Полная вероятность: Полная вероятность и формула Байеса, формула полной вероятности, примеры

Содержание

Математический анализ. (Виленкин)

Виленкин Н.Я., Шварцбурд С.И. Математический анализ. Учебное пособие для IX—X классов средних школ с математической специализацией. M., Просвещение, 1969 г.

Учебное пособие для школ с математической специализацией, снабженное большим количеством задач и упражнений. Как и вышедшая ранее (1968 г.) книга «Алгебра» того же авторского коллектива, может быть использована преподавателями и учащимися общеобразовательной школы.

8. Вычитание множеств.
9. Отображение множеств.
10. Краткие исторические сведения.
Глава I. МНОГОЧЛЕНЫ ОТ ОДНОГО ПЕРЕМЕННОГО
§ 1. Тождественные преобразования многочленов
2. Целые рациональные выражения и функции.
3. Степень с натуральным показателем и ее свойства.
4. Многочлены.
5. Умножение многочленов.
6. Числовые кольца и поля.
7. Кольцо многочленов над данным числовым полем.
8. Бином Ньютона.
§ 2. Деление многочленов. Корни многочленов
2. Теорема Безу. Схема Горнера.
3. Корни многочлена.
4. Интерполяционные формулы.
5. Кратные корни.
6. Многочлены второй степени.
7. Многочлены с целыми коэффициентами.
8. Краткие исторические сведения.
Глава II. АЛГЕБРАИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА
§ 1. Общая теория уравнений
2. Область допустимых значений.
3. Уравнения.
4. Совокупности уравнений.
5. Преобразования уравнений.
6. Теоремы о равносильности уравнений.
§ 2. Уравнения с одним неизвестным

Метод разложения на множители.
3. Метод введения нового неизвестного.
4. Биквадратные уравнения.
5. Возвратные уравнения 3-й и 4-й степеней.
§ 3. Функциональные неравенства
2. Равносильные неравенства.
3. Доказательство неравенств.
4. Линейные неравенства.
5. Решение неравенств второй степени.
6. Решение алгебраических неравенств высших степеней.
7. Краткие исторические сведения.
Глава III. ОБОБЩЕНИЕ ПОНЯТИЯ СТЕПЕНИ. ИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
§ 1. Степени с целым показателем
2. Степень с нулевым показателем.
3. Степень с целым отрицательным показателем.
§ 2. Корни. Степени с рациональными показателями
2. Степени с рациональными показателями.
3. Свойства степеней с рациональными показателями.
§ 3. Иррациональные алгебраические выражения
2. Одночленные иррациональные выражения.
3. Сокращение показателей и приведение корней к общему показателю.
4. Извлечение корня из произведения и степени.
5. Вынесение алгебраических выражений из-под корня и внесение их под корень.

6. Возведение корня в степень.
7. Извлечение корня из корня.
8. Подобные корни.
9. Сложение и вычитание корней.
10. Уничтожение иррациональности в знаменателе или в числителе алгебраической дроби.
11. Преобразование выражений вида …
12. Смешанные задачи на преобразование иррациональных выражений.
§ 4. Иррациональные уравнения и неравенства
2. Сведение иррациональных уравнений к рациональным.
3. Уединение радикала.
4. Введение нового неизвестного.
5. Особые случаи решения иррациональных уравнений.
6. Иррациональные неравенства.
7. Краткие историчесие сведения.
Глава IV. МНОГОЧЛЕНЫ ОТ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ. СИСТЕМЫ УРАВНЕНИЙ И НЕРАВЕНСТВ
§ 1. Системы алгебраических уравнений

2. Системы уравнений.
3. Геометрический смысл решений уравнений и систем уравнений с двумя неизвестными.
4. Совокупность уравнений.
5. Равносильные системы уравнений.
6. Метод подстановки.
7. Метод алгебраического сложения уравнений.

8. Метод введения новых неизвестных.
9. Системы однородных уравнений.
10. Геометрическая интерпретация решения систем двух уравнений с двумя неизвестными.
§ 2. Системы линейных уравнений
2. Теоремы о равносильности систем линейных уравнений.
3. Пример решения системы линейных уравнений методом Гаусса.
4. Метод Гаусса (приведение системы к обобщенно-треугольному виду).
5. Решение обобщенно-треугольной системы линейных уравнений.
6. Системы однородных линейных уравнений.
§ 3. Симметрические многочлены и их приложения к решению систем уравнений
2. Выражение степенных сумм
3. Основная теорема о симметрических многочленах от двух переменных.
4. Системы симметрических алгебраических уравнений.
5. Применение симметрических многочленов к решению иррациональных уравнений.
§ 4. Неравенства с многими переменными
2. Среднее арифметическое и среднее геометрическое трех чисел.
3. Неравенство Коши (двумерный вариант).
4. Задачи на наибольшие и наименьшие значения.

§ 5. Решение неравенств
2. Неравенства с двумя переменными.
3. Задание областей неравенствами и системами неравенств.
4. Понятие о линейном программировании.
5. Краткие исторические сведения.
Глава V. КОМПЛЕКСНЫЕ ЧИСЛА
§ 1. Комплексные числа в алгебраической форме
2. Комплексные числа.
3. Сложение комплексных чисел; умножение на действительные числа.
4. Умножение комплексных чисел.
5. Квадратные уравнения с действительными коэффициентами.
6. Деление комплексных чисел.
7. Сопряженные комплексные числа.

8. Извлечение квадратных корней из комплексных чисел.
§ 2. Тригонометрическая форма комплексных чисел
2. Полярная система координат.
3. Тригонометрическая форма комплексного числа.
4. Умножение и деление комплексных чисел в тригонометрической форме.
5. Возведение комплексных чисел в степень. Формула Муавра.
6. Извлечение корня из комплексного числа.
7. Функции комплексного переменного и преобразования комплексной плоскости.

§ 3. Некоторые виды алгебраических уравнений
2. Двучленные уравнения.
3. Корни из единицы и построение правильных многоугольников.
4. Трехчленные уравнения.
§ 4. Основная теорема алгебры многочленов и ее следствия
2. Многочлены с действительными коэффициентами.
3. Разложение на множители многочленов с действительными коэффициентами.
4. Краткие исторические сведения.
Глава VI. ЦЕПНЫЕ ДРОБИ

§ 1. Конечные цепные дроби
2. Пример цепной дроби.
3. Определение цепной дроби.
4. Представление рациональных чисел в виде конечной цепной дроби.
5. Подходящие дроби.
6. Свойства подходящих дробей.
8. Подходящие дроби и календарь.
9. Приближение цепной дроби подходящими дробями.
§ 2. Бесконечные цепные дроби
2. Подходящие дроби и наилучшие приближения иррациональных чисел рациональными.
3. Цепные дроби как вычислительный инструмент.
4. Краткие исторические сведения.
Глава VII. КОМБИНАТОРИКА
§ 1. Комбинаторные задачи
§ 2.

Комбинаторные задачи. Продолжение
§ 3. Определения и формулы
§ 4. Соединения с повторениями
§ 5. Комбинаторные задачи. Окончание
§ 6. Бином Ньютона и его обобщения
§ 7. Краткие исторические сведения
Глава VIII. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ

§ 2. Сложные вероятности. Теоремы сложения и умножения. Условные вероятности
§ 3. Примеры вычисления вероятностей
§ 4. Полная вероятность. Формула Байеса
§ 5. Повторение испытаний
§ 6. Примеры вычисления вероятностей. Окончание
§ 7. Краткие исторические сведения

Методическая разработка урока по теме: «Формула полной вероятности «

Практическая работа №3

Тема: «Полная вероятность и формула Байеса»

Цель:

Решение задач с использование формулы полной вероятности

и формулы Байеса.

Средства обучения:

1. Алгоритм решения задач.

2.Примеры решения задач.

3.Задачи для самостоятельного решения.

4.Учебник.

5.Вопросы по теме.

Краткие теоретические сведения:

Формула полной вероятности. Формула Байеса

Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) Н₁ Н₂,..„ Н_n образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:

Р(А) = Р(Н.) • Р(А/ Н₁) + Р(Н₂) • Р(А/ Н₂) +… + Р(Н_n) • Н(А/ H_n). (1)

Формула (1) называется формулой полной вероятности. Если до опыта вероятности гипотез были Р(Н₂),…,Р (Н₃), а в результате опыта наступило событие А, то с учетом этого события условные вероятности гипотез вычисляются по формуле Байеса. Эта формула устанавливает связь между вероятностями гипотез(условий) до испытания и после испытания в зависимости от исхода испытания(А или Ā).

Она позволяет переоценить вероятность гипотез после испытания, то есть после того, как как стал известен результат испытания.

Ход работы

1.Изучить тему “Формула полной вероятности. Формула Байеса ”.

2.Ответить на вопросы.

3.Решить задачи по алгоритму (1-4) и сверить с эталоном решения.

4.Самостоятельно решить задачи.

Вопросы:

1. Какие события называют гипотезами?

2. Напишите формулу полной вероятности.

3. Напишите формулу Байеса.

4. Какой вероятностный смысл имеют эти формулы?

Алгоритм решения задач:

1. Выясните, в чем состоит испытание, рассматриваемое в задаче,

2. Обозначьте событие А, вероятность которого нужно найти.

4. Определить вероятности гипотез Р(Н₁), P(h3),.…, Р(Н_n).

5. Найдите условные вероятности события A: P(A/H₁), Р(А/Н₂),…Р(А/Н

n).

6. По формуле (1) вычислите полную вероятность события А (или использовать формулу Байеса).

Примеры решения задач по алгоритму.

Пример 1. Имеются три партии ламп по 20,30,50 штук в каждой. Вероятность того, что лампы проработают заданное время, равна для каждой партии соответственно 0,7; 0,8 и 0,9. Какова вероятность того, что выбранная наудачу лампа из ста данных ламп проработает заданное время?

Решение.

1. Испытание состоит в том, что наудачу извлекается одна лампа из 100 .

2. Пусть событие А — извлеченная лампа проработает заданное время.

3. Рассмотрим гипотезы: Hi — принадлежит первой партии;

Н2 — второй партии;

Н₃ — третий партии.

4.Определим вероятность гипотез.

P(H₁)=20/(20+30+50)=0,2

P(H₂)=30/100=0,3

P(H₃)=50/100=0,5

5. По условию задачи условные вероятности события А равны:

Р(А/ H₁)=0,7; Р(А/ Н₂)=0_,8; Р(А/ Н₃)=0,9.

6. По формуле полной вероятности (1) вычислим Р(А).

Р(А) = Р(Н₁) • Р(А/ H₁) + Р(Н₂) • Р(А/ Н₂) + Р(Н₃)-Р(А/ Н₃) = 0.7 • 0.2 + 0,8 *

*0,3 +0,9 *0,5 = 0,83.

Пример 2. Имеются две урны. В первой урне а белых и в черных шаров, во второй — с белых и d черных шаров. Из первой урны во вторую перекладывают, не глядя, один шар. После этого из второй урны берут один шар. Найдите вероятность того, что этот шар будет белым.

Решение.

1. Испытание состоит в том, что наудачу извлекается один шар из второй урны при предварительном перекладывании одного шара из первой урны во вторую.

2. А — извлеченный шар оказался белым.

3. Гипотезы: H₁ из первой урны во вторую переложен белый шар;

Н₂ — из первой урны во вторую переложен черный шар.

Схема решения задач с помощью формулы Байеса та же самая, только в п.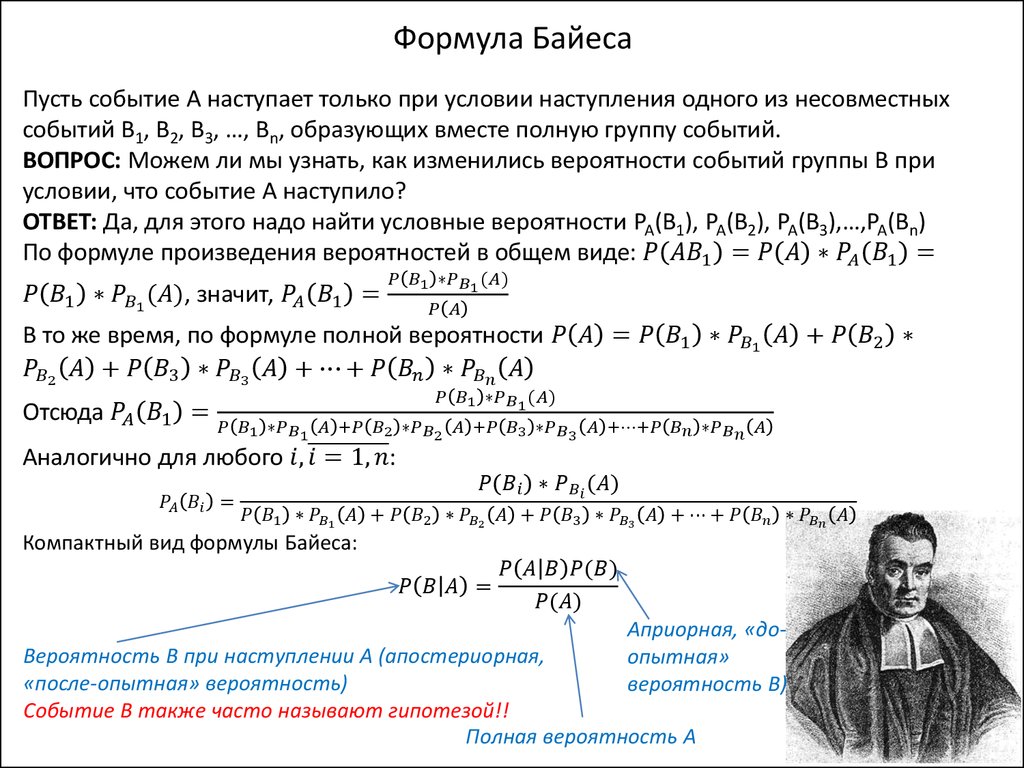 6 по формуле (2) вычисляется вероятность гипотезы Hi при условии, что событие А произошло.

Пример 3, Имеются три одинаковые по виду ящика. В первом ящике 20 белых шаров, во втором -10 белых и 10 черных шаров, в третьем — 20 черных шаров. Из выбранного наугад ящика вынули белый шар. Вычислите вероятность того, что шар вынут из первого ящика.

Решение.

1. Испытание состоит в том, что из выбранного, наугад ящика вынимают один шар.

2. А — вынут белый шар.

3. Гипотезы: H₁ — выбран первый ящик;

Н₂ — выбран второй ящик;

Н₃— выбран третий ящик,

4.Найдем вероятности гипотез. Так как выбор любого из трех одинаковых по виду ящиков, равно возможен, то

Р(Н₁)=Р(Н₂)=Р(Н₃)=1\3

5. Вычислим условные вероятности события А.

Р(А /H₁) = 1, так как все шары в первом ящике белые.

Р(А/Н₂) =1\2 , так как во втором ящике 20 шаров, из них 10 белых.

Р(А/Н₃) =0, так как в третьем ящике только черные шары.

6. Вероятность того, что белый шар вынут из первого ящика, находим по формуле Байеса:

Пример 4. Врач после осмотра больного считает, что возможно одно из двух заболеваний 1 и 2, причем степень своей уверенности в правильности диагноза оценивает как 40% и 60% соответственно. Для уточнения диагноза больного направляют на анализ, исход которого дает положительную реакцию при заболевании 1 в 90 % случаев и при заболевании 2 в 20 % случаев. Анализ дал положительную реакцию. Как изменится мнение врача после этого?

Решение.

1. Испытание состоит в том, что больному делают анализ для уточнения диагноза.

2. Событие А — анализ дал положительную реакцию.

3. Введем гипотезы: Н₁ — имеет место заболеваний 1;

Н₂ — имеет место заболевание 2.

4. Как следует из условия задачи

Р(Н₁)=0,4; Р(Н₂)=0,6.

Р(А/Н₁)=0,9; Р(А/Н₂)=0,2. Найдем P(H₁/A) по формуле Байеса:

Следовательно, врач вероятнее всего признает наличие заболевания 1.

Задачи для самостоятельного решения.

51.В продажу поступают телевизоры трех заводов. Продукция первого завода содержит 20% телевизоров со скрытым дефектом, второго — 10 % и третьего — 5 %. Определите вероятность приобрести исправный телевизор, если в магазин поступили 30 телевизоров с первого завода, 20 — со второго и 50 — с третьего?

52.Стрельбу в цель ведут 10 солдат. Для пяти из них вероятность попадания 0,6, для трех — 0,5 и для остальных — 0,3. Какова вероятность поражения?

53.Имеются пять винтовок, три из которых с оптическим прицелом. Вероятность попадания в цель при одном выстреле из винтовки с оптическим прицелом равна 0,95. без оптического прицела — 0,8. Найдите вероятность попадания в цель, если стрелок сделает один выстрел из наудачу взятой винтовки.

54.По самолету производятся три выстрела. Вероятность попадания при первом выстреле равна 0,5, при втором — 0,6, при третьем — 0,8. При одном попаданий самолет сбивается с вероятностью 0,3, при двух — с вероятностью 0,6 и при трех сбивается наверняка. Какова вероятность сбить самолет?

55.Студент знает ответы на 15 экзаменационных билетов из 20. В каком случае он имеет большую вероятность сдать экзамен, если он идет отвечать первым или если — вторым?

56.В белом ящике лежат 12 красных и 6 синих одинаковых на ощупь шаров В желтом ящике лежат 15 красных и 10 синих одинаковых на ощупь шаров. Бросается игральная кость. Если число выпавших очков кратно трем, то наудачу вынимают шар из белого ящика. Если число выпавших очков не кратно трем, то наудачу вынимают шар из желтого ящика. Какова вероятность вынуть красный шар?

57. Рабочий обслуживает три станка, на которых обрабатываются однотипные детали. Вероятность брака для первого станка равна 0,02, для второго — 0.03, для третьего — 0,04. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше_} чем второго, а третьего — в два раза меньше, чем второго. Какова вероятность того, что взятая наудачу деталь будет бракованной?

58.Для сдачи зачета студентам необходимо подготовить 30 вопросов. Из 25 студентов 10 подготовили ответы на все вопросы, 8 — на 25 вопросов, 5 — на 20 вопросов и двое — на 15. Какова вероятность того, что вызванный наудачу студент ответил на поставленный ему вопрос?

59. Для контроля продукции из 3-х партий деталей взята для испытаний одна деталь. Как велика вероятность обнаружения бракованной продукции, если в одной партии 2/3 деталей бракованные, а в двух других все годные? Считать, что вероятность выбора детали из каждой их 3-х партий одна и та же.

60. В каждой из трех урн содержится 6 черных и 4 белых шара. Из первой урны наудачу извлечен один шар и переложен во вторую урну, после чего из второй урны наудачу извлечен один шар и переложен в третью урну. Найдите вероятность того, что шар, наудачу извлеченный из третьей урны, окажется белым.

61.В группе 10 юношей, которые играют, набрасывая кольца на колышек. Для пяти из них вероятность попадания кольца на колышек равна 0,6, для трех других — 0,5 и для остальных — 0,3. Кольцо, брошенное одним из юношей, попало на колышек. Какова вероятность того, что это кольцо было брошено юношей из первой группы?

62.В одной студенческой группе обучаются 24 студента, во второй — 36 студентов и в третьей — 40 студентов. По теории вероятностей получили отличные оценки 6 студентов первой группы, 6 студентов второй группы и 4 студента третьей группы. Наугад выбранный студент оказался получившим оценку «отлично». Какова вероятность того, что он учится в первой группе?

63.В клинику поступает в среднем 50 % больных с заболеванием К, 30 % — с заболеванием L, 20 % с заболеванием М. Вероятность полного излечения болезни К равна 0,7, болезней L и М — 0,8 и 0,9 соответственно. Больной, поступивший в больницу, был выписан здоровым. Найдите вероятность того, что этот больной, страдал заболеванием К.

64.В тире имеется 9 ружей, из которых пристрелянными являются только 2. Вероятность попадания в цель из пристрелянного ружья равна 0,8, а из не пристрелянного — 0,1. Выстрелом из одного выбранного наудачу ружья мишень поражена. Определите вероятность того, что взято пристрелянное ружьё.

65. 5 % всех мужчин и 0,25 % женщин являются дальтониками. Наугад

выбранное лицо страдает дальтонизмом. Какова вероятность того, что это мужчина?

66.Из 100 студентов, пришедших сдавать экзамен, 80 подготовились к

экзамену, а 20 — нет. Вероятность того, что подготовившийся студент сдаст экзамен, равна 0,9. Аналогичная вероятность для не подготовившегося студента равна 0,05. Наудачу выбранный студент сдал экзамен. Какова вероятность того, что он к экзамену был подготовлен?

67.Перед эпидемией гриппа 90 % студентов были привиты против гриппа. Число заболевших среди привитых составляет 1 %, среди не привитых 81 %, Студент заболел гриппом. Какова вероятность того, что он не сделал прививку?

68.Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму — 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым — 0,98. Стандартное изделие при проверке было признано стандартным. Найдите вероятность того, что это изделие проверил второй товаровед.

69.В мае вероятность дождливого дня равна 0,2. Для некоторой футбольной команды вероятность выиграть в ясный день равна 0,7, но зато в дождливый день эта вероятность равна лишь 0,4. Известно, что команда выиграла матч. Какова вероятность того, что в тот день шел дождь?

70.Путешественник может купить билет в одной из трех касс железнодорожного вокзала. Вероятность того, что он направится к первой кассе, примерно равна 1\2, ко второй – 1\3 , к третьей – 1\6. Вероятности того,что билетов уже нет в кассах, примерно такие: в первой кассе — 1\5 во второй – 1\6, в третьей – 1\8. Путешественник обратился в одну из касс и получил билет. Определите вероятность того, что он направился к первой кассе.

Критерии оценки:

«3»- ответить на вопросы + решение задач(51-57).

«4»- ответить на вопросы + решение задач(51-66).

«5»- ответить на вопросы + решение задач(51-70).

Литература:

1.Виленкин Н. Я. Потапов В. Г. Задачник – практикум по теории вероятности с элементами комбинаторики и математической статистики. – М.: Просвещение, 1979.

2.Лютикас В. С. Школьнику о теории вероятности. – М.: Просвещение, 1983.

3.Лютикас В. С. Факультативный курс по математике: Теории вероятности. – М.: Просвещение, 1990

2,$$ ты прав. То есть можно просто добавить лесные массивы в каждую провинцию (раздел), чтобы получить лес площадь по всей стране. Это идея, лежащая в основе закона полной вероятности, согласно которому площадь леса заменяется вероятностью события $A$ . В частности, если вы хотите чтобы найти $P(A)$, вы можете посмотреть на раздел $S$ и добавить сумму вероятности $A$, что попадает в каждый раздел.

c).$$ Мы можем сформулировать более общую версию этой формулы, применимую к общему разбиению выборочное пространство $S$.

Закон полной вероятности:
Если $B_1, B_2, B_3,\cdots$ является разбиением выборочного пространства $S$, то для любого события $A$ имеем $$P(A)=\sum_{i} P(A \cap B_i)=\sum_{i} P(A | B_i) P(B_i).$$

Используя диаграмму Венна, мы можем графически увидеть Идея закона полной вероятности. На рис. 1.24 мы имеем $$A_1=А\шапка B_1,$$ $$A_2=A \cap B_2,$$ $$A_3=A \cap B_3.$$ Как видно из рисунка, $A_1$, $A_2$ и $A_3$ образуют разбиение множества $A$, и, таким образом, по третьей аксиоме вероятности $$P(A)=P(A_1)+P(A_2)+P(A_3).$$

Рис.1.24 — Закон полной вероятности.

Вот доказательство закона полной вероятности с использованием аксиом вероятности:

Доказательство

Поскольку $B_1, B_2, B_3,\cdots$ является разбиением выборочного пространства $S$, мы можем записать

$S$	$=\bigcup_{i} B_i$
$А$	$= A\cap S$
	$=A \cap (\bigcup_{i} B_i)$
	$=\bigcup_{i} (A \cap B_i) \hspace{20pt} \hspace{20pt}$ по дистрибутивному закону (теорема 1. 2).

Теперь заметим, что множества $A \cap B_i$ не пересекаются (поскольку множества $B_i$ не пересекаются). Таким образом, по третьей аксиоме вероятности $$P(A)=P\bigg(\bigcup_i (A \cap B_i)\bigg)=\sum_{i} P(A \cap B_i)=\sum_{i} P(A | B_i) P(B_i ).$$

Вот типичный сценарий, в котором мы используем закон полной вероятности. Мы заинтересованы в нахождение вероятности события $A$, но мы не знаем, как найти $P(A)$ напрямую. Вместо, мы знаем условную вероятность $A$ при некоторых событиях $B_i$, где $B_i$ образуют разделение пространства выборки. Таким образом, мы сможем найти $P(A)$ по закону полной вероятности, $P(A)=\sum_{i} P(A | B_i) P(B_i)$.

Пример

У меня есть три сумки, каждая из которых содержит шарики по 100 долларов:

Мешок 1 содержит красные шарики по 75$ и синие по 25$;
В сумке 2 есть красные шарики по 60 долларов и синие по 40 долларов;
В сумке 3 есть красные шарики по 45 долларов и синие по 55 долларов.

Я выбираю один из мешков наугад, а затем беру шарик из выбранных мешок, также наугад. Какова вероятность того, что выбранный шарик красный?

Раствор

← предыдущая

Печатная версия книги доступна на Amazon здесь.

Использование моделей полной вероятности для расчета вероятностей, представляющих реальный интерес для лиц, принимающих решения

. 2001 Зима; 17 (1): 17-26.

doi: 10.1017/s0266462301104034.

Ф. Э. Харрелл-младший ¹ , YC Shih

принадлежность

¹ Медицинский факультет Университета Вирджинии, США.

PMID: 11329842
DOI: 10. 1017/s0266462301104034

FE Harrell Jr et al. Int J Technol оценивает здравоохранение. 2001 Зима.

. 2001 Зима; 17 (1): 17-26.

doi: 10.1017/s0266462301104034.

Авторы

Ф. Э. Харрелл-младший ¹ , Ю. К. Ши

принадлежность

¹ Медицинский факультет Университета Вирджинии, США.

PMID: 11329842
DOI: 10.1017/s0266462301104034

Абстрактный

Цель этой статьи — проиллюстрировать преимущества байесовского подхода в количественной оценке, представлении и сообщении научных данных, а также в оказании помощи в принятии решений. Тремя основными компонентами байесовской модели являются априорное распределение, функция правдоподобия и апостериорное распределение. Априорное распределение описывает априорное мнение аналитиков, функция правдоподобия фиксирует, как данные изменяют априорные знания; а апостериорное распределение синтезирует как априорную, так и вероятностную информацию. Байесовский подход рассматривает интересующие параметры как случайные величины, использует все апостериорное распределение для количественной оценки свидетельств и сообщает свидетельства в «вероятностной» манере. Два клинических примера используются, чтобы продемонстрировать ценность байесовского подхода для лиц, принимающих решения. Используя либо неинформативное, либо скептическое априорное распределение, эти примеры показывают, что байесовские методы позволяют вычислять вероятности, которые обычно представляют больший интерес для лиц, принимающих решения, например, вероятность того, что лечение A аналогично лечению B, вероятность того, что лечение A как минимум на 5% лучше, чем лечение B, и вероятность того, что лечение A не находится в «области сходства» лечения B, и т. д. Кроме того, байесовский подход может легче работать с несколькими конечными точками, чем классический подход. Например, если лица, принимающие решения, хотят совместно изучить смертность и затраты, байесовский метод может сообщить о вероятности того, что лечение приведет к снижению смертности не менее чем на 2% и увеличению затрат менее чем на 20 000 долларов. В заключение следует отметить, что вероятности, рассчитанные с помощью байесовского подхода, предоставляют лицам, принимающим решения, более актуальную информацию и их легче интерпретировать.

Цитируется

Метод улучшения прогнозирования амбулаторных посещений для управления больницей: байесовский авторегрессионный анализ.
Вэй И, Ли В, Тан Дж, Юань Дж, Ву З, Ли И, Мао И, Хуан Д. Вэй Ю и др. Вычислительные математические методы мед. 2022 12 октября; 2022:4718157. дои: 10.1155/2022/4718157. Электронная коллекция 2022. Вычислительные математические методы мед. 2022. PMID: 36277006 Бесплатная статья ЧВК.
При перекисном окислении липидов качество пищевых углеводов более важно, чем их количество.
Цзян И, Чжао И, Милн Г, Дай Кью, Чен Кью, Чжан Х, Лань Кью, Ротман Н, Гао ЮТ, Цай Кью, Шу ХО, Чжэн В, Ян Г. Цзян И и др. Am J Clin Nutr. 2022 г., 6 июля; 116 (1): 189–196. doi: 10.1093/ajcn/nqac047. Am J Clin Nutr. 2022. PMID: 35170729 Бесплатная статья ЧВК.
Разработка и валидация номограммы для прогнозирования риска выживаемости больных плоскоклеточным раком гортани.
Цуй Дж., Ван Л., Чжун В., Чен З., Тан Х., Ян Х., Чен Дж., Лю Г. Цуй Дж. и др. Представитель Biosci, 28 августа 2020 г .; 40 (8): BSR20200228. DOI: 10.1042/BSR20200228. Представитель Biosci 2020. PMID: 32744320 Бесплатная статья ЧВК.
Стратегии скрининга для выявления сепсиса на догоспитальном этапе: проверочное исследование.
Лейн ДиДжей, Вунш Х., Саскин Р., Ческес С., Лин С., Моррисон Л.Дж., Скейлс Д.К. Лейн Диджей и др. CMAJ. 2020 9 марта; 192(10):E230-E239. doi: 10.1503/cmaj.190966. CMAJ. 2020. PMID: 32152051 Бесплатная статья ЧВК.
Разработка номограмм для прогнозирования восстановления эректильной функции после радикальной простатэктомии.
Малхолл Дж.
No related posts.

Полная вероятность: Полная вероятность и формула Байеса, формула полной вероятности, примеры

Математический анализ. (Виленкин)

Оглавление

Методическая разработка урока по теме: «Формула полной вероятности «

Использование моделей полной вероятности для расчета вероятностей, представляющих реальный интерес для лиц, принимающих решения

принадлежность

Авторы

принадлежность

Абстрактный

Похожие статьи

Цитируется

Добавить комментарий Отменить ответ