Параллелограмм. Определение, свойства и признаки
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.
Свойства параллелограмма
1. Противоположные стороны тождественны
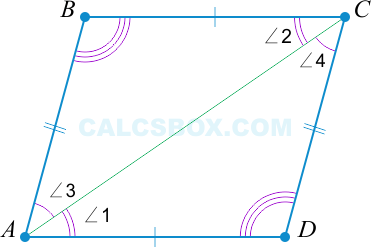
Первым делом проведем диагональ \( AC \). Получаются два треугольника: \( ABC \) и \( ADC \).
Так как \( ABCD \) — параллелограмм, то справедливо следующее:
\( AD || BC \Rightarrow \angle 1 = \angle 2 \) как лежащие накрест.
\( AB || CD \Rightarrow \angle3 = \angle 4 \) как лежащие накрест.
Следовательно, \( \triangle ABC = \triangle ADC \) (по второму признаку: \( \angle 1 = \angle 2, \angle 3 = \angle 4 \) и \( AC \) — общая).
И, значит, \( \triangle ABC = \triangle ADC \), то \( AB = CD \) и \( AD = BC \).
2. Противоположные углы тождественны
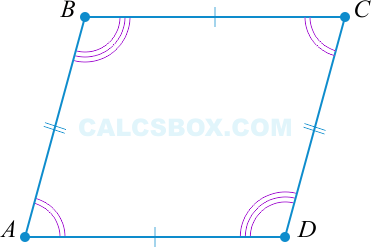
Согласно доказательству свойства 1 мы знаем, что \( \angle 1 = \angle 2, \angle 3 = \angle 4 \). Таким образом сумма противоположных углов равна: \( \angle 1 + \angle 3 = \angle 2 + \angle 4 \). Учитывая, что \( \triangle ABC = \triangle ADC \) получаем \( \angle A = \angle C \), \( \angle B = \angle D \).
3. Диагонали разделены пополам точкой пересечения
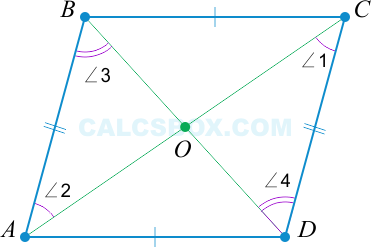
По свойству 1 мы знаем, что противоположные стороны тождественны: \( AB = CD \). Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что \( \triangle AOB = \triangle COD \) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, \( BO = OD \) (напротив углов \( \angle 2 \) и \( \angle 1 \)) и \( AO = OC \) (напротив углов \( \angle 3 \) и \( \angle 4 \) соответственно).
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны
\( AB = CD \); \( AB || CD \Rightarrow ABCD \) — параллелограмм.
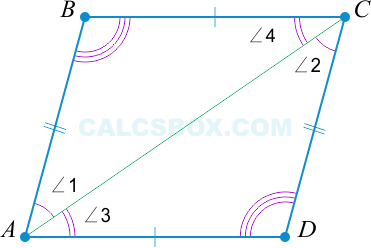
Рассмотрим подробнее. Почему \( AD || BC \)?
\( \triangle ABC = \triangle ADC \) по свойству 1: \( AB = CD \), \( \angle 1 = \angle 2 \) как накрест лежащие при параллельных \( AB \) и \( CD \) и секущей \( AC \).
Но если \( \triangle ABC = \triangle ADC \), то \( \angle 3 = \angle 4 \) (лежат напротив \( AD || BC \) (\( \angle 3 \) и \( \angle 4 \) — накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны
\( AB = CD \), \( AD = BC \Rightarrow ABCD \) — параллелограмм.
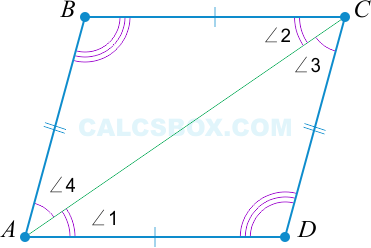
Рассмотрим данный признак. Еще раз проведем диагональ \( AC \).
По свойству 1 \( \triangle ABC = \triangle ACD \).
Из этого следует, что: \( \angle 1 = \angle 2 \Rightarrow AD || BC \) и \( \angle 3 = \angle 4 \Rightarrow AB || CD \), то есть \( ABCD \) — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны
\( \angle A = \angle C \), \( \angle B = \angle D \Rightarrow ABCD \) — параллелограмм.
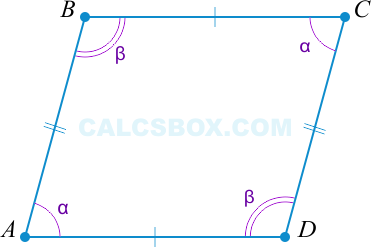
\( 2 \alpha + 2 \beta = 360^{\circ} \) (поскольку \( \angle A = \angle C \), \( \angle B = \angle D \) по условию).
Получается, \( \alpha + \beta = 180^{\circ} \). Но \( \alpha \) и \( \beta \) являются внутренними односторонними при секущей \( AB \).
И то, что \( \alpha + \beta = 180^{\circ} \) говорит и о том, что \( AD || BC \).
При этом \( \alpha \) и \( \beta \) — внутренние односторонние при секущей \( AB || CD \).
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам
\( AO = OC \); \( BO = OD \Rightarrow \) параллелограмм.
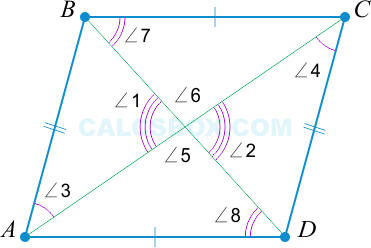
\( BO = OD \); \( AO = OC \), \( \angle 1 = \angle 2 \) как вертикальные \( \Rightarrow \triangle AOB = \triangle COD \), \( \Rightarrow \angle 3 = \angle 4 \), и \( \Rightarrow AB || CD \).
Аналогично \( BO = OD \); \( AO = OC \), \( \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8 \), и \( \Rightarrow AD || BC \).
Четвертый признак верен.
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Источник
| Определение: параллелограмм | |
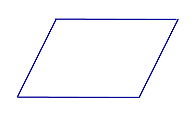 | Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны |
| Определение: диагонали параллелограмма | |
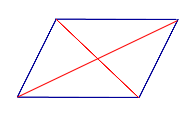 | Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины |
| Определение: высота параллелограмма | |
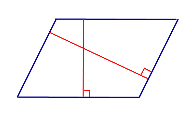 | Высотой параллелограмма называютперпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение |
| Свойство: равенство противолежащих сторон | |
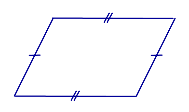 | Если четырёхугольник является параллелограммом, то его противолежащие стороны равны |
| Признак: равенство противолежащих сторон | |
| Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом |
| Признак: равенство и параллельность двух противолежащих сторон | |
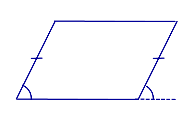 | Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом |
| Свойство: диагонали точкой пересечения делятся пополам | |
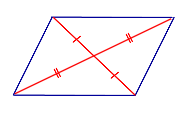 | Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам |
| Признак: диагонали точкой пересечения делятся пополам | |
| Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом |
| Свойство: суммы углов, прилежащих к сторонам | |
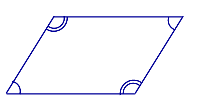 | Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180° |
| Признак: суммы углов, прилежащих к сторонам | |
| Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом |
| Свойство: равенство противолежащих углов | |
| Если четырёхугольник является параллелограммом, то его противолежащие углы равны |
| Признак: равенство противолежащих углов | |
| Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом |
| Свойство: два треугольника, на которые каждая диагональ делит четырёхугольник | |
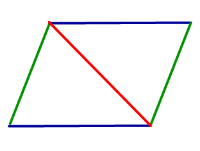 | Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника |
| Признак: два треугольника, на которые каждая диагональ делит четырёхугольник | |
| Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом |
| Свойство: четыре треугольника, на которые диагонали делят четырёхугольник | |
 | Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника) |
| Признак: четыре треугольника, на которые диагонали делят четырёхугольник | |
| Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом |
Свойства четырехугольников. Параллелограмм, прямоугольник, ромб, квадрат.
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
СОДЕРЖАНИЕ СТАТЬИ
1. Параллелограмм
Сложное слово «параллелограмм»? А скрывается за ним очень простая фигура.
Смотри:
 |
Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны |
Ну, то есть, взяли две параллельные прямые:
Пересекли ещё двумя:
И вот внутри – параллелограмм!
Какие же есть свойства у параллелограмма?
Свойства параллелограмма.
То есть, чем можно пользоваться, если в задаче дан параллелограмм?
На этот вопрос отвечает следующая теорема:
|
В любом параллелограмме:
|
Давай нарисуем все подробно.
Что означает первый пункт теоремы? А то, что если у тебя ЕСТЬ параллелограмм, то непременно
 |
и . |
Второй пункт означает, что если ЕСТЬ параллелограмм, то, опять же, непременно:
 |
и |
Ну, и наконец, третий пункт означает, что если у тебя ЕСТЬ параллелограмм, то обязательно:
 |
и |
Видишь, какое богатство выбора? Что же использовать в задаче? Попробуй ориентироваться на вопрос задачи, или просто пробуй все по очереди – какой-нибудь «ключик» да подойдёт.
А теперь зададимся другим вопросом: а как узнать параллелограмм «в лицо»? Что такое должно случиться с четырехугольником, чтобы мы имели право выдать ему «звание» параллелограмма?
На этот вопрос отвечает несколько признаков параллелограмма.
Признаки параллелограмма.
Внимание! Начинаем.
|
 |
; — параллелограмм. |
— паралелограмм.
|
 |
; – параллелограмм. |
|
 |
; – параллелограмм. |
|
 |
; – параллелограмм. |
Обрати внимание: если ты нашёл хотя бы один признак в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.
Для полной ясности посмотри на схему:
2. Прямоугольник
Думаю, что для тебя вовсе не явится новостью то, что
 |
Прямоугольник – четырехугольник, все углы которого прямые. |
Первый вопрос: а является ли прямоугольник параллелограммом?
Конечно, является! Ведь у него и — помнишь, наш признак 3?
А отсюда, конечно же, следует, что у прямоугольника, как и у всякого параллелограмма и , а диагонали точкой пересечения делятся пополам.
Но есть у прямоугольника и одно отличительноесвойство.
Свойство прямоугольника
 |
Диагонали прямоугольника равны: . |
Почему это свойство отличительное? Потому что ни у какого другого параллелограмма не бывает равных диагоналей. Сформулируем более чётко.
 |
Если у параллелограмма равны диагонали, то это — прямоугольник. |
Обрати внимание: чтобы стать прямоугольником, четырехугольнику нужно сперва стать параллелограммом, а потом уже предъявлять равенство диагоналей.
3. Ромб
 |
Ромб – четырехугольник, все стороны которого равны между собой. |
И снова вопрос: ромб – это параллелограмм или нет?
С полным правом – параллелограмм, потому что у него и (вспоминаем наш признак 2).
И снова, раз ромб – параллелограмм, то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.
Но есть и особенные свойства. Формулируем.
Свойства ромба
|
 |
(если ты забыл, напомню: — значок перпендикулярности) |
|
Посмотри на картинку:
Как и в случае с прямоугольником, свойства эти – отличительные, то есть по каждому из этих свойств можно заключить, что перед нами не просто параллелограмм, а именно ромб.
Признаки ромба
|
|
И снова обрати внимание: должен быть не просто четырехугольник, у которого перпендикулярны диагонали, а именно параллелограмм. Убедись:
 |
разве это ромб? |
Нет, конечно, хотя его диагонали и перпендикулярны, а диагональ – биссектриса углов и . Но … диагонали не делятся, точкой пересечения пополам, поэтому – НЕ параллелограмм, а значит, и НЕ ромб.
4. Квадрат
 |
Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые. |
То есть квадрат – это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.
 |
У квадрата угол между диагональю и стороной равен . |
Понятно почему? Квадрат — ромб – биссектриса угла A, который равен . Значит делит (да и тоже) на два угла по .
 |
Диагонали квадрата равны, перпендикулярны и делятся точкой пересечения пополам. |
Ну, это совсем ясно: прямоугольник диагонали равны; ромб диагонали перпендикулярны, и вообще – параллелограмм диагонали делятся точкой пересечения пополам.
 |
Если сторона квадрата равна , то его диагональ равна . |
Почему? Ну, просто применим теорему Пифагора к .
Значит, .
СРЕДНИЙ УРОВЕНЬ
Свойства четырехугольников. Параллелограмм
| Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны. |
Свойства параллелограмма
Внимание! Слова «свойства параллелограмма» означают, что если у тебя в задаче есть параллелограмм, то всем нижеследующим можно пользоваться.
Итак,
Теорема о свойствах параллелограмма.
В любом параллелограмме:
| 1) Противоположные стороны равны |  |
| 2) Противоположные углы равны |  |
| 3) Диагонали делятся пополам точкой пересечения |  |
Давай-ка поймём, почему это всё верно, иными словами ДОКАЖЕМ теорему.
Итак, почему верно 1)?
 |
Давай проведём диагональ . Что получится? Два треугольника: и . |
Раз – параллелограмм, то :
- как накрест лежащие
- как накрест лежащие.
Значит, (по II признаку: и — общая.)
Ну вот, а раз , то и – всё! – доказали.
Но кстати! Мы ещё доказали при этом и 2)!
Почему? Но ведь (смотри на картинку), то есть , а именно потому, что .
Осталось только 3).
Для этого всё-таки придётся провести вторую диагональ.
 |
Мы уже выяснили, что . Давай снова отметим равные накрест лежащие углы (посмотри и убедись, что все верно). |
И теперь видим, что — по II признаку ( угла и сторона «между» ними).
 |
Значит, (напротив углов и ) и (напротив углов и соответственно). |
Свойства доказали! Перейдём к признакам.
Признаки параллелограмма
Напомним, что признак параллелограмма отвечает на вопрос «как узнать?», что фигура является параллелограммом.
| Признак 1. Если у четырехугольника две стороны равны и параллельны, то это параллелограмм. |
В значках это так:
 |
; – параллелограмм. |
Почему? Хорошо бы понять, почему – этого хватит. Но смотри:
 |
по 1 признаку: , — общая и как накрест лежащие при параллельных и и секущей . |
А раз ,
 |
то |
Параллелограмм. Определение, свойства и признаки
Свойства параллелограмма
1. Противоположные стороны тождественны.
Доказательство
Первым делом проведем диагональ AC. Получаются два треугольника: ABC и ADC.
Так как ABCD — параллелограмм, то справедливо следующее:
AD || BC \Rightarrow \angle 1 = \angle 2 как лежащие накрест.
AB || CD \Rightarrow \angle3 = \angle 4 как лежащие накрест.
Следовательно, \triangle ABC = \triangle ADC (по второму признаку: \angle 1 = \angle 2, \angle 3 = \angle 4 и AC — общая).
И, значит, \triangle ABC = \triangle ADC, то AB = CD и AD = BC.
Доказано!
2. Противоположные углы тождественны.
Доказательство
Согласно доказательству свойства 1 мы знаем, что \angle 1 = \angle 2, \angle 3 = \angle 4. Таким образом сумма противоположных углов равна: \angle 1 + \angle 3 = \angle 2 + \angle 4. Учитывая, что \triangle ABC = \triangle ADC получаем \angle A = \angle C, \angle B = \angle D.
Доказано!
3. Диагонали разделены пополам точкой пересечения.
Доказательство
Проведем еще одну диагональ.
По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD. Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что \triangle AOB = \triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов \angle 2 и \angle 1) и AO = OC (напротив углов \angle 3 и \angle 4 соответственно).
Доказано!
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.
AB = CD; AB || CD \Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим подробнее. Почему AD || BC?
\triangle ABC = \triangle ADC по свойству 1: AB = CD, AC — общая и \angle 1 = \angle 2 как накрест лежащие при параллельных AB и CD и секущей AC.
Но если \triangle ABC = \triangle ADC, то \angle 3 = \angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (\angle 3 и \angle 4 — накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.
AB = CD, AD = BC \Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим данный признак. Еще раз проведем диагональ AC.
По свойству 1 \triangle ABC = \triangle ACD.
Из этого следует, что: \angle 1 = \angle 2 \Rightarrow AD || BC и \angle 3 = \angle 4 \Rightarrow AB || CD, то есть ABCD — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны.
\angle A = \angle C, \angle B = \angle D \Rightarrow ABCD — параллелограмм.
Доказательство
2 \alpha + 2 \beta = 360^{\circ} (поскольк
Признаки параллелограмма
Теорема 1. Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник — параллелограмм.
Пусть в четырёхугольнике AВDС (рис. 227) АВ = СD и АС = ВD. Докажем, что при этом условии АВ || СD и АС || ВD, т. е. четырёхугольник АВDC — параллелограмм.
Соединим отрезком какие-нибудь две противоположные вершины этого четырёхугольника, например С и В. Четырёхугольник ABDС разбился на два равных треугольника: \(\Delta\)СAВ и \(\Delta\)СDВ. В самом деле, сторона СВ у них общая, AB = СD и АС = ВD по условию. Таким образом, три стороны одного треугольника соответственно равны трём сторонам другого, поэтому \(\Delta\)СAВ = \(\Delta\)СDВ.
В равных треугольниках против равных сторон лежат равные углы, поэтому
∠1 = ∠2 и ∠3 = ∠4.
Углы 1-й и 2-й являются внутренними накрест лежащими углами при пересечении прямых AB и СD прямой СВ. Следовательно, AB || СD.
Точно так же углы 3-й и 4-й являются внутренними накрест лежащими углами при пересечении прямых CA и ВD прямой СВ, следовательно, CA || ВD.
Таким образом, противоположные стороны четырёхугольника ABDС попарно параллельны, следовательно, он — параллелограмм, что и требовалось доказать.
Теорема 2. Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник — параллелограмм.
Пусть в четырёхугольнике ABDС AB = СD и AB || СD. Докажем, что при этих условиях четырёхугольник ABDС — параллелограмм (рис. 228).
Соединим отрезком СВ вершины С и В. Вследствие параллельности прямых AB и СD углы 1 и 2, как углы внутренние накрест лежащие, равны.
Тогда треугольник СAB равен треугольнику СDВ, так как сторона СВ у них общая,
AB = СD по условию теоремы и ∠1 = ∠2 по доказанному.
Из равенства этих треугольников вытекает равенство углов 3 и 4, так как они лежат против равных сторон в равных треугольниках.
Но углы 3 и 4 — это внутренние накрест лежащие углы, образованные при пересечении прямых АС и ВD прямой СВ, следовательно, АС || ВD, т. е. четырёхугольник ABDС — параллелограмм.
Теорема 3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.
Рассмотрим четырехугольник ABCD. Проведем в нем две диагонали AC и BD, которые будут пересекаться в точке О и делятся этой точкой пополам.
Треугольники \(\Delta\)AOB и \(\Delta\)COD будут равны между собой по первому признаку равенства треугольников (AO = OC, BO = OD по условию, ∠AOB = ∠COD — как вертикальные углы.)
Следовательно, AB = CD и ∠1 = ∠2. Из равенства углов 1 и 2 имеем, что AB || CD.
Тогда имеем, что в четырехугольнике ABCD стороны AB = CD и AB || CD, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.
Признаки параллелограмма кратко:
1. Противоположные стороны попарно равны2. Противоположные стороны равны и параллельны
3. Диагонали пересекаются и в точке пересечения делятся пополам
Признаки параллелограмма: доказательства и рисунки
Для того, чтобы определить является ли данная фигура параллелограммом существует ряд признаков. Рассмотрим три основных признака параллелограмма.
1 признак параллелограмма
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник будет являться параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Пусть в нем стороны AB и СD параллельны. И пусть AB=CD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти треугольники равны между собой по двум сторонам и углу между ними (BD — общая сторона, AB = CD по условию, угол1 = угол2 как накрест лежащие углы при секущей BD параллельных прямых AB и CD.), а следовательно угол3 = угол4.
А эти углы будут являться накрест лежащими при пересечении прямых BC и AD секущей BD. Из этого следует что BC и AD параллельны между собой. Имеем, что в четырехугольнике ABCD противоположные стороны попарно параллельны, и, значит, четырехугольник ABCD является параллелограммом.
2 признак параллелограмма
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник будет параллелограммом.
Доказательство:
Рассмотрим четырехугольник ABCD. Проведем в нем диагональ BD. Она разделит данный четырехугольник на два равных треугольника: ABD и CBD.
Эти два треугольника буду равны между собой по трем сторонам (BD — общая сторона, AB = CD и BC = AD по условию). Из этого можно сделать вывод, что угол1 = угол2. Отсюда следует, что AB параллельна CD. А так как AB = CD и AB параллельна CD, то по первому признаку параллелограмма, четырехугольник ABCD будет являться параллелограммом.
3 признак параллелограмма
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник будет являться параллелограммом.
Рассмотрим четырехугольник ABCD. Проведем в нем две диагонали AC и BD, которые будут пересекаться в точке О и делятся этой точкой пополам.
Треугольники AOB и COD будут равны между собой, по первому признаку равенства треугольников. (AO = OC, BO = OD по условию, угол AOB = угол COD как вертикальные углы.) Следовательно, AB = CD и угол1 = угол 2. Из равенства углов 1 и 2 имеем, что AB параллельна CD. Тогда имеем, что в четырехугольнике ABCD стороны AB равны CD и параллельны, и по первому признаку параллелограмма четырехугольник ABCD будет являться параллелограммом.
Нужна помощь в учебе?
Предыдущая тема: Параллелограмм: понятие и свойства, примеры изображений
Следующая тема:   Основное тригонометрическое тождество: формулы приведения
Все неприличные комментарии будут удаляться.
Определение параллелограмма
Четырёхугольник называется параллелограммом, если его противоположные стороны попарно параллельны.
\(ABCD\) – параллелограмм \(\, \Leftrightarrow \, AB||CD\) и \(BC||AD\)
Свойства параллелограмма
1. Противоположные стороны параллелограмма равны.
2. Противоположные углы параллелограмма равны.
3. Сумма смежных углов параллелограмма равна \(180^{\circ}\).
4. Диагонали параллелограмма делятся точкой пересечения пополам.
\(ABCD\) – параллелограмм \(\Rightarrow\) \( AB=CD, \, BC=AD; \)
\(ABCD\) – параллелограмм \(\Rightarrow\) \(\angle{A}=\angle{C}, \, \angle{B}=\angle{D}; \)
\(ABCD\) – параллелограмм \(\Rightarrow\) \(\angle{A}+\angle{B}=180^{\circ}, \, \angle{A}+\angle{D}=180^{\circ}, \,
\angle{C}+\angle{B}=180^{\circ}, \, \angle{C}+\angle{D}=180^{\circ};\)
\(ABCD\) – параллелограмм, \(AC \cap BD =O\) \(\Rightarrow\) \(AO=CO, \, BO=DO \)
Признаки параллелограмма
1. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.
2. Если в четырёхугольнике противоположные углы попарно равны, то этот четырёхугольник – параллелограмм.
3. Если в четырёхугольнике две противоположные стороны параллельны и равны, то этот четырёхугольник – параллелограмм.
4. Если в четырёхугольнике диагонали точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
\( AB=CD, \, BC=AD \) \(\Rightarrow\) \(ABCD\) – параллелограмм\(;\)
\(\angle{A}=\angle{C}, \, \angle{B}=\angle{D} \) \(\Rightarrow\) \(ABCD\) – параллелограмм\(;\)
\( AB=CD, \, AB||CD \) \(\Rightarrow\) \(ABCD\) – параллелограмм\(;\)
\( AO=CO, \, BO=DO \) \(\Rightarrow\) \(ABCD\) – параллелограмм
Виды параллелограммов
Ромб, прямоугольник и квадрат являются параллелограммами. Остальные параллелограммы называют параллелограммами общего вида
Площадь параллелограмма
1. Площадь параллелограмма равна произведению его стороны на высоту, проведённую к этой стороне.
\( S=ah \) |
2. Площадь параллелограмма равна произведению его смежных сторон на синус угла между ними.
\( S=ab\sin{\gamma} \) |
3. Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними.
\( S=\frac{1}{2}d_1d_2\sin{\varphi} \) |
Квадрат, прямоугольник, ромб, трапеция, параллелограмм
Четырехугольник означает «четыре стороны»
( четырехугольник, означает четыре, боковой, означает сторону).
Четырехугольник имеет четырех сторон, , это 2-мерный (плоская форма), закрытый (линии соединяются) и имеет прямых сторон.
Попробуйте сами
(также см. Интерактивные четырехугольники)
Недвижимость
В четырехугольнике:
- четыре стороны (края)
- четыре вершины (углы)
- внутренние углы, которые добавляют к 360 градусов :
Попробуйте нарисовать четырехугольник и измерить углы.Они должны добавить к 360 °
Виды четырехугольника
Есть специальные виды четырехугольника:
Некоторые типы также включены в определение других типов! Например, квадрат , ромб и прямоугольник также являются параллелограммами . Подробности смотрите ниже.
Рассмотрим каждый вид по очереди:
Прямоугольник
маленькие квадратики в каждом углу означают «прямой угол»
Прямоугольник — это четырехсторонняя форма, каждый угол которой является прямым (90 °).
Также противоположных сторон параллельны и равной длины.
Площадь
маленькие квадратики в каждом углу означают «прямой угол»
У квадрата равные стороны (отмечены буквой «s»), и каждый угол представляет собой прямой угол (90 °)
Также противоположные стороны параллельны.
Квадрат также соответствует определению прямоугольника (все углы равны 90 °) и ромба (все стороны равной длины).
Ромб
Ромб — это четырехгранная форма, все стороны которой имеют одинаковую длину (обозначены буквой «s»).
Также противоположные стороны параллельны и противоположных углов равны.
Еще одна любопытная вещь — диагонали (пунктирные линии) пересекаются посередине под прямым углом. Другими словами, они «разрезают» друг друга пополам под прямым углом.
Ромб иногда называют ромбом или ромбом .
Параллелограмм
У параллелограмма противоположные стороны параллельны и равны по длине. Также противоположные углы равны (углы «А» такие же, а углы «В» одинаковые).
ПРИМЕЧАНИЕ: квадраты, прямоугольники и ромбы — это все Параллелограммы!
Пример:
Параллелограмм с:
- со всех сторон равны и
- угол «А» и «B» в виде прямых углов
— это квадрат !
Трапеция (UK: Trapezium)
Трапеция | Равнобедренная трапеция |
Трапеция (в Великобритании ее называют трапецией) имеет пару параллельных противоположных сторон.
И трапеция (в Великобритании называется трапецией) — четырехугольник без параллельных сторон:
| Трапеция | Трапеция | |
| В США: | Пара параллельных сторон | НЕТ параллельных сторон |
| В Великобритании: | НЕТ параллельных сторон | Пара параллельных сторон |
| (определения для США и Великобритании поменяны местами!) | ||
Трапеция Равнобедренная , как показано выше, имеет левую и правую стороны равной длины, которые соединяются с основанием под равными углами.
Воздушный змей
Эй, похоже на воздушного змея (обычно).
Имеет две пары сторон:
Каждая пара состоит из двух соединяющихся сторон равной длины.
Также:
- углы, где встречаются две пары равны.
- : диагонали, показанные выше пунктирными линиями, пересекаются в под прямым углом.
- одна из диагоналей делит пополам (делит пополам) другую.
… вот и все специальные четырехугольники.
Неправильные четырехугольники
Единственный правильный четырехугольник (все стороны равны и все углы равны) — это квадрат. Итак, все остальные четырехугольники неправильные .
Схема «Семейное древо»
Определение четырехугольника: , включая .
Пример: квадрат также является прямоугольником.
Итак, мы включаем квадрат в определение прямоугольника.
(Мы, , не говорим : «Наличие всех углов 90 ° делает его прямоугольником, за исключением случаев, когда все стороны равны, тогда это квадрат».)
Это может показаться странным, поскольку в повседневной жизни мы думаем о квадрате как о , а не о как о прямоугольнике … но в математике это .
Используя приведенную ниже таблицу, мы можем ответить на такие вопросы, как:
- Является ли квадрат разновидностью прямоугольника? (Да)
- Прямоугольник — это разновидность воздушного змея? (Нет)
Сложные четырехугольники
О да! когда две стороны пересекаются, мы называем это «сложным» или «самопересекающимся» четырехугольником, например:
У них все еще есть 4 стороны, но две стороны пересекаются.
Полигон
Четырехугольник — это многоугольник. Фактически, это четырехсторонний многоугольник, точно так же, как треугольник — трехсторонний многоугольник, пятиугольник — пятисторонний многоугольник и так далее.
Играйте с ними
Теперь, когда вы знаете различные типы, вы можете играть с интерактивными четырехугольниками.
Другие названия
Четырехугольник иногда можно назвать:
- a Quadrangle (« четыре угла »), поэтому звучит как «треугольник»
- a Tetragon (« четыре многоугольника »), поэтому он звучит как «пятиугольник», «шестиугольник» и т. Д.
Соотношение сторон параллелограмма 3: 4. Если его периметр 56 см, каковы длины сторон?
Наука
- Анатомия и физиология
- астрономия
- астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- физика
Ромб
(Перейти к области ромба или периметру ромба)
Ромб — это плоская форма с 4 равными прямыми сторонами.
Ромб похож на ромб
| Все стороны имеют одинаковую длину | |
| Противоположные стороны параллельны, а противоположные углы равны (это параллелограмм). | |
| Высота — это расстояние под прямым углом к двум сторонам | |
| И диагонали «p» и «q» ромба. разделите друг друга пополам под прямым углом. |
Играть ромбом:
Площадь ромба
Площадь можно рассчитать по:
- высота, умноженная на длину стороны:
Площадь = высота × с
- квадрат длины стороны (s 2 ), умноженный на синус угла A (или угла B):
Площадь = с 2 sin (A)
Площадь = с 2 sin (B)
- путем умножения длин диагоналей и последующего деления на 2:
Площадь = (p × q) / 2
Пример: ромб имеет диагонали 6 м и 8 м. Какова его площадь?
Площадь = (6 м × 8 м) / 2 = 24 м 2
Если вы можете нарисовать свой ромб, попробуйте инструмент «Площадь многоугольника путем рисования».
Периметр ромба
Периметр — это расстояние по краям.
Периметр равен , в 4 раза умноженным на s (длина стороны) Периметр = 4s |
Пример: длина стороны ромба 12 см. Каков его периметр?
Периметр = 4 × 12 см = 48 см
Квадрат — это ромб?
Да, потому что квадрат — это просто ромб, в котором все углы прямые.
Другие названия
Эту форму чаще называют ромбом , но некоторые люди называют ее ромбом или даже ромбом .
Множественное число — ромбов или ромбов , и, реже, ромбов или ромбов (с двойным b).
Название «ромб» происходит от греческого слова rhombos : кусок дерева крутился на веревке и издавал рев!
,треугольников — равносторонние, равнобедренные и чешуйчатые
Треугольник имеет три стороны и три угла | ||
Три угла всегда складываются в 180 ° |
Равносторонний, равнобедренный и чешуйчатый
Треугольникам даны три специальных имени, которые показывают, сколько сторон (или углов) равны.
Может быть 3 , 2 или нет равных сторон / углов:
Равносторонний треугольник Три равных стороны | |
Равнобедренный треугольник Две равные стороны | |
Скаленовый треугольник Нет равные стороны |
Как запомнить? По алфавиту идут 3, 2, нет:
- Равносторонний : «равный» — боковой («боковая сторона» означает сторону), поэтому все стороны равны
- Равнобедренный : означает «равноногие», а у нас две ноги , верно? Также i SOS celes имеет два одинаковых «S ides», соединенных стороной « O dd».
- Скален : означает «неровный» или «нечетный», поэтому нет равных сторон.
Какой тип угла?
Треугольники также могут иметь имена, которые сообщают вам, какой тип угла находится внутри :
Острый треугольникВсе углы меньше 90 ° | |
Прямой треугольникИмеет прямой угол (90 °) | |
Тупой треугольникИмеет угол более 90 ° |
Объединение имен
Иногда у треугольника будет два имени, например:Правый равнобедренный треугольникИмеет прямой угол (90 °), а также два равных угла. Вы можете угадать, каковы равные углы? |
Поиграй с ним…
Попробуйте перетащить точки и составить разные треугольники:
Вы также можете поиграть с Интерактивным треугольником.
Уголки
Три внутренних угла всегда составляют 180 °
Периметр
Периметр — это расстояние по краю треугольника: просто сложите три стороны:
Площадь
Площадь составляет , половина базовой, умноженная на высоту .
- «b» — расстояние по базе
- «h» — высота (измеренная под прямым углом к основанию)
Площадь = ½ × ш × в
Формула работает для всех треугольников.
Примечание: более простой способ записать формулу — bh / 2
Пример: Какова площадь этого треугольника?
(Примечание: 12 — это высота , а не длина левой стороны)
Высота = h = 12
База = b = 20
Площадь = ½ × b × h = ½ × 20 × 12 = 120
Основание может быть с любой стороны. Убедитесь, что «высота» измеряется под прямым углом к »основанию». :
(Примечание: вы также можете рассчитать площадь по длинам всех трех сторон, используя формулу Герона.)
Почему область «половина bh»?
Представьте, что вы «удвоили» треугольник (перевернули его вокруг одного из верхних краев), чтобы получить квадратную форму (параллелограмм), которую можно изменить на простой прямоугольник:
ЗАТЕМ вся площадь составляет bh , что соответствует обоим треугольникам, поэтому только один будет ½ × bh .
,