Записать в тригонометрической форме – Тригонометрическая форма записи комплексного числа — энциклопедический справочник и словарь для студента от А до Я

Тригонометрическая форма записи комплексного числа — энциклопедический справочник и словарь для студента от А до Я

ОПРЕДЕЛЕНИЕ

Тригонометрическая форма комплексного числа z = x + iy, не равная нулю, является обозначением , где является модулем комплексного числа z.

Кроме того, в зависимости от решаемой задачи вы можете перевести комплексное число в алгебраическую или экспоненциальную.

ПРИМЕР

Задача Чтобы выразить число z = 1-i в тригонометрической форме.

Решение. Действительной частью комплексного числа z = 1 — i является число . Мнимая часть . Чтобы найти тригонометрическую форму написания сложного числа, вам нужно найти его модуль и аргумент.

Модуль комплексного числа z является числом

Аргумент вычисляется по формуле:

Следовательно, тригонометрическая форма комплексного числа:

Ответ

Геометрическое представление комплексного числа

Если мы рассмотрим плоскость с прямоугольной системой координат, то любое комплексное число z = x + iy можно связать с точкой на этой плоскости с соответствующими координатами и радиус-вектором r комплексного числа, т. Е. A вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу (рис.1). Эта плоскость называется комплексной. Реальные числа расположены на горизонтальной (вещественной) оси, мнимые части — на вертикальной (мнимой) оси.

ОПРЕДЕЛЕНИЕ

Модуль комплексного числа z = x + iy является выражением .

ПРИМЕР

Задача

Найти модуль числа z = 3-25i.

Решение.

Действительной частью комплексного числа z = 3-25i является число x = Re z = 3, мнимая часть . Следовательно, модуль числа

Ответ

Если z — действительное число, то его модуль равен r = | z | равной абсолютному значению этого действительного числа.

Например. z = -7, r = | -7 | = 7

Свойства модуля

1.

2. | z | = 0 тогда и только тогда, когда z = 0

3.

4.

5.

6. т. Е. Модуль разности комплексных чисел равен расстоянию между этими числами на комплексной плоскости.

ПРИМЕР

Задача

Найти произведение модулей комплексных чисел .

Решение.

Модуль комплексного числа z1 = 1-i равен , модуль комплексного числа z2 = 25i равен . Следовательно,

Ответ

ОПРЕДЕЛЕНИЕ

Угол (измеренный в радианах) радиус-вектора точки, который соответствует комплексному числу z на комплексной плоскости, называется аргументом числа . В этом случае вещественные числа x, y комплексного числа z = x + iy могут быть выражены через модуль r и аргумент

Свойства аргумента Для комплексного числа аргумент определяется с точностью до

При z = 0 значение аргумента не определено.

Основным значением аргумента является число . Для инверсии следующего свойства:

Действия комплексных чисел в тригонометрической форме сравнение

Два комплексных числа и называются равными, если

умножение

Для произведения комплексных чисел в тригонометрической форме справедливо равенство:

ПРИМЕР

Задача

Найдите произведение комплексных чисел и .

Решение.

Комплекс комплексных чисел:

Ответ

Подробнее о умножении комплексных чисел читайте в отдельной статье: Умножение комплексных чисел. разделение

Фактор комплексных чисел в тригонометрической форме выполняется по формуле:

Возведение

Для поднятия до степени комплексных чисел в тригонометрической форме справедлива формула:

sciterm.ru

Тригонометрическая форма комплексного числа

Также, в зависимости от решаемой задачи, вы можете перевести комплексное число в алгебраическую или показательную форму.

Геометрическое представление комплексного числа

Если рассмотреть плоскость с прямоугольной системой координат, то любому комплексному числу можно сопоставить точку на этой плоскости с соответствующими координатами , и радиус-вектор комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу (рис. 1). Данная плоскость называется комплексной. Действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси.

Модуль и аргумент комплексного числа

Если является действительным числом, то его модуль равен абсолютной величине этого действительного числа.

Например.

Свойства модуля

2. в том и только том случае, если
6. , т.е. модуль разности комплексных чисел равен расстоянию между этими числами на комплексной плоскости.

Свойства аргумента

2. Для комплексного числа аргумент определяется с точностью до .
   Для значение аргумента не определено.
3. Главным значением аргумента называется число . Для обратного числа выполняется свойство: .

Действия над комплексными числами в тригонометрической форме

Сравнение

Два комплексных числа и называются равными, если

Умножение

Для произведения комплексных чисел в тригонометрической форме верно равенство:

   

Подробнее про умножение комплексных чисел читайте в отдельной статье: Умножение комплексных чисел.

Деление

Частное комплексных чисел в тригонометрической форме выполняется по формуле:

   

Возведение в степень

Для возведения в степень комплексных чисел в тригонометрической форме верна формула:

   

Подробнее про возведение в степень читайте в отдельной статье: Возведение в степень комплексного числа.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Тригонометрическая форма комплексного числа

Определение 1

Выражение вида $z=a+bi$ , где $a$ и $b$ — вещественные числа, а $i$ — «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=\sqrt{-1}$ или $i^2=-1$ .

Рассмотрим некоторую точку $M(a,b)$ комплексной плоскости. Введем полярную систему координат следующим образом:

• полюс полярной системы координат будет совпадать с началом координат комплексной плоскости, т.е. точкой $O(0;0)$;
• полярная ось будет совпадать с положительным направлением оси $Ox$ .

Обозначим полярные координаты рассматриваемой точки М через $r$ и $\varphi$,

где $r \ge 0$ (рис. 1).

Рис. 1

Связь координат двух систем задается следующими равенствами:

$a=r \cos \varphi $, $b=r \sin \varphi $

Подставим приведенные выше равенства в запись заданного комплексного числа в виде $z=a+bi$ и получим

$$z=r \cos \varphi + i \cdot r \sin \varphi$$

или

$$z=r(\cos \varphi + i \cdot \sin \varphi)$$

Определение 2

Запись некоторого комплексного числа $z$ в виде $z=r(\cos \varphi + i \cdot \sin \varphi)$ называется тригонометрической формой записи, при этом число $r$ — модуль данного комплексного числа $z$ , $\varphi$ — аргумент данного комплексного числа $z$ .

Модуль некоторого комплексного числа вычисляется по следующей формуле:

$z=|z|=|a+bi|=\sqrt {a^2+b^2}$.

Аргумент $\varphi$ некоторого комплексного числа $z=a+bi$ можно вычислить, используя следующие формулы:

$$\varphi = tg \frac{b}{a}; \cos \varphi = \frac {a} {\sqrt {a^2+b^2}}; \sin \varphi = \frac {b} {\sqrt {a^2+b^2}}$$

На практике для вычисления значения аргумента заданного комплексного числа $z=a+bi$ обычно пользуются формулой:

$$ \varphi = arg z = \begin{equation*} \begin{cases} arctg \frac {b}{a}, a \ge 0, (*) \\ arctg \frac{b} {a} + \pi, a или решают систему уравнений $$ \begin{equation*} \begin{cases} cos \varphi = \frac {a} {\sqrt {a^2+b^2}}, (**) \\ sin \varphi = \frac {b} {\sqrt {a^2+b^2}} \end{cases} \end{equation*}$$

Примечание 1

Аргумент вещественных чисел равен соответственно:

• 0 для положительного числа;
• $\pi$ для отрицательного числа.

Примечание 2

Аргумент чисто мнимых чисел равен соответственно:

$ \frac {\pi}{2} $ с положительной мнимой частью;

$ \frac {3\pi}{2} $ с отрицательной мнимой частью.

Примечание 3

Аргумент некоторого комплексного числа $z$ считается:

положительным $( \varphi >0)$ при отсчете против часовой стрелки от положительного направления оси $Ox$;

отрицательным $( \varphi

Примечание 4

Аргумент некоторого комплексного числа $z$ определяется не однозначно, а с точностью до слагаемого $2 \pi k$, где $k \in Z$.

Пример 1

Представить в тригонометрической форме заданные комплексные числа, для которых: 1) $r=0, \varphi=5 \pi$ ; 2) $r=10, \varphi= \frac {\pi}{2}$ ; 3) $r= \sqrt {2}, \varphi =- \frac {\pi} {3}$ ; 4) $r=3, \varphi = 0$.

Решение:

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos \varphi + i \cdot sin \varphi)$.

Для $r=0, \varphi=5 \pi$ получаем комплексное число $z=0 \cdot (cos5 \pi + i \cdot sin 5 \pi)$.

Для $r=10, \varphi = \frac {\pi}{2}$ получаем комплексное число $z=10 \cdot (cos \frac {\pi}{2} + i \cdot sin \frac {\pi} {2}$.

Для $r= \sqrt {2}, \varphi=- \frac {\pi}{3}$ получаем комплексное число $z= \sqrt {2} \cdot (cos (- \frac {\pi}{3}) + i \cdot (- \frac {\pi}{3}))$.

Для $r=3, \varphi=0$ получаем комплексное число $z=3 \cdot (cos0+i \cdot sin0)$.

Определение 3

Запись некоторого комплексного числа $z$ в виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:

• $a$ — вещественная (действительная) часть, обозначение Re$z=a$;
• $b$ — мнимая часть, обозначение Im $z=b$.

Алгоритм 1

Чтобы комплексное число $z$, записанное в алгебраической форме, привести к тригонометрической форме записи, необходимо выполнить следующее:

• вычислить модуль и аргумент;
• подставить полученные значения в выражение $z=r(cos \varphi + i \cdot sin \varphi)$.

Пример 2

Представить заданные комплексные числа в тригонометрической форме:

1) $z=3+0$ ; 2) $Z= \frac {1}{2} + \frac {1}{2} \cdot i$.

Решение:

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos \varphi + i \cdot sin \varphi)$.

1) По условию $a=3, b=0$.

Вычислим модуль исходного комплексного числа: $$ r= \sqrt {3^2 + 0^2}=3$$

Вычислим аргумент исходного комплексного числа, используя формулу (*):

$$ \varphi = artg z = arctg \frac {0}{3} = arctg0 = 0$$

Подставим полученные значения и получим:

$$z=3 \cdot (cos0+isin0)$$

Следовательно, $z=3 \cdot (cos0+isin0)$ — искомая запись комплексного числа.

2) По условию $a= \frac {1}{2}, b= \frac {1}{2}$

Вычислим модуль исходного комплексного числа:

$$r= \sqrt {\frac {1}{2}^2 + \frac {1}{2}^2} = \sqrt \frac {1}{4}+{1}{4}=\frac {1}{2}= \frac {\sqrt {2}}{2}$$

Вычислим аргумент исходного комплексного числа, используя формулу (*):

$$ \varphi = arg z = arctg \frac {1/2}{1/2} = arctgl = \frac {\pi}{4}$$

Подставим полученные значения и получим:

$$z=\frac {\sqrt {2}}{2} \cdot (cos \frac {pi}{4}+isin \frac {\pi}{4})$$

Следовательно, $z=\frac {\sqrt {2}}{2} \cdot (cos \frac {pi}{4}+isin \frac {\pi}{4})$ — искомая запись комплексного числа.

Определение 4

Запись комплексного числа $z$ в виде $z=r \cdot e^{i \varphi}$ называется показательной формой записи, где число $r$ — модуль комплексного числа $z$, определяемый по формуле $r=|z|=|a+bi|=\sqrt {a^2+b^2}$, $\varphi$ — аргумент комплексного числа $z$ , определяемый по формуле $\varphi = arctg \frac {b}{a}$ .

Алгоритм 2

Чтобы комплексное число $z$, записанное в показательной форме, привести к тригонометрической форме записи, необходимо выполнить следующее:

• определить из показательной записи числа значения модуля и аргумента;
• подставить полученные значения в выражение $z=r(cos \varphi + i \cdot \varphi)$.

Пример 3

Представить заданные комплексные числа в тригонометрической форме:

1) $z=3 \cdot e^{\frac {\pi}{3}i}$ ; 2) $z=6 \cdot e^{\pi \cdot i}$.

Решение:

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos \varphi + i \cdot sin \varphi)$.

1) Определим значения модуля и аргумента: $r=3, \varphi = \frac {\pi}{3}$.

Запись числа в тригонометрической форме имеет вид: $z=3 \cdot (cos \frac {\pi}{3} + i sin \frac {\pi}{3})$.

2) Определим значения модуля и аргумента: $r=6, \varphi = \pi$.

Запись числа в тригонометрической форме имеет вид: $z=6 \cdot (cos \pi + i sin \pi)$.

Вывод

Таким образом, можно сделать вывод о том, что в каком бы виде не было записано комплексное число $z$, его всегда можно представить в тригонометрической форме записи $z=r \cdot (cos \varphi + i sin \varphi)$.

spravochnick.ru

5. Тригонометрическая форма записи комплексного числа

6

Пример. Произведением двух комплексных чиселz1 = 3+7i иz2 = −1+2i будет комплексное числоz1z2 = (3+7i)(−1+2i)= −3−7i +6i −14= −17−i .

Произведением комплексно сопряжённых чисел является действительное число.

Действительно, (x+iy)(x−iy)= x2 +iyx−iyx−i2 y2 = x2 + y2 .

4.4 Деление комплексных чисел

Частным двух

комплексных чисел

z1= x1+iy1

и

z2= x2+iy2,

z2

≠ 0

называется

комплексное число, вычисляемое по правилу

z1

=

z1z2

=

x1x2

+ y1y2

+i

x2y1− x1y2

.

z

2

z

z

2

x2+ y2

x2

+ y

2

2

2

2

2

2

Иногда сначала

определяют при z

2

≠ 0

величину

1

=

z2

=

x2

−i

y2

. Тогда

z

x2+ y2

x2

+ y2

2

z

z

2

2

2

2

2

2

z1 = z1 1 и далее используется операцияумножения комплексных чисел.z2 z2

3 +i

(3+i)(4+3i)

12 +4i +9i −3

9 13

Пример.

=

=

=

+ 25i .

4 −3i

(4−3i)(4+3i)

16 +9

25

Тригонометрическая (или полярная) форма записи комплексного числа

z

имеет

вид

z = r (cosϕ +i sinϕ), где

r =

z

=

x2+ y2

— модуль комплексного числа.

ϕ — аргумент комплексного числа.

Аргумент

комплексного числа

z = x+iy

при

x ≠ 0 вычисляется исходя

из

того,

что

tg (Argz)= tgϕ = xy . Случай когдаx = 0 рассмотрен чуть ниже.

Главное значение аргумента комплексного числа, обозначаемое arg z , есть такое значение аргумента комплексного числа, которое удовлетворяет условию −π < arg z ≤π (иногда, для удобства, выбирают 0 ≤ arg z < 2π ). Соответственно, Argz = argz +2kπ , где k Z .

Главное значение аргумента комплексного числа можно найти по следующему правилу

Оглавление Е.Е. Красновский, В.Д. Морозова «Теория функций комплексного переменного»

7
			arctg (y x),x > 0
		π	+arctg (y x),x < 0,y ≥ 0
arg z =		π	+arctg (y x),x	<	0, y	<	0
	—
			π 2,x = 0,y > 0
			−π 2,x = 0,y > 0

Пример. Найдём модуль и главное значение аргумента для следующих комплексных чиселz1 =1+i :z1 = 2 , arg(z1 )=π4 ;

z2 =1−3i :z2 = 2 , arg(z2 )= −π3;z3 = −2+2i :z3 = 22 , arg(z3 )= 3π4;

	z4 = −1−	i		:		z4		= 2		, arg (z4 )= −5π 6 ;
									3
		3

6.Действия с комплексными числами втригонометрической форме

6.1Умножение комплексных чисел в тригонометрической форме

При умножении двух комплексных чисел z1 = r1 (cosϕ1 +i sinϕ1 )

и z2

= r2(cosϕ2+i sinϕ2)

в

тригонометрической форме их

модули

следует

перемножить,

а

аргументы сложить:

z1z2 = r1r2 (cos(ϕ1 +ϕ2 )+i sin(ϕ1 +ϕ2 )), то есть

z1z2

=

z1

z2

, Arg (z1z2 )= Argz1 +Argz2 .

6.2 Деление комплексных чисел в тригонометрической форме

При делении двух комплексных

чисел z1 = r1 (cosϕ1 +i sinϕ1 )

и z2

= r2(cosϕ2+i sinϕ2)

в

тригонометрической форме при z2 ≠ 0

(а значит, и r2

≠ 0 ) модуль делимого надо разделить на

модуль делителя, а аргумент делителя вычесть из аргумента делимого:

z1

=

r1

(cos(ϕ1 −ϕ2 )+i sin(ϕ1 −ϕ2 )).

z2

r2

То есть,

z		=		z1		, Arg	z
1							1	= Argz− Argz		.
z2				z2			z2	1	2

Оглавление Е.Е. Красновский, В.Д. Морозова «Теория функций комплексного переменного»

8

6.3 Возведение комплексного числа в целую положительную степень

При возведении комплексного числа в целую положительную степень удобно предварительно записать его в тригонометрической форме после чего воспользоваться формулой Муавра возведения комплексного числа в целую положительную степень.

zn = (r(cosϕ +i sinϕ))n = rn (cosnϕ +i sinnϕ).

3

π

π

3

3

3π

3π

Пример.

(3+3i)

2

+i sin

= (3 2)

+i sin

=

= 3

cos

4

4

cos

4

4

1

+i

1

= −54+54i .

= 54 2

−

2

2

6.4 Извлечение корня целой положительной степени из комплексного числа

arg z +2kπ

+i sin

arg z +2kπ

n z = nr

cos

n

n

,

1

k = 0,1,…,n −

Из этого соотношения называемого формулой Муавра извлечения корня целой

положительной степени из комплексного числа, следует, что среди возможных значений

n

z

(при z ≠ 0 ) различными будутn значений, соответствующих, например, значениямk =

0, n −1.

Геометрически, все значения n

располагаются на окружности с центром в точке z = 0 и

z

радиусом

и являются вершинами правильного n-угольника,вписанного в эту окружность.

n

z

Пример.

Найдём

a

,

где

a .

У

этого

корня

a

различных значений zk ,

при

1

k = 0,1,2,3a −1.

Поскольку

1 =1(cos(0)+i sin(0)), то

значения

корня имеют

вид

0 +2kπ

+i sin

0 +2kπ

2kπ

+i sin

2kπ

. Они лежат на окружности с центром в

zk =1 cos

a

a

=

1 cos

a

a

точке z = 0 и радиусом 1, являются вершинами правильногоa-угольника,вписанного в эту окружность и при этом координаты одной из вершин имеют вид(1,0).

Оглавление Е.Е. Красновский, В.Д. Морозова «Теория функций комплексного переменного»

studfiles.net

Понятие, алгебраическая и тригонометрическая форма комплексного числа

Комплексные числа вводятся в связи с тем, что действительных чисел недостаточно, чтобы решить любое квадратное уравнение с действительными коэффициентами. Простейшее из квадратных уравнений, не имеющих корней среди действительных чисел, есть

x² + 1 = 0.

Задача такова: нужно расширить систему действительных чисел до такой системы чисел, в которой это уравнение обладало бы корнем.

Решение: x² = — 1, x =√-1,

где √-1 — квадратный корень из минус единицы — мнимая единица, обозначаемая буквой i.

Продвинемся ещё на шаг к алгебрической форме записи комплексных чисел. Квадратное уравнение

имеет корни и , где i = √-1 — квадратный корень из минус единицы.

Таким образом, у комплексных чисел есть действительная и мнимая части. В алгебраической записи комплексного числа z = x + iy есть действительная часть x и мнимая часть iy.

В литературе часто встречается обобщённая алгебраическая форма комплексного числа с другими буквами: z = a + bi. Здесь же дана запись z = x + iy только для того, чтобы было более понятно отображение комплексного числа в привычной системе координат с осями x и y.

Отображая на плоскости горизонтальную ось x как ось действительных чисел, а вертикальную ось y как ось мнимых чисел, можно любое комплексное число z = x + iy отобразить как точку P в декартовой системе координат (рисунок ниже).

Поэтому возможна и запись комплексного числа в тригонометрической форме:

,

где — модуль комплексного числа, (аргумент комплексного числа) — угол, который радиус-вектор образует с осью Ox. Теперь мы видим, что более подходящим является сравнение записи комплексного числа в тригонометрической форме с отображением точки в полярной системе координат.

Обобщим ещё раз понятие модуля и аргумента комплексного числа. Модуль комплексного числа — это расстояние от начала координат до точки, в виде которой отображается комплексного числа или, что то же самое — длина радиус-вектора . Аргумент комплексного числа — это угол, который радиус-вектор образует с осью Ox.

Теперь о том, как перейти от алгебраической формы комплексного числа к тригонометрической. Доказано, что

и

.

Поэтому можем легко найти косинус и синус аргумента комплексного числа:

, .

О множествах чисел

function-x.ru

Тригонометрическая и показательная форма комплексного числа

В данном параграфе больше речь пойдет о тригонометрической форме комплексного числа. Показательная форма в практических заданиях встречается значительно реже. Рекомендую закачать и по возможности распечатать тригонометрические таблицы, методический материал можно найти на странице Математические формулы и таблицы. Без таблиц далеко не уехать.

Любое комплексное число (кроме нуля) можно записать в тригонометрической форме:

, где – этомодуль комплексного числа, а –аргумент комплексного числа.

Изобразим на комплексной плоскости число . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что:

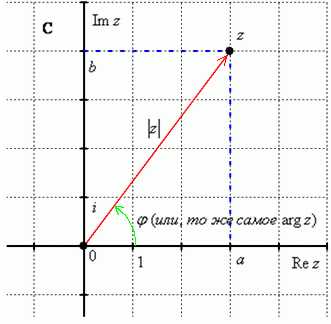
Модулем комплексного числа называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря,модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.

Модуль комплексного числа стандартно обозначают:или

По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: . Данная формула справедливадля любых значений «а» и «бэ».

Примечание: модуль комплексного числа представляет собой обобщение понятия модуля действительного числа, как расстояния от точки до начала координат.

Аргументом комплексного числа называетсяугол  между положительной полуосью действительной оси и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа:.

Рассматриваемый принцип фактически схож с полярными координатами, где полярный радиус и полярный угол однозначно определяют точку.

Аргумент комплексного числа стандартно обозначают:или

Из геометрических соображений получается следующая формула для нахождения аргумента:

. Внимание! Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой. Эти случаи мы тоже разберем.

Но сначала рассмотрим простейшие примеры, когда комплексные числа располагаются на координатных осях.

Пример 7

Представить в тригонометрической форме комплексные числа: ,,,. Выполним чертёж:

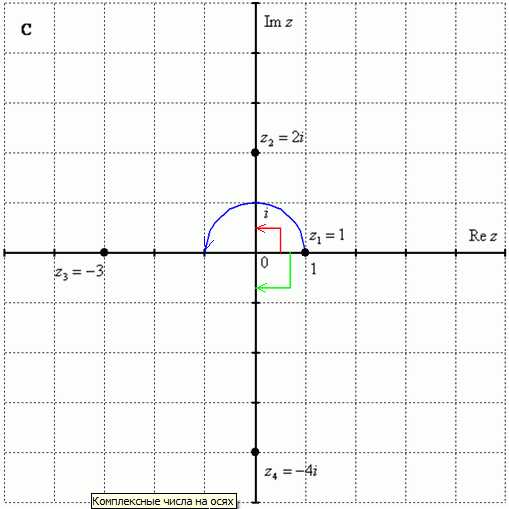
На самом деле задание устное. Для наглядности перепишу тригонометрическую форму комплексного числа:

Запомним намертво, модуль – длина (которая всегда неотрицательна), аргумент – угол

1) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:. Очевидно, что(число лежит непосредственно на действительной положительной полуоси). Таким образом, число в тригонометрической форме:.

Ясно, как день, обратное проверочное действие:

2) Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:. Очевидно, что(или 90 градусов). На чертеже угол обозначен красным цветом. Таким образом, число в тригонометрической форме:.

Используя таблицу значений тригонометрических функций, легко обратно получить алгебраическую форму числа (заодно выполнив проверку):

3) Представим в тригонометрической форме число . Найдем его модуль и

аргумент. Очевидно, что . Формальный расчет по формуле:

. Очевидно, что (или 180 градусов). На чертеже угол обозначен синим цветом. Таким образом, число в тригонометрической форме:.

Проверка:

4) И четвёртый интересный случай. Представим в тригонометрической форме число . Найдем его модуль и аргумент. Очевидно, что. Формальный расчет по формуле:.

Аргумент можно записать двумя способами: Первый способ: (270 градусов), и, соответственно:. Проверка:

Однако более стандартно следующее правило: Если угол больше 180 градусов, то его записывают со знаком минус и противоположной ориентацией («прокруткой») угла: (минус 90 градусов), на чертеже угол отмечен зеленым цветом. Легко заметить,

что и– это один и тот же угол.

Таким образом, запись принимает вид:

Внимание! Ни в коем случае нельзя использовать четность косинуса, нечетность синуса и проводить дальнейшее «упрощение» записи:

Кстати, полезно вспомнить внешний вид и свойства тригонометрических и обратных тригонометрических функций, справочные материалы находятся в последних параграфах страницы Графики и свойства основных элементарных функций. И комплексные числа усвоятся заметно легче!

В оформлении простейших примеров так и следует записывать: «очевидно, что модуль равен… очевидно, что аргумент равен…».  Это действительно очевидно и легко решается устно.

Перейдем к рассмотрению более распространенных случаев. C модулем проблем не возникает, всегда следует использовать формулу . А вот формулы для нахождения аргумента будут разными, это зависит от того, в какой координатной четверти лежит число. При этом возможны три варианта (их полезно переписать):

1) Если (1-ая и 4-ая координатные четверти, или правая полуплоскость), то аргумент нужно находить по формуле.

2) Если (2-ая координатная четверть), то аргумент нужно находить по формуле.

3) Если (3-я координатная четверть), то аргумент нужно находить по формуле.

Пример 8

Представить в тригонометрической форме комплексные числа: ,,,.

Коль скоро есть готовые формулы, то чертеж выполнять не обязательно. Но есть один момент: когда вам предложено задание представить число в тригонометрической форме, то чертёж лучше в любом случае выполнить. Дело в том, что решение без чертежа часто бракуют преподаватели, отсутствие чертежа – серьёзное основание для минуса и незачета.

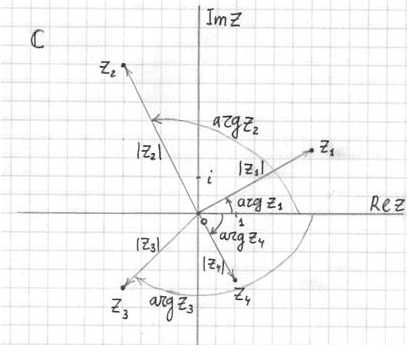
Представляем в комплексной форме числа и, первое и третье числа будут для самостоятельного решения.

Представим в тригонометрической форме число . Найдем его модуль и аргумент.

Поскольку (случай 2), то

–вот здесь нечетностью арктангенса воспользоваться нужно. К сожалению, в таблице отсутствует значение , поэтому в подобных случаях аргумент приходится оставлять в громоздком виде:– числов тригонометрической форме.

Представим в тригонометрической форме число . Найдем его модуль и аргумент.

Поскольку (случай 1), то(минус 60 градусов).

Таким образом:

–число в тригонометрической форме.

А вот здесь, как уже отмечалось, минусы не трогаем.

Кроме забавного графического метода проверки, существует и проверка аналитическая, которая уже проводилась в Примере 7. Используем таблицу значений тригонометрических функций, при этом учитываем, что угол – это в точности табличный угол(или 300 градусов):– числов исходной алгебраической форме.

Числа ипредставьте в тригонометрической форме самостоятельно. Краткое решение и ответ в конце урока.

В конце параграфа кратко о показательной форме комплексного числа.

Любое комплексное число (кроме нуля) можно записать в показательной форме:

, где – это модуль комплексного числа, а– аргумент комплексного числа.

Что нужно сделать, чтобы представить комплексное число в показательной форме? Почти то же самое: выполнить чертеж, найти модуль и аргумент. И записать число в виде .

Например, для числа предыдущего примера у нас найден модуль и аргумент:,. Тогда данное число в показательной форме запишется следующим образом:.

Число в показательной форме будет выглядеть так:

Число – так:

 И т.д.

Единственный совет – не трогаем показатель экспоненты, там не нужно переставлять множители, раскрывать скобки и т.п. Комплексное число в показательной форме записывается строго по форме .

studfiles.net

Тригонометрическая и показательная формы комплексного числа.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Тригонометрическая форма комплексного числа:

Для всякого  комплексного числа $z=x+iy$ справедливо равенство $$z=|z|(\cos\varphi+i\sin\varphi).\qquad\qquad\qquad (1)$$ Здесь $|z|=\sqrt{x^2+y^2},$ a $\varphi$ удовлетворяет условиям: $$\cos\varphi=\frac{x}{\sqrt{x^2+y^2}},\qquad \sin\varphi=\frac{y}{\sqrt{x^2+y^2}},\qquad \varphi\in[0, 2\pi).$$  

Равенство (1) называют тригонометрической формой комплексного числа $z.$  

 Примеры:

Следующие комплексные числа представить в тригонометрической форме и изобразить точками на комплексной плоскости:

1.435. $-i$

Решение.

Пусть $z=x+iy=-i,$ то есть $x=0,\,\, y=-1.$ Тогда $$|z|=\sqrt{x^2+y^2}=\sqrt 1=1.$$

$$\cos\varphi=\frac{0}{1}=0,\qquad \sin\varphi=\frac{-1}{1}=-1\Rightarrow \varphi=\frac{3\pi}{2}.$$ 

Таким образом, $z=\cos\frac{3\pi}{2}+i\sin\frac{3\pi}{2}.$

Ответ: $\cos\frac{3\pi}{2}+i\sin\frac{3\pi}{2}.$

 

1.438. $\frac{1-i}{1+i}.$

Решение.

Запишем число $z=\frac{1-i}{1+i}$ в алгебраической форме:

$$\frac{1-i}{1+i}=\frac{(1-i)(1-i)}{(1+i)(1-i)}=\frac{1-2i+i^2}{1-i^2}=\frac{1-2i-1}{1+1}=\frac{-2i}{2}=-i.$$

Тригонометрическая форма числа $-i$ найдена в предыдущемпримере (1.435):

$z=-i=\cos\frac{3\pi}{2}+i\sin\frac{3\pi}{2}.$

Ответ: $\cos\frac{3\pi}{2}+i\sin\frac{3\pi}{2}.$

 

1.441. $1+\cos\frac{\pi}{7}+i\sin\frac{\pi}{7}.$

Решение.

Пусть $z=x+iy=1+\cos\frac{\pi}{7}+i\sin{\pi}{7},$ то есть $x=1+\cos\frac{\pi}{7},\,\, y=\sin{\pi}{7}.$ Тогда $$|z|=\sqrt{x^2+y^2}=\sqrt {\left(1+\cos\frac{\pi}{7}\right)^2+\sin^2\frac{\pi}{7}}=$$ $$=\sqrt{1+2\cos\frac{\pi}{7}+\cos^2\frac{\pi}{7}+\sin^2\frac{\pi}{7}}=\sqrt{2+2\cos\frac{\pi}{7}}=$$ $$=\sqrt{4\cos^2\frac{\pi}{14}}=2\cos\frac{\pi}{14}.$$

$$\cos\varphi=\frac{x}{|z|}=\frac{1+\cos\frac{\pi}{7}}{2\cos\frac{\pi}{14}}=\frac{2\cos^2\frac{\pi}{14}}{2\cos\frac{\pi}{14}}=\cos\frac{\pi}{14}.$$

$$\sin\varphi=\frac{y}{|z|}=\frac{sin\frac{\pi}{7}}{2\cos\frac{\pi}{14}}=\frac{2\cos\frac{\pi}{14}\sin\frac{\pi}{14}}{2\cos\frac{\pi}{14}}=\sin\frac{\pi}{14}.$$

Таким образом, $\varphi=\frac{\pi}{14}.$

Отсюда находим показательную форму комплексного числа $z=x+iy=1+\cos\frac{\pi}{7}+i\sin{\pi}{7}:$

$$z=2\cos\frac{\pi}{14}\left(\cos\frac{\pi}{14}+i\sin\frac{\pi}{14}\right).$$

Ответ: $2\cos\frac{\pi}{14}\left(\cos\frac{\pi}{14}+i\sin\frac{\pi}{14}\right).$

 

Показательная форма комплексного числа:

Символом $e^{i\varphi}$ обозначается комплексное число $\cos\varphi+i\sin\varphi.$ С помощью этого обозначения всякое комплексное число $z=|z|(\cos\varphi+i\sin\varphi)$ может быть представлено в показательной форме $$z=|z|e^{i\varphi}.$$

Примеры.

Представить в показательной форме следующие комплексные числа:

1.475. $\frac{7+24i}{5}.$

Решение. 

Приведем число $z=\frac{7+24i}{5}$ к алгебраическому виду:

$$z=x+iy=\frac{7+24i}{5}=\frac{7}{5}+\frac{24}{5}i.$$

$$|z|=\sqrt{\left(\frac{7}{5}\right)^2+\left(\frac{24}{5}\right)^2}=\sqrt{\frac{49+576}{25}}=\sqrt{\frac{625}{25}}=\sqrt{25}=5.$$

$$tg\varphi=\frac{y}{x}=\frac{\frac{24}{5}}{\frac{7}{5}}=\frac{24}{7}.$$ Поскольку число $z$ принадлежит первой четверти, то $\varphi=arctg\frac{24}{7}.$

Таким образом, $z=5e^{i arctg\frac{24}{7}}.$

Ответ: $z=5e^{i arctg\frac{24}{7}}.$

  {jumi[*4]}

1.479. $\sin\alpha-i\cos\alpha.$

Решение.

$$z=x+iy=\sin\alpha-i\cos\alpha\Rightarrow \,\,x=\sin\alpha,\,\,y=-cos\alpha.$$

$$|z|=\sqrt{x^2+y^2}=\sqrt{\sin^2\alpha+\cos^2\alpha}=1.$$

$$tg\varphi=\frac{y}{x}=\frac{-\cos\alpha}{\sin\alpha}=-ctg\alpha=tg(\alpha+\frac{\pi}{2})=tg(\alpha+\frac{3\pi}{2}).$$

Кроме этого должны выполняться условия 

$$\cos\varphi=\frac{x}{|z|}=\sin\alpha;\qquad \sin\varphi=\frac{y}{|z|}=\cos\alpha.$$

Отсюда находим

$$\varphi=\alpha+\frac{3\pi}{2}.$$

Таким образом, $$z=\sin\alpha-i\cos\alpha=e^{i\left(\alpha+\frac{3\pi}{2}\right)}.$$

Ответ: $e^{i\left(\alpha+\frac{3\pi}{2}\right)}.$

 

1.482 (а). Данные числа $z_1$ и $z_2$ представить в показательной форме и выполнить указанные действия над ними:

$z_1z_2;$ $\frac{z^2_1}{z_2},$ если $z_1=2\sqrt 3-2i,$ $z_2=3-3\sqrt 3i.$

Решение.

Запишем числа $z_1$ и $z_2$ в показательной форме:

$$|z_1|=\sqrt{x^2+y^2}=\sqrt{(2\sqrt 3)^2+(-2)^2}=\sqrt{16}=4.$$

$$tg\varphi=\frac{y}{x}=\frac{-2}{2\sqrt 3}=-\frac{1}{\sqrt 3}.$$

Поскольку число $z_1$ принадлежит четвертой четверти, то $\varphi_1=arctg{-\frac{1}{\sqrt 3}}=-\frac{\pi}{6}.$

Отсюда $$z_1=4e^{-i\frac{\pi}{6}}.$$

$$|z_2|=\sqrt{x^2+y^2}=\sqrt{3^2+(-3\sqrt 3)^2}=\sqrt{36}=6.$$

$$tg\varphi=\frac{y}{x}=\frac{-3\sqrt 3}{3}=-\sqrt 3.$$

Поскольку число $z_2$ принадлежит четвертой четверти, то $\varphi_2=arctg{\sqrt 3}=-\frac{\pi}{3}.$

Отсюда $$z_2=6e^{-i\frac{\pi}{3}}.$$

Далее находим $z_1z_2$ и $\frac{z^2_1}{z_2}:$

 $$z_1z_2=4e^{-i\frac{\pi}{6}}6e^{-\frac{\pi}{3}}=24e^{i\left(\frac{-\pi}{6}-\frac{\pi}{3}\right)}=24e^{-i\frac{\pi}{2}}=$$

$$=24\left(\cos\left(-\frac{\pi}{2}\right)+i\sin\left(-\frac{\pi}{2}\right)\right)=24(0-1)=-24.$$ 

$$\frac{z^2_1}{z_2}=\frac{(4e^{-i\frac{\pi}{6}})^2}{6e^{-\frac{\pi}{3}}}=\frac{16}{6}e^{i\left(\frac{-2\pi}{6}+\frac{\pi}{3}\right)}=\frac{8}{3}e^{i\cdot 0}=\frac{8}{3}.$$

Ответ: $-24, \frac{8}{3}.$

 

Домашнее задание.

Следующие комплексные числа представить в тригонометрической форме и изобразить точками на комплексной плоскости:

1.436. $1-i\sqrt 3.$

Ответ: $2\left(\cos\frac{5\pi}{3}+i\sin\frac{5\pi}{3}\right).$

 

1.437. $-\frac{1}{2}+i\frac{\sqrt 3}{2}.$

Ответ: $\cos\frac{2\pi}{3}+i\sin\frac{2\pi}{3}.$

 

1.440. $\sin\frac{\pi}{3}+i\cos\frac{\pi}{3}.$

Ответ: $\cos\frac{\pi}{6}+i\sin\frac{\pi}{6}.$

 

 

Представить в показательной форме следующие комплексные числа:

1.476. $5-12i.$

Ответ: $13e^{-i arctg\left(-\frac{12}{5}\right)}.$

 

1.477. $-3-4i.$

Ответ:  $5e^{i arctg\left(\frac{4}{3}+\pi\right)}.$

 

 

1.479.$\sin\alpha-i\cos\alpha.$

Ответ:  $e^{i \left(\alpha+\frac{3\pi}{2}\right)}.$

 

 

1.480. $\sin\alpha+i(1-\cos\alpha).$

Ответ:  $2\sin\frac{\pi}{2}e^{i \frac{\alpha}{2}}.$

 

1.482 (б). Данные числа $z_1$ и $z_2$ представить в показательной форме и выполнить указанные действия над ними:

$z^2_1\overline z_2;$ $\frac{\overline z_2}{z_1},$ если $z_1=-\sqrt 3+i\sqrt 2,$ $z_2=\sqrt 8-\sqrt 8.$

Ответ:  $16e^{i\frac{7\pi}{4}}; 2e^{-i\frac{\pi}{2}}.$

 

 

 

mathportal.net