Примеры на тему логарифмы: Урок 3. Логарифм. Свойства логарифмов. Выражения с логарифмами. Практика

Логарифмы примеры решения задач, формулы и теоретический материал

Логарифмы (Логарифмирование) активно используются в решении задач, так как значительно упрощают обычные алгебраические операции. Использование логарифмов позволяет заменить умножение на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня заменяются соответственно на умножение и деление на показатель степени числа.

Перед изучением примеров решения задач советуем изучить теоретический материал по логарифмам, прочитать определения и все свойства логарифмов. Список тем находится в правом меню.

Свойства логарифмов

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Вычислить , если

Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения:

Ответ.

Больше примеров решений →

Натуральные логарифмы

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Вычислить

Решение. Преобразуем данное выражение, используя свойство суммы логарифмов и определение натурального логарифма:

Ответ.

Больше примеров решений →

Десятичные логарифмы

Основные ссылки — теоретический материал и примеры решений (10 шт).

Пример

Задание. Вычислить

Решение. Преобразуем данное выражение, используя свойство логарифма степени, а также тот факт, что

Материалы для подготовки к ЕГЭ по математике ЕГЭ-Студия

Предыдущую статью о показательных уравнениях мы начали с уравнения 2^x = 8. Там всё было ясно: x = 3.

А теперь рассмотрим уравнение 2^x = 7.

По графику функции y = 2^x мы видим, что это уравнение имеет корень, и притом единственный.

Ясно, что этот корень — не целое число (так как 2² = 4, 2³ = 8). Более того, оказывается, что он не является даже рациональным числом, т. е. не представляется в виде обыкновенной дроби. Интуитивно мы чувствуем лишь, что он меньше 3, но не намного.

Этот корень обозначается log₂7 (читается: «логарифм семи по основанию два». Он является иррациональным числом, т. е. бесконечной непериодической десятичной дробью. Калькулятор даёт: log₂7 = 2,807354922057604107…

Итак, наше число log₂7 — это показатель степени, в которую надо возвести 2, чтобы получить 7.

Теперь дадим общее определение логарифма. Пусть a > 0 и a ≠ 1 (условия те же, что и для основания показательной функции).

Определение. Логарифм положительного числа b по основанию a (обозначается log_ab) — это показатель степени, в которую надо возвести a, чтобы получить b.

Иными словами,

Например:

  так как  

, так как 

  так как  ;

, так как  .

Логарифм с основанием 10 называется десятичным

и обозначается lg. Например, lg 100 = 2, lg 1000 = 3, lg 0,01 = −2.

Логарифм с основанием e называется натуральным и обозначается ln.

Обратите внимание: логарифм определён только для положительных чисел. Причина заключается в том, что показательная функция может принимать лишь положительные значения. Например, число log₂(−4) не существует: в какую бы степень мы ни возводили 2, мы никогда не получим −4.

Не забывайте также про ограничения на основание логарифма: 0 < a < 1 или a > 1.

Основные формулы

По определению, log_ab — это показатель степени, в которую надо возвести число a, чтобы получить число b:

Формула (1) называется основным логарифмическим тождеством.
Вот еще один вариант записи основного логарифмического тождества:

log_aa^x=x.

Перечислим свойства логарифмов. Они являются простыми следствиями правил действия со степенями. Все логарифмы ниже считаются определёнными.

Логарифм произведения — это сумма логарифмов:

loga(bc) = logab + logac.

(2)

Логарифм частного — это разность логарифмов:

(3)

Показатель степени логарифмируемого числа «спрыгивает» перед логарифмом:

(4)

Показатель степени основания логарифма тоже «спрыгивает», но в виде обратного числа:

(5)

Формулы (4) и (5) вместе дают:

(6)

В частности, если m = n, мы получаем формулу:

(7)

 

Например, .

Наконец, важнейшая формула перехода к новому основанию:

(8)

В частности, если c = b, то log_bb = 1, и тогда:

(9)

 

Приведём несколько примеров из банка заданий.
1. (применили формулу (2) суммы логарифмов).

2. (применили основное логарифмическое тождество(1))

3. (применили формулу (4).

4. (применили формулу (9), перейдя к новому основанию 0,8).

5. (применили формулу (3) разности логарифмов)

Немного истории

Теперь вы поняли, что такое логарифмы и как ими пользоваться. Но для чего они всё-таки нужны? Или это просто такая математическая игрушка с хитрой инструкцией по применению?

Понятие логарифма и логарифмические таблицы появились в 17 веке, и значение их было огромно.

Это в наши дни вычисления не представляют труда — у каждого есть калькулятор. А как считали в «докомпьютерные» времена?

Складывать и вычитать можно было на счётах, а вот умножать и делить приходилось «в столбик» — медленно и трудно.

В 15–17 веках, в эпоху великих географических открытий, стали бурно развиваться торговля, экономика и наука. Требования к математике росли: расчёты становились более сложными, а точность — например, для решения навигационных задач — нужна была всё более высокая.

Необходим был инструмент, позволяющий упростить и ускорить расчёты, и таким инструментом явились логарифмы.

Предположим, что b и c — большие числа, которые надо перемножить. Появление таблиц логарифмов (например, с основанием 10) существенно упростило эту задачу. Теперь вычислителю достаточно было найти по таблицам десятичные логарифмы чисел b и c, сложить их (на счётах) и получить логарифм произведения: lgb + lgc = lg(bc).

А затем по таблице логарифмов найти само произведение чисел b и c.

Недаром французский математик и астроном Лаплас сказал, что изобретение логарифмов удлинило жизнь вычислителей. Логарифмическая линейка (которой инженеры пользовались до 70-х годов двадцатого века) была не менее прогрессивным изобретением, чем современный калькулятор.

Но это еще не всё! Мы не занимались бы логарифмами, если бы они имели лишь историческую, «музейную» ценность. О неожиданных применениях логарифмов мы расскажем в следующей статье, посвящённой логарифмической функции.

Логарифмы: примеры и решения

Как известно, при перемножении выражений со степенями их показатели всегда складываются (a^b*a^c = a^b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.

Определение в математике

Логарифмом называется выражение следующего вида: log_ab=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log₂8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.

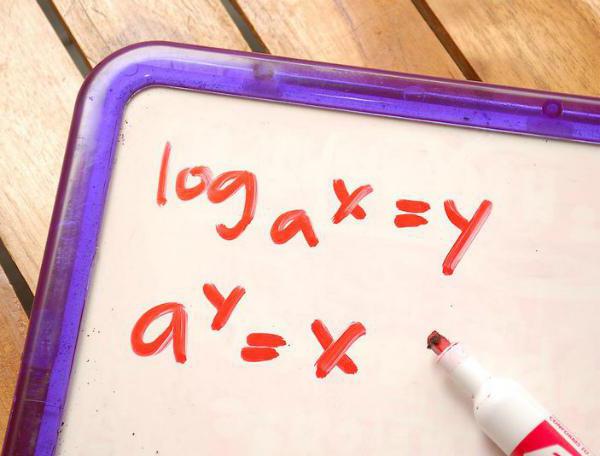
Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

1. Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
2. Десятичный логарифм lg a, где основанием служит число 10.
3. Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Правила и некоторые ограничения

В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:

• основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
• если а > 0, то и а^b>0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10^х= 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, квадратичная степень! 10²=100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log₁₀100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

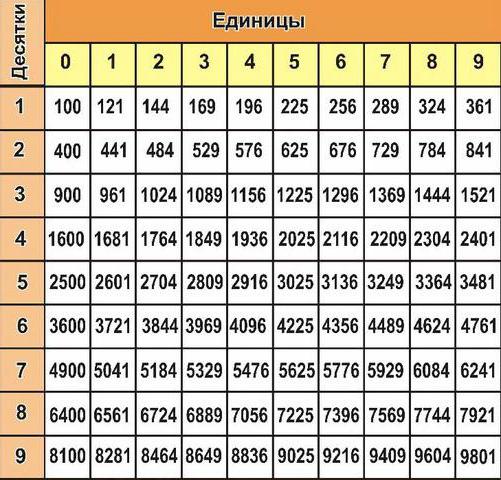
Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a^c=b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!

Уравнения и неравенства

Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3⁴=81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log₃81 = 4). Для отрицательных степеней правила такие же: 2^-5= 1/32 запишем в виде логарифма, получим log₂ (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log₂(x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм₂x = √9) подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

1. Основное тождество выглядит так: а^logaB=B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
2. Логарифм произведения можно представить в следующей формуле: log_d(s₁*s_{2) =} log_ds₁ + log_ds_2. При этом обязательным условием является: d, s₁ и s₂ > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log_as₁ = f₁ и log_as₂ = f₂, тогда a^f1= s₁, a^f2= s_2. Получаем, что s₁*s₂ = a^f1*a^f2= a^f1+f2 (свойства степеней), а далее по определению: log_a(s₁*s₂)= f₁+ f₂ = log_as1 + log_as_2, что и требовалось доказать.
3. Логарифм частного выглядит так: log_a(s_1/s₂) = log_as₁— log_as_2.
4. Теорема в виде формулы приобретает следующий вид: log_a^q bⁿ = n/q log_ab.

Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log_ab = t, получается a^t=b. Если возвести обе части в степень m: a^tn = bⁿ;

но так как a^tn= (a^q)^nt/q = bⁿ, следовательно log_a^q bⁿ = (n*t)/t, тогда log_a^q bⁿ = n/q log_ab. Теорема доказана.

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры десятичных логарифмов: ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Как использовать формулы логарифмов: с примерами и решениями

Итак, рассмотрим примеры использования основных теорем о логарифмах.

1. Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log₂4 + log₂128 = log₂(4*128) = log₂512. Ответ равен 9.
2. log₄8 = log_2² 2³ = 3/2 log₂2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log₂(2x-1) = 4. Решение:
перепишем выражение, немного его упростив log₂(2x-1) = 2², по определению логарифма получим, что 2x-1 = 2⁴, следовательно 2x = 17; x = 8,5.

Ниже даны несколько рекомендаций, следуя которым можно с легкостью решать все уравнения, содержащие выражения, которые стоят под знаком логарифма.

• Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
• Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

Логарифмы и логарифмические уравнения

Логарифмические уравнения и решение логарифмических уравнений входят в обязательный комплекс знаний и умений школьника, если он стремится сдать ЕГЭ по математике на высокий балл и поступить в ВУЗ, стать студентом. Рассмотрим, что же это такое — логарифм, логарифмические уравнения и как их решать.

Логарифм — что это

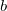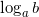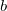Логарифмом числа   по основанию  (=c)называется такой показатель степени , в которую нужно возвести , чтобы получить   (то есть 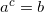). При этом задаются ограничения: 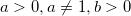. Значение логарифма может быть любым.

Вычислите:

,   .

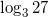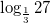1. Действуем по определению. Подберем степень, в которую нужно возвести 3, чтобы получить 27.

.

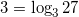2. При возведении 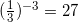, значит .

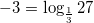Ответ: 3; -3.

Изобретенные в 17 веке для ускорения вычислений, логарифмы значительно сократили время, необходимое для умножения многозначных чисел. Они были основными в числовой работе более 300 лет, пока совершенство механических вычислительных машин в конце 19 века и компьютеров в 20 веке не сделали их устаревшими для крупномасштабных вычислений. Однако натуральный логарифм (с основанием e ≅ 2.71828 и записываемый как ln n) продолжает оставаться одной из наиболее полезных функций в математике с приложениями к математическим моделям в физических и биологических науках.

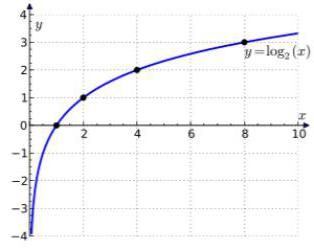
Логарифмическая функция и ее график

Помня об ограничениях, построим по точкам графики логарифмической функция в разных случаях.

Пусть 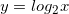.  Подставим вместо разные числа и определим соответствующие значения переменной.

Отметим координаты точек на плоскости и соединим их плавной линией.

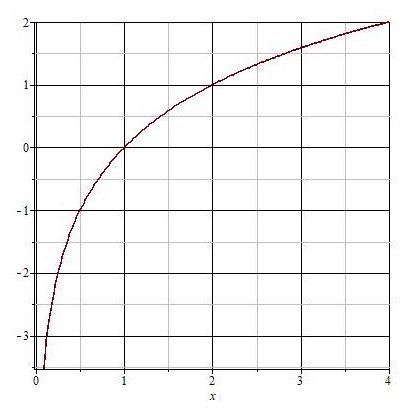
Логарифмическая функция все время возрастает.

Такое поведение характерно для всех логарифмических функций с основанием больше единицы.

Пусть теперь 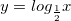. Составим таблицу значений для этого случая.

Получим следующий график функции:

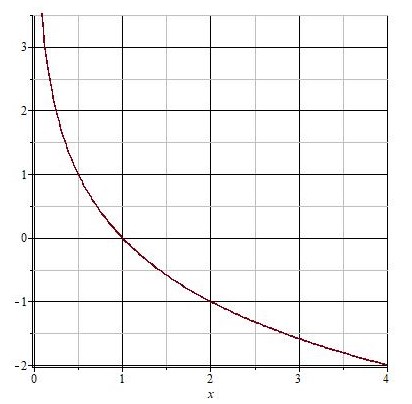
Все логарифмические функции с основанием от 0 до 1 убывают на всей области определения.

Графики всех логарифмических функций проходят через точку с координатами (1;0).

Особыми знаками принято обозначать логарифмы с основанием десять 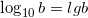  и логарифмы с натуральным основанием .

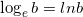Свойства логарифмов

Для упрощения вычислений при работе с логарифмами полезно знать и уметь использовать основные свойства.

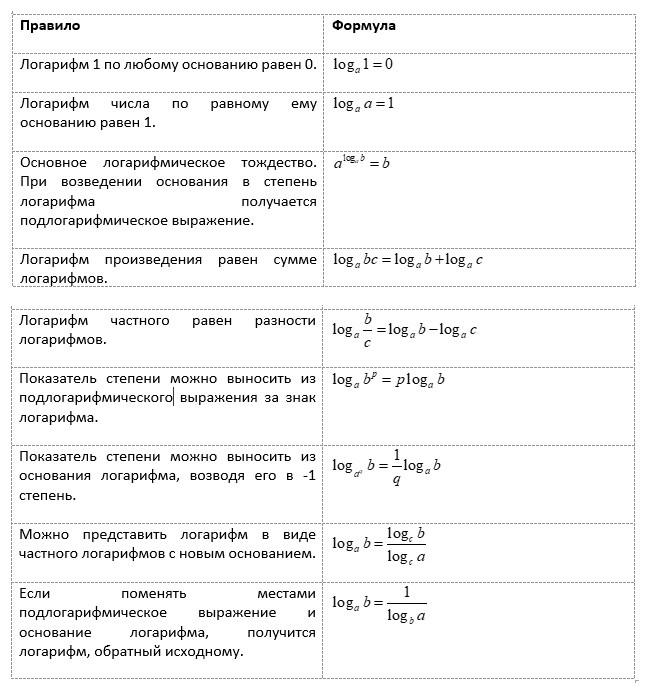
Логарифмы были быстро приняты учеными из-за различных полезных свойств, которые упростили долгие, утомительные вычисления.

В частности, ученые могли найти произведение двух чисел m и n, посмотрев логарифм каждого числа в специальной таблице, сложив логарифмы, а затем снова сверившись с таблицей, чтобы найти число с этим вычисленным логарифмом (известным как его антилогарифм). Выраженная в терминах обычных логарифмов, эта связь определяется как log m n = log m + log n.

Например, 100 × 1000 можно рассчитать, просмотрев логарифмы 100 по основанию 10 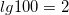и 1000 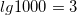. Сложив логарифмы 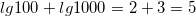, а затем найдя его антилогарифм (то есть число, стоящее под знаком логарифма, в данном случае 100000) в таблице.

Аналогично, задачи деления преобразуются в задачи вычитания с логарифмами: log m/n = log m — log n.

Это еще не все. Расчет степеней и корней может быть упрощен с использованием логарифмов. Логарифмы также могут быть преобразованы между любыми положительными основаниями (за исключением того, что 1 не может использоваться в качестве основания, поскольку все его степени равны 1).

В логарифмические таблицы обычно включались только логарифмы для чисел от 0 до 10. Чтобы получить логарифм некоторого числа вне этого диапазона, число было сначала записано в удобном виде как произведение его значащих цифр и его степени по основанию 10 —

например, 358 будет записано как 3,58 × 10 ²,

а 0,0046 будет записано как 4,6 × 10^-3.

Тогда логарифм значащих цифр — десятичная дробь между 0 и 1, известная как мантисса — будет найдена в таблице. Например, чтобы найти логарифм 358, можно посмотреть таблицу значений логарифмов 3,58 ≅ 0,55388. Следовательно, lg 358 = lg 3,58 + lg 100 = 0,55388 + 2 = 2,55388.

В примере числа с отрицательным показателем степени, такого как 0,0046, можно посмотреть lg 4,6 ≅ 0,66276. Следовательно, lg 0,0046 = lg 4,6 + lg 0,001 = 0,66276 — 3 = -2,33724.

История логарифмов

Изобретению логарифмов предшествовало сравнение арифметических и геометрических последовательностей.

В геометрической последовательности каждый член образует постоянное соотношение (знаменатель прогрессии) с предыдущим и последующим членами прогрессии: например,… 1/1000, 1/100, 1/10, 1, 10, 100, 1000… имеет общее отношение 10. В арифметической последовательности каждый последующий член отличается на константу, известную как разность прогрессии, например,… −3, −2, −1, 0, 1, 2, 3… имеет разность 1.

Обратите внимание, что геометрическая последовательность может быть записана в терминах ее общего отношения, для приведенной выше примерной геометрической последовательности:… 10⁻³, 10 ⁻², 10 ⁻¹, 10 0, 10 ¹, 10 ², 10 ³….

Умножение двух чисел в геометрической последовательности, скажем, 1/10 и 100, равно суммированию соответствующих показателей степеней с основанием 10: -1 и 2, чтобы получить 10

1 = 10. Таким образом, умножение преобразуется в сложение.

Однако первоначальное сравнение между двумя возможностями вычислений произведения не было основано на каком-либо явном использовании экспоненциальной записи: это было последующее развитие.

В 1620 году в Праге швейцарским математиком Йостом Бурги была опубликована первая таблица, основанная на концепции соотношения геометрических и арифметических последовательностей.

Шотландский математик Джон Непер опубликовал свое открытие логарифмов в 1614 году. Его целью было помочь в умножении величин, которые были связаны с вычислением синуса в прямоугольном треугольнике.

Вычисления Непера и Бригса

В сотрудничестве с английским математиком Генри Бригсом Непер приспособил свой логарифм к его современной форме. Для неперова логарифма сравнение будет происходить между точками, движущимися по градуированной прямой линии, точка L (для логарифма) движется равномерно от минус бесконечности до плюс бесконечности, точка Х (для синуса) движется от нуля до бесконечности со скоростью пропорционально его расстоянию от нуля. Кроме того, L равно нулю, когда X равно единице, и их скорость в этой точке равна.

Суть открытия Непера состоит в том, что он связал между собой арифметические и геометрические прогрессии — то есть умножение и возведение в степень значений точки X соответствуют сложению и умножению значений точки L соответственно. На практике удобно ограничивать движение L и X требованием, чтобы L = 1 при X = 10, в дополнение к условию, что X = 1 при L = 0. Это изменение привело к бригиану, или общему логарифму.

Непер умер в 1617 году, а Бригс продолжил расчеты в одиночку, опубликовав в 1624 году таблицу логарифмов, рассчитанную до 14 знаков после запятой для чисел от 1 до 20 000 и от 90 000 до 100 000. Но и в таблицах Бригса обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги появилось только в 1857 году в Берлине.

В 1620-е годы Эдмунд Уингейт и Уильям Отред изобрели первую логарифмическую линейку, до появления карманных калькуляторов — логарифмические линейки были незаменимы в инженерных расчетах.

Современное определение логарифмирования — как операции, обратной возведению в степень — впервые появилось у Валлиса и Иоганна Бернулли, а окончательно было узаконено Эйлером в XVIII веке. Эйлеру принадлежит и заслуга распространения логарифмической функции на комплексную область.

Где используются логарифмы

Некоторые области науки, где применяются логарифмы:

• Децибелы, используемые для измерения звукового давления, определяются с помощью логарифмов.
• Шкала Рихтера, которая используется для измерения интенсивности землетрясений, определяется с помощью логарифмов
• Значения pH в химии, которое используется для определения уровня кислотности вещества, также определяется с использованием понятия логарифма.
• Когда две измеренные величины оказываются связанными степенной функцией, параметры функции могут быть оценены с использованием логарифмов.
• Логарифмы могут быть использованы для решения уравнений, таких как 2^х = 3.

Решение логарифмических уравнений

Рассмотрим простейшие логарифмические уравнения и примеры их решения.

Задание 1

Решите уравнение log₅(x²+x)=log₅(x²+9)

Ответ:9

Решение: Так как основания логарифмов одинаковы, то числа, стоящие под знаком логарифмов — одинаковы:

,

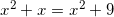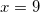
Задание 2

Решите уравнение log_x-5 49 = 2.

Если уравнение с логарифмами имеет более одного корня, в ответе укажите наибольший из них.

Ответ: 12

Решение:

(x – 5)² = 49;

x² – 10 x + 25 = 49;

x² – 10 x – 24 = 0;

a = 1 , b = -10, c = -24;

 

 

 

 

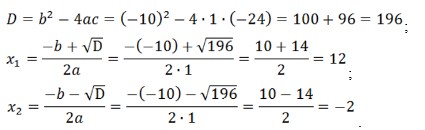
При х = –2 основание логарифма отрицательно (известно, что основание должно быть положительным). Решением является корень 12. Сделайте проверку.

Задание 3

Найдите корень уравнения log₂(4 – x) = 7.

Ответ:-124

Решение:

2⁷ = 4 – x;

128=4-х;

х = 4 – 128;

х = −124.

Задание 4

Найдите корень уравнения .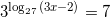

Ответ: 115

Решение: 27=3³, тогда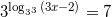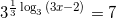

или или 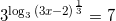 уравнения с логарифмами. По основному свойству логарифмов: при возведении числа в степень логарифма с таким же основанием, остается число, стоящее под знаком логарифма, то есть: 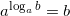. Тогда получим: .

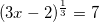Решая данное уравнение, получим: ,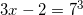

.

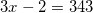
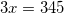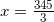
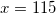
Задание 5

Решите уравнение log_x+725 = 2. Если уравнение имеет более одного корня, в ответе укажите наименьший из них.

Ответ: -2

Решение: .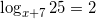

,  .

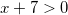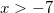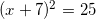
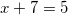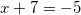
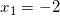и

и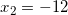

Так как x должен быть больше -7, то корень 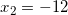 не подходит. И остается один единственный корень: .

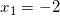Таким образом, уже не важно — наибольший это корень или наименьший, он один подходит. Поэтому в ответе указываем его.

Задание 6

Решите уравнение log₂(2 – x) = log₂(2 – 3x) + 1

Ответ: x=0,4.

Решение: мы знаем, что 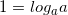, тогда пусть в нашем случае : ,

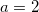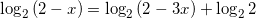применяя свойство сложения двух логарифмов с одинаковыми основаниями, получим:

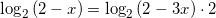
или

.

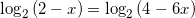
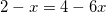
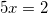
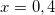Задание 7

Решите уравнение log₅(7 – x) = log₅(3 – x) + 1

Ответ: 2

Решение: мы знаем, что 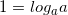, тогда пусть в нашем случае : .

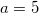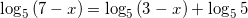применяя свойство сложения двух логарифмов с одинаковыми основаниями, получим:

.

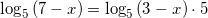
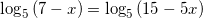
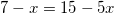
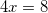
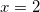Задание 8

Найдите корень уравнения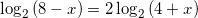

Ответ: x=-1

Решение:

.

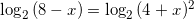
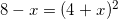
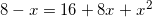
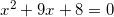
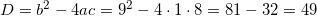
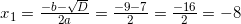
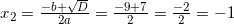так как у нас должно выполняться условие:

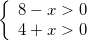, откуда 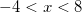, таким образом нам подходит только один корень .

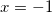Итак, мы рассмотрели решение логарифмических уравнений с подробным решением каждого из них. Вы узнали, что такое логарифм, историю возникновения логарифма и имена ученых, которые схватили идею расчета произведения через сложение и изобрели логарифм, который на многие годы облегчил расчеты инженеров, строителей, ученых.

Логарифмы. Логарифмические формулы. Свойства логарифмов

Факт 1.
\(\bullet\) Логарифм по основанию \(a\) от \(b\) – это число \(t\), которое показывает, в какую степень нужно возвести \(a\), чтобы получить \(b\).
Ограничения: числа \(a\) и \(b\) такие, что \(a>0,\ a\ne 1,\ b>0\).
\[\Large{{\color{blue}{\log_a{b}=t\quad\Leftrightarrow\quad a^t=b }}}\]
Т.к. мы имеем право возводить в любую степень, то \(t\in \mathbb{R}\).
Таким образом, верно основное логарифмическое тождество \[{\Large{a^{\log_ab}=b}}\]
\(\bullet\) Справедливы следующие формулы: \[{\large{\begin{array}{|ll|l|} \hline \qquad \qquad \qquad \qquad {\small{\text{Формулы}}} && \qquad \qquad{\small{\text{Ограничения}}}\\ &&\\ \hline \textbf{(1)} \log_a1=0&&a>0, a\ne 1\\ &&\\ \textbf{(2)} \log_aa=1 &&a>0, a\ne 1\\ &&\\ \textbf{(3)} \log_{a}{b^m}=m\log_a|b|&(m — {\small{\text{четн.}}})&a>0, a\ne 1, b\ne 0\\ &&\\ \textbf{(4)}\log_{a}{b^m}=m\log_ab& (m — {\small{\text{нечетн.}}})&a>0, a\ne 1, b>0\\ &&\\ \textbf{(5)} \log_{a^n}{b}=\frac 1n\log_{|a|}b&(n — {\small{\text{четн.}}})&a\ne 0, a\ne 1, b>0\\ &&\\ \textbf{(6)}\log_{a^n}b=\frac1n\log_ab&(n — {\small{\text{нечетн.}}})&a>0, a\ne 1, b>0\\ &&\\ \textbf{(7)} \log_a{bc}=\log_a|b|+\log_a|c|&&a>0, a\ne 1, bc\ne 0\\ &&\\ \textbf{(8)} \log_a{\dfrac bc}=\log_a|b|-\log_a|c|&&a>0, a\ne 1,bc\ne 0 \\ &&\\ \textbf{(9)} a^{\log_ab}=b &&a>0, a\ne 1, b>0\\ &&\\ \textbf{(10)}c^{\log_ab}=b^{\log_ac}&&a>0, a\ne 1, b>0, c>0\\ &&\\ \textbf{(11)} \log_ab\cdot \log_bc=\log_ac && a>0, a\ne 1,b>0, b\ne 1, c>0\\ &&\\ \textbf{(11′}) \log_bc=\dfrac{\log_ac}{\log_ab}&&a>0, a\ne 1,b>0, b\ne 1, c>0\\ &&\\ &&\\ {\small{\text{ЧАСТНЫЕ СЛУЧАИ:}}}&& \\ \textbf{(12)} \log_ab\cdot \log_ba=1 && a>0, a\ne 1, b>0, b\ne 1\\ &&\\ \textbf{(12′}) \log_ab=\dfrac1{\log_ba}&&a>0, a\ne 1, b>0, b\ne 1\\ &&\\ \hline \end{array}}}\]

Заметим, что при выполнении ограничений данные формулы верны в обе стороны!

 

Логарифмические уравнения — подготовка к ЕГЭ по Математике

Прежде чем решать логарифмические уравнения, повторим еще раз определение логарифма и основные формулы.

Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.

.

При этом .

Обратим внимание на область допустимых значений логарифма:

.

Основное логарифмическое тождество:

,

.

Основные формулы для логарифмов:

(Логарифм произведения равен сумме логарифмов)

(Логарифм частного равен разности логарифмов)
(Формула для логарифма степени)

Формула перехода к новому основанию:

.

Мы знаем, как выглядит график логарифмической функции. Эта функция монотонна. Если основание логарифма больше единицы, логарифмическая функция монотонно возрастает. Если основание больше нуля и меньше единицы, логарифмическая функция монотонно убывает. И в любом случае каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, то равны и сами числа.

Все это пригодится нам в решении логарифмических уравнений.

Простейшие логарифмические уравнения

1.Решите уравнение:

Основания логарифмов равны, сами логарифмы тоже равны – значит, равны и числа, от которых они берутся.
Обычно ученики запоминают это правило в краткой жаргонной формулировке: «Отбросим логарифмы!» Конечно, мы «отбрасываем» их не просто так, а пользуясь свойством монотонности логарифмической функции.

Получаем:

Решая логарифмические уравнения, не забываем про область допустимых значений логарифма. Помним, что выражение определено при .

Очень хорошо, если вы, найдя корень уравнения, просто подставите его в уравнение. Если после такой подстановки левая или правая часть уравнения не имеют смысла – значит, найденное число не является корнем уравнения и не может быть ответом задачи. Это хороший способ проверки на ЕГЭ.

2. Решите уравнение:

В левой части уравнения – логарифм, в правой – число 7. Применив основное логарифмическое тождество, представим число 7 в виде . Дальше все просто.

Ответ: -124

3. Решите уравнение:

Видите число 2 перед логарифмом в правой части уравнения? Сейчас оно мешает вам «отбросить логарифмы». Что с ним сделать, чтобы в левой и правой частях были просто логарифмы по основанию 5? Конечно же, поможет формула для логарифма степени.

;

;

;

4. Решите уравнение:

Область допустимых значений: Значит,

Представим 2 в правой части уравнения как — чтобы слева и справа в уравнении были логарифмы по основанию 5.

Функция монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом .

.

Ответ: 21.

5. Решите уравнение:

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: –4.

Заметим, что решения логарифмических уравнений лучше всего записывать в виде цепочки равносильных переходов. Это поможет нам не забыть про область допустимых значений.

6.Решите уравнение: .

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

Запишем решение как цепочку равносильных переходов.

Ответ: 19.

7.Решите уравнение: .

Обратите внимание: переменная х и под логарифмом, и в основании логарифма. Мы помним, что основание логарифма должно быть положительно и не равно 1.

ОДЗ:

Теперь можно «убрать» логарифмы.

— посторонний корень, поскольку должно выполняться условие .

Ответ:

8. Решите уравнение .

ОДЗ уравнения:

Сделаем замену . Как и в алгебраических уравнениях, мы делаем замену переменной всегда, когда только возможно.

Вернемся к переменной х:

9.Решите уравнение:

Выражение под логарифмом всегда положительно – поскольку к неотрицательной величине прибавляем 25. Выражение под корнем в правой части также положительно. Значит, х может быть любым действительным числом.

Представим сумму логарифмов в левой части как логарифм произведения. В правой части – перейдем к логарифму по основанию 3. И используем формулу логарифма степени.

«Отбрасываем» логарифмы.

Такое уравнение называется биквадратным. В него входят выражения и . Сделаем замену

Вернемся к переменной х. Получим:

. Мы нашли все корни исходного уравнения.

Ответ: .

Логарифмические уравнения могут встретиться вам и в задании №5 Профильного ЕГЭ по математике, и в задании №13. И если в задании №5 нужно решить простейшее уравнение, то в задаче 13 решение состоит из двух пунктов. Второй пункт – отбор корней на заданном отрезке или интервале.

Как решать логарифмические уравнения подробный разбор примеров

Чтобы ответить на вопрос как решать логарифмические уравнения давайте вспомним, что такое логарифм. Логарифм — это показатель степени, в которую нужно возвести основание логарифма, чтобы получить число.

Например,

или число 3 (показатель степени) мы можем записать так  , таким образом 

Основание логарифма всегда положительное число, не равное 1. Число под знаком логарифма — строго больше нуля.

Теперь переходим непосредственно к вопросу — как решать логарифмические уравнения из профильного и из базового ЕГЭ.

Пример 1 Найдите корень уравнения.

согласно определению логарифма:

Все неизвестные переносим в левую часть уравнения (слева от =), а известные — переносим в правую сторону.

Получим:

Делаем проверку:

Ответ:

Пример 2. Найдите корень уравнения.

Здесь для решения данного логарифмического уравнения будем использовать свойство логарифма:

То есть внесем число 3 справа под знак логарифма.

или

Если показатели степени равны, основания степени равны, то равны числа, получаемые в результате, то есть получим

Делаем проверку:

Получаем:

Ответ:

Пример 3. Найдите корень уравнения

Используем следующее свойство логарифма:

Тогда получим:

Делаем проверку:

Ответ:

Пример 4. Найдите корень уравнения.

Используя определение логарифма, получим:

Проверим:

Ответ: .

Таким образом, теперь вы можете составить четкую инструкцию, как решать логарифмические уравнения. Она заключается в следующих шагах:

1. Сделать справа и слева от знака равенства (=) логарифмы по одному основанию, избавившись от коэффициентов перед логарифмами, используя свойства логарифмов.
2. Избавляемся от логарифмов, используя правило потенцирования. Остаются только числа, которые были под знаком логарифма.
3. Решаем получившееся обычное уравнение — как найти корень уравнения смотрите здесь.
4. Делаем проверку
5. Записываем ответ.

Что такое логарифм? Определение и примеры

Что такое логарифм? В математике логарифм по основанию b положительного числа y определяется следующим образом: Если y = b ^x , то log _b y = x

Считать журнал _b y как «основание журнала b of y»

Как мы видели в уроке об экспоненциальной функции, b не равно 1, а b больше нуля.

Показатель x в экспоненциальном выражении b ^x — это логарифм в уравнении log _b y = x

Что такое простой логарифм?

Имейте в виду, что всякий раз, когда вы ищете логарифм, вы ищите показатель степени или число, которое сообщает, сколько раз умножается основание.

Например, каков логарифм выражения log ₅ 25?

2 — логарифм выражения log ₅ 25. Почему? В выражении мы видим, что база равна 5.

Поэтому спросите себя: «5 в степени того, что равно 25?»

Поскольку 5 ² = 25, log ₅ 25 = 2.

Каков логарифм выражения log ₂ 16?

Поскольку 2 в четвертой степени равно 16, log ₂ 16 = 4.

Что такое десятичный логарифм?

Десятичный логарифм — это логарифм с основанием 10. Следовательно, выражение log _b y = x становится log ₁₀ y = x

В результате вы всегда ищите, сколько раз вы умножаете 10 на получить у.

Вы можете записать десятичный логарифм как log ₁₀ y или как log y

Что такое log ₁₀ 1000?

Поскольку 10 в третьей степени = 1000, журнал ₁₀ 1000 = 3.

Запись в виде логарифма

Запишите 49 = 7 ² в виде логарифма

Запишите определение

Если y = b ^x , то логарифм _b y = x

Заменитель

Если 49 = 7 ² , то журнал ₇ 49 = 2

Логарифмическая форма 49 = 7 ² — это журнал ₇ 49 = 2

Запись 1/8 = (1 / 2) ³ в виде логарифма

Запишите определение

Если y = b ^x , то записать _b y = x

Заменитель

Если 1/8 = (1/2) ³ , то log _1/2 1/8 = 3

Логарифмическая форма 1/8 = (1/2) ³ имеет вид журнал _1/2 1/8 = 3

Новые уроки математики

Ваша электронная почта в безопасности.Мы будем использовать его только для информирования вас о новых уроках математики.

,

Логарифмы: Введение в «Связь»

Логарифмы: Введение в
«Отношения» (стр. 1 из 3)

Разделы: Введение в журналы, Упрощение выражений журнала, Общие и натурального бревна

---

Логарифмы «противоположны» экспонент, так же, как вычитание противоположно сложению, а деление противоположно умножения.Регистрирует экспоненты «отмены». Технически говоря, журналы обратные экспонент.

Практически у меня сочли полезным думать о журналах с точки зрения отношения:

The отношения

y = b x ………….. эквивалентно …………… (означает то же самое, что и) журнал b ( y ) = x

Слева вверху является экспоненциальным выражением « y = b ^x «.С правой стороны вверху: « журнал _b ( y ). = x » — эквивалентный логарифмический оператор, который произносится как «log-base-b из и равно x «; Значение нижнего индекса «b» «основание логарифма», так же как b является основанием экспоненциального выражения «b ^x «. И так же, как база b в экспоненте всегда положительна и не равна 1, так и база b поскольку логарифм всегда положителен и не равен 1.Все, что находится внутри логарифма, называется «аргументом» журнал. Обратите внимание, что основание как в экспоненциальном уравнении, так и в журнале уравнение (вверху) — «b», но что x и и переключаться на другую сторону при переключении между двумя уравнениями.

The Отношения анимированные

Если ты помнишь это отношение (что бы не было , аргумент журнала становится «равные» и что бы ни было , было «равным» становится показателем в экспоненте, и наоборот), то вам не следует слишком много проблем с логарифмами.

(я ввел термин «The Взаимосвязь ». Вы найдете , а не в своем тексте, и ваши учителя и наставники не поймут, о чем вы говорите, если вы говорите им об этом. «Отношения» совершенно нестандартны. терминология. Зачем я вообще его использую? Потому что это работает.)

Кстати: Если вы заметили что я переключил переменные между двумя полями, отображающими «The Отношения », у тебя зоркий глаз.Я сделал это специально, чтобы Подчеркните, что дело не в самих переменных, а в том, как они движутся.

• Конвертировать «6 ³ = 216 «к эквивалентному логарифмическому выражение.

Для преобразования база (то есть 6) остается то же самое, но 3 и 216 перейти на другую сторону. Это дает мне:

• Преобразовать « журнал ₄ (1024) = 5 «в эквивалентную экспоненту выражение.

Для преобразования база (то есть 4) остается прежним, но 1024 и 5 перейти на другую сторону. Это дает мне:

Верх | 1 | 2 | 3 | Вернуться к указателю Далее >>

Цитируйте эту статью как:

Стапель, Елизавета.«Логарифмы: Введение в« Отношения »». Purplemath . Доступно по номеру https://www.purplemath.com/modules/logs.htm . Доступ [Дата] [Месяц] 2016 г.

,

Обучающие логарифмы (логи) Д-р Эрик М. Баер, геологическая программа, Highline Community College

Геологический контекст: землетрясения, наводнения и наводнения, размеры зерен / седиментология, радиоактивный распад, рост населения, изменения в атмосферном CO ₂ , шкала децибел, шкала pH

---

Перейти к: Обучающие стратегии | Материалы и упражнения | Ресурсы для учащихся

Логарифмы являются обратной экспоненциальной функцией. Изначально разработанные как способ преобразования задач умножения и деления в задачи сложения и вычитания до изобретения калькуляторов, логарифмы теперь используются для решения экспоненциальных уравнений и для более элегантной работы с числами, которые простираются от очень больших к малым.Для получения дополнительной информации об экспоненциальных функциях перейдите на страницу Exponential Growth and Decay.

Функция логарифма ( log ) определяется как

y = log _b (x) тогда и только тогда, когда x = b ^y

и x> 0, b> 0 и b не равно 1.
Функция читается и читается как «y — логарифм база b для x»

Если база (b) не указана, предполагается, что база равна 10. Таким образом,

y = log (x) совпадает с y = log ₁₀ (x)

Когда в базе стоит число e (~ 2.71 …), логарифмическая функция называется «натуральным логарифмом» и обозначается как ln . Таким образом,

y = log _e (x) записывается y = ln (x)

Есть некоторые свойства логарифмических функций, которые могут быть полезны при решении проблем с журналами.

• журнал _b b ^x = x
• журнал _b b = 1
• журнал _b 1 = 0
• b ^{журнал _b X} = X

Стратегии преподавания: идеи из математического образования

Поместите количественные концепции в контекст

Существует ряд геологических условий, в которых журналы используются и могут быть введены.Некоторые из них включают:

Использовать несколько представлений

Поскольку у всех разные способы обучения, математики определили ряд способов, которыми количественные концепции могут быть представлены отдельным людям. В науках о Земле логарифмы чаще всего представляются графически.

• Графическое представление: Частота землетрясений в зависимости от магнитуды. подробности Одним из наиболее распространенных способов использования логарифмов геофизиками является построение данных в логарифмической шкале.Это используется, когда значения на графике охватывают большие значения. Примером может служить количество землетрясений разной магнитуды за год, нанесенное справа. Значения отдельных точек данных нечитаемы из-за арифметической шкалы.

  ---

  Журнал зависимости частоты землетрясений от магнитуды. Подробности Использование логарифмической шкалы позволяет более точно оценить многие значения. Однако этот график может быть труднее интерпретировать ученикам, потому что большинство авторов логарифмических графиков наносят данные в логарифмическом масштабе, но маркируют ось нелогарифмическими числами.Об этом нужно будет предупредить учащихся, потому что они часто не осознают, что шкала является логарифмической. Чтобы найти фактическое местоположение или значение точки на логарифмическом графике, необходимо вычислить логарифм исходного числа. Из-за этого учащимся очень сложно определить точное значение баллов, нанести дополнительные точки и даже вызвать неправильное толкование — например, на этом графике учащиеся могут подумать, что существует линейная зависимость между частотой и силой землетрясений, когда есть не является.

  ---

  Частота землетрясений в зависимости от магнитуды. Ось редко бывает четко и правильно помечена значениями журнала, как на этом графике.


• Логарифмическое нормальное графическое представление: Многие графические представления логарифмов построены только с одной логарифмической осью. Экспоненциальная функция (y = 10 ^x ) будет отображаться в виде линии на логарифмическом (также называемом полулогарифмическом) графике. Отношение Гутенбурга-Рихтера на логнормальном графике Согласно соотношению Гутенбурга-Рихтера частота между землетрясениями (L) и магнитудой землетрясений (M) связана соотношением

  L = 10 ^M

  Таким образом, график магнитуды и частоты землетрясений отображается в виде прямой линии на логнормальном графике.
• Лог-лог графическое представление: Диаграмма Хьюлстрома Некоторые графики имеют две логарифмические оси. Их часто называют «логарифмическими графиками». Хорошим примером является диаграмма Хьюлстрома, которая показывает скорости потока, при которых отложения будут размываться, переноситься и откладываться.


• Алгебраическое / числовое представление: Секрет журналов состоит в том, чтобы получить алгебраическое представление, чтобы можно было преобразовать между функцией журнала и экспоненциальной функцией.Студентам потребуется помощь в запоминании этого образца. В качестве примера показываю студентам

  3 ² = 9 то же самое, что 2 = log ₃ 9

  Я думаю, что использование цветного мела при написании этих чисел помогает. Некоторые студенты также находят фразу « ex ponent и equ al» полезной для запоминания этого отношения, поскольку показатель степени (2 в приведенном выше примере) сопровождается знаком равенства при преобразовании его в логарифмическую нотацию.

Используйте технологии надлежащим образом

У студентов есть любое количество технологических инструментов, которые они могут использовать для лучшего понимания количественных концепций — от калькуляторов в их рюкзаках до компьютеров в комнатах общежития. Логарифмы могут использовать эти инструменты, чтобы помочь студентам понять эту часто сложную концепцию.

• Графические калькуляторы
Графические калькуляторы — это простой способ для всех студентов ввести данные и увидеть, как выглядит кривая этих данных.Все графические калькуляторы немного отличаются, и учащимся может потребоваться помощь с их конкретной моделью. На справочном веб-сайте Prentice-Hall’s Calculator есть несколько полезных советов по использованию некоторых калькуляторов (дополнительная информация). Обратите внимание, что очень немногие калькуляторы будут вычислять журналы в базах, отличных от 10 или и . Кроме того, многие задачи с логарифмами легче решить в уме, чем правильно печатать в калькуляторе.
• Компьютеры
Логарифмы

— отличное начало для знакомства с программами работы с электронными таблицами.Студенты, вероятно, столкнутся с программами электронных таблиц во многих своих классах, и они являются отличными инструментами для визуализации формы уравнения. В Excel есть возможность переключиться на логарифмические оси, которые могут быть полезны для быстрой иллюстрации полезности логарифмов при анализе данных.

Работа в группах для решения многодневных углубленных задач

Математики также указывают, что учащиеся лучше усваивают количественные концепции, когда они работают в группах и пересматривают концепцию более одного дня.Поэтому при обсуждении количественных концепций в курсах геолого-геофизических исследований предложите студентам обсудить или применить концепции вместе. Кроме того, убедитесь, что вы либо включили задачи, которые могут быть растянуты на более чем один учебный период, либо неоднократно пересматривали концепцию. Логарифмы — это концепция, которая возникает снова и снова во вводной геонауке: радиоактивный распад, величина по шкале Рихтера, шкала pH и т. Д. Когда вводится каждая новая тема, обязательно укажите, что они видели этот тип функции раньше и должны распознать ее. ,

Учебные материалы и упражнения

• Определение вероятности и повторяемости землетрясений
  Домашнее задание / занятие в классе, где учащиеся собирают историческую информацию о землетрясениях и используют ее для прогнозирования вероятности более сильных землетрясений.
• Использование функций во вводном курсе геонаук
  Шаблон и набор упражнений, призванных помочь преподавателям повысить графическую грамотность своих студентов. Включены два упражнения — рост населения и увеличение концентрации CO ₂ в атмосфере — для помощи в обучении экспоненциальному росту и распаду.Шаблон дает общие рекомендации по обучению студентов взаимосвязи между функциями и их графическим представлением.
• Масштабирование Солнечной системы Галилея — размер глобусов
  В этом модуле студенты определяют размеры различных планет солнечной системы в таком масштабе, чтобы орбита Сатурна соответствовала территории кампуса. Учащиеся также сравнивают размеры планет в данной шкале с размерами зерен различных типов отложений. Он включает построение графиков по логарифмическим осям в Excel.
• Два потока, две истории … Как люди изменяют наводнения и потоки
  Учащиеся наносят данные о потоках на логарифмические оси, чтобы изучить наводнения.

Студенческие ресурсы

,

Логарифмы и антилогарифмы + Как найти журналы и антилогарифмы с помощью таблицы журналов

«Исследование посвящено изучению понятий и законов предмета / темы»

Привет, ребята

Спасибо, что пришли сюда. Недавно я создал видео о концепции журналов и антилогов, в котором есть еще несколько вещей, чем сама статья. Таким образом (с видео) вы можете учиться еще лучше и в интерактивном режиме, поскольку он включает мой собственный голосовой комментарий .Проверьте это по адресу:

youtube.com/watch?v=-0iKT4bdNuU

Перейдите по указанной выше ссылке, чтобы поставить лайк и подписаться на YouTube, если она вам понравилась. 🙂 Встроенное видео:

Надеюсь, вам понравится

Я заметил, что некоторые люди не понимают логарифмов (и антилогарифмов), и их трудно найти. Как и все остальное , это не очень сложная вещь. Итак, вот общих, ясных и понятных заметок по одному и тому же. Вот график для нормальной логарифмической функции:

Фото Ellywa из nl, из Wikimedia Commons, под лицензией Creative Commons Attribution-Share Alike 3.0 Unported.
Итак, сегодня я попытаюсь объяснить некоторые общие принципы , касающиеся логарифма и его использования. , я постараюсь сделать это руководство максимально точным и ясным.

Это руководство будет особенно полезным для студентов, которые недавно присоединились к классу 11 , особенно в Индии.

Я также приведу пример, чтобы изучить использование / применение логарифмов , чтобы вы могли узнать его силу.

Короче говоря, это все, что вам нужно знать о логарифмах и антилогарифмах (но не так много, как вики!): P
БАЗА И СТОИМОСТЬ

Логарифм — не очень сложная вещь для понимания (как и все остальное!).

Прежде чем изучать логарифмы, нам потребуется информация о терминах «От основания к» и «Ценность», которые я назвал.: P lol!

Логарифм и антилогарифмы имеют дело с 3 видами чисел, я называю их «основанием для», «значением» и «ответом». «База до» относится к основному условному обозначению или используемому числу.

«Значение» относится к логарифмическому значению, используемому для конкретного «Основания для».

Например,
журнал _b v = a

Здесь b = Base To, v = value, a = ответ, который мы получаем.

«База» остается в основном такой же, но «ценность» в основном меняется.

Наиболее распространенные «Base To» :
1. e (показатель степени), который похож на π (круговая диаграмма), но не имеет постоянного значения. Оно изменяется как e ^x , где «x» — любое рациональное число.

2. 10 — это число 10, которое мы используем.

Подобно логарифмам, антилогарифмы также имеют основание и значение, они просто дают значение, противоположное логарифмам, т.е. чей логарифм был вычислен (вы узнаете расчет позже в этой статье).

ЧТО ТАКОЕ ЛОГАРИФМЫ И АНТИЛОГАРИФМЫ

Фото: ddpavumba / Freedigitalphotos.нетто

Итак, теперь, когда мы знаем «основание» и «значение», мы можем видеть логарифмы.

Например, вас просят подсчитать:

Antilog (al) ₁₀ 3, тогда будет равно:

Antilog (al) ₁₀ 3 = 10 ³

^{Аналогично}

Antilog (al) _e 4 = e ^4.

^{Теперь Логарифм — это число, связанное с противоположностью антилогарифма, где «Основание для» остается прежним и наоборот. Например,}

По сравнению с примерами выше,

Логарифм (журнал) ₁₀ 10 ³ = 3

И

Логарифм (журнал) _e e ⁴ = 4.

НЕДВИЖИМОСТЬ

Итак, теперь вы будете использовать свойства логарифмов (журналов), чтобы использовать его мощность.

Некоторые свойства логарифмов:

Примечание: они применимы не только для 3 и 4, но и для всех рациональных чисел.

1. Логарифм (log) (3 * 4) = Логарифм (log) 3 + Логарифм (log) 4, где «основание до» остается неизменным с обеих сторон уравнения и может иметь любое рациональное значение.

2. Log (3/4) = Log 3 — Log 4, , где «основание до» остается неизменным с обеих сторон уравнения и может иметь любое рациональное значение.

3. Log (3 ⁴ ) = 4 * Log 3 , , где «основание до» остается одинаковым для обеих сторон уравнения и может иметь любое рациональное значение.

Подсказка: вы также можете использовать обратные уравнения.
Примечание: они не применяют антилогарифмы.

РАСЧЕТЫ С ИСПОЛЬЗОВАНИЕМ ЛОГАРИФМИЧЕСКОЙ ТАБЛИЦЫ (Таблица журнала)

Теперь, когда мы знаем логарифмические свойства, хорошо, если вы их поняли, , так что давайте начнем с использования таблиц журнала.

Таблицы журнала используют журнал ₁₀ v, поэтому я не буду писать здесь «База для», т.е. они дадут вам основу для ответа 10 журнала.

Примеры, которые я буду использовать ниже, дадут вам полную ясность по теме, так что это золотых примера, и их нужно увидеть.

Расчет логов

Учтите, что при вычислении журналов (не антилогов!) Мы используем научную нотацию, то есть десятичное число стоит только после одного числа. Но мы получаем ответ в ненаучной нотации.

Рассмотрим:

ПРИМЕР 1 . Журнал (0,8372) {База до 10 запомнить!}

запишем в научных обозначениях:

= Журнал (8,372 * 10 <sup>-1).

Теперь воспользуемся свойством логов.</sup>

= -1 + Лог (8.372)

————————————————— ————————————————— ———

Теперь мы найдем журнал (8.372), используя таблицу журналов. Процедура будет такой же для нахождения значений (в таблице) антилогов, касательных, синусов и т. Д. Однако законы и свойства будут другими.




В таблице сначала найдите 83 (для примера выше) в столбцах первого типа, затем найдите значение под 7 для 83 во втором типе столбцов и затем найдите значение 2 для 83 в столбцах третьего типа.

Теперь сложите все 3 значения, вы получите необходимое основание логарифма до 10.

9227 + 1

журнал (8,372) = 0,9228

————————————————— ————————————————— ———
Теперь в приведенном выше примере

журнал (0.8372) = -1 + Лог (8,372)
= -1 + 0,9228
= -0,0772

Что, если нам нужно значение Log _e вместо Log ₁₀ , используя таблицу логарифмов.

Так выучите правило,
Лог _e = 2.303 Лог ₁₀

Расчет антилогов

А сейчас я научу вас антилогам, и еще один золотой пример — .

ПРИМЕР 2 .Рассчитайте Antilog (86,654), используя антилогарифмическую таблицу.

Теперь для этого,

Antilog (86,654) = 10 ^86,654
А можно ли рассчитать напрямую?
Нет, конечно нет.

Поэтому используйте этот метод:


Примечание. В Antilogs мы используем ненаучную нотацию, но получаем ответ в научной нотации.

Примечание: в таблицах указано «База на 10».

Аl (86.654) = 10 ⁸⁶ * Al (0,654)

Теперь используйте антилогарифмическую таблицу так же, как описано в примере 1.

Ответ: 4,508 * 10 ⁸⁶

. Расчет антиблокировок (особый случай)

Знаете ли вы, что мы также можем вычислить Antilogs отрицательных чисел , вот еще один золотой пример, который научит вас тому же.

ПРИМЕР 3 . Antilog (-8,654) с использованием антилогарифмической таблицы.

Теперь для отрицательных чисел используйте целое число рядом с данным числом, сложите и вычтите его, математический трюк.

Al (-8,654) = Al (+9-9-8,654)

Теперь +9-8,654 дает 0,346

= Al (-9 +0,346)

= Al (0,346) * 10 ^-9

Теперь из антилогарифмической таблицы вычислите Al (0,346).

Следовательно, ответ: 2.218 * 10 ^-9

НЕКОТОРЫЕ ВАЖНЫЕ МОМЕНТЫ

Итак, здесь у меня есть необходимые золотые (или серебряные: P) точки , которые на самом деле иногда путают.
Я также суммировал важные моменты, упомянутые ранее в , так что вам, возможно, не придется перечислять их отдельно.
1. Таблицы (как журналы, так и антиблоги) имеют базу 10.

2. Если мы используем лог _и , он называется натуральным логарифмом (или ln).

3. Log _e () = 2.303 Log ₁₀ () = Ln ()

4. Процедура, выполняемая для получения значений логарифмов, антилогарифмов, синусов, тангенсов, котангетов и т. Д., Такая же, как в типичной логарифмической книге

5.Логарифмы не могут быть отрицательными, тогда как антилогарифмы могут иметь отрицательные значения.
И в целом для их ответов верно обратное. В журналах могут быть отрицательные ответы, а в антилогах — нет.

6. При вычислении журналов (не антилогов!) Мы используем научную нотацию, то есть десятичное число стоит только после одного числа. Но мы получаем ответ в ненаучной нотации.

7. В Antilogs мы используем ненаучную нотацию, но получаем ответ в научной нотации.

8.В свойствах журналов не применяются антилогарифмы.

9. Общий вид журналов:

журнал _b v = a

Здесь b = Base To, v = value, a = ответ, который мы получаем.

10. Журнал 1 с любым «Base to» равен нулю 0.

Log _x x = 1, здесь x может быть 10, e или любым другим натуральным числом.

ПРАКТИЧЕСКИЕ ПРИМЕНЕНИЯ

Итак, здесь я приведу практический пример использования логарифмов, чтобы вы могли убедиться в силе журналов.


ПРИМЕР 4 . Вычислить 245 x 35


Применение логарифмов дает
журнал (245 x 35) = журнал 245 + журнал 35
= журнал (2,45 x 10 ² ) + журнал (3,5 x 10 ¹ )
= журнал 2,45 + журнал 10 ² + журнал 3,5 + журнал 10 ¹
= 0,3892 + 2 + 0,5441 + 1
= 3.9333

Следовательно, 245 x 35 = al (3.9333) = 8576

Фактически LHS 245 x 35 = 8575
, что достаточно близко! Не так ли?

А если у вас с собой бортовой журнал, а калькулятора нет, то рассчитывать не нужно!

Примечание: я не несу ответственности за точную информацию, вы можете подтвердить ее из любого другого места.Это тезис.

Пожалуйста, ответьте своими комментариями. Даже «Спасибо» будет достаточно, чтобы я знал, что смог вам помочь. Вы также можете оставить свои вопросы или отзывы.

Фото Бойанс Чо Джу Ён / Freedigitalphotos.net

Надеюсь, Вы узнали и поняли вышеизложенное и получили ясность по теме.

НАСЛАЖДАЙТЕСЬ !!!

,