Z числа: Целое число — Википедия – Целые числа: общее представление

Целое число — Википедия

Целые числа — расширение множества натуральных чисел^[1], получаемое добавлением к нему нуля и отрицательных чисел^[2]. Необходимость рассмотрения целых чисел продиктована невозможностью в общем случае вычесть из одного натурального числа другое — можно вычитать только меньшее число из большего. Введение нуля и отрицательных чисел делает вычитание такой же полноценной операцией, как сложение^[3].

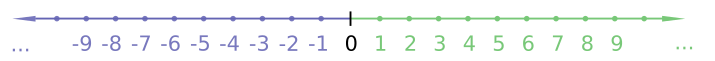
Вещественное число является целым, если его десятичное представление не содержит дробной части (но может содержать знак). Примеры вещественных чисел:

Числа 142857; 0; −273 являются целыми.

Числа 5½; 9,75 не являются целыми.

Множество целых чисел обозначается Z{\displaystyle \mathbb {Z} } (от нем. Zahlen — «числа»^[4]). Изучением свойств целых чисел занимается раздел математики, называемый теорией чисел.

Положительные и отрицательные числа[править | править код]

Согласно своему построению, множество целых чисел состоит из трёх частей:

1. Натуральные числа (или, что то же самое, целые положительные). Они возникают естественным образом при счёте (1, 2, 3, 4, 5…)^[5].
2. Ноль — число, обозначаемое 0{\displaystyle 0}. Его определяющее свойство: 0+n=n+0=n{\displaystyle 0+n=n+0=n} для любого числа n{\displaystyle n}.
3. Целые отрицательные числа.

Противоположные числа (4 и –4)

Отрицательные числа при записи помечаются спереди знаком минус: −1,−2,−3…{\displaystyle -1,-2,-3\dots } Для каждого целого числа a{\displaystyle a} существует и единственно

противоположное ему число, обозначаемое −a{\displaystyle -a} и обладающее тем свойством, что a+(−a)=0.{\displaystyle a+(-a)=0.} Если a{\displaystyle a} положительно, то противоположное ему отрицательно, и наоборот. Ноль противоположен самому себе^[2].

Абсолютной величиной целого числа a{\displaystyle a} называется это число с отброшенным знаком^[6]. Обозначение: |a|.{\displaystyle \left|a\right|.}

Примеры: |4|=4; |−5|=5; |0|=0{\displaystyle \left|4\right|=4;\ \left|-5\right|=5;\ \left|0\right|=0}

Во множестве целых чисел определены три основные арифметические операции: сложение, обратное к сложению вычитание и умножение. Имеется также важная операция, специфическая для натуральных и целых чисел: деление с остатком. Наконец, для целых чисел определён порядок, позволяющий сравнивать числа друг с другом.

Сложение и вычитание[править | править код]

Следующая таблица иллюстрирует основные свойства сложения^[7] для любых целых a,b,c{\displaystyle a,b,c}:

При сложении и вычитании целых чисел выполняются следующие правила знаков^[7][8], которые следует учитывать при раскрытии скобок:

−(−a)=a; −(a+b)=−a−b; −(a−b)=−a+b.{\displaystyle -\left(-a\right)=a;\ -\left(a+b\right)=-a-b;\ -\left(a-b\right)=-a+b.}

Правила сложения целых чисел^[9].

1. При сложении целых чисел с одинаковыми знаками надо сложить их абсолютные величины и приписать ей знак слагаемых. Пример; −14+(−28)=−42{\displaystyle -14+\left(-28\right)=-42}.
2. При сложении целых чисел с разными знаками надо сравнить их абсолютные величины, из большей вычесть меньшую и приписать результату знак того слагаемого, у которого абсолютная величина больше. Примеры: −4+9=9−4=5; −9+4=−(9−4)=−5{\displaystyle -4+9=9-4=5;\ -9+4=-\left(9-4\right)=-5}.
3. Вычитание a−b{\displaystyle a-b} для целых чисел всегда выполнимо, и результат можно найти как a+(−b).{\displaystyle a+\left(-b\right).} Пример: 26−51=26+(−51)=−25{\displaystyle 26-51=26+\left(-51\right)=-25}.
4. Геометрически сложение можно наглядно представить как смещение числа вдоль числовой оси (см. рисунок в начале статьи), причём прибавление положительного числа вызывает смещение направо, а отрицательного — налево. Например, для числа −3{\displaystyle -3} прибавление к нему 4{\displaystyle 4} означает смещение его вправо на 4 единицы; наглядно видно, что получается +1{\displaystyle +1}. Аналогично −3+(−4){\displaystyle -3+\left(-4\right)}, смещая −3{\displaystyle -3} влево на 4 единицы, получим в результате −7{\displaystyle -7}.
5. Вычитание можно наглядно представить аналогично, но в этом случае, наоборот, вычитание положительного числа вызывает смещение влево, а отрицательного — вправо. Например, 5−7{\displaystyle 5-7} смещает 5{\displaystyle 5} на 7 единиц к числу −2{\displaystyle -2}, а 5−(−7){\displaystyle 5-\left(-7\right)} смещает его вправо к числу 12{\displaystyle 12}.

Умножение и возведение в степень[править | править код]

Умножение чисел a,b{\displaystyle a,b} далее обозначается a×b{\displaystyle a\times b} или (только в случае буквенных обозначений) просто ab{\displaystyle ab}. Следующая таблица иллюстрирует основные свойства умножения^[7] для любых целых a,b,c{\displaystyle a,b,c}:

При умножении целых чисел выполняются правила знаков^[7][8], которые следует учитывать при раскрытии скобок:

(−a)b=a(−b)=−ab; (−a)(−b)=ab{\displaystyle \left(-a\right)b=a\left(-b\right)=-ab;\ \left(-a\right)\left(-b\right)=ab}

Следствие: произведение чисел с одинаковыми знаками положительно, с разными — отрицательно.

Возведение в натуральную степень целых чисел определяется так же, как и для натуральных чисел:

an=a⋅a⋅…⋅a⏟n{\displaystyle a^{n}=\underbrace {a\cdot a\cdot \ldots \cdot a} _{n}}

Свойства возведения в степень целых чисел также такие же, как у натуральных:

(ab)n=anbn;aman=am+n;(am)n=amn{\displaystyle \left(ab\right)^{n}=a^{n}b^{n};\quad a^{m}a^{n}=a^{m+n};\quad \left(a^{m}\right)^{n}=a^{mn}}

В дополнение к этому определению, принято соглашение о нулевой степени: a0=1{\displaystyle a^{0}=1} для любого целого a.{\displaystyle a.} Основанием для такого соглашения служит желание сохранить приведенные выше свойства и для нулевого показателя степени: a0an=a0+n=an,{\displaystyle a^{0}a^{n}=a^{0+n}=a^{n},} откуда ясно, что a0=1.{\displaystyle a^{0}=1.}

Упорядоченность[править | править код]

Z{\displaystyle \mathbb {Z} } — линейно упорядоченное множество. Порядок в нём задаётся соотношениями:

⋯−2<−1<0<1<2<…{\displaystyle \dots -2<-1<0<1<2<\dots }

Целое число положительно, если оно больше нуля, отрицательно, если меньше нуля. Положительными целыми числами являются натуральные числа и только они. Отрицательные числа — это числа, противоположные положительным. Ноль не является ни положительным, ни отрицательным. Любое отрицательное число меньше любого положительного^[2].

Для любых целых чисел a,b,c,d{\displaystyle a,b,c,d} справедливы следующие соотношения^[10].

1. Если a<b{\displaystyle a<b}, то для любого c{\displaystyle c} будет a+c<b+c{\displaystyle a+c<b+c}.
2. Если a<b{\displaystyle a<b} и c<d{\displaystyle c<d}, то a+c<b+d{\displaystyle a+c<b+d}.
3. Если a<b{\displaystyle a<b} и c>0{\displaystyle c>0}, то ac<bc{\displaystyle ac<bc}.
4. Если a<b{\displaystyle a<b} и c<0{\displaystyle c<0}, то ac>bc{\displaystyle ac>bc}.

Для сравнения двух отрицательных чисел существует правило: больше то число, у которого абсолютная величина меньше^[10]. Например, −6<−5{\displaystyle -6<-5}.

Делимость[править | править код]

Деление с остатком[править | править код]

Операция деления, вообще говоря, не определена на множестве целых чисел. Например, нельзя разделить 3{\displaystyle 3} на 2{\displaystyle 2} — нет такого целого числа, которое, умноженное на 2{\displaystyle 2}, даст 3{\displaystyle 3}. Но можно определить так называемое деление с остатком^[11]:

Для любых целых a,b{\displaystyle a,b} (где b≠0{\displaystyle b\neq 0}) существует единственный набор целых чисел q,r{\displaystyle q,r} такой, что a=bq+r{\displaystyle a=bq+r}, где 0⩽r<|b|.{\displaystyle 0\leqslant r<\left|b\right|.}

Здесь a — делимое, b — делитель, q — (неполное) частное, r — остаток от деления (всегда неотрицателен). Если остаток равен нулю, говорят, что деление выполняется нацело^[11].

Примеры

На операции деления с остатком основаны теория сравнений и алгоритм Евклида.

Деление нацело. Делители[править | править код]

Как определено выше, число a{\displaystyle a} делится (нацело) на число b{\displaystyle b}, если существует целое число q{\displaystyle q} такое, что a=bq{\displaystyle a=bq}. Символическая запись: b|a{\displaystyle b|a}. Существуют несколько равносильных словесных формулировок указанной делимости^[12]:

Каждое целое число n{\displaystyle n}, не равное нулю или ±1{\displaystyle \pm 1}, имеет 4 тривиальных делителя: 1,−1,n,−n{\displaystyle 1,-1,n,-n}. Если других делителей нет, число называется простым^[13].

Понятие наибольшего общего делителя двух целых чисел, разложение целого числа на простые множители и основная теорема арифметики для целых чисел практически совпадают (с возможным учётом знака) с аналогами этих понятий для натуральных чисел^[14].

Существуют практические задачи, в которых необходимо округлить вещественное значение до целого, то есть заменить его на ближайшее (в ту или иную сторону) целое. Поскольку выполнять округление можно разными способами, для уточнения можно использовать «символы Айверсона»^[15]:

⌊x⌋{\displaystyle \lfloor x\rfloor } — ближайшее к x{\displaystyle x} целое в меньшую сторону (функция «пол», англ. floor, или «целая часть»). Традиционно используются также обозначение Гаусса [x]{\displaystyle [x]} или обозначение Лежандра E(x){\displaystyle E\left(x\right)}.

⌈x⌉{\displaystyle \lceil x\rceil } — ближайшее к x{\displaystyle x} целое в бо́льшую сторону (функция «потолок», англ. ceiling).

В зависимости от особенностей постановки задачи, могут встретиться и другие методы: округлить до ближайшего целого или отсечь дробную часть (последний вариант для отрицательных x{\displaystyle x} отличается от функции «целая часть»).

Другой класс задач, связывающих целые и вещественные числа — приближение вещественного числа отношением целых, то есть рациональным числом. Доказано, что любое вещественное число можно с любой желаемой точностью приблизить рациональным, наилучшим инструментом для такого приближения служат непрерывные (цепные) дроби^[16].

Развитие математики началось с навыков практического счёта (один, два, три, четыре…), поэтому натуральные числа возникли ещё в доисторический период как идеализация конечного множества однородных, устойчивых и неделимых предметов (людей, овец, дней и т. п.). Сложение появилось как математическая модель таких важных событий, как объединение нескольких множеств (стад, мешков и т. д.) в одно, а вычитание отражало, наоборот, отделение части множества. Умножение для натуральных чисел появилось в качестве, так сказать, пакетного сложения: 3 × 4 означало сумму «3 раза по 4», то есть 4 + 4 + 4. Свойства и взаимосвязь операций открывались постепенно^[17][18].

Начальным шагом на пути расширения натуральных чисел стало появление нуля; первыми этот символ стали применять, по-видимому, индийские математики. Вначале ноль применялся не как число, а как цифра при позиционной записи чисел, затем постепенно стал признаваться и как полноценное число, обозначающее отсутствие чего-либо (например, полное разорение торговца)^[19].

Отрицательные числа впервые стали использовать в древнем Китае и в Индии, где их рассматривали как математический образ «долга». Древний Египет, Вавилон и Древняя Греция не использовали отрицательных чисел, а если получались отрицательные корни уравнений (при вычитании), они отвергались как невозможные. Исключение составлял Диофант, который в III веке уже знал «правило знаков» и умел умножать отрицательные числа. Однако он рассматривал их лишь как промежуточный этап, полезный для вычисления окончательного, положительного результата. Полезность и законность отрицательных чисел утверждались постепенно. Индийский математик Брахмагупта (VII век) уже рассматривал их наравне с положительными

[20].

В Европе признание наступило на тысячу лет позже, да и то долгое время отрицательные числа называли «ложными», «мнимыми» или «абсурдными». Первое описание их в европейской литературе появилось в «Книге абака» Леонарда Пизанского (1202 год), который также трактовал отрицательные числа как долг. Бомбелли и Жирар в своих трудах считали отрицательные числа вполне допустимыми и полезными, в частности, для обозначения нехватки чего-либо. Свободно использовали отрицательные числа Никола Шюке (1484 год) и Михаэль Штифель (1544)^[20].

В XVII веке, с появлением аналитической геометрии, отрицательные числа получили наглядное геометрическое представление на числовой оси. С этого момента наступает их полное равноправие. Легализация отрицательных чисел привела к многочисленным удобствам — например, перенос слагаемых уравнения в другую его часть стал возможен независимо от знака этого слагаемого (ранее, скажем, уравнения x3+ax=b{\displaystyle x^{3}+ax=b} и x3=ax+b{\displaystyle x^{3}=ax+b} считались принципиально различными)

[21].

Тем не менее теория отрицательных чисел долго находилась в стадии становления. Паскаль, например, считал, что 0−4=0{\displaystyle 0-4=0}, так как «ничто не может быть меньше, чем ничто»^[22]. Оживлённо обсуждалась странная пропорция 1:(−1)=(−1):1{\displaystyle 1:\left(-1\right)=\left(-1\right):1} — в ней первый член слева больше второго, а справа — наоборот, и получается, что большее равно меньшему («парадокс Арно»). Валлис считал, что отрицательные числа меньше нуля, но в то же время больше, чем бесконечность^[23]. Непонятно было также, какой смысл имеет умножение отрицательных чисел, и почему произведение отрицательных положительно; на эту тему проходили жаркие дискуссии. Отголоском тех времён является то обстоятельство, что в современной арифметике операция вычитания и знак отрицательных чисел обозначаются одним и тем же символом (минус), хотя алгебраически это совершенно разные понятия. Гаусс в 1831 году считал нужным разъяснить, что отрицательные числа принципиально имеют те же права, что и положительные, а то, что они применимы не ко всем вещам, ничего не означает, потому что дроби тоже применимы не ко всем вещам (например, неприменимы при счёте людей)^[24].

Полная и вполне строгая теория отрицательных чисел была создана только в XIX веке (Уильям Гамильтон и Герман Гюнтер Грассман)^[25].

В прикладных науках[править | править код]

Целые числа: общее представление

В данной статье определим множество целых чисел, рассмотрим, какие целые называются положительными, а какие отрицательными. Также покажем, как  целые числа используются для описания изменения некоторых величин. Начнем с определения и примеров целых чисел.

Целые числа. Определение, примеры

Вначале вспомним про натуральные числа ℕ. Само название говорит о том, что это такие числа, которые естественно использовались для счета с незапамятных времен. Для того, чтобы охватить понятие целых чисел, нам нужно расширить определение натуральных чисел.

Определение 1. Целые числа

Целые числа — это натуральные числа, числа, противоположные им, и число нуль. 

Множество целых чисел обозначается буквой ℤ.

Множество натуральных чисел ℕ — подмножество целых чисел ℤ. Любое натуральное число является целым, но не любое целое число является натуральным.

Из определения следует, что целым является любое из чисел 1, 2, 3.., число 0, а также числа -1, -2, -3,..

В соответствии с этим, приведем примеры. Числа 39, -589, 10000000, -1596, 0 являются целыми числами.

Целые числа и координатная прямая

Пусть координатная прямая проведена горизонтально и направлена вправо. Взглянем на нее, чтобы наглядно представить расположение целых чисел на прямой.

Началу отсчета на координатной прямой соответствует число 0, а точкам, лежащим по обе стороны от нуля соответствуют положительные и отрицательные целые числа. Каждой точке соответствует единственное целое число. 

В любую точку прямой, координатой которой является целое число, можно попасть, отложив от начала координат некоторое количество единичных отрезков.

Положительные и отрицательные целые числа

Из всех целых чисел логично выделить положительные и отрицательные целые числа. Дадим их определения.

Определение 2. Положительные целые числа

Положительные целые числа — это целые числа со знаком «плюс».

Например, число 7 — целое число со знаком плюс, то есть положительное целое число. На координатной прямой это число лежит справа от точки отсчета, за которую принято число 0. Другие примеры положительных целых чисел: 12, 502, 42, 33, 100500.

Определение 3. Отрицательные целые числа

Отрицательные целые числа — это целые числа со знаком «минус».

Примеры целых отрицательных чисел: -528, -2568, -1.

Число 

Целые числа. Определение. | tutomath

Существуют множество разновидностей чисел, одни из них – это целые числа. Целые числа появились для того, чтобы облегчить счет не только в положительную сторону, но и в отрицательную.

Рассмотрим пример:
Днем на улице была температура 3 градуса. К вечеру температура снизилась на 3 градуса.
3-3=0
На улице стало 0 градусов. А ночью температура снизилась на 4 градуса и стало показывать на термометре -4 градуса.
0-4=-4

Ряд целых чисел.

Натуральными числами мы такую задачу описать мы не сможем, рассмотрим эту задачу на координатной прямой.

У нас получился ряд чисел:
…, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, …

Этот ряд чисел называется рядом целых чисел.

Целые положительные числа. Целые отрицательные числа.

Ряд целых чисел состоит из положительных и отрицательных чисел. Справа от нуля идут натуральные числа или их еще называют целыми положительными числами. А слева от нуля идут целые отрицательные числа.

Нуль не является ни положительным ни отрицательным числом. Он является границей между положительными и отрицательными числами.

Целые числа – это множество чисел, состоящие из натуральных чисел, целых отрицательных чисел и нуля.

Ряд целых чисел в положительную и в отрицательную сторону является бесконечным множеством.

Если мы возьмём два любых целых числа, то числа, стоящие между этими целыми числами, будут называться конечным множеством.

Например:
Возьмем целые числа от -2 до 4. Все числа, стоящие между этими числами, входят в конечное множество. Наше конечное множество чисел выглядит так:
-2, -1, 0, 1, 2, 3, 4.

Натуральные числа обозначаются латинской буквой N.
Целые числа обозначаются латинской буквой Z. Все множество натуральных чисел и целых чисел можно изобразить на рисунке.

Неположительные целые числа другими словами – это отрицательные целые числа.
Неотрицательные целые числа – это положительные целые числа.

Вопросы по теме:
Как называются числа, находящиеся в ряду целых чисел: а) справа от нуля; б) слева от нуля?
Ответ: а) натуральные числа или целые положительные числа. Оба термина несут один и тот же смысл.
б) целые отрицательные числа.

Назовите наибольшее целое число?
Ответ: ряд положительных целых чисел бесконечен, поэтому наибольшего целого числа не существует.

Какое наименьшее целое число?
Ответ: ряд отрицательных чисел бесконечен, поэтому наименьшего целого числа не существует.

Пример №1:
Сколько целых чисел расположено между числами -33 и 102?
Решение:
У нас 32 отрицательных числа, есть нуль и 101 положительных чисел.
32+1+101=134
Ответ: 134

Пример №2:
Приведите пример целого числа.
Целое число: -16523, -100, -1, 0, 1, 2, 3, 4, 5, 6, 7, 1009, 1984.

Пример №3:
Сколько четных целых чисел расположено между числами -4 и 5?
Ответ: -2, 2, 4.

Числа: натуральные, целые, рациональные, иррациональные, действительные, комплексные

Тестирование онлайн

• Округление чисел

Натуральные числа

Это числа, которые используются при счете: 1, 2, 3… и т.д.

Ноль не является натуральным.

Натуральные числа принято обозначать символом N.

Целые числа. Положительные и отрицательные числа

Два числа отличающиеся друг от друга только знаком, называются противоположными, например, +1 и -1, +5 и -5. Знак «+» обычно не пишут, но предполагают, что перед числом стоит «+». Такие числа называются положительными. Числа, перед которыми стоит знак «-«, называются отрицательными.

Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.

Рациональные числа

Это конечные дроби и бесконечные периодические дроби . Например,

Множество рациональных чисел обозначается Q. Все целые числа являются рациональными.

Иррациональные числа

Бесконечная непериодическая дробь называется иррациональным числом. Например:

Множество иррациональных чисел обозначается J.

Действительные числа

Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.

Действительные числа обозначаются символом R.

Округление чисел

Рассмотрим число 8,759123… . Округлить до целой части означает записать лишь ту часть числа, которая находится до запятой. Округлить до десятых означает записать целую часть и после запятой одну цифру; округлить до сотых — после запятой две цифры; до тысячных — три цифры и т.д.

Округлить 8,759123… с точностью до целой части.

Округлить 8,759123… с точностью до десятой части.

Округлить 8,759123… с точностью до сотой части.

Округлить 8,759123… с точностью до тысячной части.

Целые числа

К целым числам относятся натуральные числа, ноль, а также числа, противоположные натуральным.

Натуральные числа — это положительные целые числа.

Латинской буквой \( \mathbb{Z} \) обозначается множество целых чисел.

К примеру: 1, 3, 7, 19, 23 и т.д. Такие числа мы используем для подсчета (на столе лежит 5 яблок, у машины 4 колеса и др.)

Латинской буквой \( \mathbb{N} \) — обозначается множество натуральных чисел.

К натуральным числам нельзя отнести отрицательные (у стула не может быть отрицательное количество ножек) и дробные числа (Иван не мог продать 3,5 велосипеда).

Числами, противоположными натуральным, являются отрицательные целые числа: −8, −148, −981, … . 

Арифметические действия с целыми числами

Что можно делать с целыми числами? Их можно перемножать, складывать и вычитать друг из друга. Разберем каждую операцию на конкретном примере.

Сложение целых чисел

Два целых числа с одинаковыми знаками складываются следующим образом: производится сложение модулей этих чисел и перед полученной суммой ставится итоговый знак:

\( (+11) + (+9) = +20 \)

Вычитание целых чисел

Два целых числа с разными знаками складываются следующим образом: из модуля большего числа вычитается модуль меньшего и перед полученным ответом ставят знак большего по модулю числа:

\( (-7) + (+8) = +1 \)

Умножение целых чисел

Чтобы умножить одно целое число на другое нужно выполнить перемножение модулей этих чисел и поставить перед полученным ответом знак «+», если исходные числа были с одинаковыми знаками, и знак «−», если исходные числа были с разными знаками:

\( (-5) \cdot (+3) = -15 \)

\( (-3) \cdot (-4) = +12 \)

Следует запомнить следующее

правило перемножения целых чисел:

\( + \cdot + = + \)

\( + \cdot — = — \)

\( — \cdot + = — \)

\( — \cdot — = + \)

Существует правило перемножения нескольких целых чисел. Запомним его:

Знак произведения будет «+», если количество множителей с отрицательным знаком четное и «−», если количество множителей с отрицательным знаком нечетное.

\( (-5) \cdot (-4) \cdot (+1) \cdot (+6) \cdot (+1) = +120 \)

Деление целых чисел

Деление двух целых чисел производится следующим образом: модуль одного числа делят на модуль другого и если знаки чисел одинаковые, то перед полученным частным ставят знак «+», а если знаки исходных чисел разные, то ставится знак «−».

\( (-25) : (+5) = -5 \)

Свойства сложения и умножения целых чисел

Разберем основные свойства сложения и умножения для любых целых чисел \( a \), \( b \) и \( c \):

1. \( a + b = b + a \) – переместительное свойство сложения;
2. \( (a + b) + c = a + (b + c) \) – сочетательное свойство сложения;
3. \( a \cdot b = b \cdot a \) – переместительное свойство умножения;
4. \( (a \cdot c) \cdot b = a \cdot (b \cdot c) \) – сочетательное свойства умножения;
5. \( a \cdot (b \cdot c) = a \cdot b + a \cdot c \) – распределительное свойство умножения.

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Не можешь написать работу сам?

Доверь её нашим специалистам

от 100 р.стоимость заказа

2 часамин. срок

Узнать стоимость

Множество натуральных чисел — N, множество целых чисел Z, множество рациональных чисел Q, множество иррациональные чисел, множество действительных = вещественных чисел R. Понятия и обозначения, русский и английский = международный подходы. Обозначения

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа.  / / Множество натуральных чисел — N, множество целых чисел Z, множество рациональных чисел Q, множество иррациональные чисел, множество действительных = вещественных чисел R. Понятия и обозначения, русский и английский = международный подходы. Обозначения Поделиться:    Действительные (= вещественные) числа R: натуральные числа — множество N, целые числа — множество Z, рациональные числа — множество Q, иррациональные числа — множество R. Понятия и обозначения. Поиск в инженерном справочнике DPVA. Введите свой запрос:

Целые числа — это… Что такое Целые числа?

Множество целых чисел 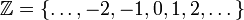определяется как замыкание множества натуральных чисел 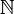относительно арифметических операций сложения (+) и вычитания (-). Таким образом, сумма, разность и произведение двух целых чисел есть снова целые числа. Оно состоит из положительных натуральных чисел (1, 2, 3), чисел вида -n (n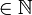) и числа нуль.

Необходимость рассмотрения целых чисел продиктована невозможностью (в общем случае) вычесть из одного натурального числа другое. Целые числа являются кольцом относительно операций сложения и умножения.

Отрицательные числа ввёл в математический обиход Михаэль Штифель (M. Stiffel), 1487—1567), в книге «Полная арифметика» 1544 года, и Никола Шюке (N. Chuquet, 1445—1500) — его работа была обнаружена в 1848 году.

Алгебраические свойства

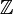не замкнуто относительно деления двух целых чисел (например, 1/2). Следующая таблица иллюстрирует несколько основных свойств сложения и умножения для любых целых a, b и c.

На языке абстрактной алгебры первые пять вышеперечисленных свойств сложения говорят о том, что 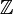является абелевой группой относительно бинарной операции сложения, и, следовательно, также циклической группой, так как каждый ненулевой элемент 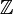может быть записан в виде конечной суммы 1 + 1 + … 1 или (−1) + (−1) + … + (−1). Фактически, 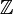является единственной бесконечной циклической группой по сложению в силу того, что любая бесконечная циклическая группа изоморфна группе .

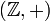Первые четыре свойства умножения говорят о том, что 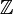— коммутативный моноид по умножению. Однако стоит заметить, что не каждое целое имеет противоположное по умножению, например, нет такого x из 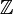, что 2x = 1, так как левая часть уравнения четна, а правая нечетна. Из этого следует, что 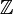не является группой по умножению, а также не является полем. Наименьшее поле, содержащее целые числа, — множество рациональных цисел ().

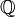Совокупность всех свойств таблицы означает, что 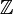является коммутативным кольцом с единицей относительно сложения и умножения.

Обычное деление не определено на множестве целых чисел, но определено так называемое деление с остатком: для любых целых a и b, 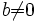, существует единственный набор целых чисел q и r, что a = bq + r и 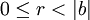, где |b| — абсолютная величина (модуль) числа b. Здесь a — делимое, b — делитель, q — частное, r — остаток. На этой операции основан алгоритм Евклида нахождения наибольшего общего делителя двух целых чисел.

Теоретико-множественные свойства

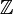— линейно упорядоченное множество без верхней и нижней границ. Порядок в нём задается соотношениями:

… < −2 < −1 < 0 < 1 < 2 < …

Целое число называется положительным, если оно больше нуля, отрицательным, если меньше нуля. Нуль не является положительным или отрицательным.

Для целых чисел справедливы следующие соотношения:

1. если a < b и c < d, тогда a + c < b + d.
2. если a < b и 0 < c, тогда ac < bc. (Отсюда легко показать, что если c < 0, то ac > bc.)

Целые числа в вычислительной технике

Тип целое число — зачастую один из основных типов данных в языках программирования. Тем не менее эти «целые числа» — лишь имитация класса 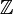в математике, так как это множество бесконечно и всегда найдётся целое число, которое данный компьютер не сможет хранить в своей памяти. Целые типы данных обычно реализуются как фиксированный набор битов, но любые представления в конце концов приведут к тому, что свободное место на носителе (жёстком диске) закончится. С другой стороны, теоретические модели цифровых компьютеров имеют потенциально бесконечное (но счётное) пространство.

См. также

Ссылки

Wikimedia Foundation. 2010.