Примеры на тему логарифмы – Свойства логарифмов и примеры решений

Логарифмы: примеры и решения

Как известно, при перемножении выражений со степенями их показатели всегда складываются (a^b*a^c = a^b+c). Этот математический закон был выведен Архимедом, а позже, в VIII веке, математик Вирасен создал таблицу целых показателей. Именно они послужили для дальнейшего открытия логарифмов. Примеры использования этой функции можно встретить практически везде, где требуется упростить громоздкое умножение на простое сложение. Если вы потратите минут 10 на прочтение этой статьи, мы вам объясним, что такое логарифмы и как с ними работать. Простым и доступным языком.

Определение в математике

Логарифмом называется выражение следующего вида: log_ab=c, то есть логарифмом любого неотрицательного числа (то есть любого положительного) «b» по его основанию «a» считается степень «c», в которую необходимо возвести основание «a», чтобы в итоге получить значение «b». Разберем логарифм на примерах, допустим, есть выражение log₂8. Как найти ответ? Очень просто, нужно найти такую степень, чтобы из 2 в искомой степени получить 8. Проделав в уме некоторые расчеты, получаем число 3! И верно, ведь 2 в степени 3 дает в ответе число 8.

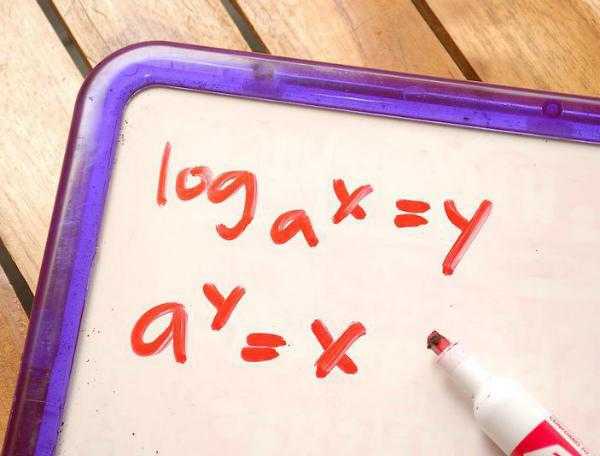
Разновидности логарифмов

Для многих учеников и студентов эта тема кажется сложной и непонятной, однако на самом деле логарифмы не так страшны, главное — понять общий их смысл и запомнить их свойста и некоторые правила. Существует три отдельных вида логарифмических выражений:

1. Натуральный логарифм ln a, где основанием является число Эйлера (e = 2,7).
2. Десятичный логарифм lg a, где основанием служит число 10.
3. Логарифм любого числа b по основанию a>1.

Каждый из них решается стандартным способом, включающим в себя упрощение, сокращение и последующее приведение к одному логарифму с помощью логарифмических теорем. Для получения верных значений логарифмов следует запомнить их свойства и очередность действий при их решениях.

Правила и некоторые ограничения

В математике существует несколько правил-ограничений, которые принимаются как аксиома, то есть не подлежат обсуждению и являются истиной. Например, нельзя числа делить на ноль, а еще невозможно извлечь корень четной степени из отрицательных чисел. Логарифмы также имеют свои правила, следуя которым можно с легкостью научиться работать даже с длинными и емкими логарифмическими выражениями:

• основание «a» всегда должно быть больше нуля, и при этом не быть равным 1, иначе выражение потеряет свой смысл, ведь «1» и «0» в любой степени всегда равны своим значениям;
• если а > 0, то и а^b>0, получается, что и «с» должно быть больше нуля.

Как решать логарифмы?

К примеру, дано задание найти ответ уравнения 10^х= 100. Это очень легко, нужно подобрать такую степень, возведя в которую число десять, мы получим 100. Это, конечно же, квадратичная степень! 10²=100.

А теперь давайте представим данное выражение в виде логарифмического. Получим log₁₀100 = 2. При решении логарифмов все действия практически сходятся к тому, чтобы найти ту степень, в которую необходимо ввести основание логарифма, чтобы получить заданное число.

Для безошибочного определения значенияя неизвестной степени необходимо научиться работать с таблицей степеней. Выглядит она следующим образом:

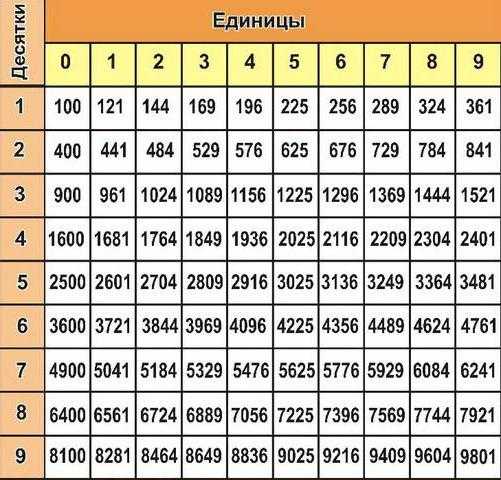
Как видите, некоторые показатели степени можно угадать интуитивно, если имеется технический склад ума и знание таблицы умножения. Однако для больших значений потребуется таблица степеней. Ею могут пользоваться даже те, кто совсем ничего не смыслит в сложных математических темах. В левом столбце указаны числа (основание a), верхний ряд чисел — это значение степени c, в которую возводится число a. На пересечении в ячейках определены значения чисел, являющиеся ответом (a^c=b). Возьмем, к примеру, самую первую ячейку с числом 10 и возведем ее в квадрат, получим значение 100, которое указано на пересечении двух наших ячеек. Все так просто и легко, что поймет даже самый настоящий гуманитарий!

Уравнения и неравенства

Получается, что при определенных условиях показатель степени — это и есть логарифм. Следовательно, любые математические численные выражения можно записать в виде логарифмического равенства. Например, 3⁴=81 можно записать в виде логарифма числа 81 по основанию 3, равному четырем (log₃81 = 4). Для отрицательных степеней правила такие же: 2^-5= 1/32 запишем в виде логарифма, получим log₂ (1/32) = -5. Одной из самых увлекательных разделов математики является тема «логарифмы». Примеры и решения уравнений мы рассмотрим чуть ниже, сразу же после изучения их свойств. А сейчас давайте разберем, как выглядят неравенства и как их отличить от уравнений.

Дано выражение следующего вида: log₂(x-1) > 3 — оно является логарифмическим неравенством, так как неизвестное значение «х» находится под знаком логарифма. А также в выражении сравниваются две величины: логарифм искомого числа по основанию два больше, чем число три.

Самое главное отличие между логарифмическими уравнениями и неравенствами заключается в том, что уравнения с логарифмами (пример — логарифм₂x = √9)_{подразумевают в ответе одно или несколько определенных числовых значений, тогда как при решении неравенства определяются как область допустимых значений, так и точки разрыва этой функции. Как следствие, в ответе получается не простое множество отдельных чисел как в ответе уравнения, а а непрерывный ряд или набор чисел.}

Основные теоремы о логарифмах

При решении примитивных заданий по нахождению значений логарифма, его свойства можно и не знать. Однако когда речь заходит о логарифмических уравнениях или неравенствах, в первую очередь, необходимо четко понимать и применять на практике все основные свойства логарифмов. С примерами уравнений мы познакомимся позже, давайте сначала разберем каждое свойство более подробно.

1. Основное тождество выглядит так: а^logaB=B. Оно применяется только при условии, когда а больше 0, не равно единице и B больше нуля.
2. Логарифм произведения можно представить в следующей формуле: log_d(s₁*s_{2) =} log_ds₁ + log_ds_2. При этом обязательным условием является: d, s₁ и s₂ > 0; а≠1. Можно привести доказательство для этой формулы логарифмов, с примерами и решением. Пусть log_as₁ = f₁ и log_as₂ = f₂, тогда a^f1= s₁, a^f2= s_2. Получаем, что s₁*s₂ = a^f1*a^f2= a^f1+f2 (свойства степеней), а далее по определению: log_a(s₁*s₂)= f₁+ f₂ = log_as1 + log_as_2, что и требовалось доказать.
3. Логарифм частного выглядит так: log_a(s_1/s₂) = log_as₁— log_as_2.
4. Теорема в виде формулы приобретает следующий вид: log_a^q_{bⁿ = n/q logab.}

Называется эта формула «свойством степени логарифма». Она напоминает собой свойства обычных степеней, и неудивительно, ведь вся математика держится на закономерных постулатах. Давайте посмотрим на доказательство.

Пусть log_ab = t, получается a^t=b. Если возвести обе части в степень m: a^tn = bⁿ;

но так как a^tn= (a^q)^nt/q = bⁿ, следовательно log_a^q_{bⁿ = (n*t)/t, тогда loga^qbⁿ = n/q logab. Теорема доказана.}

Примеры задач и неравенств

Самые распространенные типы задач на тему логарифмов — примеры уравнений и неравенств. Они встречаются практически во всех задачниках, а также входят в обязательную часть экзаменов по математике. Для поступления в университет или сдачи вступительных испытаний по математике необходимо знать, как правильно решать подобные задания.

К сожалению, единого плана или схемы по решению и определению неизвестного значения логарифма не существует, однако к каждому математическому неравенству или логарифмическому уравнению можно применить определенные правила. Прежде всего следует выяснить, можно ли упростить выражение или привести к общему виду. Упрощать длинные логарифмические выражения можно, если правильно использовать их свойства. Давайте скорее с ними познакомимся.

При решении же логарифмических уравнений, следует определить, какой перед нами вид логарифма: пример выражения может содержать натуральный логарифм или же десятичный.

Вот примеры десятичных логарифмов: ln100, ln1026. Их решение сводится к тому, что нужно определить ту степень, в которой основание 10 будет равно 100 и 1026 соответственно. Для решений же натуральных логарифмов нужно применить логарифмические тождества или же их свойства. Давайте на примерах рассмотрим решение логарифмических задач разного типа.

Как использовать формулы логарифмов: с примерами и решениями

Итак, рассмотрим примеры использования основных теорем о логарифмах.

1. Свойство логарифма произведения можно применять в заданиях, где необходимо разложить большое значение числа b на более простые сомножители. Например, log₂4 + log₂128 = log₂(4*128) = log₂512. Ответ равен 9.
2. log₄8 = log_2² 2³ = 3/2 log₂2 = 1,5 — как видите, применяя четвертое свойство степени логарифма, удалось решить на первый взгляд сложное и нерешаемое выражение. Необходимо всего лишь разложить основание на множители и затем вынести значения степени из знака логарифма.

Задания из ЕГЭ

Логарифмы часто встречаются на вступительных экзаменах, особенно много логарифмических задач в ЕГЭ (государственный экзамен для всех выпускников школ). Обычно эти задания присутствуют не только в части А (самая легкая тестовая часть экзамена), но и в части С (самые сложные и объемные задания). Экзамен подразумевает точное и идеальное знание темы «Натуральные логарифмы».

Примеры и решения задач взяты из официальных вариантов ЕГЭ. Давайте посмотрим, как решаются такие задания.

Дано log₂(2x-1) = 4. Решение:
перепишем выражение, немного его упростив log₂(2x-1) = 2², по определению логарифма получим, что 2x-1 = 2⁴, следовательно 2x = 17; x = 8,5.

Ниже даны несколько рекомендаций, следуя которым можно с легкостью решать все уравнения, содержащие выражения, которые стоят под знаком логарифма.

• Все логарифмы лучше всего приводить к одному основанию, чтобы решение не было громоздким и запутанным.
• Все выражение, стоящие под знаком логарифма, указываются как положительные, поэтому при вынесении множителем показателя степени выражения, который стоит под знаком логарифма и в качестве его основания, остающееся под логарифмом выражение должно быть положительно.

fb.ru

Логарифмы. Свойства логарифмов. Формулы с логарифмами. Десятичные, натуральные логарифмы, основное логарифмическое тождество

Определение логарифма

Логарифмом положительного числа b по основанию a (a>0, a не равно 1) называют такое число с, что a^c = b: logab=c⇔ac=b(a>0,a≠1,b>0)&nbsp&nbsp&nbsp&nbsp&nbsp&nbsp

Обратите внимание: логарифм от неположительного числа не определен. Кроме того, в основании логарифма должно быть положительное число, не равное 1. Например, если мы возведем -2 в квадрат, получим число 4, но это не означает, что логарифм по основанию -2 от 4 равен 2.

Основное логарифмическое тождество

alogab=b(a>0,a≠1) (2)

Важно, что области определения правой и левой частей этой формулы отличаются. Левая часть определена только при b>0, a>0 и a ≠ 1. Правая часть определена при любом b, а от a вообще не зависит. Таким образом, применение основного логарифмического «тождества» при решении уравнений и неравенств может привести к изменению ОДЗ.

Два очевидных следствия определения логарифма

logaa=1(a>0,a≠1) (3)
loga1=0(a>0,a≠1) (4)

Действительно, при возведении числа a в первую степень мы получим то же самое число, а при возведении в нулевую степень — единицу.

Логарифм произведения и логарифм частного

loga(bc)=logab+logac(a>0,a≠1,b>0,c>0) (5)

logabc=logab−logac(a>0,a≠1,b>0,c>0) (6)

Хотелось бы предостеречь школьников от бездумного применения данных формул при решении логарифмических уравнений и неравенств. При их использовании «слева направо» происходит сужение ОДЗ, а при переходе от суммы или разности логарифмов к логарифму произведения или частного — расширение ОДЗ.

Действительно, выражение loga(f(x)g(x)) определено в двух случаях: когда обе функции строго положительны либо когда f(x) и g(x) обе меньше нуля.

Преобразуя данное выражение в сумму logaf(x)+logag(x), мы вынуждены ограничиваться только случаем, когда f(x)>0 и g(x)>0. Налицо сужение области допустимых значений, а это категорически недопустимо, т. к. может привести к потере решений. Аналогичная проблема существует и для формулы (6).

Степень можно выносить за знак логарифма

logabp=plogab(a>0,a≠1,b>0) (7)

И вновь хотелось бы призвать к аккуратности. Рассмотрим следующий пример:

loga(f(x)2=2logaf(x)

Левая часть равенства определена, очевидно, при всех значениях f(х), кроме нуля. Правая часть — только при f(x)>0! Вынося степень из логарифма, мы вновь сужаем ОДЗ. Обратная процедура приводит к расширению области допустимых значений. Все эти замечания относятся не только к степени 2, но и к любой четной степени.

Формула перехода к новому основанию

logab=logcblogca(a>0,a≠1,b>0,c>0,c≠1) (8)

Тот редкий случай, когда ОДЗ не изменяется при преобразовании. Если вы разумно выбрали основание с (положительное и не равное 1), формула перехода к новому основанию является абсолютно безопасной.

Если в качестве нового основания с выбрать число b, получим важный частный случай формулы (8):

logab=1logba(a>0,a≠1,b>0,b≠1) (9)

Десятичные и натуральные логарифмы

Десятичным логарифмом числа x называется логарифм по основанию 10. Десятичные логарифмы используются довольно часто, поэтому для них введено специальное обозначение: log₁₀x = lg x. Все перечисленные выше формулы сохраняют актуальность для десятичных логарифмов. Например, lg(xy)=lgx+lgy(x>0,y>0).

Натуральным логарифмом числа x (обозначение lnx) называется логарифм х по основанию e. Число e — иррациональное, приближенно равно 2,71. Например, ln e = 1. Пользуясь формулой (8), можно любой логарифм свести к десятичным или натуральным логарифмам: logab=lgblga=lnblna(a>0,a≠1,b>0)

Несколько простых примеров с логарифмами

Пример 1. Вычислите: lg2 + lg50.
Решение. lg2 + lg50 = lg100 = 2. Мы воспользовались формулой суммы логарифмов (5) и определением десятичного логарифма.

Пример 2. Вычислите: lg125/lg5.
Решение. lg125/lg5 = log₅125 = 3. Мы использовали формулу перехода к новому основанию (8).

Таблица формул, связанных с логарифмами

alogab=b(a>0,a≠1)

logaa=1(a>0,a≠1)

loga1=0(a>0,a≠1)

loga(bc)=logab+logac(a>0,a≠1,b>0,c>0)

logabc=logab−logac(a>0,a≠1,b>0,c>0)

logabp=plogab(a>0,a≠1,b>0)

logab=logcblogca(a>0,a≠1,b>0,c>0,c≠1)

logab=1logba(a>0,a≠1,b>0,b≠1)

Возможно, вас заинтересуют также:

www.repetitor2000.ru

Логарифм. Свойства логарифмов

Логарифм. Свойства логарифмов

Рассмотрим равенство . Пусть нам известны значения  и и мы хотим найти значение .

То есть мы ищем показатель степени, в которую нужно взвести чтобы получить .

Пусть переменная  может принимать любое действительное значение, тогда на переменные  и накладываются такие ограничения: ,  ,  

Если нам известны значения  и , и перед нами стоит задача найти неизвестное , то для этой цели вводится математическое  действие, которое называется логарифмирование.

Чтобы найти значение , мы берем логарифм числа  по основанию :

Итак,

Логарифмом числа  по основанию  называется показатель степени, в которую надо возвести  , чтобы получить .

То есть основное логарифмическое тождество:

            ,  ,  

является по сути математической записью определения логарифма.

Математическая операция  логарифмирование является обратной по отношению к операции возведения в степень, поэтому свойства логарифмов тесно связаны со свойствами степени.

Перечислим основные свойства логарифмов:

(,  ,   ,  ,  

1. 

2. 

3. 

4. 

5. 

Следующая группа свойств позволяет представить  показатель степени выражения, стоящего под знаком логарифма, или стоящего в основании логарифма в виде коэффициента  перед знаком логарифма:

6. 

7. 

8. 

9. 

Следующая группа формул позволяет перейти от логарифма с данным основанием к логарифму с произвольным основанием, и называется формулами перехода к новому основанию:

10. 

11. 

12. (следствие из свойства 11)

Следующие три свойства не очень известны, однако они часто используются при решении логарифмических уравнений, или при упрощении выражений, содержащих логарифмы:

13. 

14. 

15. 

 

Частные случаи:

— десятичный логарифм

 —  натуральный логарифм

При упрощении выражений, содержащих логарифмы  применяется общий подход:

1. Представляем десятичные дроби в виде обыкновенных.

2. Смешанные числа представляем в виде неправильных дробей.

3. Числа, стоящие в основании логарифма и под знаком логарифма раскладываем на простые множители.

4. Стараемся привести все логарифмы к одному основанию.

5. Применяем свойства логарифмов.

Давайте рассмотрим примеры упрощения выражений, содержащих логарифмы.

Пример 1.

Вычислить:

Упростим все показатели степеней: наша задача привести их к логарифмам, в основании которых стоит то же число, что и в основании степtни.

==(по свойству 7)=(по свойству 6) =

Подставим показатели, которые у нас получились в исходное выражение. Получим:

Ответ: 5,25

 

Пример 2. Вычислить:

Приведем все логарифмы к основанию 6 (при этом логарифмы из знаменателя дроби «перекочуют» в числитель):

Разложим числа, стоящие под знаком логарифма на простые множители:

Применим свойства 4 и 6:

Введем замену  

Получим:

Ответ:  1 

 

Скачать таблицу логарифм и его свойства

И.В. Фельдман, репетитор по математике.

ege-ok.ru

Свойства логарифма. Примеры решения логарифма

ЛЕКЦИЯ 2 Свойства логарифма

Вспомним полученные знания из лекции1 по данной теме и ответим на вопросы (устно):

1. Дайте определение логарифма числа.

2. Дайте определение десятичного логарифма.

3. Сформулируйте основное логарифмическое тождество

4. Перечислите изученные свойства логарифмов.

Вычислите (в тетрадях):

1. 5 10. 2+

2. 11.

3. 2 12. —

4. 13. 2

5. 14.

9. ()

Если возникли трудности, то вспомни свойства степеней и корней:

Введем новые свойства логарифмов, с помощью которых вы должны научиться решать и упрощать выражения, содержащие логарифмы

В тетради оформляем таблицу (переписываем и разбираемся по каждому свойству!)

log _a1 = 0, a > 0, a  1.

log₃₂1 =0

2.

Логарифм основания.

log _aa = 1, a > 0, a  1.

Log₃₂8 + Log₃₂4

Логарифм произведения.

log _a(xy) = log 

_ax + log_ay,

a > 0, a  1, x > 0, y > 0.

log₃₂8 + log₃₂4 = =log₃₂32 =1

4.

Логарифм дроби.

log _a  = log _ax – log_ay,

a > 0, a ? 1, x > 0, y > 0.

 

log₃ 54-log₃2 = =log₃27 =3

5.

Логарифм степени.

log _ax =  log _ax,
x > 0, a > 0, a  1,   R.

  log₃ 27⁶⁷ = 67log₃ 27=

67*3 = 201

 log₃ (-27)⁸ = 8 log_{3 | —}27|=

8*3 = 24(под логарифмом не может быть отрицательного числа !!!)

Замечание.

log _ax^2k = 2k log 

_a  |x| , 
a > 0, a  1, k N , x  R, 
x  0.

6.

Логарифм выражения по основанию, которое является степенью.

log _a x =  log _ax, a > 0, 
a  1, x > 0,   R,   0 .

 Этого свойства в учебнике нет, но оно важное!

=¹/₄log₂ 2 = ¼₌ 0,25

(т.о, показатель основания «выходит» из логарифма обратным числом)

Лишний раз проверь при вынесения показателя – под логарифмом должно остаться положительное число!!!

= ⁷/₄log₂ 2 = ⁷/₄=1,75

(если сразу использовать свойства 5 и 6)

Замечание:

1. log _a^2kx =  log  _|a|x,
a  0, a  1, x > 0, k  N.
2. log _a x  =  log_ax, a > 0,
a  1,   R, R,   0 , x > 0.

7.

Переход к новому основанию.

=

a > 0, a  1, c > 0, c  1, b > 0.

 

= ; =

= (это свойство используется когда основание надо поменять местами с подлогарифмируемым выражением)

Замечание.

log _ab = , 
a > 0, a  1, b > 0, b  1.

Вся теория логарифмов строится на определении и свойствах. Определение надо выучить, а свойства отработать на упражнениях. Приступим!

Из учебника в тетради выполнить задания №488, №489, №490, №495, 496.

У многих из вас возникает вопрос «А где же эти логарифмы встречаются и применяются в жизни?»

Историческая справка по теме.

«Зачем и где применяются логарифмы»

Знания логарифмов и основных логарифмических свойств необходимы для людей многих профессий: физиков, химиков, астрономов, психологов, географов и экологии.

Логарифмы по основанию 10 до изобретения калькуляторов широко применялись для вычислений. Неравномерная шкала десятичных логарифмов обычно наносится и на логарифмические линейки

Логарифмическая линейка хорошо знакома нашим родителям. Она позволяет выполнять умножение и деление чисел, возведение в степень и вычисление квадратных и кубических корней.

Шкала Рихтера— классификация силы землетрясений, созданная и представленная в 1935 г. геологом Чарльзом Рихтером. Шкала основана на принципе логарифма: каждое деление увеличивается в 10 раз, и его основанием является общая энергия, выделяемая при землетрясении.

В 1858 году немецкий физик и психолог Густав Фехнер доказал, основной психофизический закон, в котором говорится,что интенсивность воспринимаемого нами ощущения пропорциональна логарифму силы раздражения. Его формулируют так: «При изменении силы раздражителя в геометрической прогрессии, интенсивность ощущения меняется в арифметической прогрессии».

Логарифмы применяются и в психических явлениях. «Шкала Ландау» самый яркий пример.Знаменитый физик по ней оценивал заслуги своих коллег. Шкала была логарифмическая (классу 2 отвечали достижения в 10 раз меньше, чем для класса 1). Из физиков имел класс 0,5, Бор, Дирак, Гейзенберг имели класс 1

Астрономы измеряют «блеск» небесных светил в звездных величинах. Блеск в астрономии — величина пропорциональная логарифмусветового потока. Её направление обратное: чем больше значение звездной величины, тем слабее блеск объекта.

Xимическая шкала кислотности очень близка к шкале звездных величин. Чем выше кислотность, тем ниже значение индекса, основанием логарифма служит число 10.

Играя на рояле, пианист играет на логарифмах. Ступени темперированной хроматической гаммы представляют логарифмы этих величин с основанием

Логарифмическая спираль часто встречается в природе. Впервые логарифмическая спираль описана Декартом, а потом была исследована Бернулли.

Паук Эпейра сплетая паутину, закручивает паутину, скручивая нити вокруг центра по логарифмической спирали.

Живые существа обычно растут во всех направлениях , сохраняя общее начертание своей формы. Раковины морских животных могут расти лишь в одном направлении. Чтобы не слишком вытягиваться в длину им приходится скручиваться.

Многие Галактики закручены по логарифмической спирали. Солнечная система, как одна из Галактик тоже закручена по такой спирали.

Предлагаю творческую работу — презентацию по данной теме (можно объединиться в творческую группу)

Вы сегодня погрузились в логарифмы,

Безошибочно их надо вычислять,

На экзамене, конечно, вы их встретите,

Остаётся вам успехов пожелать.

На следующем занятии продолжим изучать свойства логарифмов на более сложном уровне.

infourok.ru

их решение, что есть основание, виды и примеры

При изучении математики приходится решать такие интересные выражения, как логарифмы. Но для начала необходимо тщательно разобраться с основаниями и произвести подсчеты, которые дадут правильный ответ. Разберем подробнее, как решать логарифмы разной сложности.

Для начала рассмотрим уравнение вида 3^x=8. На первый взгляд, может показаться, что данное выражение не имеет решения. Но если разобраться, то решение такого примера становится несложным. Число 3 является основанием, в которое надо возвести x, чтобы получить в результате 8. Именно это и есть логарифмическим выражением, которое нередко встречается в математических задачах, особенно на экзаменах.

Виды

Логарифмы бывают следущих видов:

1. Десятичные. К таким относят равенства, в основании которых заложено число 10. Запись уравнения производится в виде log10а. Означает следующее: для получения нужного числа необходимо возвести в десятую степень неизвестное число. Это простые выражение, не требующих значительных математических манипуляций. В качестве варианта записи иногда выступает lg а.
2. Натуральные — выражения, где в качестве основания выступает константа e. Ее называют числом Эйлера, оно составляет 2,7. Эти равенства записываются в виде ln x, что является общепринятым обозначением в математической литературе.
3. Другие логарифмы. Например, уравнения с двойкой в основании называются двоичными, а если внизу располагается цифра 16, то это шестнадцатеричный тип выражения. А если он имеет основание 64, то его сложность достаточно высока. Решением будет искаться как адаптивное управление по геометрической точности под названием ACG.

Остальные подобные равенства попадают в ту или иную группу. Их объединяет одинаковый способ решения, а именно возведение числа в степень основания для получения правильного результата.

Свойства

Они применяются при решении логарифмов и показательных уравнений. Причем верны они только в том случае, когда и основание, и аргумент равенства имеют положительный знак. Также есть небольшой нюанс: основание не может иметь степень 0 и 1.

1. Свойство 1. Loga (xy)=logaX+logaY. Расшифровка этой записи: логарифм произведения числа x и y равен сумме каждого из них или сумма логарифмов равна произведению их аргументов. В качестве примера приведем следующее выражение: log2 (16)=log2 (8)+log2 (2).
2. Свойство 2. Loga (x/y)=loga (x)-loga (y). В этом выражении логарифм от деления двух аргументов равен разности одного уравнения от другого. Пример: loga (5/3)=loga (5)-loga (3).
3. Свойства 3. loga (x^r)=r*loga (x). Показатель аргумента может быть вынесен за скобки.
4. Свойство 4. loga (1/x)=-loga (x). Поскольку (1/x)=x^-1, то можно вынести -1 за скобки по аналогии с предыдущим свойством.
5. Свойство 5. loga (a)=1. Если основание и аргумент равны между собой, то такой пример равняется 1, то есть число a в первой степени остается таким же. Сюда же можно отнести и такое свойство, согласно которому число в степени ноль равняется единице.
6. Свойство 6. (logb (x)/logb (a))=loga (x). Это особенное свойство, согласно которому уравнения с одинаковыми основаниями заменяются одним, где основание равняется аргументу делителя, аргумент такой же, как у делимого. То есть, аргумент нижнего логарифма идет вниз, а верхнего располагается наверху.

С помощью вышеописанных свойств можно решать равенства любой степени сложности. Они не очень сложные в применении, но их нужно уметь грамотно использовать и понимать, когда возможно использовать и что для этого следует сделать. Имеются и другие, особые свойства логарифмов, которые можно отыскать в специализированной математической литературе.

Логарифмы — интересный тип равенств. Несмотря на то, что поначалу все кажется сложным и не особенно понятным, при углубленном изучении они превращаются в довольно простые. Главное запомнить: внизу располагается основание, в которое возводится число для получения ответа. Также стоит хорошо изучить свойства логарифмов, потому что они значительно облегчают решение, особенно сложных примеров.

Видео

В этом видео рассматриваются свойства логарифмов.

liveposts.ru

Свойства логарифмов, формулы | Подготовка к ЕГЭ по математике

Категория: Справочные материалы

Елена Репина 2013-02-18 2013-07-07

Логарифм числа по основанию определяется как показатель степени, в которую нужно возвести основание , чтобы получить число .

Обозначение читается как логарифм по основанию .

Например, , так как  (2 – основание степени, 3 – показатель степени).

 

Логарифмы

Определение

Основное логарифмическое тождество

Свойства логарифмов

Чаще всего используют логарифмы с основаниями (натуральный логарифм, например, ), (десятичный, например, ) и (двоичный).

 

Автор: egeMax | комментариев 12 | Метки: Логарифмы, шпаргалки-таблицы

egemaximum.ru

Логарифмические уравнения и неравенства

Автор Сергей Валерьевич

Суббота, Февраль 18, 2012

Логарифмическим уравнениям и неравенствам в вариантах ЕГЭ по математике посвящена задача C3. Научиться решать задания C3 из ЕГЭ по математике должен каждый ученик, если он хочет сдать предстоящий экзамен на «хорошо» или «отлично». В данной статье представлен краткий обзор часто встречающихся логарифмических уравнений и неравенств, а также основных методов их решения.

Итак, разберем сегодня несколько примеров логарифмических уравнений и неравенств, которые предлагались учащимся в вариантах ЕГЭ по математике прошлых лет. Но начнет с краткого изложение основных теоретических моментов, которые нам понадобятся для их решения.

Логарифмическая функция

Определение

Функцию вида

   

называют логарифмической функцией.

Основные свойства

Основные свойства логарифмической функции y = log_a x:

	a > 1	0 < a < 1
Область определения	D(f) = (0; +∞)	D(f) = (0; +∞)
Область значений	E(f) = (-∞; +∞)	E(f) = (-∞; +∞)
Монотонность	Возрастает на (0; +∞)	Убывает на (0; +∞)
Непрерывность	Непрерывная	Непрерывная
Выпуклость	Выпукла вверх	Выпукла вниз

График логарифмической функции

Графиком логарифмической функции является логарифмическая кривая:

Свойства логарифмов

• Логарифм произведения двух положительных чисел равен сумме логарифмов этих чисел:

   

• Логарифм частного двух положительных чисел равен разности логарифмов этих чисел:

   

• Если a и b — положительные числа, причем a ≠ 1, то для любого числа r справедливо равенство:

   

•  Равенство log _a t = log _a s, где a > 0, a ≠ 1, t > 0, s > 0, справедливо тогда и только тогда, когда t = s.

• Если a, b, c — положительные числа, причем a и c отличны от единицы, то имеет место равенство (формула перехода к новому основанию логарифма):

   

yourtutor.info

No related posts.