Целые числа (Z). Рациональные числа (Q), их сложение, вычитание, умножение и деление. Сравнение рациональных чисел
Возьмем какое-нибудь натуральное число, например, 11. Противоположное ему будет число -11. На координатной прямой, оно находится на том же расстоянии от начала отсчета, что и число 11, только 11 находится справа, а -11 — слева. Числа 11 и -11 называются противоположными. Противоположные числа – это числа, отличающиеся только знаком. Понятно, что 0 = -0. Поэтому, число 0 противоположно самому себе.
Целые числа – это натуральные числа, противоположные им числа и 0.
Примеры целых чисел: -8, 111, 0, 1285642, -20051 и т. д.
Рациональные числа – это числа, которые можно представить в виде дроби , где m и n – целые числа, n ? 0. Пример: ; ; ; 1,01; 12 и т.д. Все целые числа являются рациональными.
Действительно, любое целое число n можно представить в виде дроби . Например, целое число
18 – это .
Две дроби считаются равными, если .
Пример: = , так как 3 • 2 = 6 • 1.
Очевидно, что дроби равны. На этом свойстве основано сокращение дробей. Для того чтобы сократить дробь, находим общий делитель числителя и знаменателя и на этот делитель делим числитель и знаменатель — полученная дробь будет равна исходной.
Пример: Сократить дробь .
Над рациональными числами операции сложения, умножения и деления определены следующим образом:
1. Операция сложения:.
Пример: .
2. Операция умножения: .
Пример: .
3. Операция деления:, то есть, делитель «переворачиваем»
Пример: .
При сравнении рациональных чисел применяют следующие правила:
1. Всякое положительное рациональное число всегда больше всякого отрицательного рационального числа.
2. Если два числа положительны, то число больше , если , для отрицательных — наоборот.
Пример: , так как 3 • 6 > 5 • 2.
studyport.ru
N натуральные числа Z целые числа Q
N –натуральные числа Z – целые числа Q — рациональные числа
Найдите значения выражений: 3+3+3+3= 2+2+2+2= Упростите выражение: х+х+х+…+х+х= п слагаемых
Найдите площадь квадрата со стороной 10 см. S = а 2 S = 102 = 100(см 2) Найдите объем куба с ребром 0, 5 см. V = а 3 V = 0, 53= 0, 125 (см 3)
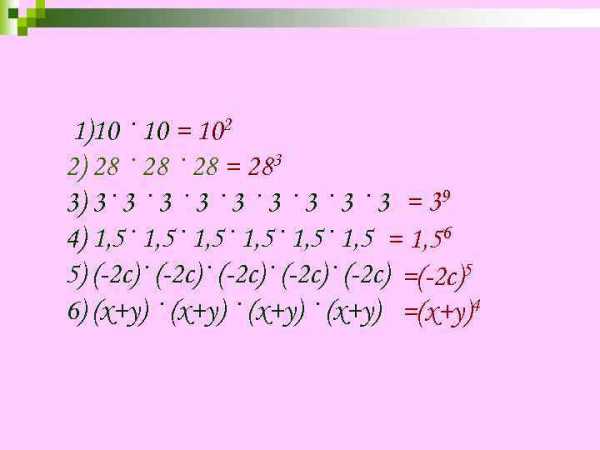1)10 · 10 = 102 2) 28 · 28 = 283 3) 3· 3 · 3 = 39 4) 1, 5· 1, 5· 1, 5 = 1, 56 5) (-2 с)· (-2 с) =(-2 с)5 6) (х+y) · (х+y) =(х+y)4
Степень с натуральным показателем
Степень с натуральным показателем показатель степени ап =а • а • … • а n множителей основание степени 56; 3, 75; 04; (-4, 8)6
Степенью числа а с натуральным показателем n(п≥ 2)называется произведение n множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а. (а 1=а) Операцию отыскания степени называют возведением в степень.
№ 1. Представьте в виде произведения третью степень числа 4 и найдите ее числовое значение. 43 = 4· 4· 4 =64 № 2. Чему равна сумма кубов чисел 5 и 3 ? 53 + 33 = 125 + 27 =152
№ 3. Вычислите: = 125 1) 5 3 2) 24 – 62 = -20 3) (-4) 2+ 25 = 48 4) 1 7 – 92 + 10 3 = 920 № 4. Представьте данное число в виде степени какого-либо числа с показателем, отличным от 1. 1) 64 =43 2)36 =62 3)121 =112 4)27 =33
№ 5. Найдите х, если 1) 2 х = 32; 2) х 3 = 125 2 х= 2 5 х 3= 5 3 х=5 № 6. Вычислите квадрат куба числа: 1)2 (23) 2 =64 2)4 (43)2=4096
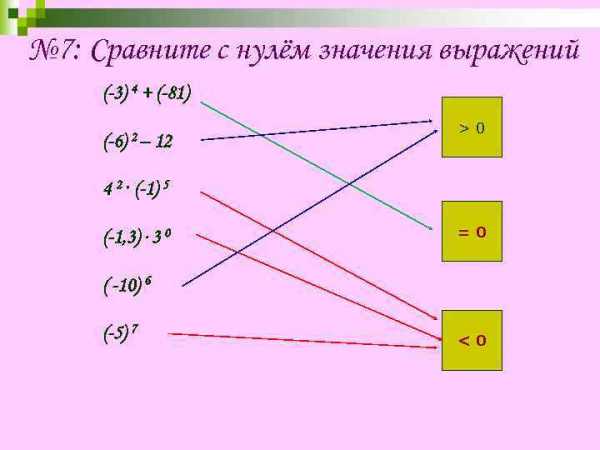№ 7: Сравните с нулём значения выражений (-3) 4 + (-81) (-6) 2– 12 >0 4 2 · (-1) 5 (-1, 3) · 3 0 =0 ( -10) 6 (-5) 7
Какую закономерность можно заметить? (-2)1 =(- 2) = -2 (-2)2 = (- 2) = 4 (-2)3 = (- 2) = -8 (-2)4 = (- 2) = 16 (-2)5 = (- 2) (- 2) = -32 (-2)6 = (- 2) (- 2) = 64 (-2)7 = (- 2) (- 2) = -128 (-2)8 = (- 2) (- 2) = 256 (-2)9 = (- 2) (- 2) (- 2) = -512 (-2)10 = (- 2) (- 2) (- 2) = 1024
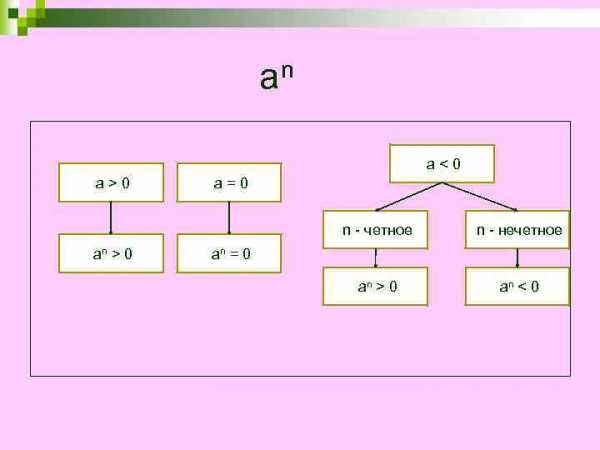an a0 a=0 n — четное an > 0 n — нечетное an > 0 an
5) -24 и (-2)4
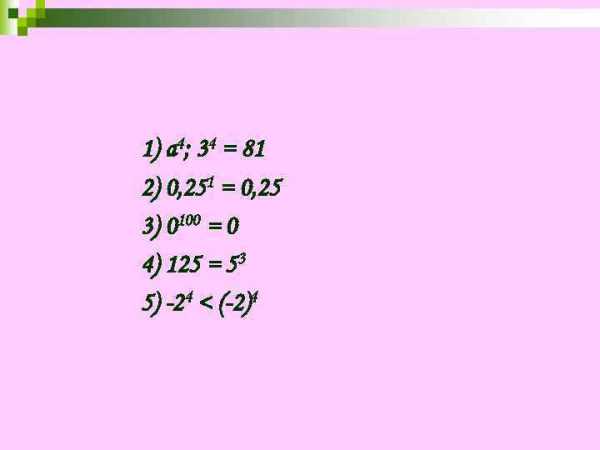1) а 4; 34 = 81 2) 0, 251 = 0, 25 3) 0100 = 0 4) 125 = 53 5) -24
Из истории степеней У древних вавилонян, египтян и китайцев имелись некоторые отдельные знаки – иероглифы для немногих математических понятий. Однако лишь в «Арифметике » Диофанта (3 в) встречаются зачатки алгебраической буквенной символики.
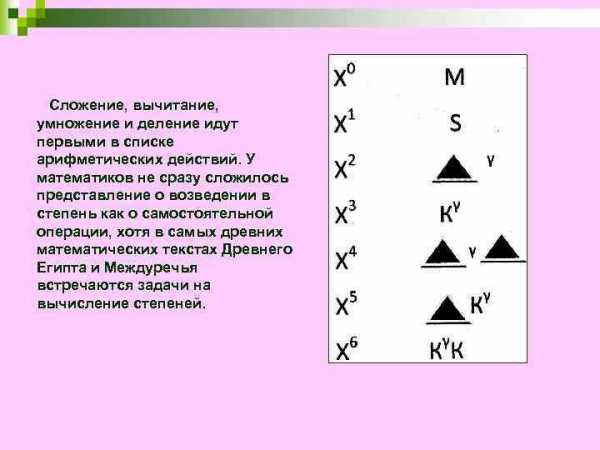Сложение, вычитание, умножение и деление идут первыми в списке арифметических действий. У математиков не сразу сложилось представление о возведении в степень как о самостоятельной операции, хотя в самых древних математических текстах Древнего Египта и Междуречья встречаются задачи на вычисление степеней.
Европейские математики 16 века вторую степень неизвестного называли «сила» , а также «квадрат» , третью степень – «куб» . Немецкие математики Средневековья стремились ввести единое обозначение и сократить число символов. Книга Михаэля Штифеля «Полная арифметика» (1544 г. ) сыграла в этом значительную роль.
Вильям Оутред (15751660)– английский математик Aq вместо A 2 Ac вместо A 3 Aqqвместо A 4
Франсуа Виет (15401603) – французский матемматик Виет применял сокращения: N для первой степени, Q для второй степени, C для третьей степени, QQ для четвертой и т. д. Например 1 C-8 Q+16 N aequatur 40 означает : x 3 – 8 x 2 + 16 x = 40
Михаэль Штифель (1487 г. -19. 04. 1567 г. ) немецкий математик ААА вместо А 3
Рене Декарт (15961650) –французский математик Рене Декарт в его «Геометрии» (1637) впервые ввёл современное обозначение степеней
Использование записи в виде степени. В физике: 10 = 101 100 = 102 (санти) 1000 = 103 (кило) 1000000 = 106 (Мега) 100000 = 109 (Гига) При переводе единиц измерения: 72 км = 72000 м = 72∙ 103 м 5 кг = 5000 г = 5∙ 103 г
Использование записи в виде степени в астрономии. В астрономии расстояния до звезд измеряют в астрономических единицах (а. е. ). 1 а. е. = 1, 496∙ 108 км 1 световой год = 9, 46 ∙ 108 км Самая близкая к нам звезда (из созвездия Центавра) находится на расстоянии: 206265 а. е. =3, 08∙ 1013 км = 3, 26 св. лет
Миаил Васильевич Ломоносов (1711 -1765)русский учёный “Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь” М. В. Ломоносов
Дополнительное задание: Найти значение выражения n 2 + k 2 , если 2 n = 32 и 3 k = 9.
present5.com
Целые числа — Википедия
Материал из Википедии — свободной энциклопедии
Целые числа — расширение множества натуральных чисел[1], получаемое добавлением к нему нуля и отрицательных чисел[2]. Необходимость рассмотрения целых чисел продиктована невозможностью в общем случае вычесть из одного натурального числа другое — можно вычитать только меньшее число из большего. Введение нуля и отрицательных чисел делает вычитание такой же полноценной операцией, как сложение
Вещественное число является целым, если его десятичное представление не содержит дробной части (но может содержать знак). Примеры:
- Числа 142857; 0; −273 являются целыми.
- Числа 5½; 9,75 не являются целыми.
Множество целых чисел обозначается Z{\displaystyle \mathbb {Z} } (от нем. Zahlen — «числа»[4]). Изучением свойств целых чисел занимается раздел математики, называемый теорией чисел.
Положительные и отрицательные числа[ | ]
Согласно своему построению, множество целых чисел состоит из трёх частей:
- Натуральные числа (или, что то же самое, целые положительные). Они возникают естественным образом при счёте (1, 2, 3, 4, 5…)[5].
- Ноль — число, обозначаемое 0{\displaystyle 0}. Его определяющее свойство: 0+n=n+0=n{\displaystyle 0+n=n+0=n} для любого числа n{\displaystyle n}.
- Целые отрицательные числа.
encyclopaedia.bid
что значит Z в алгебре??? множество каких чисел?
целые числа (имхо)
множество целых чисел
целые числа, но не знаю входят ли туда отрицательные?
множество целых чисел
Множество целых чисел 1,2,3,4,5,6…
touch.otvet.mail.ru