«Координаты. Координатная плоскость». 6-й класс
Место урока в общей теме:
Общая тема «Положительные и отрицательные числа»
Это 1 урок по теме «Координаты»
- учащиеся знают определения положительных и отрицательных чисел
- учащиеся знают понятие координатной прямой
- умеют определять координаты точек координатной прямой
- умеют отмечать точки на координатной прямой по заданным координатам
Цели урока:
1) образовательные:
- ввести понятие координат
- ввести понятие системы координат, координатных осей и координатной плоскости
- ввести понятие координат точки: абсциссы и ординаты
- научить определять координаты точек
- научить отмечать точки на координатной плоскости по заданным ее координатам
- закрепить полученные знания в ходе выполнения упражнений
2) развивающие:
- создать у учащихся положительную мотивацию к выполнению умственных и практических действий
- развитие коммуникативной и информационной компетентностей учащихся
- помочь развитию интереса у учащихся не только к содержанию, но и к процессу овладения знаниями
- развивать умение применять полученные знания в конкретной ситуации
- развивать логическое мышление, память, самостоятельность
3) воспитывающие:
- воспитывать у учащихся чувство удовлетворения от возможности показать на уроке свои знания не только по математике, но и в других областях школьных знаний
- развитие интереса к изучению математики
- расширить умственный кругозор учащихся, помочь школьникам лучше понять роль математики в истории общества
- воспитание дисциплинированности, организованности
Тип урока: урок усвоения новых знаний
В соответствие с типом урока выбраны следующие этапы урока
- организационный момент
- актуализация
- подготовка к активному и сознательному усвоению нового материала
- усвоение нового материала
- упражнения на понимание
- обобщение и систематизация знаний
- подведение итогов урока
- оглашение домашнего задания
Ход урока
I. Организационный момент.
Организационный момент.
Приветствие. Постановка пред учащимися долговременных целей по теме и задач по уроку.
II. Устная работа
Направлена на подготовку учащихся к активному и сознательному усвоению нового материала.
Координаты в жизненных ситуациях используются очень широко.
1. Привести примеры того, как в жизни используются координаты.
2. Предложить учащимся на основе рассмотренных примеров дать понятие координат.
III. Изучение нового материала.
1. Ввести понятие системы координат и координатной плоскости.
Учащимся предлагается рассмотреть рисунок и рассказать, что на нем изображено или ответить на вопросы.
— Можно ли утверждать, что на рисунке изображены координатные прямые? Почему?
— Под каким углом расположены эти прямые к друг другу?
— Охарактеризовать точку пересечения этих
прямых.
— Что напоминает запись ? Чем она отличается от записи координаты точки на координатной прямой?
— Под каким углом из точки А проведены стрелки к координатным прямым и ?
— Какая связь между точками координатных прямых, на которые указывают стрелки, и записью ?
Выслушать ответы учащихся. Сделать выводы и ввести понятие системы координат, координатных осей, координатной плоскости, координат точки.
Координаты точки – пара чисел, по которым определяется положение точки на плоскости, где на первом месте стоит абсцисса, а на втором - ордината этой точки.
2. Ввести правило позволяющее определять координаты указанных точек.
Учащимся предлагается рассмотреть рисунок и определить координаты отмеченных точек.
Попросить учащихся сформулировать правило, позволяющее определить координаты точки. Повторить его.
Чтобы определить координаты точки — надо из
точки опустить перпендикуляры на координатные
оси и определить, какому числу координатной оси
соответствует основание перпендикуляра.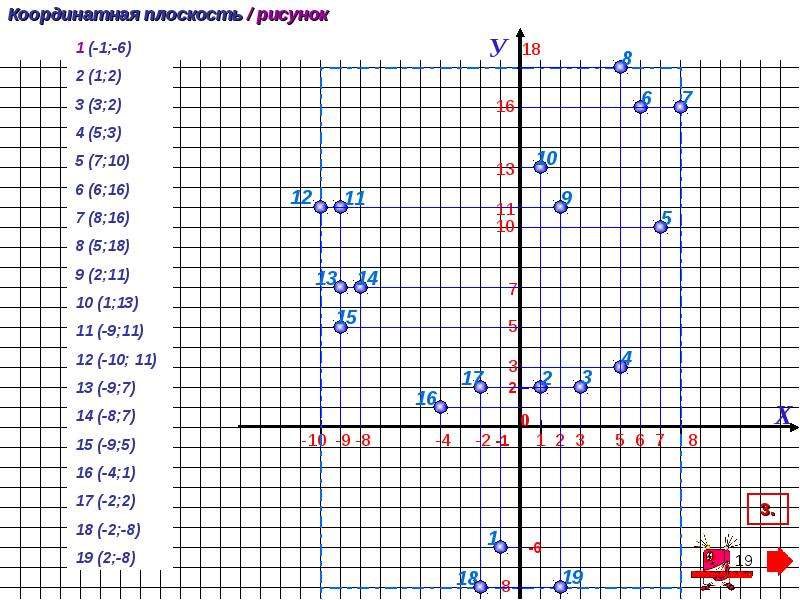
Для закрепления этого правила учащимся предлагается самостоятельно определить координаты отмеченных точек координатной плоскости, изображенных на экране. А затем проверить свое решение с тем, что на экране.
3. Определение положения точки на координатной плоскости по известным координатам.
Учащимся дается точка с заданными координатами. Задание – по известным координатам определить положение точки на координатной плоскости.
Сформулировать правило, позволяющее определять положение точки на координатной плоскости.
Чтобы определить положение точки на координатной плоскости – надо провести прямые, перпендикулярные осям, и найти точку их пересечения.
IV. Закрепление изученного материала.
1. Учащимся предлагается построить
координатную плоскость в тетрадях и отметить
точки с указанными координатами, с последующей
проверкой.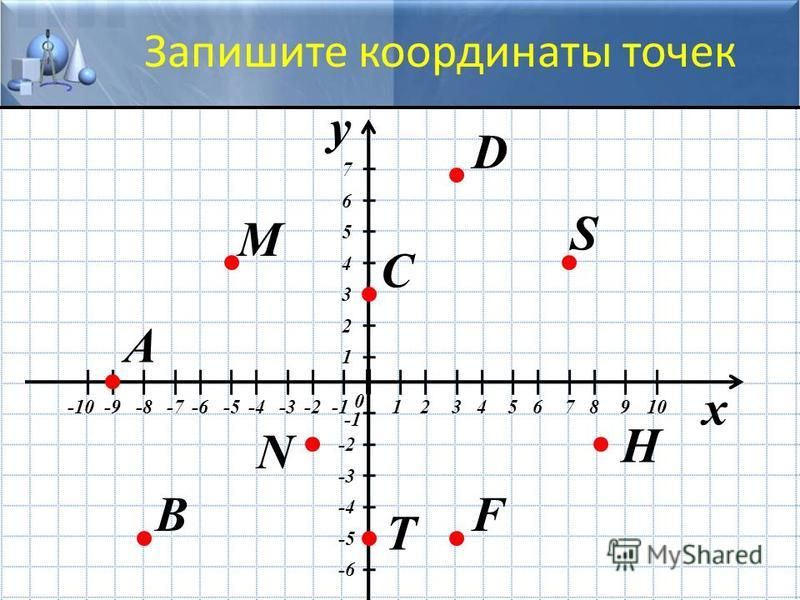
2. Резервное задание. Найти площадь прямоугольника, если известны координаты его вершин.
V. Подведение итогов урока. Выставление оценок.
— Что нового узнали сегодня на уроке? Чему научились?
— С какими понятиями познакомились?
— Какие правила сегодня изучили?
VI. Домашнее задание.
Практическое задание: начертить на листе бумаги в клетку систему координат, взяв единичные отрезок длиной 1 см (две тетрадные клетки). Отметить произвольно десять точек, не указывая их координаты.
Приложение.
Как найти Координаты Точки? Примеры
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете.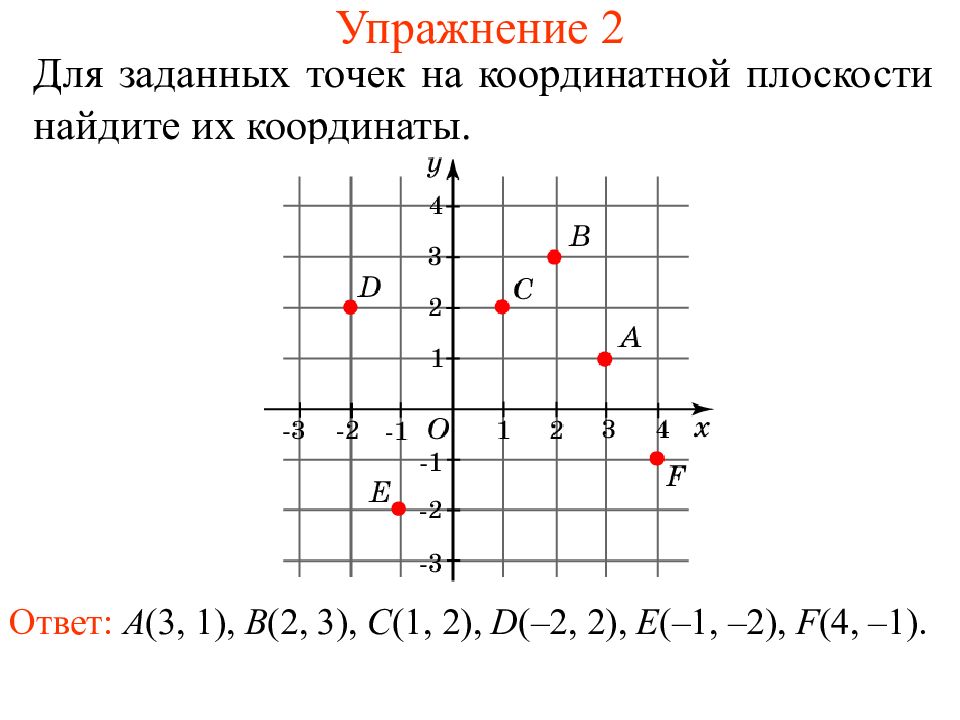 С точками на плоскости та же история.
С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O.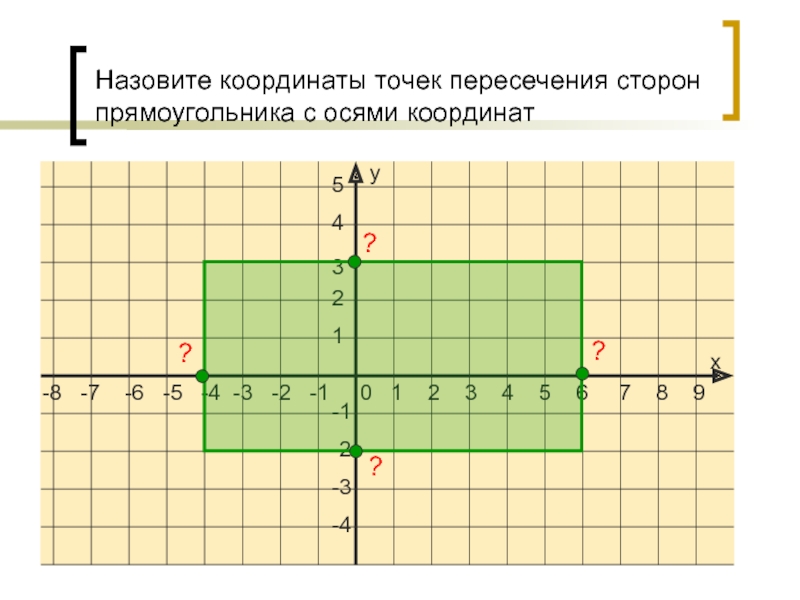 Начало координат делит оси на две части: положительную и отрицательную.
Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV ;
Правила координат:
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.

- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).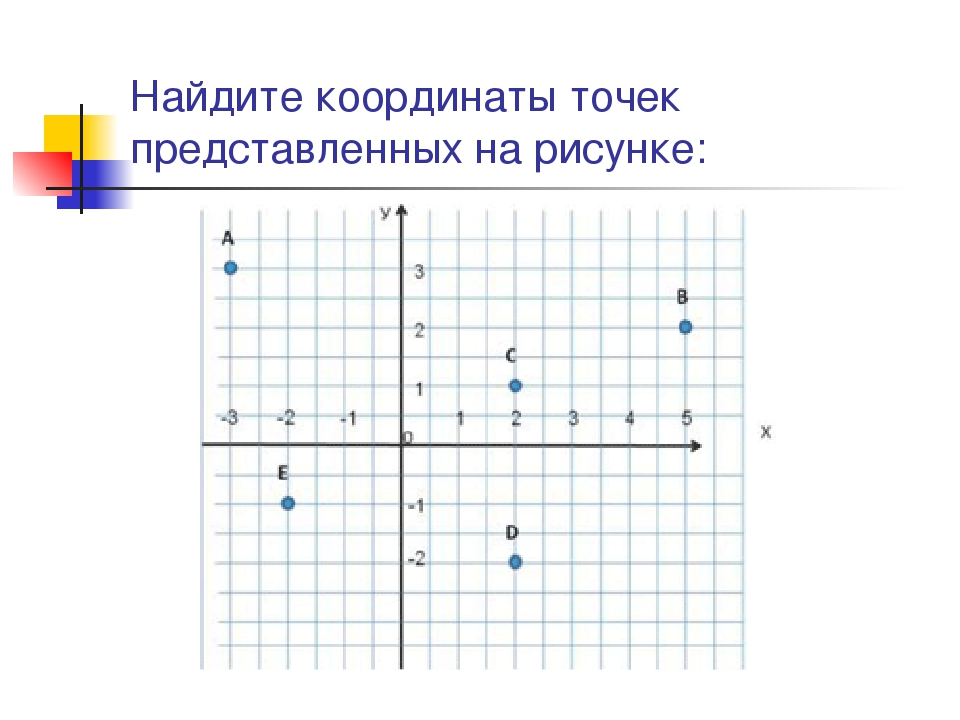
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.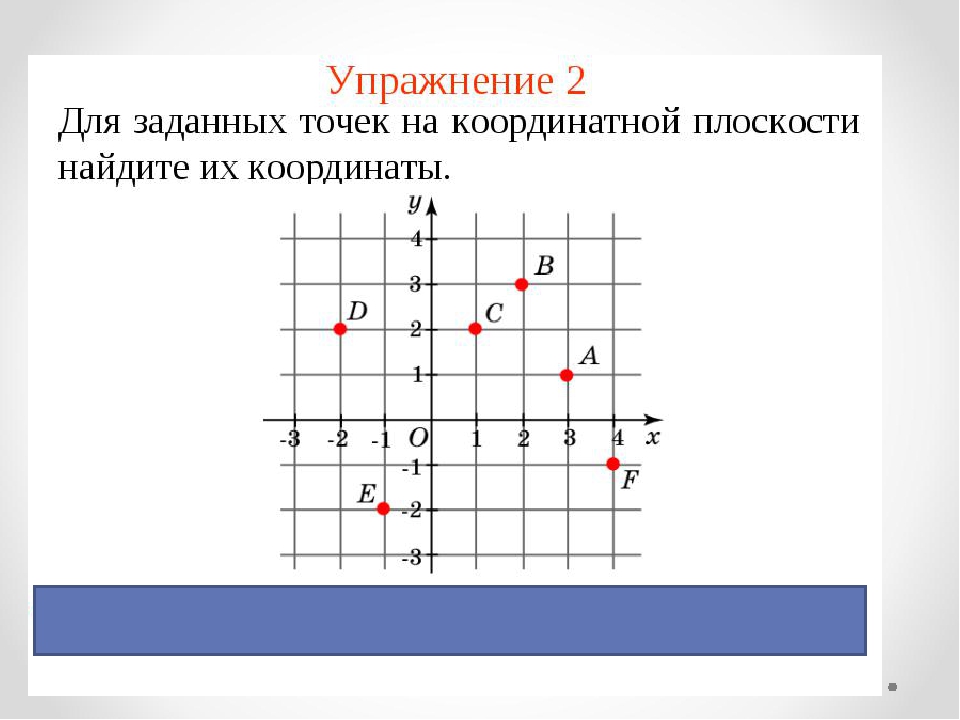
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
что это такое? Как отмечать точки и строить фигуры на координатной плоскости? II
§ 1 Система координат: определение и способ построения
В этом уроке познакомимся с понятиями «система координат», «координатная плоскость», «оси координат», научимся строить точки на плоскости по координатам.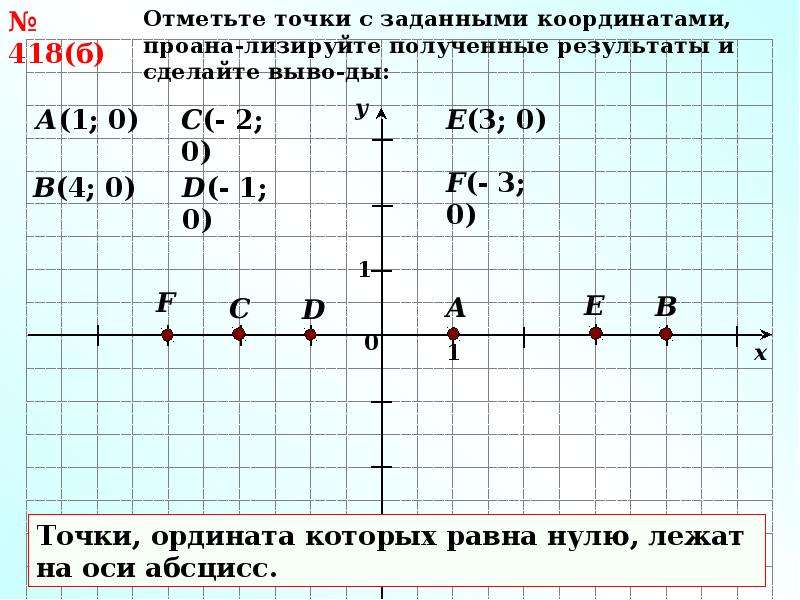
Возьмем координатную прямую х с началом координат точкой О, положительным направлением и единичным отрезком.
Через начало координат точку О координатной прямой х проведем еще одну координатную прямую y, перпендикулярную х, положительное направление зададим вверх, единичный отрезок такой же. Таким образом, мы построили систему координат.
Дадим определение:
Две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом координат каждой из них, образуют систему координат.
§ 2 Координатная ось и координатная плоскость
Прямые, которые образуют систему координат, называют координатными осями, каждая из которых имеет свое название: координатная прямая х — ось абсцисс, координатная прямая y — ось ординат.
Плоскость, на которой выбрана система координат, называется координатной плоскостью.
Описанная система координат называется прямоугольной. Часто ее называют декартовой системой координат в честь французского философа и математика Рене Декарта.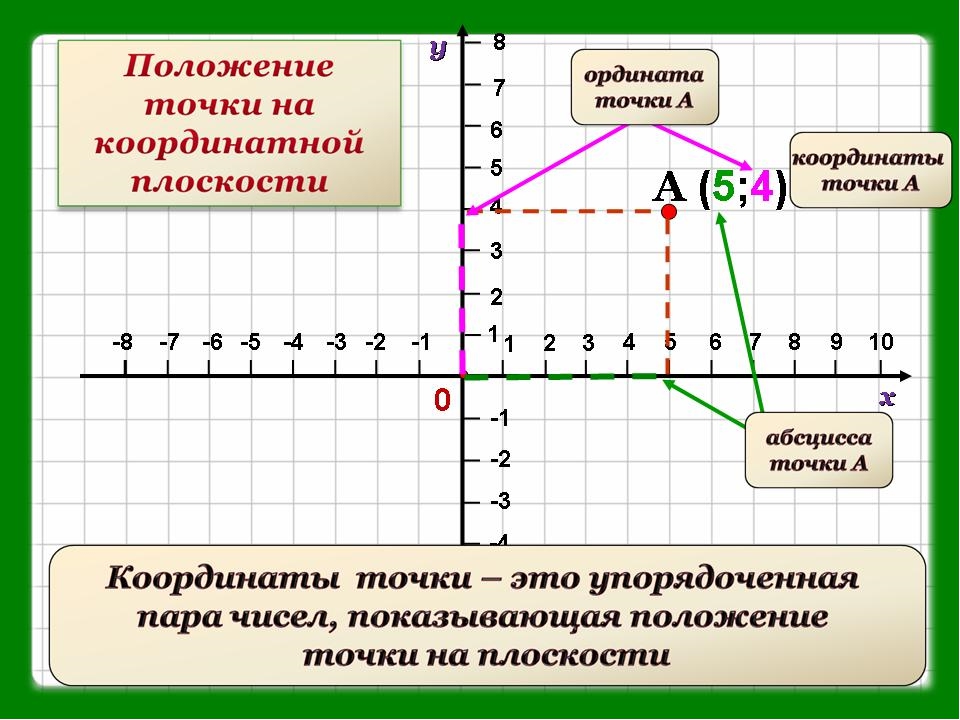
Каждая точка координатной плоскости имеет две координаты, которые можно определить, опустив из точки перпендикуляры на оси координат. Координаты точки на плоскости — это пара чисел, из которых первое число — абсцисса, второе число — ордината. Абсциссу показывает перпендикуляр к оси х, ординату — перпендикуляр к оси y.
Отметим на координатной плоскости точку А, проведем из неё перпендикуляры к осям системы координат.
По перпендикуляру к оси абсцисс (ось х) определяем абсциссу точки А, она равна 4, ординату точки А — по перпендикуляру к оси ординат (ось у) — это 3. Координаты нашей точки 4 и 3. А (4;3). Таким образом, координаты можно найти для любой точки координатной плоскости.
§ 3 Построение точки на плоскости
А как построить точку на плоскости с заданными координатами, т.е. по координатам точки плоскости определить её положение? В данном случае действия выполняем в обратном порядке. На координатных осях находим точки соответствующие заданным координатам, через которые проводим прямые, перпендикулярные осям х и y. Точка пересечения перпендикуляров и будет искомой, т.е. точкой с заданными координатами.
Точка пересечения перпендикуляров и будет искомой, т.е. точкой с заданными координатами.
Выполним задание: построить на координатной плоскости точку М (2;-3).
Для этого на оси абсцисс находим точку с координатой 2, проводим через данную точку прямую перпендикулярную оси х. На оси ординат найдем точку с координатой -3, через нее проведем прямую перпендикулярную оси y. Точка пересечения перпендикулярных прямых и будет заданной точкой М.
А теперь рассмотрим несколько частных случаев.
Отметим на координатной плоскости точки А (0; 2), В (0; -3), С (0; 4).
Абсциссы данных точек равны 0. На рисунке видно, что все точки находятся на оси ординат.
Следовательно, точки, абсциссы которых равны нулю, лежат на оси ординат.
Поменяем координаты данных точек местами.
Получится А (2;0), В (-3;0) С (4; 0). В этом случае все ординаты равны 0 и точки находятся на оси абсцисс.
Значит, точки, ординаты которых равны нулю, лежат на оси абсцисс.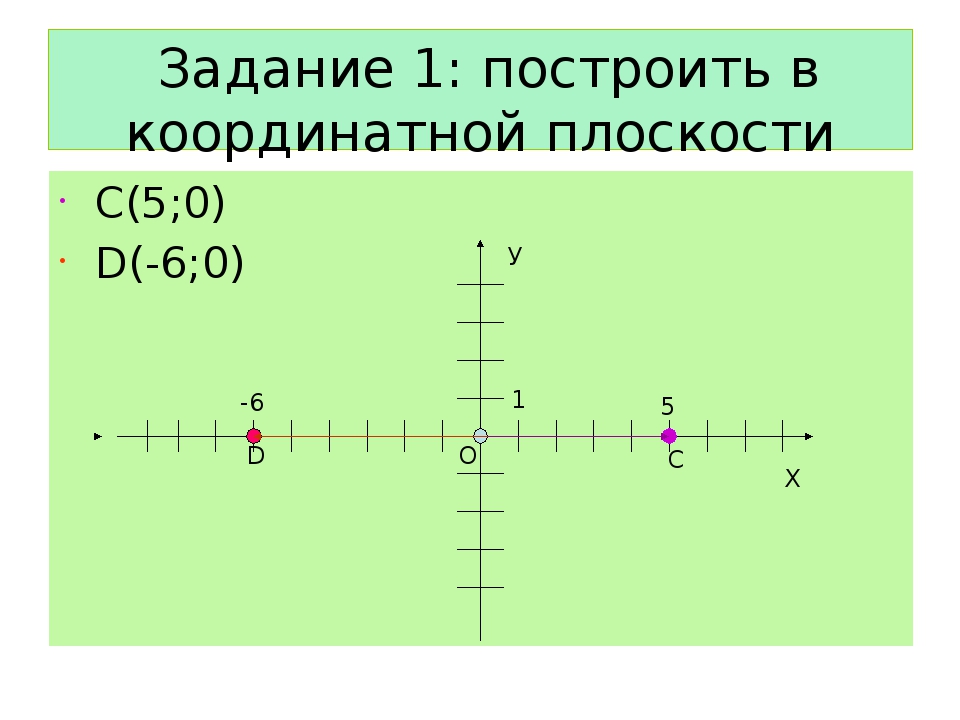
Разберем еще два случая.
На координатной плоскости отметим точки М (3; 2), N (3; -1), Р (3; -4).
Легко заметить, что все абсциссы точек одинаковые. Если эти точки соединить, получится прямая, параллельная оси ординат и перпендикулярная оси абсцисс.
Напрашивается вывод: точки, имеющие одну и ту же абсциссу, лежат на одной прямой, которая параллельна оси ординат и перпендикулярна оси абсцисс.
Если поменять координаты точек М, N, Р местами, то получится М (2; 3), N (-1; 3), Р (-4; 3). Одинаковыми станут ординаты точек. В данном случае, если эти точки соединить, получится прямая параллельная оси абсцисс и перпендикулярная оси ординат.
Таким образом, точки, имеющие одну и ту же ординату, лежат на одной прямой параллельной оси абсцисс и перпендикулярной оси ординат.
В этом уроке Вы познакомились с понятиями «система координат», «координатная плоскость», «оси координат — ось абсцисс и ось ординат». Узнали, как найти координаты точки на координатной плоскости и научились строить точки на плоскости по ее координатам.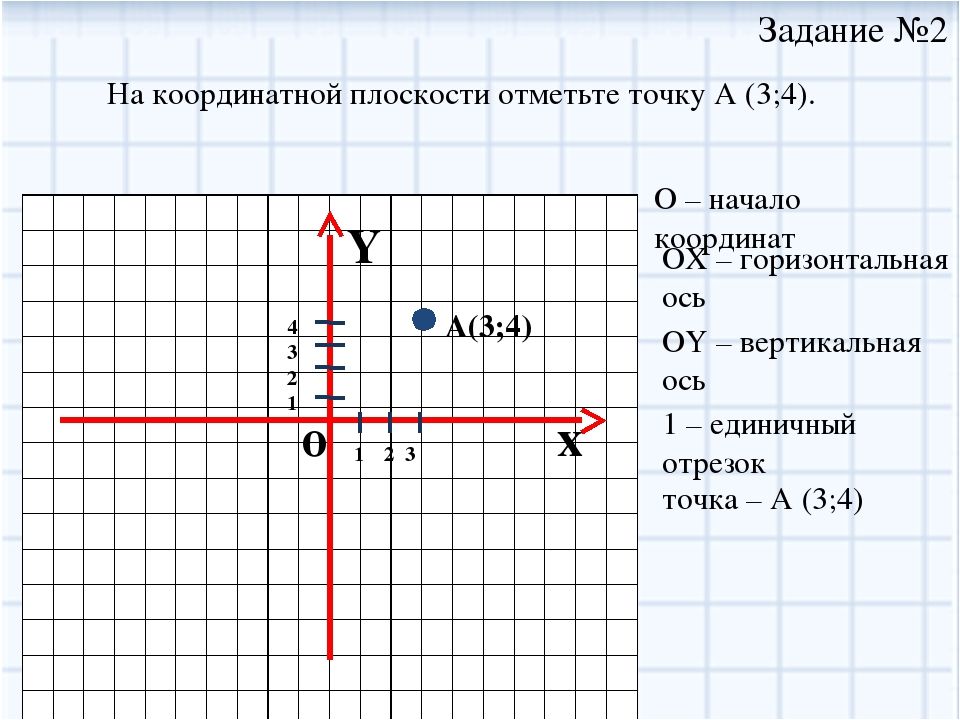
Список использованной литературы:
- Математика. 6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича//автор-составитель Л.А. Топилина. – Мнемозина, 2009.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И.Зубарева, А.Г.Мордкович.- М.: Мнемозина, 2013.
- Математика. 6 класс: учебник для общеобразовательных учреждений/Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др./по редакцией Г.В. Дорофеева, И.Ф. Шарыгина; Рос.акад.наук, Рос.акад.образования. — М.: «Просвещение», 2010
- Справочник по математике — http://lyudmilanik.com.ua
- Справочник для учащихся в средней школе http://shkolo.ru
Математика — наука довольно сложная. Изучая ее, приходится не только решать примеры и задачи, но и работать с различными фигурами, и даже плоскостями. Одной из наиболее используемых в математике является система координат на плоскости. Правильной работе с ней детей учат не один год. Поэтому важно знать, что это такое и как правильно с ней работать.
Давайте же разберемся, что представляет собой данная система, какие действия можно выполнять с ее помощью, а также узнаем ее основные характеристики и особенности.
Определение понятия
Координатная плоскость — это плоскость, на которой задана определенная система координат. Такая плоскость задается двумя прямыми, пересекающимися под прямым углом. В точке пересечения этих прямых находится начало координат. Каждая точка на координатной плоскости задается парой чисел, которые называют координатами.
В школьном курсе математики школьникам приходится довольно тесно работать с системой координат — строить на ней фигуры и точки, определять, какой плоскости принадлежит та или иная координата, а также определять координаты точки и записывать или называть их. Поэтому поговорим подробнее обо всех особенностях координат. Но прежде коснемся истории создания, а затем уже поговорим о том, как работать на координатной плоскости.
Историческая справка
Идеи о создании системы координат были еще во времена Птоломея.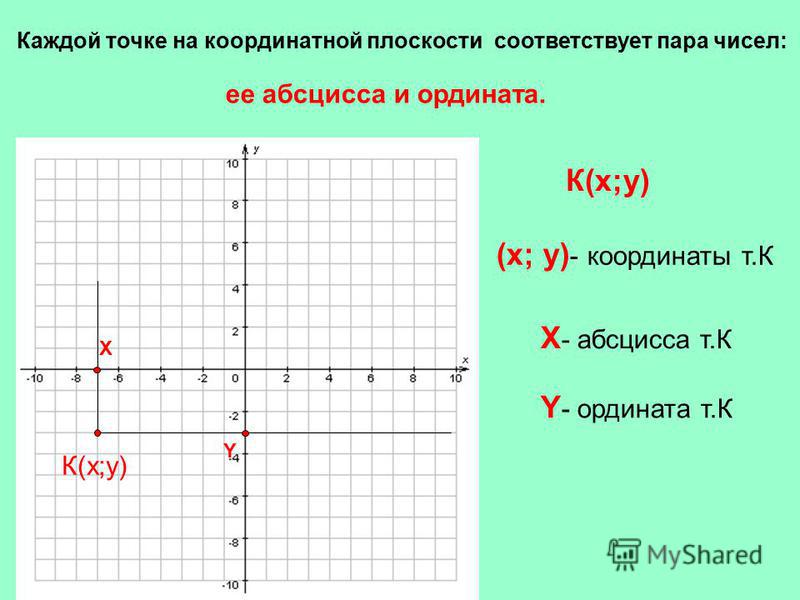 Уже тогда астрономы и математики думали о том, как научиться задавать положение точки на плоскости. К сожалению, в то время еще не было известной нам системы координат, и ученым приходилось пользоваться другими системами.
Уже тогда астрономы и математики думали о том, как научиться задавать положение точки на плоскости. К сожалению, в то время еще не было известной нам системы координат, и ученым приходилось пользоваться другими системами.
Изначально они задавали точки с помощью указания широты и долготы. Долгое время это был один из наиболее используемых способов нанесения на карту той или иной информации. Но в 1637 году Рене Декарт создал собственную систему координат, названную впоследствии в честь «декартовой».
Уже в конце XVII в. понятие «координатная плоскость» стало широко использоваться в мире математики. Несмотря на то что с момента создания данной системы прошло уже несколько веков, она до сих пор широко используется в математике и даже в жизни.
Примеры координатной плоскости
Прежде чем говорить о теории, приведем несколько наглядных примеров координатной плоскости, чтобы вы смогли представить ее себе. В первую очередь координатная система используется в шахматах. На доске каждый квадрат имеет свои координаты — одну координату буквенную, вторую — цифровую. С ее помощью можно определить положение той или иной фигуры на доске.
На доске каждый квадрат имеет свои координаты — одну координату буквенную, вторую — цифровую. С ее помощью можно определить положение той или иной фигуры на доске.
Вторым наиболее ярким примером может служить любимая многими игра «Морской бой». Вспомните, как, играя, вы называете координату, например, В3, таким образом указывая, куда именно целитесь. При этом, расставляя корабли, вы задаете точки на координатной плоскости.
Данная система координат широко применяется не только в математике, логических играх, но и в военном деле, астрономии, физике и многих других науках.
Оси координат
Как уже говорилось, в системе координат выделяют две оси. Поговорим немного о них, так как они имеют немалое значение.
Первая ось — абсцисс — горизонтальная. Она обозначается как (Ox ). Вторая ось — ординат, которая проходит вертикально через точку отсчета и обозначается как (Oy ). Именно эти две оси образуют систему координат, разбивая плоскость на четыре четверти.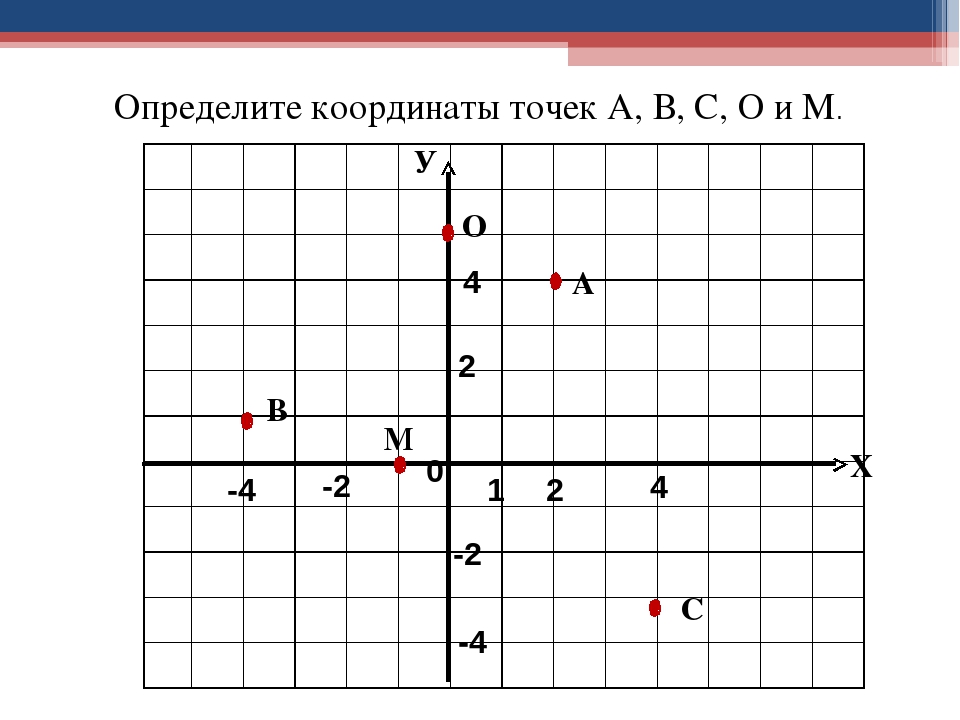 Начало отсчета находится в точке пересечения этих двух осей и принимает значение 0 . Только в случае если плоскость образована двумя пересекающимися перпендикулярно осями, имеющими точку отсчета, это координатная плоскость.
Начало отсчета находится в точке пересечения этих двух осей и принимает значение 0 . Только в случае если плоскость образована двумя пересекающимися перпендикулярно осями, имеющими точку отсчета, это координатная плоскость.
Также отметим, что каждая из осей имеет свое направление. Обычно при построении системы координат принято указывать направление оси в виде стрелочки. Кроме того, при построении координатной плоскости каждая из осей подписывается.
Четверти
Теперь скажем пару слов о таком понятии, как четверти координатной плоскости. Плоскость разбивается двумя осями на четыре четверти. Каждая из них имеет свой номер, при этом нумерация плоскостей ведется против часовой стрелки.
Каждая из четвертей имеет свои особенности. Так, в первой четверти абсцисса и ордината положительная, во второй четверти абсцисса отрицательная, ордината — положительная, в третьей и абсцисса, и ордината отрицательные, в четвертой же положительной является абсцисса, а отрицательной — ордината.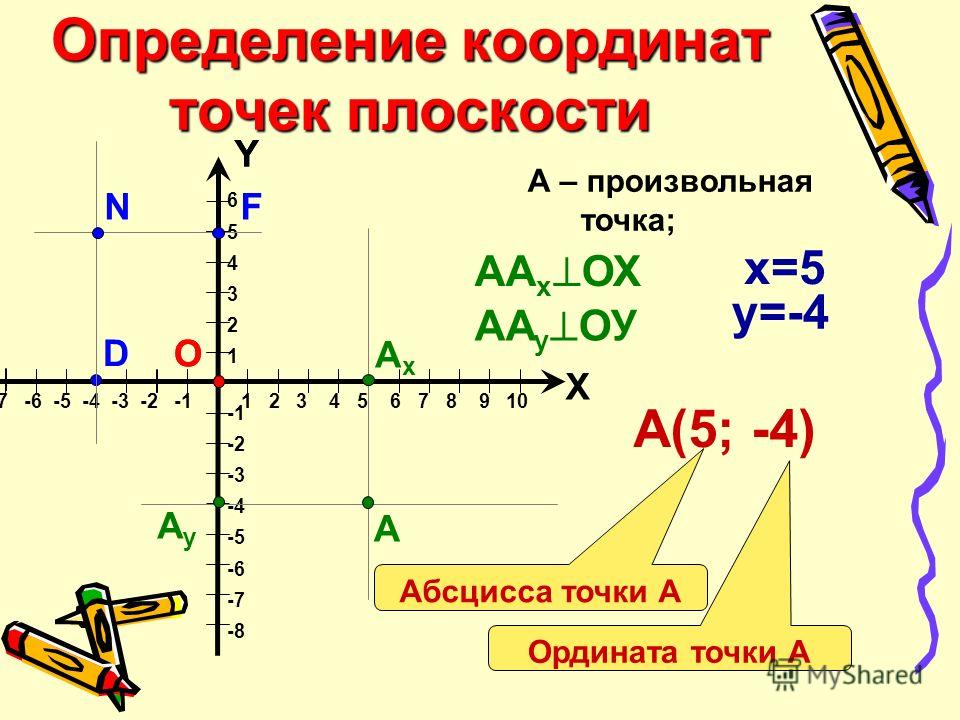
Запомнив эти особенности, можно с легкостью определить, к какой четверти относится та или иная точка. Кроме того, эта информация может пригодиться вам и в том случае, если придется делать вычисления, используя декартову систему.
Работа с координатной плоскостью
Когда мы разобрались с понятием плоскости и поговорили о ее четвертях, можно перейти к такой проблеме, как работа с данной системой, а также поговорить о том, как наносить на нее точки, координаты фигур. На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.
В первую очередь строится сама система, на нее наносятся все важные обозначения. Затем уже идет работа непосредственно с точками или фигурами. При этом даже при построении фигур сначала на плоскость наносятся точки, а затем уже прорисовываются фигуры.
Правила построения плоскости
Если вы решили начать отмечать на бумаге фигуры и точки, вам понадобится координатная плоскость. Координаты точек наносятся именно на нее.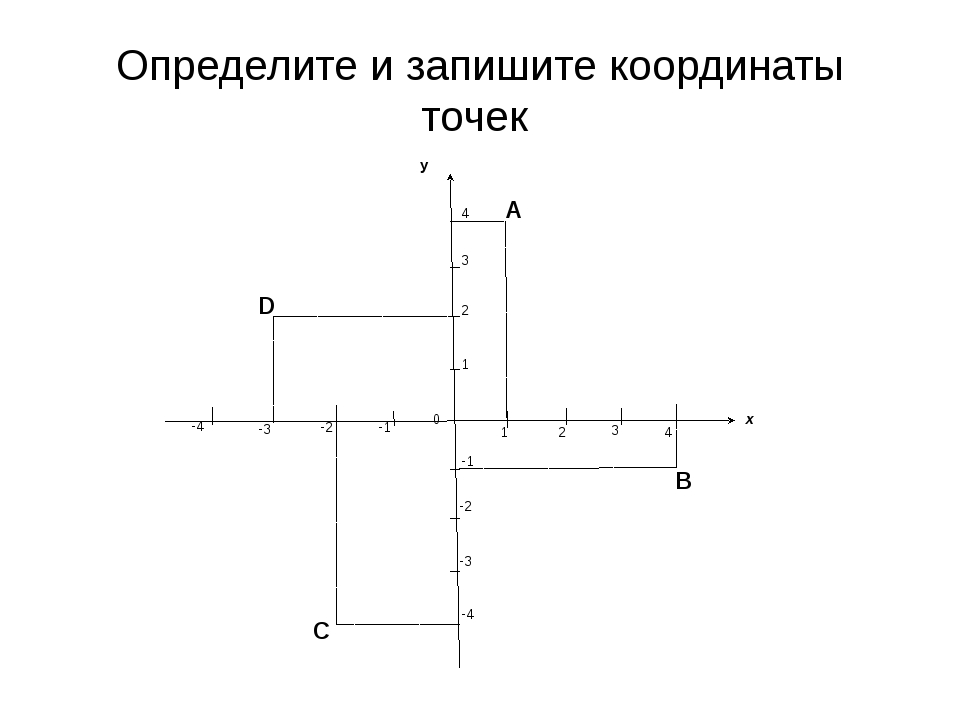 Для того чтобы построить координатную плоскость, понадобится только линейка и ручка или карандаш. Сначала рисуется горизонтальная ось абсцисс, затем вертикальная — ординат. При этом важно помнить, что оси пересекаются под прямым углом.
Для того чтобы построить координатную плоскость, понадобится только линейка и ручка или карандаш. Сначала рисуется горизонтальная ось абсцисс, затем вертикальная — ординат. При этом важно помнить, что оси пересекаются под прямым углом.
Следующим обязательным пунктом является нанесение разметки. На каждой из осей в обоих направлениях отмечаются и подписываются единицы-отрезки. Это делается для того, чтобы затем можно было работать с плоскостью с максимальным удобством.
Отмечаем точку
Теперь поговорим о том, как нанести координаты точек на координатной плоскости. Это основа, которую следует знать, чтобы успешно размещать на плоскости разнообразные фигуры, и даже отмечать уравнения.
При построении точек следует помнить, как правильно записываются их координаты. Так, обычно задавая точку, в скобках пишут две цифры. Первая цифра обозначает координату точки по оси абсцисс, вторая — по оси ординат.
Строить точку следует таким образом. Сначала отметить на оси Ox заданную точку, затем отметить точку на оси Oy . Далее провести воображаемые линии от данных обозначений и найти место их пересечения — это и будет заданная точка.
Далее провести воображаемые линии от данных обозначений и найти место их пересечения — это и будет заданная точка.
Вам останется только отметить ее и подписать. Как видите, все довольно просто и не требует особых навыков.
Размещаем фигуру
Теперь перейдем к такому вопросу, как построение фигур на координатной плоскости. Для того чтобы построить на координатной плоскости любую фигуру, следует знать, как размещать на ней точки. Если вы умеете это делать, то разместить фигуру на плоскости не так уж и сложно.
В первую очередь вам понадобятся координаты точек фигуры. Именно по ним мы и будем наносить на нашу систему координат выбранные вами Рассмотрим нанесение прямоугольника, треугольника и окружности.
Начнем с прямоугольника. Наносить его довольно просто. Сначала на плоскость наносятся четыре точки, обозначающие углы прямоугольника. Затем все точки последовательно соединяются между собой.
Нанесение треугольника ничем не отличается. Единственное — углов у него три, а значит, на плоскость наносятся три точки, обозначающие его вершины.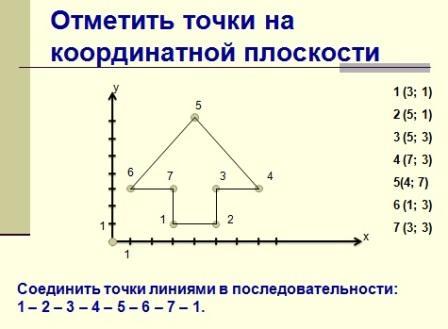
Касательно окружности тут следует знать координаты двух точек. Первая точка — центр окружности, вторая — точка, обозначающая ее радиус. Эти две точки наносятся на плоскость. Затем берется циркуль, измеряется расстояние между двумя точками. Острие циркуля ставится в точку, обозначающую центр, и описывается круг.
Как видите, тут также нет ничего сложного, главное, чтобы под рукой всегда были линейка и циркуль.
Теперь вы знаете, как наносить координаты фигур. На координатной плоскости это делать не так уж и сложно, как может показаться на первый взгляд.
Выводы
Итак, мы рассмотрели с вами одно из наиболее интересных и базовых для математики понятий, с которым приходится сталкиваться каждому школьнику.
Мы с вами выяснили, что координатная плоскость — это плоскость, образованная пересечением двух осей. С ее помощью можно задавать координаты точек, наносить на нее фигуры. Плоскость разделена на четверти, каждая из которых имеет свои особенности.
Основной навык, который следует выработать при работе с координатной плоскостью, — умение правильно наносить на нее заданные точки. Для этого следует знать правильное расположение осей, особенности четвертей, а также правила, по которым задаются координаты точек.
Для этого следует знать правильное расположение осей, особенности четвертей, а также правила, по которым задаются координаты точек.
Надеемся, что изложенная нами информация была доступна и понятна, а также была полезна для вас и помогла лучше разобраться в данной теме.
Что такое координатная плоскость?
Термин «координаты» в переводе с латинского языка значит слово «упорядоченный».
Допустим, нам нужно обозначить положение точки на плоскости. Для этого мы берем 2 перпендикулярные прямые, которые называются осями координат, где Х будет осью абсцисс, У- осью ординат, а началом координат будет точка О. Образованные с помощью осей координат прямые углы, будут называться координатными углами.
Так мы подошли к определению и теперь знаем, что координатной плоскостью является плоскость с заданной системой координат.
А теперь давайте посмотрим, нумерацию координатных углов:
Теперь давайте с вами отобразим прямоугольную систему координат и отметим в ней точку M.
Далее нам нужно прочертить через точку М прямую, которая будет параллельна оси У. Теперь, смотрим, что у нас вышло. Как видим, что прямая пересекает ось Х в той точке, в которой координата будет равна −2. Данная координата является абсциссой точки M.
Теперь нам нужно прочертить через точку М прямую, которая будет параллельна оси Х.
Мы с вами видим, что эта прямая пересекает ось Х в той точке, координата которой равняется трем. Вот эта координата будет ординатой точки М.
Запись координат токи М будет выглядеть так:
В такой записи всегда на первое место ставят абсциссу, а на второе – ординату. Если рассмотреть на примере координат точки М(-2;3), то -2 выступает в роли абсциссы точки М, а ординатой этой точки будет число 3.
Из этого следует, что на координатной плоскости каждой точке М соответствует такая пара чисел, как ее абсцисса и ордината. Верным будет и утверждение наоборот, то есть, каждой такой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.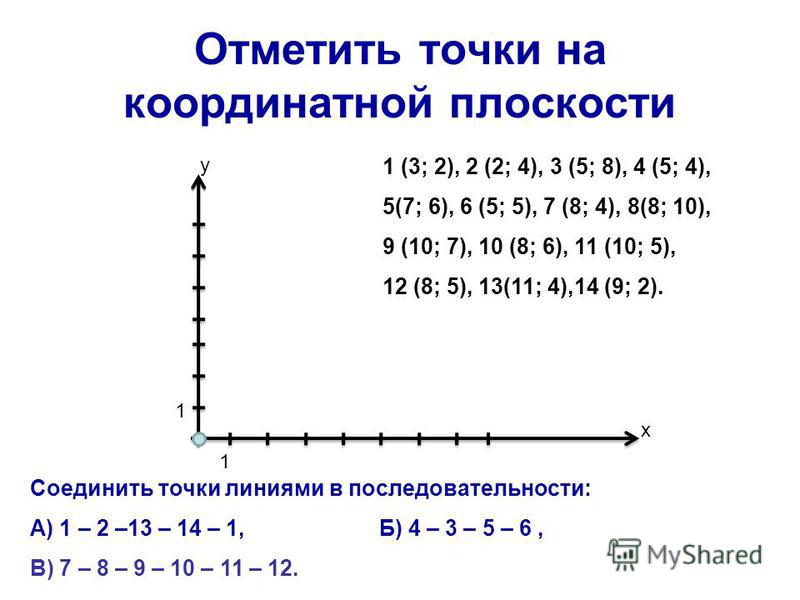
Задание:
Координатная плоскость в жизни
Как по вашему, может ли пригодиться в повседневной жизни знания о координатной плоскости? И доводилось ли вам слышать такую фразу, как «оставьте свои координаты» или «по каким координатам вас можно найти»? И задумывались ли вы над тем, что может обозначать эти выражения?
Оказывается все очень просто и банально и это значит местонахождение того или иного объекта, по которому легко найти человека или какое-то определенное место. Можно уверенно утверждать, что системы координат необходимы в практической жизни человека повсеместно.
Такой системой координат может быть как домашний адрес, так и номер телефона, место работы и т.д.
Ведь даже при покупке билетов на поезд, вы знаете не только его номер и место назначения, но и обязательно должен быть указан номер вагона и места.
Чтобы пойти в гости к однокласснику, недостаточно знать только дом, в котором он живет, а нужно еще и знать номер квартиры.
Задание
1. Какими сведениями вы должны владеть, чтобы занять место в театре?
2. Какие данные нужно иметь, чтобы определить точки на земной поверхности?
3. По каким координатам можно определить место в кинотеатре?
4. Что необходимо знать, чтобы определелить положения фигуры на шахматной доске?
5. Какими координатами вы пользуетесь при игре в морской бой?
Историческая справка
Идея использования координат появилась еще в глубокой древности. Первоначально их применять начали астрономы, для определения небесных светил и географы – для определения местонахождения и объектов на поверхности Земли.
Благодаря трудам древнегреческого астронома Клавдия Плотомея уже во втором веке ученые научились определять долготу и широту.
А известно ли вам, почему в математике существует такое понятие, как «Декартова система координат»? Оказывается метод координат, который имеет общематематическое значение, был открыт французскими математиками Пьером Ферма и Рене Декартом в XVII в.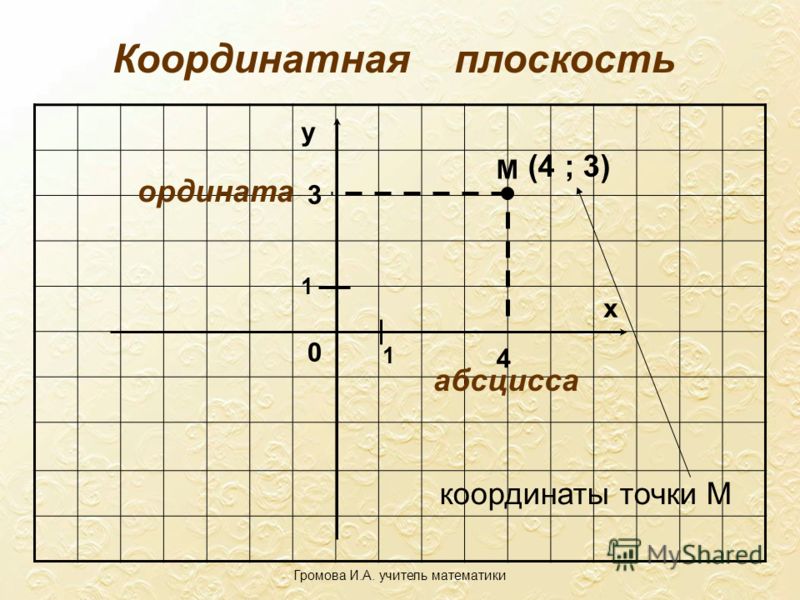 , а в 1637 году Рене Декарт впервые описал его в книге по геометрии.
, а в 1637 году Рене Декарт впервые описал его в книге по геометрии.
А вот термины «абсцисса», «ордината» и «координаты» были впервые введены Вильгельмом Лейбницем в семнадцатом веке.
Домашнее задание:
Для указания взаимного расположения каких-то исследуемых объектов используются:
- координатный луч, когда их размещение или движение происходят вдоль прямой линии по одну сторону от заданного объекта, принятого за начало отсчёта;
- координатная прямая, когда их размещение или движение происходят вдоль прямой линии по разные стороны от заданного объекта, принятого за начало отсчёта;
- координатная плоскость, когда их размещение или движение происходят вдоль произвольной непрямой линии.
Элементы координатной плоскости
Координатная плоскость отличается от обычной плоскости тем, что на неё наносится система координат. Примером может служить изображение любого материка с нанесёнными на него параллелями и меридианами, которые и задают систему географических координат, позволяющих находить или задавать положение любого объекта на карте.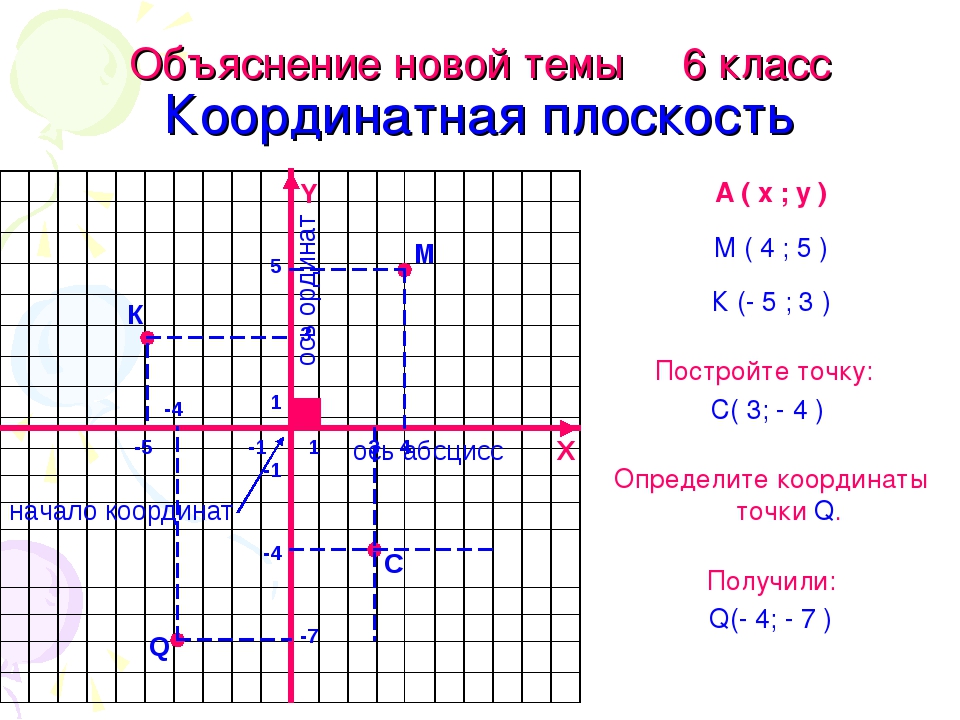
Система координат представляет собой две взаимно пересекающиеся под прямым углом координатные прямые в точках начала отсчёта. Горизонтальную координатную прямую принято называть осью абсцисс (абсцисса с лат. яз. – отрезок). Вертикальную прямую – осью ординат (ордината с лат. яз. – выстраивание по порядку).
Аналогично, координатная прямая отличается от обычной прямой тем, что на ней выбирают какую-то точку за начало отсчёта; выбирают масштаб единичного отрезка в зависимости от того, какие расстояния предстоит изображать; положительное направление отсчёта, обозначаемое на координатной прямой стрелкой.
Положение объекта на такой плоскости обозначают точкой с двумя числами – координатами: абсциссой и ординатой.
Использование координатных плоскостей
Координатные плоскости широко используются для решения геометрических и физических задач. Причём в физике за ось абсцисс часто принимают ось времени. Тогда ось ординат задаёт координату тела на координатной прямой, располагаемой вдоль прямолинейной траектории движения тела.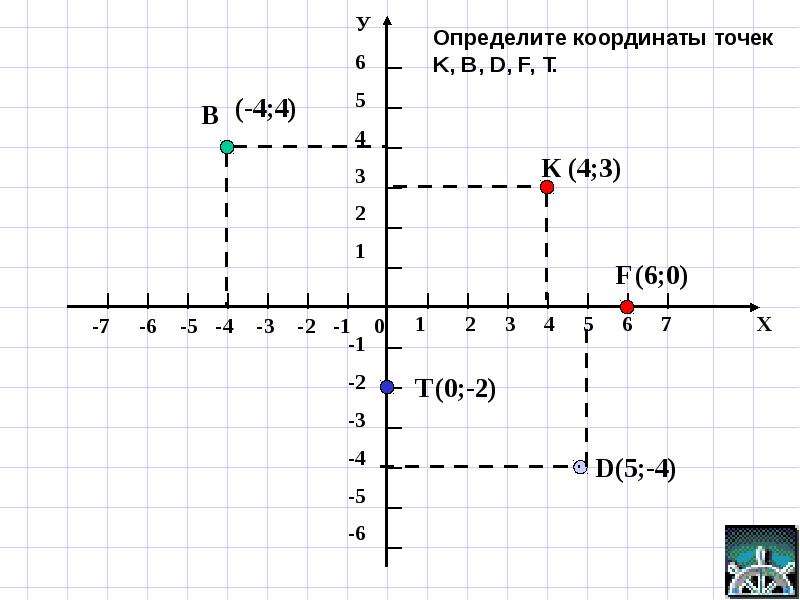
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат , на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).
Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой.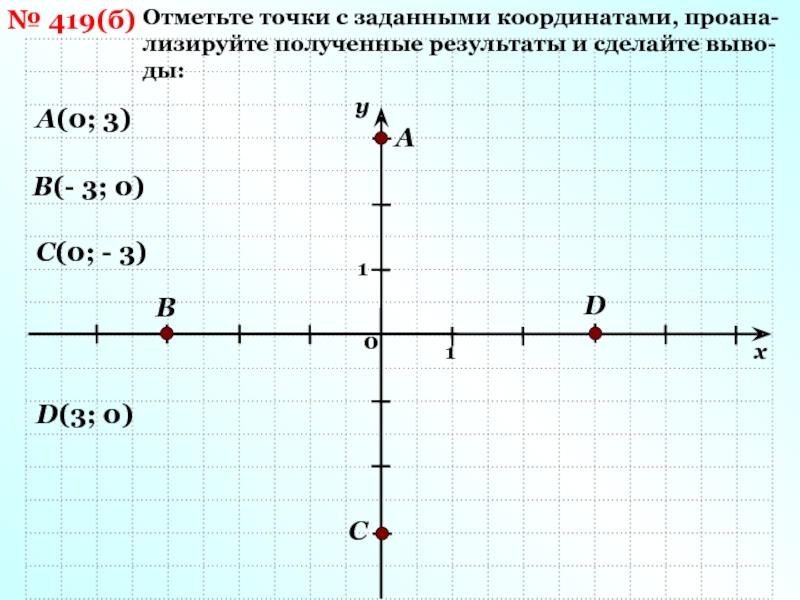 Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).
Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).
Орты
Прямоугольная система координат (любой размерности) также описывается набором ортов , сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
В трёхмерном случае такие орты обычно обозначаются i j k или e x e y e z . При этом в случае правой системы координат действительны следующие формулы с векторным произведением векторов :
- [i j ]=k ;
- [j k ]=i ;
- [k i ]=j .
История
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году . Поэтому прямоугольную систему координат называют также — Декартова система координат . Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма , однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
См.
 также
такжеСсылки
Wikimedia Foundation . 2010 .
Смотреть что такое «Координатная плоскость» в других словарях:
плоскость резания — (Pn) Координатная плоскость, касательная к режущей кромке в рассматриваемой точке и перпендикулярная основной плоскости. [ …
В топографии сеть воображаемых линий, опоясывающих земной шар в широтном и меридиональном направлениях, с помощью которой можно точно определить положение любой точки на земной поверхности. Отсчет широт ведется от экватора – большой окружности,… … Географическая энциклопедия
В топографии сеть воображаемых линий, опоясывающих земной шар в широтном и меридиональном направлениях, с помощью которой можно точно определить положение любой точки на земной поверхности. Отсчет широт ведется от экватора большой окружности,… … Энциклопедия Кольера
У этого термина существуют и другие значения, см. Фазовая диаграмма. Фазовая плоскость координатная плоскость, в которой по осям координат откладываются какие либо две переменные (фазовые координаты), однозначно определяющие состояние системы… … Википедия
главная секущая плоскость — (Pτ) Координатная плоскость, перпендикулярная линии пересечения основной плоскости и плоскости резания.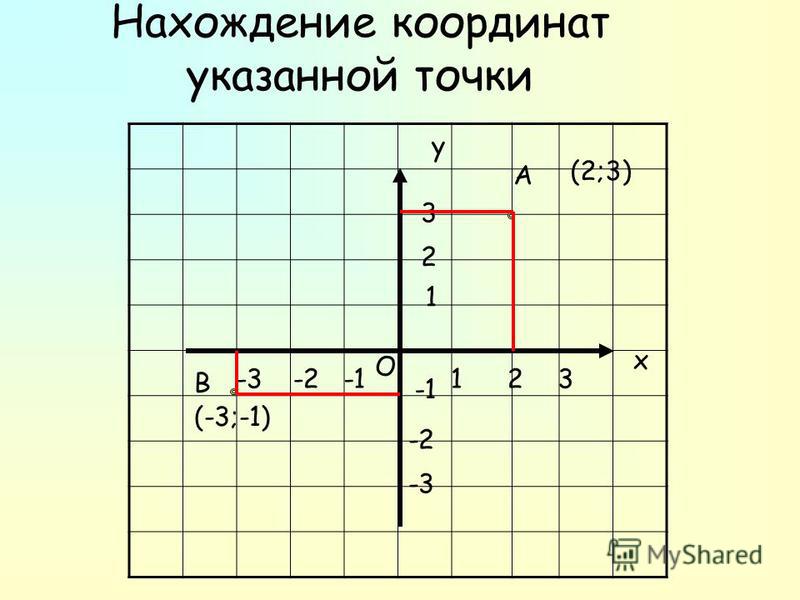 [ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и координатные плоскости … Справочник технического переводчика
[ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и координатные плоскости … Справочник технического переводчика
инструментальная главная секущая плоскость — (Pτи) Координатная плоскость, перпендикулярная линии пересечения инструментальных основной плоскости и плоскости резания. [ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и координатные плоскости … Справочник технического переводчика
инструментальная плоскость резания — (Pnи) Координатная плоскость, касательная к режущей кромке в рассматриваемой точке и перпендикулярная инструментальной основной плоскости. [ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и… … Справочник технического переводчика
кинематическая главная секущая плоскость — (Pτк) Координатная плоскость, перпендикулярная линии пересечения кинематических основной плоскости и плоскости резания … Справочник технического переводчика
кинематическая плоскость резания — (Pnк) Координатная плоскость, касательная к режущей кромке в рассматриваемой точке и перпендикулярная кинематической основной плоскости … Справочник технического переводчика
основная плоскость — (Pv) Координатная плоскость, проведенная через рассматриваемую точку режущей кромки перпендикулярно направлению скорости главного или результирующего движения резания в этой точке.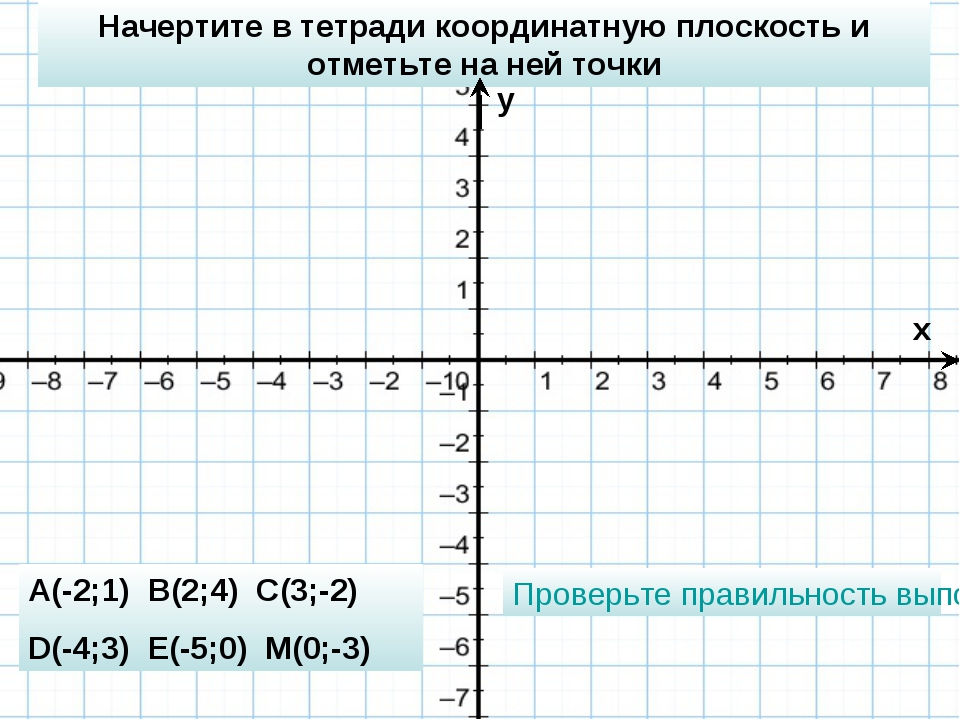 Примечание В инструментальной системе координат направление… … Справочник технического переводчика
Примечание В инструментальной системе координат направление… … Справочник технического переводчика
что это такое? Как отмечать точки и строить фигуры на координатной плоскости?
Математика – наука довольно сложная. Изучая ее, приходится не только решать примеры и задачи, но и работать с различными фигурами, и даже плоскостями. Одной из наиболее используемых в математике является система координат на плоскости. Правильной работе с ней детей учат не один год. Поэтому важно знать, что это такое и как правильно с ней работать.
Давайте же разберемся, что представляет собой данная система, какие действия можно выполнять с ее помощью, а также узнаем ее основные характеристики и особенности.
Определение понятия
Координатная плоскость — это плоскость, на которой задана определенная система координат. Такая плоскость задается двумя прямыми, пересекающимися под прямым углом. В точке пересечения этих прямых находится начало координат. Каждая точка на координатной плоскости задается парой чисел, которые называют координатами.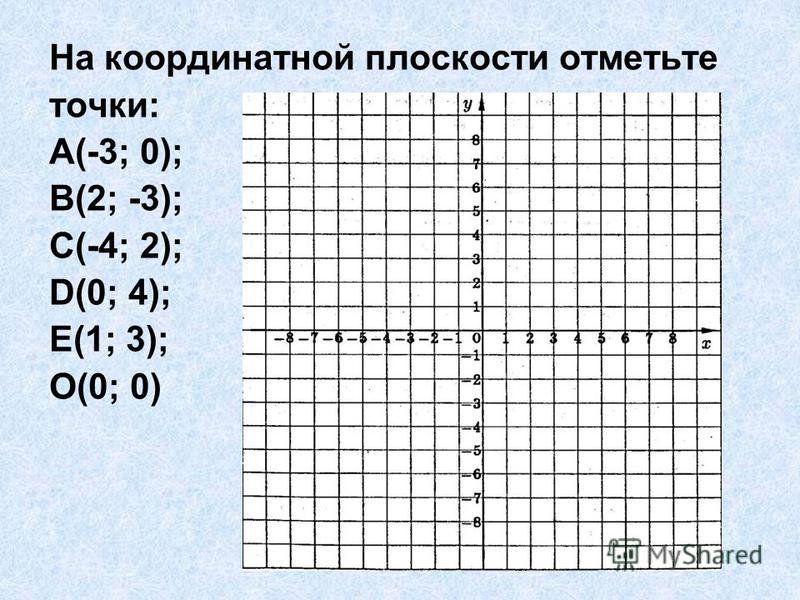
В школьном курсе математики школьникам приходится довольно тесно работать с системой координат – строить на ней фигуры и точки, определять, какой плоскости принадлежит та или иная координата, а также определять координаты точки и записывать или называть их. Поэтому поговорим подробнее обо всех особенностях координат. Но прежде коснемся истории создания, а затем уже поговорим о том, как работать на координатной плоскости.
Историческая справка
Идеи о создании системы координат были еще во времена Птоломея. Уже тогда астрономы и математики думали о том, как научиться задавать положение точки на плоскости. К сожалению, в то время еще не было известной нам системы координат, и ученым приходилось пользоваться другими системами.
Изначально они задавали точки с помощью указания широты и долготы. Долгое время это был один из наиболее используемых способов нанесения на карту той или иной информации. Но в 1637 году Рене Декарт создал собственную систему координат, названную впоследствии в честь великого математика «декартовой».
После опубликования труда «Геометрия» система координат Рене Декарта завоевала признание в научных кругах.
Уже в конце XVII в. понятие «координатная плоскость» стало широко использоваться в мире математики. Несмотря на то что с момента создания данной системы прошло уже несколько веков, она до сих пор широко используется в математике и даже в жизни.
Примеры координатной плоскости
Прежде чем говорить о теории, приведем несколько наглядных примеров координатной плоскости, чтобы вы смогли представить ее себе. В первую очередь координатная система используется в шахматах. На доске каждый квадрат имеет свои координаты – одну координату буквенную, вторую – цифровую. С ее помощью можно определить положение той или иной фигуры на доске.
Вторым наиболее ярким примером может служить любимая многими игра «Морской бой». Вспомните, как, играя, вы называете координату, например, В3, таким образом указывая, куда именно целитесь. При этом, расставляя корабли, вы задаете точки на координатной плоскости.
Данная система координат широко применяется не только в математике, логических играх, но и в военном деле, астрономии, физике и многих других науках.
Оси координат
Как уже говорилось, в системе координат выделяют две оси. Поговорим немного о них, так как они имеют немалое значение.
Первая ось — абсцисс — горизонтальная. Она обозначается как (Ox). Вторая ось — ординат, которая проходит вертикально через точку отсчета и обозначается как (Oy). Именно эти две оси образуют систему координат, разбивая плоскость на четыре четверти. Начало отсчета находится в точке пересечения этих двух осей и принимает значение 0. Только в случае если плоскость образована двумя пересекающимися перпендикулярно осями, имеющими точку отсчета, это координатная плоскость.
Также отметим, что каждая из осей имеет свое направление. Обычно при построении системы координат принято указывать направление оси в виде стрелочки. Кроме того, при построении координатной плоскости каждая из осей подписывается.
Четверти
Теперь скажем пару слов о таком понятии, как четверти координатной плоскости. Плоскость разбивается двумя осями на четыре четверти. Каждая из них имеет свой номер, при этом нумерация плоскостей ведется против часовой стрелки.
Каждая из четвертей имеет свои особенности. Так, в первой четверти абсцисса и ордината положительная, во второй четверти абсцисса отрицательная, ордината — положительная, в третьей и абсцисса, и ордината отрицательные, в четвертой же положительной является абсцисса, а отрицательной — ордината.
Запомнив эти особенности, можно с легкостью определить, к какой четверти относится та или иная точка. Кроме того, эта информация может пригодиться вам и в том случае, если придется делать вычисления, используя декартову систему.
Работа с координатной плоскостью
Когда мы разобрались с понятием плоскости и поговорили о ее четвертях, можно перейти к такой проблеме, как работа с данной системой, а также поговорить о том, как наносить на нее точки, координаты фигур. На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.
На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.В первую очередь строится сама система, на нее наносятся все важные обозначения. Затем уже идет работа непосредственно с точками или фигурами. При этом даже при построении фигур сначала на плоскость наносятся точки, а затем уже прорисовываются фигуры.
Далее мы поговорим подробнее о построении системы и непосредственно нанесении точек и фигур.
Правила построения плоскости
Если вы решили начать отмечать на бумаге фигуры и точки, вам понадобится координатная плоскость. Координаты точек наносятся именно на нее. Для того чтобы построить координатную плоскость, понадобится только линейка и ручка или карандаш. Сначала рисуется горизонтальная ось абсцисс, затем вертикальная — ординат. При этом важно помнить, что оси пересекаются под прямым углом.
Далее на каждой оси указывают направление и подписывают их с помощью общепринятых обозначений x и y. Также отмечается точка пересечения осей и подписывается цифрой 0.
Следующим обязательным пунктом является нанесение разметки. На каждой из осей в обоих направлениях отмечаются и подписываются единицы-отрезки. Это делается для того, чтобы затем можно было работать с плоскостью с максимальным удобством.
Отмечаем точку
Теперь поговорим о том, как нанести координаты точек на координатной плоскости. Это основа, которую следует знать, чтобы успешно размещать на плоскости разнообразные фигуры, и даже отмечать уравнения.
При построении точек следует помнить, как правильно записываются их координаты. Так, обычно задавая точку, в скобках пишут две цифры. Первая цифра обозначает координату точки по оси абсцисс, вторая — по оси ординат.
Строить точку следует таким образом. Сначала отметить на оси Ox заданную точку, затем отметить точку на оси Oy. Далее провести воображаемые линии от данных обозначений и найти место их пересечения — это и будет заданная точка.
Вам останется только отметить ее и подписать. Как видите, все довольно просто и не требует особых навыков.
Размещаем фигуру
Теперь перейдем к такому вопросу, как построение фигур на координатной плоскости. Для того чтобы построить на координатной плоскости любую фигуру, следует знать, как размещать на ней точки. Если вы умеете это делать, то разместить фигуру на плоскости не так уж и сложно.
В первую очередь вам понадобятся координаты точек фигуры. Именно по ним мы и будем наносить на нашу систему координат выбранные вами геометрические фигуры. Рассмотрим нанесение прямоугольника, треугольника и окружности.
Начнем с прямоугольника. Наносить его довольно просто. Сначала на плоскость наносятся четыре точки, обозначающие углы прямоугольника. Затем все точки последовательно соединяются между собой.
Нанесение треугольника ничем не отличается. Единственное – углов у него три, а значит, на плоскость наносятся три точки, обозначающие его вершины.
Касательно окружности тут следует знать координаты двух точек. Первая точка – центр окружности, вторая – точка, обозначающая ее радиус.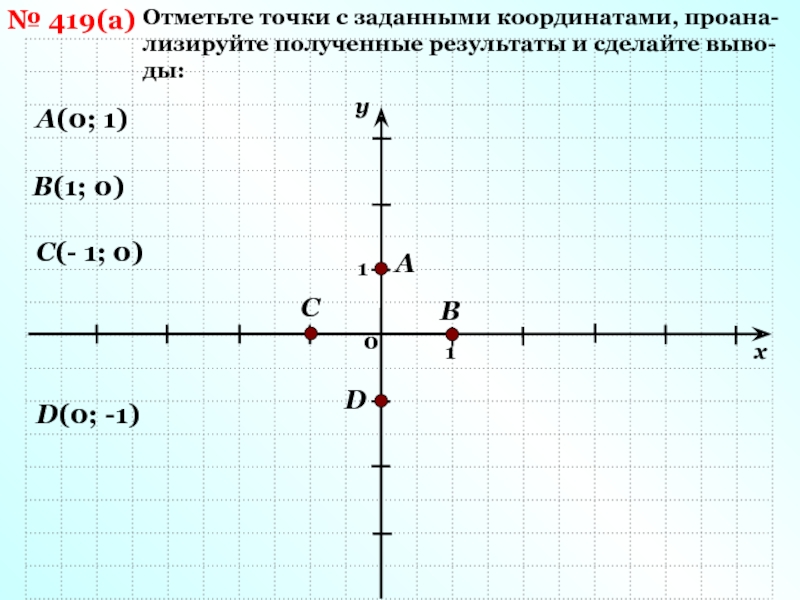 Эти две точки наносятся на плоскость. Затем берется циркуль, измеряется расстояние между двумя точками. Острие циркуля ставится в точку, обозначающую центр, и описывается круг.
Эти две точки наносятся на плоскость. Затем берется циркуль, измеряется расстояние между двумя точками. Острие циркуля ставится в точку, обозначающую центр, и описывается круг.
Как видите, тут также нет ничего сложного, главное, чтобы под рукой всегда были линейка и циркуль.
Теперь вы знаете, как наносить координаты фигур. На координатной плоскости это делать не так уж и сложно, как может показаться на первый взгляд.
Выводы
Итак, мы рассмотрели с вами одно из наиболее интересных и базовых для математики понятий, с которым приходится сталкиваться каждому школьнику.
Мы с вами выяснили, что координатная плоскость – это плоскость, образованная пересечением двух осей. С ее помощью можно задавать координаты точек, наносить на нее фигуры. Плоскость разделена на четверти, каждая из которых имеет свои особенности.
Основной навык, который следует выработать при работе с координатной плоскостью, – умение правильно наносить на нее заданные точки. Для этого следует знать правильное расположение осей, особенности четвертей, а также правила, по которым задаются координаты точек.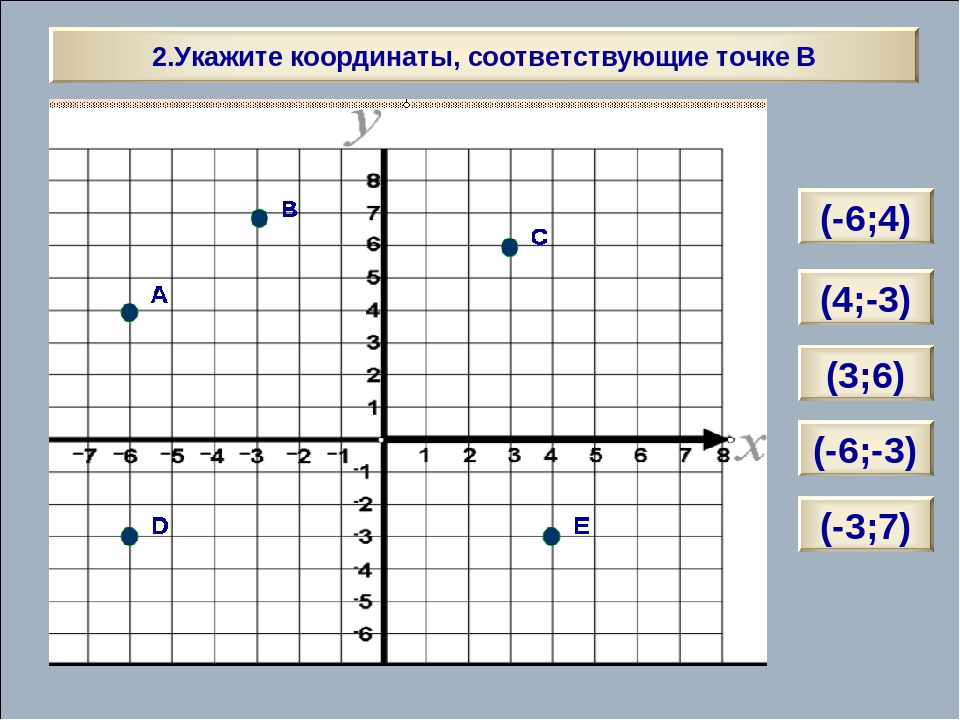
Надеемся, что изложенная нами информация была доступна и понятна, а также была полезна для вас и помогла лучше разобраться в данной теме.
что это такое? Как отмечать точки и строить фигуры на координатной плоскости
В повседневной жизни часто можно услышать фразу: «Оставь мне свои координаты». В ответ человек обычно оставляет свой адрес или номер телефона, то есть данные, по которым его можно найти.
Координаты могут обозначаться самыми разными наборами цифр или букв.
Например, номер автомобиля — это координаты, потому что по номеру машины можно определить из какого она города и кто ёё владелец.
Координаты — это набор данных, по которому определяется положение того или иного объекта.
Примерами координат являются: номер вагона и места в поезде, широта и долгота на географической карте, запись положения фигуры на шахматной доске, положение точки на числовой оси и т.д.
Всегда, когда мы по определенным правилам однозначно обозначаем какой-то объект набором букв, чисел или других символов, мы задаём координаты объекта.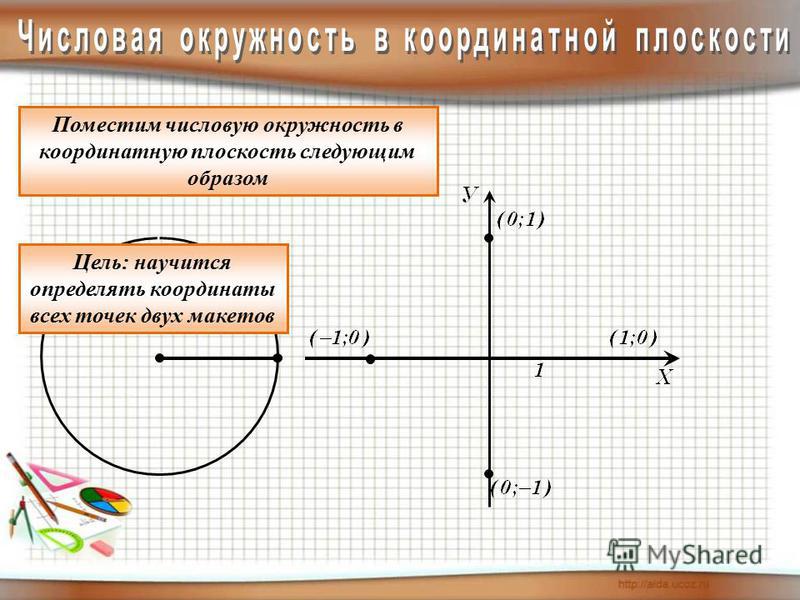
Декартова система координат
Французкий математик Рене Декарт (1596 — 1650) предложил задавать положение точки на плоскости с помощью двух координат.
Для нахождения координат нужны ориентиры, от которых ведётся отсчёт.
- На плоскости такими ориентирами будут служить две числовые оси. На чертеже обычно первую ось рисуют горизонтально, её называютосью АБСЦИСС и обозначают буквой X, записывают ось Ox. Положительное направление на оси абсцисс выбирают слева направои показывают стрелкой.
- Вторую ось проводят вертикально, её называют осью ОРДИНАТ и обозначают буквой Y, записывают ось Oy. Положительное направление на оси ординат выбирают снизу вверх и показывают стрелкой.
Оси взаимно перпендикулярны (т.е. угол между ними равен 90°) и пересекаются в точке, которую обозначают O. Точка O является началом отсчёта для каждой из осей.
Система координат — это две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом отсчёта для каждой из них.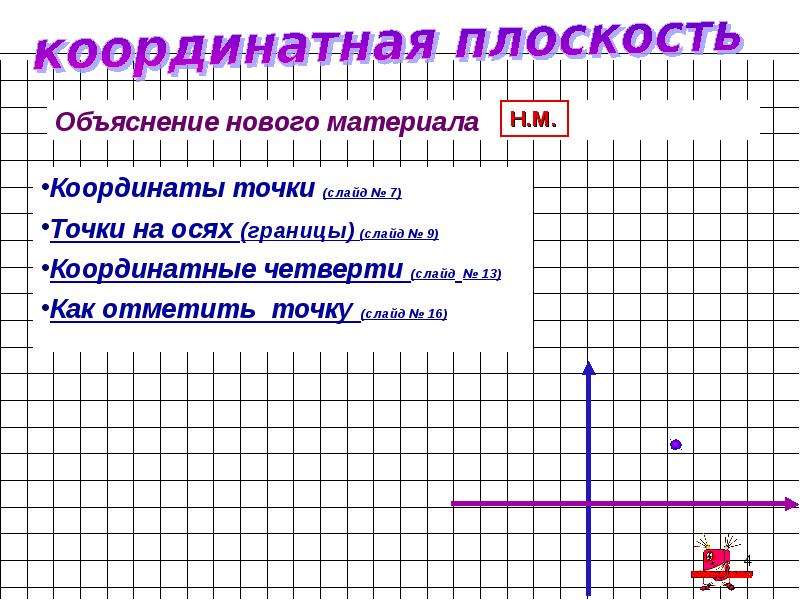
Координатные оси — это прямые, образующие систему координат.
Ось абсцисс (Ox) — горизонтальная ось.
Ось ординат (Oy) — вертикальная ось.
Координатная плоскость — плоскость, в которой построена система координат. Обозначается плоскость как x0y.
Обращаем ваше внимание на выбор длины единичных отрезков по осям.
Цифры, обозначающие числовые значения на осях можно располагать как справа, так и слева от оси Oy. Цифры на оси Ox, как правило, пишут внизу под осью.
Обычно единичный отрезок на оси 0y равен единичному отрезку на оси 0x. Но бывают случаи, когда они не равны друг другу.
Оси координат делят плоскость на 4 угла, которые называюткоординатными четвертями . Четверть, образованная положительными полуосями (правый верхний угол), считают первой (I).
Отсчитываем четверти (или координатные углы) против часовой стрелки.
Если расположить единичную числовую окружность на координатной плоскости, то для ее точек можно найти координаты. Числовую окружность располагают так, чтобы ее центр совпал с точкой начала координат плоскости, т. е. точкой O (0; 0).
Числовую окружность располагают так, чтобы ее центр совпал с точкой начала координат плоскости, т. е. точкой O (0; 0).
Обычно на единичной числовой окружности отмечают точки соответствующие от начала отсчета на окружности
- четвертям — 0 или 2π, π/2, π, (2π)/3,
- серединам четвертей — π/4, (3π)/4, (5π)/4, (7π)/4,
- третям четвертей — π/6, π/3, (2π)/3, (5π)/6, (7π)/6, (4π)/3, (5π)/3, (11π)/6.
На координатной плоскости при указанном выше расположении на ней единичной окружности можно найти координаты, соответствующие этим точкам окружности.
Координаты концов четвертей найти очень легко. У точки 0 окружности координата x равна 1, а y равен 0. Можно обозначить так A (0) = A (1; 0).
Конец первой четверти будет располагаться на положительной полуоси ординат. Следовательно, B (π/2) = B (0; 1).
Конец второй четверти находится на отрицательной полуоси абсцисс: C (π) = C (-1; 0).
Конец третьей четверти: D ((2π)/3) = D (0; -1).
Но как найти координаты середин четвертей? Для этого строят прямоугольный треугольник. Его гипотенузой является отрезок от центра окружности (или начала координат) к точке середины четверти окружности. Это радиус окружности. Поскольку окружность единичная, то гипотенуза равна 1. Далее проводят перпендикуляр из точки окружности к любой оси. Пусть будет к оси x. Получается прямоугольный треугольник, длины катетов которого — это и есть координаты x и y точки окружности.
Четверть окружности составляет 90º. А половина четверти составляет 45º. Поскольку гипотенуза проведена к точке середины четверти, то угол между гипотенузой и катетом, выходящим из начала координат, равен 45º. Но сумма углов любого треугольника равна 180º. Следовательно, на угол между гипотенузой и другим катетом остается также 45º. Получается равнобедренный прямоугольный треугольник.
Из теоремы Пифагора получаем уравнение x 2 + y 2 = 1 2 . Поскольку x = y, а 1 2 = 1, то уравнение упрощается до x 2 + x 2 = 1.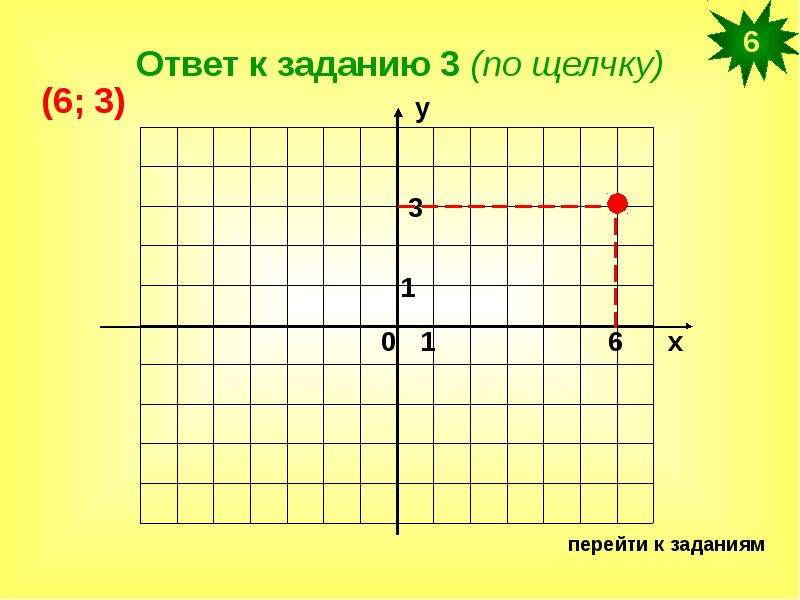 Решив его, получаем x = √½ = 1/√2 = √2/2.
Решив его, получаем x = √½ = 1/√2 = √2/2.
Таким образом, координаты точки M 1 (π/4) = M 1 (√2/2; √2/2).
В координатах точек середин других четвертей будут меняться только знаки, а модули значений оставаться такими же, так как прямоугольный треугольник будет только переворачиваться. Получим:
M 2 ((3π)/4) = M 2 (-√2/2; √2/2)
M 3 ((5π)/4) = M 3 (-√2/2; -√2/2)
M 4 ((7π)/4) = M 4 (√2/2; -√2/2)
При определении координат третьих частей четвертей окружности также строят прямоугольный треугольник. Если брать точку π/6 и проводить перпендикуляр к оси x, то угол между гипотенузой и катетом, лежащим на оси x, составит 30º. Известно, что катет, лежащий против угла в 30º, равен половине гипотенузы. Значит, мы нашли координату y, она равна ½.
Зная длины гипотенузы и одного из катетов, по теореме Пифагора находим другой катет:
x 2 + (½) 2 = 1 2
x 2 = 1 — ¼ = ¾
x = √3/2
Таким образом T 1 (π/6) = T 1 (√3/2; ½).
Для точки второй трети первой четверти (π/3) перпендикуляр на ось лучше провести к оси y.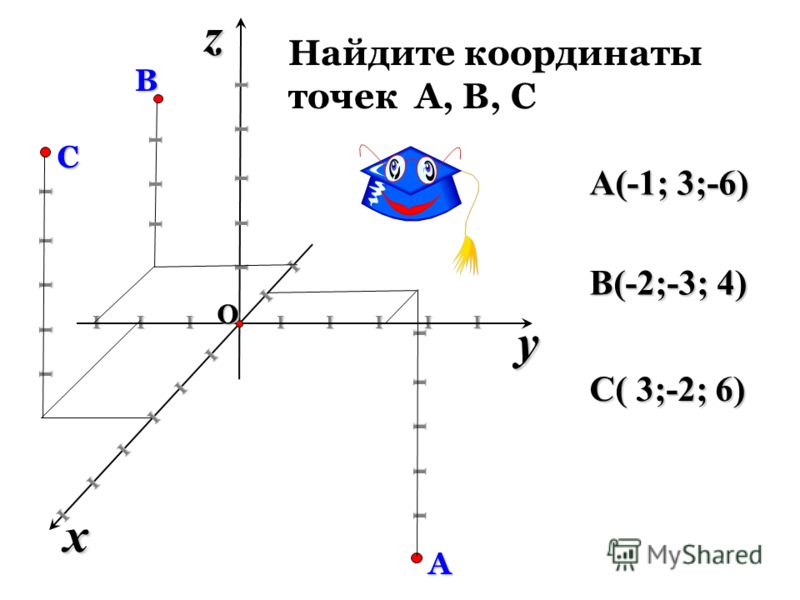 Тогда угол при начале координат также будет 30º. Здесь уже координата x будет равна ½, а y соответственно √3/2: T 2 (π/3) = T 2 (½; √3/2).
Тогда угол при начале координат также будет 30º. Здесь уже координата x будет равна ½, а y соответственно √3/2: T 2 (π/3) = T 2 (½; √3/2).
Для других точек третей четвертей будут меняться знаки и порядок значений координат. Все точки, которые ближе расположены к оси x будут иметь по модулю значение координаты x, равное √3/2. Те точки, которые ближе к оси y, будут иметь по модулю значение y, равное √3/2.
T 3 ((2π)/3) = T 3 (-½; √3/2)
T 4 ((5π)/6) = T 4 (-√3/2; ½)
T 5 ((7π)/6) = T 5 (-√3/2; -½)
T 6 ((4π)/3) = T 6 (-½; -√3/2)
T 7 ((5π)/3) = T 7 (½; -√3/2)
T 8 ((11π)/6) = T 8 (√3/2; -½)
Математика — наука довольно сложная. Изучая ее, приходится не только решать примеры и задачи, но и работать с различными фигурами, и даже плоскостями. Одной из наиболее используемых в математике является система координат на плоскости. Правильной работе с ней детей учат не один год. Поэтому важно знать, что это такое и как правильно с ней работать.
Давайте же разберемся, что представляет собой данная система, какие действия можно выполнять с ее помощью, а также узнаем ее основные характеристики и особенности.
Определение понятия
Координатная плоскость — это плоскость, на которой задана определенная система координат. Такая плоскость задается двумя прямыми, пересекающимися под прямым углом. В точке пересечения этих прямых находится начало координат. Каждая точка на координатной плоскости задается парой чисел, которые называют координатами.
В школьном курсе математики школьникам приходится довольно тесно работать с системой координат — строить на ней фигуры и точки, определять, какой плоскости принадлежит та или иная координата, а также определять координаты точки и записывать или называть их. Поэтому поговорим подробнее обо всех особенностях координат. Но прежде коснемся истории создания, а затем уже поговорим о том, как работать на координатной плоскости.
Историческая справка
Идеи о создании системы координат были еще во времена Птоломея. Уже тогда астрономы и математики думали о том, как научиться задавать положение точки на плоскости. К сожалению, в то время еще не было известной нам системы координат, и ученым приходилось пользоваться другими системами.
Изначально они задавали точки с помощью указания широты и долготы. Долгое время это был один из наиболее используемых способов нанесения на карту той или иной информации. Но в 1637 году Рене Декарт создал собственную систему координат, названную впоследствии в честь «декартовой».
Уже в конце XVII в. понятие «координатная плоскость» стало широко использоваться в мире математики. Несмотря на то что с момента создания данной системы прошло уже несколько веков, она до сих пор широко используется в математике и даже в жизни.
Примеры координатной плоскости
Прежде чем говорить о теории, приведем несколько наглядных примеров координатной плоскости, чтобы вы смогли представить ее себе. В первую очередь координатная система используется в шахматах. На доске каждый квадрат имеет свои координаты — одну координату буквенную, вторую — цифровую. С ее помощью можно определить положение той или иной фигуры на доске.
Вторым наиболее ярким примером может служить любимая многими игра «Морской бой».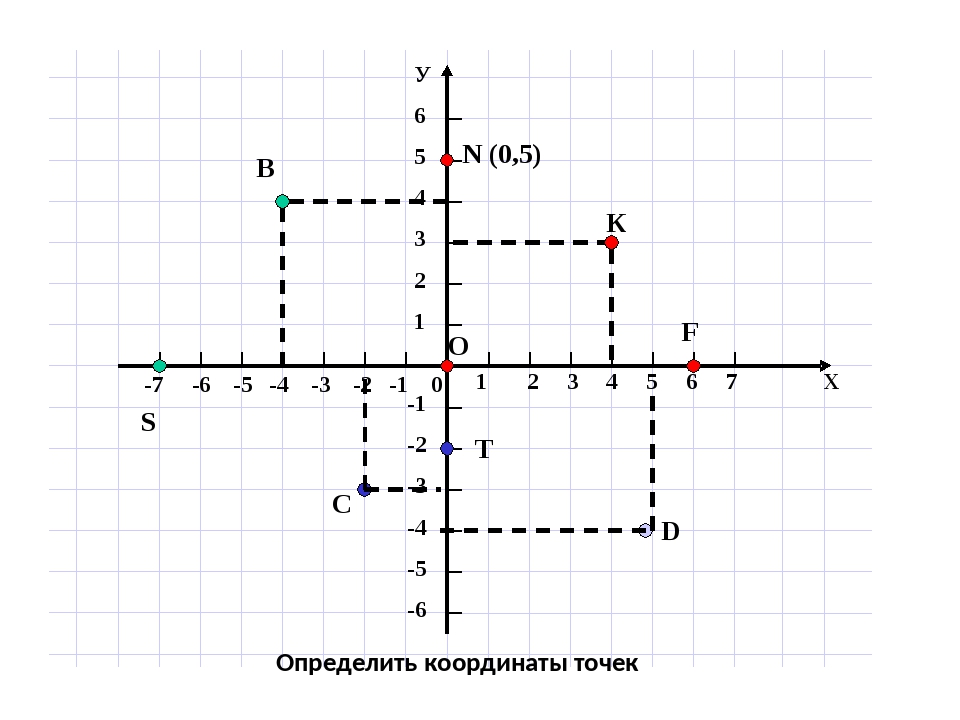 Вспомните, как, играя, вы называете координату, например, В3, таким образом указывая, куда именно целитесь. При этом, расставляя корабли, вы задаете точки на координатной плоскости.
Вспомните, как, играя, вы называете координату, например, В3, таким образом указывая, куда именно целитесь. При этом, расставляя корабли, вы задаете точки на координатной плоскости.
Данная система координат широко применяется не только в математике, логических играх, но и в военном деле, астрономии, физике и многих других науках.
Оси координат
Как уже говорилось, в системе координат выделяют две оси. Поговорим немного о них, так как они имеют немалое значение.
Первая ось — абсцисс — горизонтальная. Она обозначается как (Ox ). Вторая ось — ординат, которая проходит вертикально через точку отсчета и обозначается как (Oy ). Именно эти две оси образуют систему координат, разбивая плоскость на четыре четверти. Начало отсчета находится в точке пересечения этих двух осей и принимает значение 0 . Только в случае если плоскость образована двумя пересекающимися перпендикулярно осями, имеющими точку отсчета, это координатная плоскость.
Также отметим, что каждая из осей имеет свое направление. Обычно при построении системы координат принято указывать направление оси в виде стрелочки. Кроме того, при построении координатной плоскости каждая из осей подписывается.
Обычно при построении системы координат принято указывать направление оси в виде стрелочки. Кроме того, при построении координатной плоскости каждая из осей подписывается.
Четверти
Теперь скажем пару слов о таком понятии, как четверти координатной плоскости. Плоскость разбивается двумя осями на четыре четверти. Каждая из них имеет свой номер, при этом нумерация плоскостей ведется против часовой стрелки.
Каждая из четвертей имеет свои особенности. Так, в первой четверти абсцисса и ордината положительная, во второй четверти абсцисса отрицательная, ордината — положительная, в третьей и абсцисса, и ордината отрицательные, в четвертой же положительной является абсцисса, а отрицательной — ордината.
Запомнив эти особенности, можно с легкостью определить, к какой четверти относится та или иная точка. Кроме того, эта информация может пригодиться вам и в том случае, если придется делать вычисления, используя декартову систему.
Работа с координатной плоскостью
Когда мы разобрались с понятием плоскости и поговорили о ее четвертях, можно перейти к такой проблеме, как работа с данной системой, а также поговорить о том, как наносить на нее точки, координаты фигур.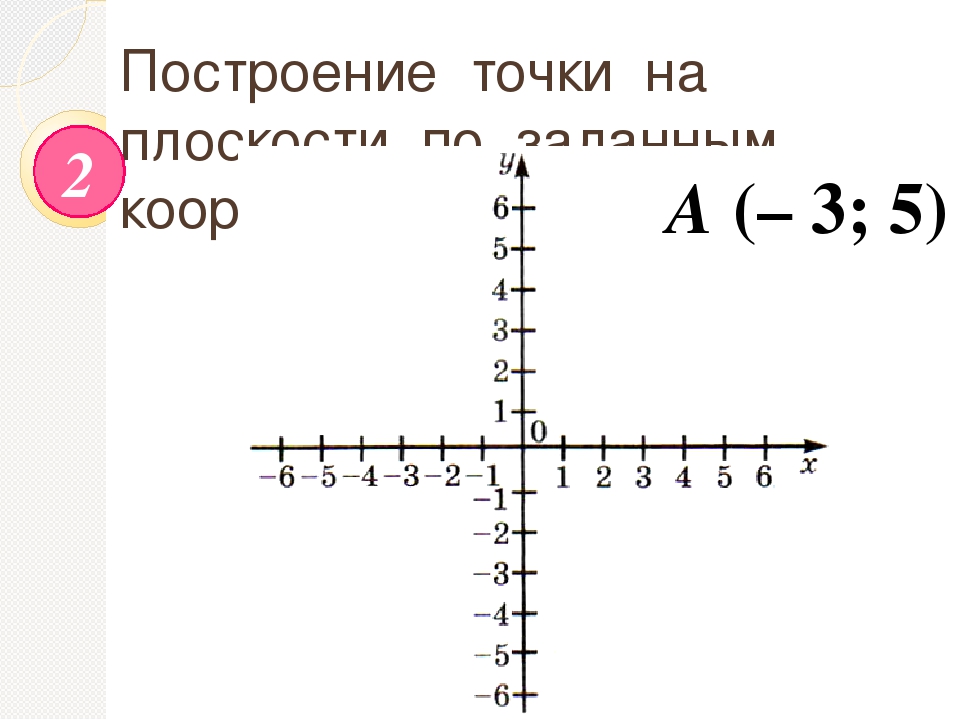 На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.
На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.
В первую очередь строится сама система, на нее наносятся все важные обозначения. Затем уже идет работа непосредственно с точками или фигурами. При этом даже при построении фигур сначала на плоскость наносятся точки, а затем уже прорисовываются фигуры.
Правила построения плоскости
Если вы решили начать отмечать на бумаге фигуры и точки, вам понадобится координатная плоскость. Координаты точек наносятся именно на нее. Для того чтобы построить координатную плоскость, понадобится только линейка и ручка или карандаш. Сначала рисуется горизонтальная ось абсцисс, затем вертикальная — ординат. При этом важно помнить, что оси пересекаются под прямым углом.
Следующим обязательным пунктом является нанесение разметки. На каждой из осей в обоих направлениях отмечаются и подписываются единицы-отрезки. Это делается для того, чтобы затем можно было работать с плоскостью с максимальным удобством.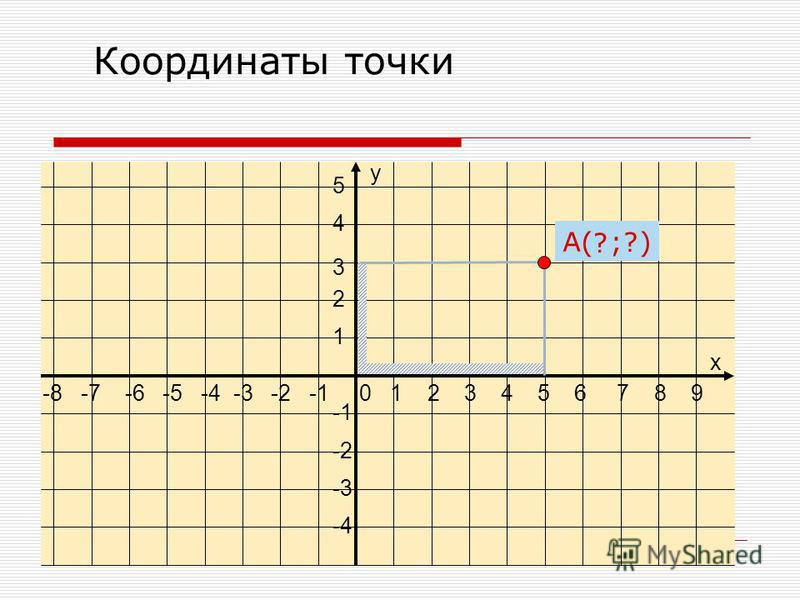
Отмечаем точку
Теперь поговорим о том, как нанести координаты точек на координатной плоскости. Это основа, которую следует знать, чтобы успешно размещать на плоскости разнообразные фигуры, и даже отмечать уравнения.
При построении точек следует помнить, как правильно записываются их координаты. Так, обычно задавая точку, в скобках пишут две цифры. Первая цифра обозначает координату точки по оси абсцисс, вторая — по оси ординат.
Строить точку следует таким образом. Сначала отметить на оси Ox заданную точку, затем отметить точку на оси Oy . Далее провести воображаемые линии от данных обозначений и найти место их пересечения — это и будет заданная точка.
Вам останется только отметить ее и подписать. Как видите, все довольно просто и не требует особых навыков.
Размещаем фигуру
Теперь перейдем к такому вопросу, как построение фигур на координатной плоскости. Для того чтобы построить на координатной плоскости любую фигуру, следует знать, как размещать на ней точки.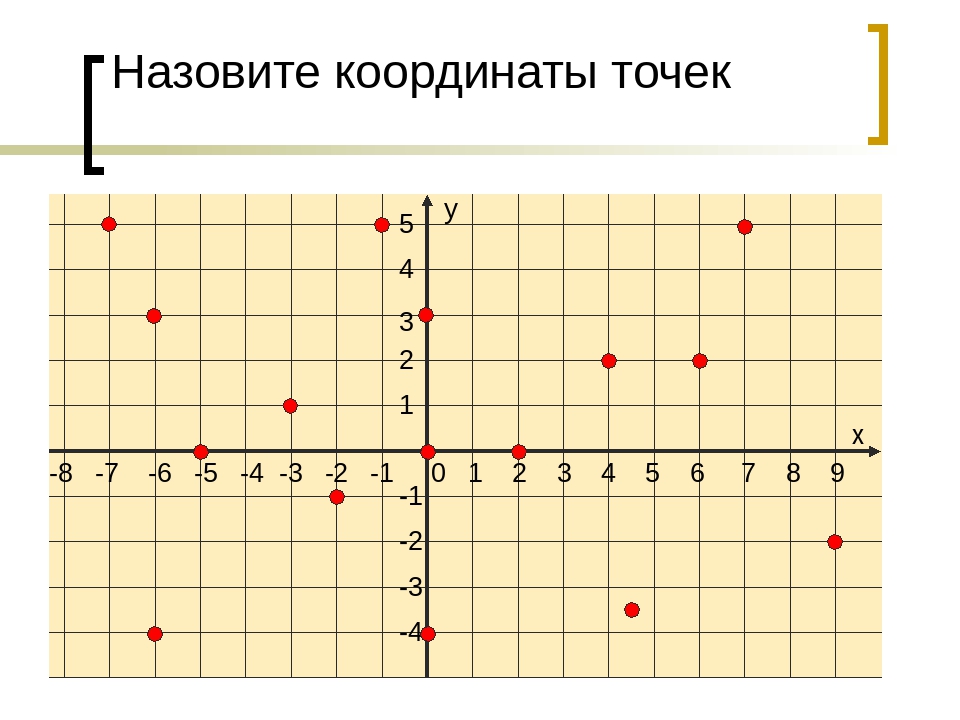 Если вы умеете это делать, то разместить фигуру на плоскости не так уж и сложно.
Если вы умеете это делать, то разместить фигуру на плоскости не так уж и сложно.
В первую очередь вам понадобятся координаты точек фигуры. Именно по ним мы и будем наносить на нашу систему координат выбранные вами Рассмотрим нанесение прямоугольника, треугольника и окружности.
Начнем с прямоугольника. Наносить его довольно просто. Сначала на плоскость наносятся четыре точки, обозначающие углы прямоугольника. Затем все точки последовательно соединяются между собой.
Нанесение треугольника ничем не отличается. Единственное — углов у него три, а значит, на плоскость наносятся три точки, обозначающие его вершины.
Касательно окружности тут следует знать координаты двух точек. Первая точка — центр окружности, вторая — точка, обозначающая ее радиус. Эти две точки наносятся на плоскость. Затем берется циркуль, измеряется расстояние между двумя точками. Острие циркуля ставится в точку, обозначающую центр, и описывается круг.
Как видите, тут также нет ничего сложного, главное, чтобы под рукой всегда были линейка и циркуль.
Теперь вы знаете, как наносить координаты фигур. На координатной плоскости это делать не так уж и сложно, как может показаться на первый взгляд.
Выводы
Итак, мы рассмотрели с вами одно из наиболее интересных и базовых для математики понятий, с которым приходится сталкиваться каждому школьнику.
Мы с вами выяснили, что координатная плоскость — это плоскость, образованная пересечением двух осей. С ее помощью можно задавать координаты точек, наносить на нее фигуры. Плоскость разделена на четверти, каждая из которых имеет свои особенности.
Основной навык, который следует выработать при работе с координатной плоскостью, — умение правильно наносить на нее заданные точки. Для этого следует знать правильное расположение осей, особенности четвертей, а также правила, по которым задаются координаты точек.
Надеемся, что изложенная нами информация была доступна и понятна, а также была полезна для вас и помогла лучше разобраться в данной теме.
Прямоугольная система координат на плоскости задаётся двумя взаимно перпендикулярными прямыми.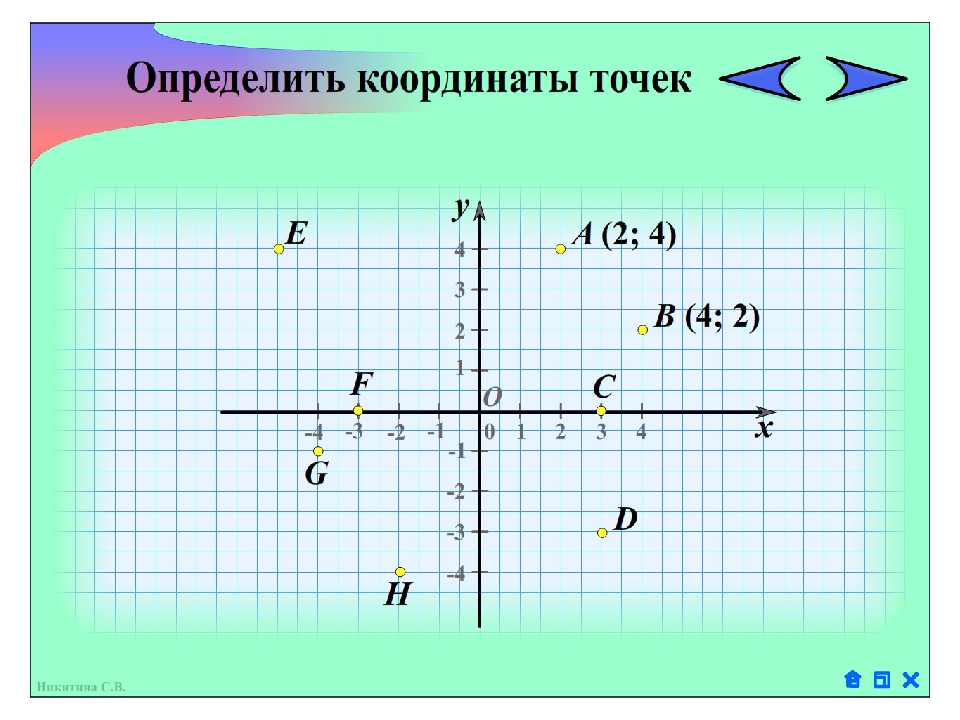 Прямые называют осями координат (или координатными осями). Точку пересечения этих прямых называют началом отсчёта и обозначают буквой O.
Прямые называют осями координат (или координатными осями). Точку пересечения этих прямых называют началом отсчёта и обозначают буквой O.
Обычно одна из прямых горизонтальна, другая — вертикальна. Горизонтальную прямую обозначают как ось x (или Ox) и называют осью абсцисс, вертикальную — ось y (Oy), называют осью ординат. Всю систему координат обозначают xOy.
Точка O разбивает каждую из осей на две полуоси, одну из из которых считают положительной (её обозначают стрелкой), другую — отрицательной.
Каждой точке F плоскости ставится в соответствие пара чисел (x;y) — её координаты.
Координата x называется абсциссой. Она равна Ox, взятому с соответствующим знаком.
Координата y называется ординатой и равна расстоянию от точки F до оси Oy (с соответствующим знаком).
Расстояния до осей обычно (но не всегда) измеряют одной и той же единицей длины.
Точки, расположенные справа от оси y, имеют положительные абсциссы. У точек, которые лежат левее оси ординат, абсциссы отрицательны.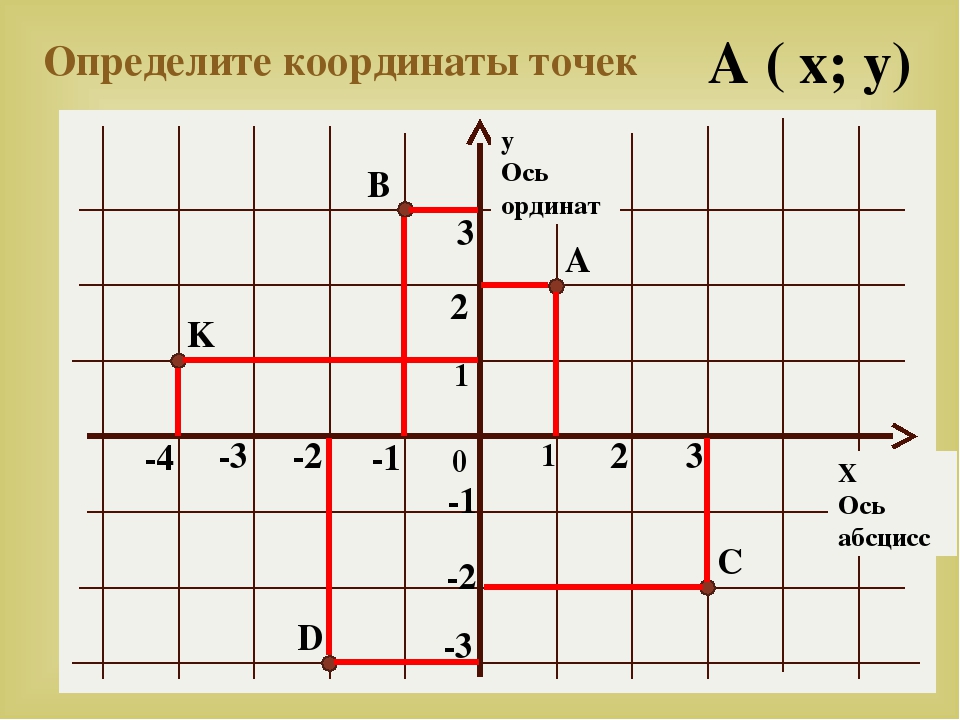 Для любой точки, лежащей на оси Oy, её координата x равна нулю.
Для любой точки, лежащей на оси Oy, её координата x равна нулю.
Точки с положительной ординатой лежат выше оси x, с отрицательной — ниже. Если точка лежит на оси Ox, её координата y равна нулю.
Координатные оси разбивают плоскость на четыре части, которые называют координатными четвертями (или координатными углами или квадрантами).
1 координатная четверть расположена в правом верхнем углу координатной плоскости xOy. Обе координаты точек, расположенных в I четверти, положительны.
Переход от одной четверти к другой ведётся против часовой стрелки.
2 координатная четверть находится в левом верхнем углу. Точки, лежащие во II четверти, имеют отрицательную абсциссу и положительную ординату.
3 координатная четверть лежит в левом нижнем квадранте плоскости xOy. Обе координаты точек, принадлежащей III координатному углу, отрицательны.
4 координатная четверть — это правый нижний угол координатной плоскости. Любая точка из IV четверти имеет положительную первую координату и отрицательную вторую.
Пример расположения точек в прямоугольной системе координат:
что это такое? Как отмечать точки и строить фигуры на координатной плоскости? Работа с координатной плоскостью
Основные сведения о координатной плоскости
Каждый объект (например, дом, место в зрительном зале, точка на карте) имеет свой упорядоченный адрес (координаты), который имеет числовое или буквенное обозначение.
Математики разработали модель, которая позволяет определять положение объекта и называется координатной плоскостью .
Чтобы построить координатную плоскость нужно провести $2$ перпендикулярные прямые , на конце которых указываются с помощью стрелок направления «вправо» и «вверх». На прямые наносятся деления, а точка пересечения прямых является нулевой отметкой для обеих шкал.
Определение 1
Горизонтальная прямая называется осью абсцисс и обозначается х, а вертикальная прямая называется осью ординат и обозначается у.
Две перпендикулярные оси х и у с делениями составляют прямоугольную , или декартовую , систему координат , которую предложил французский философ и математик Рене Декарт.
Координатная плоскость
Координаты точки
Точка на координатной плоскости определяется двумя координатами.
Чтобы определить координаты точки $A$ на координатной плоскости нужно через нее провести прямые, которые будут параллельны координатным осям (на рисунке выделены пунктирной линией). Пересечение прямой с осью абсцисс дает координату $x$ точки $A$, а пересечение с осью ординат дает координату у точки $A$. При записи координат точки сначала записывается координата $x$, а затем координата $y$.
Точка $A$ на рисунке имеет координаты $(3; 2)$, а точка $B (–1; 4)$.
Для нанесения точки на координатную плоскость действуют в обратном порядке.
Построение точки по заданным координатам
Пример 1
На координатной плоскости построить точки $A(2;5)$ и $B(3; –1).$
Решение .
Построение точки $A$:
- отложим число $2$ на оси $x$ и проведем перпендикулярную прямую;
- на оси у отложим число $5$ и проведем перпендикулярную оси $y$ прямую.
 На пересечении перпендикулярных прямых получим точку $A$ с координатами $(2; 5)$.
На пересечении перпендикулярных прямых получим точку $A$ с координатами $(2; 5)$.
Построение точки $B$:
- отложим на оси $x$ число $3$ и проведем перпендикулярную оси х прямую;
- на оси $y$ отложим число $(–1)$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $B$ с координатами $(3; –1)$.
Пример 2
Построить на координатной плоскости точки с заданными координатами $C (3; 0)$ и $D(0; 2)$.
Решение .
Построение точки $C$:
- отложим число $3$ на оси $x$;
- координата $y$ равна нулю, значит точка $C$ будет лежать на оси $x$.
Построение точки $D$:
- отложим число $2$ на оси $y$;
- координата $x$ равна нулю, значит, точка $D$ будет лежать на оси $y$.
Замечание 1
Следовательно, при координате $x=0$ точка будет лежать на оси $y$, а при координате $y=0$ точка будет лежать на оси $x$.
Пример 3
Определить координаты точек A, B, C, D.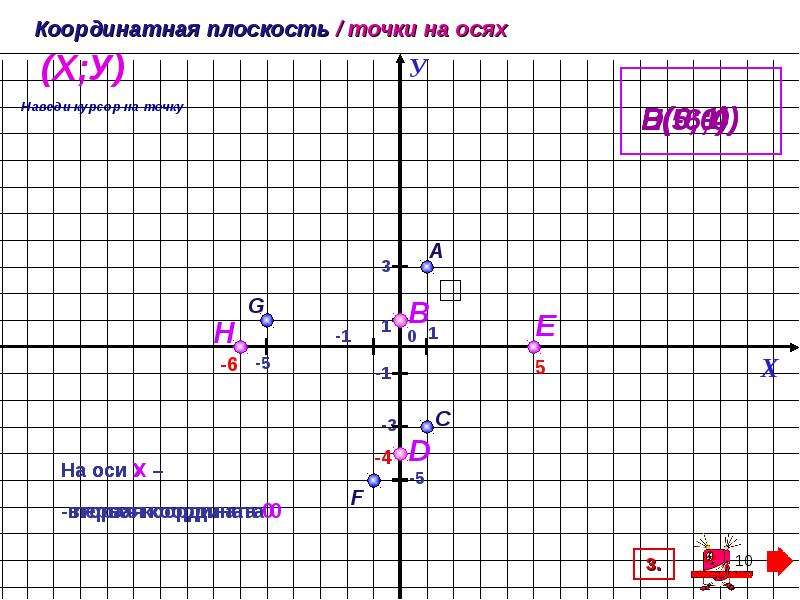 $
$
Решение .
Определим координаты точки $A$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Таким образом, получаем, что точка $A (1; 3).$
Определим координаты точки $B$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Получаем, что точка $B (–2; 4).$
Определим координаты точки $C$. Т.к. она расположена на оси $y$, то координата $x$ этой точки равна нулю. Координата у равна $–2$. Таким образом, точка $C (0; –2)$.
Определим координаты точки $D$. Т.к. она находится на оси $x$, то координата $y$ равна нулю. Координата $x$ этой точки равна $–5$. Таким образом, точка $D (5; 0).$
Пример 4
Построить точки $E(–3; –2), F(5; 0), G(3; 4), H(0; –4), O(0; 0).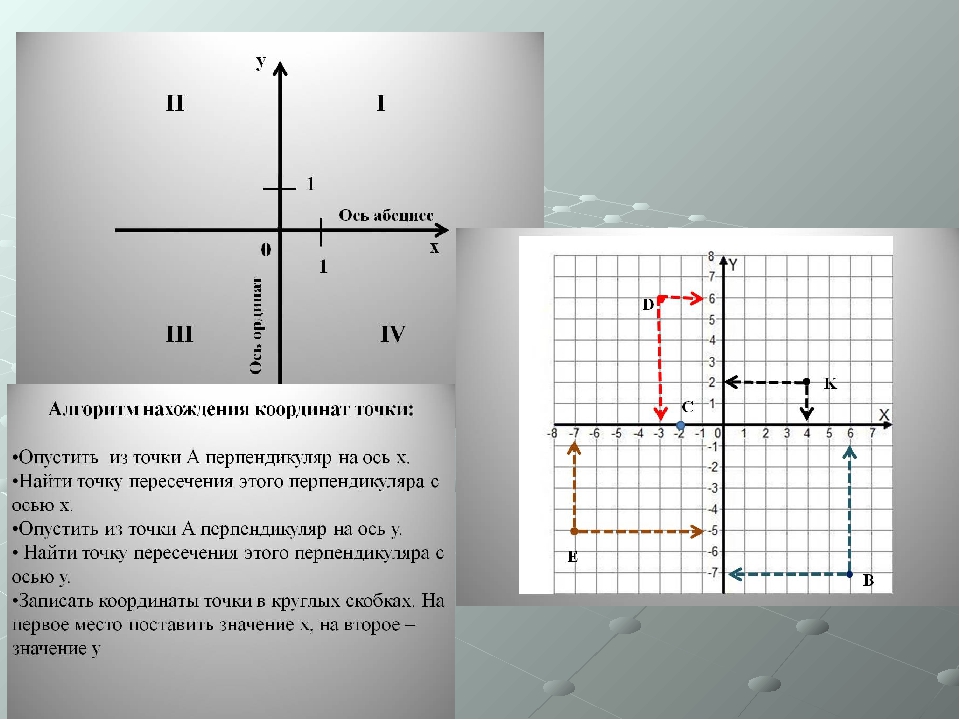 $
$
Решение .
Построение точки $E$:
- отложим число $(–3)$ на оси $x$ и проведем перпендикулярную прямую;
- на оси $y$ отложим число $(–2)$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $E (–3; –2).$
Построение точки $F$:
- координата $y=0$, значит, точка лежит на оси $x$;
- отложим на оси $x$ число $5$ и получим точку $F(5; 0).$
Построение точки $G$:
- отложим число $3$ на оси $x$ и проведем перпендикулярную прямую к оси $x$;
- на оси $y$ отложим число $4$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $G(3; 4).$
Построение точки $H$:
- координата $x=0$, значит, точка лежит на оси $y$;
- отложим на оси $y$ число $(–4)$ и получим точку $H(0; –4).$
Построение точки $O$:
- обе координаты точки равны нулю, значит, точка лежит одновременно и на оси $y$, и на оси $x$, следовательно является точкой пересечения обеих осей (началом координат).

«прописаны» точки — «жильцы», у каждой точки есть свой «номер дома» — ее координата. Если же точка берется в плоскости, то для ее «прописки» нужно указывать не только «номер дома», но и «номер квартиры». Напомним, как это делается.
Проведем две взаимно-перпендикулярные координатные прямые и будем считать началом отсчета на обеих прямых точку их пересечения — точку О. Тем самым на плоскости задана прямоугольная система координат (рис. 20), которая превращает обычную плоскость в координатную. Точку О называют началом координат, координатные прямые (ось х и ось у) называют осями координат, а прямые углы, образованные осями координат, называют координатными углами. Координатные прямоугольная углы нумеруют так, как показано на рисунке 20.
А теперь обратимся к рисунку 21, где изображена прямоугольная система координат и отмечена точка М. Проведем через нее прямую, параллельную оси у. Прямая пересекает ось х в некоторой точке, у этой точки есть координата — на оси х.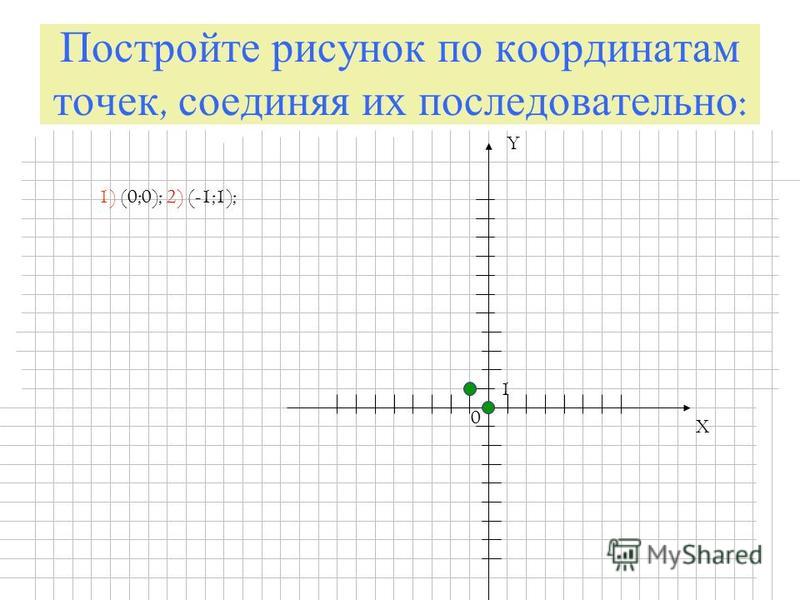 Для точки, изображенной на рисунке 21, эта координата равна -1,5, ее называют абсциссой точки М. Далее проведем через точку М прямую, параллельную оси х. Прямая пересекает ось у в некоторой точке, у этой точки есть координата — на оси у.
Для точки, изображенной на рисунке 21, эта координата равна -1,5, ее называют абсциссой точки М. Далее проведем через точку М прямую, параллельную оси х. Прямая пересекает ось у в некоторой точке, у этой точки есть координата — на оси у.
Для точки М, изображенной на рисунке 21, эта координата равна 2, ее называют ординатой точки М. Коротко пишут так: М(-1,5; 2). Абсциссу записывают на первом месте, ординату — на втором. Используют, если в этом есть необходимость, и другую форму записи: х = -1,5; у = 2.
Замечание 1 . На практике для отыскания координат точки М обычно вместо прямых, параллельных осям координат и проходящих через точку М, строят отрезки этих прямых от точки М до осей координат (рис. 22).
Замечание 2. В предыдущем параграфе мы ввели разные обозначения для числовых промежутков. В частности, как мы условились, запись (3, 5) означает, что на координатной прямой рассматривается интервал с концами в точках 3 и 5. В настоящем же параграфе пару чисел мы рассматриваем как координаты точки; например, (3; 5) — это точка на координатной плоскости с абсциссой 3 и ординатой 5.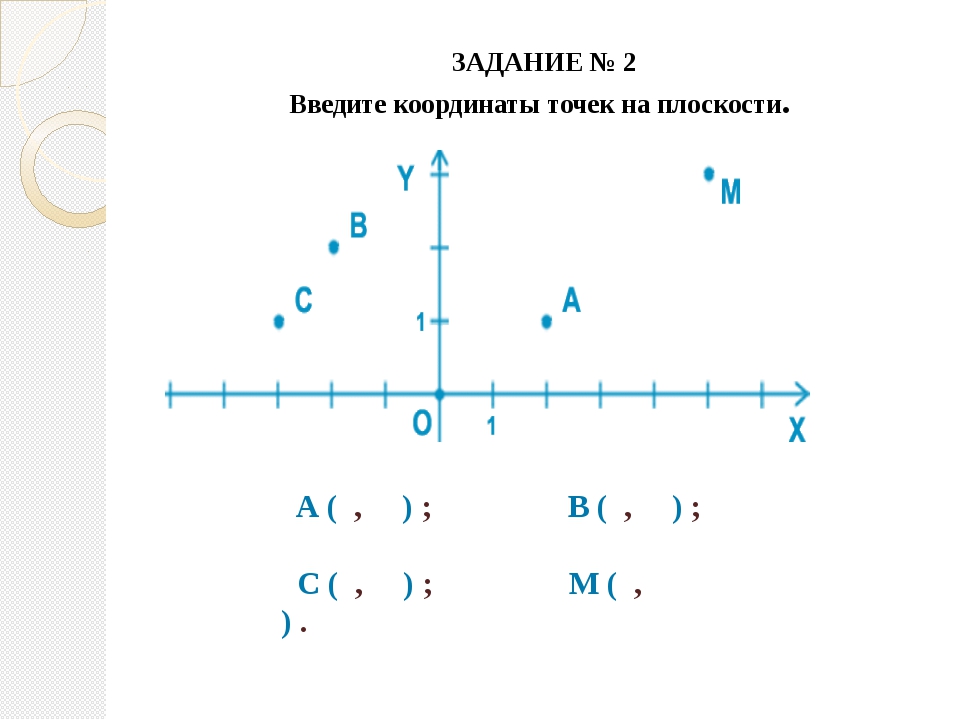 Как же правильно по символической записи определить, о чем идет речь: об интервале или о координатах точки? Чаще всего это бывает ясно по тексту. А если не ясно? Обратите внимание на одну деталь: в обозначении интервала мы использовали запятую, а в обозначении координат — точку с запятой. Это, конечно, не очень существенное, но все-таки различие; будем его применять.
Как же правильно по символической записи определить, о чем идет речь: об интервале или о координатах точки? Чаще всего это бывает ясно по тексту. А если не ясно? Обратите внимание на одну деталь: в обозначении интервала мы использовали запятую, а в обозначении координат — точку с запятой. Это, конечно, не очень существенное, но все-таки различие; будем его применять.
Учитывая введенные термины и обозначения, горизонтальную координатную прямую называют абсцисс, или осью х, а вертикальную координатную прямую — осью ординат, или осью у. Обозначения х, у используют обычно при задании на плоскости прямоугольной системы координат (см. рис. 20) и часто говорят так: дана система координат хОу. Впрочем, встречаются и другие обозначения: например, на рисунке 23 задана система координат tOs.
Алгоритм отыскания координат точки М, заданной в прямоугольной системе координат хОу
Именно так мы и действовали, находя координаты точки М на рисунке 21. Если точка М 1 (х; у) принадлежит первому координатному углу, то х > 0, у > 0; если точка М 2 (х; у) принадлежит второму координатному углу, то х 0; если точка М 3 (х; у) принадлежит третьему координатному углу, то х О, у
А что будет, если точка, координаты которой надо найти, лежит на одной из осей координат? Пусть точка А лежит на оси х, а точка В — на оси у (рис.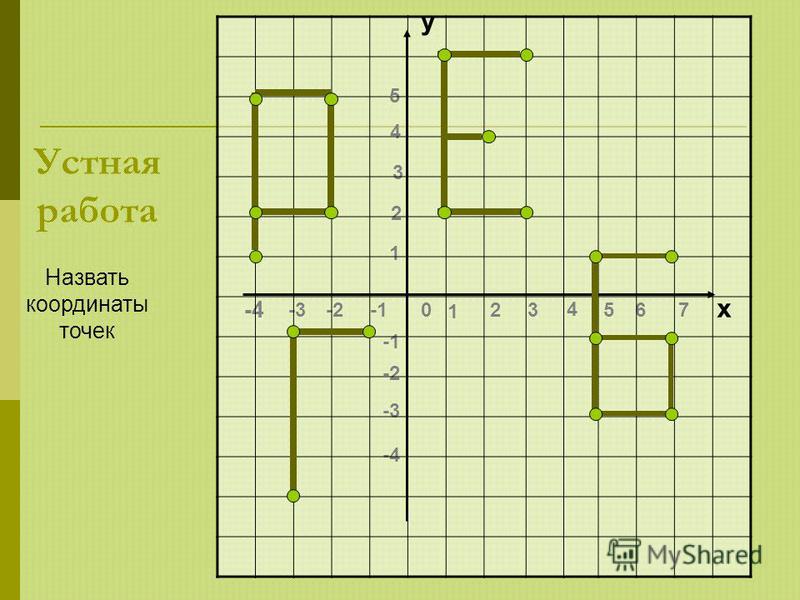 25). Проводить через точку А прямую, параллельную оси у, и находить точку пересечения этой прямой с осью х не имеет смысла, поскольку такая точка пересечения уже есть — это точка А, ее координата (абсцисса) равна 3. Точно так же не нужно проводить через точку А прямую, параллельную оси х, — этой прямой является сама ось х, которая пересекает ось у в точке О с координатой (ординатой) 0. В итоге для точки А получаем А(3; 0). Аналогично для точки В получаем В(0; — 1,5). А для точки О имеем О(0; 0).
25). Проводить через точку А прямую, параллельную оси у, и находить точку пересечения этой прямой с осью х не имеет смысла, поскольку такая точка пересечения уже есть — это точка А, ее координата (абсцисса) равна 3. Точно так же не нужно проводить через точку А прямую, параллельную оси х, — этой прямой является сама ось х, которая пересекает ось у в точке О с координатой (ординатой) 0. В итоге для точки А получаем А(3; 0). Аналогично для точки В получаем В(0; — 1,5). А для точки О имеем О(0; 0).
Вообще, любая точка на оси х имеет координаты (х; 0), а любая точка на оси у — координаты (0; у)
Итак, как находить координаты точки в координатной плоскости, мы обсудили. А как решать обратную задачу, т. е. как, задав координаты, построить соответствующую точку? Чтобы выработать алгоритм, проведем два вспомогательных, но в то же время важных рассуждения.
Первое рассуждение. Пусть в системе координат хОу проведена I, параллельная оси у и пересекающая ось х в точке с координатой (абсциссой) 4
(рис. 26). Любая точка, лежащая на этой прямой, имеет абсциссу 4. Так, для точек М 1 , М 2 , М 3 имеем М 1 (4; 3), М 2 (4; 6), М 3 (4; — 2). Иными словами, абсцисса любой точки М прямой удовлетворяет условию х = 4. Говорят, что х = 4 — уравнение прямой l или что прямая I удовлетворяет уравнению х = 4.
26). Любая точка, лежащая на этой прямой, имеет абсциссу 4. Так, для точек М 1 , М 2 , М 3 имеем М 1 (4; 3), М 2 (4; 6), М 3 (4; — 2). Иными словами, абсцисса любой точки М прямой удовлетворяет условию х = 4. Говорят, что х = 4 — уравнение прямой l или что прямая I удовлетворяет уравнению х = 4.
На рисунке 27 изображены прямые, удовлетворяющие уравнениям х = — 4 (прямая I 1), x = — 1
(прямая I 2) x = 3,5 (прямаяI 3). А какая прямая удовлетворяет уравнению х = 0? Догадались? Ось у.
Второе рассуждение. Пусть в системе координат хОу проведена прямая I, параллельная оси х и пересекающая ось у в точке с координатой (ординатой) 3 (рис. 28). Любая точка, лежащая на этой прямой, имеет ординату 3. Так, для точек М 1 , М 2 , М 3 имеем: М 1 (0; 3), М 2 (4; 3), М 3 (- 2; 3). Иными словами, ордината любой точки М прямой I удовлетворяет условию у = 3. Говорят, что у = 3 — уравнение прямой I или что прямая I удовлетворяет уравнению у = 3.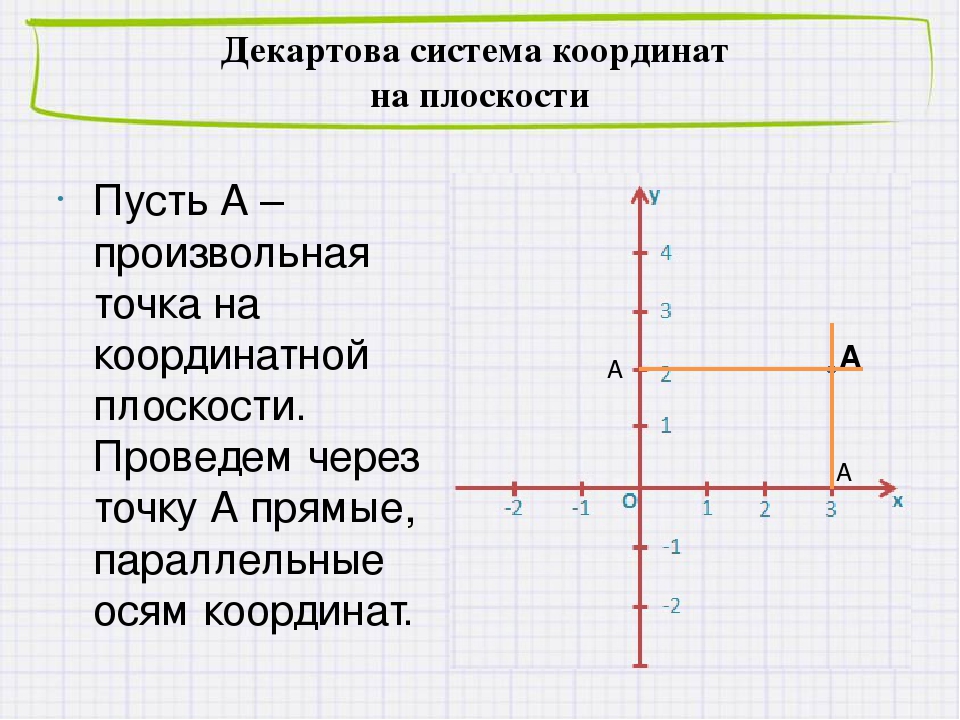
На рисунке 29 изображены прямые, удовлетворяющие уравнениям у = — 4 (прямая l 1), у = — 1 (прямая I 2), у = 3,5 (прямая I 3)- A какая прямая удовлетворяет уравнению у = 01 Догадались? Ось х.
Заметим, что математики, стремясь к краткости речи, говорят «прямая х = 4», а не «прямая, удовлетворяющая уравнению х = 4». Аналогично, они говорят «прямая у = 3», а не «прямая, удовлетворяющая равнению у = 3 ». Мы будем поступать точно так же. Вернемся теперь к рисунку 21. Обратите внимание, что точка М (- 1,5; 2), которая там изображена, есть точка пересечения прямой х = -1,5 и прямой у = 2. Теперь, видимо, будет понятен алгоритм построения точки по заданным ее координатам.
Алгоритм построения точки М (а; Ь) в прямоугольной системе координат хОу
П р и м е р. В системе координат хОу построить точки: А (1; 3), В (- 2; 1), С (4; 0), D (0; — 3).
Решение. Точка А есть точка пересечения прямых х = 1 и у = 3 (см. рис. 30).
Точка В есть точка пересечения прямых x = — 2 и y = 1 (рис.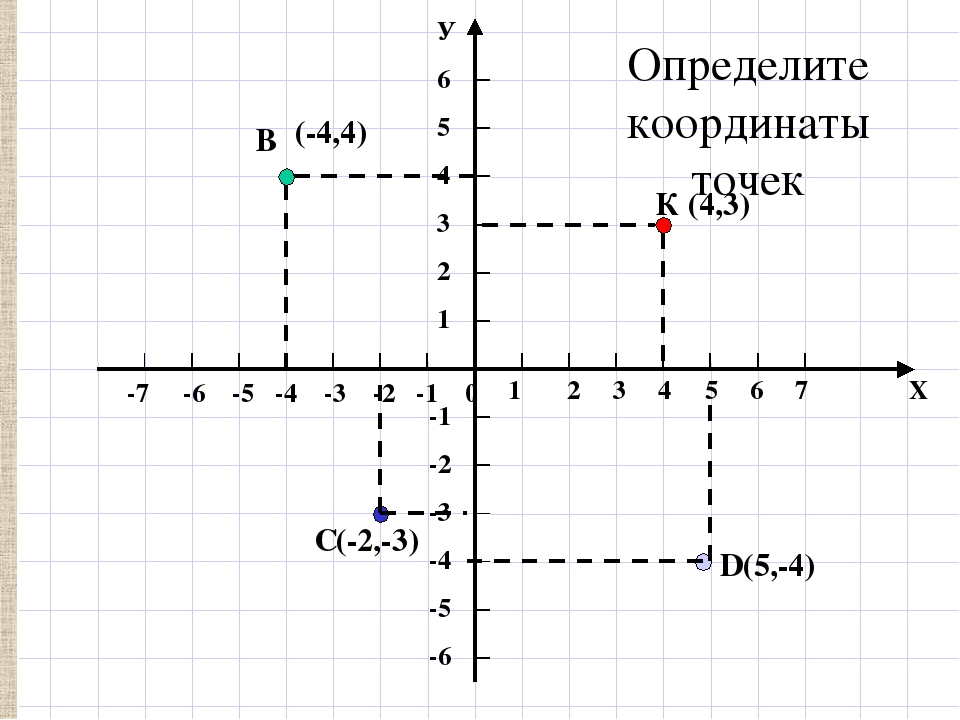 30). Точка С принадлежит оси х, а точка D — оси у (см. рис. 30).
30). Точка С принадлежит оси х, а точка D — оси у (см. рис. 30).
В заключение параграфа заметим, что впервые прямоугольную систему координат на плоскости стал активно использовать для замены алгебраических моделей геометрическими французский философ Рене Декарт (1596-1650). Поэтому иногда говорят «декартова система координат», «декартовы координаты».
Полный перечень тем по классам, календарный план согласно школьной программе по математике онлайн , видеоматериал по математике для 7 класса скачать
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные урокиДля указания взаимного расположения каких-то исследуемых объектов используются:
- координатный луч, когда их размещение или движение происходят вдоль прямой линии по одну сторону от заданного объекта, принятого за начало отсчёта;
- координатная прямая, когда их размещение или движение происходят вдоль прямой линии по разные стороны от заданного объекта, принятого за начало отсчёта;
- координатная плоскость, когда их размещение или движение происходят вдоль произвольной непрямой линии.

Элементы координатной плоскости
Координатная плоскость отличается от обычной плоскости тем, что на неё наносится система координат. Примером может служить изображение любого материка с нанесёнными на него параллелями и меридианами, которые и задают систему географических координат, позволяющих находить или задавать положение любого объекта на карте.
Система координат представляет собой две взаимно пересекающиеся под прямым углом координатные прямые в точках начала отсчёта. Горизонтальную координатную прямую принято называть осью абсцисс (абсцисса с лат. яз. – отрезок). Вертикальную прямую – осью ординат (ордината с лат. яз. – выстраивание по порядку).
Аналогично, координатная прямая отличается от обычной прямой тем, что на ней выбирают какую-то точку за начало отсчёта; выбирают масштаб единичного отрезка в зависимости от того, какие расстояния предстоит изображать; положительное направление отсчёта, обозначаемое на координатной прямой стрелкой.
Положение объекта на такой плоскости обозначают точкой с двумя числами – координатами: абсциссой и ординатой.
Использование координатных плоскостей
Координатные плоскости широко используются для решения геометрических и физических задач. Причём в физике за ось абсцисс часто принимают ось времени. Тогда ось ординат задаёт координату тела на координатной прямой, располагаемой вдоль прямолинейной траектории движения тела.
Основные сведения о координатной плоскости
Каждый объект (например, дом, место в зрительном зале, точка на карте) имеет свой упорядоченный адрес (координаты), который имеет числовое или буквенное обозначение.
Математики разработали модель, которая позволяет определять положение объекта и называется координатной плоскостью .
Чтобы построить координатную плоскость нужно провести $2$ перпендикулярные прямые , на конце которых указываются с помощью стрелок направления «вправо» и «вверх». На прямые наносятся деления, а точка пересечения прямых является нулевой отметкой для обеих шкал.
Определение 1
Горизонтальная прямая называется осью абсцисс и обозначается х, а вертикальная прямая называется осью ординат и обозначается у.
Две перпендикулярные оси х и у с делениями составляют прямоугольную , или декартовую , систему координат , которую предложил французский философ и математик Рене Декарт.
Координатная плоскость
Координаты точки
Точка на координатной плоскости определяется двумя координатами.
Чтобы определить координаты точки $A$ на координатной плоскости нужно через нее провести прямые, которые будут параллельны координатным осям (на рисунке выделены пунктирной линией). Пересечение прямой с осью абсцисс дает координату $x$ точки $A$, а пересечение с осью ординат дает координату у точки $A$. При записи координат точки сначала записывается координата $x$, а затем координата $y$.
Точка $A$ на рисунке имеет координаты $(3; 2)$, а точка $B (–1; 4)$.
Для нанесения точки на координатную плоскость действуют в обратном порядке.
Построение точки по заданным координатам
Пример 1
На координатной плоскости построить точки $A(2;5)$ и $B(3; –1). $
$
Решение .
Построение точки $A$:
- отложим число $2$ на оси $x$ и проведем перпендикулярную прямую;
- на оси у отложим число $5$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $A$ с координатами $(2; 5)$.
Построение точки $B$:
- отложим на оси $x$ число $3$ и проведем перпендикулярную оси х прямую;
- на оси $y$ отложим число $(–1)$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $B$ с координатами $(3; –1)$.
Пример 2
Построить на координатной плоскости точки с заданными координатами $C (3; 0)$ и $D(0; 2)$.
Решение .
Построение точки $C$:
- отложим число $3$ на оси $x$;
- координата $y$ равна нулю, значит точка $C$ будет лежать на оси $x$.
Построение точки $D$:
- отложим число $2$ на оси $y$;
- координата $x$ равна нулю, значит, точка $D$ будет лежать на оси $y$.

Замечание 1
Следовательно, при координате $x=0$ точка будет лежать на оси $y$, а при координате $y=0$ точка будет лежать на оси $x$.
Пример 3
Определить координаты точек A, B, C, D.$
Решение .
Определим координаты точки $A$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Таким образом, получаем, что точка $A (1; 3).$
Определим координаты точки $B$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Получаем, что точка $B (–2; 4).$
Определим координаты точки $C$. Т.к. она расположена на оси $y$, то координата $x$ этой точки равна нулю. Координата у равна $–2$. Таким образом, точка $C (0; –2)$.
Определим координаты точки $D$.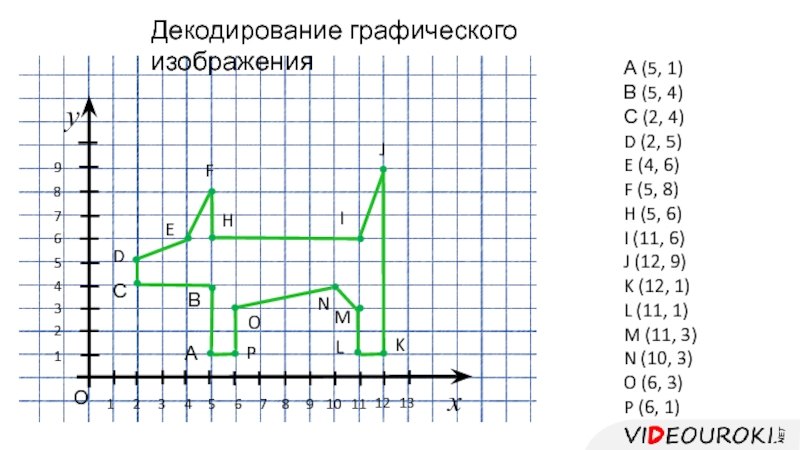 Т.к. она находится на оси $x$, то координата $y$ равна нулю. Координата $x$ этой точки равна $–5$. Таким образом, точка $D (5; 0).$
Т.к. она находится на оси $x$, то координата $y$ равна нулю. Координата $x$ этой точки равна $–5$. Таким образом, точка $D (5; 0).$
Пример 4
Построить точки $E(–3; –2), F(5; 0), G(3; 4), H(0; –4), O(0; 0).$
Решение .
Построение точки $E$:
- отложим число $(–3)$ на оси $x$ и проведем перпендикулярную прямую;
- на оси $y$ отложим число $(–2)$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $E (–3; –2).$
Построение точки $F$:
- координата $y=0$, значит, точка лежит на оси $x$;
- отложим на оси $x$ число $5$ и получим точку $F(5; 0).$
Построение точки $G$:
- отложим число $3$ на оси $x$ и проведем перпендикулярную прямую к оси $x$;
- на оси $y$ отложим число $4$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $G(3; 4).$
Построение точки $H$:
- координата $x=0$, значит, точка лежит на оси $y$;
- отложим на оси $y$ число $(–4)$ и получим точку $H(0; –4).
 $
$
Построение точки $O$:
- обе координаты точки равны нулю, значит, точка лежит одновременно и на оси $y$, и на оси $x$, следовательно является точкой пересечения обеих осей (началом координат).
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат , на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).
Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).
Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ.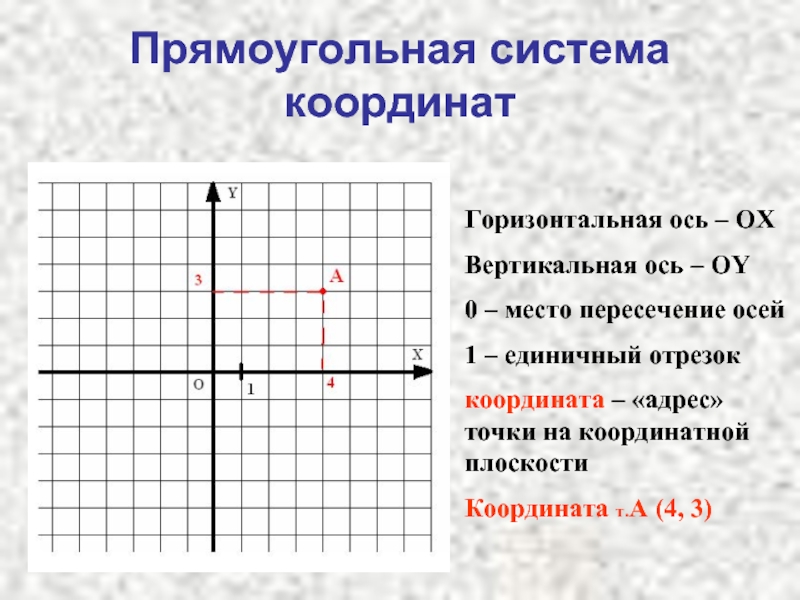 Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).
Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).
Орты
Прямоугольная система координат (любой размерности) также описывается набором ортов , сонаправленных с осями координат.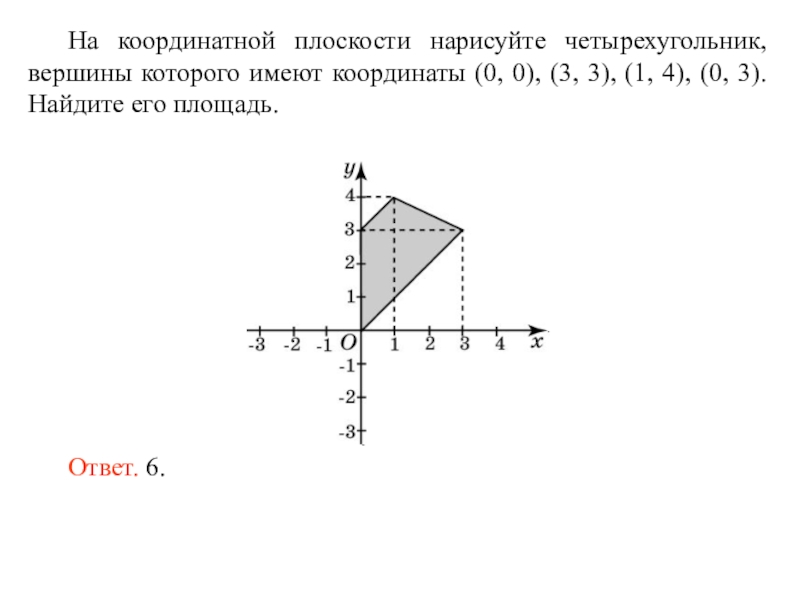 Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
В трёхмерном случае такие орты обычно обозначаются i j k или e x e y e z . При этом в случае правой системы координат действительны следующие формулы с векторным произведением векторов :
- [i j ]=k ;
- [j k ]=i ;
- [k i ]=j .
История
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году . Поэтому прямоугольную систему координат называют также — Декартова система координат . Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма , однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.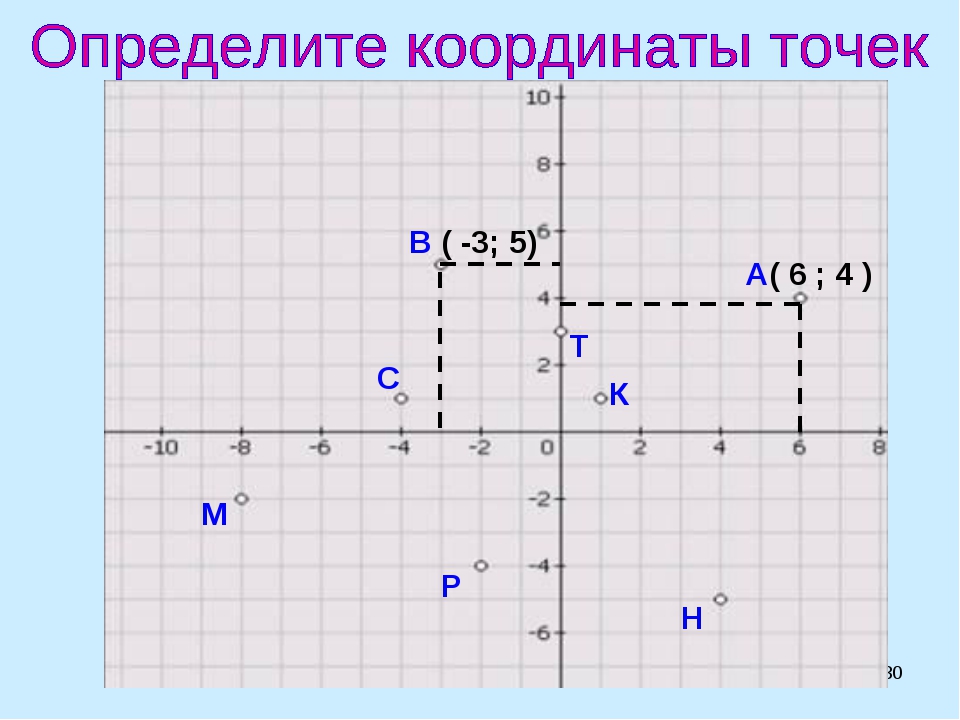
См. также
Ссылки
Wikimedia Foundation . 2010 .
Смотреть что такое «Координатная плоскость» в других словарях:
плоскость резания — (Pn) Координатная плоскость, касательная к режущей кромке в рассматриваемой точке и перпендикулярная основной плоскости. [ …
В топографии сеть воображаемых линий, опоясывающих земной шар в широтном и меридиональном направлениях, с помощью которой можно точно определить положение любой точки на земной поверхности. Отсчет широт ведется от экватора – большой окружности,… … Географическая энциклопедия
В топографии сеть воображаемых линий, опоясывающих земной шар в широтном и меридиональном направлениях, с помощью которой можно точно определить положение любой точки на земной поверхности. Отсчет широт ведется от экватора большой окружности,… … Энциклопедия Кольера
У этого термина существуют и другие значения, см. Фазовая диаграмма. Фазовая плоскость координатная плоскость, в которой по осям координат откладываются какие либо две переменные (фазовые координаты), однозначно определяющие состояние системы… … Википедия
главная секущая плоскость — (Pτ) Координатная плоскость, перпендикулярная линии пересечения основной плоскости и плоскости резания. [ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и координатные плоскости … Справочник технического переводчика
инструментальная главная секущая плоскость — (Pτи) Координатная плоскость, перпендикулярная линии пересечения инструментальных основной плоскости и плоскости резания. [ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и координатные плоскости … Справочник технического переводчика
инструментальная плоскость резания — (Pnи) Координатная плоскость, касательная к режущей кромке в рассматриваемой точке и перпендикулярная инструментальной основной плоскости. [ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и… … Справочник технического переводчика
кинематическая главная секущая плоскость — (Pτк) Координатная плоскость, перпендикулярная линии пересечения кинематических основной плоскости и плоскости резания … Справочник технического переводчика
кинематическая плоскость резания — (Pnк) Координатная плоскость, касательная к режущей кромке в рассматриваемой точке и перпендикулярная кинематической основной плоскости … Справочник технического переводчика
основная плоскость — (Pv) Координатная плоскость, проведенная через рассматриваемую точку режущей кромки перпендикулярно направлению скорости главного или результирующего движения резания в этой точке. Примечание В инструментальной системе координат направление… … Справочник технического переводчика
что это такое? Как отмечать точки и строить фигуры на координатной плоскости? Элементы координатной плоскости
Основные сведения о координатной плоскости
Каждый объект (например, дом, место в зрительном зале, точка на карте) имеет свой упорядоченный адрес (координаты), который имеет числовое или буквенное обозначение.
Математики разработали модель, которая позволяет определять положение объекта и называется координатной плоскостью .
Чтобы построить координатную плоскость нужно провести $2$ перпендикулярные прямые , на конце которых указываются с помощью стрелок направления «вправо» и «вверх». На прямые наносятся деления, а точка пересечения прямых является нулевой отметкой для обеих шкал.
Определение 1
Горизонтальная прямая называется осью абсцисс и обозначается х, а вертикальная прямая называется осью ординат и обозначается у.
Две перпендикулярные оси х и у с делениями составляют прямоугольную , или декартовую , систему координат , которую предложил французский философ и математик Рене Декарт.
Координатная плоскость
Координаты точки
Точка на координатной плоскости определяется двумя координатами.
Чтобы определить координаты точки $A$ на координатной плоскости нужно через нее провести прямые, которые будут параллельны координатным осям (на рисунке выделены пунктирной линией). Пересечение прямой с осью абсцисс дает координату $x$ точки $A$, а пересечение с осью ординат дает координату у точки $A$. При записи координат точки сначала записывается координата $x$, а затем координата $y$.
Точка $A$ на рисунке имеет координаты $(3; 2)$, а точка $B (–1; 4)$.
Для нанесения точки на координатную плоскость действуют в обратном порядке.
Построение точки по заданным координатам
Пример 1
На координатной плоскости построить точки $A(2;5)$ и $B(3; –1).$
Решение .
Построение точки $A$:
- отложим число $2$ на оси $x$ и проведем перпендикулярную прямую;
- на оси у отложим число $5$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $A$ с координатами $(2; 5)$.
Построение точки $B$:
- отложим на оси $x$ число $3$ и проведем перпендикулярную оси х прямую;
- на оси $y$ отложим число $(–1)$ и проведем перпендикулярную оси $y$ прямую. На пересечении перпендикулярных прямых получим точку $B$ с координатами $(3; –1)$.
Пример 2
Построить на координатной плоскости точки с заданными координатами $C (3; 0)$ и $D(0; 2)$.
Решение .
Построение точки $C$:
- отложим число $3$ на оси $x$;
- координата $y$ равна нулю, значит точка $C$ будет лежать на оси $x$.
Построение точки $D$:
- отложим число $2$ на оси $y$;
- координата $x$ равна нулю, значит, точка $D$ будет лежать на оси $y$.
Замечание 1
Следовательно, при координате $x=0$ точка будет лежать на оси $y$, а при координате $y=0$ точка будет лежать на оси $x$.
Пример 3
Определить координаты точек A, B, C, D.$
Решение .
Определим координаты точки $A$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Таким образом, получаем, что точка $A (1; 3).$
Определим координаты точки $B$. Для этого проведем через эту точку $2$ прямые, которые будут параллельными к координатным осям. Пересечение прямой с осью абсцисс дает координату $x$, пересечение прямой с осью ординат дает координату $y$. Получаем, что точка $B (–2; 4).$
Определим координаты точки $C$. Т.к. она расположена на оси $y$, то координата $x$ этой точки равна нулю. Координата у равна $–2$. Таким образом, точка $C (0; –2)$.
Определим координаты точки $D$. Т.к. она находится на оси $x$, то координата $y$ равна нулю. Координата $x$ этой точки равна $–5$. Таким образом, точка $D (5; 0).$
Пример 4
Построить точки $E(–3; –2), F(5; 0), G(3; 4), H(0; –4), O(0; 0).$
Решение .
Построение точки $E$:
- отложим число $(–3)$ на оси $x$ и проведем перпендикулярную прямую;
- на оси $y$ отложим число $(–2)$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $E (–3; –2).$
Построение точки $F$:
- координата $y=0$, значит, точка лежит на оси $x$;
- отложим на оси $x$ число $5$ и получим точку $F(5; 0).$
Построение точки $G$:
- отложим число $3$ на оси $x$ и проведем перпендикулярную прямую к оси $x$;
- на оси $y$ отложим число $4$ и проведем перпендикулярную прямую к оси $y$;
- на пересечении перпендикулярных прямых получаем точку $G(3; 4).$
Построение точки $H$:
- координата $x=0$, значит, точка лежит на оси $y$;
- отложим на оси $y$ число $(–4)$ и получим точку $H(0; –4).$
Построение точки $O$:
- обе координаты точки равны нулю, значит, точка лежит одновременно и на оси $y$, и на оси $x$, следовательно является точкой пересечения обеих осей (началом координат).
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат X’X и Y’Y. Оси координат пересекаются в точке O, которая называется началом координат , на каждой оси выбрано положительное направление.Положительное направление осей (в правосторонней системе координат) выбирают так, чтобы при повороте оси X’X против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси Y’Y. Четыре угла (I, II, III, IV), образованные осями координат X’X и Y’Y, называются координатными углами (см. Рис. 1).
Положение точки A на плоскости определяется двумя координатами x и y. Координата x равна длине отрезка OB, координата y — длине отрезка OC в выбранных единицах измерения. Отрезки OB и OC определяются линиями, проведёнными из точки A параллельно осям Y’Y и X’X соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A. Записывают так: A(x, y).
Если точка A лежит в координатном угле I, то точка A имеет положительные абсциссу и ординату. Если точка A лежит в координатном угле II, то точка A имеет отрицательную абсциссу и положительную ординату. Если точка A лежит в координатном угле III, то точка A имеет отрицательные абсциссу и ординату. Если точка A лежит в координатном угле IV, то точка A имеет положительную абсциссу и отрицательную ординату.
Прямоугольная система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения одинаковы для всех осей. OX — ось абсцисс, OY — ось ординат, OZ — ось апликат. Положительное направление осей выбирают так, чтобы при повороте оси OX против часовой стрелки на 90° её положительное направление совпало с положительным направлением оси OY, если этот поворот наблюдать со стороны положительного направления оси OZ. Такая система координат называется правой. Если большой палец правой руки принять за направление X, указательный за направление Y, а средний за направление Z, то образуется правая система координат. Аналогичными пальцами левой руки образуется левая система координат. Правую и левую системы координат невозможно совместить так, чтобы совпали соответствующие оси (см. Рис. 2).
Положение точки A в пространстве определяется тремя координатами x, y и z. Координата x равна длине отрезка OB, координата y — длине отрезка OC, координата z — длине отрезка OD в выбранных единицах измерения. Отрезки OB, OC и OD определяются плоскостями, проведёнными из точки A параллельно плоскостям YOZ, XOZ и XOY соответственно. Координата x называется абсциссой точки A, координата y — ординатой точки A, координата z — аппликатой точки A. Записывают так: A(a, b, c).
Орты
Прямоугольная система координат (любой размерности) также описывается набором ортов , сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу.
В трёхмерном случае такие орты обычно обозначаются i j k или e x e y e z . При этом в случае правой системы координат действительны следующие формулы с векторным произведением векторов :
- [i j ]=k ;
- [j k ]=i ;
- [k i ]=j .
История
Впервые прямоугольную систему координат ввел Рене Декарт в своей работе «Рассуждение о методе» в 1637 году . Поэтому прямоугольную систему координат называют также — Декартова система координат . Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма , однако его работы были впервые опубликованы уже после его смерти. Декарт и Ферма применяли координатный метод только на плоскости.
Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке.
См. также
Ссылки
Wikimedia Foundation . 2010 .
Смотреть что такое «Координатная плоскость» в других словарях:
плоскость резания — (Pn) Координатная плоскость, касательная к режущей кромке в рассматриваемой точке и перпендикулярная основной плоскости. [ …
В топографии сеть воображаемых линий, опоясывающих земной шар в широтном и меридиональном направлениях, с помощью которой можно точно определить положение любой точки на земной поверхности. Отсчет широт ведется от экватора – большой окружности,… … Географическая энциклопедия
В топографии сеть воображаемых линий, опоясывающих земной шар в широтном и меридиональном направлениях, с помощью которой можно точно определить положение любой точки на земной поверхности. Отсчет широт ведется от экватора большой окружности,… … Энциклопедия Кольера
У этого термина существуют и другие значения, см. Фазовая диаграмма. Фазовая плоскость координатная плоскость, в которой по осям координат откладываются какие либо две переменные (фазовые координаты), однозначно определяющие состояние системы… … Википедия
главная секущая плоскость — (Pτ) Координатная плоскость, перпендикулярная линии пересечения основной плоскости и плоскости резания. [ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и координатные плоскости … Справочник технического переводчика
инструментальная главная секущая плоскость — (Pτи) Координатная плоскость, перпендикулярная линии пересечения инструментальных основной плоскости и плоскости резания. [ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и координатные плоскости … Справочник технического переводчика
инструментальная плоскость резания — (Pnи) Координатная плоскость, касательная к режущей кромке в рассматриваемой точке и перпендикулярная инструментальной основной плоскости. [ГОСТ 25762 83] Тематики обработка резанием Обобщающие термины системы координатных плоскостей и… … Справочник технического переводчика
кинематическая главная секущая плоскость — (Pτк) Координатная плоскость, перпендикулярная линии пересечения кинематических основной плоскости и плоскости резания … Справочник технического переводчика
кинематическая плоскость резания — (Pnк) Координатная плоскость, касательная к режущей кромке в рассматриваемой точке и перпендикулярная кинематической основной плоскости … Справочник технического переводчика
основная плоскость — (Pv) Координатная плоскость, проведенная через рассматриваемую точку режущей кромки перпендикулярно направлению скорости главного или результирующего движения резания в этой точке. Примечание В инструментальной системе координат направление… … Справочник технического переводчика
§ 1 Система координат: определение и способ построения
В этом уроке познакомимся с понятиями «система координат», «координатная плоскость», «оси координат», научимся строить точки на плоскости по координатам.
Возьмем координатную прямую х с началом координат точкой О, положительным направлением и единичным отрезком.
Через начало координат точку О координатной прямой х проведем еще одну координатную прямую y, перпендикулярную х, положительное направление зададим вверх, единичный отрезок такой же. Таким образом, мы построили систему координат.
Дадим определение:
Две взаимно перпендикулярные координатные прямые, пересекающиеся в точке, которая является началом координат каждой из них, образуют систему координат.
§ 2 Координатная ось и координатная плоскость
Прямые, которые образуют систему координат, называют координатными осями, каждая из которых имеет свое название: координатная прямая х — ось абсцисс, координатная прямая y — ось ординат.
Плоскость, на которой выбрана система координат, называется координатной плоскостью.
Описанная система координат называется прямоугольной. Часто ее называют декартовой системой координат в честь французского философа и математика Рене Декарта.
Каждая точка координатной плоскости имеет две координаты, которые можно определить, опустив из точки перпендикуляры на оси координат. Координаты точки на плоскости — это пара чисел, из которых первое число — абсцисса, второе число — ордината. Абсциссу показывает перпендикуляр к оси х, ординату — перпендикуляр к оси y.
Отметим на координатной плоскости точку А, проведем из неё перпендикуляры к осям системы координат.
По перпендикуляру к оси абсцисс (ось х) определяем абсциссу точки А, она равна 4, ординату точки А — по перпендикуляру к оси ординат (ось у) — это 3. Координаты нашей точки 4 и 3. А (4;3). Таким образом, координаты можно найти для любой точки координатной плоскости.
§ 3 Построение точки на плоскости
А как построить точку на плоскости с заданными координатами, т.е. по координатам точки плоскости определить её положение? В данном случае действия выполняем в обратном порядке. На координатных осях находим точки соответствующие заданным координатам, через которые проводим прямые, перпендикулярные осям х и y. Точка пересечения перпендикуляров и будет искомой, т.е. точкой с заданными координатами.
Выполним задание: построить на координатной плоскости точку М (2;-3).
Для этого на оси абсцисс находим точку с координатой 2, проводим через данную точку прямую перпендикулярную оси х. На оси ординат найдем точку с координатой -3, через нее проведем прямую перпендикулярную оси y. Точка пересечения перпендикулярных прямых и будет заданной точкой М.
А теперь рассмотрим несколько частных случаев.
Отметим на координатной плоскости точки А (0; 2), В (0; -3), С (0; 4).
Абсциссы данных точек равны 0. На рисунке видно, что все точки находятся на оси ординат.
Следовательно, точки, абсциссы которых равны нулю, лежат на оси ординат.
Поменяем координаты данных точек местами.
Получится А (2;0), В (-3;0) С (4; 0). В этом случае все ординаты равны 0 и точки находятся на оси абсцисс.
Значит, точки, ординаты которых равны нулю, лежат на оси абсцисс.
Разберем еще два случая.
На координатной плоскости отметим точки М (3; 2), N (3; -1), Р (3; -4).
Легко заметить, что все абсциссы точек одинаковые. Если эти точки соединить, получится прямая, параллельная оси ординат и перпендикулярная оси абсцисс.
Напрашивается вывод: точки, имеющие одну и ту же абсциссу, лежат на одной прямой, которая параллельна оси ординат и перпендикулярна оси абсцисс.
Если поменять координаты точек М, N, Р местами, то получится М (2; 3), N (-1; 3), Р (-4; 3). Одинаковыми станут ординаты точек. В данном случае, если эти точки соединить, получится прямая параллельная оси абсцисс и перпендикулярная оси ординат.
Таким образом, точки, имеющие одну и ту же ординату, лежат на одной прямой параллельной оси абсцисс и перпендикулярной оси ординат.
В этом уроке Вы познакомились с понятиями «система координат», «координатная плоскость», «оси координат — ось абсцисс и ось ординат». Узнали, как найти координаты точки на координатной плоскости и научились строить точки на плоскости по ее координатам.
Список использованной литературы:
- Математика. 6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича//автор-составитель Л.А. Топилина. – Мнемозина, 2009.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И.Зубарева, А.Г.Мордкович.- М.: Мнемозина, 2013.
- Математика. 6 класс: учебник для общеобразовательных учреждений/Г.В. Дорофеев, И.Ф. Шарыгин, С.Б. Суворова и др./по редакцией Г.В. Дорофеева, И.Ф. Шарыгина; Рос.акад.наук, Рос.акад.образования. — М.: «Просвещение», 2010
- Справочник по математике — http://lyudmilanik.com.ua
- Справочник для учащихся в средней школе http://shkolo.ru
Что такое координатная плоскость?
Термин «координаты» в переводе с латинского языка значит слово «упорядоченный».
Допустим, нам нужно обозначить положение точки на плоскости. Для этого мы берем 2 перпендикулярные прямые, которые называются осями координат, где Х будет осью абсцисс, У- осью ординат, а началом координат будет точка О. Образованные с помощью осей координат прямые углы, будут называться координатными углами.
Так мы подошли к определению и теперь знаем, что координатной плоскостью является плоскость с заданной системой координат.
А теперь давайте посмотрим, нумерацию координатных углов:
Теперь давайте с вами отобразим прямоугольную систему координат и отметим в ней точку M.
Далее нам нужно прочертить через точку М прямую, которая будет параллельна оси У. Теперь, смотрим, что у нас вышло. Как видим, что прямая пересекает ось Х в той точке, в которой координата будет равна −2. Данная координата является абсциссой точки M.
Теперь нам нужно прочертить через точку М прямую, которая будет параллельна оси Х.
Мы с вами видим, что эта прямая пересекает ось Х в той точке, координата которой равняется трем. Вот эта координата будет ординатой точки М.
Запись координат токи М будет выглядеть так:
В такой записи всегда на первое место ставят абсциссу, а на второе – ординату. Если рассмотреть на примере координат точки М(-2;3), то -2 выступает в роли абсциссы точки М, а ординатой этой точки будет число 3.
Из этого следует, что на координатной плоскости каждой точке М соответствует такая пара чисел, как ее абсцисса и ордината. Верным будет и утверждение наоборот, то есть, каждой такой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Задание:
Координатная плоскость в жизни
Как по вашему, может ли пригодиться в повседневной жизни знания о координатной плоскости? И доводилось ли вам слышать такую фразу, как «оставьте свои координаты» или «по каким координатам вас можно найти»? И задумывались ли вы над тем, что может обозначать эти выражения?
Оказывается все очень просто и банально и это значит местонахождение того или иного объекта, по которому легко найти человека или какое-то определенное место. Можно уверенно утверждать, что системы координат необходимы в практической жизни человека повсеместно.
Такой системой координат может быть как домашний адрес, так и номер телефона, место работы и т.д.
Ведь даже при покупке билетов на поезд, вы знаете не только его номер и место назначения, но и обязательно должен быть указан номер вагона и места.
Чтобы пойти в гости к однокласснику, недостаточно знать только дом, в котором он живет, а нужно еще и знать номер квартиры.
Задание
1. Какими сведениями вы должны владеть, чтобы занять место в театре?
2. Какие данные нужно иметь, чтобы определить точки на земной поверхности?
3. По каким координатам можно определить место в кинотеатре?
4. Что необходимо знать, чтобы определелить положения фигуры на шахматной доске?
5. Какими координатами вы пользуетесь при игре в морской бой?
Историческая справка
Идея использования координат появилась еще в глубокой древности. Первоначально их применять начали астрономы, для определения небесных светил и географы – для определения местонахождения и объектов на поверхности Земли.
Благодаря трудам древнегреческого астронома Клавдия Плотомея уже во втором веке ученые научились определять долготу и широту.
А известно ли вам, почему в математике существует такое понятие, как «Декартова система координат»? Оказывается метод координат, который имеет общематематическое значение, был открыт французскими математиками Пьером Ферма и Рене Декартом в XVII в., а в 1637 году Рене Декарт впервые описал его в книге по геометрии.
А вот термины «абсцисса», «ордината» и «координаты» были впервые введены Вильгельмом Лейбницем в семнадцатом веке.
Домашнее задание:
Тема данного видео урока: Координатная плоскость .
Цели и задачи урока:
Ознакомиться с прямоугольной системой координат на плоскости
— научить свободно ориентироваться на координатной плоскости
— строить точки по заданным её координатам
— определять координаты точки, отмеченной на координатной плоскости
— хорошо воспринимать на слух координаты
— четко и аккуратно выполнять геометрические построения
— развитие творческих способностей
— воспитание интереса к предмету
Термин «координаты » произошел от латинского слова — «упорядоченный»
Чтобы указать положение точки на плоскости берут две перпендикулярные прямые Х и У.
Ось Х — ось абсцисс
Ось У- ось ординат
Точка О- начало координат
Плоскость, на которой задана система координат, называется координатной плоскостью .
Каждой точке М на координатной плоскости соответствует пара чисел: её абсцисса и ордината. Наоборот, каждой паре чисел соответствует одна точка плоскости, для которой эти числа являются координатами.
Рассмотрены примеры:
- по построению точки по её координатам
- нахождение координат точки расположенной на координатной плоскости
Немного дополнительной информации:
Идея задавать положение точки на плоскости зародилась в древности — прежде всего у астрономов. Во II в. Древнегреческий астроном Клавдий Птоломей пользовался широтой и долготой в качестве координат. Описание применения координат дал в книге «Геометрия» в 1637 г.
Описание применения координат дал в книге «Геометрия» в 1637 г. французский математик Рене Декарт, поэтому прямоугольную систему координат часто называют декартовой.
Слова «абсцисса », «ордината », «координаты » первым начал использовать в конце XVII.
Для лучшего понимания координатной плоскости, представим что нам даны: географический глобус, шахматная доска, театральный билет.
Для определения положения точки на земной поверхности надо знать долготу и широту.
Для определения положения фигуры на шахматной доске нужно знать две координаты, например: е3.
Места в зрительном зале определяются по двум координатам: ряд и место.
Дополнительное задание.
После изучения видео урока, для закрепления материала, предлагаю Вам взять ручку и листик в клеточку, начертить координатную плоскость и построить фигуры по заданным координатам:
Грибок
1) (6; 0), (6; 2), (5; 1,5), (4; 3), (2; 1), (0; 2,5), (- 1,5; 1,5), (- 2; 5), (- 3; 0,5), (- 4; 2), (- 4; 0).
2) (2; 1), (2,2; 2), (2,3; 4), (2,5; 6), (2,3; 8), (2; 10), (6; 10), (4,8; 12), (3; 13,3), (1; 14),
(0; 14), (- 2; 13,3), (- 3,8; 12), (- 5; 10), (2; 10).
3) (- 1; 10), (- 1,3; 8), (- 1,5; 6), (- 1,2; 4), (- 0,8;2).
Мышонок 1) (3; — 4), (3; — 1), (2; 3), (2; 5), (3; 6), (3; 8), (2; 9), (1; 9), (- 1; 7), (- 1; 6),
(- 4; 4), (- 2; 3), (- 1; 3), (- 1; 1), (- 2; 1), (-2; — 1), (- 1; 0), (- 1; — 4), (- 2; — 4),
(- 2; — 6), (- 3; — 6), (- 3; — 7), (- 1; — 7), (- 1; — 5), (1; — 5), (1; — 6), (3; — 6), (3; — 7),
(4; — 7), (4; — 5), (2; — 5), (3; — 4).
2) Хвост: (3; — 3), (5; — 3), (5; 3).
3) Глаз: (- 1; 5).
Лебедь
1) (2; 7), (0; 5), (- 2; 7), (0; 8), (2; 7), (- 4; — 3), (4; 0), (11; — 2), (9; — 2), (11; — 3),
(9; — 3), (5; — 7), (- 4; — 3).
2) Клюв: (- 4; 8), (- 2; 7), (- 4; 6).
3) Крыло: (1; — 3), (4; — 2), (7; — 3), (4; — 5), (1; — 3).
4) Глаз: (0; 7).
Верблюд
1) (- 9; 6), (- 5; 9), (- 5; 10), (- 4; 10), (- 4; 4), (- 3; 4), (0; 7), (2; 4), (4; 7), (7; 4),
(9; 3), (9; 1), (8; — 1), (8; 1), (7; 1), (7; — 7), (6; — 7), (6; — 2), (4; — 1), (- 5; — 1), (- 5; — 7),
(- 6; — 7), (- 6; 5), (- 7;5), (- 8; 4), (- 9; 4), (- 9; 6).
2) Глаз: (- 6; 7).
Слоник
1) (2; — 3), (2; — 2), (4; — 2), (4; — 1), (3; 1), (2; 1), (1; 2), (0; 0), (- 3; 2), (- 4; 5),
(0; 8), (2; 7), (6; 7), (8; 8), (10; 6), (10; 2), (7; 0), (6; 2), (6; — 2), (5; — 3), (2; — 3).
2) (4; — 3), (4; — 5), (3; — 9), (0; — 8), (1; — 5), (1; — 4), (0; — 4), (0; — 9), (- 3; — 9),
(- 3; — 3), (- 7; — 3), (- 7; — 7), (- 8; — 7), (- 8; — 8), (- 11; — 8), (- 10; — 4), (- 11; — 1),
(- 14; — 3), (- 12; — 1), (- 11;2), (- 8;4), (- 4;5).
3) Глаза: (2; 4), (6; 4).
Конь
1) (14; — 3), (6,5; 0), (4; 7), (2; 9), (3; 11), (3; 13), (0; 10), (- 2; 10), (- 8; 5,5),
(- 8; 3), (- 7; 2), (- 5; 3), (- 5; 4,5), (0; 4), (- 2; 0), (- 2; — 3), (- 5; — 1), (- 7; — 2),
(- 5; — 10), (- 2; — 11), (- 2; — 8,5), (- 4; — 8), (- 4; — 4), (0; — 7,5), (3; — 5).
2) Глаз: (- 2; 7).
точек графика на координатной плоскости (видео и примеры)
Координатная плоскость — это организованный способ определения местоположений в двух измерениях с использованием сетки и координат по оси x и оси y. Изучение того, как перемещаться и как наносить точки на координатную плоскость, поможет вам понять геометрию.
Содержание
- Определение координатной плоскости
- Квадранты координатной плоскости
- Нанесение точек на координатную плоскость
- Графические точки на координатной плоскости с использованием уравнений
Определение координатной плоскости
Координатная плоскость имеет две оси (множественные оси).Они называются осью x и осью y. Чтобы обеспечить понимание, все математики маркируют точки на координатной плоскости сначала значением оси x, затем значением оси y.
- Ось x идет влево и вправо по горизонтали
- Ось Y идет вверх и вниз, вертикально
Эти две оси делят координатную сетку (наложение пересекающихся перпендикулярных линий на координатной плоскости) на четыре области, называемые квадрантами .
Только один квадрант, Квадрант I, будет иметь положительные числа как для значения x, так и для значения y.Один квадрант, Квадрант III, будет иметь отрицательные числа как для значений x, так и для значений y. В двух других квадрантах, II и IV, будут отрицательные и положительные числа.
Квадранты координатной плоскости
С осью X, разрезающей горизонтально поперек координатной плоскости, и осью Y, разрезающей вертикально, координатная плоскость аккуратно делится на четыре квадранта, помеченных римскими цифрами в направлении против часовой стрелки от верхнего правого (I) до нижнего правого (IV). ).
- Квадрант I, вверху справа, будет иметь два положительных числа, например: (+, +)
- Квадрант II, вверху слева, будет иметь отрицательное значение x и положительное значение y, например: (-, +)
- Квадрант III, внизу слева, будет иметь два отрицательных числа, например: (-, -)
- Квадрант IV, нижний правый, будет иметь положительное значение x и отрицательное значение y, например: (+, -)
Вот несколько самопроверок.Посмотрите, сможете ли вы определить квадрант каждой упорядоченной пары:
- (-3, -6)
- (3, -6)
- (-3, 6)
- (3, 6)
Мы надеемся, что вы сказали (-3, -6) в квадранте III, (3, -6) в квадранте IV, (-3, 6) в квадранте II и (3, 6) в квадранте I
Ось Y (вертикальная ось) является разделителем между левым и правым. Все значения x слева от оси y всегда равны отрицательным ; Значения x справа от оси y всегда равны положительному значению .
Точно так же ось x является разделителем между верхним и нижним краями: значения y над осью x всегда положительные , а значения y под осью x всегда отрицательные .
Нанесение точек на координатную плоскость
Держите доминирующую руку перед собой, вытянув указательный палец и большой палец вверх, как это:
[вставить мультяшную руку, указывающую как пистолет]
Видите длинный указательный палец, он кажется более важным? Это первая координата, значение оси x.Короткий ползунок — это значение по оси Y. Поэтому вы всегда помещаете их в таком порядке: (x, y)
Чтобы изобразить конкретную точку на координатной сетке, начните с начала координат , (0, 0). Каждая сетка имеет начало, точку пересечения двух осей.
Посмотрите на заказанную пару; скажем, это (3, 6).
- Пройдите вправо на три единицы (потому что 3, x-значение, положительно).
- Поднимитесь на шесть единиц (потому что 6, значение y, также положительно).
- Отметьте пересечение перпендикулярных линий, которые вы видите в этом месте, 3 положительных единицы справа и шесть положительных единиц вверх.Это точка на координатной сетке (3, 6).
Давайте попробуем другой из нашего предыдущего списка, (-3, -6):
[вставить координатную сетку, показывающую квадрант III]
- Перейдите на три единицы влево, потому что -3 — отрицательное значение x.
- Спуститесь на шесть единиц, потому что -6 — отрицательное значение y.
- Отметьте пересечение перпендикулярных линий, которые вы видите в точке на 3 отрицательных единицы слева и 6 отрицательных единиц вниз. То есть (-3, -6).
Не забывайте всегда отмечать пересечение линий, а не пустое пространство между ними. Думайте о сетке как о сети; вы только «улавливаете» то, что находится на линиях, пока не попадете в суетливые пары координат, такие как (-3,5, -6,75), где вам, возможно, придется оценить эти доли единиц внутри ящиков.
Большинство координатных сеток выделены целыми числами. Они также могут быть кратными 10 или десятичными значениями, чтобы у вас по-прежнему оставались перпендикулярные линии для таких точек, как -3.5 или 6.5 и так далее.
Графические точки на координатной плоскости с использованием уравнений
Уравнение, требующее построения графиков на координатной сетке, может быть одного из двух типов:
- Координаты появляются в уравнении, или
- Координаты не появляются в уравнении
Если вам дано уравнение без координат, вы должны выбрать случайное значение для одного из двух чисел, поместить его в уравнение и посмотреть, каким станет другое значение. Повторите это, введя, скажем, случайное значение x и посмотрев, какое значение y дает уравнение.Вам нужно достаточное количество проходов по уравнению, чтобы построить график всех пар (x, y) и соединить их.
Вот линейное уравнение:
Выберите какое-нибудь значение для x, например 1, и выскочит значение y: 4.
Повторите это с другим значением x, 2, и другим, 3:
у = 2 + 3 = 5
у = 3 + 3 = 6
Теперь у вас есть три заказанные пары:
Рисование их в квадранте I дает вам прямую линию.
[вставить рисунок квадранта I с этой линией]
Вот что-то более сложное, квадратное уравнение для параболы:
у = х2 + 3
Сохраняйте ту же стратегию.Начните с 0 (это самый простой первый шаг):
у = 02 + 3 = 3
Это дает вам (0, 3) для минимума параболы, поэтому вы знаете, что ее направление направлено вверх в квадранты I и II. Постройте некоторые другие точки, используя маленькие значения x:
у = 12 + 3 = 4
у = 22 + 3 = 7
у = 32 + 3 = 12
Нанесение всего нескольких точек на координатную сетку даст вам макет, по крайней мере, правой стороны параболы. Добавьте несколько отрицательных значений x, чтобы убедиться, что вы также найдете точки в квадранте II.(Они будут зеркальными отрицаниями x-значений квадранта I.)
[вставьте чертеж этой параболы, если возможно]
Линейные уравнения производят линии; квадратные уравнения производят кривые. Если вы рисуете круг, вам понадобятся две точки, если вам дан центр, и три точки, если вам не дан центр. Для парабол также требуются три точки, а для гипербол — шесть точек (три по оси x, три по оси y).
Следующий урок:
Геометрические конструкции
графиков
графиков Цели
Изучив этот блок, вы сможете:
- Определите оси x и y .
- Определите происхождение . на графике.
- Определите координаты точки x и y .
- Нанесите точки на график.
Элементы графа
Мы часто используем графики, чтобы дать нам представление о отношения между переменными. Давайте сначала посмотрим на основные построение графов.
|
Координаты точек
Точка — это основная взаимосвязь, отображаемая на графике.Каждая точка определяется парой чисел, содержащей две координаты. Координата — одно из набора чисел используется для определения местоположения точки на графике. Каждый Точка обозначается как x , так и координатой y . В этом модуле вы узнаете, как найти обе координаты для любого точка. Вы также узнаете правильные обозначения для обозначения координаты точки. Сначала вы начнете с определения Координата x точки.
Определение координаты x
Координата x балла — это значение, которое сообщает вам, как далеко от начала координат находится точка по горизонтали, или x — ось. Чтобы найти координату x точка на графике:
Справа график с двумя точками, B и D. На этом рисунок:
|
Определение координаты y
Как мы уже упоминали, каждая точка определяется двумя координатами , координаты x и y .Теперь, когда ты знаешь как чтобы найти координату точки x , вы должны уметь найти координату y . В y — координата точки — это значение, которое говорит вам, как далеко от исходной точки точка находится на вертикальной оси y . Найти y — координата точки на графике:
Оглядываясь на график с нашими точками B и D, мы определите координату y для каждого.
|
Обозначение для обозначения точек
Когда у вас есть координаты точки, вы можете использовать заказанный парное обозначение для маркировки точек.Обозначения просты. Точки идентифицируются указанием их координат в виде ( x , y ). Обратите внимание, что координата x всегда идет первый. Например, на рисунке, который мы использовали, мы определили координаты x и y для каждой точки B и D.
|
Точки на осях
Если точка лежит на оси, рисовать линии не нужно. для определения координат точки.На рисунке ниже точка A лежит на оси y , а точка C лежит на оси x . Когда точка лежит на оси, одна из ее координат должна быть равна нулю.
|
- Точка C — Если вы посмотрите, как далеко точка
от начала координат по оси y ответ равен нулю.
Следовательно, координата y равна нулю. Любая точка, которая лежит
на оси x имеет нулевую координату y .
Если вы двигаетесь по оси x , чтобы найти координату x , точка находится в 200 от начала координат. Координаты точки C являются (200, 0)
Пример
|
Ответы на пример
- Какая точка находится на оси y ? Пункт А
- Какая точка помечена (20, 60)? Пункт B
- Какие точки имеют координату y из 30? Пункты A и C
[решение для примера]
Нанесение точек на график
Бывают случаи, когда вам ставят точку, и вам нужно будет найти его расположение на графике.Этот процесс часто называют построение точки и использует те же навыки, что и определение координат точки на графике. Показан процесс построения точки. на примере.
Пример
Постройте точку (200, 300).
| Шаг первый | Шаг второй | Шаг третий |
|---|---|---|
| Сначала нарисуйте линию, идущую от оси x на x — координата точки.В нашем примере это по адресу 200. | Затем нарисуйте линию, идущую от оси y на y — координата точки. В нашем примере это по адресу 300. | Точка пересечения этих двух линий находится в точке, где мы строят, (200, 300). |
Теперь вы готовы попробовать практическую задачу.Если у вас уже есть выполнил первую практическую задачу для этого блока, который вы, возможно, пожелаете попробовать дополнительную практику.
декартовых координат
Декартовы координаты могут использоваться, чтобы точно определить, где мы находимся на карте или графике.
Декартовы координаты
Используя декартовы координаты, мы отмечаем точку на графике с помощью , насколько далеко по и насколько далеко она находится вверх по :
| Точка (12,5) проходит на 12 единиц вперед и на 5 единиц вверх. |
Их также называют прямоугольными координатами , потому что это похоже на то, как мы формируем прямоугольник.
Ось X и Y
| Направление влево-вправо ( по горизонтали ) обычно называется X . | |
| Направление вверх-вниз ( вертикальное ) обычно называется Y . |
| Сложите их вместе на графике … | |
… и мы готовы к работе | |
Там, где они пересекаются, это точка «0»,
| |
Ось : опорная линия, от которой расстояние измеряются.
Множественное число Axis — Axes , произносится как ax-eez
Пример:
точка (6,4) это
6 единиц в поперечнике (в направлении x ) и
На 4 единицы вверх (в направлении и )
Так (6,4) означает:
Идите по 6, затем вверх по 4, затем «начертите точку».
И вы можете вспомнить, какая ось какая, по:
x — это КРЕСТ, поэтому x — ПОПЕРЕЧНО страницы.
Сложить как 2 числовые строки
Это похоже на то, как если бы мы соединили две числовые линии, одна идет влево-вправо, а другая — вниз-вверх.
Направление
По мере увеличения x точка перемещается дальше вправо . | |
По мере увеличения y точка перемещается дальше на вверх на . |
Запись координат
Координаты всегда пишутся в определенном порядке:
- сначала горизонтальное расстояние,
- , затем вертикальное расстояние.
Это называется «заказанной парой » ( пара номеров в специальном заказе )
И обычно числа разделяются запятыми, а вокруг всего этого ставятся круглые скобки:
(3,2)
Пример: (3,2) означает 3 единицы вправо и 2 единицы вверх
Пример: (0,5) означает 0 единиц вправо и 5 единиц вверх.
Другими словами, всего на 5 единиц больше.
Происхождение
Точке (0,0) присваивается специальное имя «Начало», а иногда и буква «О».
абсцисса и ордината
Вы можете услышать слова «абсцисса» и «ордината» … это просто значения x и y:
- Абсцисса: значение по горизонтали («x») в паре координат: как далеко от точки вдоль находится точка
- Ордината: значение по вертикали («y») в паре координат: как далеко вверх или вниз точка
«Декартово»…?
Они называются декартовыми , потому что идея была развита математиком и философом Рене Декартом , который был также известен как Картезиус .
Он также известен тем, что сказал «Я думаю, следовательно, я» .
А как насчет отрицательных значений X и Y?
Как и в случае с числовой линией, у нас могут быть и отрицательные значения.
Отрицательный: начало с нуля и направление в противоположном направлении :
- Отрицательный x идет влево
- Отрицательный y идет вниз
Итак, для отрицательного числа:
|
Четыре квадрантаКогда мы включаем отрицательные значения, оси x и y делят пространство на 4 части: Квадранты I, II, III и IV (пронумерованы против часовой стрелки) |
В квадранте I и x, и y положительны, но…
- в квадранте II x отрицательно (y все еще положительно),
- в квадранте III и x, и y отрицательны, а
- в квадранте IV x снова положительно, а y отрицательно.
Как это:
|
Пример: точка «А» (3,2) находится на 3 единицы вперед и на 2 единицы вверх.
И x, и y положительны, поэтому эта точка находится в «квадранте I»
Пример: точка «C» (-2, -1) проходит на 2 единицы в отрицательном направлении и на 1 единицу вниз (т. Е. В отрицательном направлении).
И x, и y отрицательны, поэтому эта точка находится в «Квадранте III»
Примечание: слово Quadrant происходит от quad , что означает четыре . Например, четвероногих малышей, рожденных при одном рождении, называют четвероногих , четвероногих — четвероногих .а четырехугольник — четырехсторонний многоугольник.
Размеры: 1, 2, 3 и более …
Подумайте об этом:
| 1 | В числовую строку можно заходить только: , поэтому для любой позиции нужно всего один номер |
|---|---|
| 2 | Декартовы координаты могут идти: , поэтому для любой позиции нужно два числа |
| 3 | Как определить точку в реальном мире (например, кончик носа)? Нам нужно знать:
, то есть три числа , или 3 измерения! |
3 Размеры
Декартовы координаты могут использоваться для определения местоположения точек в 3 измерениях, как в этом примере:
| Здесь точка (2, 4, 5) показана в трехмерных декартовых координатах . |
На самом деле, эту идею можно продолжить в четырех и более измерениях — я просто не могу придумать, как вам это проиллюстрировать!
Координатная плоскость — математическая открытая ссылка
Координатная плоскость — математическая открытая ссылкаДвумерная поверхность, на которой точки нанесены и расположены по их координатам x и y.
Попробуй это Перетащите точку A. При перетаскивании обратите внимание на два числа, определяющих ее положение на плоскости.Перетащите начало координат, чтобы изменить положение осей.Координатная плоскость — это двумерная поверхность, на которой мы можем рисовать точки, линии и кривые. Он имеет две шкалы, называемые осью x и осью y , расположенной под прямым углом друг к другу. Множественное число оси — это «оси» (произносится «AX-easy»). Точки на плоскости располагаются с помощью двух чисел — координат x и y. Это горизонтальные и вертикальные расстояния точки от определенного места, называемого исходной точкой.
X ось Горизонтальный масштаб называется осью x . Когда вы переходите вправо по шкале от нуля, значения становятся положительными и увеличиваются. По мере того, как вы идете налево от нуля, они становятся все более и более отрицательными. Y ось Вертикальный масштаб называется осью y . По мере роста от нуля числа увеличиваются в положительном направлении. По мере того, как вы спускаетесь с нуля, они становятся все более и более отрицательными.Маркировка осей
Вдоль каждой оси вы увидите маленькие галочки с цифрами.Эти метки помогают судить о масштабе. Они показаны через каждые 5 единиц на рисунке выше, но могут иметь любое приращение и не обязательно должны быть одинаковыми по обеим осям.Происхождение
Точка пересечения двух осей (нулевое значение на обеих шкалах) называется началом координат. Начало координат — это точка, от которой измеряются все расстояния по осям x и y. На рисунке выше вы можете перетащить исходную точку, чтобы переместить ее в более подходящее место в любое время.Квадранты
Две оси делят плоскость на четыре области, называемые квадрантами.Первый квадрант, по соглашению, верхний правый, а затем они вращаются против часовой стрелки. На диаграмме выше они обозначены квадрантами 1,2 и т. Д. Их принято обозначать цифрами. но мы говорим о них как о «первом, втором, третьем и четвертом квадрантах». Иногда они обозначаются римскими цифрами: I, II, III и IV.
На диаграмме выше вы можете перетащить начало координат в любой угол и отображать только один квадрант за раз. если хотите.
Что стоит попробовать
На рисунке вверху страницы сначала нажмите «сброс».- Перетащите исходную точку, в том числе перетащите ее полностью в угол, чтобы отобразить только один квадрант.
- Перетащите точку A в каждый квадрант. Первое число после A — это координата x , а второе — координата y . Обратите внимание, как знаки каждого изменения в каждом квадранте. Подробнее об этом см. Координаты точки
Другие темы о координатной геометрии
(C) Открытый справочник по математике, 2011 г.
Все права защищены.
— определение, факты и примеры
Координатная плоскость — это двумерная плоскость, образованная пересечением вертикальной линии, называемой осью y, и горизонтальной линии, называемой осью x. Это перпендикулярные линии, которые пересекаются друг с другом в нуле, и эта точка называется началом координат.
Что такое координатная плоскость?
Координатная плоскость — это двумерная поверхность, образованная двумя числовыми линиями.Он образуется, когда горизонтальная линия, называемая осью X, и вертикальная линия, называемая осью Y, пересекаются в точке, называемой началом координат. Числа на координатной сетке используются для определения точек. Координатная плоскость может использоваться для точек графика, линий и многого другого. Он действует как карта и дает точные указания от одной точки к другой.
Определение координатной плоскости
Определение координатной плоскости следующее: Координатная плоскость , также известная как сетка прямоугольной координатной плоскости , представляет собой двумерную плоскость, образованную пересечением вертикальной линии, называемой осью Y, и горизонтальной линии, называемой X -ось.
Координатная плоскость
График координат , иногда называемый координатной плоскостью , состоит из двух числовых линий, называемых осями, которые проходят перпендикулярно друг другу.
Координаты
Координаты — это набор из двух значений, которые определяют местоположение определенной точки на сетке координатной плоскости, более известной как координатная плоскость. Точка в координатной плоскости называется ее упорядоченной парой в форме (x, y), которая записывается в круглых скобках, что соответствует координате X и координате Y.Эти координаты могут быть положительными, нулевыми или отрицательными, в зависимости от положения точки в соответствующих квадрантах.
Квадранты
Квадрант можно определить как область / часть декартовой плоскости, полученную при пересечении двух осей друг друга
- Первый квадрант: x> 0, y> 0
- Второй квадрант: x <0, y> 0
- Третий квадрант: x <0, y <0
- Четвертый квадрант: x> 0, y <0
Определение точки на координатной плоскости
Теперь, когда мы уже знакомы с координатной плоскостью и ее частями, давайте обсудим, как определять точки на координатной плоскости.Чтобы найти точку на координатной плоскости, выполните следующие действия:
- Шаг 1. Найдите точку.
- Шаг 2: Найдите квадрант, глядя на знаки его координат X и Y.
- Шаг 3: Найдите координату X или абсциссу точки, считывая количество единиц, в которых точка находится справа / слева от начала координат по оси X.
- Шаг 4: Найдите координату Y или ординату точки, считывая количество единиц, в которых точка находится выше / ниже начала координат по оси Y.
Давайте посмотрим на примеры координатной плоскости. Посмотрите на рисунок, показанный ниже.
- Шаг 1: Обратите внимание на синюю точку на графике координат.
- Шаг 2: Он находится во втором квадранте.
- Шаг 3: точка находится на расстоянии 3 единиц от начала координат по отрицательной оси X.
- Шаг 4: точка находится на расстоянии 2 единиц от начала координат вдоль положительной оси Y.
Таким образом, точка на графике имеет координаты (-3, 2).
Построение точки на координатной плоскости
В этом разделе мы узнаем, как построить точку на координатной плоскости. Возьмем для примера точку P = (5,6). Чтобы нанести точку на координатную плоскость, выполните следующие действия:
- Шаг 1. Постройте два перпендикуляра, ось X и ось Y.
- Шаг 2: Начните с начала координат. Переместите 5 единиц вправо по положительной оси X.
- Шаг 3. Переместите на 6 единиц вверх вдоль положительной оси Y.
- Шаг 4: Отметьте точку пересечения. Обозначьте это как (5, 6).
Обратите внимание, что P находится в первом квадранте. Кроме того, это называется положительной координатной плоскостью, поскольку значение обеих координат для любой точки в этом квадранте будет положительным.
Важные моменты
- Первый квадрант (+, +), известный как квадрант положительных координат, представлен римской цифрой I .
- Второй квадрант (-, +) представлен римской цифрой II .
- Третий квадрант (-, -) представлен римской цифрой III .
- Четвертый квадрант (+, -) представлен римской цифрой IV .
- Координаты любой точки заключены в скобки
Попробуйте решить этот сложный вопрос:
Найдите любые три точки, которые лежат в положительной координатной плоскости и для которых абсцисса и ордината равны и также неотрицательны.
Темы, связанные с координатной плоскостью
Пример 1. Давайте поможем Оливии и Джейн построить следующие точки на декартовой плоскости:
А (2,5, 3,5)
Б (- 2, 4)
К (6.5, 1)
D (4, — 2.2)
Решение:
A и C находятся в первом квадранте.
B находится во втором квадранте.
D находится в четвертом квадранте.Пример 2: Вот несколько точек, нанесенных на координатную плоскость:
A (1,2), B (3, -2), C (-3, -3), D (-4, 2), E (-1, 2), F (3,0), G (0, -3)
Посмотрите на точки, нанесенные на график ниже, и ответьте на следующие вопросы:a) В каких квадрантах лежат точки C, D и E?
б) Какие точки лежат в первом или четвертом квадранте?
в) Какие точки лежат на одной из двух осей?
Решение:a) D и E лежат во втором квадранте, а C лежит в третьем квадранте.
б) A лежит в первом квадранте, а B лежит в четвертом квадранте.
c) F лежит на положительной стороне оси X, а G лежит на отрицательной стороне оси Y.Пример 3: Человек одновременно бросает две катящиеся кости. Пусть числа, которые отображаются на Die — 1 и Die — 2, представлены как x и y соответственно. После каждого броска на плоскости наносится точка P (x, y). Постройте все возможные позиции P и выделите те позиции, для которых сумма x и y равна 8.
Решение:
Обратите внимание, что на каждом кубике может быть 6 чисел (целые числа от 1 до 6). Таким образом, если вы сложите возможные числа на обеих костях, у вас получится 36 пар. Теперь пары, для которых сумма x и y равна 8: (2,6), (3,5), (4,4), (5,3), (6,2). На следующем рисунке построено всего 36 пар, и эти 5 пар выделены:
перейти к слайду перейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом в решении проблем, используя логику, а не правила.Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Забронируйте бесплатную пробную версию Класс
Часто задаваемые вопросы о координатной плоскости
Какие части координатной плоскости?
Координатные плоскости включают оси (ось X и ось Y), начало координат (0,0) и четыре квадранта.
Что такое начало на координатной плоскости?
Точка пересечения двух осей координатной плоскости является началом координатной плоскости.Координаты начала координат (0, 0).
Что такое координата XY?
Координата XY — это двумерная плоскость с осями координат, осью X и осью Y, перпендикулярными друг другу.
Как построить координатную плоскость?
Координатная плоскость может быть построена следующим образом:
- Шаг 1. Возьмите лист миллиметровой или сеточной бумаги.
- Шаг 2: Проведите горизонтальную линию. Эта линия называется осью x и используется для определения значений x.
- Шаг 3: Проведите вертикальную линию. Эта линия называется осью y и используется для определения значений y. Чтобы показать, что ось на самом деле
Примечание: чтобы показать, что эти оси на самом деле идут вечно в обоих направлениях, используйте маленькие стрелки на каждом конце линии.
Когда бы вы использовали координатную плоскость?
Декартова плоскость координат x и y хорошо работает во многих ситуациях в реальной жизни, например, при планировании размещения различных предметов мебели в комнате, можно нарисовать двумерную сетку, представляющую комнату и, таким образом, подходящую можно использовать единицу измерения.
Сколько квадрантов на координатной плоскости?
В координатной плоскости четыре квадранта.
Как прочитать координатную плоскость?
Мы можем считать координатную плоскость следующим образом:
- Шаг 1: Найдите квадрант, в котором расположена данная точка, посмотрев на знаки ее координат x и y.
- Шаг 2: Считайте количество единиц, в которых точка находится справа / слева от начала координат по оси x, чтобы найти ее координату x.
- Шаг 3: Считайте количество единиц, в которых точка находится по направлению вверх / вниз от начала координат по оси y, чтобы найти ее координату y.
точек графика на координатной плоскости | Как построить график координат — Видео и стенограмма урока
Графические точки на координатной плоскости
Теперь давайте посмотрим, как построить график координат на координатной плоскости. Шаги построения графика координат:
- Найдите значение x на оси x .
- Если значение y отрицательное, переместитесь на правильное количество тактов, чтобы найти значение y ; если значение y положительное, переместитесь на правильное количество тактов, чтобы найти значение y .
- Отметьте точку
Графические примеры пар координат
Давайте посмотрим, как построить график следующей пары координат (6, 3).
- Значение x всегда идет первым, поэтому значение x равно 6
- Значение y равно 3, что означает, что оно должно увеличиться на 3
- Отметьте пересечение этих двух точек как точку
Теперь давайте посмотрим, как построить график пары координат (-4, 2)
- Значение x всегда идет первым, поэтому значение x равно -4
- Значение y равно 2, что означает, что оно должно увеличиться на 2
- Отметьте пересечение этих двух точек как точку
Теперь давайте посмотрим, как построить график пары координат (-3, -2)
- Значение x всегда идет первым, поэтому значение x равно -3
- Значение y равно -2.Поскольку он отрицательный, на этот раз нам нужно спуститься вниз 2
- Отметьте пересечение этих двух точек как точку
Теперь давайте посмотрим, как построить график пары координат (0, 5)
- Значение x всегда идет первым, поэтому значение x равно 0. Поскольку оно равно 0, оно остается равным 0. или где пересекаются оси x и y .
- Значение y равно 5, что означает, что оно должно увеличиться на 5
- Отметьте пересечение этих двух точек как точку
- Обратите внимание, что он находится на оси y . Когда значение x равно 0, точка находится на оси y .Когда значение y равно 0, точка находится на оси x .
Использование координатного плоского графика
Теперь давайте посмотрим, как использовать координатный график. Какую информацию показывает этот график?
Глядя на этот график, мы можем определить пары координат в каждом месте.Начните с выбранной координаты x ‘-3’.
- Проведите вертикальную линию, перпендикулярную -3
- Посмотрите, где линия пересекает линию графика
- Проведите горизонтальную линию
- Посмотрите, где линия пересекает ось y
В этом случае он пересекает ось y в точке -5. Это означает, что пара координат (-3, -5).
Мы также можем найти пару координат, начинающуюся с координаты y .Давайте найдем пару координат для y = 2:
- Проведите горизонтальную линию через 2 на оси y .
- Найдите место пересечения линии графика — обратите внимание, что в этом примере есть 2 места, где линия пересекает линию графика
- Проведите вертикальную линию через ось x (для обоих мест)
- Посмотрите, какие числа находятся там, где нарисованные линии пересекают ось x
Обратите внимание, что в этом примере есть два ответа.Иногда граф координат может иметь две пары координат для одной точки x или y . В этом случае наши пары координат: (-1, 2) и (1.5, 2).
Координатный график может помочь визуализировать, как данные меняются при различных входных данных. Обычно x является входом, а y — выходом. В приведенных выше примерах предположим, что график показывает, насколько хорошо кто-то думал, что им понравится шоколадный батончик, исходя из названия и внешнего вида (значения x ), в сравнении с тем, насколько им действительно понравился шоколадный батончик после его дегустации ( y -значения).
Мы можем видеть, где находятся точки максимума и минимума. По вкусу больше всего понравился шоколадный батончик, получивший оценку «6». Судя по внешнему виду моноблока, это произошло при x — значениях 1 и -4. Таким образом, этот моноблок понравился больше всего, когда они думали, что он выглядит не очень хорошо (с оценкой -4), и когда они думали, что он выглядел немного лучше, чем посредственный (с оценкой 1). Наименее понравившийся шоколадный батончик, исходя из вкуса, получил оценку «-6». Однако его значение x , равное «4», указывает на то, что он выглядел довольно хорошо.
Итак, шоколадный батончик, который выглядел наименее привлекательно (с оценкой -6 по оси x ), показал очень хорошие вкусовые качества с оценкой 5, в то время как шоколадный батончик, который выглядел лучше всего (с 6 баллов по оси x ) оказался посредственным по вкусовым качествам, получив 1 балл по оси x .
В целом этот график говорит нам, что внешний вид и вкус шоколадного батончика не сильно коррелированы, а это означает, что даже если шоколадный батончик выглядит хорошо, это не означает, что он приятный на вкус.
Сводка урока
График координат — это график, на котором отображаются точки x и y по горизонтали x по оси и по вертикали y по оси . Пара координат — это точка на графике, которая указывает, где находятся значения x и y . Его можно найти:
- Поиск значения x на оси x
- Если значение y отрицательное, переместитесь на нужное количество тактов вниз, чтобы найти значение y .Если значение y положительное, переместитесь на правильное количество тактов, чтобы найти значение y .
- Разметка точки
Координатный график может быстро показать, как один вход (значения x ) влияет на выход (значения y ).
Построение точек (упорядоченных пар) в координатной плоскости
Чтобы построить точку в плоскости координат xy (также называемой декартовой координатной плоскостью), вам просто нужно знать, как читать значения или числа в упорядоченной паре, которая определяет точку.В этом уроке мы узнаем, как именно это сделать!
объявление
Точки построения — это все о чтении чисел
Каждое число в упорядоченной паре называется «координатой». Первое число называется «координатой x», а второе число — «координатой y». Эти два числа говорят вам, в какой части координатной плоскости находится ваша точка.
Примеры
Чтобы построить точку, начните с начала координат, которое является центром графика (точка (0,0)).Затем координата x скажет вам, на сколько единиц нужно переместиться влево или вправо, а координата y скажет вам, на сколько единиц переместиться вверх или вниз.
Если координата x отрицательная, вы переместитесь влево, а не вправо.
То же самое с отрицательной координатой y. Вы будете двигаться вниз от начала координат, а не вверх.
Что делать, если координаты являются дробными или десятичными?
Координаты в упорядоченной паре могут быть любыми действительными числами.Это означает, что они могут быть не только положительными или отрицательными, но также дробными или десятичными. Даже в этом случае применима та же общая идея. Но, в зависимости от десятичной или дробной части, вам, возможно, придется немного оценить местоположение точки.
Сводка
Точка состоит из двух координат: координаты x и координаты y. Каждый из них дает вам часть информации, которую вы можете использовать для построения точки на координатной плоскости.
Дополнительное обучение
Как только вы научитесь наносить точки, вы сможете строить линейные уравнения или работать с такими идеями, как наклон линии или расстояние между двумя точками.

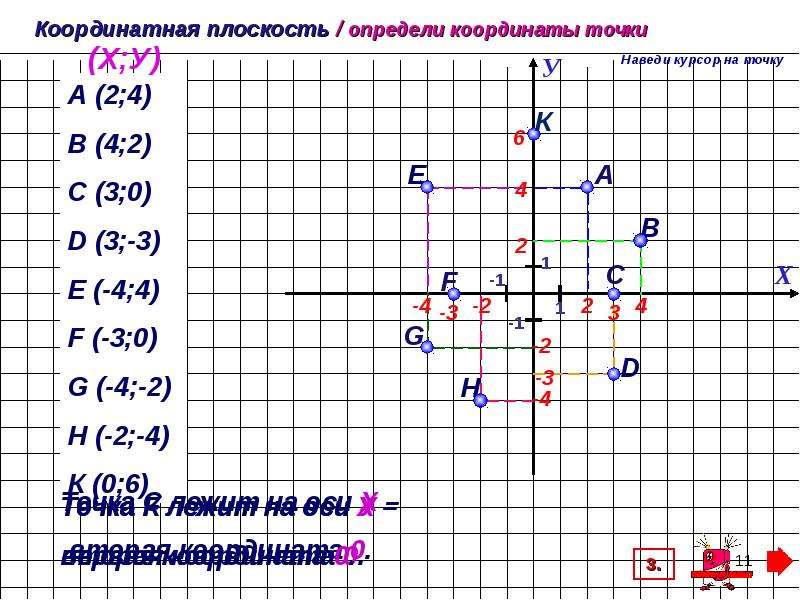
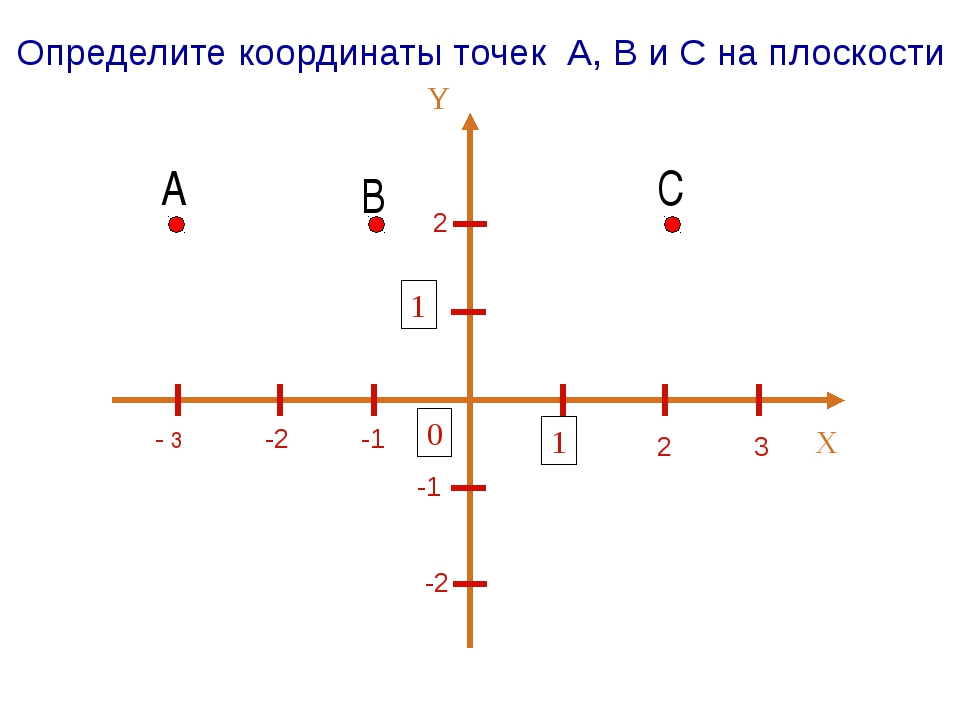 На пересечении перпендикулярных прямых получим точку $A$ с координатами $(2; 5)$.
На пересечении перпендикулярных прямых получим точку $A$ с координатами $(2; 5)$.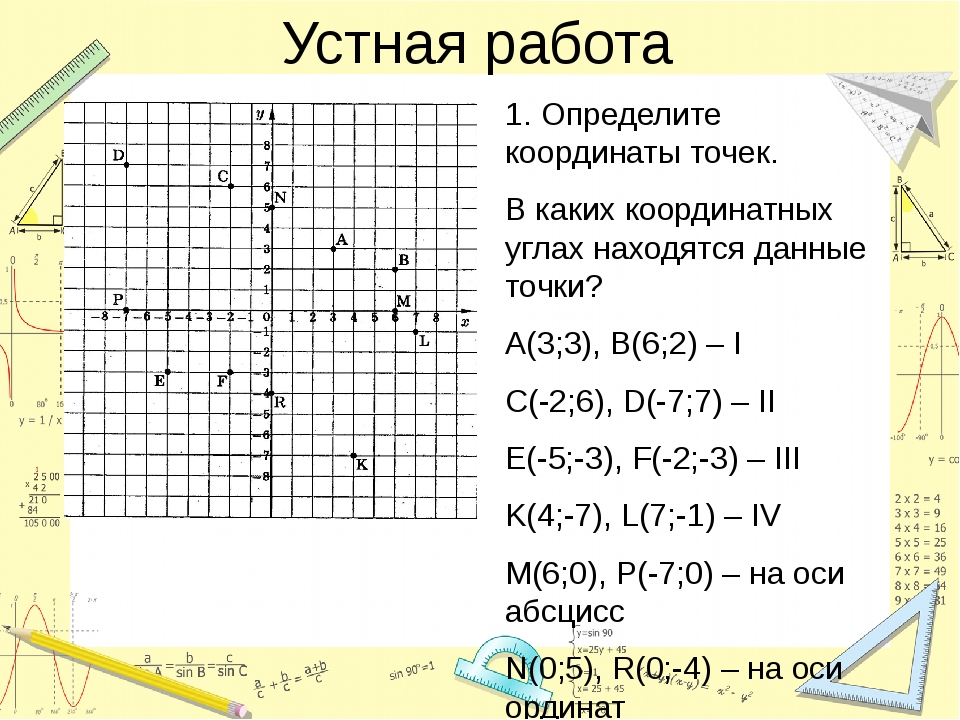

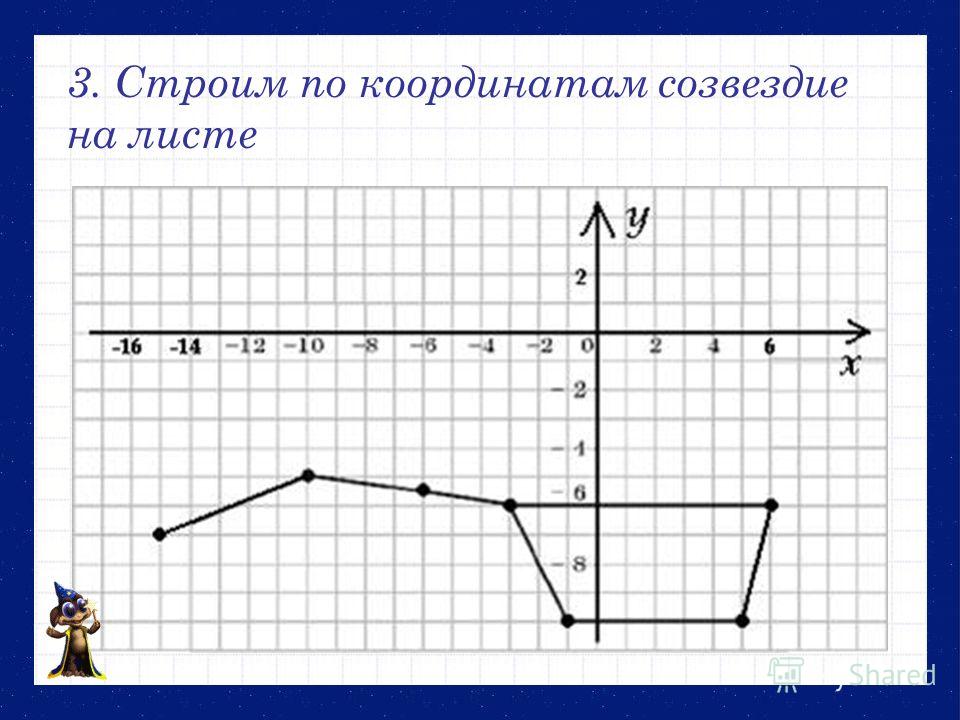
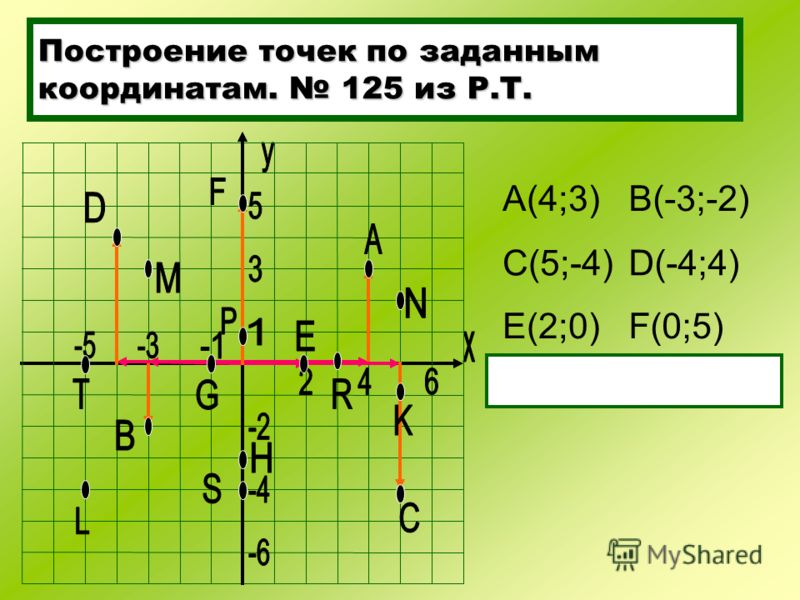 $
$