Нахождение обратной матрицы примеры – , , , .

Нахождение обратной матрицы с примеры решения. Описание основных методов вычисления обратной матрицы

Задание. Для матрицы $ A=\left( \begin{array}{ll}{7} & {4} \\ {5} & {3}\end{array}\right) $ найти обратную методом присоединенной матрицы.

Решение. Приписываем к заданной матрице справа единичную матрицу второго порядка:

$$ A\left|E=\left( \begin{array}{cc|cc}{7} & {4} & {1} & {0} \\ {5} & {3} & {0} & {1}\end{array}\right)\right. $$

От первой строки отнимаем вторую (для этого от элемента первой строки отнимаем соответствующий элемент второй строки):

$$ A\left|E = \left( \begin{array}{rr|rr}{2} & {1} & {1} & {-1} \\ {5} & {3} & {0} & {1}\end{array}\right)\right. $$

От второй строки отнимаем две первых:

$$ A\left|E \sim \left( \begin{array}{rr|rr}{2} & {1} & {1} & {-1} \\ {1} & {1} & {-2} & {3}\end{array}\right)\right. $$

Первую и вторую строки меняем местами:

$$ A\left|E \sim \left( \begin{array}{rr|rr}{1} & {1} & {-2} & {3} \\ {2} & {1} & {1} & {-1}\end{array}\right)\right. $$

От второй строки отнимаем две первых:

$$ A\left|E \sim \left( \begin{array}{rr|rr}{1} & {1} & {-2} & {3} \\ {0} & {-1} & {5} & {-7}\end{array}\right)\right. $$

Вторую строку умножаем на (-1), а к первой строке прибавляем вторую:

$$ A\left|E \sim \left( \begin{array}{rr|rr}{1} & {0} & {3} & {-4} \\ {0} & {1} & {-5} & {7}\end{array}\right)\right. $$

Итак, слева получили единичную матрицу, а значит матрица, стоящая в правой части (справа от вертикальной черты), является обратной к исходной.

Таким образом, получаем, что $ A^{-1}=\left( \begin{array}{rr}{3} & {-4} \\ {-5} & {7}\end{array}\right) $

Ответ. $ A^{-1}=\left( \begin{array}{rr}{3} & {-4} \\ {-5} & {7}\end{array}\right) $

www.webmath.ru

§3. Обратная матрица

1. Как известно, для каждого числа 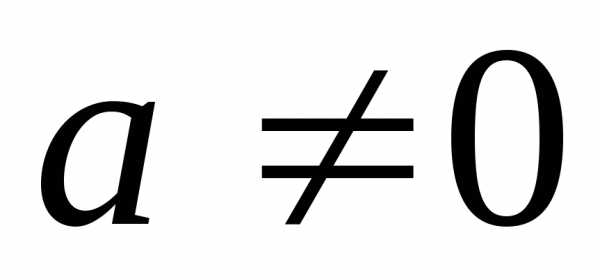существует такое числ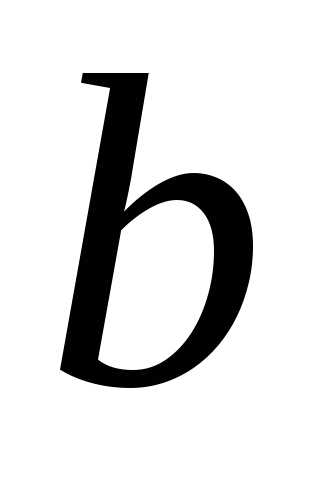о, что. Число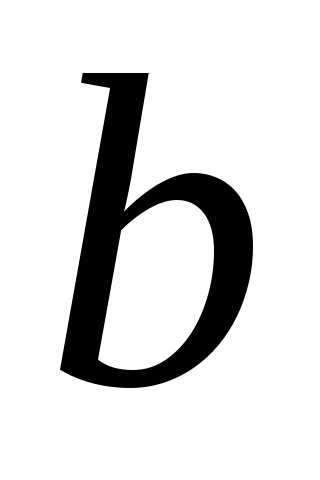называется обратным для. Если мы зафиксируем натуральное числои будем рассматривать квадратные матрицы-го порядка, то в этом множестве матриц единичная матрицабудет играть роль единицы. Естественно поставить вопрос о существовании обратной матрицы, т.е. такой матрицы, которая в произведении с данной матрицей дает единичную.

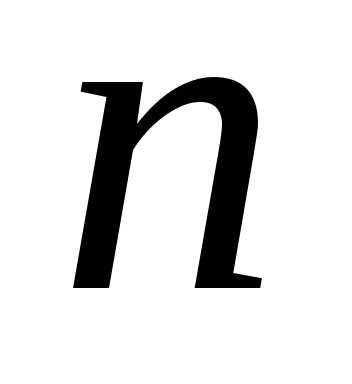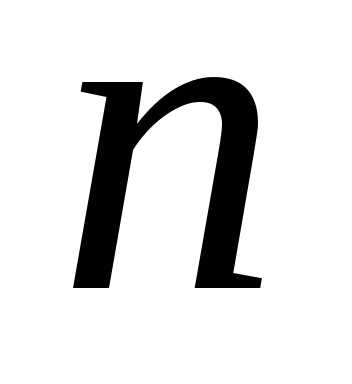Пусть – квадратная матрица-го порядка. Квадратная матрица(того же порядка) называется обратной для, если

.

Матрицу, обратную к матрице

, принято обозначать символом.

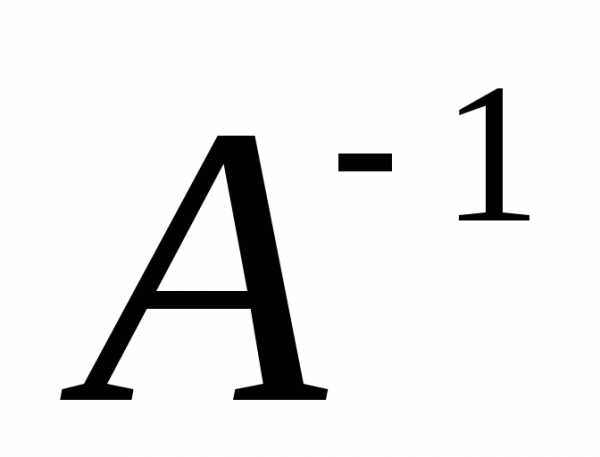2. Способы вычисления обратной матрицы

Если для квадратной матрицы существует обратная матрица, то справедливо равенство, где– единичная матрица. Переходя в этом равенстве к определителям (и учитывая свойство 9 определителей), имеем, или. Отсюда заключаем, что(в противном случае левая часть последнего равенства равнялась бы нулю). Этим доказано, что если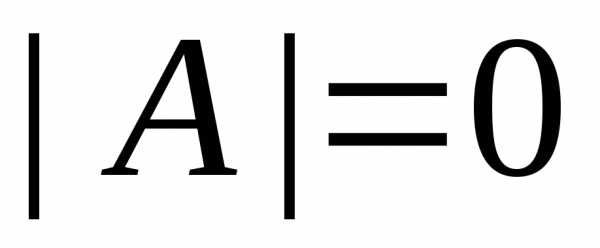, то для матрицыне существует обратной. Другими словами, условие

является необходимым условием существования обратной матрицы. Оказывается, это условие является и достаточным.

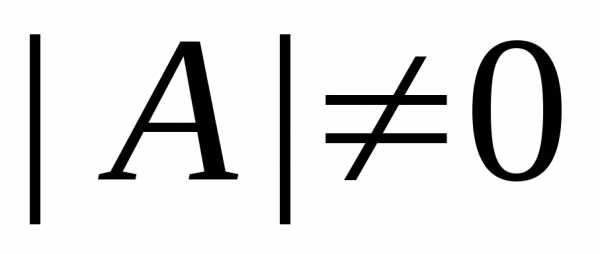
Лемма

Если обратная матрица существует, то она единственна.

Квадратная матрица называетсяневырожденной, если ее определитель не равен нулю ( 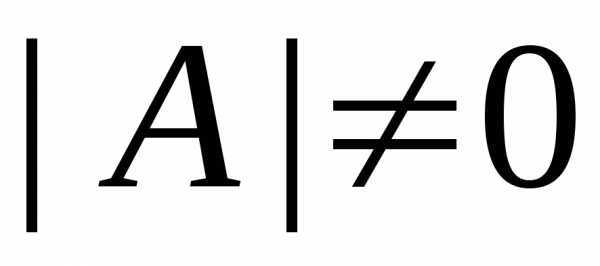). В противном случае матрицаназываетсявырожденной ( ).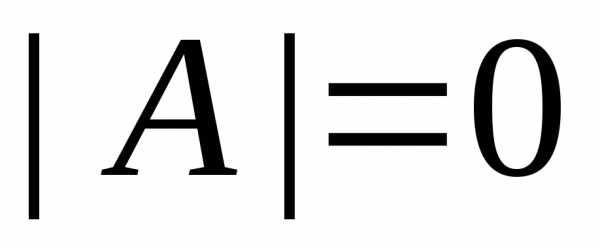

Пусть матрица имеет вид

.

ТЕОРЕМА. Если – невырожденная матрица, то для нее существует обратная матрица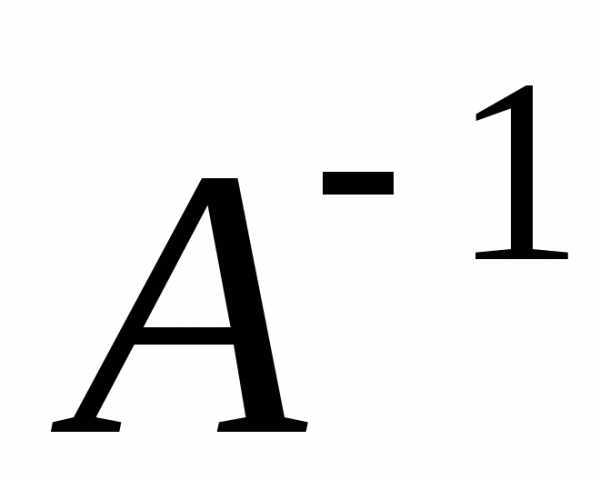, которая вычисляется по формуле

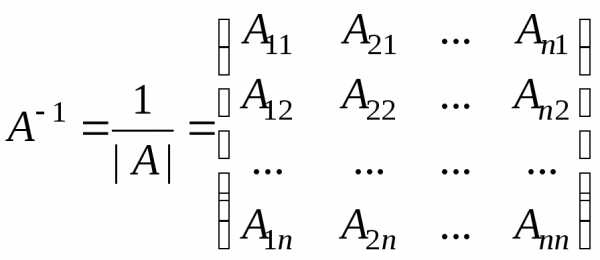, (5)

где – алгебраическое дополнение для элементаматрицы.

Замечание

Обратим внимание на расположение чисел в правой части формулы (5): число

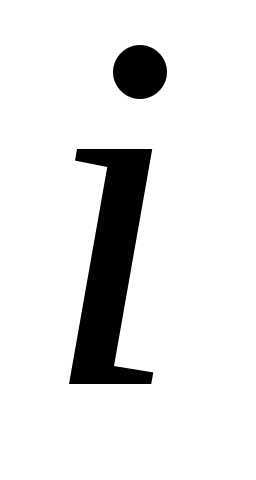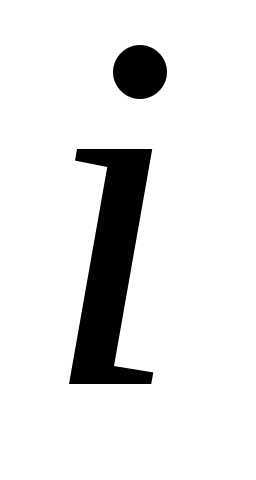расположено не в -й строке и-м столбце, а наоборот, в-й строке и-м столбце. Таким образом, матрица, стоящая в правой части (5), является транспонированной матрицей алгебраических дополнений элементов матрицы.

Типовой пример. Найдите 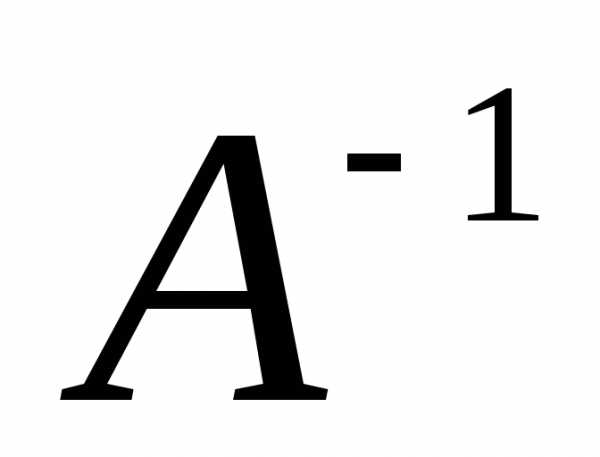, если.

► .

– невырожденная матрица, следовательно, обратная для нее существует. Найдем ее по формуле:

.

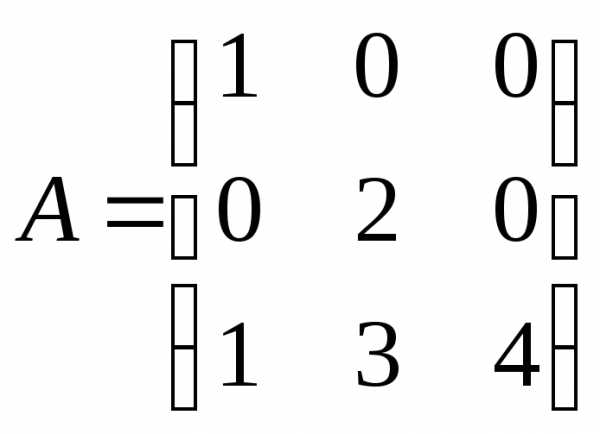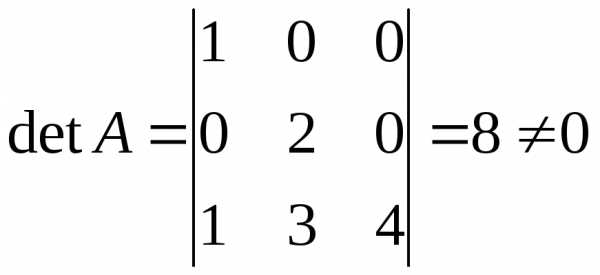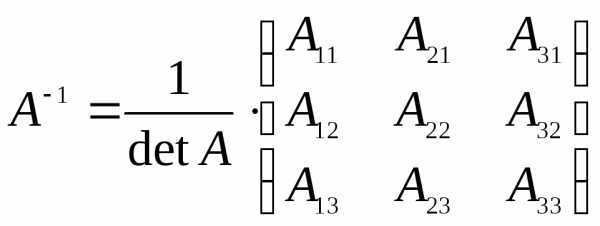Обратите внимание на индексацию алгебраических дополнений. Вычисляем алгебраические дополнения

; ; ;

; ; ;

; ; .

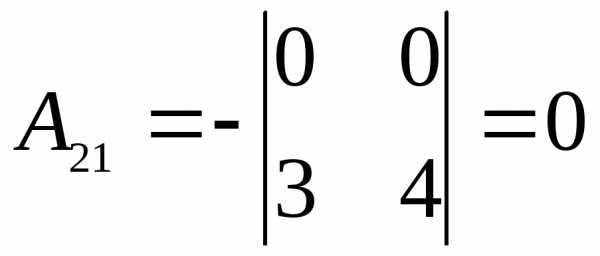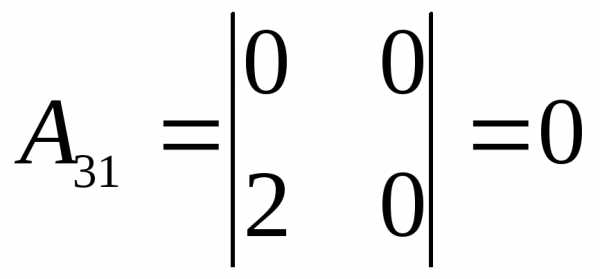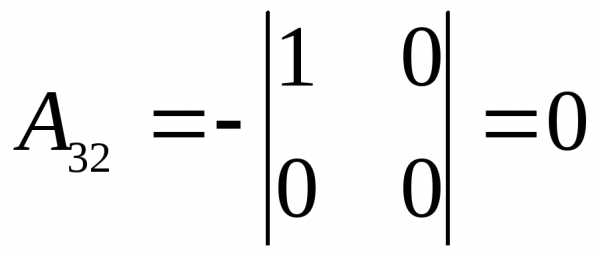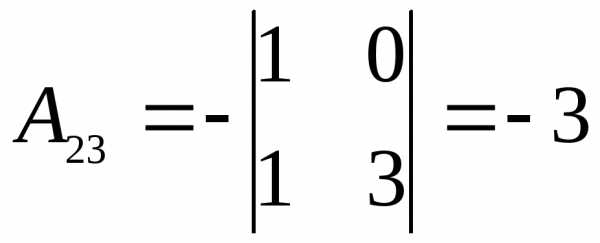Тогда

.

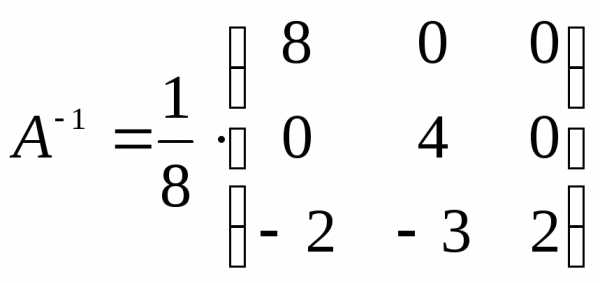
Можно сделать проверку:

.

Значит, обратная матрица найдена верно.◄

3. Вычисление обратной матрицы методом элементарных преобразований. Элементарные преобразования матрицы

1. Перестановка строк (столбцов).

2. Умножение строки (столбца) на число .

3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на любое число.

Чтобы найти матрицу, обратную данной, делаем следующее:

для матрицы 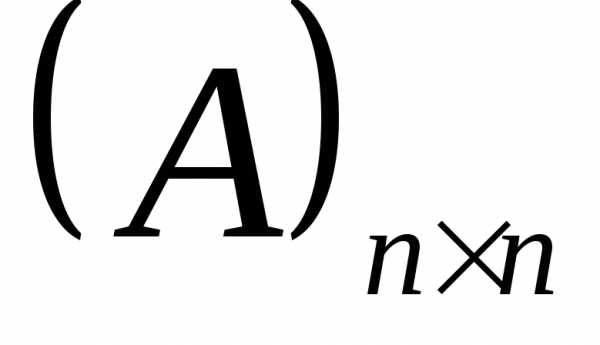записываем прямоугольную матр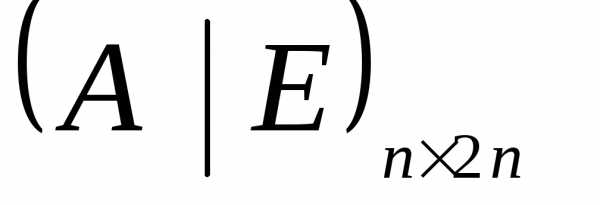ицу, приписывая справа единичную матрицу;

с помощью элементарных преобразований приводим матрицу

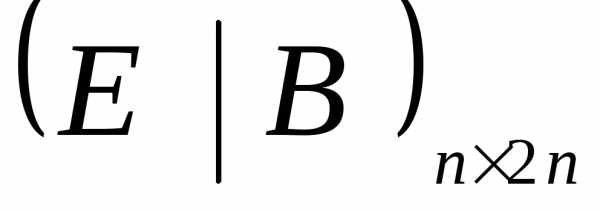к виду. Тогда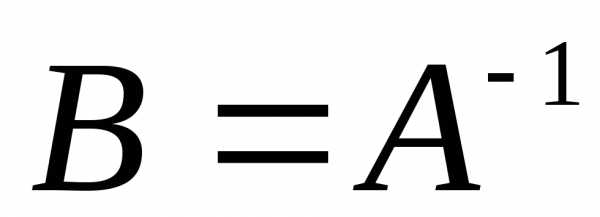. Эквивалентные матрицы обозначаются.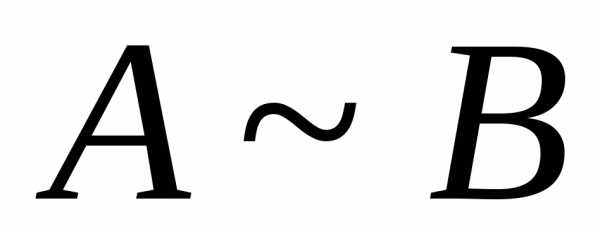

Типовой пример

Найти матрицу, обратную данной: .

►~(первую строку матрицы умножили на ) ~~~~

. Следовательно, .

Проверка: . ◄

С помощью обратной матрицы можно решать простейшие матричные уравнения, где неизвестной является матрица X. Это уравнения следующего вида

.

В этих уравнениях – матрицы таких размеров, что все операции умножения возможны и с обеих сторон от знаков равенств находятся матрицы одинаковых размеров. Если в первых двух уравнениях матрица

невырожденная, то их единственное решение записывается следующим образом соответственнои. Если в третьем матричном уравнении матрицы и невырождены, то его решение записывается в виде . Пример

В табл. 6 приведены данные о дневной производительности пяти предприятий, выпускающих четыре вида продукции с потреблением трех видов ресурсов, а также количество рабочих дней в году каждого предприятия и цены каждого вида сырья.

Таблица 6

Вид продукции	Производительность предприятий (изд. в день)					Затраты ресурсов, ед. веса/изд.
	1	2	3	4	5	1	2	3
1	4	5	3	6	7	2	3	4
2	0	2	4	3	0	3	5	6
3	8	15	0	4	6	4	4	5
4	3	10	7	5	4	5	8	6
	Кол-во раб. дней в году					Цены ед.сырья
	200	150	170	120	140	40	50	60

Требуется найти:

1) годовую производительность каждого предприятия по каждому виду продукции;

2) годовую потребность каждого предприятия по каждому виду ресурса;

3) годовую сумму кредитования каждого предприятия для закупки ресурсов, необходимых для выпуска продукции указанных видов и при определенном количестве рабочих дней.

►Введем следующие обозначения:

а) Данная матрица является матрицей производительности пяти предприятий по всем четырем видам продукции. Каждый столбец этой матрицы соответствует дневной производительности отдельного предприятия по каждому виду изделий. Следовательно, годовая производительность 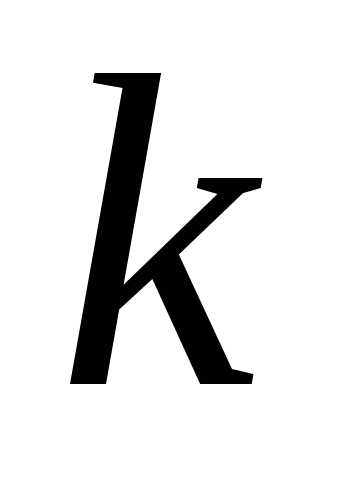-го предприятия по каждому виду изделий получается умножением-го столбца матрицы А на количество рабочих дней в году для этого предприятия (к = 1,2,3,4,5)

А₁₁=0,79 А₂₁=0,16 А₃₁=0,02

А₁₂=0,16 А₂₂=0,8 А₃₂=0,1

А₁₃=0,02 А₂₃=0,1 А₃₃=0,96,

тогда .

Это матрица коэффициентов полных материальных затрат.

б) , т.е. валовой выпуск продукции 1-го, 2-го и 3-го цехов будут соответственно.

в) Найдем производственную программу каждого цеха (промежуточный продукт) по формуле (;)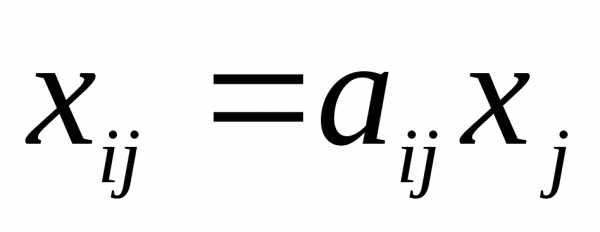

;

;

;

;

;

;

;

;

.

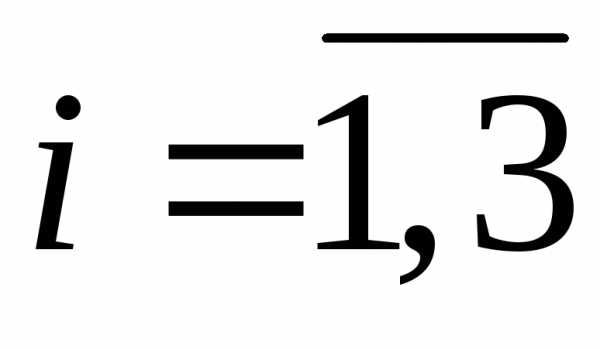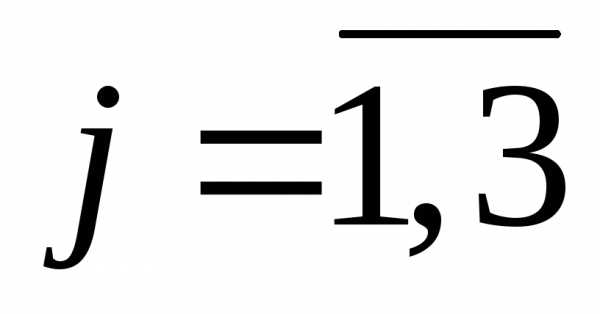Результаты представим в таблице 7:

Таблица 7

Цех	Внутрипроизводственные потребления			Итого	Конечный продукт	Валовый выпуск
	1	2	3
1 2 3	0 48 0	37 0 19	0 40 80	37 88 99	200 100 300	237 186 400

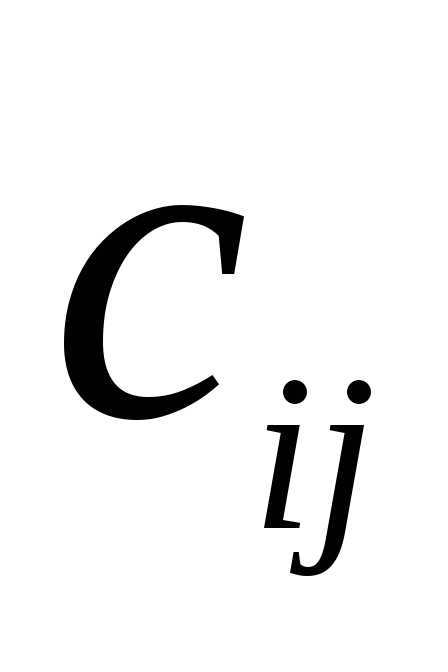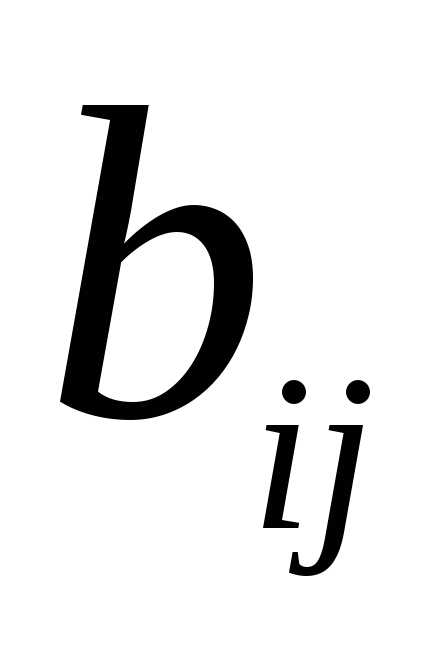г) Коэффициенты косвенных затрат определяются как разности полных внутрипроизводственных затрат и прямых затрат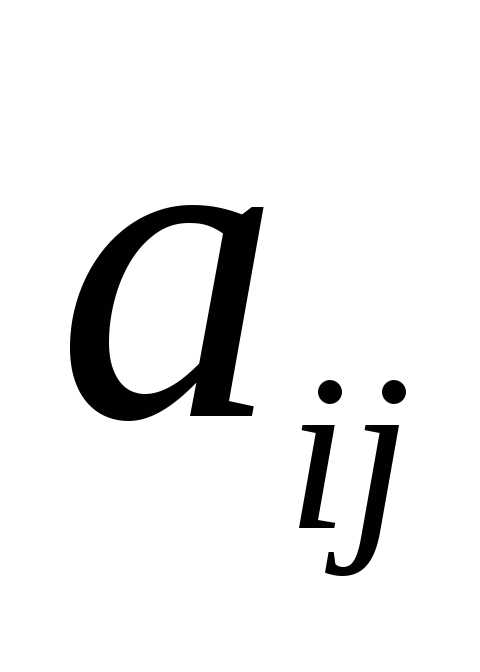. В матричной форме:

; .◄

4. Невырожденная квадратная матрица , для которой, называетсяортогональной. Свойства ортогональных матриц, играющих важную роль во многих приложениях, можно сформулировать в виде следующих теорем.

ТЕОРЕМА. Для ортогональной матрицы справедливо равенство.

ТЕОРЕМА. Каждая ортогональная матрица второго порядка , для которойможет быть представлена в виде, где — некоторое число, а каждая ортогональная матрица с — в виде.

studfiles.net

Ιιι Обратная матрица.

Обратная матрица определяется только для квадратных матриц.

Определение 1. Матрицы В называется обратной к матрице А, если АВ = ВА = Е.

Матрица, имеющая обратную, называется обратимой. Обратная матрица обозначается А^-1.

Свойства обратной матрицы.

1^˚. Если В обратна к А, то А обратна к В.

Доказательство этого свойства следует непосредственно из определения. Таким образом, имеем (А^-1) ^-1 = А

2^˚. Если у матрицы А есть обратная, то она единственна.

Доказательство. Пусть Х и Y — две матрицы, обратные к А. Тогда XA = AX = E и YA = AY = E.

Рассмотрим X(AY) = XE = X.

С другой стороны X(AY) = (XA)Y = EY = Y.

Следовательно Х = У.

3^˚. Если матрицы А и В имеют обратные, то АВ имеет обратную, причем (АВ) ^-1 = В^-1А^-1.

Доказательство.

Явная формула обратной матрицы.

Пусть дана матрица

Пусть матрица А имеет ненулевой определитель. Тогда обратную к A матрицу можно найти по формуле

где — определитель матрицы А, — алгебраическое дополнение к элементам

матрицы А. Т.е. =,здесь- определитель, полученный из определителя матрицы А вычеркиванием i-той строки и j-того столбца.

Доказательство формулы.

Для того, чтобы доказать, что эта формула задает обратную для А, необходимо показать, что . Сделаем это для матрицы порядка 3. (В общем случае доказательство точно такое же).

=

Здесь по главной диагонали стоит сумма произведений элементов j-того столбца на их алгебраические дополнения, тогда по теореме о разложении по любому столбцу это выражение равно определителю матрицы А. Вне главной диагонали стоит сумма произведений элементов j-того столбца на алгебраические дополнения к элементам к-того столбца (на месте kj), а это равно нулю по теореме о разложении по любому столбцу.

Применяем теорему о разложении по любой строке.

Например, ++= 0как сумма произведений элементов первой строки на алгебраические дополнения к элементам второй строки, + += 0как сумма произведений элементов третьей строки на алгебраические дополнения к элементам второй строки, + +=как сумма произведений элементов второй строки (на свои) на алгебраические дополнения к элементам второй строки.

Теорема 1. Определитель произведения матриц равен произведению определителей.

Теорема 2. (критерий обратимости). Матрица имеет обратную тогда и только тогда, когда ее определитель отличен от нуля.

Доказательство. Необходимость. Пусть матрица А имеет обратную. Тогда . Тогда det,detE = 1. det= detA (по теореме1). Следовательно

detA= 1. Значит detA.

Достаточность. Пусть определитель матрицы А отличен от 0. Тогда

Значит обратная матрица для А существует.

Нахождение обратной матрицы по методу Гаусса.

Рассмотрим следующие преобразования матрицы А:

1. поменять 2 строки местами

2. умножить строку на ненулевое число

3. к любой строке прибавить другую строку, умноженную на любое число.

К матрице А порядка n припишем единичную матрицу того же порядка

Применим к матрице (А|E) метод Гаусса (аналогично тому, как описано при вычислении определителя по методу Гаусса) так, чтобы на месте матрицы А получить единичную матрицу. То, что при этом получится на месте матрицы Е, будет обратной к А. Здесь можно применять только преобразования строк.

Пример 1. Показать, что матрица Аобратима и найти ее обратную

(Метод присоединения матрицы).

Вычислим определитель detA = 64 + 25 — 70 — 24 = -5 0.Т.к. определитель отличен от нуля, то А имеет обратную, т.е. обратима.

Проверка:

A

Пример2. Решить матричное уравнение AX + B = C, где А = ,

В = , С = .

Вычислим detC = (-2)(-4) — (-1)(-7) = 8 — 7 = 10

detA = (-2)(-3) – 15 = 6 — 5 = 10.

Значит матрицы С и А — обратимы. Найдем из уравнения матрицу Х.

AX = C- В

А(АХ) = А( C-В)

(АА)Х = А( C-В)

ЕХ = А( C-В)

Х = А( C-В)

Находим А^-1:

Находим C^-1:

C^-1— B =

X = A( C- B) =

Проверка. Подставим Х в исходное уравнение

Пример 3. Найти обратную к А методом элементарных преобразований (методом Гаусса)

~ ~

поменяем первую и четвертую строки меняем местами. Умножим первую строку на (-2) прибавим ко второй и четвертой, домножим первую строку на (-3) и прибавим к третьей

~~

чтобы не переходить к дробным компонентам домножим четвертую строку на (-2) и прибавим ее ко второй строке.

~~~ ~~

Ниже главной диагонали стоят только нулевые элементы. Проведем “обратный ход” снизу вверх, чтобы получить над главной диагональю нулевые элементы.

~~~

Четвертую строку умножим на (-4) и прибавим к третьей, четвертую строку умножим на (-2) и прибавим ко второй и к первой.

~

Таким образом

Можно сделать проверку. AА^-1 должно равняться Е.

studfiles.net

Тема: Нахождение обратной матрицы

⇐ ПредыдущаяСтр 3 из 12Следующая ⇒

Цель: Формирование навыков нахождения обратной матрицы.

На выполнение практической работы отводится 2 часа.

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Теоретический материал

Матрица, состоящая из строк и столбцов, называется квадратной матрицей порядка :

.

Элементы образуют главную диагональ матрицы.

У единичной матрицы порядка элементы главной диагонали равны единицы, а остальные элементы равны нулю: то есть

.

Для — матриц справедливы равенства .

Каждой — матрице соответствует определитель -го порядка, который состоит из тех же элементов, расположенных в том же порядке, что и в матрице:

.

Произведение двух квадратных матриц всегда определено; при этом определитель матрицы – произведения равен произведению определителей матриц – сомножителей: .

Квадратная матрица называется невырожденной, если ее определитель отличен от нуля , и вырожденной в противном случае .

Всякая невырожденная матрица порядка имеет обратную матрицу того же порядка , удовлетворяющую соотношениям

.

Обратная матрица имеет вид

, (1)

где — алгебраическое дополнение элемента в определителе матрицы , то есть элементы обратной матрицы находятся по формулам .

Свойства обратной матрицы

(здесь — матрицы, — число)

1. ;

2. ;

3. ;

4. ;

5. .

Пример

Задание: Для матрицы найти обратную матрицу и проверить, что .

Решение: Так как , то матица имеет обратную матрицу, элементы которой равны .

Вычислим алгебраические дополнения элементов для :

; ;

; ;

; ;

; ;

.

Теперь, используя формулу (1), находим обратную матрицу

.

Далее вычислим произведение

=

= .

Аналогично находим

. Итак, обратная матрица вычислена правильно.

Задания для самостоятельной работы

1. Для заданной матрицы найти указанные элементы обратной матрицы : 1) ; 2) ; 3) ;

4) ; 5) ; 6) .

1. Для матриц и найдите обратные матрицы, и . Проверить, верно, ли они найдены.

Вопросы для самоконтроля:

1. Какая матрица называется квадратной?

2. Какая матрица называется единичной, верхнетреугольной, нижнетреугольной, диагональной?

3. Дайте определение обратной матрицы. Всегда ли существует обратная матрица?

4. Как найти обратную матрицу?

Практическое занятие №3

Тема: Решение систем алгебраических уравнений по правилу Крамера и матричным методом

Цель: Формирование навыков решения СЛАУ по правилу Крамера и матричным методом.

На выполнение практической работы отводится 2 часа.

Требования к выполнению практической работы:

1.Ответить на теоретические вопросы.

2.Оформить задания в тетради для практических работ.

Пример

Задание: Показать, что система имеет единственное решение и найти его двумя способами: а) по правилу Крамера;

б) матричным методом.

Решение: Данная система имеет размер (три уравнения и три неизвестных). Составим матрицу из коэффициентов при неизвестных:

. Матрица квадратная . Вычислим определитель матрицы , используя формулу его разложения по элементам первой строки:

.

Так как определитель системы , то данная система имеет единственное решение. Это решение можно найти по правилу Крамера: ; ; , где — главный определитель системы; , , — вспомогательные определители, которые получаются из главного путем замены соответствующего столбца на столбец свободных членов, и вычисляются аналогично определителю .

;

;

Отсюда по правилу Крамера имеем:

; ;

.

Решение системы единственно, это совокупность чисел .

Проверка: Подставим найденное решение во все уравнения исходной системы линейных алгебраических уравнений.

Так как все уравнения системы обратились в равенства, то решение найдено верно.

Ответ: .

Решим данную систему матричным способом. Рассмотрим матрицы:

; ; ;

— матрица коэффициентов при неизвестных, — матрица – столбец неизвестных, — матрица – столбец свободных членов.

Данную систему можно записать в виде:

;

При умножении матриц каждая строка матрицы умножается на столбец матрицы и в результате получается соответствующий элемент матрицы . Таким образом, последняя матричная запись содержит все три уравнения данной системы линейных алгебраических уравнений. Коротко ее можно записать так:

(1)

Рассмотрим матрицу , обратную к матрице . Это такая матрица, которая при умножении на данную матрицу дает единичную матрицу : , где .

Умножая обе части матричного равенства (2) на матрицу слева, получим:

,

, и окончательно имеем:

(2)

Формула (2) используется для нахождения решения системы линейных алгебраических уравнений. Предварительно нужно вычислить обратную матрицу. Обратная матрица вычисляется по формуле: (3), где — алгебраическое дополнение всех элементов матрицы ,

— главный определитель системы .

В нашем примере .

Найдем теперь алгебраические дополнения для всех элементов матрицы :

; ;

; ;

; ;

; ;

.

Составим матрицу алгебраических дополнений:

.

Транспонируем ее, то есть поменяем местами столбцы и строки с одинаковыми номерами:

.

Обратную матрицу получим по формуле (3), умножая каждый элемент последней матрицы на число, равное :

.

Решение системы линейных алгебраических уравнений находим по формуле (2) умножением матрицы на матрицу свободных членов :

=

Отсюда следует, что , , .

Найденное решение было проверено выше, и совпадает с результатом, полученным по правилу Крамера.

Ответ: — единственное решение системы.

Задания для самостоятельной работы

Показать, что система линейных уравнений имеет единственное решение и найти его двумя способами: а) по правилу Крамера;

б) матричным методом.

 

.

Вопросы для самоконтроля:

1. Что называется решение СЛАУ?
2. Какие случаи могут представиться при решении СЛАУ?
3. Какие СЛАУ называются совместными, несовместными?
4. Напишите формулу Крамера. В каком случае они применимы?
5. При каком условии СЛАУ имеет единственное решение?
6. Что можно сказать о СЛАУ, если ее определитель равен нулю?
7. Как записать СЛАУ в матричном виде?
8. В чем состоит матричный метод решения СЛАУ?

Практическое занятие №4

Рекомендуемые страницы:

lektsia.com

Способы вычисления обратной матрицы

Если для квадратной матрицы существует обратная матрица , то справедливо равенство , где – единичная матрица. Переходя в этом равенстве к определителям (и учитывая свойство 9 определителей), имеем , или . Отсюда заключаем, что (в противном случае левая часть последнего равенства равнялась бы нулю). Этим доказано, что если , то для матрицы не существует обратной. Другими словами, условие является необходимым условием существования обратной матрицы. Оказывается, это условие является и достаточным.

Лемма

Если обратная матрица существует, то она единственна.

Квадратная матрица называется невырожденной, если ее определитель не равен нулю ( ). В противном случае матрица называется вырожденной ( ).

Пусть матрица имеет вид

.

ТЕОРЕМА. Если – невырожденная матрица, то для нее существует обратная матрица , которая вычисляется по формуле

, (5)

где – алгебраическое дополнение для элемента матрицы .

Замечание

Обратим внимание на расположение чисел в правой части формулы (5): число расположено не в -й строке и -м столбце, а наоборот, в -й строке и -м столбце. Таким образом, матрица, стоящая в правой части (5), является транспонированной матрицей алгебраических дополнений элементов матрицы .

Типовой пример. Найдите , если .

► . – невырожденная матрица, следовательно, обратная для нее существует. Найдем ее по формуле:

.

Обратите внимание на индексацию алгебраических дополнений. Вычисляем алгебраические дополнения

; ; ;

; ; ;

; ; .

Тогда

.

Можно сделать проверку:

.

Значит, обратная матрица найдена верно.◄

 

3. Вычисление обратной матрицы методом элементарных преобразований. Элементарные преобразования матрицы

1. Перестановка строк (столбцов).

2. Умножение строки (столбца) на число .

3. Прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на любое число.

Чтобы найти матрицу, обратную данной, делаем следующее:

для матрицы записываем прямоугольную матрицу , приписывая справа единичную матрицу;

с помощью элементарных преобразований приводим матрицу к виду . Тогда . Эквивалентные матрицы обозначаются .

Типовой пример

Найти матрицу, обратную данной: .

► ~(первую строку матрицы умножили на ) ~ ~ ~ ~

. Следовательно, .

Проверка: . ◄

С помощью обратной матрицы можно решать простейшие матричные уравнения, где неизвестной является матрица X. Это уравнения следующего вида

.

В этих уравнениях – матрицы таких размеров, что все операции умножения возможны и с обеих сторон от знаков равенств находятся матрицы одинаковых размеров. Если в первых двух уравнениях матрица невырожденная, то их единственное решение записывается следующим образом соответственно и . Если в третьем матричном уравнении матрицы и невырождены, то его решение записывается в виде .
Пример

В табл. 6 приведены данные о дневной производительности пяти предприятий, выпускающих четыре вида продукции с потреблением трех видов ресурсов, а также количество рабочих дней в году каждого предприятия и цены каждого вида сырья.

Таблица 6

Вид продукции	Производительность предприятий (изд. в день)	Затраты ресурсов, ед. веса/изд.
	Кол-во раб. дней в году	Цены ед.сырья

 

Требуется найти:

1) годовую производительность каждого предприятия по каждому виду продукции;

2) годовую потребность каждого предприятия по каждому виду ресурса;

3) годовую сумму кредитования каждого предприятия для закупки ресурсов, необходимых для выпуска продукции указанных видов и при определенном количестве рабочих дней.

►Введем следующие обозначения:

 

 

а) Данная матрица является матрицей производительности пяти предприятий по всем четырем видам продукции. Каждый столбец этой матрицы соответствует дневной производительности отдельного предприятия по каждому виду изделий. Следовательно, годовая производительность -го предприятия по каждому виду изделий получается умножением -го столбца матрицы А на количество рабочих дней в году для этого предприятия (к = 1,2,3,4,5)

 

А₁₁=0,79 А₂₁=0,16 А₃₁=0,02

А₁₂=0,16 А₂₂=0,8 А₃₂=0,1

А₁₃=0,02 А₂₃=0,1 А₃₃=0,96,

 

тогда .

Это матрица коэффициентов полных материальных затрат.

б) , т.е. валовой выпуск продукции 1-го, 2-го и 3-го цехов будут соответственно .

в) Найдем производственную программу каждого цеха (промежуточный продукт) по формуле ( ; )

;

;

;

;

;

;

;

;

.

Результаты представим в таблице 7:

Таблица 7

Цех	Внутрипроизводственные потребления	Итого	Конечный продукт	Валовый выпуск

 

г) Коэффициенты косвенных затрат определяются как разности полных внутрипроизводственных затрат и прямых затрат . В матричной форме:

; .◄

 

4.Невырожденная квадратная матрица , для которой , называется ортогональной. Свойства ортогональных матриц, играющих важную роль во многих приложениях, можно сформулировать в виде следующих теорем.

ТЕОРЕМА. Для ортогональной матрицы справедливо равенство .

ТЕОРЕМА. Каждая ортогональная матрица второго порядка , для которой может быть представлена в виде , где j — некоторое число, а каждая ортогональная матрица с — в виде .

Ранг матрицы

1. Ранее для квадратной матрицы -го порядка было введено понятие минора элемента . Напомним, что так был назван определитель порядка , полученный из определителя вычеркиванием -й строки и -го столбца.

Введем теперь понятие минора матрицы. Рассмотрим некоторую, не обязательно квадратную матрицу . Выберем какие-нибудь номеров строк и номеров столбцов .

Минором порядка матрицы (соответствующим выбранным строкам и столбцам) называется определитель порядка , образованный элементами, стоящими на пересечении выбранных строк и столбцов, т.е. число

.

Каждая матрица имеет столько миноров данного порядка , сколькими способами можно выбрать номера строк и столбцов .

В матрице размеров минор порядка называется базисным, если он отличен от нуля, а все миноры порядка равны нулю или миноров порядка вообще нет, т.е. совпадает с меньшим из чисел или .

Ясно, что в матрице может быть несколько разных базисных миноров. Все базисные миноры имеют один и тот же порядок. Действительно, если все миноры порядка равны нулю, то равны нулю и все миноры порядка , а, следовательно, и всех бόльших порядков. Это становится очевидным, если разложить минор порядка по элементам какой-либо строки (столбца): все миноры элементов этой строки являются определителями порядка , а поэтому равны нулю.

Рангом матрицы называется порядок базисного минора, или, иначе, самый большой порядок, для которого существуют отличные от нуля миноры. Если все элементы матрицы равны нулю, то ранг такой матрицы, по определению, считают нулем.

Ранг матрицы будем обозначать символом . Из определения ранга следует, что для матрицы размеров справедливо соотношение .

2. Два способа вычисления ранга матрицы.

а) Метод окаймляющих миноров. Пусть в матрице найден минор -го порядка, отличный от нуля. Рассмотрим лишь те миноры -го порядка, которые содержат в себе (окаймляют) минор : если все они равны нулю, то ранг матрицы равен . В противном случае среди окаймляющих миноров найдется ненулевой минор -го порядка, и вся процедура повторяется.

Типовой пример

Вычислить методом окаймления ранг матрицы

.

Минор второго порядка, стоящий в левом верхнем углу, отличен от нуля:

.

Теперь вычислим миноры, окаймляющие данный. Таковых два:

,

 

.

Таким образом, оба окаймляющих минора равны нулю и, следовательно, ранг исходной матрицы равен двум: .

Ясно, что перебирать таким способом миноры в поисках базисного – задача, связанная с большими вычислениями, если размеры матрицы не очень малы. Существует, однако, более простой способ нахождения ранга матрицы – при помощи элементарных преобразований.

б) Метод элементарных преобразований. Напомним, элементарными преобразованиями матрицы называют следующие преобразования:

1) умножение строки на число, отличное от нуля;

2) прибавление к одной строке другой строки;

3) перестановку строк;

4) такие преобразования столбцов.

Преобразования 1 и 2 выполняются поэлементно. Комбинируя преобразования первого и второго вида, мы можем к любой строке прибавить линейную комбинацию остальных строк.

ТЕОРЕМА. Элементарные преобразования не меняют ранга матрицы.

Рекомендуемые страницы:

lektsia.com

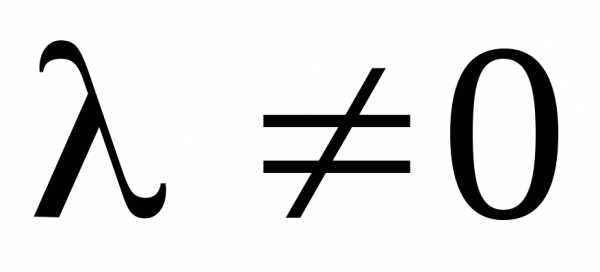No related posts.