Задачи по статистике с решениями и выводами
Фонды рабочего времениИзложена методика расчета календарного, табельного и максимально-возможного фондов рабочего времени, а также коэффициентов их использования. Содержатся сведения по составлению балансов рабочего времени на предприятии. Рассматриваются коэффициенты использования рабочего дня, рабочего периода, а также интегральный показатель использования рабочего времени.
Индексы средней производительности трудаРешена задача с вычислением уровня и динамики производительности труда. Рассчитаны индексы средней производительности труда — индекс переменного состава, постоянного состава и структурных сдвигов. Показано разложение на факторы прироста продукции, вычисление числа высвободившихся работников в связи с ростом производительности.
Индексы средней заработной платыВ представленной на странице задаче вычислены индексы средней заработной платы переменного состава, постоянного состава, структурных сдвигов, показано разложение на факторы изменения средней заработной платы и фонда заработной платы.
Страница содержит краткое описание показателей движения рабочей силы, также на примере показаны расчеты коэффициентов текучести кадров, оборота по приему и увольнению, общего оборота и постоянства кадров.
Статистика основных фондовРассмотрены основные показатели статистики основых фондов — полная и остаточная стоимость основных фондов, коэффициенты годности и износа, коэффициенты обновления и выбытия, показатели фондоотдачи и фондоемкости.
Показатели эффективности использования оборотных средствРассмотрена краткая теория и решена задача по статистике оборотных средств предприятия. На примере показаны расчеты показателей эффективности использования оборотных средств — коэффициента оборачиваемости, закрепления, продолжительности одного оборота.
Задачи по статистике с решениями
Примеры решения задач по статистике
Задача Статистическая сводка и группировка.
Теория по решению задачи.Статистическая сводка – научно обработанный материал статистического наблюдения в целях получения обобщенной характеристики изучаемого явления.
Группировка – распределение единиц изучаемого объекта на однородные типичные группы по существенным для них признакам.
Интервал – разница между максимальным и минимальным значением признака в каждой группе.
 , где
, где
i – величина интервала;
R – размах колебания (R=xmax-xmin)
n – принятое число групп;
xmax, xmin – наибольшее и наименьшее значение признака в изучаемой совокупности.
 , где
, где
N – число наблюдений
Типовая задача № 1
Распределите потребительские общества по размеру товарооборота на 3 группы с равными интервалами. В каждой группе подсчитайте количество потребительских обществ, сумму товарооборота, сумму издержек обращения. Результаты группировок представьте в табличной форме. К какому виду статистических таблиц относится составление вами таблица, и какой вид группировки она содержит?
Имеются основные экономические показатели потребительских обществ за отчетный период:
Таблица № 1
|
№ п/п |
Товарооборот в млн. грн. |
Издержки обращения, в млн. грн. |
Прибыль, в млн. грн. |
|
1 |
390 |
14 |
40 |
|
2 |
190 |
8 |
15 |
|
3 |
180 |
8 |
15 |
|
4 |
450 |
16 |
42 |
|
5 |
200 |
10 |
20 |
|
6 |
390 |
14 |
40 |
|
7 |
180 |
10 |
13 |
|
8 |
250 |
|
25 |
|
9 |
330 |
12 |
25 |
|
10 |
240 |
8 |
21 |
|
11 |
300 |
11 |
24 |
|
12 |
230 |
10 |
15 |
|
13 |
420 |
12 |
36 |
|
14 |
190 |
14 |
12 |
|
15 |
450 |
15 |
42 |
|
16 |
200 |
8 |
23 |
|
Итого |
4590 |
181 |
408 |
Ход решения задачи:
Т. к. нам известен группировочный признак, работу необходимо начать в определения величины интервала по формуле:

Образец 3 группы потребительских обществ по размеру товарооборота.

Определяем границы групп:
1 группа: 180+90=270 (180-270)
2 группа: 270+90=360 (270-360)
3 группа: 360+90+450 (360-450)
После того, как выбран группировочный признак, намечено число групп и образованы сами группы, необходимо отобрать показатели, которыми будут характеризоваться группы, и определить их величину по каждой группе.
В нашем примере каждую группу необходимо охарактеризовать следующими показателями:
а) количеством потребительских обществ;
б) суммой товарооборота;
в) суммой издержек обращения.
Для заполнения итоговой таблицы составим предварительно рабочие таблицы № 2, 3, 4.
Группа потребительских обществ с товарооборотом от 180 до 270 млн. грн.
Таблица № 2
|
№ п/п |
Номер потребительского общества |
Товарооборот, в млн. грн. |
Сумма издержек обращения, в млн. грн. |
|
1 |
2 |
190 |
8 |
|
2 |
3 |
180 |
8 |
|
3 |
5 |
200 |
10 |
|
4 |
7 |
180 |
10 |
|
5 |
8 |
250 |
11 |
|
6 |
10 |
240 |
8 |
|
7 |
12 |
230 |
10 |
|
8 |
14 |
190 |
14 |
|
9 |
16 |
200 |
8 |
|
Итого |
9 |
1860 |
87 |
Группа потребительских обществ с товарооборотом от 270 до 3660 млн. грн.
Таблица № 3
|
№ п/п |
Номер потребительского общества |
Товарооборот, в млн. грн. |
Сумма издержек обращения, в млн. грн. |
|
1 |
9 |
330 |
12 |
|
2 |
11 |
300 |
11 |
|
Итого |
2 |
630 |
23 |
Группа потребительских обществ с товарооборотом от 360 до 450 млн. грн.
Таблица № 4
|
№ п/п |
Номер потребительского общества |
Товарооборот, в млн. грн. |
Сумма издержек обращения, в млн. грн. |
|
1 |
1 |
390 |
14 |
|
2 |
4 |
450 |
16 |
|
3 |
6 |
390 |
14 |
|
4 |
13 |
420 |
12 |
|
5 |
15 |
450 |
15 |
|
Итого |
5 |
2100 |
71 |
Итоговые показатели рабочих таблиц занесем в окончательную итоговую таблицу и получим групповую таблицу № 5.
Группировка потребительских обществ, по размеру товарооборота:
Таблица № 5
|
Группы потребительских обществ по размеру товарооборота, млн. грн. |
Количество потребительских обществ |
Товарооборот, в млн. грн. |
Сумма издержек обращения, в млн. грн. |
|
180-270 |
9 |
1860 |
87 |
|
270-360 |
2 |
630 |
23 |
|
360-450 |
16 |
4590 |
181 |
Вывод: По результатам итоговой таблицы можно сделать вывод, что с увеличением объема товарооборота потребительских обществ, относительный показатель уровня издержек обращения снижается. Следовательно, между ними существует обратная связь. Составленная нами таблица является групповой таблицей, т. к. ее подлежащее содержит группы потребительских обществ по размеру товарооборота. Она содержит аналитический вид группировки.
Задача — Ряды распределения и статистические таблицы.
Теория по решению задачи.
Статистический ряд распределения – упорядоченное распределение единиц совокупности на группы по определенному варьирующему признаку.
Дискретный вариационный ряд – характеризует распределение единиц совокупности по дискретному (прерывному) признаку.
Интервальный вариационный ряд – характеризует распределение единиц совокупности по интервальному (непрерывному) признаку.
Для изображения дискретных вариационных рядов распределения используется «полигон распределения». Для графического изображения интервального вариационного ряда применяются «гистограмма» и «кумулята».
Задача 1.
На экзамене по истории студенты получили оценки:
3 4 4 4 3 4
3 4 3 5 4 4
5 5 2 3 2 3
3 4 4 5 3 3
5 4 5 4 4 4
Построить дискретный вариационный ряд распределения студентов по баллам и изобразить его графически.
Ход решения задачи:
Определяем элементы ряда распределения: варианты, частоты, частоты.
|
Оценка, баллы |
Кол-во студентов с такой оценкой, человек |
В процентах к итогу |
|
2 |
2 |
6,7 |
|
3 |
9 |
30 |
|
4 |
13 |
43,3 |
|
5 |
6 |
20 |
|
Итого |
30 |
100 |
Теперь графически изобразим дискретный ряд распределения в виде помпона распределения.

Можно сделать вывод о том, что преобладающее большинство студентов получило «4» (43,3 %).
Задача 2.
Во время выборочной проверки было установлено, что продолжительность одной покупки в кондитерском отделе магазина была такой: (секунды).
77 70 82 81 81
82 75 80 71 80
81 89 75 67 78
73 76 78 73 76
82 69 61 66 84
72 74 82 82 76
Построить интервальный вариационный ряд распределения покупок по продолжительности, создав 4 группы с одинаковыми интервалами. Обозначить элементы ряда. Изобразить его графически, сделать вывод.
Ход решения задачи по статистике:
Определяем элементы ряда распределения: варианты, частоты, частости, накопленные частоты.
Но прежде рассчитаем границы 4 заданных групп с одинаковыми интервалами:
Величину интервала определим по формуле 
 .
.
В нашем случае 
Границы групп соответственно равны:
I 61+7=68 (61-68)
II 68+7=75 (68-75)
III 75+7=82 (75-82)
IV 82+7=89 (82-89)
|
Группы покупок по продолжительности, сек. |
Число покупок |
В процентах к итогу |
Накопленные частоты |
|
61-68 |
3 |
10 |
3 |
|
68-75 |
9 |
30 |
12 |
|
75-82 |
16 |
53,3 |
28 |
|
82-89 |
2 |
6,7 |
30 |
|
Итого |
30 |
100 |
Теперь графически отобразим наш интервальный вариационный ряд в виде гистограммы и кумуляты.

По таблице и графика можно сделать вывод о том, что преобладающее большинство покупок (16 или 53.3%) находится во временном интервале 75-82, сек.
Статистика задача — Абсолютные и относительные величины.
Теория по решению статистической задачи.
Абсолютные величины – показатели, которые выражают размеры общественных явлений и процессов числом единиц совокупности.
Относительные величины – показатели, выражающие количественные соотношения численностей или величин признаков изучаемых явлений.
Виды относительных величин:
1) Относительная величина выполнения плана:

2) Относительная величина планового задания:

3) Относительная величина динамики:

4) Относительная величина структуры:

5) Относительная величина сравнения отражает соотношение двух объемов или уровней в пространстве: соотношение производства автомобилей в Украине и России, соотношение уровней оплаты труда в разных хозяйствах, соотношение уровней производительности на разных предприятиях отрасли и т. д.
6) Относительная величина координации получается посредством деления друг на друга разноименных исходных показателей, она дает типичную характеристику соотношения одно-порядковых по значимости исходных показателей, во-первых, непосредственно связанных между собой, во-вторых, обладающих некоторой общностью.
7) Относительная величина интенсивности:

Типовая задача № 1
Два консервных завода выработали по 100 тыс. шт. банок виноградного сока. На первом заводе емкость каждой банки составляет 500 см3, а на втором – 200 см3. Можно ли сказать, что оба завода работали одинаково?
Ход решения задачи по статистике:
Для того, чтобы ответить на этот вопрос необходимо установить коэффициенты перевода фактического объема банок в условные банки и затем умножить количество выпущенных банок на эти коэффициенты. Представим расчет в таблице № 1.
Таблица № 1
|
Заводы |
Количество выпущенных банок, тыс. шт. |
Объем банки см3 |
Коэффициенты перевода |
Количество выпущенных условных банок, тыс. шт. |
|
№ 1 |
100 |
500 |
|
100*1,414=141,4 |
|
№ 2 |
100 |
200 |
|
100*0,566=56,6 |
Таким образом, завод № 1 по сравнению с заводом № 2 выпустил виноградного сока на 84,8 тыс. Банок больше (141,4-56,6).
Статистика — Типовая задача № 2
Имеются следующие данные розничного товарооборота:
Таблица № 2
|
Универмаги |
Розничный товарооборот (млн. грн.) |
||
|
Фактически за базисный год |
Отчетный год |
||
|
По плану |
Фактически |
||
|
«Крым» |
105 |
110 |
98 |
|
«Центральный» |
137 |
148 |
150 |
Определить:
1. Относительную величину выполнения плана.
2. Относительную величину планового задания.
3. Относительную величину динамики.
Ход решения задачи:
1. Определяем относительную величину выполнения плана по двум универмагам:

2. Определим относительную величину планового задания:

3. Определяем относительную величину динамики:

Статистическая задача — Средние и структурные средние величины.
Теория по решению статистической задачи:
Средние величины – это показатели. Выражающие типичные черты и дают обобщающую количественную характеристику уровня признака по совокупности однородных явлений.
1. Средняя арифметическая:

2. Средняя гармоническая:

3. Средняя квадратическая:

4. Средняя хронологическая:

5. Средняя геометрическая:

К1, К2, К3 и Кn – коэффициенты динамики по отношению к предыдущему периоду.
6. мода интервальных рядов распределения вычисляется по следующей формуле:

х0 – минимальная граница модального интервала;
i – величина интервала;
f2 – частота модального интервала;
f1 – частота интервала, предшествующего модальному;
f3 – частота интервала, следующего за модальным.
Мода для дискретных рядов распределения – это наиболее часто встречающаяся величина признака в данной совокупности.
7. Медиана для интервальных рядов распределения вычисляется по формуле:

x0 – нижняя граница медианного интервала;
i – величина медианного интервала;
∑f – сумма частот ряда;
SМЕ-1 – сумма накопленных частот, предшествующих медианному интервалу;
fМЕ – частота медианного интервала.
Чтобы определить медиану в дискретном вариационном ряду. Необходимо сумму частот разделить пополам и к полученному результату добавить ½.
Типовая задача № 1
Имеются следующие данные о заработной плате рабочих:
Таблица № 1
|
Месячная заработная плата (грн.) (х) |
Число рабочих (f) |
х*f |
|
х1=120 |
27 |
3240 |
|
х2=145 |
33 |
4785 |
|
х4=200 |
48 |
9600 |
|
х5=208 |
51 |
10608 |
|
х6=250 |
16 |
4000 |
|
х7=337 |
28 |
9436 |
|
Итого |
203 |
41669 |
Определите среднюю заработную плату одного рабочего.
Ход решения:
Среднюю заработную плату определим по формуле средней арифметической взвешенной:

Т. о. средняя заработная плата рабочего составила 205,27 грн.
Типовая задача (статистика) № 2
Имеются, следующие данные выпуска литья в литейном цехе завода за пятилетний период:
Таблица № 2
|
Годы |
1-й |
2-й |
3-й |
4-й |
5-й |
|
Выпуск литья, тонн |
528,34 |
336,98 |
439,24 |
297,55 |
672,17 |
|
В % к предыдущему году |
- |
63,8 |
130,3 |
67,7 |
225,9 |
Требуется определить средний темп выпуска литья.
Ход решения задачи:
Для определения среднего темпа выпуска литья используем формулу средней геометрической:

Типовая задача № 3
Имеются следующие данные:
Таблица № 3
|
Група рабочих по размеру заработной платы (в грн.) |
Число рабочих |
SМЕ |
|
150-200 |
28 |
28 |
|
200-250 |
54 |
82 |
|
250-300 |
30 |
112 |
|
300-350 |
47 |
159 |
|
350-400 |
63 |
222 |
|
400-450 |
18 |
240 |
|
450-500 |
22 |
262 |
|
Итого |
262 |
- |
Определить моду и медиану.
Ход решения задачи:
1. Определяем моду:

2. Определяем медиану:

Практические задачи по статистике для самостоятельного решения с ответами
Задача по статистике 1.
Имеются следующие данные об урожайности зерновых культур:
|
Урожайность зерновых культур |
Количество хозяйств |
|
До 20 |
30 |
|
20-30 |
40 |
|
30-40 |
60 |
|
40 и выше |
20 |
Определить среднюю урожайность зерновых культур, моду и медиану.
Ответ.
средняя урожайность: 30,3 ц/га
мода: 33,3
медиана: 30,8
Задача 2.
|
Годы |
97г. |
98г. |
99г. |
2000г. |
2001г. |
|
Производства зерна, тыс. тонн |
150 |
168 |
179 |
186 |
191 |
Требуется определить: (цепным и базисным способом):
1) абсолютный прирост;
2) темп роста и прироста;
3) средний абсолютный прирост;
4) средние темпы роста и прироста.
Ответ 2.
цепным способом базисным способом
абсолютный прирост 18 абсолютный прирост 18
11 29
7 36
5 41
темп роста 1,12 темп роста 1,12
1,07 1,19
1,04 1,24
1,03 1,27
темп прироста 0,12 темп прироста 0,12
0,07 0,19
0,04 0,24
0,03 0,27
средний абсолютный прирост: 31 средний абсолютный прирост: 31
средний темп роста 1,02 средний темп роста: 1,05
средний темп прироста 0,02 средний темп прироста: 0,05
Задача 3.
Методом случайной повторной выборки было взято для проверки на вес 200 шт. деталей. В результате проверки был установлен средний вес детали 30 г. при среднем квадратическом отклонении 4 г. С вероятностью 0,954 требуется определить предел в котором находится средний вес деталей в генеральной совокупности.
Ответ.
Средний вес детали колеблется в пределах 29,44 ‹ х ‹ 30,56.
Задача 4.
По имеющимся данным определить индивидуальные и общий индексы себестоимости и экономию (перерасход) от снижения (роста) себестоимости.
|
Вид товара |
Общие затраты, грн. |
Имеющие единицы себестоимость в отчетном году, % |
|
|
Базисный год |
Отчетный год |
||
|
Электробритва |
9500 |
10244 |
-1,5 |
|
Электрофен |
600 |
612 |
+2,0 |
Ответ.
Индивидуальный индекс себестоимости по электробритве 0,985
Индивидуальный индекс себестоимости электрофену 1,02
Общий индекс себестоимости 0,99.
Перерасход денежных средств от роста себестоимости 144 грн.
Задача 5.
Полная первоначальная стоимость оборудования 250,4 тыс. грн. Это оборудование может работать 20 лет при условии проведения в капитальных ремонтов на сумму 2,5 тыс. грн. каждый. После полного износа оборудования может быть реализовано как металлолом за 1 тыс. грн. Затраты на модернизацию в течении срока службы 62,6 тыс. грн. Определить сумму ежегодных амортизационных отчислений, общую норму амортизации.
Ответ.
Сумма ежегодных отчислений 16,6 тыс. грн.
Общая норма амортизации 6,6 %.
Задача по статистике 6.
Определить календарный, режимный, располагаемый (плановый) и фактический фонды станочного времени по 2 видам станков и коэффициенты использования станочного времени за апрель по таким данным:
|
Виды станков |
Количество установленных станков |
Фактически отработано станкочасов |
Запланировано на ремонт станков, станкочасов |
|
Токарные |
48 |
15127 |
60 |
|
Фрезерные |
52 |
16420 |
80 |
Число рабочих дней в апреле 22. Режим работы – 2 смены. Установленная продолжительность смены: 8 часов.
Ответ.
Календарный фонд 72000 станкочасов
Режимный фонд 35200 станкочасов
Плановый фонд 35060 станкочасов
Фактический фонд 31547 станкочасов
Коэффициент использования календарного фонда 43,8 %
Коэффициент использования режимного фонда 89,6 %
Коэффициент использования планового фонда 90 %
Задача 7.
В квартале 62 рабочих дня, отработало 136400 человеко-дней; целодневные простои 930 человеко-дней; неявок по различным причинам (включая праздничные и выходные) 69670 человеко-дней. Определить: коэффициенты использования среднесписочной и среднеявочной численности.
Ответ.
К использования среднесписочной численности 0,96 %
Коэффициент использования среднеявочной численности 0,99 %
Задача 8.
На заводе с численностью персонала 3000 человек производительность труда выросла на 25 %, а на заводе, где работают 5000 человек, снизилась на 5 %. Как изменилась производительность труда на 2-х заводах вместе.
Ответ.
Увеличилась на 6 % производительность на двух заводах.
Задача 9 по статистике
Объем продукции в натуральном выражении на предприятии вырос за отчетный период на 28 %, а производственные затраты в целом возросли на 19 %. Определить как изменилась себестоимость единицы продукции.
К задаче 9 ответ
Себестоимость единицы продукции снизилась на 7 %.
Задача 10.
Какой была численность населения в начале и конце года, если среднегодовой показатель ее за этот год составил 800 тыс. человек, сальдо миграции + 32 тысячи человек, коэффициент естественного прироста 30 % 0.
Ответ — Численность на начало года 772000 человек.
К задаче 10.
Численность на конец года 828000 человек.

Статистическая сводка и группировка. Задачи по статистике с решением онлайн
Группировка — это разграничение изучаемой совокупности по значениям одного или нескольких признаков на качественно однородные группы и характеристика их системой показателей. В зависимости от поставленной цели и конкретного содержания исследуемого материала посредством группировок решают три основные задачи:
- выделяются социально-экономические типы явлений;
- выявляются состав и структура совокупности;
- устанавливаются, изучаются причинно-следственные связи между признаками явлений.
Соответственно этим задачам используются три вида группировок — типологические, структурные и факторные.
На основе типологических группировок осуществляется образование однокачественных групп или типов явлений. Структурные группировки позволяют выявить внутреннее состояние явлений. При построении структурных группировок по количественным признакам устанавливаются границы выделяемых групп. Решая вопрос о величине интервала групп (или, что то же, о числе групп), необходимо иметь в виду, что следует выбирать такое число групп, чтобы при этом не наблюдалось существенных отклонений от равномерного распределения внутри каждой группы. Величина равного интервала в этом случае определяется по формуле:
и -минимальное и максимальное значения группировочного признака; n — число выделяемых групп. Хороший способ приближенного определения интервала группировки может быть получен на основе формулы Стерджесса:
где - число единиц совокупности.
Статистические ряды, в которых показывается только распределение единиц в изучаемой совокупности в зависимости от величины признака, обычно называют рядами распределения или вариационными рядами.
Величина равного интервала при построении вариационных рядов распределения используется в тех случаях, если соотношение максимального и минимального значений группировочного признака не превышает десятикратного значения. В случаях значительной вариации группировочного признака целесообразно применять кратные интервалы. В практике статистических исследований обычно используют удвоенные кратные интервалы, т. е. величина каждого последующего интервала по сравнению с предыдущим удваивается. Для выявления специфических особенностей распределений, допустим изучение характера концентрации производства, могут быть использованы неравные интервалы.
Интервалы группировки считаются обоснованными, если коэффициент вариации признака в них не превышают 33%. Посредством факторной группировки устанавливаются и изучаются причинно-следственные связи между признаками однородных явлений.
Условие задачи
Имеются следующие данные об урожайности картофеля и количеством внесенных минеральных удобрений по 10 сельскохозяйственным предприятиям:
| Номер колхоза | Урожайность, ц/га | Внесено минеральных удобрений на 1 га, кг | Номер колхоза | Урожайность, ц/га | Внесено минеральных удобрений на 1 га, кг |
| 1 | 128 | 140 | 6 | 183 | 197 |
| 2 | 179 | 262 | 7 | 201 | 246 |
| 3 | 221 | 289 | 8 | 195 | 276 |
| 4 | 136 | 191 | 9 | 141 | 187 |
| 5 | 164 | 202 | 10 | 192 | 253 |
Для изучения зависимости между урожайностью картофеля и внесенными минеральными удобрениями произведите группировку сельскохозяйственных предприятий, образовав 3 группы предприятий с равными интервалами. По каждой группе и по совокупности в целом подсчитайте:
- число предприятий;
- среднюю урожайность картофеля;
- средний объем внесенных минеральных удобрений на 1 га, кг.
Результаты представьте в таблице и сделайте выводы.
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение задач, контрольных или онлайн-помощь на зачете/экзамене 〉〉
Если вам сейчас не требуется помощь, но может потребоваться в дальнейшем, то, чтобы не потерять контакт, вступайте в группу ВК.
Решение задачи
Расположим предприятия в таблице по возрастанию урожайности.
Произведем расчет групп:
Длина интервала:
1-я группа: 128 –159 ц/га
2-я группа: 159 –190 ц/га
3-я группа: 190 –221 ц/га
| Номер колхоза | Урожайность, ц/га | Внесено минеральных удобрений на 1 га, кг |
| 128 — 159 | ||
| 1 | 128 | 140 |
| 4 | 136 | 191 |
| 9 | 141 | 187 |
| Итого | 405 | 518 |
| 159 – 190 | ||
| 5 | 164 | 202 |
| 2 | 179 | 262 |
| 6 | 183 | 197 |
| Итого | 526 | 661 |
| 190 – 221 | ||
| 10 | 192 | 253 |
| 8 | 195 | 276 |
| 7 | 201 | 246 |
| 3 | 221 | 289 |
| Итого | 809 | 1064 |
Получаем следующую группировку:
Группировка сельскохозяйственных предприятий по урожайности
| Урожайность, ц/га | Число предприятий | Средняя урожайность, ц/га | Средний объем внесенных минеральных удобрений на 1 га, кг |
| 128 – 159 | 3 | 135,0 | 172,7 |
| 159 – 190 | 3 | 175,3 | 220,3 |
| 190 -221 | 4 | 202,3 | 266,0 |
| Итого | 10 | 174,0 | 224,3 |
Таким образом получаем, что между урожайностью и внесением минеральных удобрений существует прямая зависимость. Чем больше урожайность на предприятии, тем больше предприятие вносило минеральных удобрений на 1 га.
К оглавлению решебника по статистике 〉
Решение задач онлайн 📝 по статистике без посредников.
Статистику, как прикладную часть теории вероятностей, нельзя отнести к очень сложным наукам. Но практические задания, направленные на усвоение и запоминание материала, отличаются большой трудоёмкостью и отнимают много времени. Поэтому заказать решение задач по статистике студенты предпочитают не столько из-за нехватки знаний, сколько по причине банального недостатка времени.
Портал «ВсёСдал!» имеет огромную базу исполнителей (аспиранты, преподаватели, кандидаты и доктора наук), готовых не только выполнить решение задач по математической статистике, но и взяться за объемную и сложную социальную статистику.
За такие проекты берется далеко не каждая фирма, которая предлагает сегодня в сети помощь студентам. Дело здесь состоит в больших объёмах данных, набор и обработка которых отнимают много сил и времени.
Выгодно заказать решение задач по статистике
Портал «ВсёСдал!» не является фирмой-посредником, зарабатывающей на студентах. Это свободная виртуальная площадка, на страницах которой вы размещаете заказ на решение задач по статистике онлайн, в электронном или письменном виде. Программа автоматически рассылает вашу заявку исполнителям, а те в свою очередь связываются с вами.
Чем подробнее вы заполните форму, тем проще специалисту будет определиться, по его ли профилю задание. Например, если вам нужно решение задач по мат статистике, профессионалу-экономисту нет смысла отвечать на ваш проект. И наоборот, специалист по высшей математике и математической статистике вряд ли в оперативно выполнит решение задач по эконометрике онлайн, когда требуется максимально быстро дать решение в условиях реального времени экзамена или зачета.
Поэтому постарайтесь дать полное описание того задания, выполнение которого вы планируете возложить на плечи исполнителя (решение задач по статистике индексы, решение задач по химии, написание курсовой по истории, решение задач по статистике онлайн в режиме реального времени, проработка методички по марковским цепям, решение задач экономической статистики и т.д.).
Также укажите количество заданий (одна-две с подробным описанием для самостоятельного изучения или же решение задач по математической статистике в объеме полной контрольной работы – от этого напрямую зависит стоимость проекта).
К примеру, только решение задач по статистике на индексы имеет огромное количество разновидностей:
· индексы цен структурных сдвигов, себестоимости, цен постоянного состава
· индексы в однородной совокупности, анализы сезонных колебаний, модели сезонной волны
· индексы зарплаты (переменный, постоянный состав, структурные сдвиги).
Есть общие индексы динамики, ряды динамики. Решение статистики, как видим, многообразно и очень объемно. Неудивительно, что у некоторых студентов с изучением дисциплины порой возникают сложности.
На портале «ВсёСдал!» вы можете заказать эти и массу других студенческих работ, которые требуют от студентов преподаватели ВУЗов:
· статистика — выборочное наблюдение и решение задач
· марковские цепи — решение задач
· статистика средние величины — решение задач
· решение задач по статистике (индексы)
· общая теория статистики — решение задач
· решение задач по математической статистике
а также заказать дипломную, курсовую, практическую работу, реферат или веб-презентацию.
Решение задач по статистике онлайн
Из-за того, что решение задач по статистике (средние величины, индексы, ряды) действительно представляет собой обширную работу (набор данных в таблицы, ранжирование, построение интервального ряда, создание расчетных таблиц, построение графиков и диаграмм, др.), многие студенты считают, что решение задач по статистике онлайн невозможно. Это далеко не так!
На письменной контрольной или экзамене вам даются ограниченные данные, работа с которыми не представляет труда для опытного профессионала. Вы можете заказать задачи по статистике с развернутыми пояснениями и потом на наглядном примере изучить предмет непосредственно перед сдачей.
Если же на самоподготовку времени не осталось, так же, как вы заказываете помощь по английскому языку онлайн, можно поручить профессионалу решение задач по статистике онлайн, что подразумевает оперативное выполнение задания из экзаменационного билета или контрольной в режиме реального времени.
Задачи с решением для студентов
Раздел содержит подробные готовые решения типовых задач по высшей математике, теории вероятностей, статистике, финансовой математике, эконометрике, методам оптимальных решений (линейному программированию, экономико-математическим моделям). Решение многих задач предваряет теория в сжатом виде, что будет небесполезно для студентов, пытающихся самостоятельно разобраться с ходом решения.
На этой странице выложено большое количество решенных задач по статистике — от простых до сложных, с запутанными условиями. Эти типовые примеры предназначены для самостоятельной работы студентов экономических и управленческих специальностей ВУЗов. Тематика охватывает весь курс общей теории статистики, основные разделы курса социально-экономической статистики и статистики предприятия. Решения содержат пояснения и выводы.
В разделе размещены подробно разобранные задачи по теории вероятностей и математической статистике, перед решением которых излагается теория в сжатом виде, где содержаться основные формулы разбираемой темы. Примеры упорядочены в соответствии с содержанием курса теории вероятностей в ВУЗах. Задачи будут полезны для студентов экономических и технических специальностей.
На странице выложены решения типовых задач по высшей математике для студентов 1-го и 2-го курсов экономических и технических специальностей. Перед большинством решений кратко изложены основные теоретические сведения. Приведенная выборка решенных задач может служить базой для подготовки к семестровым экзаменам и зачетам по высшей математике в качестве решебника.
В этом разделе можно найти примеры решенных задач по финансовой математике (другие названия — основы финансовых вычислений, актуарная математика). Приведены основные, чаще всего используемые на практике схемы простых и сложных процентов, дисконтирование, учет инфляции, финансовые ренты, оценка доходности финансовых операций, преобразование и эквивалентность денежных потоков и т.д. Перед решением задач приведена краткая теория.
В этом разделе разобраны типовые задачи методов оптимальных решений. Подробным образом рассматриваются задачи линейного программирования (графический и симплексный методы), транспортная задача. Перед примерами некоторых задач кратко изложены основные теоретические сведения.
В этом разделе выложены примеры решения задач по эконометрике для самостоятельной работы студентов экономических специальностей.
Задачи по статистике с решением
Задачи по статистике с решением — Выборочное наблюдение
Задача 1 по статистике
При проверке импортирования груза на таможне методом случайной выборки было обработано 200 изделий. В результате был установлен средний вес изделия 30г., при СКО=4г с вероятностью 0,997. Определите пределы в которых находится средний вес изделий генеральной совокупности.
Решение.
В данном примере – случайный повторный отбор.
n=200
 =30г
=30г
 =4г — СКО
=4г — СКО
p=0,997, тогда t=3
Формула средней ошибки для случайного повторного отбора:

 =0,84 г
=0,84 г
 г
г
Определяем величину средней ошибки.

Ответ: пределы в которых находится средний вес изделий: г
г
Задача 2
В городе проживает 250тыс. семей. Для определения среднего числа детей в семье была организована 2%-я бесповторная выборка семей. По ее результатам было получено следующее распространение семей по числу детей:
P=0,954. Найти пределы в которых будет находится среднее число детей в генеральной совокупности.
|
Число детей в семье, xi |
0 |
1 |
2 |
3 |
4 |
5 |
|
Кол-во детей в семье |
1000 |
2000 |
1200 |
400 |
200 |
200 |
Решение
2%-я выборка означает:
n=250000*0,02= 5000 семей было исследовано.
Т.к. выборка бесповторная, используем следующую формулу для определения средней величины ошибки:

Найдем среднее число детей в выборочной совокупности:
 ребенка
ребенка
Определим дисперсию

 ребенка – средняя величина ошибки
ребенка – средняя величина ошибки
Т.к p = 0,954, то t = 2
 ребенка
ребенка
 ребенка
ребенка
Вывод: из-за слишком малой величины ошибки, среднее число детей в генеральной совокупности можно принять за 1,5 ребенка.
Задача 3
С целью определения средней фактической продолжительности рабочего дня в гос. учреждении с численностью служащих 480 человек была проведена 25%-ная механическая выборка. По результатам наблюдения оказалось, что у 10% обследованных потери рабочего времени достигали более 45 мин.в день. С вероятностью 0,683 установите пределы, в которых находится генеральная доля служащих с потерями рабочего времени более 45 мин. в день.
Решение. Определим объем выборочной совокупности: n=480*0.25=120 чел.
Выборочная доля w по условию 10%.Учитывая, что показатели точности механической и собственно случайной бесповторной выборки определяются одинаково, а также то, что при P=0,683 t=1, предельная ошибка выборочной доли:  =
=
Ответ: пределы в которых находится средняя доля  % или:
% или: г
г
Т.о., с вероятностью 0,683 можно утверждать, что доля работников учреждения с потерями рабочего времени более 45 мин. в день находится в пределах от 7,6 до 12,4 %.
Задача 4 по статистике
В АО 200 бригад рабочих. Планируется проведение выборочного обследования с целью определения удельного веса рабочих, имеющих профессиональные заболевания. Известно, что дисперсия доли бесповторной выборки равна 225. с вероятностью 0,954 рассчитайте необходимое количество бригад для обследования рабочих, если ошибка выборки не должна превышать 5%.
Численность выборки для бесповторного отбора:
 бригад
бригад
Относительные величины динамики и интенсивности
Сопоставление статистических данных осуществляется в различных формах и по разным направлениям. В соответствии с различными задачами и направлениями сопоставления статистических данных применяются различные виды относительных величин.
Относительная величина динамики характеризует изменение явления во времени и показывает, во сколько раз изменился уровень показателя по сравнению с каким-либо предшествующим периодом. Относительные величины имеют форму коэффициентов, если они исчисляются делением сравниваемой величины на базу сравнения. Если коэффициент умножить на 100, то получим результат сопоставления в процентах.
Отношения между разноименными абсолютными величинами называют относительными величинами интенсивности. В их числе можно назвать показатели жизненного уровня населения, к которым относятся, например, показатели потребления продуктов питания и непродовольственных товаров на душу населения. Учитывая экономическую сущность относительных величин интенсивности, они характеризуют уровень социального и экономического развития.
В процессе статистического анализа абсолютные и относительные величины должны рассматриваться во взаимосвязи, т. е. пользоваться ими нужно не формально, а представлять, какая абсолютная величина скрывается за каждым относительным показателем. Особенно важно соблюдать это положение при расчете относительных величин динамики. Одно из главных требований, которое предъявляется при исчислении относительных величин, заключается в необходимости обеспечения сопоставимости сравниваемой величины и величины, принятой за базу сравнения.
Условие задачи
Определить относительные величины динамики и интенсивности на основании данных, приведенных в таблице.
| Годы | Промышленность СССР, млрд.р. |
| 1965 | 229.4 |
| 1970 | 374.3 |
| 1975 | 511.2 |
| 1980 | 616.3 |
| 1985 | 717.0 |
Численность населения в СССР в 1985 г. составляла 268,8 млн.человек.
Решение задачи
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение задач, контрольных или онлайн-помощь на зачете/экзамене 〉〉
Если вам сейчас не требуется помощь, но может потребоваться в дальнейшем, то, чтобы не потерять контакт, вступайте в группу ВК.
Вычислим относительные величины динамики — цепные (по отношению к предыдущему году) и базисные (по отношению к 1965 году).
Относительные величины динамики по отношению к предыдущему году:
1970 г.
1975 г.
1980 г.
1985 г.
Относительные величины динамики по отношению к базисному 1965 году:
1970 г.
1975 г.
1980 г.
1985 г.
| Годы | 1965 | 1970 | 1975 | 1980 | 1985 |
| Вся промышленность, млрд.р. | 229.4 | 374.3 | 511.2 | 616.3 | 717 |
| Относительные величины динамики (цепные), % | —- | 163.2 | 136.6 | 120.6 | 116.3 |
| Относительные величины динамики (базисные), % | —— | 163.2 | 222.8 | 268.7 | 312.6 |
Вычислим относительные величины интенсивности — стоимость промышленной продукции на одного человека в СССР:
1965 г.
1970 г.
1975 г.
1980 г.
1985 г.
| Годы | Вся промышленность, млрд.р. | Стоимость на одного человека, тыс.р. |
| 1965 | 229.4 | 0.853 |
| 1970 | 374.3 | 1.392 |
| 1975 | 511.2 | 1.902 |
| 1980 | 616.3 | 2.293 |
| 1985 | 717 | 2.667 |
Таким образом, в течение исследуемого периода стоимость промышленной продукции постоянно увеличивалась. В 1985 году по сравнению с 1965 годом показатель увеличился на 3,216 раз или на 212,6%. Промышленная продукция в расчете на одного человека также значительно увеличилась на этом временном отрезке.
К оглавлению решебника по статистике 〉
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение задач, контрольных или онлайн-помощь на зачете/экзамене 〉〉
Если вам сейчас не требуется помощь, но может потребоваться в дальнейшем, то, чтобы не потерять контакт, вступайте в группу ВК.
На цену сильно влияет срочность решения (от суток до нескольких часов). Онлайн-помощь на экзамене/зачете осуществляется по предварительной записи.
Заявку можно оставить прямо в чате, предварительно скинув условие задач и сообщив необходимые вам сроки решения. Время ответа — несколько минут.
Статистика Проблемы с решениями
Проблема 1
В одном штате 52% избирателей — республиканцы, а 48% — демократы. Во втором штате 47% избирателей — республиканцы, а 53% — Демократы. Предположим, что простая случайная выборка из 100 избирателей опрошены из каждого штата.
Какова вероятность того, что опрос покажет больший процент республиканских избирателей в во втором состоянии чем в первом состоянии?
(А) 0.04
(В) 0,05
(С) 0,24
(D) 0,71
(E) 0,76
Решение
Правильный ответ — C. Для этого анализа пусть P 1 = доля избирателей-республиканцев в первом штате, P 2 = доля избирателей-республиканцев во втором штате, p 1 = доля избирателей-республиканцев в образец из первого состояния, и p 2 = доля избирателей-республиканцев в образец из второго состояния.Количество избирателей, отобранных из первое государство (n 1 ) = 100, а количество избирателей выборка из второго состояния (n 2 ) = 100.
Решение состоит из четырех шагов.
- Убедитесь, что размер выборки достаточно велик для моделирования различий с нормальным населением. Так как n 1 P 1 = 100 * 0,52 = 52, n 1 (1 — P 1 ) = 100 * 0.48 = 48, n 2 P 2 = 100 * 0,47 = 47, и n 2 (1 — P 2 ) = 100 * 0,53 = 53 каждый больше 10, размер выборки достаточно велик.
- Найдите среднее значение разницы в пропорциях образца: E (p 1 — p 2 ) = P 1 — P 2 = 0,52 — 0,47 = 0,05.
- Найдите стандартное отклонение разницы.
σ г = sqrt {[P 1 (1 — P 1 ) / n 1 ] + [P 2 (1 — P 2 ) / n 2 ]}
σ г = sqrt {[(0,52) (0,48) / 100] + [(0,47) (0,53) / 100]}
σ г = sqrt (0,002496 + 0,002491) = sqrt (0,004987) = 0,0706 - Найдите вероятность.Эта проблема требует от нас найти
вероятность того, что p 1 меньше p 2 .
Это эквивалентно нахождению вероятности того, что
p 1 — p 2 меньше нуля. Чтобы найти это
вероятность, нам нужно преобразовать случайную величину
(p 1 — p 2 ) в
z-оценка.
Это преобразование показано ниже.
z с 1 — с 2 = (х — μ с 1 — с 2 ) / σ d = = (0-0.05) /0,0706 = -0,7082
Использование Stat Trek’s Калькулятор нормального распределения, мы находим, что вероятность того, что z-оценка будет -0,7082 или меньше составляет 0,24.
Следовательно, вероятность того, что опрос покажет больший процент республиканских избирателей в второе состояние, чем в первом состоянии, составляет 0,24.
.Statistics Problem Solver — Бесплатная загрузка и обзоры программного обеспечения
Pros
Это программное обеспечение отличается высокой точностью и стабильностью. Простой поиск данных, хороший регрессионный анализ, очень хорошая бесплатная лицензия. в целом очень хорошее приложение
Минусы
Отсутствуют некоторые статистические измерения, трудно редактировать данные
Сводка
Действительно помогает выполнять совместную работу, имеет хорошие инструменты для поиска необходимых файлов или части разговора.вы также можете проверить с https://www.tutorspoint.com/blog/online-statistics-assignment-help/
Pros
Было здорово видеть, как программа вырабатывает решения, которые можно было бы адаптировать к проблемам «реальной жизни». Этот процесс помогает понять решения нескольких статистических проблем.
Минусы
Было бы неплохо увидеть добавление коробчатых диаграмм с усами.
Резюме
В целом, эта программа делает именно то, что обещает.Скорость нормальная, особенно поначалу, когда вы видите, как разворачивается решение. С небольшими дополнениями это было бы одним из лучших и наименее дорогих решений статистических задач.
Pros
Он не только дает вам решения, но и учит, как их решать.
Минусы
К нему нужно немного привыкнуть, прежде чем вы сможете решать с ним различные проблемы.
Pros
Он выполняет те задачи, которые он утверждает.
Минусы
Вычисления идут медленно. Это не столько замедление вычислений как таковое, сколько из-за потерь, сделанных на ненужную анимацию каждого отдельного вычисления. Кроме того, слишком много времени тратится на форму без достаточной функциональности.
Еще меня раздражало то, что программа загружает страницу продукта каждый раз, когда программа завершается.
И последнее: хотя он делает кое-что из того, что мне нужно, в конце концов, этого недостаточно.
А, и это не совсем бесплатно. Будет работать нормально, но полная программа стоит денег.
Pros
Качество обучающих программ по статистике хорошее. Впечатляет, как вы можете просто заполнить пробелы и посмотреть, как программа шаг за шагом решает эту проблему.
Плюсы
Красивый пользовательский интерфейс.Очень проста в использовании. Хорошие описательные пошаговые решения статистических задач. Рекомендуется всем, кто изучает статистику.
.статистических выбросов: обнаружение и обработка
Большинство реальных наборов данных включает определенное количество аномальных значений, обычно называемых «выбросами». Эти наблюдения существенно отклоняются от общей тенденции, поэтому важно изолировать эти выбросы для повышения качества исходных данных и уменьшения негативного воздействия, которое они оказывают на процесс анализа наборов данных. Практически почти все образцы экспериментальных данных, вероятно, будут загрязнены выбросами, что снижает эффективность и надежность статистических методов.Выбросы анализируются, чтобы увидеть, можно ли объяснить их необычное поведение. Иногда выбросы имеют «плохие» значения, возникающие в результате необычных, но объяснимых событий. Причины выбросов не всегда случайны или случайны. Следовательно, прежде чем выбросить выброс, необходимо провести исследование.
Обнаружение статистических выбросов
Статистические выбросы чаще встречаются в распределениях, не соответствующих нормальному распределению. Например, в распределении с длинным хвостом статистические выбросы встречаются чаще, чем в случае нормального распределения.
Самый простой метод определения того, является ли экстремальное значение выбросом, — использовать межквартильный размах. IQR показывает, насколько распределена средняя половина нашего набора данных.
Межквартильный размах, или IQR, определяется вычитанием первого квартиля из третьего квартиля.
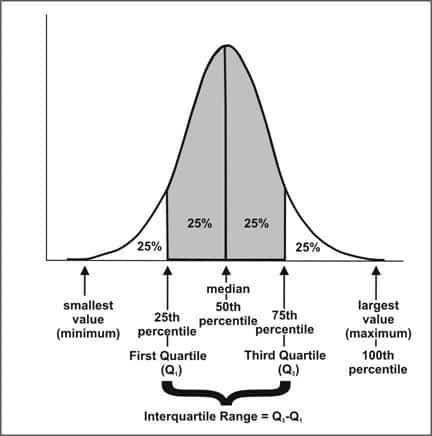
Начнем с IQR и умножим его на 1,5. Затем вычтите это число из первого квартиля и прибавьте его к третьему квартилю. Эти два числа из нашего внутреннего ограждения .Для внешних ограждений мы начинаем с IQR и умножаем его на 3. Затем мы вычитаем это число из первого квартиля и добавляем его к третьему квартилю. Эти два числа — это наши внешние ограждения .
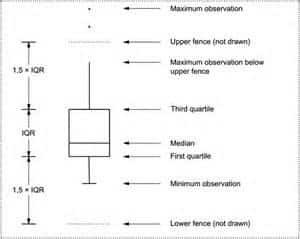
Выбросы теперь можно обнаружить, определив место наблюдения относительно внутренних и внешних ограждений. Если отдельное наблюдение более экстремально, чем любое из наших внешних ограждений, то оно является выбросом, и более конкретно его называют сильным выбросом .Если значение наших данных находится между соответствующими внутренними и внешними ограничениями, то это значение является предполагаемым выбросом или слабым выбросом .
Пример
Предположим, что мы вычислили первый и третий квартили наших данных и обнаружили, что эти значения равны 40 и 50 соответственно. Межквартильный размах IQR = 50-40 = 10. Затем мы видим, что 1,5 x IQR = 15. Это означает, что внутренние границы находятся на уровне 40-15 = 25 и 50 + 15 = 65. Это на 1,5 x IQR меньше, чем первый квартиль и больше третьего квартиля.
Теперь мы вычисляем 3 x IQR, то есть 3 x 10 = 30. Внешние ограждения на 3 x IQR более экстремальны, чем первый и третий квартили. Это означает, что внешние ограждения 40 — 30 = 10 и 50 + 30 = 80.
Любые значения данных меньше 10 или больше 80 считаются выбросами. Любые значения данных от 10 до 25 или от 65 до 80 являются предполагаемыми выбросами.
Причины выявления выбросов
Наличие выбросов указывает на ошибки в измерениях или возникновение неожиданного и ранее неизвестного явления.Чрезвычайно важно проверять выбросы в каждом статистическом анализе, поскольку они влияют на всю описательную статистику, поскольку чувствительны к ним. Среднее значение, стандартное отклонение и коэффициент корреляции в парных данных — это лишь некоторые из этих типов статистики. Это может ввести аналитиков в заблуждение и сделать неверные выводы, поскольку вся эта статистика искажается.
ПРИМЕЧАНИЕ:
Некоторые статистические оценщики могут работать со статистическими выбросами и являются надежными, в то время как другие не могут справиться с ними.Типичный пример — медиана. Это наиболее устойчивая статистика с пределом пробоя 50%. Это означает, что пока не более половины данных загрязнены или отсутствуют, медиана не будет отклоняться на произвольно большую или малую величину.
На практике выброс может нанести серьезный ущерб бизнесу, основанному на данных. Например, выбросы в транзакционных данных розничных продавцов или дистрибьюторов могут привести к неправильному расчету прогнозов спроса. Это приводит к несоответствию спроса и предложения, поскольку бизнес либо в конечном итоге испытывает дефицит, либо избыточный запас запасов.Другие неблагоприятные исходы также могут включать; неточное планирование бюджета, неоптимальное использование ресурсов, плохой выбор поставщиков, убыточная модель ценообразования и т. д.
Выбросы могут отрицательно повлиять даже на инженерные фирмы или производители. Ошибки в измерениях, снятых датчиками (например, термометрами, барометрами) во время проверки качества производимых продуктов, могут привести к неожиданному выходу из строя продуктов, неправильному измерению гарантийных сроков, инициировать перепроектирование продуктов и так далее.
Неблагоприятные эффекты выбросов могут даже повлиять на жизнь граждан, если данные, собранные правительством, содержат выбросы. Предвзятые выборки в государственных опросах, содержащие наблюдения, которые считались бы выбросами по сравнению со всем населением, могли бы оправдать разработку политики, которая может нанести ущерб обществу. Таким образом, крайне важно разработать методы работы с выбросами в статистическом анализе.
Обработка выбросов
Обработка выбросов значений может быть достигнута с помощью следующих категорий действий, которые могут быть предприняты:
Преобразование данных : Преобразование данных — это один из способов смягчить влияние выбросов, поскольку наиболее часто используемые выражения, квадратный корень и логарифмы, влияют на большие числа в гораздо большей степени, чем на меньшие.Трансформации могут не всегда укладываться в теорию модели, поскольку они могут повлиять на ее интерпретацию. Преобразование переменной делает больше, чем просто делает распределение менее искаженным; он изменяет отношения между переменными в модели.
Удаление значений: Если есть допустимые ошибки, которые не могут быть исправлены или лежат настолько далеко за пределами диапазона данных, что искажают статистические выводы, выбросы должны быть удалены. Если есть сомнения, мы можем сообщить результаты модели как с выбросами, так и без них, чтобы увидеть, насколько они меняются.Преобразование и удаление данных — важные инструменты, но их не следует рассматривать как средство решения проблем распределения, связанных с выбросами. Преобразования и / или устранение выбросов должны быть осознанным выбором, а не рутинной задачей. В некоторых случаях удаление значения выброса может также привести к неверным выводам, сделанным в отношении данных. В таких случаях замена наблюдения мерой центральной тенденции (Среднее, Медианное или Модное), в зависимости от ситуации.
Согласование ценностей: Один очень эффективный план — использовать методы, устойчивые к наличию выбросов.Непараметрические статистические методы относятся к этой категории и должны более широко применяться к непрерывным или интервальным данным. Когда выбросы не являются проблемой, исследования с помощью моделирования показали, что их способность обнаруживать существенные различия лишь немного меньше, чем у соответствующих параметрических методов. Существуют также различные формы надежных регрессионных моделей и вычислительно-ресурсоемких подходов, которые заслуживают дальнейшего рассмотрения.
Если вы хотите внедрить программное обеспечение для прогнозирования для своего бизнеса, вы можете связаться с нами, используя нашу контактную форму или по адресу sales @ bistasolutions.com.
.PPT — Проблемы со статистическими методами в исследованиях управления… и некоторые решения Презентация в PowerPoint
Проблемы со статистическими методами в исследованиях управления… и несколько решений Презентация для Ежегодного собрания INFORMS, Остин, США, ноябрь 2010 г. Майкл Вуд, Портсмутский университет, Великобритания [email protected] http://userweb.port.ac.uk/~woodm/presentations.htm Презентация на основе пересмотренной версии Wood (2010)
Пример использования типичная журнальная статья приводит к трем выводам : • Ценность любого статистического подхода серьезно ограничена различными факторами: e.грамм. трудности обобщения на контексты, отличные от исследуемой выборки. • Традиционный формат проверки гипотез делает результаты почти бессмысленными: вместо этого я предлагаю использовать уровни достоверности для гипотез и предлагаю два способа сделать это (один — метод начальной загрузки в электронной таблице). • Анализ должен быть более удобным для пользователя. Я начну с 3, затем с 2. Наверное, нет времени для 1.
Пример из практики: Glebbeek and Bax (2004) • … хотел проверить гипотезу «текучесть кадров и эффективность фирмы имеют перевернутую U-образные отношения: слишком высокая или низкая текучесть кадров вредна.• Для этого они проанализировали производительность (рентабельность) «110 офисов агентства по временному трудоустройству», построив регрессионные модели, используя «чистый результат на офис» (стр. 281) в качестве меры производительности и текучести кадров, и квадрат оборота как независимые переменные, а также три управляющие переменные.
Часть таблицы 2 в Glebbeek and Bax (2004)
Может быть проще для пользователя: Результаты и криволинейные прогнозы для Региона 1 и среднего количества прогулов и возраста (Модель 4)
или… Эквивалент модели 4…
Проверка нулевой гипотезы и значения p не являются хорошей идеей • Многие люди не знают, что они имеют в виду, или неправильно их интерпретируют • Не говорят вам, насколько велик эффект, или насколько вероятно, что криволинейная гипотеза верна • Гипотеза перевернутой U-образной формы слишком очевидна, чтобы ее стоило доказывать? Вместо этого… используйте доверительные интервалы, но, возможно, только для одного параметра, или…
Используйте начальную загрузку: жирная линия — это прогноз данных, другие строки — это прогнозы из повторных выборок, представляющих другие выборки из того же источника.
Очевидно, что некоторые из этих повторных выборок не подтверждают гипотезу об обратной U-образной форме , некоторые подтверждают • Таблица показывает, что 65% из 10 000 повторных выборок дают предсказания перевернутой U-образной формы • Таким образом, достоверность гипотезы составляет 65% … это то, что мы хотим знать! • Обратите внимание, что два значения p (оба> 10%) не дают вам этой информации. • См. Wood (2009b). В анализе используется эта электронная таблица: http://userweb.port.ac.uk/~woodm/BRQ.xls
Иногда можно использовать значения p для определения уровней достоверности • Значение P для оборота в (линейной) модели 3 равно 0.7%, нестандартная рег. коэффициент равен –1 778 • Таким образом, уверенность в том, что коэффициент отрицательный = 99,65%… снова позволяет избежать нулевых гипотез (Wood (2009a)
Подумайте, может ли какой-либо статистический подход быть полезным … Преимущество статистических методов в том, что они позволяют Мы можем заглянуть сквозь туман шумовых переменных и увидеть закономерности. Но для того, чтобы статистический анализ был полезным, необходимо проверить четыре вопроса: • Вредит ли необходимость сосредоточения внимания на легко измеримых переменных достоверности результатов • Является ли целевая группа вероятно, будет представлять постоянный интерес • Будет ли объем объясненных вариаций достаточным для оправдания усилий, и, принимая во внимание эти факторы, • Вносит ли исследование полезное дополнение к существующим знаниям (включая «здравый смысл»).
Выводы • Рассмотреть полезность любого статистического подхода • Избегать серии гипотез для проверки. Вместо этого посмотрите на размер / характер эффектов • Используйте доверительные интервалы, а не значения p • Или уровни достоверности для гипотез • полученные из значений p • полученные из начальной загрузки • Сделайте результаты как можно более удобными для пользователя
Ссылки • Glebbeek, AC, & Bax, EH (2004). Действительно ли вредна высокая текучесть кадров? Эмпирический тест с использованием записей компании.Журнал Академии управления, 47 (2), 277-286. • Вуд, М. (2009a). Освобождение исследования от нулевых гипотез: уровни достоверности для основных гипотез вместо значений p. http://arxiv.org/abs/0912.3878. • Вуд, М. (2009b). Уровни достоверности начальной загрузки для гипотез о моделях регрессии. Http://arxiv.org/abs/0912.3880. • Вуд, М. (2010). Использование статистических методов в исследованиях управления: предложения из тематического исследования. http://arxiv.org/abs/0908.0067v2
Спасибо • Есть мысли? • Все комментарии получены с благодарностью ([email protected])


