Задачки с числами
День рождения
Позавчера мне было 25. А в следующем году мне исполнится 28.
Какой день — день моего рождения?
Простая дедукция
Учитель сказал, что задумал два последовательных числа от 1 до 10. После этого он сообщил одному студенту одно из этих чисел, а второму – другое. Последовал такой разговор:
1-й студент: «Я не знаю другого числа.»
2-й студент: «Я тоже не знаю другог числа.»
1-й студент: «Теперь я знаю другое число.»
Найдите все 4 возможные комбинации из двух чисел.
Сложная дедукция
Эта задачка – одна из самых сложных в этом разделе.
Учитель сообщил, что задумал два натуральных числа больше единицы.
1-й студент: «Я не знаю сумму.»
2-й студент: «Я знал, что ты не знаешь. Сумма меньше 14.»
1-й студент: «Теперь я знаю эти числа.»
2-й студент: «Я тоже.»
Найдите эти два числа.
Сколько лет детям?
Два друга разговаривают:
— Питер, сколько лет твоим детям?
— Знаешь, Томас, у меня их трое. И если перемножить их возраста, то получится 36.
— Этого недостачно…
— Сумма их возрастов равна количеству бутылок пива, что мы сегодня выпили.
— Этого всё ещё недостаточно.
— Хорошо. Последнее, что могу сказать – старший сын носит зеленую кепку.
Сколько лет детям Питера?
Математический знак
Какой математический знак можно поставить между цифрами 5 и 9, чтобы получилось число больше, чем 5 и меньше, чем 9?
Дробь
Расставьте все 9 цифр: 1, 2, 3, 4, 5, 6, 7, 8, и 9 в числителе и знаменателе дроби, использовав каждую цифру один и только один раз, так чтобы получилась дробь равная 1/3.
Пятизначное число
Если приписать цифру 1 впереди некоего 5-тизначного числа, то получится число в 3 раза меньше, чем если приписать цифру 1 в конце этого же числа. Найдите это число.
Шифр
Найдите число, если:
- Это число состоит из 6 разных цифр.
- Чётные и нечётные цифры чередуются (ноль также может чередоваться и будет считаться четным числом).
- Каждые две соседние цифры отличаются больше, чем на 1.
- Число, состоящие из первых двух цифр, как и число, состоящие из средних двух цифр, делятся без остатка на число, составленное двумя последними цифрами.
У этой задачи существует больше одного варианта решения.
Кроссворд с числами
Составьте таблицу из трёх чисел, расположенных вертикально, и трёх – горизонтально, как показано на примере ниже. Числа можно брать только из приведённого списка. Можно использовать одно и то же число несколько раз. Составив таблицу, подсчитайте сумму всех цифр в ней. Какова максимальная сумма, которую можно получить?
Таблица Список чиселПример с использованием каждого из чисел: 40067 04802 78215 дважды
Сумма в этом примере: 73.
Но, конечно, этот результат можно улучшить.
Загадочное число
Найдите число обозначенное звёздочками, если известно следующее:
- Все 4 цифры неизвестого числа – разные.
- Ни одна из цифр не равна нулю.
- Каждый «+» справа от числа означает, что в этом числе есть совпадающая цифра стоящая в той же позиции, как и цифра искомого числа.
6152 +0 4182 00 5314 00 5789 + ---------- ****
1996
Пользуясь цифрами: «1», «9», «9» и «6» и знаками арифметических операций: «+», «-», «х», «:», знаком извлечения корня и скобками, получите следющие результаты:
29, 32, 35, 38, 70, 73, 76, 77, 100 и 1000.
Все четыре цифры должны быть использованны только в заданном порядке, каждая цифра только один раз, и нельзя переворачивать цифры вверх ногами.
100
Используя четыре семёрки (7) и одну еденицу (1), получите число 100. Кроме 5-ти цифр, можно пользоваться обычными арифметическими операциями: «+», «-», «х», «:», знаком извлечения корня и скобками.
Уравнение
Переставьте только одну цифру, так чтобы получилось равенство:
101 – 102 = 1
Последовательности
Существует бесконечное множество формул (функций), которые удовлетворет заданная конечная последовательность чисел. Постарайтесь найти самые простые формулы для следующих последовательностей.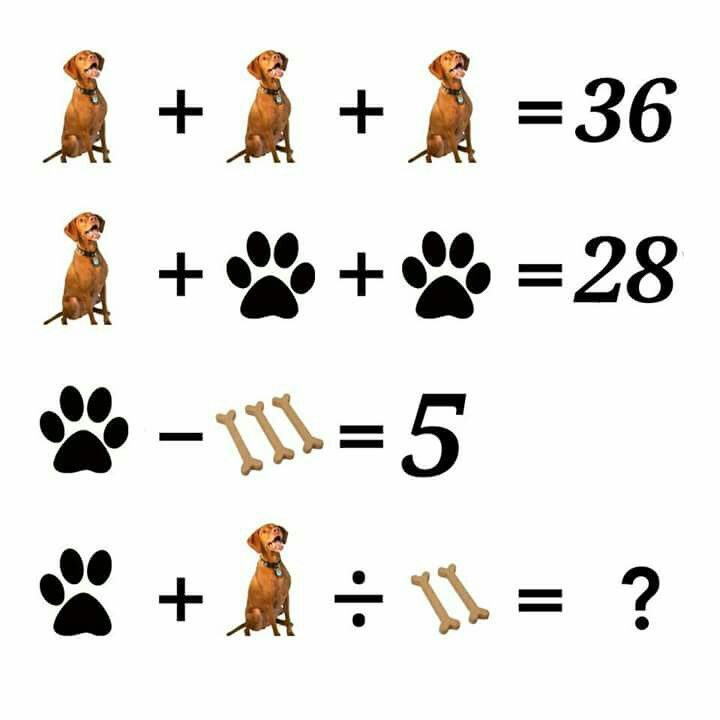
- 8723, 3872, 2387, ?
- 1, 4, 9, 18, 35, ?
- 23, 45, 89, 177, ?
- 7, 5, 8, 4, 9, 3, ?
- 11, 19, 14, 22, 17, 25, ?
- 3, 8, 15, 24, 35, ?
- 2, 4, 5, 10, 12, 24, 27, ?
- 1, 3, 4, 7, 11, 18, ?
- 99, 92, 86, 81, 77, ?
- 0, 4, 2, 6, 4, 8, ?
- 1, 2, 2, 4, 8, 11, 33, ?
- 1, 2, 6, 24, 120, ?
- 1, 2, 3, 6, 11, 20, 37, ?
- 5, 7, 12, 19, 31, 50, ?
- 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, ?
- 126, 63, 190, 95, 286, 143, 430, 215, 646, 323, 970, ?
- 4, 7, 15, 29, 59, 117, ?
- 2, 3, 2, 3, 2, 4, 2, 3, 2, 3, 2, 5, 2, 3, 2, 3, 2, 4, 2, 3, 2, 3, 2, 5, 2, 3, 2, 3, 2, 4, 2, 3, 2, 3, 2, 5, ?
- 4, 4, 341, 6, 4, 4, 6, 6, 4, 4, 6, 10, 4, 4, 14, 6, 4, 4, 6, 6, 4, 4, 6, 22, 4, 4, 9, 6, ?
Математические головоломки >>
Девиз
Наука не является и никогда не будет являться законченной книгой.
Альберт Эйнштейн
Загадки про цифры 0-9 в стихах и с подвохом
На палочку она похожа,
И на худую спицу тоже.
Прямая, ровная всегда,
В строю стоит после ноля.
(Единица)
С острым носиком сестрица
Счёт открывает…
Сколько солнышек за тучкой,
Сколько стержней в авторучке,
Сколько у слона носов,
Сколько на руке часов?
Сколько ног у мухомора
И попыток у сапера,
Знает и собой гордится
Цифра эта…
(Единица)
На столе лежали фрукты:
Слива, персик, апельсин.
Ваня скушал два продукта,
И остался фрукт…
(Один)
Загадки про цифру 2
Два молоденьких пингвинаПлавают весь день на льдине.
Свою шею выгибает,
И красива, и стройна,
Хвостик чуть приподнимает
Словно лебедь, цифра…
(Два)
В школе есть такая птица:
Если сядет на страницу,
То с поникшей головой
Возвращаешься домой.
(Два)
Лебедь плавает в тетрадке,
Значит что-то не в порядке.
Если ты совсем Незнайка,
Цифру эту получай-ка.
(Два)
Сколько крыльев у синицы,
Сколько лап у каждой птицы?
Сколько берегов у речки,
Сколько ушек у овечки?
Сколько глаз у злого льва
Знает только цифра…
(Два)
Маша в города играла,
Называла и считала:
Кемерово и Москва,
Городов назвала…
(Два)
Синие часы у Гриши,
Красные часы у Миши,
Сколько же всего часов
У мальчишек близнецов?
(Двое)
Яблоко у Маши,
И груша у Наташи.
Скорее фрукты эти
Сосчитайте, дети!
(Два)
Пять пирожков лежало в миске.
Два пирожка взяла Лариска,
Ещё один стащила киска.
Так сколько их осталось в миске?
(Два)
Загадки про цифру 3
Три утёнка на пруду
Учатся учатся искать еду.
Необычна цифра эта,
Круглолица, так и знай.
И на букву З похожа,
Что за цифра? Отгадай!
(Три)
Эта цифра просто чудо.
У нее родня повсюду.
Даже в алфавите есть
У неё сестра-близнец.
(Три)
Букву З ты обведи,
К цифрам в гости приведи.
Повнимательней смотри —
Буква З как цифра…
(Три)
Шар один в руке у Саши,
Два шара в руке у Маши.
Сосчитаем все шары
И получим ровно…
(Три)
Начинаем вычислять:
От восьми отнимем пять.
Результат проговори
И запишем цифру…
(Три)
На треугольник посмотри,
Углов здесь сколько?
Ровно…
(Три)
Под деревом четыре льва,
Один ушёл, осталось…
(Три)
Возле леса, на опушке
Трое их живет в избушке.
Там три стула и три кружки.
Три кроватки, три подушки.
Угадайте без подсказки,
Кто герои этой сказки?
(Три медведя)
Золотая рыбка плавает, ныряет,
Сколько пожеланий рыбка исполняет?
(Три)
Загадки про цифру 4
Четыре конька под водою играют,
Морские коньки цвет легко поменяют!
Кто-то ночью старый стул
Спинкой вниз перевернул.
И теперь у нас в квартире
Стал он цифрою…
(Четыре)
Эта цифра так похожа
На красивый парус!
Раздувается всё шире
Циферка…
(Четыре)
Делал маленький Егорка
Генеральную уборку,
Опрокинул стул в квартире,
Стал похож стул на…
(Четыре)
Здесь режиссер и сценарист
Еще заслуженный артист,
Ведущая в прямом эфире,
Подскажешь, сколько нас?…
(Четыре)
Я у бабушки гостила,
У нее в квартире
Кошки две и два кота,
А всего — …
(Четыре)
Чтоб одеть тепло сыночков,
Не хватает двух носочков.
Сколько же в семье сынков,
Если в доме шесть носков?
(Четыре)
Нашёл пять ягодок в траве
И съел одну, осталось…
(Четыре)
Горело пять свечей
Четыре задул Елисей
Сколько свечей осталось?
(Четыре, одна сгорела)
Загадки про цифру 5
Пять котят весь день играли,
Весело клубок катали.
Если два перевернуть
И внимательно взглянуть,
Так и сяк взглянуть опять,
То увидим цифру…
(Пять)
Отгадайте-ка, друзья,
Что за цифра буду я?
Ручку вправо повернула,
Ножку круто изогнула?
(Пять)
Эти счёты всегда рядом,
Загибать их только надо.
Пальчики легко считать,
На руке их ровно…
(Пять)
Сколько пальцев на руке
И копеек в пятачке,
У морской звезды лучей,
Клювов у пяти грачей,
Лопастей у листьев клена
И углов у бастиона,
Про все это рассказать
Нам поможет цифра…
(Пять)
Младшая сестренка Света
Любит пальчики считать!
Ежедневно их считает,
Каждый день выходит…
(Пять)
В школе надо не лениться:
Рисовать, писать, учиться,
На уроках отвечать
И в дневник поставят…
(Пять)
Загадки про цифру 6
Появились у скворцов
Шесть хорошеньких птенцов.
Отгадайте-ка, ребятки,
Что за цифра-акробатка?
Если на голову встанет,
Ровно на три больше станет.
(Шесть)
Если навесной замок
Вверх поднимет хоботок,
То тогда увидим здесь
Не замок, а цифру…
(Шесть)
Циферка, как бегемотик,
Круглый у неё животик,
Шейку ловко изгибает,
За пятёркою ступает.
(Шесть)
Как-то раз соседу Толе
Довелось на ламу сесть,
И у Толи вместе с ламой
Ножек сразу стало…
(Шесть)
Яблоки в саду поспели.
Мы отведать их успели.
Три румяных, наливных,
Три с кислинкой. Сколько их?
(Шесть)
Сколько букв есть у дракона
И нулей у миллиона,
Разных шахматных фигур,
Крыльев у трех белых кур,
Ног у майского жука
И сторон у сундука.
Коль не можем сами счесть,
Нам подскажет цифра…
(Шесть)
Сколько концов
У трех огурцов?
(Шесть)
Загадки про цифру 7
Семь трудолюбивых пчёлок
Прилетели к нам в поселок.
На косу она похожа,
Но косить траву не может-
Не наточена совсем
И не косит цифра
(Семь)
Она похожа на топор,
Но не наколет дров во двор.
Как коса, но не совсем,
Просто это цифра…
(Семь)
Есть пословица у нас
И она известна всем —
Отрезаешь только раз,
А отмерить надо ..
(Семь)
Сколько в радуге цветов,
Дней в неделе у китов.
Гномиков у Белоснежки,
Братьев-близнецов у пешки,
Нот, что знают даже дети,
И всего чудес на свете,
Разобраться с этим всем
Нам поможет цифра…
(Семь)
Совушки в лесу сидели
Вшестером на ветках ели.
Прилетела к ним подружка
Длиннохвостая кукушка.
Им не колются иголки,
Сколько птиц сидит на елке?
(Семь)
Загадки про цифру 8
Восемь маленьких мышат
Скушать вкусный сыр спешат.
Два кружка соединили,
Что за цифру получили?
(Восемь)
Два кольца, но без конца,
В середине нет гвоздя.
Если я перевернусь,
То совсем не изменюсь.
Узнавай скорей меня,
Так какая цифра я?
(Восемь)
Два кружочка рядом встали —
Что за дивные очки?
Поверни хоть вверх ногами,
Одинаковы они!
(Восемь)
Цифра с виду как игрушка —
Неваляшка-погремушка.
Не удариться ей о земь.
Всем понятно — это…
(Восемь)
Цифра есть у нас с секретом.
И зимой, и жарким летом
Различишь едва-едва,
Где в живот, где голова.
(Восемь)
У этого цветка
Четыре лепестка.
А сколько лепестков
У двух таких цветков?
(Восемь)
По траве бежал котенок,
А за ним бежал щенок,
Кто, ребята, сосчитает,
Сколько там бежало ног?
(Восемь)
Загадки про цифру 9
Девять мартышек на пальме сидят,
Пальцы считают, бананы едят.
Это цифра акробатка
А зовут её —…
(Девятка)
Цифра эта так хитра,
Ты её переверни,
И начнутся чудеса —
Цифру шесть увидишь ты!
(Девять)
Вот так цифра, посмотри,
У нее секрет свой есть:
Листик с ней переверни,
Превратится цифра в шесть!
(Девять)
Цифра эта старше восьмерки
И немного младше десятки.
Это сумма шестерки и тройки,
Отгадаешь такую загадку?
(Девять)
Я цифра-фокус и сюрприз
Люблю держаться за карниз.
А если я перевернусь,
То цифрой шесть вмиг окажусь.
(Девять)
Загадки про цифру 0
Плохой у паука улов —
Ноль мух попалось и жуков.
Он похож на букву О,
Он не значит ничего.
Но любую цифру враз
Увеличит в десять раз!
(Ноль)
Не похож я на пятак,
Не похож на рублик.
Круглый я, да не дурак,
С дыркой, но не бублик.
(Ноль)
Сколько лет в яйце цыпленку,
Сколько крыльев у котенка,
Сколько в алфавите цифр,
Сколько гор проглотит тигр,
Сколько мышка весит тонн,
Сколько в стае рыб ворон,
Сколько зайцев съела моль,
Знает только цифра…
(Ноль)
Тигр огромный в клетке жил,
И по свободе он тужил.
Как-то тигр открыл замок
И пустился наутек.
Отменяется гастроль,
Стало в клетке тигров…
(Ноль)
Загадки с ответом «цифры»
Проживают в умной книжке
Хитроумные братишки.
Десять их, но братья эти
Сосчитают все на свете.
(Цифры)
Все на свете мы считаем,
Складываем, умножаем.
Создаем программы, шифры
Девять знаков — это…
(Цифры)
Восемнадцать, тридцать шесть —
В этих числах знаки есть.
Каждый ребенок должен их знать,
Чтобы легко научиться считать.
(Цифры)
Вернуться в раздел Загадки для детей.
Числовые задачи с решениями
Задача 1 :
Сумма пяти чисел, умноженных на 8, равна 48. Найдите число.
Решение:
Пусть число будет «х».
(5x + 8) — 8 = 48 — 8
5x = 40
Разделите обе части на 5.
5x/5 = 40/50005
Задача 2 :
Число состоит из трех цифр, из которых средняя цифра равна нулю, а сумма остальных цифр равна 9. Число, полученное путем перестановки первой и третьей цифр, больше исходного числа на 297. , Найдите число.
Решение:
Пусть «x0y» будет требуемым трехзначным числом. (Согласно приведенной информации, средняя цифра равна нулю)
«Сумма остальных цифр равна 9» —-> x + y = 9 ——(1)
«Поменять местами первую и третью цифры» ———> y0x
Из информации, указанной в вопросе, мы можем получить
y0x — x0y = 297
(100y + x) — (100x + y) = 297
100y + x — 100x -y = 297
-99x + 99y = 297
-x + y = 3 ———(2)
Решение (1) & (2), мы получаем x = 3 и y = 6
Итак,
x0y = 306
Итак, искомое число равно 306.
Задача 3 :
Из двух чисел 1/5 большего равно 1/3 меньшего, а их сумма равна 16. Найдите числа.
Решение:
Пусть «x» и «y» будут такими двумя требуемыми числами, что
x > y.
Из точки «1/5 большей части равна 1/3 меньшей» имеем
(1/5)x = (1/3)y
3x = 5y
3x — 5 y = 0 ———(1)
Из точки «их сумма равна 16» имеем
x + y = 16 ———-(1)
Решая (1) и (2), получаем x = 10 и y = 6.
Итак, два числа 10 и 6.
Задача 4:
Число от 10 до 100 в пять раз больше суммы своих цифр. Если к нему добавить 9, цифры меняются местами. Найдите число.
Решение:
Пусть «xy» будет искомым числом от 10 до 100. (Двузначное число)
«Число от 10 до 100 в пять раз больше суммы своих цифр»
Из приведенной выше информации имеем
xy = 5(x+y)
10x + y = 5x + 5y
5x — 4y = 0 ——-(1)
«Если 9
Из приведенной выше информации имеем
xy + 9 = yx
10x + y + 9 = 10y + x
9x — 9y — 9y = -9
= -1 ———(2)
Решая (1) и (2), получаем x = 4 и y = 5.
Итак, искомое число равно 45.
Задача 5 :
Одно число в три раза больше другого на 2. Если меньшее число в 4 раза больше большего на 5, найдите числа.
Решение:
Пусть «x» и «y» будут двумя числами такими, что x > y
Дано: одно число больше, чем в три раза, другое число на 2
Итак, мы имеем x = 3y + 2 ———(1)
Дано : меньшее число в 4 раза больше большего в 5
Итак, имеем 4y = x + 5 ———(2)
Подключение (1) В (2) мы получаем
4y = 3y + 2 + 5
4y = 3y + 7
4y = 3y + 7
y = 7
Подключение y = 7 дюймов (1 (1 ), получаем x = 3(7) + 2
Следовательно, x = 23
Итак, два числа 23 и 7.
Задача 6 :
цифры. Число, образованное перестановкой цифр, на 18 меньше заданного числа. Найдите заданное число.
Решение:
Пусть «xy» будет требуемым двузначным числом.
Дано: Двузначное число в 7 раз больше суммы своих цифр.
Итак, мы имеем
xy = 7 (x + y)
10x + y = 7x + 7y
10x + y = 7x + 7y
3x — 6y = 0
x — 2y = 0 — ——(1)
Дано: Число, полученное путем перестановки цифр, на 18 меньше заданного числа
Итак, мы имеем
xy — yx = 18
(10x + y) — (10y + x) = 18
10x + y — 10y — x = 18
9x — 9y = 18
x — y = 2 ———(2)
Решая (1) и (2), получаем x = 4 и y = 2
xy = 42
Итак, искомое число равно 42. 296 дает остаток 75, найдите остаток при делении этого числа на 37.
Решение:
Пусть число будет ‘x’
Тогда x = 296k + 75, где «k» — это частное от деления «x» на «296». В этой форме мы рассматриваем число 75 как остаток при делении числа x на 296.
Мы хотим найти остаток при делении числа «x» на 37. Для этого нам нужно иметь 37 при делении числа x на 296. место, где у нас есть 296 в приведенном выше уравнении.
Таким образом, мы можем записать 296 как 37 умножить на 8 и 75 как 37 умножить на 2 плюс 1.
Это показано ниже.
x = 37 × 8k + 37 × 2 + 1
x = 37(8k + 2) + 1
Таким образом, остаток равен 1 при делении числа x на 37.
Задача 8 :
Найдите наименьшее число, которое при делении на 35 дает в остатке 25, при делении на 45 дает в остатке 35, а при делении на 55 дает в остатке 45.
каждого делителя и соответствующего остатка, мы должны найти разницу.
35 — 25 = 10
45 — 35 = 10
55 — 45 = 10
Мы получаем разницу 10 (для всех делителей и соответствующих остальных)
Теперь мы должны найти Л.С. 35,45,55) и вычесть разницу из L.C.M.
L.C.M of (35, 45, 55) = 3465
Таким образом, требуемое наименьшее число равно
= 3465 — 10
= 3455
Помимо математики, указанной выше , пожалуйста, используйте наш пользовательский поиск Google здесь.
Пожалуйста, отправьте ваш отзыв на [email protected]
Мы всегда ценим ваши отзывы.
©Все права защищены. onlinemath5all.com
Изучите логику для задач «Найди число»
Purplemath
Словесные задачи «Числа» обычно довольно надуманы, но они также довольно стандартны, поэтому вам следует научиться решать их. В конце концов, суть этих задач не в их отношении к «реальной жизни», а в вашей способности извлечь математику из английского языка.
Эти упражнения — отличный способ размять свои умственные мышцы, использовать то, что вы уже знаете, применить свою логику (и здравый смысл) и быстро найти решение.
Содержание продолжается ниже
MathHelp.com
Словесные задачи по алгебре
Какой пример решения словесной задачи «число»?
- Сумма двух последовательных целых чисел равна 15. Найдите числа.
Здесь мне дали много информации.
- Я складываю (то есть суммирую) две вещи
- это числа (например, −4,628 и 17 / 32 )
- числа являются целыми числами (например, −3 и 6)
- второе число больше первого на 1
- результатом сложения будет 15
Откуда мне знать, что второе число будет больше первого на 1? Потому что два целых числа «последовательны», что означает «одно сразу за другим, не пропуская ничего между ними».
(Примерами последовательных целых чисел могут быть −12 и −11, 1 и 2 и 9.9 и 100.)
«Целые числа» — это число ноль, целые числа и отрицательные значения целых чисел. При переходе от одного целого числа к следующему последовательному целому я поднимусь на одну единицу.
Мне нужно выяснить, какие два числа я добавляю. Второе число определяется через первое число, поэтому я выберу переменную для обозначения этого числа, которое мне еще неизвестно:
1-е число: n
Второе число на единицу больше первого. во-первых, поэтому мое выражение для второго числа:
2-е число: n + 1
Я знаю, что я должен сложить эти два числа, и что в результате будет (другими словами, я должен установить его равным) 15. Это, наряду с мои навыки перевода позволяют мне составить уравнение, являющееся алгебраическим эквивалентом «(это число), добавленное к (следующему числу), равно (пятнадцать)»:
n + ( n + 1) = 15
Это линейное уравнение, которое я могу решить:
n + ( п + 1) = 15
2 н + 1 = 15
2 n = 14
n = 7
Упражнение не спрашивало меня о значении переменной n ; он запросил идентичность двух номеров.
Так что мой ответ не « n = 7″; фактический ответ, принимая во внимание и второе число, таков:
Цифры 7 и 8.
Обычно не требуется, чтобы вы записывали свой ответ таким образом; иногда очень минимальная «7, 8» считается приемлемой формой. Но упражнение задавало мне полными предложениями вопрос о двух числах; Я чувствую, что это хорошая форма, чтобы ответить на этот вопрос в форме полного предложения.
Какой пример поиска последовательных четных/нечетных чисел?
- Произведение двух последовательных отрицательных четных целых чисел равно 24. Найдите эти числа.
Я начну с извлечения информации, которую они мне дали.
- Я умножаю (то есть нахожу произведение) двух вещей
- эти две вещи — числа
- эти два числа равны
- эти два числа являются целыми числами
- эти два числа отрицательные
- одно число на 2 больше другого
- при умножении получится 24
Откуда мне знать, что одно число будет на 2 больше другого? Потому что эти числа являются последовательными четными целыми числами; «последовательная» часть означает «один сразу после другого», а «четная» часть означает, что числа разделены двумя единицами.
(Примерами последовательных четных целых чисел являются 10 и 12, −14 и −16, а также 0 и 2.)
Второе число определяется через первое число, поэтому я выберу переменную для первого числа. Тогда второе число будет на две единицы больше этого.
1-й номер: №
2-е число: n + 2
Когда я умножаю эти два числа, я должен получить 24. Это дает мне уравнение:
( n )( n + 2) = 24
Вот квадратное уравнение, которое я могу решить:
( n ) ( N + 2) = 24
N 2 + 2 N = 24
N 2 + 2 N – 240340 – 240340 – 240340 – 240340 – 240340 – 240340 – 240340 – 240340 – 240340 № 2 + 2
N ( n + 6)( n — 4) = 0
Очевидно, что это уравнение имеет два решения: n = −6 и n = 4.
Поскольку числа, которые я ищу, отрицательны, я можно игнорировать значение решения «4» и вместо этого использовать решение n = −6.
Тогда следующее число, которое больше первого на 2, должно быть n + 2 = -4, и мой ответ:
Числа -6 и -4.
В приведенном выше упражнении каждый из ответов 4 и n = −6 был одним из решений уравнения; другое решение уравнения имело знак, противоположный другому ответу на упражнение.
Не думайте, что вы можете использовать оба решения, если просто измените знаки на то, что вам нравится. Хотя это часто «работает», это не всегда работает , и это обязательно разозлит вашего учителя. Вместо этого отбрасывайте неверные результаты и правильно решайте правильные.
- Удвоенное большее из двух чисел в три раза больше меньшего в пять раз, а сумма четырехкратного большего и трехкратного меньшего равна 71. Что это за числа?
Смысл подобных упражнений в том, чтобы дать мне возможность попрактиковаться в развертывании и раскручивании этих слов и превращении слов в алгебраические выражения и уравнения.
Дело в решении, а не в относительной «реальности» проблемы. Тем не менее, как мне это решить? Лучший первый шаг — начать маркировку.
Мне нужно найти два числа, и на этот раз они не дали мне никакой связи между ними, например, «два последовательных четных целых числа». Поскольку ни одно число не определяется другим, мне понадобятся две буквы для обозначения двух неизвестных. Мне нужно не забыть пометить переменные их определениями.
большее число: x
меньшее число: y
Теперь я могу создавать выражения, а затем уравнение для первого отношения, которое они мне дают:
в два раза больше: 2 x
три больше, чем в пять раз меньше: 5 y + 3
отношение между («есть»): 2 x = 5 y + 3
А теперь другое отношение, которое мне дали:
в четыре раза больше: 4 x
в три раза меньше: 3 y
отношение между («сумма»): 4 x + 3 y = 71
Теперь у меня есть два уравнения с двумя переменными:
2 x = 5 y + 3
4 х + 3 у = 71
Я решу, скажем, первое уравнение для х =:
х = (5/2) у + (30/05)9
Затем я подставлю правую часть этого уравнения во второе уравнение вместо « x »:
4[ (5/2) у + (3/2) ] + 3 у = 71
10 у + 6 + 3 у = 71
13 у + 6 = 71
13 y = 65
y = 65/13 = 5
Теперь, когда у меня есть значение для y , я могу выполнить обратное решение для x :
x = (50339 x =) у + (3/2)
х = (5/2)(5) + (3/2)
х = (25/2) + (3/2)
x = 28/2 = 14
Как всегда, мне нужно не забыть ответить на вопрос, который на самом деле был задан.
Решение здесь не « x = 14″, а следующее предложение:
Большее число равно 14, а меньшее число равно 5.
Каковы шаги для решения «числовых» словесных задач?
Шаги для решения задач с числами следующие:
- Прочтите упражнение один раз; не пытайтесь начать решать его, прежде чем вы даже знаете, что он говорит.
- Выясните, что вы знаете (например, вы складываете или умножаете?).
- Выясните, чего вы не знаете; это, вероятно, будут значения чисел.
- Выберите одну или несколько полезных переменных для неизвестных, которые вам нужно найти.
- Используйте переменные и известную информацию для создания выражений.
- Используйте эти выражения и известную информацию для создания одного или нескольких уравнений.
- Решите уравнение(я) относительно неизвестного(ых).
- Проверьте свое определение (я) для своей переменной (переменных).
