 2+n-72)=1/(n+9)
2+n-72)=1/(n+9)Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Решено
В классе 27 детей, из них 12 ходят на вокал, 19 на танцы, 5 человек участвуют в обоих кружках. Сколько детей этого класса не заняты в кружках
Сколько детей этого класса не заняты в кружках
Найдите значение выражение 4\25+15\4 Напишите решение пожалуйста срочно надо
Решено
Кто сможет решить?
Решено
Найдите точку максимума функции y = (2x –3) cos x – 2sin x + 5 принадлежащую промежутку (0;П/2)
Определите трудоемкость единицы продукции по плану и фактически, а также рост производительности труда на основе следующих данных: 1. трудоемкость…
Если Log 4 (x) = 12, то чему равно log 2 (x / 4)?
Цитата страницы Начать эссе значок-вопрос Спросите репетитораНачать бесплатную пробную версию
Скачать PDF PDF Цитата страницы Цитировать Поделиться ссылкой ДелитьсяСсылайтесь на эту страницу следующим образом:
«Если Log 4 (x) = 12, то чему равно log 2 (x / 4)?» eNotes Editorial , 11 февраля 2011 г.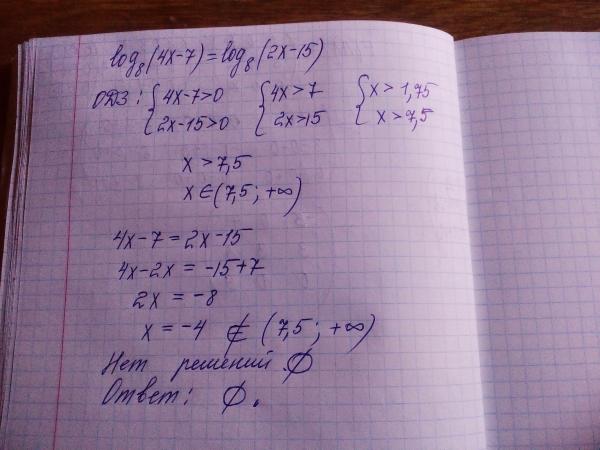 2 = 2*log2 2 = 2
2 = 2*log2 2 = 2
==> log2 (x/4) = log2 x — 2………….(1)
Теперь нам дано, что log4 x = 12
Перепишем.
==> log4 x = log2 x / log2 4 = log2 x/ 2 = (1/2)log2 x= 12
==> log2 x = 2*12 = 24
==> log2 x/4 = 24 -2 = 22
Тогда значения log2 (x/4) = 22
Утверждено редакцией eNotes
Математика
Последний ответ опубликован 07 сентября 2010 г. в 12:47:25.
Что означают буквы R, Q, N и Z в математике?
14 ответов воспитателя
математика
Последний ответ опубликован 09 октября 2017 г. в 00:54:39
Добавьте 1 плюс 2 плюс 3 плюс 4. . . вплоть до 100.
3 Ответы воспитателя
Математика
Последний ответ опубликован 3 октября 2011 г.
Этот предел представляет собой производную некоторой функции f при некотором числе a. укажите это f и a. lim h->0 [(4-й корень из)(16+h)-2]/h a=? ф=?
1 Ответ учителя
Математика
Последний ответ опубликован 17 августа 2010 г. в 8:49:11.
Учитывая f(x) и g(x), найдите (туман)(X) и (gof)(x) f(x) = 2x g(x) = x+3 9[(log_{2} x) + 4] = 32 и Найдите значение x
- Математические сомнения
- Проблемы
- Логарифмы
$x$ — это переменная, и сумма логарифма $x$ по основанию $2$ и числа $4$ становится показателем степени литерала $x$. Полная функциональная стоимость равна $32$. Чтобы найти значение $x$, можно решить экспоненциально-логарифмическое уравнение.
Шаг: 1
Выразите это уравнение экспоненциальной формы в логарифмической форме, используя фундаментальное соотношение между логарифмической и экспоненциальной функциями. 95 -\large \log_{2} x \normalsize = 4$
95 -\large \log_{2} x \normalsize = 4$
Шаг: 2
Используйте правило степени логарифмирования, чтобы записать первый логарифмический член в простой форме.
$\подразумевает 5 \times \large \log_{x} \normalsize 2 -\large \log_{2} x \normalsize = 4$
$\ подразумевает 5 \large \log_{x} \normalsize 2 -\ большой \log_{2} x \normalsize = 4$
Запомните это логарифмическое уравнение, и оно решается двумя разными способами, чтобы получить значение $x$. Используйте изменение основного правила логарифмирования, чтобы преобразовать либо $\large \log_{x} \normalsize 2$ в $\large \log_{2} x$, либо наоборот.
Метод: 1
$\ подразумевает 5 \large \log_{x} \normalsize 2 -\large \log_{2} x \normalsize = 4$
В этом методе выражение $\large \log_{x} \normalsize 2$ в обратной форме с использованием правила изменения основания логарифмов.
$\подразумевается 5 \times \large \dfrac{1}{\log_{2} x} -\log_{2} x \normalsize = 4$
$\подразумевается \large \dfrac{\normalsize 5}{ \log_{2} x} -\log_{2} x \normalsize = 4$
Шаг: 3
Возьмем $\large \log_{2} x \normalsize = y$ и преобразуем это логарифмическое уравнение в $ у $.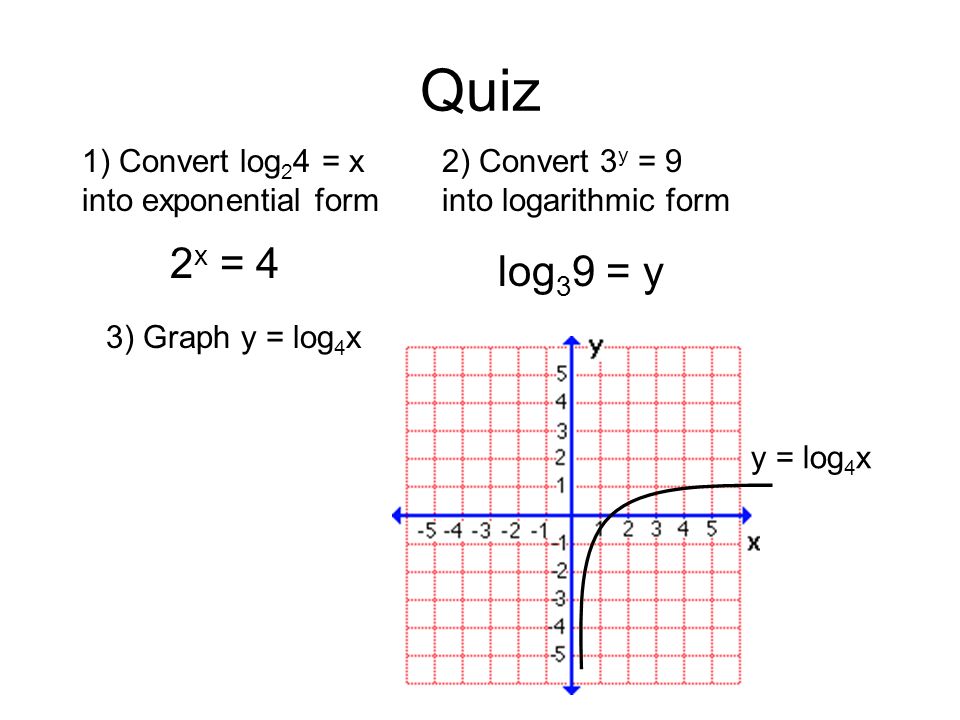

 06.17
06.17