Применение векторов к решению задач (продолжение) 8 класс онлайн-подготовка на Ростелеком Лицей
Теорема о двух неколлинеарных векторах
В предыдущих уроках мы неоднократно решали следующую задачу: даны два неколлинеарных вектора, через которые в многоугольнике нужно выразить некоторые другие векторы. Выполним обобщение такого типа задач.
Теорема
Заданы векторы и . Векторы неколлинеарны. Доказать, что любой третий вектор однозначно выражается через векторы и , то есть найдутся такие числа х и у, что: .
Если данная теорема будет доказана, то в некотором смысле можно сказать, что, зная два неколлинеарных вектора, мы владеем всеми остальными векторами на плоскости.
Доказательство:
Из точки С, конца вектора , проведем прямые, параллельные векторам и . Получим точки А, В – пересечения построенных прямых с продолжениями векторов. Концы векторов обозначим за F и К соответственно (см. Рис. 1). Воспользуемся правилом треугольника и выразим вектор :
Вектор коллинеарен вектору , так как они
Рис. 1
1
принадлежат одной прямой согласно построению. Отсюда найдется такое число х, которое в произведении с вектором даст вектор : . С другой стороны, вектор равен вектору по построению, вектор коллинеарен вектору , значит, аналогично сказанному ранее, .
Таким образом, , то есть вектор является линейной комбинацией неколлинеарных векторов и . Кроме того, нашлась такая пара чисел х и у, с помощью которых любой вектор на плоскости можно выразить через два заданных неколлинеарных вектора.
Докажем, что такая пара единственная. Предположим противное: пусть существует такая пара чисел х1 и у1, что . Мы предположили, что есть еще одна линейная комбинация тех же двух неколлинеарных векторов для того же третьего вектора. Выполним вычитание полученных выражений:
Слева в выражении стоит нулевой вектор, справа – линейная комбинация двух неколлинеарных векторов, которые друг через друга не выражаются, таким образом, чтобы выполнялось равенство, коэффициенты при векторах в правой части должны быть нулевыми, то есть .
Вывод: разложение вектора по двум неколлинеарным векторам однозначно.
Задача о трапеции
Пример 1 – задача 790: докажите, что отрезок, соединяющий середины диагоналей трапеции, параллелен основаниям и равен их полуразности (см. Рис. 2).
Доказать: ; (при условии, что AD – большее основание, обозначим его за b, а ВС – меньшее основание, обозначим его за а).
Рис. 2
Доказательство:
Введем вектор . Выразим его через другие векторы, пользуясь правилом многоугольника. Напомним, что вектор , :
С другой стороны:
Выполним сложение полученных выражений:
Векторы очевидно противоположны, и их сумма составляет нулевой вектор, аналогично и векторы сокращаются. Получаем:
Поделим обе части выражения на два:
Из полученного равенства следует, что отрезок, соединяющий середины диагоналей трапеции, равен полуразности ее оснований. Кроме того, из равенства векторов в правой и левой частях следует, что они коллинеарны между собой, а также коллинеарны векторам и , таким образом, отрезок, соединяющий середины диагоналей трапеции, параллелен ее основаниям, что и требовалось доказать.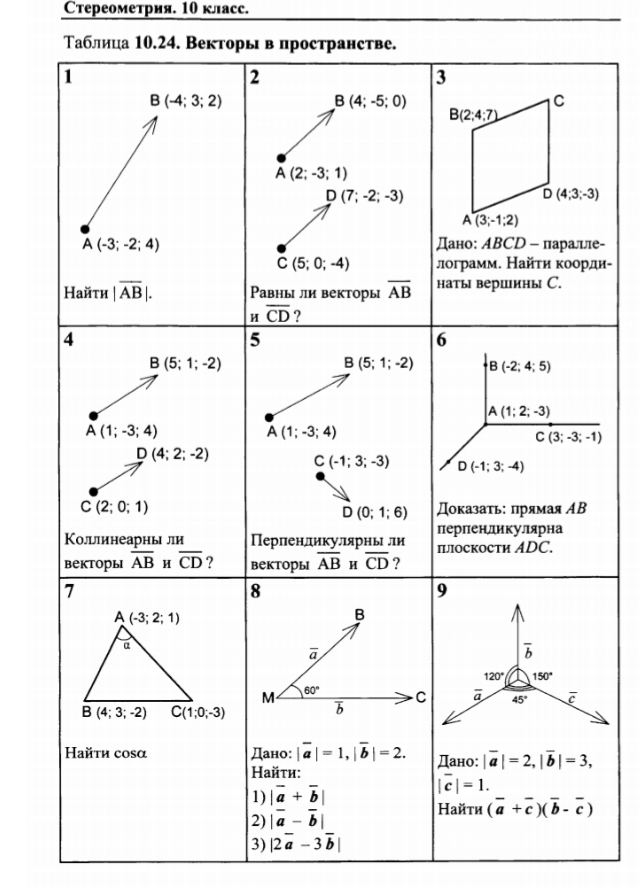
Обратим внимание, что несложно доказывается тот факт, что отрезок MN принадлежит средней линии трапеции, и данным фактом можно пользоваться при решении различных задач (см. Рис. 3). Напомним, что отрезок средней линии ММ1 – средняя линия треугольника , отсюда . Аналогично . Таким образом, можно найти длину отрезка, не пользуясь
Рис. 3
векторами, для этого следует вычесть из длины средней линии трапеции (она равна полусумме оснований) длины только что найденных отрезков:
Итак, мы рассмотрели применение векторов при решении различных задач, доказали некоторые свойства фигур и решили наиболее распространенные типы задач.
Список литературы
- Александров А.Д. и др. Геометрия, 8 класс. – М.: Просвещение, 2006.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В. Геометрия, 8 класс. – М.: Просвещение, 2011.
- Мерзляк А.Г., Полонский В.Б., Якир С.М. Геометрия, 8 класс. – М.: ВЕНТАНА-ГРАФ, 2009.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Terver.ru (Источник).
- Cleverstudents.ru (Источник).
Домашнее задание
1. Задание 1: точки M и N – середины диагоналей АС и BD четырехугольника ABCD. Докажите, что
2. Задание 2: дан произвольный треугольник . Докажите, что существует треугольник, стороны которого соответственно параллельны и равны медианам треугольника
3. Задание 3: докажите, что отрезки, соединяющие середины противоположных сторон произвольного четырехугольника, точкой пересечения делятся пополам.
Применение векторов к решению задач
Урок 9. Геометрия 9 класс ФГОС
Этот урок посвящён решению геометрических задач, в которых применяются все знания о векторах. Материал данного урока научит учащихся решать задачи более рациональным способом, применяя при этом векторы.
Конспект урока «Применение векторов к решению задач»
Сегодня
мы продолжим работать с векторами, поэтому повторим основные сведения о них.
Отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом, называется направленным отрезком или вектором.
На рисунках вектор изображают в виде отрезка со стрелкой, показывающей направление вектора.
Обозначают вектор двумя заглавными буквами со стрелкой над ними. При этом первая буква обозначает начало вектора, а вторая — конец.
Также вектор можно называть одной строчной латинской буквой со стрелкой над ней.
Любую точку плоскости также считают вектором и называют нулевым вектором.
Длиной ненулевого вектора называется длина отрезка АB.
Длина любого нулевого вектора равна 0.
Мы с вами рассматривали особый случай расположения векторов относительно друг друга.
Если
ненулевые векторы лежат на одной прямой либо на параллельных прямых, то они
являются коллинеарными. Нулевой вектор считается коллинеарным
любому вектору.
Среди коллинеарных векторов выделяют два случая: сонаправленные векторы (они имеют одинаковое направление) и противоположно направленные векторы (они имеют противоположные направления). Нулевой вектор считается сонаправленным любому вектору.
Равными называют векторы, если их длины равны и они сонаправлены.
Если же длины векторов равны, но они противоположно направлены, то такие векторы называют противоположными.
Так же вы уже владеете следующими операциями над векторами: сложением, вычитанием и умножением вектора на число.
Для сложения двух векторов существует два правила: правило треугольника и правило параллелограмма. А вот складывать несколько векторов нужно по правилу многоугольника.
Для построения вектора разности мы выделили два способа.
Можно
от некоторой точки отложить векторы и
. При этом вектором их разности будет вектор, направленный от конца
вектора-вычитаемого к концу вектора-уменьшаемого.
При этом вектором их разности будет вектор, направленный от конца
вектора-вычитаемого к концу вектора-уменьшаемого.
Так же, пользуясь теоремой о разности двух векторов, разность векторов и можно представить в виде суммы вектора и вектора .
Тогда, последовательно друг за другом отложив векторы и , по правилу треугольника получим вектор их суммы, который в свою очередь равен вектору разности .
Последнее действие, которое мы рассмотрели — это умножение вектора на число.
Произведением ненулевого вектора на число k называется такой вектор , длина которого равна произведению модуля числа k и длины данного вектора . Причем векторы сонаправлены, если k больше либо равно 0, и противоположно направлены, если k меньше 0.
Стоит
обратить внимание на то, что в каждом из этих случаев векторы коллинеарны, а
значит вектор и
вектор произведения вектора на
число k всегда будут
коллинеарны.
Произведение ненулевого вектора на ноль, а также произведение на число k равны .
Владея таким большим багажом знаний о векторах, будет естественным применить его при решении различных задач.
Но перед тем как приступить к их решению, выполним задание.
параллелограмм,. Выразить и через и .
Обратите внимание, по правилу параллелограмма сумма векторов и равна вектору .
.
Теперь рассмотрим прямоугольник, . Выразить и через и .
.
Рассмотрим второй способ. По правилу треугольника вектор равен сумме векторов и .
Вектор сонаправлен вектору , и его длина . Ну, а вектор является противоположным вектору , то есть равен .
Тогда вектор равен сумме и , и равен разности .
Видим,
что, выражая векторы по различным правилам, в итоге мы получаем одинаковый
результат.
Теперь приступим к решению задач.
Задача. В треугольнике проведена медиана .
Доказать: .
Доказательство
Что и требовалось доказать.
В следующей задаче докажем теорему о средней линии треугольника.
Задача. Доказать, что средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
Доказательство
Что и требовалось доказать.
Задача. Доказать, что прямая, проведённая через середины оснований трапеции,
проходит через точку пересечения продолжений боковых сторон.
Доказать: .
Доказательство
и коллинеарны
Что и требовалось доказать.
Подведём
итоги урока.
Сегодня, обобщив многочисленные знания о векторах, мы с вами применили их при решении геометрических задач.
Предыдущий урок 8 Произведение вектора на число
Следующий урок 10 Средняя линия трапеции
Получите полный комплект видеоуроков, тестов и презентаций Геометрия 9 класс ФГОС
Чтобы добавить комментарий зарегистрируйтесь или войдите на сайт
Решение задач по теме Векторы на плоскости 9 класс презентация, доклад, проект
Презентация к уроку геометрии в 9 классе
«Решение задач по теме «Векторы на плоскости»
Материал подготовила Белякова Людмила Калениковна, учитель математики МБОУ «Веревская средняя общеобразовательная школа» Гатчинского района Ленинградской области
Тема урока : «Решение задач по теме «Векторы на плоскости».
Цель урока: Обобщить знания учащихся по теме, совершенствовать навыки в решении задач.
Задачи урока:
Повторить определение вектора, понятия равных, противоположных, коллинеарных векторов.
Развивать умения в выполнении действий над векторами.
Формирование логического мышления, умений в отыскании способа решения задач.
Развитие умений аргументировать, доказывать правильность выполнения задания.
Устная работа с использованием чертежа
Дайте определение вектора.
Назовите начало и конец указанного вектора.
Какие векторы называют коллинеарными?
Назовите коллинеарные векторы.
Какие векторы называют равными?
Назовите равные векторы.
А
В
С
Д
М
К
Р
Т
Работа в тетради по повторению.
Постройте в тетради сумму данных векторов двумя способами.
Постройте в тетради разность данных векторов двумя способами.
К
Р
Т
Д
(Т)
Построение разности векторов.
КР — ТД
К
Р
Т
Д
2 способ
КР + (-ТД)
К
Р (Т)
Д
Устная работа по готовому чертежу
АВСД – параллелограмм.
Укажите равные векторы. Назовите вектор, равный ВА, АД.
Укажите противоположные векторы.
Назовите вектор, равный – ВО, — АО.
Чему равна сумма противоположных векторов?
А
В
С
Д
О
О
Устная работа по готовому чертежу
АВСД – параллелограмм.
Укажите верные равенства и докажите их равенство
1) АО = ОС, ВО = ОД, ВС = АД,
2) АВ + ВО = ОД, ВО + ОС = АД, АО – АВ = ОВ
А
В
С
Д
О
О
Устная работа по готовому чертежу
Задача
А
В
С
М
N
К
М, N и К –середины сторон треугольника АВС.
Назовите вектор, равный
ВN, АК, К N,
2МК, — 2MK, — МК
-2МN, 2МN, — MN
МВ + NС, АМ + КС
АК-АМ, КN- ВN
Устная работа по готовому чертежу
А
В
С
М
К
Р
С помощью векторов
МК и КР выразите векторы:
МР, АС, ВС, АВ, РК, СК.
Задача для самостоятельного решения с последующей проверкой
С помощью векторов ОА и ОД выразите векторы
АД, ДА, АВ, СД, ВД, ДВ, СА, АС.
Запишите полученные равенства.
А
В
С
Д
О
Проверка выполнения работы.
А
В
С
Д
О
АД = — ОА + ОД ДА = — ОД + ОА
АВ = — ОА – ОД СД = ОА + ОД
ВД = 2ОД ДВ = — 2ОД
СА = 2ОА АС = — 2ОА
Задача для самостоятельной работы с последующей проверкой
Известно, что МК = КР = РТ = ТД.
С помощью векторов ОМ и ОД выразите вектор ОТ
М
К
Р
Т
Д
О
Проверка решения задачи
ОТ = ОД + ДТ
ДТ = 0,25ДМ
ДМ = — ОД + ОМ
ДТ = 0,25(- ОД + ОМ)
ОТ = ОД + 0,25( — ОД + ОМ)
ОТ = 0,75ОД + 0,25 ОМ
О
Задача для самостоятельного решения
В трапеции АВСД основание АД больше основания ВС в 2 раза. О – точка пересечения диагоналей трапеции.
С помощью векторов АВ и ВС выразите следующие векторы: АД, АС, СА,ВД, СД, ВО, ОД, СО, ОА
А
В
С
Д
Проверка выполнения работы
АД = 2 ВС,
АС = АВ + ВС
СА = -ВС — АВ
ВД= — АВ + 2ВС
СД = -ВС – АВ + 2 ВС = — АВ + ВС
Треугольники АОВ и ВОС подобны, коэффициент подобия к = 2
Значит, ОД = 2ВО, ВД = 3ВО
Следовательно, ВО = 1/3ВД, т. е. ВО = 1/3 ( -АВ + 2ВС)
е. ВО = 1/3 ( -АВ + 2ВС)
ОД = 2/3 ВД, ОД = 2/3 (-АВ + 2ВС)
Аналогично, СО =1/3 СА, т.е. СО = 1/3(-ВС – АВ)
ОА= 2/3 СА, т. е. ОА = 2/3 (-ВС – АВ)
Самостоятельная работа по вариантам
Точки М и К – середины сторон треугольника АВС.
Пользуясь векторами ОМ и ОК выразите векторы
ОВ, ВК, АМ, АВ. ОВ, СК, ВС, ВА.
1 вариант 2 вариант
А
В
С
О
М
К
А
В
С
О
М
К
Подведение итога урока.
Повторили определение вектора, его обозначение.
Понятия равных векторов, коллинеарных векторов.
Закрепили умения в выполнении действий над векторами – сложение, вычитание, умножение вектора на число.
Рассмотрели решение задач в выражении векторов через данные вектора с помощью изученных действий.
Скачать презентацию
1
Первый слайд презентации: Решение задач по теме «векторы в пространстве»
Изображение слайда
2
Слайд 2
От конца вектора а отложить вектор в, равный вектору в ; Провести вектор из начала вектора а в конец вектора в. ВЫВОД: полученный вектор и будет суммой векторов а и в. ПРАВИЛО ТРЕУГОЛЬНИКА а+в в а а в в а
Изображение слайда
3
Слайд 3
а + в
ПРАВИЛО ПАРАЛЛЕЛОГРАММА
От начала вектора а отложить вектор в, равный вектору в;
На векторах а и в как на сторонах построить параллелограмм ;
Провести из общего начала векторов а и в вектор –диагональ параллелограмма.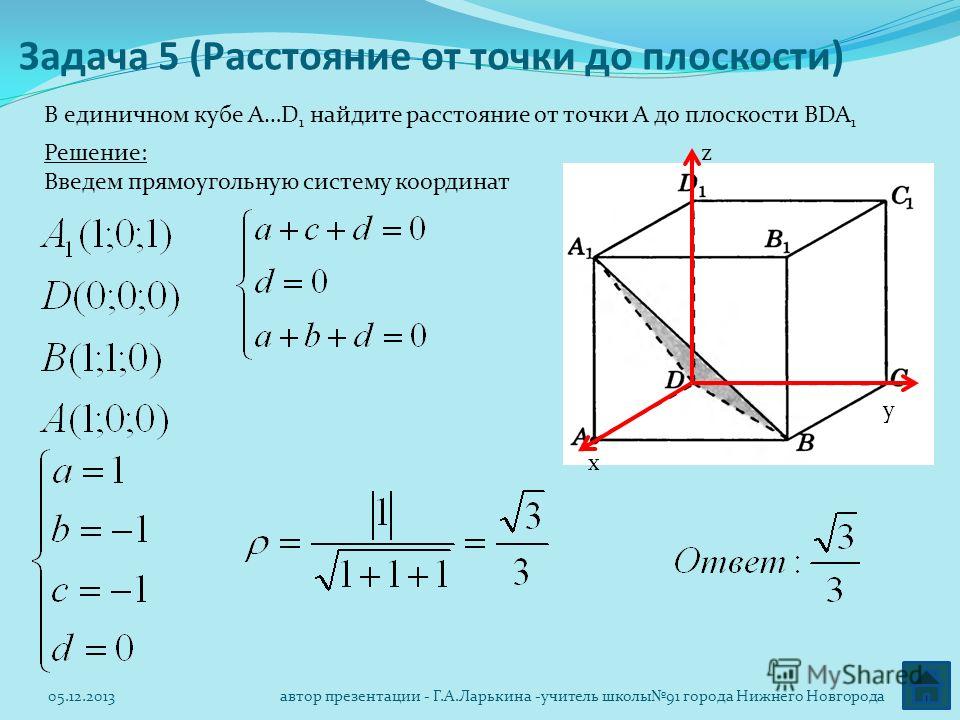
Изображение слайда
4
Слайд 4
ПРАВИЛО МНОГОУГОЛЬНИКА а 1 а 2 а 3 а 4 А 1 А 2 А 3 А 4 А 5 1 ) От конца вектора а 1 отложить вектор а 2, равный вектору а 2; 2) Повторить откладывание векторов столько раз, сколько векторов нужно отложить; 3) Провести вектор из конца вектора а n в начало а. ВЫВОД: полученный вектор в и будет суммой векторов а 1, а 2, а 3,… и а n а 1 а 2 а 3 а 4
Изображение слайда
5
Слайд 5
ЗАКОНЫ СЛОЖЕНИЯ ВЕКТОРОВ Для любых векторов а, в и с справедливы равенства: 1) а + в = в + а — переместительный закон 2) ( а + в ) + с = а + ( в + с ) — сочетательный закон
Изображение слайда
6
Слайд 6
ПЕРЕМЕСТИТЕЛЬНЫЙ ЗАКОН
1. Доказательство: Рассмотрим случай,когда векторы а и в не коллинеарные.
А
В
а
D
в
С
а
в
а + в
ОТ произвольной точки А отложим векторы
АВ = а и А D = в и на этих векторах построим параллелограмм АВС D. По правилу треугольника АС = АВ + А D = а + в.
Аналогично АС= А D + D С = в + а. Отсюда
Следует,что а + в = в + а,
Доказательство: Рассмотрим случай,когда векторы а и в не коллинеарные.
А
В
а
D
в
С
а
в
а + в
ОТ произвольной точки А отложим векторы
АВ = а и А D = в и на этих векторах построим параллелограмм АВС D. По правилу треугольника АС = АВ + А D = а + в.
Аналогично АС= А D + D С = в + а. Отсюда
Следует,что а + в = в + а,
Изображение слайда
7
Слайд 7
СОЧЕТАТЕЛЬНЫЙ ЗАКОН 2. Доказательство : От произвольной точки А отложим вектор АВ = а, а от точки В вектор ВС = в, от точки С вектор С D =с. Применяя правило треугольника, получаем: (а + в ) + с = ( АВ + ВС )+ С D = А C +С D =А D а + ( в + с) = АВ + (ВС + С D)= АВ + ВС = А D. Отсюда следует, что ( а + в ) + с = а + ( в + с). Теорема доказана. . А В а в с С D
Изображение слайда
8
Слайд 8
ВЫЧИТАНИЕ ВЕКТОРОВ а в а- в Разностью векторов а и в называется такой вектор, сумма которого с вектором в равна вектору а а в а в
Изображение слайда
9
Слайд 9
Теорема : Для любых векторов а и в справедливо равенство
а – в = а +( — в ). Доказательство. По определению разности векторов
( а – в ) + в = а Прибавив к обеим частям этого равенства
вектор (-в), получим (а – в ) + в + (-в)= а + (-в),или
(а – в ) +0=(-в), откуда а – в = а + (-в).
а
в
.
В
А
О
-в
а
а -в
Доказательство. По определению разности векторов
( а – в ) + в = а Прибавив к обеим частям этого равенства
вектор (-в), получим (а – в ) + в + (-в)= а + (-в),или
(а – в ) +0=(-в), откуда а – в = а + (-в).
а
в
.
В
А
О
-в
а
а -в
Изображение слайда
10
Слайд 10
Задача 1. Сложить коллинеарные противоположно направленные векторы. а в О а + в .
Изображение слайда
11
Слайд 11
а в Векторы а и в коллинеарные, найти сумму векторов. ПОСТРОЕНИЕ: О С а + в а а в Задача 2. ДАНО:
Изображение слайда
12
Слайд 12
Задача 3. ПОСТРОЕНИЕ:
Дано:
х
у
z
А)
х + y
В)
x +z
C)
z + y
ПОСТРОЕНИЕ:
Дано:
х
у
z
А)
х + y
В)
x +z
C)
z + y
Изображение слайда
13
Слайд 13
Задача 4. ПОСТРОИТЬ а +в +с + d +е ПОСТРОЕНИЕ: Дано: а в с d е а +в +с + d +е а в с d e
Изображение слайда
14
Слайд 14
Задача 5. Дано: Построение: х z y — х -z -y y х — у z — y x -z x x z у z
Изображение слайда
15
Слайд 15
ЗАДАЧА 6 : используя правило треугольника, постройте векторы ОА = а +в ДАНО: ПОСТРОЕНИЕ: а в в ОА а
Изображение слайда
16
Слайд 16
ЗАДАЧА 7: используя правило параллелограмма
постройте векторы ОР =х + у
Х+У= ОР
O
P
х. у
х
у
у
х
у
Изображение слайда
17
Слайд 17
( ) Задача 8. АВ + AD – DC – OD ABCD — прямоугольник А B C D АВ + AD – DC – OD = АС – DC – OD = АС + CD + DO = АО О 3 4 5
Изображение слайда
18
Слайд 18
Задачи 9-10 (решить самостоятельно) : Используя правило треугольника, найдите сумму векторов: а) РМ и МТ, б) СН и НС, в) АВ + 0,г) 0 +СЕ.
Изображение слайда
19
Слайд 19
Задача 10. АВ + ВС = АО + ОР = MN + NR = MK + KM = MK + OM = А S + S С = NM + ML = RP + PR = ZK + KZ = DE + KD = ON = AS = XH = MD = OP = OB = RA = KX = AD = FO =
Изображение слайда
20
Последний слайд презентации: Решение задач по теме «векторы в пространстве»
ИСПОЛЬЗУЕМЫЕ ИСТОЧНИКИ :
1) https://ru. wikipedia.org/wiki/%D0%92%D0%B5%D0%BA%D1%82%D0%BE%D1%80_(%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F)#.D0.9E.D1.82.D0.BD.D0.BE.D1.88.D0.B5.D0.BD.D0.B8.D1.8F_.D0.BC.D0.B5.D0.B6.D0.B4.D1.83_.D0.B2.D0.B5.D0.BA.D1.82.D0.BE.D1.80.D0.B0.D0.BC.D0.B8
2) http://animashki.kak2z.org/category.php?cat=17
3) Геометрия.Учебник для 10-11классов. Атанасян Л.С. и др.
wikipedia.org/wiki/%D0%92%D0%B5%D0%BA%D1%82%D0%BE%D1%80_(%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F)#.D0.9E.D1.82.D0.BD.D0.BE.D1.88.D0.B5.D0.BD.D0.B8.D1.8F_.D0.BC.D0.B5.D0.B6.D0.B4.D1.83_.D0.B2.D0.B5.D0.BA.D1.82.D0.BE.D1.80.D0.B0.D0.BC.D0.B8
2) http://animashki.kak2z.org/category.php?cat=17
3) Геометрия.Учебник для 10-11классов. Атанасян Л.С. и др.
Изображение слайда
Применение векторов при решении задач и доказательстве теорем
Разработал студент группы А-11
Мельников Лев
Содержание
ВВЕДЕНИЕ
1 КРАТКАЯ ИСТОРИЧЕСКАЯ СПРАВКА
2 ОСНОВНЫЕ ПОНЯТИЯ И ТЕОРЕМЫ
2.2. ВЕКТОРЫ
3 КООРДИНАТЫ
4 РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ВЕКТОРОВ И СКАЛЯРНОГО
ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
4.2 ДОКАЗАТЕЛЬСТВО НЕКОТОРЫХ ТЕОРЕМ
4.3 НАХОЖДЕНИЕ РАССТОЯНИЙ И УГЛОВ
5 РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ МЕТОДА КООРДИНАТ
5.2 ЗАДАЧИ НА ПОСТРОЕНИЯ
5.3 ЗАДАЧИ НА ВЫЧИСЛЕНИЯ РАССТОЯНИЙ И УГЛОВ
ЗАКЛЮЧЕНИЕ
СПИСОК ЛИТЕРАТУРЫ
3
4
5
5
7
8
8
9
10
10
12
14
15
ВВЕДЕНИЕ
Учёные всегда стремились упростить себе жизнь – придумывали новые, простые
методы решения, универсальные для множества задач, позволяющие быстро решить
даже самую трудную задачу. Именно таким методом и является векторнокоординатный.
Именно таким методом и является векторнокоординатный.
«Векторный» путь построения геометрии предложил в 1918 году известный
немецкий математик Герман Вейль. Векторы можно использовать как для решения
планиметрических задач, так и для стереометрических.
Векторно-координатный метод решения задач позволяет с лёгкостью решать даже
самые большие и сложные задачи, избегать долгих доказательств теорем. С
помощью векторов можно вычислять расстояния и углы, доказывать теоремы,
строить перпендикулярные и параллельные прямые и отрезки, строить сечения,
доказывать равенство геометрических фигур и многое другое.
В настоящее время векторно-координатный метод используется в алгебре,
геометрии, физике, механике; понятие векторного пространства используется в
теории вероятностей, математической экономике, биологии, лингвистике и т.д.
3
КРАТКАЯ ИСТОРИЧЕСКАЯ
СПРАВКА
Интерес к векторам и векторному исчислению пробудился у математиков в XIX веке
в связи с потребностями механики и физики. Однако истоки исчисления с
Однако истоки исчисления с
направленными отрезками возникли в далеком прошлом. В Древней Греции
пифагорейцы, открыв иррациональные числа, которые нельзя выразить дробями
(например:√2, √5), не решились ввести более широкое толкование числа. Математики
того времени попытались свести вопросы арифметики и алгебры к решению задач
геометрическим путем. Таким образом, было положено начало геометрической
теории отношений Евдокса (408-355 гг. до н.э.), а позднее «геометрической алгебре».
В геометрическом исчислении, изложенном, а труде Евклида «Начала», сложения и
вычитания сводились к сложению и вычитанию отрезков, а умножение — к
построению прямоугольников на отрезках, соответствующих по длине множителям.
Термин «вектор» происходит от латинского слова vector, что означает несущий или
ведущий, влекущий, переносящий
В современной математике раздел, в котором излагается учение о действиях над
векторами, называют векторной алгеброй, так как эти действия имеют много общих
свойств с алгебраическими действиями.
4
ОСНОВНЫЕ ПОНЯТИЯ И
ТЕОРЕМЫ
2.2. ВЕКТОРЫ
Вектор-это отрезок, для которого указано, какой из его концов считается началом, а
какой – концом. Направление вектора на рисунке (от начала к концу) отмечается
стрелкой.(рисунок 1)
Рисунок 1 — Изображение вектора
Любая точка пространства также может считаться вектором. В таком случае
вектор называется нулевым. Начало и конец этого вектора совпадают.
5
ОСНОВНЫЕ ПОНЯТИЯ И
ТЕОРЕМЫ
Рисунок 2 — Изображение правила
треугольника
Рисунок 4 — Изображение правила
многоугольника
Рисунок 3 — Изображение правила
параллелограмма
Рисунок 5 — Изображения правила
параллелепипеда
6
КООРДИНАТЫ
Если через некоторую точку пространства проведены три попарно
перпендикулярные прямые, на каждой из них выбрано направление (оно
обозначается стрелкой) и выбрана единица измерения отрезков, то говорят,
что выбрана прямоугольная система координат в пространстве. Прямые с
выбранными направлениями называются осями координат, а их общая
точка – началом координат. Она обычно обозначается буквой О. Оси
Она обычно обозначается буквой О. Оси
обозначаются так: Ох, Оу, Оz – и имеют названия: «ось абсцисс», «ось
ординат», «ось аппликат». Вся система координат называется Oxyz. Три
плоскости, проходящие через оси координат называются координатными
плоскостями. Точка О разделяет каждую из осей координат на на два
дополнительных луча. Луч, направление которого совпадает с
направлением оси, называется положительной полуосью, а
дополнительный к нему луч – отрицательной полуосью.
7
РЕШЕНИЕ ЗАДАЧ С
ПОМОЩЬЮ ВЕКТОРОВ
4.2 Доказательство некоторых теорем
Пусть точки А, В, С и Р такие, что ОР=mOA+nOB+рОС (OА, ОС и ОВ линейно
независимы).Тогда необходимое и достаточное условие их принадлежности одной
прямой состоит в следующем: m+n+р=1. (рис 7)
Пусть точки А, В, С и Р лежат в одной плоскости, тогда векторы
АР=ОР-ОА, АВ=ОВ-ОА, АС=ОС-ОА будут линейно зависимыми,
следовательно
ОР-ОА=n(OB-OA)+p(OC-OA),
OP=(1- n- p)OA+nOB+pOC. И в силу единственности разложения вектора
OP по векторам ОА, ОВ, ОС получим
m=1- n –p или m+ n+ p=1
Доказательство достаточности:
Рисунок 7 Пусть m+n+p=1, тогда
OP-OA=mOA+nOB+pOC-OA=mOA+nOB+pOC-(m+n+p)*OA=n(OB- Изображение фигуры
OA)+p(OC-OA)
8
Отсюда АР=nAB+pAС и по определению P принадлежит плоскости АВС.
РЕШЕНИЕ ЗАДАЧ С
ПОМОЩЬЮ ВЕКТОРОВ
4.3 Нахождение расстояний и углов
На рёбрах DA,DB,AC тетраэдра DABC взяты соответственно точки L, N, F так, что
DL=1/2DA,DN=1/3DB,AF=1/4AC. В каком отношении плоскость, проходящая через
точки L,N,F делит ребро BC? (рис 8)
Решение:
Пусть М – точка пересечения рассматриваемой плоскости с ребром BC и
DA=a, DB=b, DC=c.
Так как точки M,N,L,F лежат в одной плоскости, причём последние три
точки не лежат на одной прямой, то по формуле
DM=kDL+lDN+(1 – k – l)DF=ka/2+lb/3+(1 – k – l)(3/4a+1/4c).
Рисунок 8 С другой стороны, по формуле (1)
Изображение фигуры
DM=(1-m)b+mc
где m – отношение ВМ:ВС. Так как векторы а,b,с не компланарны, то на основании
утверждения о разложении вектора по трём некомпланарным, мы получим систему:
k/2+(1 – k – l)3/4=0, l/3=1 – m,
(1 – k – l)1/4=m.
9
Отсюда m=2/5 и ВМ:МС=2/3.
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ
МЕТОДА КООРДИНАТ
5.2 Задачи на построения
Вершина В прямоугольного параллелепипеда АВСDA1B1C1D1 с отношением
рёбер AB:DA:AA1=1:2:3 принята за начало прямоугольной системы координат, а
векторы ВА, 1/2ВС и 1/3ВВ1 приняты соответственно за единичные векторы i, j, k.
Построить сечение параллелепипеда плоскостью α , заданной в этой системе
координат уравнением 4x + y — 2z — 2=0. (рис 9)
Рисунок 9 Изображение фигуры
Для построения данного сечения найдём три точки,
принадлежащие плоскости α, но не лежащие на одной
прямой, например, точки пересечения плоскости α с
осями координат. Так, если плоскость α пересекает ось
Вх в точке К, то точка К имеет координаты (к;0;0).
Подставляя эти координаты в уравнение плоскости α
,получим к=1/2. Таким образом, плоскость α пересекает
ось Вх в точке К(1/2;0;0). Построим эту точку.
10
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ
МЕТОДА КООРДИНАТ
Аналогично если плоскость α пересекает ось Ву в точке L, то точка L имеет
координаты (0;l;0). Подставляя эти координаты в уравнение плоскости α , найдем,
что L(0;2;0). Построим точку L (она совпала с точкой С).
Точно так же находим, что плоскость α пересекает ось Вz в точке М(0;0;-построим
эту точку и затем построим сечение призмы плоскостью α, проходящей через точки
К,L,M. Получаем четырёхугольник КСD2A2.
Получаем четырёхугольник КСD2A2.
11
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ
МЕТОДА КООРДИНАТ
5.3 Задачи на вычисления расстояний и углов
В основании пирамиды МАВС лежит равнобедренный треугольник с прямым углом
при вершине С. каждое боковое ребро образует с плоскостью основания угол,
равный 45 гр. На ребре МВ взята точка К – середина этого ребра. Найдём угол между
прямой АК и плоскостью МВС. (рис 10)
Установив, что медианно МО грани МАВ является высотой
пирамиды, т.е. МО┴АВ и МО┴ОС, и что ОА =ОС=ОМ, зададим
в пространстве прямоугольную систему координат Охуz, как
показано на рисунке.
OA=i ; OC=j ; OM=k
В этой системе координат O(0;0;0), A(1;0;0), C(0;1;0), M(0,0,1)
Находим далее координаты точек В и К, вектора АК,
коллинеарного прямой АК, и
12
РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ
МЕТОДА КООРДИНАТ
векторов ВС и ВМ. Получаем B(-1;0;0;), K(-1/2;0;1/2), AK(-3/2;0;1/2), BC(1;1;0), BM
(1;0;1).
Если вектор n(k;l;m) перпендикулярен плоскости МВС, то n┴BC и n┴BM, или в
координатах:
k*1+l*1+m*0=0
k*1+l*0+m*1=0
откуда, полагая, например, что k=1, находим, что l=-1, m=-1, т. е. n(1;-1;-1).
е. n(1;-1;-1).
Пусть φ – это искомый угол. Тогда
Рисунок 11 — продолжение решения задачи
Таким образом, угол между прямой АК и плоскостью МВС равен
arcsin (2√30)/15
Содержание
13
ЗАКЛЮЧЕНИЕ
Обобщая вышеизложенные доводы, мы удостоверились, что
использование векторно-координатного метода позволяет с лёгкостью
решать множество задач самых разных видов, избегать больших
доказательств теорем. Решение таким методом задачи, помогает
сэкономить время и силы. Такое решение задач хорошо тем, что
человек не механически действует по образцу решения задач данного
типа, повторяя одни и те же действия, а творчески подходит к работе.
14
СПИСОК ИСПОЛЬЗОВАННЫХ
ИСТОЧНИКОВ
1.
В.Б. Некрасов, Б.М. Беккер, «Применение векторов для решения задач»,
СПб, СМИО Пресс 2002г.
2.
В.Н. Литвиненко «Сборник задач по стереометрии с методами решений»
М., изд. «Просвещение», 1998г
3.
Н.М. Рогановский, А.А. Столяр «Векторное построение стереометрии» изд.
«Народная асвета»,1974г.
4.
Ионин Ю.И., Некрасов В.Б. «Векторы в геометрических задачах»
5.
Болтянский В.Г., Ягиом И.Н. «Векторы и их применение в геометрии в
книге: Энциклопедия элементарной математики», том 4 М., Главное издательство
физмат литературы, 1963г.
6.
Журнал «Математика», №39, 2001г.
7.
Зив Б.Г. «Задачи к урокам геометрии 7-11»СПб, МПО «Мир и семья – 95»,
изд. ООО «Акация», 1996г.
8.
Атанасян Л.С., Бутузов В.Ф. и др. учебник «Геометрия 9-10»Изд.
«Просвещение», 1982г.
15
Задачи с векторами
Научись решать задачи ЕГЭ за пару минут!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2013-11-10
Задачи с векторами на ЕГЭ. Дорогие друзья! Вы знаете, что в состав экзамена по математике входят такие задания. Не факт, что такая задача попадёт именно вам, но готовиться к этому и понимать тему в любом случае нужно. На блоге мы уже рассмотрели несколько задач на сумму (разность) векторов, длину вектора, в этой же статье есть необходимая теория. Посмотрите её, прежде чем рассматривать задачи представленные ниже.
Посмотрите её, прежде чем рассматривать задачи представленные ниже.
Также загляните в справочник на блоге. Если нужно вспомнить, что такое абсцисса и ордината точки, тогда посмотрите эту статью. Кратко повторим:
Чтобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты начала:
Формула для определения длины вектора, если известны координаты его начала и конца:
Формула для определения длины вектора, если известны его координаты:
27725. Вектор АВ с началом в точке A(2;4) имеет координаты (6;2). Найдите ординату точки B.
Как уже сказано координаты вектора находятся следующим образом: из соответствующих координат конца вычитаются координаты начала вектора. То есть:
Координаты вектора нам даны, координаты его начала тоже, значит:
Следовательно можем найти координаты точки В:
х2 – 2 = 6 у2 – 4 = 2
х2 = 8 у2 = 6
Таким образом, ордината точки В равна 6.
Ответ: 6
27726. Вектор АВ с началом в точке A(3;6) имеет координаты (9;3). Найдите сумму координат точки B.
Задача по процессу решения такая же как и предыдущая, но иначе поставлен вопрос. Вычисления так же находятся в пределах устного счёта. Ещё раз запишем координаты вектора, когда известны координаты его начала и конца:
Координаты вектора и координаты его начала даны, значит:
Можем найти координаты точки В:
х2 – 3 = 9 у2 – 6 = 3
х2 = 12 у2 = 9
Таким образом, сумма координат точки В равна 21.
Ответ: 21
27727. Вектор АВ с концом в точке B (5;3) имеет координаты (3;1). Найдите абсциссу и ординату точки A, также сумму её координат.
Нам известны координаты вектора и координаты его конца, значит:
Можем найти координаты точки А:
5 – х1 = 3 3 – у1 = 1
х1 = 2 у1 = 2
Таким образом, абсцисса точки А равна двум, ордината тоже равна двум, а сумма координат равна 2+2 = 4.
Ответ: 4
27731 Найдите квадрат длинны вектора a+b.
В данной задаче необходимо найти координаты вектора, который является суммой указанных векторов, затем найти его длину и возвести её в квадрат. Запишем формулу длины вектора, если известны его координаты:
Или в другой форме:
Найдём координаты вектора, который является суммой данных векторов. Для этого сначала найдём координаты данных векторов.
Рассмотрим вектор:
Рассмотрим вектор:
*Можно было глядя на эскиз сразу их записать, так как точки их начал совпадают с началом координат.
Теперь найдём координаты вектора являющегося их суммой:
(2 + 8; 6 + 4) = (10;10)
Таким образом, длина вектора являющегося суммой векторов a и b равна:
Следовательно квадрат длины будет равен 200.
*Имея опыт в решении подобных задач, можно сразу записывать:
Как видите, вычисления можно осуществить устно. Здесь для вас умышленно представлено подробное решение.
Ответ: 200
27733. Найдите квадрат длины вектора a – b.
Задача аналогична предыдущей. Необходимо найти координаты вектора, который является разностью представленных векторов, затем найти его длину и результат возвести в квадрат.
Координаты данных векторов нам уже известны (из предыдущей задачи):
Теперь найдём координаты вектора, который является их разностью:
(2 – 8; 6 – 4) = (–6;2)
Таким образом, длина вектора, который является разностью векторов
Следовательно квадрат её длины будет равен 40.
*Можно сразу записывать и вычислять:
Ответ: 40
27723. Найдите сумму координат вектора АВ.
Посмотреть решение
27724.Вектор АВ с началом А(2;4) имеет координаты (6;2) Найдите абсциссу точки В.
Посмотреть решение
27730. Найдите сумму координат вектора а + b.
Посмотреть решение
27732. Найдите сумму координат вектора а–b.
Посмотреть решение
27736. Найдите сумму координат вектора а + b
Найдите сумму координат вектора а + b
Посмотреть решение
27739. Найдите квадрат длины вектора а–b.
Посмотреть решение
Вы убедились, что задачи с векторами на ЕГЭ это одни из самых простых заданий. Есть, конечно, задания со скалярным произведением векторов, но о они сложности не представляют, нужно лишь знать формулу скалярного произведения. Такие задачи мы также рассмотрим, не пропустите!
На этом всё. Если что-то непонятно, пишите. Успеха Вам!
С уважением, Александр Крутицких
Уроки сделаны… Мама охрипла… Сын оглох … Соседи выучили всё наизусть, собака пересказала!!!..
P.S: Делитесь этой статьёй в сетях.
Категория: Векторы | ЕГЭ-№1
Подготовка к ОГЭ по математике. Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Вектор – задачи и решения
Вектор и скаляр
1. Среди следующих вариантов, представляющих собой пары скаляр-вектор…
A. Сила – ускорение
B. Давление – сила C.
7 90 – скорость
D. Электрический ток – давление
Решение:
Сила = вектор, ускорение = вектор
Давление = скаляр, сила = вектор
Перемещение = вектор, скорость = скаляр
Электрический ток = скаляр, давление = скаляр
Правильный ответ B.
2.
Правильный ответ показан цифрой… . 2 и 3
D. 3 и 4
Решение:
Speed = Скаляр
Смещение = вектор
Вес = вектор
Ускорение = вектор
Правильный ответ — C.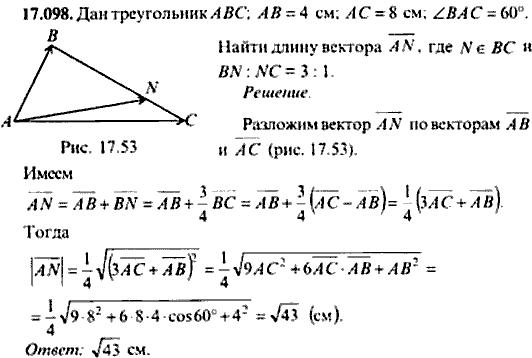
Компоненты векторов векторов.
3. Два вектора, F 1 = 20 Н и F 2 = 30 Н, имеют направление, как показано на рисунке ниже. Определите равнодействующую компонентов векторов по осям x и y.
A. 5√3 N и -25 N
B. -5√3 N и 25 N
C. 25 N и 5√3 N
D. 30 N и 25√3 N
Известны :
F 1 = 20 ньютонов
Угол между F 1 и осью x = 30 o
F 2 = 30 Newton
Угол между F 2 и x Axis = 30 O
Разыскивается: F x и F Y
Решение:
9002 F 10007Решение:
9002 F 10007 .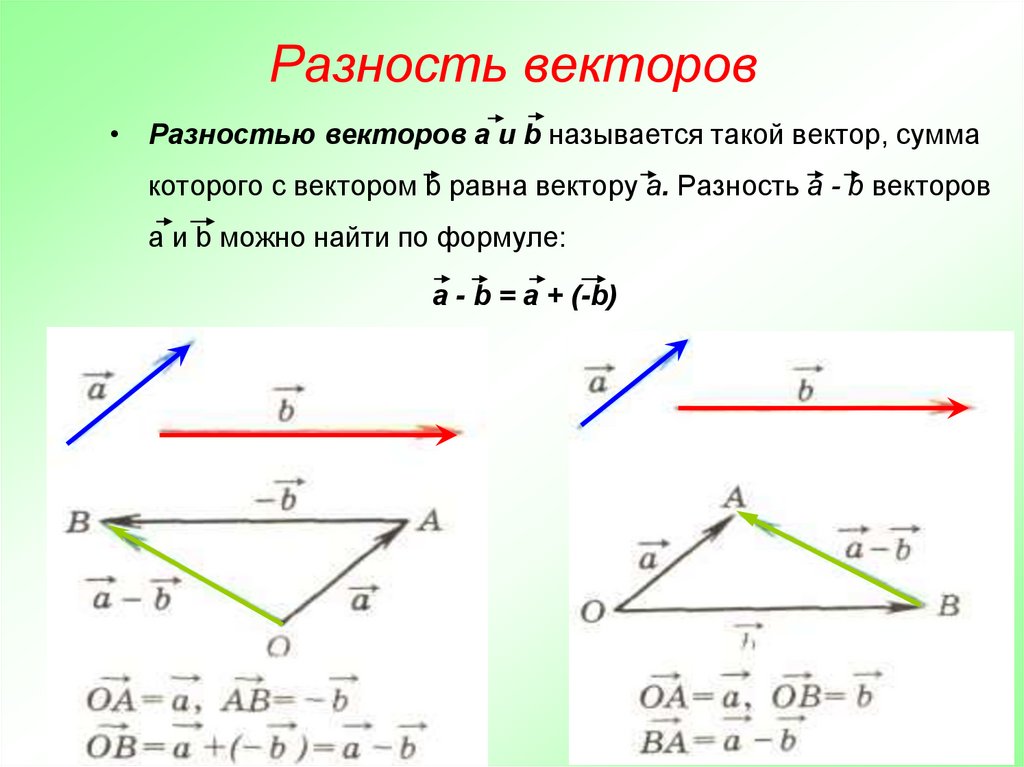 F 1 cos 30 o = (20)(0,5√3) = 10√3 Ньютон (знак плюс, поскольку указывает на ось +x)
F 1 cos 30 o = (20)(0,5√3) = 10√3 Ньютон (знак плюс, поскольку указывает на ось +x)
F 1y = F 1 sin 30 8 = (20)(0,5) = 10 ньютонов (знак плюс, потому что указывает на ось +y) F 2x = F 2 cos 30 o = (30)(0,5√3) = -15√3 Ньютона (знак минус, поскольку указывает на ось -x) F 2y = F 2 sin 30 900 o
Результат компонента x:
F x = F 1x + F 2x = 10√ 3 N – 15√3 N = -5√3 Ньютона
Результат компонента y:
F y = F 1y + F 2y = 10 N + 15 N = 25 ньютонов
Правильный ответ: B.
Результат двух векторов
4.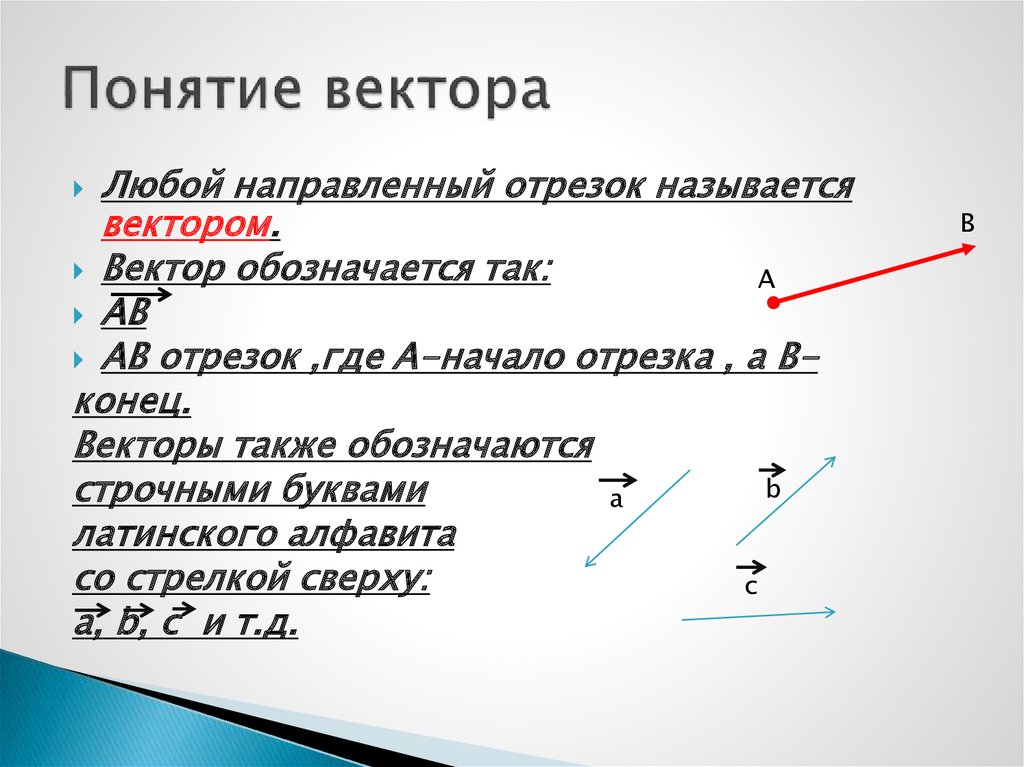 Двое детей A и B толкают блок, если A толкает блок на юг с силой 400 Н и одновременно В толкают брусок на восток с силой 300 Н, затем определяют равнодействующую сил А и В. С юго-восток
Двое детей A и B толкают блок, если A толкает блок на юг с силой 400 Н и одновременно В толкают брусок на восток с силой 300 Н, затем определяют равнодействующую сил А и В. С юго-восток
D. 700 С юго-восток
Известно:
U = север, T = восток, S = юг, B = запад
TL = северо-восток, TG = юго-восток, BD = юго-запад, BL = северо-запад
A = 400 Ньютон на юг
B = 300 Newton Eastward
Разыскивается: величина и направление чистой силы (R)
Решение:
Правильный ответ C.
5. Кто-то едет на мотоцикле от дома 6 км на север, затем 8 км на восток. Определить конечное положение человека по начальному положению.
A. 14 км к северо -востоку
B. 14 км юго -запада
C. 10 км северо -востока
10 км северо -востока
D. 10 км северо -запад
Известно:
Разыскивается: .
Решение:
Правильный ответ C.
6.
Исходя из рисунка выше, если 1 квадрат представляет 1 км, то каково полное перемещение.
Решение:
Расстояние = A + B + C = 6 + 6 + 2 = 14 км
Перемещение = R = 12 км
7. Автомобиль едет из А в В вдоль 30 км на север, затем 60 км на восток, затем 110 км на юг. Определить перемещение автомобиля из A в D.
Решение:
AA’ = 60 км
A’D = 110 км – 30 км = 80 км
8. Автомобиль едет из города A до города B 100 км к северу, затем до города C 60 км на восток, а затем до города D 20 км к югу. Определить водоизмещение автомобиля. 92+2\cdot|\vec{a}|\cdot |\vec{b}|\cdot \cos \alpha}[/tex]
Определить водоизмещение автомобиля. 92+2\cdot|\vec{a}|\cdot |\vec{b}|\cdot \cos \alpha}[/tex]
Угол между векторами
Задача 1
Найти сумму векторов $\overrightarrow{u}=⟨2,-1⟩$ и $ \overrightarrow{v}=⟨3,5⟩$
⟨4, 3⟩
⟨4, 5⟩
⟨5, 4⟩
⟨3, 4⟩
Задача 2
Данные векторы $\overrightarrow{u}=⟨2,-1,3⟩$ $\overrightarrow{v}=⟨3,5,0⟩$ $\overrightarrow{w}=⟨-2,0 ,3⟩$
$\alpha =2\qquad \beta =-2\qquad \gamma =4$
Найти $\alpha \overrightarrow{u}+\beta \overrightarrow{v}+\gamma \overrightarrow{w } = $
$⟨-10,-12,18⟩$
$⟨10,-14,18⟩$
$⟨-10,10,8⟩$
$⟨2,-2,4⟩$
Задача 3
Найти направление вектора $\overrightarrow{v}=⟨3,5⟩$
$\arctan(\frac{3}{5})$
$\tan(\frac{5 }{3})$
$\arctan(\frac{5}{3})$
$\arcsin(\frac{5}{3})$
Задача 4
Найти модуль вектора $\alpha \overrightarrow{u}$, если $\alpha =2$ и $\overrightarrow{u}=⟨-2,4,1⟩$
$2\sqrt{ 22}$
$2\sqrt{21}$
9
$\sqrt{80}$
Задача 5
Даны два вектора $\overrightarrow{u}=⟨2,3,1⟩$ и $\overrightarrow{v}=⟨-2,5,1⟩. $
$
Найдите величину вектора $\ overrightarrow{z}=2\overrightarrow{u}-3\overrightarrow{v}$
$\sqrt{181}$
$\sqrt{82}$
$10$
$\sqrt{182}$
Задача 6
Найдите величину $\overrightarrow{v}$.
Задача 7
Найдите векторную сумму $\overrightarrow{AB}+\overrightarrow{CA}$, если $A=⟨2,0,-3⟩$, $B=⟨1,1,-2⟩$ и $С=⟨0,3,2⟩$
⟨1, -2, -4⟩
⟨1, 4, -2⟩
⟨-1, 2, -4⟩
⟨2, -2, -4⟩
Задача 8
Найдите сумму векторов $\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{w}$.
Задача 9
Использование графа метода треугольника $\overrightarrow{u}-\overrightarrow{v}$
Вам не нужно предоставлять решение. Просто откройте решение.
Задача 10
Даны три вектора $\overrightarrow{u}=⟨2,3,1⟩$, $\overrightarrow{v}=⟨-2,5,1⟩$ и $\overrightarrow{z}=\overrightarrow {u}-2\overrightarrow{v}$. Найди
величина вектора $3\overrightarrow{z}$
Найди
величина вектора $3\overrightarrow{z}$
$28$
$3\sqrt{86}$
$22$
$\sqrt{775}$
Задача 11
Найдите результирующий вектор $\overrightarrow{u}-2\overrightarrow{v}+3\overrightarrow{w}$.
$⟨-3,-19⟩$
$⟨-9,19⟩$
$⟨-3,19⟩$
$⟨-4,19⟩$
Задача 12
Найдите вектор $\left( \left\vert \overrightarrow{u}\right\vert +\left\vert \overrightarrow{v}\right\vert-\left\vert \overrightarrow{w}\ вправо\верт\вправо) \влево(\overrightarrow{w}-\overrightarrow{u}\вправо) $
$5⟨5,1⟩$
$(5+\sqrt{5}-\sqrt{17})⟨5,1⟩$
$(5-\sqrt{17})⟨5,1⟩
$$(5-\sqrt{5})⟨5,5⟩$
Задача 13
Найти направление
вектор
$-\left\vert \overrightarrow{u}\right\vert \cdot \overrightarrow{u}$.
$\overrightarrow{u}=⟨-2,3⟩$
$\arctan (\sqrt{-3})$
$\arctan (\frac{-3}{2})$
$\ загар (\frac{-3}{2})$
$\загар (\sqrt{-3})$
Задача 14
Найдите вектор $\left( \frac{\left\vert \overrightarrow{u}\right\vert +\left\vert \overrightarrow{v}\right\vert }{\left\vert \overrightarrow {w}\right\vert }\right) \left( \overrightarrow{u}-\overrightarrow{v}+\overrightarrow{w}\right)$
$\left( \frac{2\sqrt{5}}{\sqrt{26}}\right) ⟨-1,-2⟩$
$\left( \frac{2\sqrt{5}+ 5}{\sqrt{26}}\right) ⟨-1,-2⟩$
$\sqrt{26} ⟨-1,-2⟩$
$3 ⟨-1,-2⟩$
Задача 15
Координаты точек A, B и C равны
$A=(-1,1,2)$, $B=(1,-2,3)$, $C=(-2, 1,1)$.
Найдите векторную сумму $\overrightarrow{u}+\overrightarrow{v}-\overrightarrow{w}$
, если $\overrightarrow{u}=\overrightarrow{AB},\overrightarrow{v}=\overrightarrow{CB },\overrightarrow{w}=\overrightarrow{CA}$
$⟨6,-9,3⟩$
$⟨6,-6,2⟩$
$⟨4,-6,2⟩$
$⟨6,-9,2⟩$
Задача 16
Даны точки A, B и C и константы $\alpha, \beta, \gamma$ такие, что $A=(-1,2,1)$, $B=(0,2,-3) $, $C=(1,2,-1)$ и $\alpha=-2$, $\beta=2$, $\gamma =3$
$\overrightarrow{u}=\overrightarrow{CB} $
$\overrightarrow{v}=\overrightarrow{AC}$
$\overrightarrow{w}=\overrightarrow{BA}$
Найдите вектор $\alpha \overrightarrow{u}+\beta \overrightarrow{v}+ \gamma\overrightarrow{w}$
$⟨-1,0,4⟩$
$⟨2,0,-2⟩$
$⟨-1,0,4⟩$
$⟨3,0,12⟩$
Сообщите о проблеме на этой странице.
Правильно:
Неправильно:
Неразрешенные задачи:
Практические решения векторов — Physics-prep.
 com
comПрактические задачи: векторы Решения
1. (Легкий) Вектор A Recrevents 5.0 M.0 M.0 M.0 M.0 M.0.0. . Если вектор B представляет 10,0 м смещения на север, найдите сумму двух перемещений ( Р ).
R = (5 2 + 10 2 ) 1/2 = 11 м
tanθ = 10/5 = 2
θ = 63°
2. (просто) Определить компоненты a x и y водоизмещение, величина которого составляет 30,0 м под углом 23° от оси x.
x-comp = 30cos23 = 28 м
y-comp = 30sin23 = 12 м
3. (умеренная) Автомобиль движется на 150,0 м под углом 63° к «северо-востоку» (это просто означает 63° от оси x). ). Некоторое время он остается в покое, а затем перемещается на 300 м под углом 34° к юго-западу (это означает, что он находится на расстоянии 214° от оси x). Найдите полное перемещение автомобиля.
| вектор | маг (м) | угол | x-комп (м) | y-комп (м) |
| 1 | 150 | 63 | 68 | 134 |
| 2 | 300 | 214 | -249 | -168 |
| Р | 184 | 191 | -181 | -34 |
4. (легко) На объект действуют две силы, но в разных направлениях. Например, вы и ваш друг можете дергать за веревочки, прикрепленные к одному деревянному бруску. Найдите величину и направление равнодействующей силы при следующих обстоятельствах.
(легко) На объект действуют две силы, но в разных направлениях. Например, вы и ваш друг можете дергать за веревочки, прикрепленные к одному деревянному бруску. Найдите величину и направление равнодействующей силы при следующих обстоятельствах.
а) Первая сила имеет величину 10 Н и действует на восток. Вторая сила имеет величину 4 Н и действует на запад.
F = 6N, восток
b) Первая сила имеет величину 10 N и действует на восток. Вторая сила имеет величину 4 Н и действует на север.
Силы расположены под прямым углом. Используйте теорию Пифагора.
F = (10 2 + 4 2 ) ½ = 11 Н
tanθ = 4/10
θ = 22º
5. (умеренная) Найдите описанную здесь систему уравновешивающих сил:
Сила A : 20 Н при 20°
Сила B : 40 Н при 230°
| Сила | магн. (Н) | угол | x-comp (N) | y-комп (N) |
| А | 20 | 20 | 18,8 | 6,8 |
| Б | 40 | 230 | -25,7 | -30,6 |
| ЭКВ | 24,8 | 74 | 6,9 | 23,8 |
| Р | 0 | 0 | 0 |
6.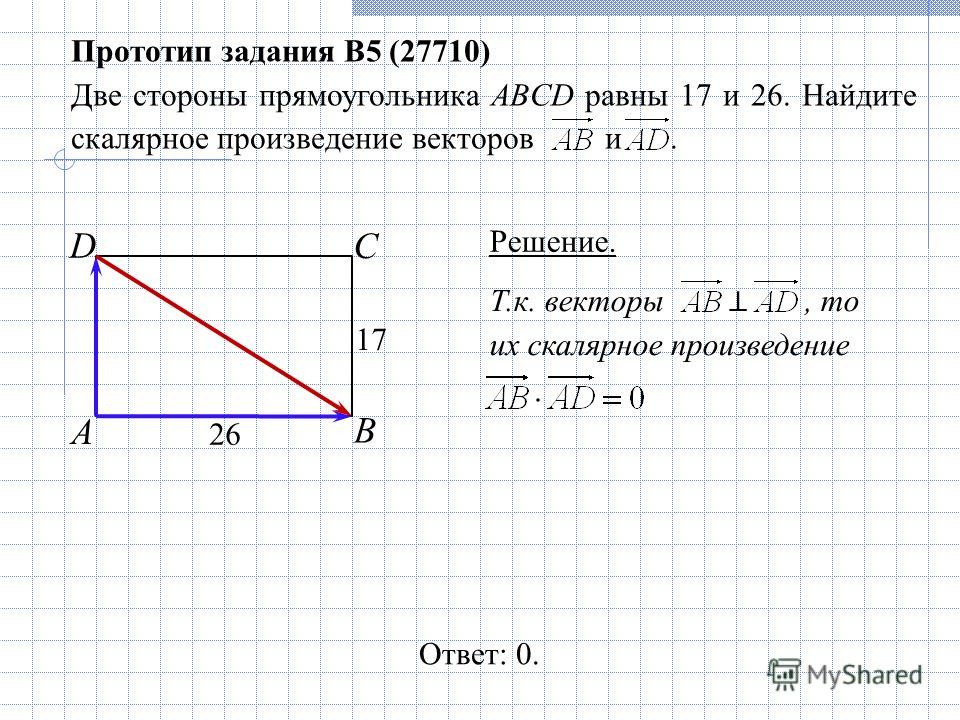 (умеренный) Вектор A представляет смещение.
(умеренный) Вектор A представляет смещение.
A = 20 м, 70°
Вектор B представляет второе смещение.
B = 50 м, 30°
Найдите скалярное произведение двух векторов и векторное произведение двух векторов.
Угол между двумя векторами равен 40°
Скалярное произведение:
A • B = ABcosθ = 20(50)cos(40) = 766 м 2
Величина векторного произведения:
| А х В | = ABsinθ = 20(50)sin(40) = 643 м 2
Чтобы получить угол перекрестного произведения, используйте RHR: пальцы на 70°, затем согните их до 30° (все в плоскости x/y) и ваш большой палец будет указывать в направлении -z.
7. (умеренная) Вектор D = 3 i — 4 j + 2 k и вектор: E = 4 i — j — 2 k .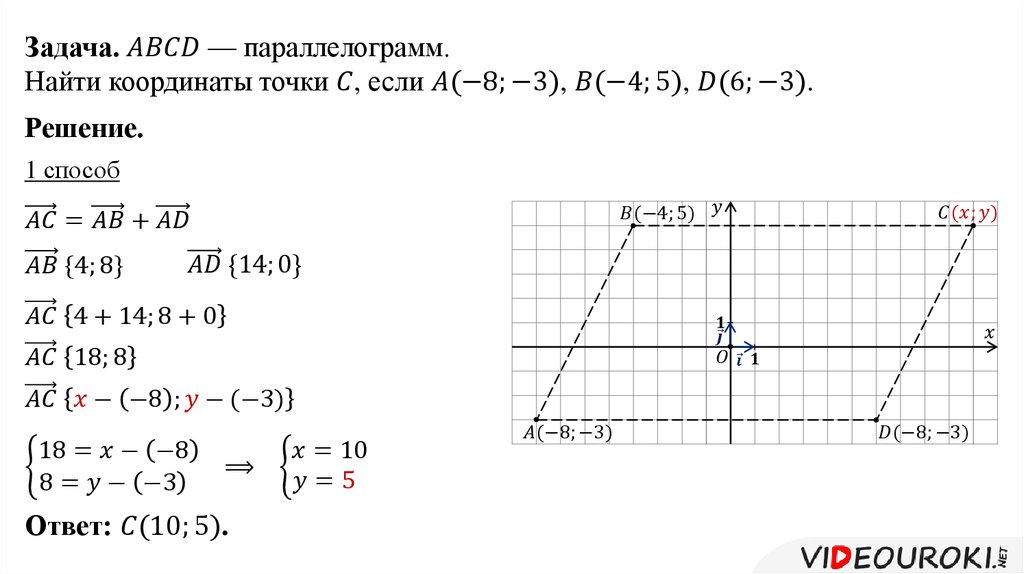 Найдите величину D + E и величину D — E .
Найдите величину D + E и величину D — E .
D + E = 7 i — 5 j
Таким образом, величина равна | D + E | = (7 2 + (-5) 2 ) 1/2 = 8,6
D — E = — i — 3 j + 4 k
Итак, величина равна | D — E | = (1 2 + (-3) 2 + 4 2 ) 1/2 = 5,1
8. (Умеренный), если сильный вектор F 1 имеет малышу 30 N. направление -z и вектор силы F 2 имеет величину 60 Н, направленное в направлении +x, определите скалярное произведение ( F 1 • F 2 ) и перекрестное произведение ( F 1 x F 2 ). Как изменились бы ответы, если бы векторы поменялись местами в уравнениях?
Как изменились бы ответы, если бы векторы поменялись местами в уравнениях?
F 1 • F 2 = (F 1 )(F 2 )cos90 = (30)(60)(0) = 0, поскольку произведение не имеет точки векторы находятся под углом 90° друг к другу)
| F 1 x F 2 | = (30)(60)sin 90 = 1800 Н 2
(величина перекрестного произведения)
Чтобы определить направление, используйте RHR:
Пальцы в направлении -z
Изгиб в направлении +x
Большой палец указывает в направлении -y.
(Кросс-произведение направлено вниз на экране)
Ответ скалярного произведения не изменится, если векторы поменяются местами, но векторное произведение будет иметь противоположное направление (+y) при сохранении той же величины (1800 м 2 ) .
9. (умеренное) Два смещения с величинами 10 м и 12 м могут быть объединены для формирования результирующих векторов с множеством различных величин.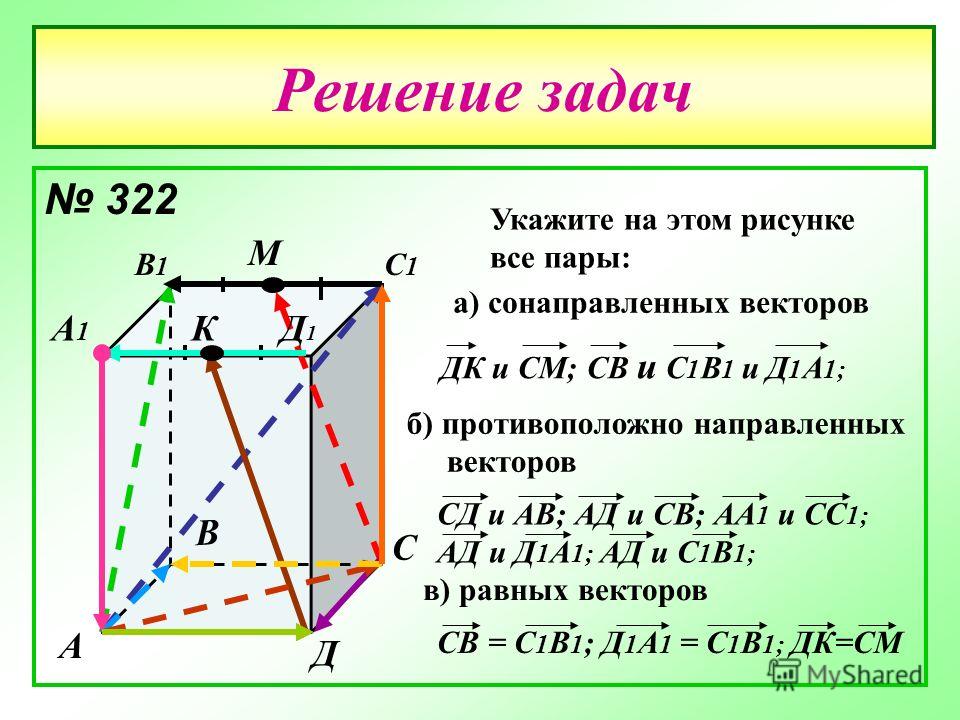 Какая из следующих величин может быть результатом этих двух смещений? 22 м, 2 м, 30,9м, 15,6 м. Какой угол существует для возможных равнодействующих между первоначальными смещениями?
Какая из следующих величин может быть результатом этих двух смещений? 22 м, 2 м, 30,9м, 15,6 м. Какой угол существует для возможных равнодействующих между первоначальными смещениями?
Если смещения параллельны (угол между ними 0°): R = 22 м
Если смещения антипараллельны (угол между ними 180°): R = 2 м
Если смещения перпендикулярны (угол 90° между ними) : R = 15,6 м
(Примечание: используйте закон косинусов, чтобы получить угол для R = 15,6 м)
Результат больше 22 м невозможен.
10. (умеренная) Велосипедная шина (Радиус = R = 0,4 м) катится по земле (без проскальзывания) на три четверти оборота. Рассмотрим точку на шине, которая изначально касалась земли. На какое расстояние он сместился от своего исходного положения?
Точка перемещается на три четверти окружности плюс 1 радиус вдоль земли (в направлении x) и 1 радиус вверх (в направлении y)
Результат = [(0,75)π(2R) + R] i + R J
РЕЗУЛЬТАЛЬНЫЙ = 2,28 I + 0,4 J
РЕЗУЛЬТАЛЬНАЯ МАСЧИНА = (2,28 2 + 0,4 2 ) ½ = 2,31 м
См. С. С. (умеренная) Учащийся несет кусок глины от двери первого этажа небоскреба (на Грант-стрит) к лифту, находящемуся на расстоянии 24 м. Затем она поднимается на лифте на 11-й этаж. Наконец, она выходит из лифта и несет глину 12 м обратно в сторону Грант-стрит. Определить полное перемещение глины, если каждый этаж находится на 4,2 м выше нижнего этажа.
С. С. (умеренная) Учащийся несет кусок глины от двери первого этажа небоскреба (на Грант-стрит) к лифту, находящемуся на расстоянии 24 м. Затем она поднимается на лифте на 11-й этаж. Наконец, она выходит из лифта и несет глину 12 м обратно в сторону Грант-стрит. Определить полное перемещение глины, если каждый этаж находится на 4,2 м выше нижнего этажа.
| Рабочий объем | Величина (м) | Угол (°) | x-комп (м) | у-комп (м) |
| 1 | 24 | 0 | 24 | 0 |
| 2 | 42 | 90 | 0 | 42 |
| 3 | 12 | 180 | -12 | 0 |
| Р | 44 | 74 | 12 | 42 |
Рабочие проблемы
Рабочие проблемы
Далее: Об этом документе. .. Up: Движение в двух измерениях Предыдущий: Процедура решения снаряда
.. Up: Движение в двух измерениях Предыдущий: Процедура решения снаряда
Найдите сумму следующих векторов смещения:
| знак равно | 5.0 м в 37 o N из E | ||
| знак равно | 6,0 м в 45 o N из W | ||
| знак равно | 4.0 м в 30 o Ю из Вт | ||
| знак равно | 3.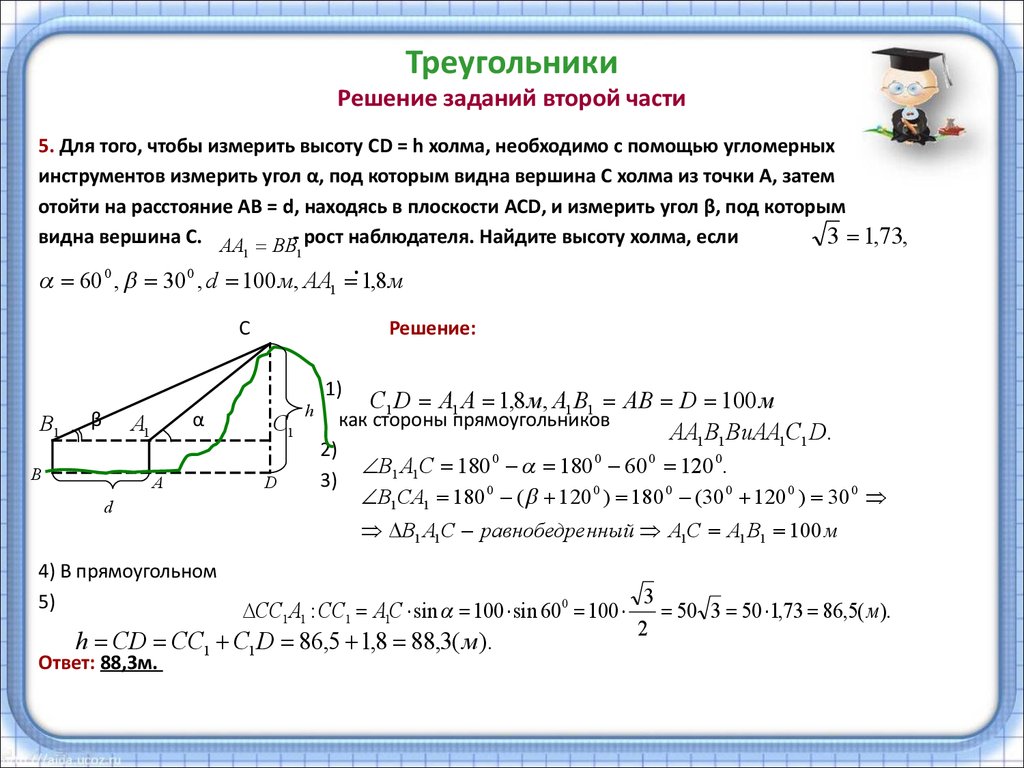 0 м в 60 o S из E 0 м в 60 o S из E |
Решение:
- а)
- Разложите каждый вектор на компоненты:
А х знак равно 5cos 37 o = 3,99 м А у знак равно 5sin 37 o = 3,01 м В х знак равно — 6cos 45 o = — 4,24 м Б у знак равно 6sin 45 o = 4,24 м С х знак равно — 4cos 30 o = — 3,46 м С у знак равно — 4sin 30 o = — 2,00 м Д х знак равно 3cos 60 o = 1,50 м Д у знак равно — 3sin 60 o = — 2,60 м - б)
- Сложите все x-компоненты и все y-компоненты:
R x знак равно A x + B x + C x + D x = — 2,21 м 7 Р у знак равно A y + B y + C y + D y = 2,65 м . 
- в)
- Найти || а также :
R = = 3,45 м = = 50 o С из С
Течение в реке 1,0 м / с . Женщина проплывает 300 м вниз по течению, а затем обратно к исходной точке без остановки. Если она может плыть со скоростью 2,0 м/с в стоячей воде, найти время пути туда и обратно.
Решение:
Нам нужно найти скорость женщины относительно берега для каждого
часть плавания. Пусть вниз по течению будет положительное направление и пусть v w будет
скорость воды. v w/w — скорость женщины относительно
вода и v w/s скорость женщины относительно берега.
Затем: (i) движение вниз по течению v w/s = v w + v w/w = 1,0 + 2,0 = 3,0 m / s (ii) движение
вверх по течению v w/s = 1,0 — 2,0 = — 1,0 м / с .
Пусть вниз по течению будет положительное направление и пусть v w будет
скорость воды. v w/w — скорость женщины относительно
вода и v w/s скорость женщины относительно берега.
Затем: (i) движение вниз по течению v w/s = v w + v w/w = 1,0 + 2,0 = 3,0 m / s (ii) движение
вверх по течению v w/s = 1,0 — 2,0 = — 1,0 м / с .
Чтобы найти время, чтобы пойти 300 м в каждом направлении использования x = v 0 t + в 2 . С a = 0 мы имеем t = х / v 0 .
Это дает (i) вниз по течению:
| т д = = 100 с |
| т и = = 300 с |
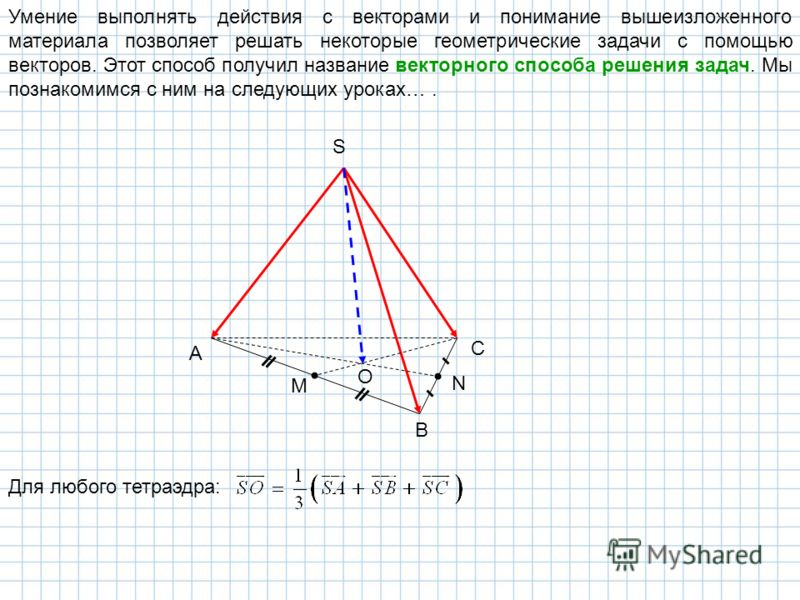
Женщина в предыдущей задаче переплывает реку к противоположный берег и обратно. Ширина реки 300 м, и она плавает перпендикулярно течению, поэтому она оказывается ниже по течению от того места, где она началась. Найдите время обратного пути.
Решение:
Поскольку женщина плывет перпендикулярно течению, мы можем определить ось Y как
параллельны реке и обрабатывают движение по осям x и y независимо друг от друга. Мы только
интересует движение в направлении х. Для первой половины ее плавать
у нас есть:
| а х | знак равно | ||
| v x0 | знак равно | v x = 2,0 м / с | |
| х | знак равно | 300 м . |
| t = = = 150 с . | (3) |
(Пример 3.4) Самолет сбрасывает пакет с продовольствием в застрявшая группа исследователей. Самолет движется горизонтально на 40,0 м/с на высоте 100 м над землей. Найдите а) место, где пакет ударяется о землю относительно места падения и б) скорость пакета как раз до того, как он упадет на землю.
Решение:
Настройте систему координат, как показано на рисунке 3.5. Рассмотрим компоненты x и y
отдельно. Нам дано:
Нам дано:
| X-Motion | Y-движение |
| х =? | г = — 100 м |
| v 0x = 40 м / с | v 0y = 0 |
| а х = 0 | а г = — 9,8 м / с 2 |
- а)
- Сначала найдем время пролета по y-движению.
Затем мы можем найти x из,г знак равно v oy t + a y t 2 — 100 знак равно (- 9,8) т 2 т знак равно 4,5 с . 
(4) х знак равно v x0 t + a x т 2 х знак равно 40(4,5) + 0 знак равно 180 м . (5) - б)
- Находим v y от,
в г знак равно v у0 + в знак равно 0 — 9,8(4,5) = — 44,1 м / с . 
| против | знак равно | = 59,5 м / с | |
| знак равно | = 48 о . | (6) |
Снаряд выпущен с начальной скоростью 113 м/с с
угол 60 o над горизонтом от вершины обрыва 49м
высокий (см. рис. 3.6). Найти)
время достижения максимальной высоты, б) максимальная высота, в) общее время
в воздухе, г) горизонтальная дальность и д) компоненты конечного
скорость непосредственно перед ударом снаряда о землю.
рис. 3.6). Найти)
время достижения максимальной высоты, б) максимальная высота, в) общее время
в воздухе, г) горизонтальная дальность и д) компоненты конечного
скорость непосредственно перед ударом снаряда о землю.
Решение:
Настройте систему координат.
Рассмотрим x- и y-движение отдельно. Нам дано:
| X-Motion | Y-движение |
| х =? | г В = — 49 м |
| v 0x = 113cos 60 или | v 0y = 113sin 60 или |
| v 0x = v Ax = в Вх | v Да = 0 |
| а х = 0 | а г = — 9,8 м / с 2 |
- а)
- Найдите время достижения максимальной высоты:
v Ай знак равно v 0 лет + a y t A т А знак равно знак равно = 9,99 с . 
(7) - б)
- Найдите максимальную высоту:
г А знак равно v 0y t A + a y t A 2 знак равно 113sin 60(9,99) — (9,8)(9,99) 2 = 489 м . (8) - в)
- Найти общее время t B в воздухе:
Решая квадратное уравнение, получаем,г Б знак равно V 0Y T B + A Y T B 2 9944449999999999999999999999999999999999999999999999999999999999999999999999444444444444444444444449н — 49 мзнак равно (113sin 60) t B — (9.  8) t 2 B
8) t 2 B 0 знак равно 4,9 т Б 2 — 97,9 т Б — 49. (9)
который дает, t B = 20,5 с или t B = — 0,49 с . Мы отказываемся от второго решение (это дает время, когда снаряд оторвался бы от земли, если бы он был брошен оттуда).т В = (97,9 ) - г)
- Найти диапазон по горизонтали ( x B ):
x В знак равно V 0x T B + A x T B 2 9944449999999999999999999999999999999999999999999999999999999999999999999999999999999744444444444444444444449нзнак равно (113cos 60)(20,5) = 1158 м . 
(10) - д)
- Найдите составляющие конечной скорости ( v Bx , v By ):
Обратите внимание, что отрицательное значение v By правильно указывает направление вниз.v Вх знак равно v 0x = 113cos 60 = 56,5 м / с против По знак равно v 0y + a y т Б знак равно 113sin 60 — 9,8(20,5) = — 103 м / с . 
(11)
(задача 3.50) Снаряд выпущен по падающей цели. снаряд покидает орудие в тот же момент, когда цель падает из состояния покоя. Считая, что ружье первоначально наведено на цель, показать, что пуля попадет в цель.
Решение:
Пусть x B и y B будут положениями пули x и y ,
а также
пусть x T и y T будут x и y позициями цели.
Мы
нужно показать, что y B = y T и x B = x T в некоторый общий момент времени т с ,
время попадания пули в цель.
Движение пули описывается двумя уравнениями:
| x В | знак равно | v 0 cos t | |
| г Б | знак равно | v 0 sin t — gt 2 . |
 Таким образом, мы имеем в момент времени т с :
Таким образом, мы имеем в момент времени т с : | x T = x B = v 0 cos t c |
Чтобы пуля попала в цель, позиции и должны быть равны при т с . Положение цели y определяется выражением
| y T = y 0 — gt c 2 |
y B = v 0 sin t c — gt c 2 . |
Чтобы показать это, рассмотрите Рисунок 3.7:
| загар = = | |||
| г 0 = х Т . |
y 0 = = v 0 sin t c . |
Далее: Об этом документе… Up: Движение в двух измерениях Предыдущий: Процедура решения снаряда [email protected]
9/10/1997
практических задач на ведущем уроке 92}$.
(16 задач)
Для любого скаляра $c$ и вектора $\mathbf{x}$ $|c \mathbf{x} | = |c|\ |\mathbf{x} |$.
(4 задачи)
Единичный вектор — это вектор длины 1.
(5 задач)
Найдите единичный вектор в том же направлении, что и $\bfx$, разделите $\bfx$ на его длину.
(3 задачи)
(9 задач)
Направление вектора $\mathbf{x}$ определяется как $\text{dir } \mathbf{x} = \frac{\mathbf{x}}{| \mathbf{х} | }.$
(4 задачи)
Чтобы построить $\bfx$ по длине и направлению, напишите: $\bfx = \left| \bfx\право| \text{каталог} \bfx.$
(4 задачи)
(7 задач)
Угол между двумя векторами — это угол, образуемый дугой, которая непосредственно их соединяет, при условии, что векторы имеют одно и то же основание.
(7 задач)
Угол между векторами всегда находится в диапазоне от 0 до $\pi$ включительно. Он равен 0, если векторы имеют одинаковое направление, и $\pi$, если векторы направлены в противоположные стороны.
(2 задачи)
(10 задач)
$\langle x_1, x_2\rangle + \langle y_1, y_2\rangle = \langle x_1+y_1, x_2+y_2\rangle$.

(2 задачи)
Сумма двух векторов — это вектор, полученный путем совмещения хвоста одного вектора с началом другого:
(6 задач)
Когда объект имеет скорость относительно движущейся среды, его результирующая скорость является суммой его относительной скорости и скорости среды.
(1 проблема)
(20 задач)
$\langle y_1, y_2\rangle — \langle x_1, x_2\rangle = \langle y_1-x_1, y_2-x_2\rangle$.
(3 задачи)
Вектор из $\bfx$ в $\bfy$ задается как $\bfy — \bfx$.
(14 задач)
Вычитание вектора аналогично сложению отрицательного значения вектора: $$\bfy — \bfx = \bfy + (- \bfx).$$
(1 проблема)
(13 задач)
$c \mathbf{x}$ — это вектор, полученный умножением длины $\bfx$ на $c$.

(6 задач)
$c \langle x_1, x_2, x_3 \rangle = \langle c x_1, c x_2, c x_3 \rangle.$
(2 задачи)
Для любого скаляра $c$ и вектора $\mathbf{x}$ $|c \mathbf{x} | = |c|\ |\mathbf{x} |$.
(4 задачи)
(6 задач)
Начните геометрическое доказательство, пометив важные точки как можно меньшим числом переменных.
(5 задач)
Середина между двумя векторами $\mathbf{x}$ и $\mathbf{y}$ равна $\frac{\mathbf{x} + \mathbf{y}}{2}$.
(3 задачи)
92+\frac{1}{2}$. При каком значении $c$ $\mathbf{i} + c \mathbf{j}$ является касательным вектором к $y(x)$ в точке $x=1$?
Решение
Найдите длину двумерного вектора $2 \\bfi + 3 \\bfj$ и трехмерного вектора $\langle2, 3, 4 \rangle$.
Решение
Нарисуйте все трехмерные векторы, угол которых по отношению к вектору $\bfi$ равен
- $\pi/6$
- $\pi/2$
- $5\pi/6$
Решение
Нарисуйте все единичные векторы в 3d, которые имеют угол $\pi/6$ по отношению к вектору $\bfi$.
Решение
Оцените угол между следующими парами векторов:
Решение
Нарисуйте все единичные векторы в 2d, которые имеют угол $\pi/4$ по отношению к вектору $\bfi$.
Решение
Векторы $\mathbf{a}$, $\mathbf{b}$, $\mathbf{c}$ и $\mathbf{d}$ показаны ниже. Используя только сложение векторов, выразите один из векторов через другие.
Решение
Следующий параллелограмм имеет один угол в начале координат. Два соседних угла задаются векторами $\mathbf{a}$ и $\mathbf{b}$. Выразите четвертый угол в виде вектора.
Два соседних угла задаются векторами $\mathbf{a}$ и $\mathbf{b}$. Выразите четвертый угол в виде вектора.
Решение
Река течет со скоростью $10$ м/с в северо-восточном направлении. Конкретная лодка может двигаться со скоростью $20$ м/с относительно воды. В каком направлении должна быть направлена лодка, чтобы двигаться строго на запад?
Решение
Решение
Решение задач с векторами
Задача 1 :
Показать, что векторы a = 2i + 3j + 6k, b = 6i + 2j − 3k и c = 3i − 6j + 2k взаимно ортогональны.
Решение:
Взаимно ортогональные означает, что они перпендикулярны друг другу.
вектор a ⋅ вектор b = (2i + 3j + 6k) ⋅ (6i + 2j − 3k)
= 2(6) + 3(2) + 6(-3)
= 12 + 6 — 18
= 18 — 18
= 0
вектор b ⋅ вектор c = (6i + 2j − 3k) ⋅ (3i − 6j + 2k)
= 6(3) + 2(-6) + (-3)2
= 18 — 12 — 6
= 18 — 18
= 0
вектор c ⋅ вектор = (3i − 6j + 2k) ⋅ (2i + 3j + 6k)
= 3(2) + (-6)(3) + 2(6)
= 6 — 18 + 12
= 18 — 18
= 0
Поскольку a ⋅ b = b ⋅ c = c ⋅ a = 0, заданные векторы взаимно ортогональны.
Задача 2 :
Пусть -i — 2j — 6k, 2i — j + k и -i + 3j + 5k стороны треугольника. Докажите, что указанные выше векторы образуют прямоугольный треугольник.
Решение :
Данные векторы являются сторонами прямоугольного треугольника. Чтобы показать, что треугольник прямоугольный, достаточно доказать, что две его стороны перпендикулярны.
Пусть
a = -i — 2j — 6k
b = 2i — j + k
c = = -i + 3j + 5k
a ⋅ b = (-i — 2j — 6k) ⋅ ( 2i — j + k)
= -1(2) + (-2)(-1) + (-6)(1)
= -2 + 2 — 6
= -6 ≠ 0
b ⋅ c = (2i — j + k) ⋅ (-i + 3j + 5k)
= 2(-1) + (-1)(3) + 1(5)
= -2 — 3 + 5
= 0
Поскольку b ⋅ c = 0, вектор b и вектор c перпендикулярны .
Итак, данные векторы образуют прямоугольный треугольник.
Задача 3 :
Если |вектор| = 5, |b вектор| = 6, |с вектор| = 7 и вектор + вектор b + вектор c = 0 вектор, найти a ⋅ b + b ⋅ c + c ⋅ a .
Решение:
вектор a + вектор b + вектор c = 0 вектор
|вектор a + вектор b + вектор c| = 0
Возьмите квадрат с обеих сторон.
|вектор a + вектор b + вектор c| 2 = 0 2
|а| 2 + |b| 2 + |с| 2 + 2(а ⋅ б) + 2(б ⋅ в) + 2(в ⋅ а) = 0
|а| 2 + |b| 2 + |с| 2 + 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0
Подставьте данные значения.
5 2 + 6 2 + 7 2 + 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0
25 + 36 + 49+ 2(a ⋅ b + b ⋅ c + c ⋅ a) = 0
110 + 2 (a ⋅ b + b ⋅ c + c ⋅ a) = 0
Вычтите 110 с каждой стороны.
2(a ⋅ b + b ⋅ c + c ⋅ a) = -110
Разделите каждую сторону на 2.
a ⋅ b + b ⋅ c + c ⋅ a = -55
Задача 0 5: 90 4 0 5: 90 4
Покажите, что точки (2, — 1, 3), (4, 3, 1) и (3, 1, 2) лежат в одной плоскости.
Решение:
Пусть
a = 2i — j + 3k
b = 4i + 3j + k
c = 3i + j + 2k
Если три вектора коллинеарны, то их скалярное произведение равно нулю.
= (1/2)[2(6 — 1) + 1(8 — 3) + 3(4 — 9)]
= (1/2)[ 2(5) + 1(5) + 3 (-5)]
= (1/2) [10 + 5 — 15]
= (1/2)[15 — 15]
= 0
Так как скалярное произведение трех векторов a, b и c ноль, данные точки компланарны.
Задача 5 :
Если вектор и вектор b являются единичными векторами, а θ – это угол между ними, покажите, что
(i) sin(θ/2) = (1/2)|вектор a — вектор b|
Решение :
На первом шаге возьмем квадрат для |вектор a — вектор b|.
Поскольку вектор и вектор b являются единичными векторами, мы должны применить 1 вместо вектора и вектора b.
|вектор а — вектор б| 2 = 1 2 + 1 2 — 2(1)(1)cosθ
|вектор a — вектор b| 2 = 2 — 2cosθ
|вектор a — вектор b| 2 = 2(1- cosθ)
|вектор a — вектор b| 2 = 2 (2sin 2 (θ/2))
|вектор a — вектор b| = 2sin(θ/2)
sin(θ/2) = (1/2)|вектор a — вектор b| —-(1)
Отсюда доказано
(ii) cos(θ/2) = (1/2) |a вектор + b вектор|
Решение:
На первом шаге возьмем квадрат для |a вектор + b вектор|
Поскольку вектор и вектор b являются единичными векторами, мы должны применить 1 вместо вектора и вектора b.
|вектор a + вектор b| 2 = 1 2 + 1 2 + 2(1)(1)cosθ
|вектор a — вектор b| 2 = 2 + 2cosθ
|вектор a — вектор b| 2 = 2(1 + cosθ)
|вектор a — вектор b| 2 = 2(2 cos 2 (θ/2))
|вектор a — вектор b| = 2cos(θ/2)
cos(θ/2) = (1/2)|вектор a + вектор b| —-(2)
Отсюда доказано
(ii) tan(θ/2) = |a вектор-b вектор| / |вектор-b вектор|
Решение:
Мы можем доказать приведенный выше результат, используя (1) и (2).
sin(θ/2) = (1/2)|вектор a — вектор b|
cos(θ/2) = (1/2)|вектор a + вектор b|
(1)/(2) :
sin(θ/2)/cos(θ/2)
= (1/2)|вектор a — вектор b|/(1/2)|вектор + б вектор |
tan(θ/2)
= (1/2)|вектор a — вектор b|/(1/2)|вектор a + вектор b|
Задача 6 :
Пусть вектор a, вектор b, вектор c — три вектора такие, что |a вектор| = 3, |b вектор|= 4, |c вектор|= 5, Если все три вектора перпендикулярны друг другу, найти значение | вектор a + вектор b + вектор c|.


