Метод присоединенной матрицы — Студопедия
Поделись
Определение обратной матрицы
ОБРАТНЫЕ МАТРИЦЫ
ЛЕКЦИЯ 3
Обратная матрица Метод присоединенной матрицы. Матричные уравнения. Матричный способ решения систем линейных уравнений. Ранг матрицы. Метод окаймляющих миноров. Метод элементарных преобразований. Теорема о базисном миноре.
Матрица А–1 называется обратной матрицей по отношению к матрице А, если выполняется равенство
AA–1 = A–1A = E. (3.1)
Из данного определения следует, что взаимообратные матрицы перестановочны. Это означает, что только квадратные матрицы могут иметь обратные. Однако не каждая квадратная матрица имеет обратную. Для того чтобы матрица А имела обратную, необходимо и достаточно, чтобы ее определитель был отличен от нуля: detA¹0.
% Действительно, из определения обратной матрицы и свойств определителей получаем: det(A–1A)=detA–1detA=detE=1, откуда следует необходимое условие существования обратной матрицы: detA¹0 или detA–1¹0. Вопрос о доказательстве достаточности этого условия несколько сложнее. Для этого нужно указать алгоритм построения такой матрицы. Поэтому мы вернемся к этому вопросу позднее (см. метод присоединенной матрицы).
Отметим, что если обратная матрица существует, то такая матрица только одна. Действительно, пусть существует еще одна матрица В, удовлетворяющая условию АВ=ВА=Е, тогда можно написать:
BAA–1=(BA)A–1=EA–1=A–1,
BAA–1=B(AA–1)=BE=B,
откуда получаем В=А–1, т.е. обратные матрицы совпадают. &
Матрица, определитель которой отличен от нуля, называется невырожденной, или неособенной; в противном случае она называется вырожденной, или особенной. Необходимое и достаточное условие существования обратной матрицы можно сформулировать следующим образом: обратная матрица существует, причем только одна, тогда и только тогда, когда исходная матрица невырожденная.
Необходимое и достаточное условие существования обратной матрицы можно сформулировать следующим образом: обратная матрица существует, причем только одна, тогда и только тогда, когда исходная матрица невырожденная.
Для невырожденных матриц справедливы следующие свойства:
| 1) detA–1=(detA)–1, | 2) (AB)–1=B–1A–1, | 3) (AT)–1=(A–1)T, |
| 4) (A–1)–1=A, | 5) ( |
Матрица AÚназывается присоединенной к матрице A, если она является транспонированной к матрице A, а вместо элементоввзяты их алгебраические дополнения, т.е.
Теорема 3. 1. Обратная и присоединенная матрицы связаны соотношением
1. Обратная и присоединенная матрицы связаны соотношением
(3.2)
% Действительно, рассмотрим произведение матриц
При этом учтем, что сумма произведений элементов некоторой строки или столбца на их алгебраические дополнения равно определителю матрицы (см. теорему о разложении определителя по строке или столбцу).Дополнительно мы воспользуемся еще одним свойством определителей: сумма произведений алгебраических дополнений некоторой строки или столбца на соответствующие элементы другой строки или столбца равно нулю
. Это связано с тем, что такая сумма эквивалентна определителю, у которого две одинаковые строки или столбца, и, следовательно, он будет равен нулю. Таким образом, перемножая рассматриваемые матрицы, получимОтсюда следует справедливость приведенной теоремы. Более того, фактически мы указали алгоритм построения обратной матрицы при помощи присоединенной матрицы и тем самым доказали достаточное условие существования обратной матрицы. &
&
Общая схема нахождения обратной матрицы
(метод присоединенной матрицы):
1) Вычисляем определитель заданной матрицы, если он равен нулю, то обратной матрицы не существует.
2) Транспонируем заданную матрицу.
3) Вычисляем все алгебраические дополнения транспонированной матрицы.
4) Составляем присоединенную матрицу, т.е. вместо элементов транспонированной матрицы ставим их алгебраические дополнения.
5) Записываем обратную матрицу. Для этого каждый элемент присоединенной матрицы делим на определитель исходной матрицы.
6) Делаем проверку.
Пример 3.1. Найти A–1, если
Решение. 1) detA = –4.
2)
3) Ищем алгебраические дополнения транспонированной матрицы (не забывать учитывать знаки алгебраических дополнений!):
4) Составляем присоединенную матрицу:
5) Записываем обратную матрицу:
6) Делаем проверку: AA–1 = A–1A = E:
Следовательно, обратная матрица найдена правильно. à
à
Пример 3.2. Найти обратную матрицу
Решение. Поскольку
и A11 = d, A12 = –c, A 21 = –b, A22 = a, то
Эту формулу можно использовать для нахождения обратных матриц второго порядка. à
| Алгебраические дополнения. | ∆ 1,2 = -(2·4-(-2·(-2))) = -4 | ∆ 2,1 = -(2·4-5·3) = 7 | ∆ 2,3 = -(-1·5-(-2·2)) = 1 | ∆ 3,2 = -(-1·(-2)-2·3) = 4 |
| A -1 = |
|
Другой алгоритм нахождения обратной матрицы
Приведем другую схему нахождения обратной матрицы.
- Находим определитель данной квадратной матрицы A .
- Находим алгебраические дополнения ко всем элементам матрицы A .
- Записываем алгебраические дополнения элементов строк в столбцы (транспонирование).
- Делим каждый элемент полученной матрицы на определитель матрицы A .
Особый случай : Обратной, по отношению к единичной матрице E , является единичная матрица E .
Для обратной матрицы существует уместная аналогия с обратным числом. Для каждого числа a , не равного нулю, существует такое число b , что произведение a и b равно единице: ab = 1 . Число b называется обратным для числа b . Например, для числа 7 обратным является число 1/7, так как 7*1/7=1.
Обратной матрицей , которую требуется отыскать для данной квадратной матрицы А , называется такая матрица
произведение на которую матрицы А справа является единичной матрицей, т. е,
е,
. (1)
Единичной матрицей называется диагональная матрица, у которой все диагональные элементы равны единице.
Нахождение обратной матрицы — задача, которая чаще решается двумя методами:
- методом алгебраических дополнений, при котором требуется находить определители и транспонировать матрицы;
- методом исключения неизвестных Гаусса, при котором требуется производить элементарные преобразования матриц (складывать строки, умножать строки на одно и то же число и т. д.).
Для особо любознательных существуют и другие методы, например, метод линейных преобразований. На этом уроке разберём три упомянутых метода и алгоритмы нахождения обратной матрицы этими методами.
Теорема. Для каждой неособенной (невырожденной, несингулярной) квадратной матрицы можно найти обратную матрицу, и притом только одну. Для особенной (вырожденной, сингулярной) квадратной матрицы обратная матрица не существует.
Квадратная матрица называется неособенной (или невырожденной , несингулярной ), если её определитель не равен нулю, и особенной (или вырожденной , сингулярной ), если её определитель равен нулю.
Обратная матрица может быть найдена только для квадратной матрицы. Естественно, обратная матрица также будет квадратной и того же порядка, что и данная матрица. Матрица, для которой может быть найдена обратная матрица, называется обратимой матрицей.
Нахождение обратной матрицы методом исключения неизвестных Гаусса
Первый шаг для нахождения обратной матрицы методом исключения неизвестных Гаусса — приписать к матрице A единичную матрицу того же порядка, отделив их вертикальной чертой. Мы получим сдвоенную матрицу . Умножим обе части этой матрицы на , тогда получим
,
Алгоритм нахождения обратной матрицы методом исключения неизвестных Гаусса
1. К матрице A приписать единичную матрицу того же порядка.
2. Полученную сдвоенную матрицу преобразовать так, чтобы в левой её части получилась
единичная матрица, тогда в правой части на месте
единичной матрицы автоматически получится обратная матрица. Матрица A в левой части
преобразуется в единичную матрицу путём элементарных преобразований матрицы.
2. Если в процессе преобразования матрицы A в единичную матрицу в какой-либо строке или в каком-либо столбце окажутся только нули, то определитель матрицы равен нулю, и, следовательно, матрица A будет вырожденной, и она не имеет обратной матрицы. В этом случае дальнейшее нахождение обратной матрицы прекращается.
Пример 2. Для матрицы
найти обратную матрицу.
и будем её преобразовывать, так чтобы в левой части получилась единичная матрица. Начинаем преобразования.
Умножим первую строку левой и правой матрицы на (-3) и сложим её со второй строкой, а затем умножим первую строку на (-4) и сложим её с третьей строкой, тогда получим
.
Чтобы по возможности не было дробных чисел при последующих преобразованиях, создадим предварительно единицу во второй строке в левой части сдвоенной матрицы. Для этого умножим вторую строку на 2 и вычтем из неё третью строку, тогда получим
.
Сложим первую строку со второй, а затем умножим вторую строку на (-9) и сложим её
с третьей строкой. Тогда получим
Тогда получим
.
Разделим третью строку на 8, тогда
.
Умножим третью строку на 2 и сложим её со второй строкой. Получается:
.
Переставим местами вторую и третью строку, тогда окончательно получим:
.
Видим, что в левой части получилась единичная матрица, следовательно, в правой части получилась обратная матрица . Таким образом:
.
Можно проверить правильность вычислений, умножим исходную матрицу на найденную обратную матрицу:
В результате должна получиться обратная матрица.
онлайн калькулятора для нахождения обратной матрицы .
Пример 3. Для матрицы
найти обратную матрицу.
Решение. Составляем сдвоенную матрицу
и будем её преобразовывать.
Первую строку умножаем на 3, а вторую на 2, и вычитаем из второй, а затем первую строку умножаем на 5, а третью на 2 и вычитаем из третьей строки, тогда получим
.
Первую строку умножаем на 2 и складываем её со второй, а затем из третьей строки вычитаем вторую, тогда получим
.
Видим, что в третьей строке в левой части все элементы получились равными нулю. Следовательно, матрица вырожденная и обратной матрицы не имеет. Дальнейшее нахождение обратной марицы прекращаем.
Проверить решение можно с помощью
Определение 1: матрица называется вырожденной, если её определитель равен нулю.
Определение 2: матрица называется невырожденной, если её определитель не равен нулю.
Матрица «A» называется обратной матрицей , если выполняется условие A*A-1 = A-1 *A = E (единичной матрице).
Квадратная матрица обратима только в том случае, когда она является невырожденной.
Схема вычисления обратной матрицы:
1) Вычислить определитель матрицы «A», если ∆ A = 0, то обратной матрицы не существует.
2) Найти все алгебраические дополнения матрицы «A».
3) Составить матрицу из алгебраических дополнений (Aij )
4) Транспонировать матрицу из алгебраических дополнений (Aij )T
5) Умножить транспонированную матрицу на число, обратное определителю данной матрицы.
6) Выполнить проверку:
На первый взгляд может показаться, что это сложно, но на самом деле всё очень просто. Все решения основаны на простых арифметических действиях, главное при решении не путаться со знаками «-» и «+», и не терять их.
А теперь давайте вместе с Вами решим практическое задание, вычислив обратную матрицу.
Задание: найти обратную матрицу «A», представленную на картинке ниже:
Решаем всё в точности так, как это указано в план-схеме вычисления обратной матрицы.1. Первое, что нужно сделать, это найти определитель матрицы «A»:
Пояснение:
Мы упростили наш определитель, воспользовавшись его основными функциями. Во первых, мы прибавили ко 2 и 3 строке элементы первой строки, умноженные на одно число.
Во-вторых, мы поменяли 2 и 3 столбец определителя, и по его свойствам поменяли знак перед ним.
В-третьих, мы вынесли общий множитель (-1) второй строки, тем самым, снова поменяв знак, и он стал положительным. Также мы упростили 3 строку также, как в самом начале примера.
Также мы упростили 3 строку также, как в самом начале примера.
У нас получилась треугольный определитель, у которого элементы ниже диагонали равны нулю, и по 7 свойству он равен произведению элементов диагонали. В итоге мы получили ∆ A = 26, следовательно обратная матрица существует.
А11 = 1*(3+1) = 4
А12 = -1*(9+2) = -11
А13 = 1*1 = 1
А21 = -1*(-6) = 6
А22 = 1*(3-0) = 3
А23 = -1*(1+4) = -5
А31 = 1*2 = 2
А32 = -1*(-1) = -1
А33 = 1+(1+6) = 7
3. Следующий шаг — составление матрицы из получившихся дополнений:
5. Умножаем эту матрицу на число, обратное определителю, то есть на 1/26:
6. Ну а теперь нам просто нужно выполнить проверку:
В ходе проверки мы получили единичную матрицу, следовательно, решение было выполнено абсолютно верно.
2 способ вычисления обратной матрицы.
1. Элементарное преобразование матриц
2. Обратная матрица через элементарный преобразователь.
Обратная матрица через элементарный преобразователь.
Элементарное преобразование матриц включает:
1. Умножение строки на число, не равное нулю.
2. Прибавление к любой строке другой строки, умноженной на число.
3. Перемена местами строк матрицы.
4. Применяя цепочку элементарных преобразований, получаем другую матрицу.
А-1 = ?
1. (A|E) ~ (E|A-1 )
2. A-1 * A = E
Рассмотрим это на практическом примере с действительными числами.
Задание: Найти обратную матрицу.
Решение:
Выполним проверку:
Небольшое разъяснение по решению:
Сперва мы переставили 1 и 2 строку матрицы, затем умножили первую строку на (-1).
После этого умножили первую строку на (-2) и сложили со второй строкой матрицы. После чего умножили 2 строку на 1/4.
Заключительным этапом преобразований стало умножение второй строки на 2 и прибавлением с первой. 2
2
Матрица
Инверсия: Для матриц есть нет такого понятия, как деление. Можете добавить, вычитать и умножать матрицы, но разделить их нельзя. Однако существует родственное понятие, который называется «инверсия». Сначала я расскажу, почему инверсия полезно, а потом я покажу вам, как сделать это. Вспомните, когда вы
впервые узнал, как решить
линейные уравнения. Эта терминология и эти
факты очень важны для матриц. Если вам дано матричное уравнение
как АКС = C , где вы
даны А и С и просят вычислить X ,
вы хотите «отделить» матрицу A . Как появился « A 1 AX »
в левой части уравнения превратиться в » Х «?
Вспомните природу инверсий для правильных чисел. Если у вас есть
число (например, 3/2)
и обратное ему (в данном случае 2/3)
и вы умножаете их, вы получите 1.
И 1
это тождество, так называемое, потому что 1 x = x для любого числа х .
Аналогично работает и с матрицами. Если вы умножаете матрицу (например, А )
и обратное ему (в данном случае Следует отметить, что
порядок в умножении
выше, важно и вовсе не произвольно. Напомним, что для матриц
умножение не коммутативно. то есть АВ почти никогда не равен BA .
Таким образом, умножая матричное уравнение «слева» (чтобы получить A 1 AX )
совсем не то же самое, что умножать «справа» (на
получить AXA 1 ).
И нельзя сказать, что продукт AXA 1 равно А 1 ТОПОР ,
потому что вы не можете изменить порядок умножения. Вместо,
надо умножить на А 1 слева, поставив рядом с A в исходном матричном уравнении. И так как вы должны сделать то же самое
к обеим частям уравнения, когда вы решаете, вы должны умножить «слева» и в правой части уравнения,
в результате получается A 1 C . Как вы видели выше, обратные матрицы могут быть очень полезны для решения матрицы уравнения. Но, учитывая матрицу, как ее инвертировать? Как вы находите обратный? Техника обращения матриц довольно хитрая. За заданная матрица A и обратный A 1 , мы знаем, что у нас есть A 1 А = I . Собирались использовать идентификационную матрицу I в процесс обращения матрицы.
Сначала я записываю записи матрицы A , но я их пишу в матрице двойной ширины: В другой половине двойной ширины, я пишу единичную матрицу: Сейчас сделаю матрицу
операции со строками
чтобы преобразовать левую часть двойной ширины в тождество. Теперь, когда левый сторона двойной ширины содержит идентификатор, правая сторона содержит обратный. То есть обратная матрица такая: Обратите внимание, что мы можем подтвердить что эта матрица обратна A умножая две матрицы и подтверждая, что мы получаем тождество: Авторские права Элизабет Stapel 2003-2011 Все права защищены Имейте в виду, что в «реальных
жизни», обратная сторона редко представляет собой матрицу, заполненную красивыми, аккуратными целыми
номера такие. Однако, если повезет, особенно если вы делаете инверсии
вручную, вам дадут хорошие, подобные этому, чтобы сделать. Топ | 1 | 2 | Возвращаться к индексу Далее >>
|
|
|
линейная алгебра — еще один способ найти обратную матрицу
спросил
Изменено
7 лет, 2 месяца назад 9{-1} = \ frac1 {\ det (M)} \ mathrm {adj} (M) $. Однако очень сложно найти, когда матрица большая.
Однако очень сложно найти, когда матрица большая.
Я нашел очень интересный способ получить обратную матрицу и хочу знать, почему это можно сделать так. Например, если вы хотите найти обратную $M=\begin{bmatrix}1 & 2 \\ 3 & 4\end{bmatrix}$$
Сначала напишите единичную матрицу в правой части и выполните несколько шагов:
$$\begin{bmatrix}1 & 2 &1 &0 \\ 3 & 4&0&1\end{bmatrix}\to\begin{bmatrix}1 & 2 &1 &0 \\ 3/2 & 2&0&1/2\end {bmatrix}\to\begin{bmatrix}1/2 & 0 &-1 &1/2 \\ 3/2 & 2&0&1/2\end{bmatrix}\to\begin{bmatrix}3/2 & 0 &-3 &3/2 \\ 3/2 & 2&0&1/2\end{bmatrix}$$ $$\to\begin{bmatrix}3/2 & 0 &-3 &3/2 \\ 0 & 2&3&-1\end{bmatrix}\to\begin{bmatrix}1 & 0 &-2 &1 \\ 0 & 2&3&-1\end{bmatrix}\to\begin{bmatrix}1 & 0 &-2 &1 \\ 0 & 1&3/2&-1/2\end{bmatrix}$$ 9{-1}=\begin{bmatrix}-2 &1 \\3/2&-1/2\end{bmatrix}$$
Как доказать, что этот метод работает?
- линейная алгебра
- матрицы
$\endgroup$
$\begingroup$
Это очень стандартный метод; если вы обнаружили это самостоятельно, поздравляю! Это работает, потому что каждая из элементарных операций со строками, которые вы выполняете, эквивалентна умножению на элементарную матрицу. Чтобы преобразовать $A$ в $I$, вы выполняете некоторую последовательность элементарных операций над строками, которые фактически умножают $A$ на последовательность элементарных матриц: 9{-1}\end{bmatrix}$ именно так, как вы обнаружили.
Чтобы преобразовать $A$ в $I$, вы выполняете некоторую последовательность элементарных операций над строками, которые фактически умножают $A$ на последовательность элементарных матриц: 9{-1}\end{bmatrix}$ именно так, как вы обнаружили.
$\endgroup$
4
$\begingroup$
Метод, который вы описываете, называется методом Гаусса-Джордана. Здесь есть хорошее описание и неформальное обсуждение того, почему это работает.
Гораздо эффективнее и стабильнее, чем метод, основанный на детерминантах и адъюгатах. На практике вы не будете использовать метод детерминанта/сопряжения, за исключением очень маленьких матриц (размера 2 или 3). 9н$.
Таким образом, чтобы вычислить обратную $A$, нам нужно решить уравнения $Ax_1 = e_1,\ldots, Ax_n = e_n$. Все эти уравнения решаются сразу методом исключения Гаусса описанным вами методом.
$\endgroup$
$\begingroup$
Потому что, когда вы выполняете преобразование и исключение Гаусса до
$$ (А\\верт\I)\ , $$
на самом деле вы находите решения всех этих линейных систем:
9{-1}) \ , $$ инверсия $A$ появляется там, где должна.
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Обратные матрицы
Цели
- Поймите, что означает обратимость квадратной матрицы.
- Узнайте об обратимых преобразованиях и поймите взаимосвязь между обратимыми матрицами и обратимыми преобразованиями.
- Рецепты: вычислить обратную матрицу, решить линейную систему, взяв обратные.
- Изображение: обратное преобразование.
- словарных слов: обратная матрица , обратное преобразование .
В разделе 3.1 мы научились перемножать матрицы. В этом разделе мы научимся «делить» по матрице. Это позволяет нам элегантно решить матричное уравнение Ax=b:
Ах=b⇐⇒x=A−1b.
Однако при «делении на матрицы» следует соблюдать осторожность, поскольку не каждая матрица имеет обратную, а порядок умножения матриц важен.
Взаимная или обратное ненулевого числа a есть число b, которое характеризуется тем свойством, что ab=1. Например, обратное число 7 равно 1/7. Мы используем эту формулировку для определения обратной матрицы.
Например, обратное число 7 равно 1/7. Мы используем эту формулировку для определения обратной матрицы.
Определение
Пусть A — матрица размера n × n (квадратная). Мы говорим, что A является обратимым , если существует матрица B размера n × n такая, что
AB=In и BA=In.
В этом случае матрица B называется обратной матрицы A, и мы пишем B=A−1.
Мы должны потребовать AB=In и BA=In, потому что в общем случае умножение матриц не является коммутативным. Однако в этом следствии в разделе 3.6 мы покажем, что если A и B являются матрицами размера n × n, такими что AB = In, то автоматически BA = In.
Пример
Факты об обратимых матрицах
Пусть A и B — обратимые матрицы размера n × n.
- A−1 обратим, и его обращение равно (A−1)−1=A. Число
- AB обратимо, и обратное ему число равно (AB)−1=B−1A−1 (обратите внимание на порядок).
Доказательство
- Уравнения AA-1=In и A-1A=In одновременно отображают A-1 как инверсию A и A как инверсию A-1.

- Мы вычисляем
(B-1A-1)AB=B-1(A-1A)B=B-1InB=B-1B=In.
Здесь мы использовали ассоциативность матричного умножения и тот факт, что InB=B. Это показывает, что B−1A−1 является инверсией AB.
Почему инверсия AB не равна A−1B−1? Если бы это было так, то у нас было бы
In=(AB)(A-1B-1)=ABA-1B-1.
Но нет никаких оснований для того, чтобы ABA-1B-1 равнялась единичной матрице: нельзя поменять порядок A-1 и B, поэтому в этом выражении нечего отменять. На самом деле, если In=(AB)(A−1B−1), то мы можем умножить обе части справа на BA, чтобы сделать вывод, что AB=BA. Другими словами, (AB)-1=A-1B-1 тогда и только тогда, когда AB=BA.
В более общем смысле обратным произведением нескольких обратимых матриц является произведение обратных в обратном порядке; доказательство такое же. Например,
(АВС)-1=С-1В-1А-1.
До сих пор мы определяли обратную матрицу, не давая никакой стратегии ее вычисления. Мы делаем это сейчас, начиная со специального случая матриц 2×2. Затем мы дадим рецепт для случая n×n.
Затем мы дадим рецепт для случая n×n.
Определение
Определитель матрицы 2×2 есть число
detFabcdG=ad-bc.
Предложение
Пусть A=FabcdG.
- Если det(A)A=0, то A обратим, и A-1=1det(A)Fd-b-caG.
- Если det(A)=0, то A необратима.
Существует аналогичная формула для обратной матрицы размера n×n, но она не так проста и требует больших вычислительных ресурсов. Заинтересованный читатель может найти его в этом подразделе Раздела 4.2.
Пример
Следующая теорема дает общую процедуру вычисления A−1.
Теорема
Пусть A — матрица размера n × n, и пусть (A|In) — матрица, полученная путем увеличения A единичной матрицей. Если редуцированная ступенчатая форма строки (A|In) имеет форму (In|B), то A обратима и B=A−1. В противном случае A необратима.
Доказательство
Сначала предположим, что приведенная ступенчатая форма строки (A|In) не имеет формы (In|B). Это означает, что в первых n столбцах (нерасширенная часть) содержится менее n опорных точек, поэтому у A меньше n опорных точек. Отсюда следует, что Nul(A)A={0} (уравнение Ax=0 имеет свободную переменную), поэтому в Nul(A) существует ненулевой вектор v. Предположим, что существует матрица B такая, что BA=In. Затем
Это означает, что в первых n столбцах (нерасширенная часть) содержится менее n опорных точек, поэтому у A меньше n опорных точек. Отсюда следует, что Nul(A)A={0} (уравнение Ax=0 имеет свободную переменную), поэтому в Nul(A) существует ненулевой вектор v. Предположим, что существует матрица B такая, что BA=In. Затем
v=Inv=BAv=B0=0,
, что невозможно, так как vA=0. Следовательно, A необратима.
Теперь предположим, что сокращенная ступенчатая форма строки (A|In) имеет вид (In|B). В этом случае все опорные точки содержатся в нерасширенной части матрицы, поэтому расширенная часть не играет роли в сокращении строк: элементы расширенной части не влияют на выбор используемых операций над строками. Следовательно, редукция строк (A|In) эквивалентна решению n систем линейных уравнений Ax1=e1,Ax2=e2,…,Axn=en, где e1,e2,…,en стандартные векторы координат :
Ax1=e1:C1041000120100-3-4001DAx2=e2:C1041000120100-3-4001DAx3=e3:C1041000120100-3-4001D. Столбцы x1,x2,. ..,xn матрицы B в приведенной по строкам форме являются решениями следующих уравнений:
..,xn матрицы B в приведенной по строкам форме являются решениями следующих уравнений:
В соответствии с этим фактом в разделе 3.3 произведение Bei является просто i-м столбцом xi матрицы B, поэтому
ei=Axi=ABei
для всех i. По тому же факту i-й столбец матрицы AB равен ei, а это означает, что матрица AB единична. Таким образом, B является обратным A.
Пример (обратимая матрица)
Пример (необратимая матрица)
В этом подразделе мы научимся решать Ax=b путем «деления на A».
Теорема
Пусть A — обратимая матрица размера n × n, а b — вектор в Rn. Тогда матричное уравнение Ax=b имеет ровно одно решение:
х=А-1б.
Доказательство
Считаем:
Ax=b=⇒A-1(Ax)=A-1b=⇒(A-1A)x=A-1b=⇒Inx=A-1b=⇒x=A-1b.
Здесь мы использовали ассоциативность матричного умножения и тот факт, что Inx=x для любого вектора b.
Пример (Решение системы 2 × 2 с использованием инверсий)
Пример (Решение системы 3 × 3 с использованием инверсий)
Преимущество решения линейной системы с использованием обратных величин заключается в том, что решение матричного уравнения Ax=b для других или даже неизвестных значений b становится намного быстрее. Например, в приведенном выше примере решение системы уравнений
E2x1+3×2+2×3=b1x1+3×3=b22x1+2×2+3×3=b3,
, где b1,b2,b3 неизвестны, равно
Cx1x2x3D=C232103223D-1Cb1b2b3D=C-6-5932−422−3DCb1b2b3D=C−6b1−5b2+9b33b1+2b2−4b32b1+2b2−3b3D.
Как и в случае умножения матриц, обращение матриц полезно понимать как операцию линейных преобразований. Напомним, что тождественное преобразование на Rn обозначается IdRn.
Определение
Преобразование T:Rn→Rn является обратимым , если существует преобразование U:Rn→Rn такое, что T◦U=IdRn и U◦T=IdRn. В этом случае преобразование U называется обратным к T, и мы пишем U=T−1.
Инверсия U к T «отменяет» все, что сделал T. У нас есть
T◦U(x)=xandU◦T(x)=x
для всех векторов x. Это означает, что если вы примените T к x, затем примените U, вы получите вектор x обратно, и то же самое в другом порядке.
Пример (функции одной переменной)
Пример (Расширение)
Пример (вращение)
Пример (Отражение)
Не пример (проекция)
Предложение
- Преобразование T:Rn→Rn обратимо тогда и только тогда, когда оно взаимно однозначно и на.
- Если уже известно, что Т обратимо, то U:Rn→Rn является инверсией T при условии, что либо T◦U=IdRn, либо U◦T=IdRn: необходимо проверить только одно.
Как и следовало ожидать, матрица, обратная линейному преобразованию, является обратной матрицей преобразования, как утверждает следующая теорема.
Теорема
Пусть T:Rn→Rn — линейное преобразование со стандартной матрицей A. Тогда T обратимо тогда и только тогда, когда A обратимо, и в этом случае T−1 линейно со стандартной матрицей A−1.
Доказательство
Предположим, что T обратим. Пусть U:Rn→Rn — обратное к T. Мы утверждаем, что U линейно. Нам нужно проверить определяющие свойства в Разделе 3.3. Пусть u,v — векторы в Rn. Затем
u+v=T(U(u))+T(U(v))=T(U(u)+U(v))
по линейности T. Применение U к обеим сторонам дает
U(u+v)=UAT(U(u)+U(v))B=U(u)+U(v).
Пусть c — скаляр. Затем
cu=cT(U(u))=T(cU(u))
по линейности T. Применение U к обеим сторонам дает
U(cu)=UAT(cU(u))B=cU(u).
Поскольку U удовлетворяет определяющим свойствам в разделе 3.3, это линейное преобразование.
Теперь, когда мы знаем, что U является линейным, мы знаем, что у него есть стандартная матрица B. Согласно совместимости матричного умножения и композиции в разделе 3.4, матрица для T◦U равна AB. Но T◦U — это тождественное преобразование IdRn, а стандартной матрицей для IdRn является In, поэтому AB=In. Аналогичным образом показано, что BA=In. Следовательно, A обратим и B=A−1.
Обратно, предположим, что A обратим. Пусть B=A−1, и определим U:Rn→Rn как U(x)=Bx. По совместимости матричного умножения и композиции в разделе 3.4 матрица для T◦U есть AB=In, а матрица для U◦T есть BA=In. Следовательно,
T◦U(x)=ABx=Inx=xandU◦T(x)=BAx=Inx=x,
, который показывает, что T обратим с обратным преобразованием U.
Пример (Расширение)
Пример (вращение)
Пример (Отражение)
Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)
Обратная матрица
Обратная матрица
Определение и примеры
Напомним, что функции f и g обратны, если
f(g(x)) = г (f (х)) = х
Позже мы увидим, что матрицы можно рассматривать как функции из R n до R m и что матричное умножение равно состав этих функций. Обладая этим знанием, мы следующее:
Пусть А и B быть n x n матриц, то A и B являются обратными друг друга, то
AB = BA = I n
Пример
Рассмотрим матрицы
Мы
можно проверить, что когда мы умножаем A и B
в любом порядке мы получаем единичную матрицу. (Проверьте это.)
(Проверьте это.)
Нет у всех квадратных матриц есть обратные. Если матрица имеет обратную, мы называем ее неединственное число или обратимый . Иначе он называется единственное число . В следующем разделе мы увидим, как определить, матрица вырожденная или невырожденная.
Свойства инверсий
Ниже приведены четыре свойства инверсий.
- Если А
неособый, то и A -1 и
(A -1 ) -1 = А - Если А
и Б
невырожденные матрицы, то
АБ
неособый и
(AB) -1 = B -1 A -1
-1
- Если А
неособо тогда
(А Т ) -1 = (А -1 ) Т
- Если А
и Б
матрицы с
АВ = I н
затем и Б являются инверсиями друг друга.
Обратите внимание, что четвертое свойство подразумевает, что если AB = I затем BA = I.
Доказательство первых трех свойств элементарно, а четвертого слишком продвинутый для этого обсуждения. Докажем второе.
Доказательство того, что (AB) -1 = B -1 А -1
По свойству 4 нам нужно только показать, что
(AB)(B -1 A -1 ) = I
У нас есть
(AB)(B -1 A -1 ) = A(BB -1 )A -1 ассоциативная собственность
= АИА -1 определение обратного
= АА -1 определение идентификационная матрица
= I определение обратного
Нахождение обратного
Теперь, когда мы поняли, что такое инверсия, мы хотели бы найти способ
вычисление и обращение невырожденной матрицы. Мы используем определения
обратное и матричное умножение. Пусть А
— невырожденная матрица, а B — обратная к ней.
Затем
Мы используем определения
обратное и матричное умножение. Пусть А
— невырожденная матрица, а B — обратная к ней.
Затем
АВ = Я
Напомним, что мы находим j -й столбец произведения путем умножения A на j th столбец B. Теперь некоторые обозначения. Позволять e j быть м x 1 матрица, то есть j th столбец единичной матрицы и x j быть j й столбец B. Затем 90 009
Топор j = е j
Мы можем записать это в расширенной форме
[A|e j ]
Вместо того, чтобы решать эти расширенные задачи по одной за раз, используя строку операций, мы можем решать их одновременно. Решаем
[А | я]
Пример
Найти обратную матрицу
Раствор
обратная матрица — это правая часть окончательной расширенной матрицы
.
Это Пример показывает, что если A эквивалентна по строкам единичной матрице, то A неособый.
Линейные системы и инверсии
Мы можем использовать обратную матрицу для решения линейных систем. Предполагать что
Топор = б
Тогда так же, как мы делим на коэффициент, чтобы изолировать x, мы можем применить A -1 с обеих сторон для изолировать х.
A -1 Топор = А -1 б
IX = A -1 b x = А -1 б
Пример
Решить
х + 4z = 2
х + у + 6z = 3
-3x — 10z = 4
Раствор
Мы представить эту систему в матричной форме
Топор = b
с
Решение
x = A -1 б
Мы уже вычислили обратное. Мы прибываем в
решение
х = -18 y = -9 z = 5
Уведомление что если b нулевой вектор, то
Топор = 0
может решить с помощью
х = А -1 0 = 0
Это демонстрирует теорему
Теорема неособых эквивалентностей
Следующие эквивалентны (TFAE)
- А неособый
- Топор = 0 имеет только тривиальное решение
- А является строковым эквивалентом I
- линейная система Ax = b имеет единственный решение для каждой матрицы n x 1 б
Назад на главную страницу матриц и приложений
Назад на домашнюю страницу линейной алгебры
Назад к математике Домашняя страница отдела
электронная почта Вопросы и предложения
Математические слова: обратная матрица
Математические слова: обратная матрица
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 Тогда из равенстваследует,
что.
Если же матрицавырожденная,
то ее упрощенный видотличается
от единичной матрицы, а матрицане
имеет обратной.
Тогда из равенстваследует,
что.
Если же матрицавырожденная,
то ее упрощенный видотличается
от единичной матрицы, а матрицане
имеет обратной.
 Свойства частных решений
однородных СЛАУ.
Свойства частных решений
однородных СЛАУ. Другими
словами, функции y 1 (x ), y 2 (x ),
…, y n (x ) линейно
зависимы на
интервале (a , b ),
если существует равная нулю на (a , b ) их
нетривиальная линейная комбинация.
Функции y 1 (x ),y 2 (x ),
…, y n (x ) линейно
независимы на
интервале (a , b ),
если только тривиальная их линейная
комбинация тождественно равна нулю
на (a , b ).
Другими
словами, функции y 1 (x ), y 2 (x ),
…, y n (x ) линейно
зависимы на
интервале (a , b ),
если существует равная нулю на (a , b ) их
нетривиальная линейная комбинация.
Функции y 1 (x ),y 2 (x ),
…, y n (x ) линейно
независимы на
интервале (a , b ),
если только тривиальная их линейная
комбинация тождественно равна нулю
на (a , b ).
 теорему 3.4).
теорему 3.4).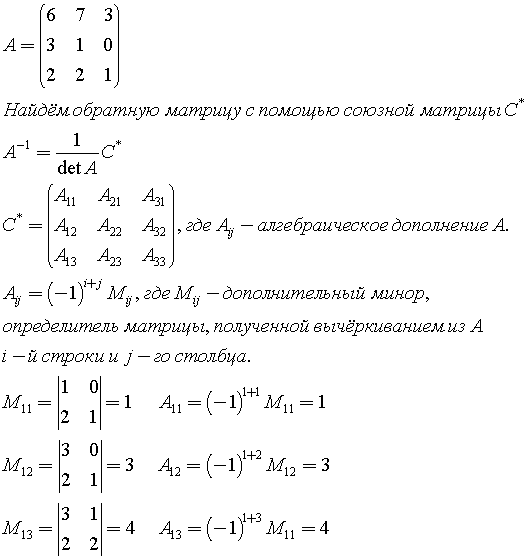 Ранг нулевой матрицы по определению
считают 0.
Ранг нулевой матрицы по определению
считают 0. 1.
Правило параллелограмма. Чтобы сложить
векторы и,
помещаем начала обоих в одну точку.
Достраиваем до параллелограмма
и из той же точки проводим
диагональ параллелограмма. Это и будет
сумма векторови.
1.
Правило параллелограмма. Чтобы сложить
векторы и,
помещаем начала обоих в одну точку.
Достраиваем до параллелограмма
и из той же точки проводим
диагональ параллелограмма. Это и будет
сумма векторови. Если
векторы перпендикулярны, их скалярное
произведение равно нулю.
А вот
так скалярное произведение выражается
через координаты векторов и .
Если
векторы перпендикулярны, их скалярное
произведение равно нулю.
А вот
так скалярное произведение выражается
через координаты векторов и .

 Рассмотрим алгоритм обращения матрицы. Пусть дана неособенная матрица n -го порядка:
Рассмотрим алгоритм обращения матрицы. Пусть дана неособенная матрица n -го порядка:
 см. пример оформления .
см. пример оформления .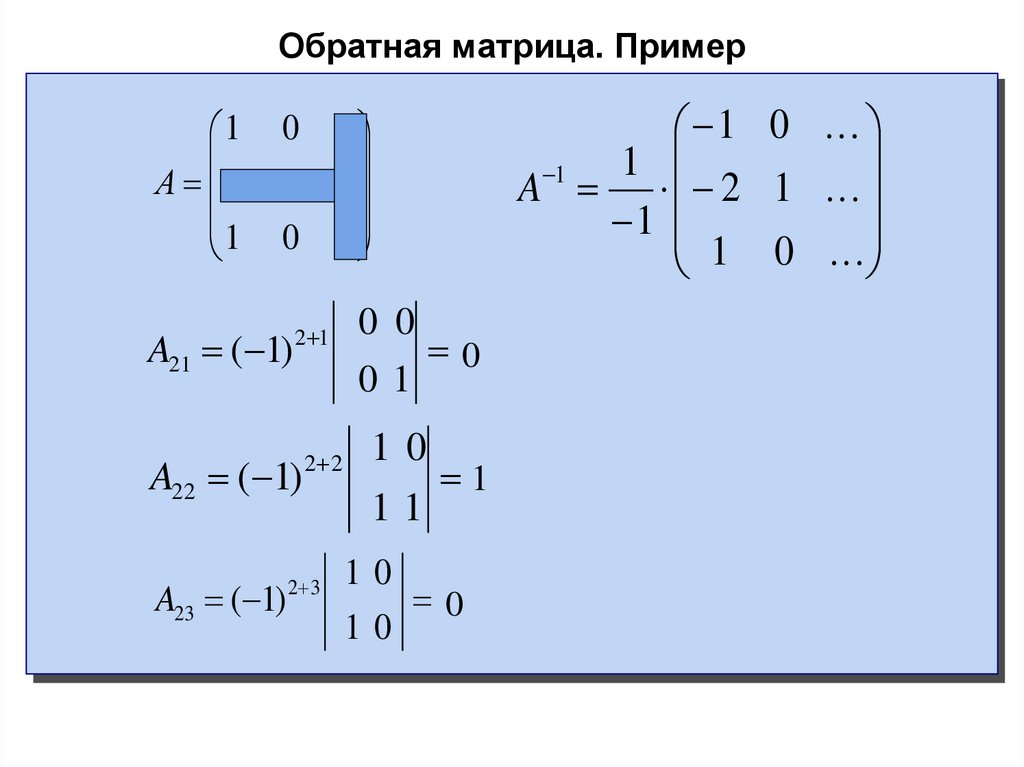
 Если вам дали что-то вроде «3 х = 6″, вы бы
решить, разделив обе части на 3.
Так как умножить на 1/3
то же, что деление
на 3,
вы также можете умножить обе части на 1/3
чтобы получить тот же ответ: х =
2. Если вам нужно решить
что-то вроде «(3/2) x = 6″, вы можете
по-прежнему делим обе части на 3/2,
но, вероятно, было проще умножить обе части на 2/3.
Обратная дробь
2/3 это
инверсия 3/2
потому что если умножить
две дроби, вы получите 1,
что в этом контексте называется «(мультипликативной) идентичностью»:
1
называется тождеством, потому что умножение чего-либо на 1
не меняет своего значения.
Если вам дали что-то вроде «3 х = 6″, вы бы
решить, разделив обе части на 3.
Так как умножить на 1/3
то же, что деление
на 3,
вы также можете умножить обе части на 1/3
чтобы получить тот же ответ: х =
2. Если вам нужно решить
что-то вроде «(3/2) x = 6″, вы можете
по-прежнему делим обе части на 3/2,
но, вероятно, было проще умножить обе части на 2/3.
Обратная дробь
2/3 это
инверсия 3/2
потому что если умножить
две дроби, вы получите 1,
что в этом контексте называется «(мультипликативной) идентичностью»:
1
называется тождеством, потому что умножение чего-либо на 1
не меняет своего значения. Но вы не можете делать деление с матрицами. С другой стороны, что, если вы
можно найти обратное число А ,
что-то похожее на нахождение обратной дроби выше? Обратное А ,
записывается как « А 1 »
и произносится « А инверсия», позволит вам отменить A из матричного уравнения, а затем решить для X .
Но вы не можете делать деление с матрицами. С другой стороны, что, если вы
можно найти обратное число А ,
что-то похожее на нахождение обратной дроби выше? Обратное А ,
записывается как « А 1 »
и произносится « А инверсия», позволит вам отменить A из матричного уравнения, а затем решить для X . А смысл матрицы идентичности в том, что IX = X для любой матрицы х (разумеется, конечно, «любая матрица правильного размера»).
А смысл матрицы идентичности в том, что IX = X для любой матрицы х (разумеется, конечно, «любая матрица правильного размера»). Вы не можете быть случайным с размещением матриц; Ты должен быть
точным, правильным и последовательным. Это единственный способ успешно
отменить А и решить матричное уравнение.
Вы не можете быть случайным с размещением матриц; Ты должен быть
точным, правильным и последовательным. Это единственный способ успешно
отменить А и решить матричное уравнение. (Как всегда с операциями со строками, не существует единственно «правильного» способа
сделать это. Ниже приведены лишь шаги, которые произошли с
мне. Ваши расчеты могут легко выглядеть совершенно по-другому.)
(Как всегда с операциями со строками, не существует единственно «правильного» способа
сделать это. Ниже приведены лишь шаги, которые произошли с
мне. Ваши расчеты могут легко выглядеть совершенно по-другому.)


 Когда
А умножается на А -1 результатом является единичная матрица I. Неквадратные матрицы не имеют обратных.
Когда
А умножается на А -1 результатом является единичная матрица I. Неквадратные матрицы не имеют обратных. Ярлык для матриц 2×2
Ярлык для матриц 2×2 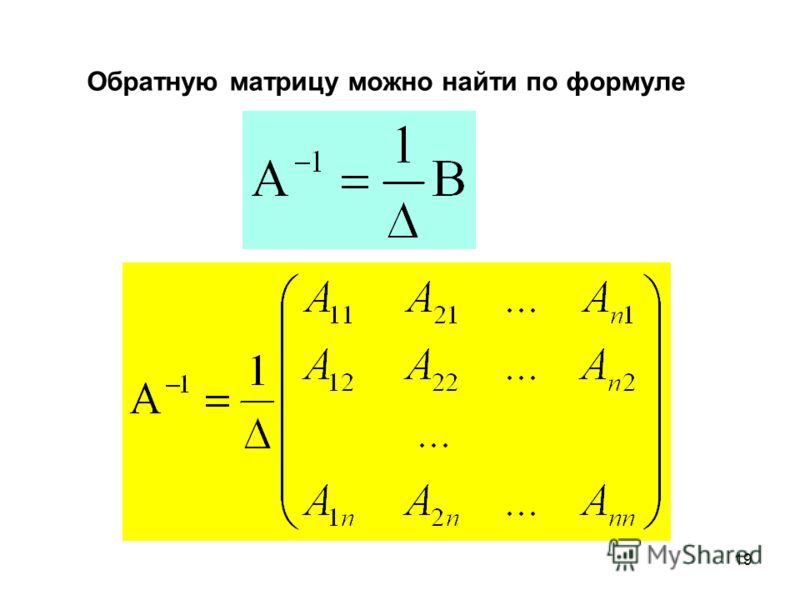
 Например, оказывается, что обратная матрица
Например, оказывается, что обратная матрица
 В третьем используется так называемая теорема Кэли-Гамильтона: в одних курсах она рассматривается, а в других нет.
В третьем используется так называемая теорема Кэли-Гамильтона: в одних курсах она рассматривается, а в других нет.