Авторизация
Размер:
AAA
Цвет: C C C
Изображения Вкл. Выкл.
Обычная версия сайта
Сведения об образовательной организации Контакты Старая версия сайта Версия для слабовидящих Версия для слабовидящих
Южно-Уральский государственный медицинский университет
- Университет
- События
- Новости
- ЮУГМУ сегодня
- Историческая справка
- Руководство
- Выборы ректора
- Лицензия, аккредитация и сертификаты
- Организационная структура
- Противодействие коррупции
- Первичная профсоюзная организация ЮУГМУ Профсоюза работников здравоохранения РФ
- Абитуриенту
- Новости для абитуриентов
- Центр довузовской подготовки
- Поступающим на специалитет
- Поступающим в ординатуру
- Поступающим в аспирантуру
- Поступающим в медицинский колледж
- Документы на право ведения образовательной деятельности
- Положения о приемной, экзаменационной и апелляционной комиссиях
- Информация об общежитиях
- Часто задаваемые вопросы
- Результаты приема студентов
- Информация для инвалидов
- Обучающемуся
- Факультеты
- Кафедры
- Медицинский колледж
- Ординатура
- Аспирантура
- Научная библиотека
- Образовательный портал
- Расписания
- Этический кодекс студентов медицинских вузов
- Совет студентов Минздрава России
- О допуске студентов к работе в медицинских организациях
- Иностранным обучающимся
- Медицинское обслуживание
- Информация об общежитиях
- Стипендиальное обеспечение
- Порядок перехода обучающихся с платного на бесплатное обучение
- Часто задаваемые вопросы
- Анкетирование
- Студенческие отряды
- Противодействие терроризму и экстремизму
- Специалисту
- Институт дополнительного профессионального образования
- Аккредитация специалистов
- Пациенту
- Клиника ФГБОУ ВО ЮУГМУ Минздрава России
- Профилактика новой коронавирусной инфекции, гриппа, ОРВИ, вакцинация
- ЗОЖ
- Научная работа
- Управление по научной и инновационной работе
- Экспериментально-биологическая клиника (виварий)
- Отдел международных связей
- НИИ иммунологии
- Центральная научно-исследовательская лаборатория
- НОЦ «Проблемы фундаментальной медицины»
- НОЦ «Клиническая фармакология»
- Конференции и другие мероприятия
- Диссертационные советы
- Журнал «Непрерывное медицинское образование и наука»
- Студенческое научное общество
- Совет молодых ученых и специалистов
Дифференциальные и интегральные законы распределения случайной величины
Случайная величина наилучшим и исчерпывающим образом характеризуется в теории вероятностей законом ее распределения.
Этот закон устанавливает связь между возможными значениями случайной величины и соответствующими этим значениям вероятностям их появления. Существует две формы описания закона распределения случайной величины — дифференциальная и интегральная. Причем, в метрологии в основном используется дифференциальная форма — закон распределения плотности вероятностей случайной величины.
Дифференциальный закон распределения характеризуется плотностью распределения вероятностей f(x) случайной величины х. Вероятность Р попадания случайной величины в интервал от х1 до х2 при этом дается формулой:
Графически эта вероятность представляет собой отношение площади под кривой f(x) в интервале от х1 до х2
к общей площади, ограниченной всей кривой распределения. Как правило, площадь под всей кривой распределения вероятностей нормируют на единицу.
В данном случае представлено распределение непрерывной случайной величины. Кроме них существуют и дискретные случайные величины, принимающие ряд определенных значений, которые можно пронумеровать.
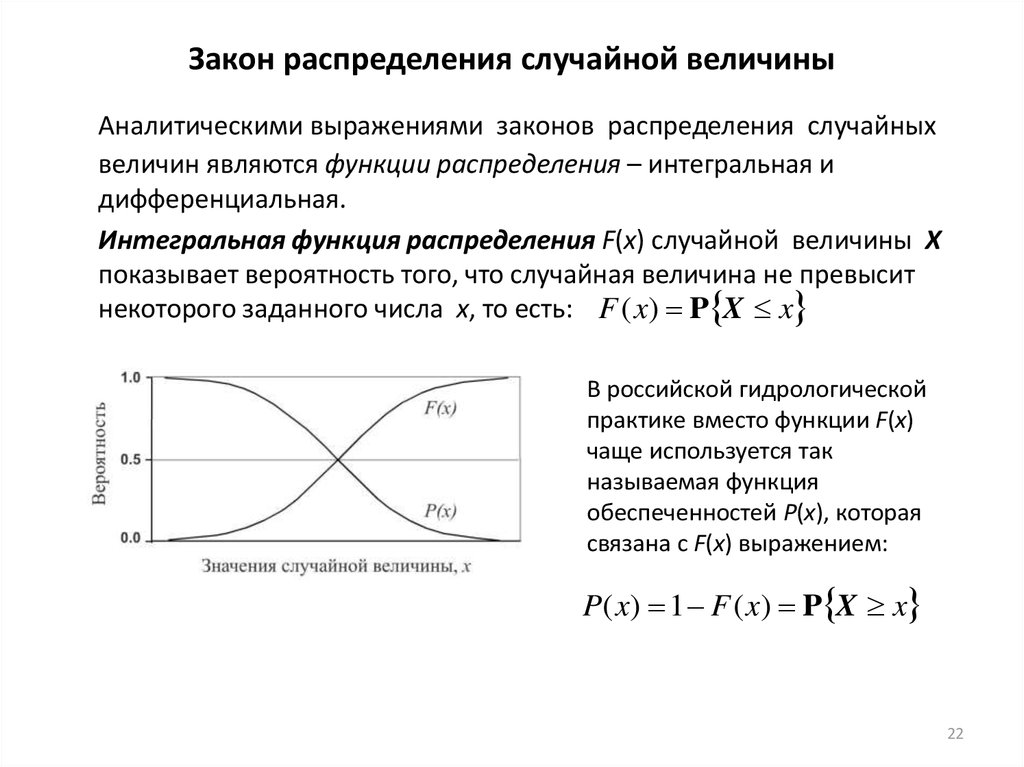
Интегральный закон распределения случайной величины представляет собой функцию F(x), определяемую формулой
Вероятность, что случайная величина будет меньше х1 дается значением функции F(х) при х = х1 :
Хотя закон распределения случайных величин является их полной вероятностной характеристикой, нахождение этого закона является довольно трудной задачей и требует проведения многочисленных измерений. Поэтому на практике для описания свойств случайной величины используют различные числовые характеристики распределений . К ним относятся моменты
случайных величин: начальные и центральные, которые представляют собой некоторые средние значения.
При этом если усредняются величины, отсчитываемые от начала координат, то моменты называются начальными, а если от центра распределения – то центральными.
Начальный момент k-го порядка определяется формулой:
Наибольший практический интерес представляет начальный момент первого порядка — математическое ожидание случайной величины m1 (k=1):
Математическое ожидание определяет положение центра группирования случайной величины, вокруг которого наблюдается ее рассеяние. Экспериментальной оценкой математического ожидания при многократных измерениях является
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас.
Бесплатные
корректировки и доработки. Узнайте стоимость своей работы.
Расчет стоимостиГарантииОтзывы
Центральный момент k-го порядка определяется формулой:
Особую роль играет центральный момент второго порядка. Он называется дисперсией D случайной величины и характеризует рассеяние отдельных ее значений:
На практике чаще используется среднее квадратическое отклонение σ (СКО) случайной величины, определяемое формулой:
При более подробном изучении распределений случайной величины используются моменты более высоких порядков. Так, любой нечетный центральный момент характеризует асимметрию распределения. Например, третий момент используют для нахождения коэффициента асимметрии
кривой распределения относительно математического ожидания.
Четвертый центральный момент характеризует остроту вершины кривой распределения.
Поможем написать любую работу на аналогичную тему
Реферат
Дифференциальные и интегральные законы распределения случайной величины
От 250 руб
Контрольная работа
Дифференциальные и интегральные законы распределения случайной величины
От 250 руб
Курсовая работа
Дифференциальные и интегральные законы распределения случайной величины
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
вероятность — Существование закона случайной величины
спросил
Изменено 7 лет, 2 месяца назад
Просмотрено 10 тысяч раз
$\begingroup$
Вот определение закона случайной величины.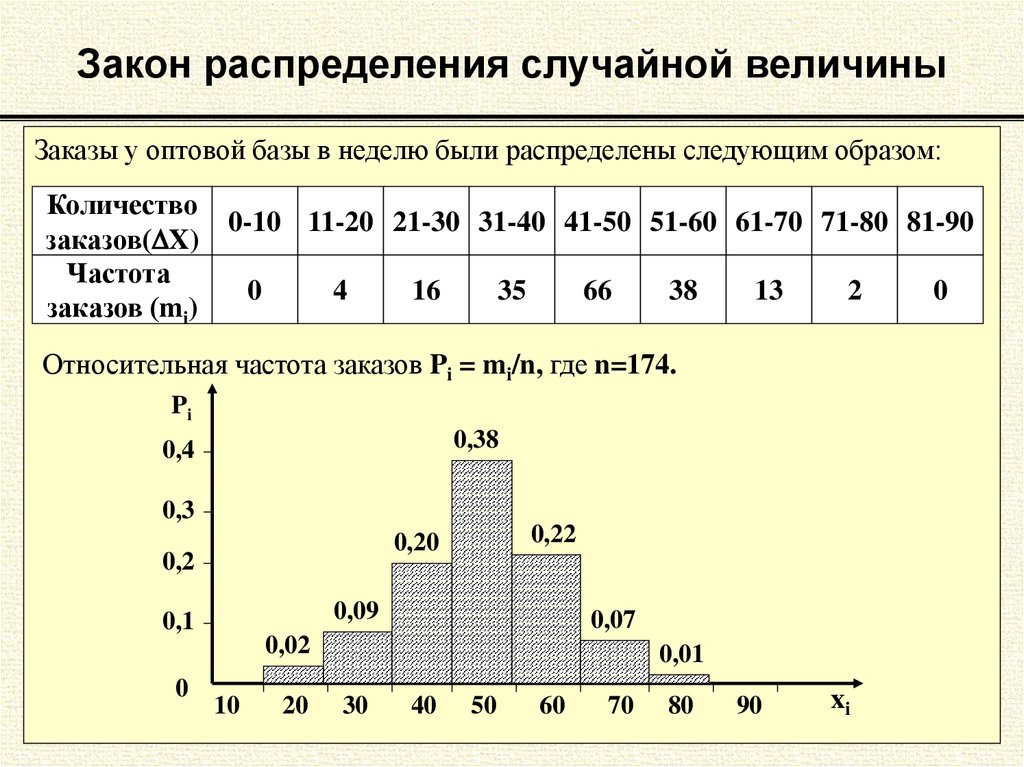
Пусть $X$ — случайная величина на $(\Omega,\mathcal{F}, \mathbb{P})$. Тогда закон $X$, обозначаемый $L_{X}$, представляет собой вероятностную меру на $(\mathbb{R},\mathcal{B}(\mathbb{R}))$ такую, что для всех $ B \in \mathcal{B}$, $L_X(B) = \mathbb{P}(X \in B)$, где $\mathcal{B}$ обозначает борелевское множество $\mathbb{R}$.
Я понимаю определение, но мне интересно, как мы узнаем, что такие $L_X$, как в этом определении, существуют?
Можем ли мы создать его явно? или мы знаем по какой-то теореме, что существует по крайней мере один $L_X$? 9{-1}(B) = \{\omega\in\Omega : X(\omega)\in B\}.
$$
Тогда у нас есть
$$
L_X(B) = \mathbb P\big( \{\omega\in\Omega : X(\omega)\in B\} \big).
$$
Это определенно определяет неотрицательную функцию , областью определения которой является $\mathcal B(\mathbb R)$. Далее возникает проблема доказательства того, что это действительно вероятностная мера. Он должен сопоставлять $\mathbb R$ меру $1$ и должен быть счетно-аддитивным.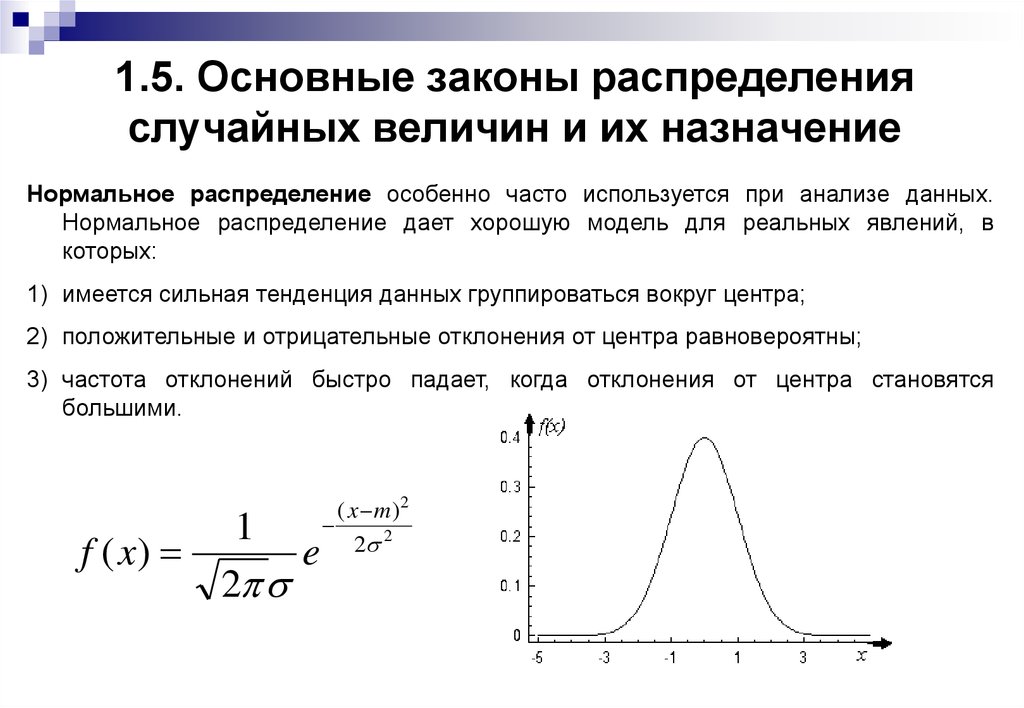
\infty \{\omega\in\Omega : X (\omega) \in B_i \}.
$$
Если $B$s попарно не пересекаются, то $X(\omega)$ не может быть в обоих $B_i$ и $B_j$ для $i\ne j$, поэтому $\omega$ не может быть в обоих $\{ \omega\in\Omega : X(\omega) \in B_i \}$ и $\{\omega\in\Omega : X(\omega) \in B_j \}$, так что они также попарно не пересекаются. Тогда мы можем использовать счетную аддитивность $\mathbb P$, чтобы показать счетную аддитивность $L_X$.
«Закон $X$» является синонимом «распределения вероятностей $X$».
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Найти закон распределения функции случайной величины
Задавать вопрос
спросил
Изменено 7 лет, 3 месяца назад
Просмотрено 756 раз
$\begingroup$
Пусть $X$ — случайная величина с экспоненциальным распределением $X\sim\operatorname{Exp}(\lambda)$, такая, что ее ожидаемое значение $\mathbb E[X] = 2$.
Пусть $f$ будет такой функцией, что:
$$f(x) = \begin{cases}\lceil x\rceil,& x\in[0,3)\\ 6,& x\geqslant 3\end{cases}$$
Определить закон распределения случайной величины $Y=f(X).$
Первое, что я сделал, это определил, что $\lambda$ равно $1/2$.