Этапы урока, содержание (задания) | Время | Деятельность учителя (описание, прямая речь) | Деятельность учащихся (описание, предполагаемые ответы) | Формы, методы и приемы обучения | Формируемые УУД |
1. Организационный момент. | 1 мин. | Приветствует учащихся. Проверяет готовность к уроку. Проверьте, чтобы у вас на партах был учебник и рабочая тетрадь. Начинается урок, | Приветствуют учителя. | Словесный (беседа) | КУУД – вступать в диалог с учителем |
2. Актуализация знаний. | 5 мин. | Повторение Давайте проверим ваши знания с прошлых уроков. Что такое неравенство? Что мы называем множеством решений неравенства? Давайте вспомним, какие виды решений неравенства существуют. Множество решений, бесконечное множество решений и пустое множество решений. — Что значит пустое множество? Теперь я вам представлю три неравенства, скажите в каком неравенстве множество решений, в каком бесконечное множество решений, а в каком пустое множество решений? B+5 10Y a 200 Запиши неравенства. Я буду говорить неравенства словами, а вы будете записывать его цифрами. а) 15 меньше или равно 34 б) 72 больше или равно 27 в) 37 больше 22 г) 46 меньше 92 д) 55 = 55 Какие знаки используются при решении неравенств? Молодцы! | Внимательно слушают учителя. Отвечают на вопросы. -выражение, показывающее, что одна величина больше или меньше другой — Пустое множество Во множестве нет элементов. — множество решений — пустое множество решений — бесконечное множество решений Слушают учителя. Выполняют задание. Выходят к доске желающие и записывают неравенства под диктовку. — Используются знаки «», «=» и «≤», и «≥». | Словесный (беседа, рассказ), наглядный (доска, рабочая тетрадь), практический (работа у доски, в тетради; ответы на вопросы) Фронтальная работа | КУУД – формулировать собственное мнение, вступать в диалог с учителем, учитывать мнение других; РУУД – принимать и сохранять учебную задачу, планировать свои действия; ЛУУД – интерес к новому содержанию; ПУУД — анализировать информацию, выбирать рациональный способ решения задачи. |
3. Целеполагание. | 3 мин. | Давайте запишем число и классная работа. Обратите внимание, сейчас я запишу на доске выражение : 5 Ребята, а что я записала? А что в нем не так? Правильно, ребята! Как вы думаете, как называются такие неравенства, в которых два знака? Кто сможет назвать тему нашего урока? Правильно. Мы будем говорить о двойном неравенстве. | Слушают учителя. Отвечают на вопросы учителя: — Неравенство. — В нем два знака неравенства. — Двойное; — Сложное. — Двойное неравенство. | Словесный (беседа), наглядный (интерактивная доска) | КУУД – формулировать собственное мнение; РУУД – принимать и сохранять учебную задачу, умение формулировать тему и цель урока; ПУУД — находить сходства, различия, закономерности. |
4. Изучение нового материала. | 10 – 12 минут | Ознакомляет с новым материалом с помощью практической работы. Откройте учебник на странице 10. Давайте прочитаем 1 задание. Я читаю, слушайте внимательно. О чем говорится в задании? Отметьте на числовом луче эти числа. Какие это числа? Назовите их. Правильно. Напишите карандашиком в учебнике эти числа. Как вы думаете, как можно записать это множество с помощью знаков неравенства? Числа 4, 5, 6 можно заменить буквой х, то есть она будет обозначать числа от 4 до 6. Это будет выглядеть так: 3 Запишите себе это неравенство в тетрадь. Теперь давайте, ознакомимся с правилом в учебнике в рамочке. Я читаю, вы слушаете. Прочитайте каждый про себя данное правило. — Кто может объяснить: Что такое двойное неравенство? Почему неравенство называется двойным? Как читают двойное неравенство, например, из нашего правила. Какие числа будут являться решением неравенства? Почему именно эти числа? Правильно. Обратите внимание на линейку, мы видим, что нам нужны числа больше 5, но меньше 10. Еще раз назовите эти числа. А что происходит, если в записи двойного неравенства используется, к примеру, знак «больше или равно»? Да, конечно. Обратите внимание на двойные неравенства, что мы видим? Молодцы! | Открывают учебник на нужной странице и внимательно слушают чтение задания учителя. — Нам нужно отметить на числовом луче множество чисел, которые одновременно больше 3 и меньше 7. — Отмечают числа. — 4, 5, 6. — 3 — 3 Слушают учителя и записывают выражение в тетрадь. Учащиеся смотрят на страницу 10 и слушают правило, прочтенное учителем. Далее читают каждый про себя данное правило. — Например, арбуз. В правиле сказано, что он тяжелее одной 5-килограммовой гири, но легче двух таких гирь. Как показано на картинке. — Потому что в нем объединили два неравенства. — х больше пяти и меньше десяти. — 6, 7, 8, 9. Потому что они входят в промежуток между числами 5 и 10. Смотрят на линейку в правиле и отвечают: 6, 7, 8, 9. — Множество решений расширяется. — Что когда появляется знак «меньше или равно», то число, которое меньше, тоже входит во множество решений данного неравенства. | Словесный (беседа, рассказ, рассуждение), наглядный (учебник, доска, презентация), практический (выполнение заданий по новому материалу | КУУД – вступать в диалог с учителем и одноклассниками, формулировать собственное мнение, учитывать мнение других; РУУД – принимать и сохранять учебную задачу, планировать этапы решения задачи; ПУУД — анализировать информацию, выбирать рациональный способ решения задачи; — устанавливать зависимости, соотношения между объектами в процессе наблюдения и сравнения; — находить сходства, различия, закономерности; ЛУУД – интерес к новому содержанию. |
5. Физическая минутка. | 1 – 2 мин. | Учитель показывает движения со словами: Поворот, наклон, прыжок, Улыбнись давай, дружок. Еще попрыгай: раз, два, три! На соседа посмотри, Руки вверх и тут же вниз И за парту вновь садись. Мульдимедийная презентация Организует выполнение гимнастики для глаз | Повторяют движения за учителем под стихотворение. Выполняют гимнастику для глаз по упражнениям презентации | Словесный (беседа), наглядный (действия учителя), практический (выполнение упражнений) | КУУД – вступать в диалог с учителем; РУУД – принимать и сохранять учебную задачу. |
6. Практическая работа | 7 – 10 минут | Давайте выполним задание на странице 10, №2. Прочитай неравенства. Первый ряд начинает читать, остальные слушают. Молодцы! Справились с заданием. Следующее задание №3. Прочитайте задание про себя. Что от нас требуют в задании? Хорошо. Два человека идут к доске, остальные решают у себя в тетради и позже мы проверим, что у вас получилось. Итак, что получилось у ребят? Проверяем. Правильно? Следующее смотрим. Верно? У всех так? Молодцы! Присаживайтесь. Справились с трудным заданием. Впереди ждет еще одно задание под номером 5. Прочитайте задание. Что нужно сделать в задании? Хорошо. Два человека выходят к доске и записывают неравенства. Один под буквами а и б, другой – под буквами – в и г. Каждый выполняет задание в тетради, и потом мы проверим, что у вас получилось. Приступайте. Смотрим на доску и проверяем. У всех такие равенства получились? Молодцы! Мы справились с еще одним трудным и интересным заданием. | Открывают учебник на странице 10. Читают неравенства по цепочке. — а больше 7 и меньше 12; — b больше 15 и меньше или равно 96 и т. — Замени двойное неравенство двумя неравенствами. — Заменить двойные неравенства двумя неравенствами. Двое идут к доске и пишут неравенства. — Первое неравенство делится на: х больше или равно 9, а второе: х меньше 18. — Правильно. — у больше 3 и второе: у меньше или равно 11. — Да, верно. Смотрят и читают задание №5. — Записать двойные неравенства. Выходят к доске и работают, остальные выполняют задание в тетради. — 4 — 5 “больше или равно» k — 10 m “меньше или равно» 25 и т.д. Да. | Словесный (беседа, рассказ), наглядный (учебник, доска, дидактический материал), практический (выполнение заданий в учебнике и в тетради) | КУУД – формулировать собственное мнение; РУУД – принимать и сохранять учебную задачу, планировать этапы решения задачи; ПУУД — анализировать информацию, выбирать рациональный способ решения задачи; ЛУУД – интерес к новому содержанию. |
7. Самостоятельная работа. | 5 мин. | Теперь я проверю, как вы усвоили наш сегодняшний материал, самостоятельно задание 5. | Получают карточки, подписывают их и решают задания. | Словесный (беседа), наглядный (дидактический материал), практический (выполнение заданий) | КУУД — вступать в диалог с учителем; РУУД – принимать и сохранять учебную задачу, планировать свои действия. |
8. Подведение итогов. | 1 – 2 мин. | — Что нового мы узнали на уроке? — Какие задания мы выполняли на уроке? Да, мы сегодня много с вами сделали. | — Мы узнали, что такое двойное неравенство. — Как они читаются. — Их состав. — Составляли двойные неравенства, читали их. — Из двойного неравенства делали два неравенства. | Словесный (беседа), наглядный (презентация) | КУУД – формулировать собственное мнение, учитывать другие мнения; ЛУУД – интерес к новому содержанию. |
9. Рефлексия. | 2 мин. | Мне хочется узнать, как вы оцените свою работу. В этом мне помогут смайлики разного цвета. На партах лежат смайлики разных цветов. Я рада, что вы честно оценили свою работу. Спасибо за урок. | Дети оценивают свою работу на уроке. | Словесный (беседа), наглядный (дидактический материал), практический (работа с карточками) | КУУД – вступать в диалог с учителем; РУУД – адекватно воспринимать оценку учителя и сверстников, принимать и сохранять учебную задачу |
Проверяет свою готовность к уроку.
Значит масса арбуза заключена в промежутке от 5 кг до 10 кг. И чтобы не писать два неравенства, пишут одно двойное неравенство.
д.
Двойные неравенства. 2 способа решения
Например:
\(5<11<17\)
\(-2\leq3x+5\leq2\)
\(2x-5\leq3x+7\leq8x\)
Двойное неравенство по своей сути – это система из двух неравенств, записанных в одну строку. Поэтому их всегда можно представить в виде системы.
Например:
\(-2\leq3x+5\leq2\Leftrightarrow\begin{cases}-2\leq3x+5\\3x+5\leq2\end{cases}\)
\(2x-5\leq3x+7\leq8x\Leftrightarrow\begin{cases}2x-5\leq3x+7\\3x+7\leq8x\end{cases}\)
Но делать это нужно не всегда.
1) Если в крайней левой и крайней правой частях двойного неравенства нет неизвестных, то удобнее оставить его как есть. При этом в процессе решения стремится равносильными преобразованиями привести неравенство к виду \([число]\)\(<\)\(x\)\(<\)\([число]\).
Пример: Решите двойное неравенство:
|
\(-2\leq3x+5\leq2\) \(|-5\) |
Здесь нет неизвестных по краям, поэтому к системе переходить не будем. Вместо этого делаем такие преобразования, чтоб в центре остался голый икс, а по краям — числа. |
|
|
\(-7≤3x≤-3\) \(|:3\) |
Теперь нам мешает \(3\). Поделим все три части неравенства на \(3\). |
|
|
\(-\)\(\frac{7}{3}\)\(\leq x \leq-1\) |
Готово, наш икс «голый». Можно записывать ответ. |
Ответ: \([-\)\(\frac{7}{3}\)\(;-1]\)
2) Если в крайних частях двойного неравенства есть неизвестные лучше перевести неравенство в систему и решать его как обычную систему неравенств.
Пример: Решите двойное неравенство:
|
\(2x-5<3x+7≤8x\) |
В крайней левой и крайней правой частях есть неизвестные –значит переходим к системе. |
|
\(\begin{cases}2x-5<3x+7\\3x+7\leq8x\end{cases}\) |
Решаем обычные линейные неравенства: все, что с иксами переносим в левую сторону, все что без иксов — в правую. |
|
\(\begin{cases}2x-3x<7+5\\3x-8x\leq-7\end{cases}\) |
Приводим подобные слагаемые |
|
\(\begin{cases}-x<12 \\-5x\leq-7 \end{cases}\) |
«Оголим» иксы, поделив верхнее неравенство на \((-1)\), нижнее на \((-5)\). Не забываем при этом перевернуть знаки сравнения, так как мы делим на отрицательное число. |
|
\(\begin{cases}x>-12 \\x\geq \frac{7}{5}\end{cases}\) |
Отметим на числовой оси оба решения |
|
Так как у нас система, то мы ищем значения иксов, которые подойдут обоим неравенствам, т. |
е. интервал, где есть двойная штриховка: и сверху, и снизу. Его и запишем ответ.
Ответ: \([\)\(\frac{7}{5}\)\(;\infty)\)
Вопрос Видео: Решение двойных неравенств с переменными по трем сторонам
Стенограмма видео
Найдите все значения 𝑥, удовлетворяющие неравенству минус 20 минус 𝑥 меньше или равно трем 𝑥 плюс два, что меньше 18 минус два 𝑥 . Запишите ответ в виде интервала.
Для начала мы решим эту задачу, разделив ее на две части: первое неравенство слева, а затем второе неравенство справа. Итак, мы можем приступить к решению нашего первого неравенства. Итак, у нас есть минус 20 минус 𝑥 меньше или равно трем 𝑥 плюс два. Итак, мы собираемся решить это неравенство, но помня так же, как мы решаем уравнение. Итак, первое, что мы собираемся сделать, это на самом деле мы собираемся вычесть два с каждой стороны, что дает нам минус 22 минус 𝑥 меньше или равно трем 𝑥.
Хорошо, теперь наш следующий шаг, мы на самом деле собираемся добавить 𝑥 к каждой стороне, что дает нам минус 22 меньше или равно четырем 𝑥.
Хорошо, теперь мы можем решить это неравенство, потому что мы собираемся разделить три на четыре, что дает минус 22, если четыре меньше или равны 𝑥. Просто чтобы привести это в порядок, мы упростим эту дробь в левой части. Таким образом, мы можем сказать, что минус 11 больше двух меньше или равно 𝑥. Большой! Итак, наше первое неравенство решено.
Теперь мы продолжим и решим правую часть, наше второе неравенство. И это второе неравенство говорит нам, что три 𝑥 плюс два меньше, чем 18 минус два 𝑥. Хорошо, снова решим это так, как мы решаем уравнение, поэтому первое, что мы собираемся сделать, это на самом деле мы собираемся вычесть два из каждой стороны, что дает нам три 𝑥 меньше, чем 16 минус два 𝑥. Итак, теперь мы добавим по две 𝑥 с каждой стороны. Таким образом, мы получаем, что пять 𝑥 меньше 16.
И затем, наконец, чтобы решить наше неравенство, мы делим обе части на пять, что дает нам, что 𝑥 меньше 16 на пять. Так здорово! Мы решили оба неравенства. Итак, давайте теперь соберем их вместе, чтобы увидеть, какими могут быть наши возможные значения 𝑥.
Если мы объединим наши решения, мы увидим, что 𝑥 больше или равно минус 11 для двух и меньше 16 для пяти. Хорошо, давайте покажем, что это на самом деле означает. Итак, если мы посмотрим на это на числовой прямой, мы увидим это вот так, где мы фактически получили заполненную точку над нашим минусом 11 над двумя. И это потому, что он меньше или равен. И тогда у нас фактически есть открытый круг над нашими 16 против пяти. И это потому, что он просто говорит, что это больше, чем 𝑥.
Итак, мы решили эту проблему. И мы знаем, где лежат наши ценности. Но мы закончили? Ну, нет, потому что на самом деле наш вопрос просит нас записать наш ответ в виде интервала. Таким образом, в интервальной записи это будет наше решение со скобкой слева. И это потому, что он меньше или равен. И снова это то же самое, что когда мы показываем на числовой строке. У нас там другое обозначение и у нас есть цветной кружок.
Но когда мы используем обозначение интервала, мы фактически используем для этого скобки.
А справа у нас скобки. И мы используем эту скобку в правой части, потому что, как мы видим, здесь просто 𝑥 меньше 16 на пять, не меньше или равно. И снова мы получили обозначение открытого круга. Итак, мы подошли к окончательному ответу. И это написано как интервал.
1.4: Составные неравенства — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19681
- Дэвид Арнольд
- Колледж секвойи
В этом разделе обсуждается метод, используемый для решения составных неравенств, который представляет собой фразу, которая обычно относится к паре неравенств, соединенных либо словом «и», либо словом «или».
Простые линейные неравенства
Как и при решении уравнений, вы можете прибавить или вычесть одинаковую сумму из обеих частей неравенства.
Свойство \(\PageIndex{1}\)
Пусть \(a\) и \(b\) — действительные числа с \(a \[a+c и \[a-c Эта утилита одинаково действительна, если вы замените «less чем» с \(>, \leq\) или \(\geq\). Пример \(\PageIndex{1}\) Решить неравенство \(x + 3 < 8\) для \(x.\) Решение Вычесть \(3\) с обеих сторон неравенство и упростить. \[\begin{align*} x+3 &<8 \\ x+3-3 &<8-3 \\ x &<5 \end{align*}\] Таким образом, все действительные числа меньше чем \(5\) являются решениями неравенства. Традиционно набор решений неравенств изображается на числовой прямой. Мы можем описать набор решений, используя построитель набора и нотацию интервала. Решение: \[(-\infty, 5)=\{x : x<5\}\nonumber\] Важным понятием является идея эквивалентных неравенств. Эквивалентные неравенства. Два неравенства называются эквивалентными тогда и только тогда, когда они имеют одно и то же множество решений. Обратите внимание, что это определение аналогично определению эквивалентных уравнений. То есть два неравенства эквивалентны, если все решения первого неравенства являются также решениями второго неравенства, и наоборот. Таким образом, в примере \(\PageIndex{1}\) вычитание трех из обеих частей исходного неравенства дает эквивалентное неравенство. То есть неравенства \(x+3 < 8\) и \(x < 5\) имеют одно и то же множество решений, а именно, все действительные числа, меньшие 5. Неслучайно инструменты в Свойстве \( \PageIndex{1}\) производят эквивалентные неравенства. Всякий раз, когда вы добавляете или вычитаете одинаковую сумму из обеих частей неравенства, полученное неравенство эквивалентно исходному (у них один и тот же набор решений). Давайте посмотрим на другой пример. Пример \(\PageIndex{2}\) Решите неравенство \(x-5 \geq 4\) для \(x.\) Решение Добавьте 5 к обеим частям неравенства и упрощать. \[\begin{align*} x-5 & \geq 4 \\ x-5+5 & \geq 4+5 \\ x & \geq 9 \end{align*}\] Закрасить раствор на числовой строке. В построителе наборов и интервальных обозначениях решение: \[[9, \infty)=\{x : x \geq 9\} \nonumber\] Вы также можете умножить или разделить обе стороны на одно и то же положительное число. Свойство \(\PageIndex{2}\) Пусть \(a\) и \(b\) – действительные числа с \(a \[a c и \[\frac{a}{c}<\frac{b}{c}\] Опять же, эта утилита одинаково действительна, если вы замените символ «меньше чем» на \(>, \leq, \text{или} \geq.\) Инструменты в свойстве 4 всегда производят эквивалентные неравенства. Пример \(\PageIndex{3}\) Решить неравенство \(3x \leq −18\)для \(x.\) Решение Разделить обе части неравенства на \(3 \) и упростить. \[\begin{align*} 3 x & \leq-18 \\ \frac{3 x}{3} & \leq \frac{-18}{3} \\ x & \leq-6 \end {align*}\] Нарисуйте решение на числовой прямой. В построителе наборов и интервальных обозначениях решение: \[(-\infty,-6]=\{x : x \leq-6\} \nonumber\] На данный момент нет никакой разницы между техникой решения неравенств и методикой решения уравнений. Однако есть одно важное исключение. Рассмотрим на мгновение истинное утверждение \[-2<6 \label{eq6}\] Если вы умножите обе части неравенства \ref{eq6} на \(3,\), вы все равно получите истинное утверждение; т. е. \[-6<18 \nonumber\] Но если вы умножите обе части неравенства \ref{eq6} на \(−3,\), вам нужно «обратить символ неравенства», чтобы сохранить истинное заявление; то есть \[6>-18 \nonumber\] Это обсуждение приводит к следующему свойству. Свойство \(\PageIndex{3}\) Пусть \(a\) и \(b\) — действительные числа с \(a < b\). Если \(c\) - любое действительное отрицательное число, то \[a c>b c\] и \[\frac{a}{c}>\frac{b}{c}\] Обратите внимание, что вы «переворачиваете знак неравенства», когда умножаете или делите обе части неравенства на отрицательное число. Опять же, эта утилита одинаково действительна, если вы замените символ «меньше» на \(>, \leq,\) или \(\geq\). Инструменты в Property \(\PageIndex{3}\) всегда производят эквивалентные неравенства. Пример \(\PageIndex{4}\) Решить неравенство \(−5x > 10\) для \(x.\) Решение Разделить обе части неравенства на \(−5 \) и перевернуть знак неравенства. Упрощать. \[\begin{array}{r}{-5 x>10} \\ {\dfrac{-5 x}{-5}<\dfrac{10}{-5}} \\ {\quad x <-2}\end{array} \nonumber\] Нарисуйте решение на числовой прямой. В построителе наборов и интервальной нотации решение равно \[(-\infty,-2)=\{x : x<-2\} \nonumber\] Теперь обратим наше внимание на решение составных неравенств. В этом случае лучший способ учиться — это делать. Начнем с примера. Пример \(\PageIndex{5}\) Решите следующее составное неравенство для \(x.\) \[3-2 x<-1 \quad \text { or } \quad 3-2 x > Решение Сначала решим каждое из неравенств независимо. В первом неравенстве прибавьте \(−3\) к обеим частям неравенства, затем разделите на \(−2,\), поменяв знак неравенства на противоположный. \[\begin{align*} 3-2 x &<-1 \\-2 x &<-4 \\ x &>2 \end{align*}\] Заштрихуйте решение на числовой прямой. Точно такую же последовательность операций можно использовать для решения второго неравенства \[\begin{align*} 3-2 x &>1 \\-2 x &>-2 \\ x &<1 \end{align*}\] Хотя вы решаете каждую часть неравенства независимо друг от друга, вам нужно организовать свою работу следующим образом, расположив решение числового ряда для первого неравенства над решением второго неравенства. \[\begin{array}{rllllrll}{3-2 x}&{<}&{-1} & {\text {или}} & {\quad 3-2 x}&{>}&{ 1} \\ {-2 x}&{<}&{-4} & &{-2 x}&{> (2, \infty)=\{x : x<1 \text { or } x>2\} \nonumber\] Давайте рассмотрим другой пример. Пример \(\PageIndex{6}\) Решите следующее составное неравенство для \(x.\) \[-1<3-2 x<1 \label{eq12}\] Решение Напомним, что \(a < x < b\) идентично утверждению \(x > a\) и \(x < b.\). Таким образом, мы можем записать составное неравенство \(−1 < 3 − 2x < 1\) в виде \[3-2 x>-1 \quad \text { and } \quad 3-2 x<1 \label{eq13}\] Решите каждое неравенство самостоятельно, организовав работу следующим образом. \[\begin{array}{rllllrll}{3-2 x}&{>}&{-1} & {\text {и}} & {\quad 3-2 x}&{<}&{ 1} \\ {-2 x}&{>}&{-4} & &{-2 x}&{<}&{-2} \\ {x}&{<}&{2} && {x }&{>}&{1}\end{array} \label{eq14}\] Заштрихуйте решение каждого неравенства на отдельных действительных линиях, одну поверх другой Решение, как в интервальных, так и в обозначениях построителя множеств, равно \[(1,2)=\{x : 1 Обратите внимание, что в нашем ответе мы использовали компактную форму составного неравенства. С тем же успехом мы могли бы использовать \[(1,2)=\{x : x>1 \text { and } x<2\} \nonumber\] Обе формы записи построителя наборов одинаково допустимы. . Вы можете использовать любой из них, но вы должны понимать оба. Альтернативный подход. Возможно, вы заметили, что при решении второго неравенства в \ref{eq14} вы повторяете те же операции, что и при решении первого неравенства. То есть вы вычли \(3\) из обеих частей неравенства, а затем разделили обе части неравенства на \(−2,\), поменяв знак неравенства на противоположный. Это повторение раздражает и предлагает возможный короткий путь в данной конкретной ситуации. Вместо того, чтобы разбивать составное неравенство \ref{eq12} на две части (как в \ref{eq13}), давайте сохраним неравенство вместе, как в \[-1<3-2 x<1 \label{eq16}\] Теперь правила работы с этой формой. Свойство \(\PageIndex{4}\) При работе с составным неравенством вида \[a можно прибавлять (или вычитать) ту же сумму к (из) все три части неравенства, как в \[a+c или \[a-c Вы также можете умножить все три части на то же самое положительное число \(c > 0,\) как в \[c a Однако, если вы умножите все три части на одно и то же отрицательное число \(c < 0,\) тогда не забудьте поменять местами знаки неравенства, как в \[c a>c x>c b\] Правила деления идентичны правилам умножения. Если \(c > 0\) (положительно), то \[\frac{a}{c}<\frac{x}{c}<\frac{b}{c}\] Если \( c < 0\) (отрицательно), то при делении знаки неравенства меняются местами. \[\frac{a}{c}>\frac{x}{c}>\frac{b}{c}\] Каждый из инструментов в свойстве \(\PageIndex{4}\) всегда производят эквивалентные неравенства. Итак, вернемся к составному неравенству \ref{eq16} и вычтем \(3\) из всех трех членов неравенства. \[\begin{array}{c}{-1<3-2 x<1} \\ {-1-3<3-2 x-3<1-3} \\ {-4<-2 x<-2}\end{array} \nonumber\] Затем разделите все три члена на \(−2,\), меняя при этом знаки неравенства. \[\begin{array}{c}{-4<-2 x<-2} \\ {\dfrac{-4}{-2}>\dfrac{-2 x}{-2}>\ dfrac{-2}{-2}} \\ {2>x>1}\end{array} \nonumber\] Принято менять порядок этого последнего неравенства. Читая неравенство справа налево, мы получаем \[1 , которое описывает действительные числа больше 1 и меньше \(2.\) Решение рисуется на следующую реальную строку. Обратите внимание, что это идентично решению, установленному на реальной линии на рисунке \(\PageIndex{2}\). Обратите также внимание, что этот второй альтернативный метод более эффективен, особенно если вы немного поработаете в уме. Рассмотрим следующую последовательность, в которой мы вычитаем три из всех трех членов, затем делим все три члена на \(−2,\), меняя знаки неравенства, а затем, наконец, читаем неравенство в противоположном направлении. \[\begin{array}{c}{-1<3-2 x<1} \\ {-4<-2 x<-2} \\ {\quad 2>x>1} \\ { \quad 1 Давайте посмотрим на другой пример. Пример \(\PageIndex{7}\) Решите следующее составное неравенство для \(x.\) \[-1 Решение Сначала умножим все три члена на \(2,\), чтобы очистить дроби. \[2(-1)<2\left(x-\frac{x+1}{2}\right) \leq 2(2) \nonumber\] \[-2<2(x) -2\left(\frac{x+1}{2}\right) \leq 4 \nonumber\] Отмена. Обратите внимание на использование круглых скобок, что очень важно, когда используется знак минус. \[-2<2 x-\cancel{2}\left(\frac{x+1}{\cancel{2}}\right) \leq 4 \nonnumber\] \[-2<2 x-(x+1) \leq 4 \nonumber\] Распределите знак минус и упростите. \[\begin{align*} -2 &< &&2x-x-1 &&\leq 4 \\ -2 &< &&x-1&& \leq 4\end{align*}\] Добавить \(1\ ) всем трем участникам. \[-1 Это решение описывает действительные числа больше \(-1\) и меньше \(5,\), включая \(5. Ответ, описанный как в нотации интервала, так и в нотации построителя множеств, следует за \[(-1,5]=\{x :-1 Давайте посмотрим на другой пример Пример \(\PageIndex{8}\) Решите следующее составное неравенство для \(x.\) \[x \leq 2 x-3 \leq 5 \nonumber\] Решение Предположим, что мы пытаемся изолировать \(x\), как мы это делали в примере \(\PageIndex{7}\). Возможно, мы попытаемся добавить \(−x\) ко всем трем элементам. \[\begin{align*} x &\leq &&2x-3 &&\leq 5 \\ x-x &\leq &&2x-3-x &&\leq 5-x \\ 0 &\leq &&x-3 &&\leq 5-x \end{align*}\] Ну, это мало помогло, просто перенес задачу с \(x\) на другой конец неравенства. Подобные попытки не помогут выделить \(x. Решение: разделим неравенство (со словом «и», разумеется). \[x \leq 2 x-3 \quad \text { и } \quad 2 x-3 \leq 5 \nonumber\] Мы можем решить первое неравенство, вычитая \(2x\) из обеих частей неравенства, затем умножая обе части на \(−1,\), обращая неравенство в процессе \[\begin{align*} x & \leq 2 x-3 \\-x & \leq-3 \\ x & \geq 3 \end{align*}\] Чтобы решить второе неравенство, прибавьте \(3\) к обеим частям, затем разделите обе стороны на \(2\): \[\begin{align*} 2 x-3 & \leq 5 \\ 2 x & \leq 8 \\ x & \leq 4 \end{align*} \] Конечно, вы, вероятно, захотите организовать свою работу следующим образом \[\begin{array}{rllrl} x & \leq 2 x-3 & \text{and} &2 x-3 & \leq 5 \\ -x & \leq-3 && 2 x & \leq 8 \\ x & \geq 3 & & x & \leq 4\end{array} \nonumber\] Таким образом, нам нужно заштриховать на числовой прямой все действительные числа, которые больше или равны \(3\) и меньше или равно \(4,\), как показано на рисунке \(\PageIndex{5}\).
Составные неравенства
В предыдущем разделе мы изучили тонкости «и» и «или», пересечения и объединения, а также рассмотрели некоторые простые составные неравенства. В этом разделе мы опираемся на эти основы и обращаем внимание на более сложные примеры.
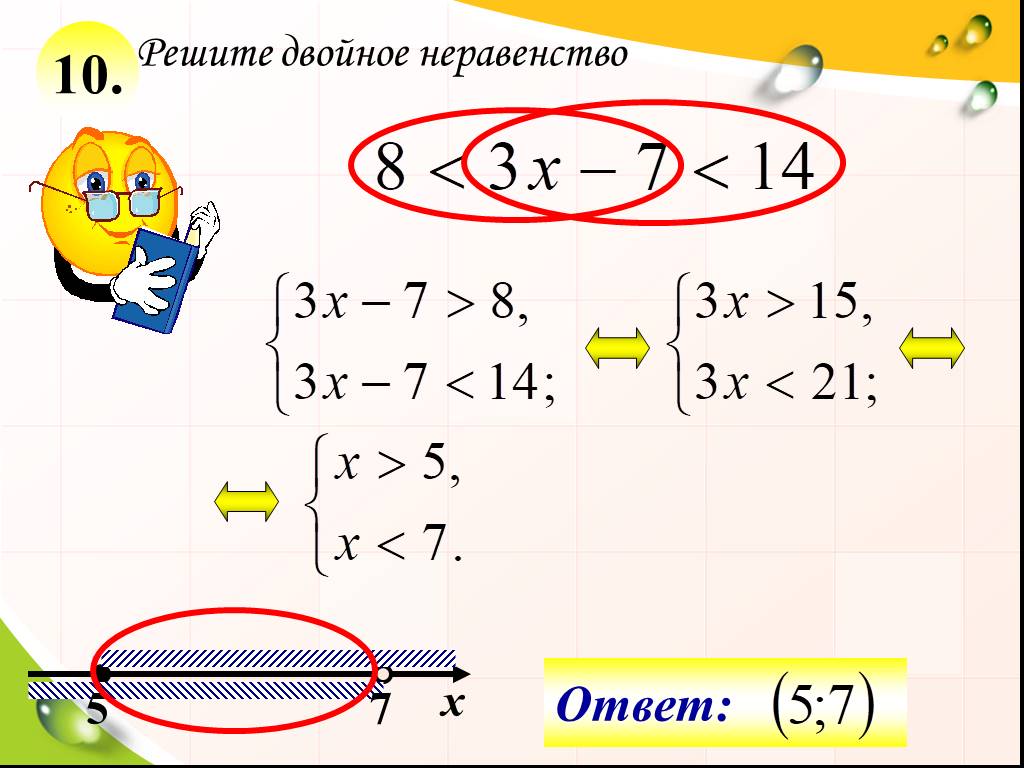
Решение составного неравенства \(−1 < 3 − 2x < 1.\)
\) Это то есть действительные числа, находящиеся между \(-1\) и \(5,\), включая \(5,\), заштрихованные на вещественной линии на рисунке \(\PageIndex{4}\).
\) Итак, что же нам делать?