Запись в тригонометрической форме комплексного числа: Представьте комплексное чтсло в тригонометрической форме z=2i

alexxlab / / Разное

Содержание

Алгебраическая и тригонометрическая формы записи комплексных чисел

Похожие презентации:

Действия над комплексными числами в алгебраической форме

Комплексные числа

Комплексные числа

Комплексные числа

Элементы теории функций комплексного переменного

Комплексные числа и последовательности комплексных чисел. Лекция № 1

Комплексные числа

Множество комплексных чисел

Комплексные числа и последовательности комплексных чисел. Лекция № 1

Комплексные числа

п.23 Алгебраическая и
тригонометрическая формы
записи комплексных чисел
Выписать основные понятия, определения,
формулы, разобрать задачи. Выполнить задания
№1; №2 слайды 19; 20
Определение
Комплексным числом называется
число вида z x yi,
где i 1 , а x и y – вещественные
числа.
2
Основная теорема алгебры
Выражение
z x iy
называется алгебраической формой
записи комплексного числа.
Число x называется действительной частью,

y–мнимой частью комплексного числа z.
Это записывают следующим образом:
x Rez,
y Im z.
Если x 0 , то число
чисто мнимым.
z называют
Если y 0, то получается z x 0 i
вещественное число.
Два комплексных числа
z x iy
и
z x iy
называются сопряженными.
Два комплексных числа z1 x1 iy1 и
z2 x2 iy2 равны друг другу, если
x1 x2 и y1 y2
Комплексное число z считается
равным нулю, если x=y=0.
Всякое
комплексное
число можно
изобразить точкой на плоскости, т.к.
каждому z соответствует упорядоченная
пара вещественных чисел (x;y).
Число z=0 ставится в соответствие
началу координатной плоскости. Такую
плоскость мы в дальнейшем будем
называть комплексной плоскостью, ось
абсцисс–действительной, а ось ординат–
мнимой осью комплексной плоскости.
у
M(x,y)
r
O
Y
X
х
Модуль комплексного числа
Число x 2 y 2 называется модулем
комплексного числа z x iy
и
обозначается z .
Тригонометрическая форма записи
комплексного числа
Для определения положения точки на
плоскости можно пользоваться полярными
координатами ,
где r–расстояние точки от начала координат,
а φ–угол, который составляет радиус–вектор
этой точки с положительным
направлением оси Ox.
,
Положительным направлением
изменения угла φ считается
направление против часовой стрелки.
Воспользовавшись связью декартовых
и полярных координат:
x r cos , y r sin ,
получим тригонометрическую форму
записи комплексного числа
z r cos i sin
r x , y
2
,
2
φ – аргумент комплексного числа,
который находят из формул
x
cos
r
y
sin
r
или в силу того, что ,
y
tg
x
y
arctg
x
При переходе от алгебраической формы комплексного числа к
тригонометрической
достаточно определить лишь главное значение
аргумента комплексного числа, т.е. считать φ=arg z.
y
Так как arg z , то из формулы tg
получаем, что
x
y
— для внутренних точек I, IV четвертей;
arg z arctg
x
y
arg z arctg — для внутренних точек II четверти;
x
y
arg z arctg — для внутренних точек III четверти.
x
Пример 1. Представить комплексные числа
тригонометрической форме.
z1 1 i
и z2
1
3
в
i
2
2
Решение.
Комплексное число z=x+iy в тригонометрической форме
y
r x y , arctg .
x
1) z1=1+i (число z1 принадлежит I четверти), x=1, y=1.
1
2
2
arctg
arctg
1
.
r 1 1 2,
1
4
Таким образом, z1 2 cos i sin .
4
4
1
3
1
3
2) z 2
i (число z2 принадлежит II четверти) x , y
.
2
2
2
2
имеет вид z=r(cosφ +isinφ), где
2
1 3
r
1,
2 2
2
2
2
arctg 3 .
Так как z2 II ч., то Arg z 2
3
3
2
.
3
2
2
i sin
Следовательно, z 2 cos
.
3
3
2
2
i sin
.
Ответ: z1 2 cos i sin , z 2 cos
4
4
3
3
1) Записать число z 2 2 3 i
тригонометрической форме:
r z
2
2
2 3
2
2 3
-2
0
4 12 16 4
a 2
1
cos
2
r
4
2
3
b 2 3
3
sin
r
4
2
у
в
х
2
2
z 2 2 3 i 4 cos
i sin
3
3
25
25
z 2 cos
i sin
3
3
2) Записать число
в алгебраической форме:
25 24
8 2 4
3
3
3
3
3
z 2 cos 2 4 i sin 2 4 2 cos i sin
3
3
3
3
1
3
1 i 3
2 i
2
2
Тригонометрическая форма
комплексного числа
2
2
r z a b
z a bi
у
М(a,b)
b
z
a
cos
r a r cos
b b r sin
sin
r
0
a
х
z a bi r (cos i sin )
Выполнить №1 и №2
№1 Записать в тригонометрической форме
комплексное число
z 1 i 3
.
.
z 2 cos i sin
6
6
№2 Записать число
в алгебраической форме:

English     Русский Правила

Тригонометрическая форма комплексных чисел. Лекция на тему:»Тригонометрическая форма комплексного числа» Представить следующие комплексные числа в тригонометрической форме

КОМПЛЕКСНЫЕ ЧИСЛА XI

§ 256. Тригонометрическая форма комплексных чисел

Пусть комплексному числу а + bi соответствует вектор OA > с координатами (а, b ) (см. рис. 332).

Обозначим длину этого вектора через r , а угол, который он образует с осью х , через φ . По определению синуса и косинуса:

a /

r = cos φ , b / r = sin φ .

Поэтому а = r cos φ , b = r sin φ . Но в таком случае комплексное число а + bi можно записать в виде:

а + bi = r cos φ + ir sin φ = r (cos φ + i sin φ ).

Как известно, квадрат длины любого вектора равен сумме квадратов его координат. Поэтому r 2 = a 2 + b 2 , откуда r = √a 2 + b 2

Итак, любое комплексное число а + bi можно представить в виде :

а + bi = r (cos

φ + i sin φ ), (1)

где r = √a 2 + b 2 , а угол φ определяется из условия:

Такая форма записи комплексных чисел называется тригонометрической .

Число r в формуле (1) называется модулем , а угол φ — аргументом , комплексного числа а + bi .

Если комплексное число а + bi не равно нулю, то модуль его положителен; если же а + bi = 0, то а = b = 0 и тогда r = 0.

Модуль любого комплексного числа определен однозначно.

Если комплексное число а + bi не равно нулю, то аргумент его определяется формулами (2) однозначно с точностью до угла, кратного 2π . Если же а + bi

= 0, то а = b = 0. В этом случае r = 0. Из формулы (1) легко понять, что в качестве аргумента φ в данном случае можно выбрать любой угол: ведь при любом φ

0 (cos φ + i sin φ ) = 0.

Поэтому аргумент нуля не определен.

Модуль комплексного числа r иногда обозначают | z |, а аргумент arg z . Рассмотрим несколько примеров на представление комплексных чисел в тригонометрической форме.

Пример. 1 . 1 + i .

Найдем модуль r и аргумент φ этого числа.

r = √ 1 2 + 1 2 = √ 2 .

Следовательно, sin φ = 1 / √ 2 , cos φ = 1 / √ 2 , откуда φ = π / 4 + 2n π .

Таким образом,

1 + i = √ 2 ,

где п — любое целое число. Обычно из бесконечного множества значений аргумента комплексного числа выбирают то, которое заключено между 0 и 2π . В данном случае таким значением является π / 4 . Поэтому

1 + i = √ 2 (cos π / 4 + i sin π / 4)

Пример 2. Записать в тригонометрической форме комплексное число √ 3 — i . Имеем:

r = √ 3+1 = 2, cos φ = √ 3 / 2 , sin φ = — 1 / 2

Поэтому с точностью до угла, кратного 2π , φ = 11 / 6 π ; следовательно,

√ 3 — i = 2(cos 11 / 6 π + i sin 11 / 6 π ).

Пример 3 Записать в тригонометрической форме комплексное число i .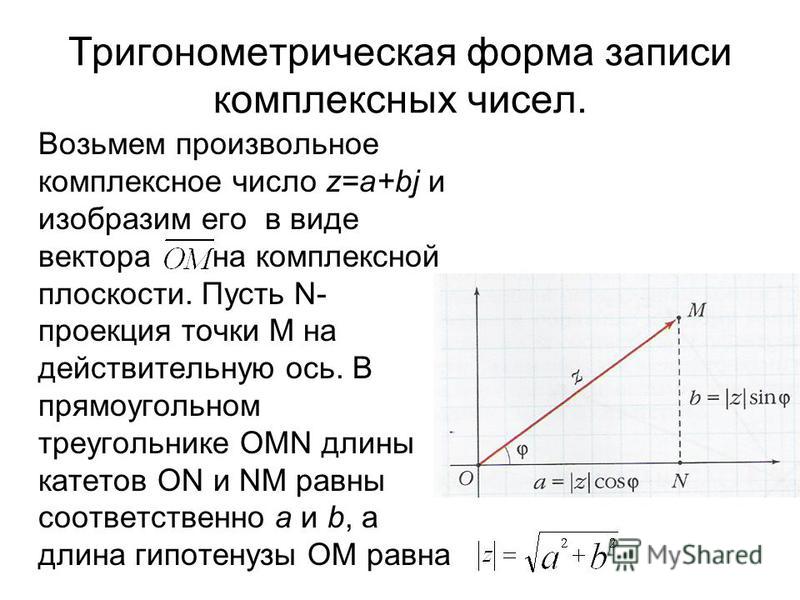

Комплексному числу i соответствует вектор OA > , оканчивающийся в точке А оси у с ординатой 1 (рис. 333). Длина такого вектора равна 1, а угол, который он образует с осью абсцисс, равен π / 2 . Поэтому

i = cos π / 2 + i sin π / 2 .

Пример 4. Записать в тригонометрической форме комплексное число 3.

Комплексному числу 3 соответствует вектор OA > х абсциссой 3 (рис. 334).

Длина такого вектора равна 3, а угол, который он образует с осью абсцисс, равен 0. Поэтому

3 = 3 (cos 0 + i sin 0),

Пример 5. Записать в тригонометрической форме комплексное число -5.

Комплексному, числу -5 соответствует вектор OA > , оканчивающийся в точке оси х с абсциссой -5 (рис. 335). Длина такого вектора равна 5, а угол, который он образует с осью абсцисс, равен

π . Поэтому

5 = 5(cos π + i sin π ).

Упражнения

2047. Данные комплексные числа записать в тригонометрической форме, определив их модули и аргументы:

1) 2 + 2√3 i , 4) 12i — 5; 7).3i ;

2) √3 + i ; 5) 25; 8) -2i ;

3) 6 — 6i ; 6) — 4; 9) 3i — 4.

2048. Указать на плоскости множества точек, изображающих комплексные числа, модули г и аргументы ф которых удовлетворяют условиям:

1) r = 1, φ = π / 4 ; 4) r φ π / 6 ;

2) r =2; 5) 2 r φ

3) r 3; 6) φ = π / 3 ; 9) 1 r

10) 0 φ π / 2 .

2049. Могут ли модулем комплексного числа одновременно быть числа r и — r ?

2050. Могут ли аргументом комплексного числа одновременно быть углы φ и — φ ?

Данные комплексные числа представить в тригонометрической форме, определив их модули и аргументы:

2051*. 1 + cos α + i sin α . 2054*. 2(cos 20° — i sin 20°).

2052*. sin φ + i cos φ . 2055*. 3(- cos 15° — i sin 15°).

3.1. Полярные координаты

На плоскости часто применяется полярная система координат . Она определена, если задана точка O, называемая полюсом , и исходящий из полюса луч (для нас это ось Ox) – полярная ось. Положение точки M фиксируется двумя числами: радиусом (или радиус-вектором) и углом φ между полярной осью и вектором . Угол φ называется полярным углом; измеряется в радианах и отсчитывается от полярной оси против часовой стрелки.

Положение точки в полярной системе координат задается упорядоченной парой чисел (r; φ). У полюса r = 0, а φ не определено. Для всех остальных точек r > 0, а φ определено с точностью до слагаемого кратного 2π. При этом парам чисел (r; φ) и (r 1 ; φ 1) сопоставляется одна и та же точка, если .

Для прямоугольной системы координат xOy декартовы координаты точки легко выражаются через ее полярные координаты следующим образом:

3.2. Геометрическая интерпретация комплексного числа

Рассмотрим на плоскости декартову прямоугольную систему координат xOy .

Любому комплексному числу z=(a, b) ставится в соответствие точка плоскости с координатами (x, y ), где координата x = a, т.е. действительной части комплексного числа, а координата y = bi – мнимой части.

Плоскость, точками которой являются комплексные числа – комплексная плоскость.

На рисунке комплексному числу z = (a, b) соответствует точка M(x, y) .

Задание. Изобразите на координатной плоскости комплексные числа:

3.3. Тригонометрическая форма комплексного числа

Комплексное число на плоскости имеет координаты точки M (x; y) . При этом:

Запись комплексного числа — тригонометрическая форма комплексного числа.

Число r называется модулем комплексного числа z и обозначается . Модуль – неотрицательное вещественное число. Для .

Модуль равен нулю тогда и только тогда, когда z = 0, т.е. a = b = 0 .

Число φ называется аргументом z и обозначается . Аргумент z определен неоднозначно, как и полярный угол в полярной системе координат, а именно с точностью до слагаемого кратного 2π.

Тогда принимаем: , где φ – наименьшее значение аргумента. Очевидно, что

.

При более глубоком изучении темы вводится вспомогательный аргумент φ*, такой, что

Пример 1 . Найти тригонометрическую форму комплексного числа .

Решение. 1) считаем модуль: ;

2) ищем φ: ;

3) тригонометрическая форма:

Пример 2. Найти алгебраическую форму комплексного числа .

Здесь достаточно подставить значения тригонометрических функций и преобразовать выражение:

Пример 3. Найти модуль и аргумент комплексного числа ;

1) ;

2) ; φ – в 4 четверти:

3. 4. Действия с комплексными числами в тригонометрической форме

· Сложение и вычитание удобнее выполнять с комплексными числами в алгебраической форме:

· Умножение – при помощи несложных тригонометрических преобразований можно показать, что при умножении модули чисел перемножаются, а аргументы складываются: ;

Лекция

Тригонометрическая форма комплексного числа

План

1.Геометрическое изображение комплексных чисел.

2.Тригонометрическая запись комплексных чисел.

3.Действия над комплексными числами в тригонометрической форме.

Геометрическое изображение комплексных чисел.

а) Комплексные числа изображают точками плоскости по следующему правилу: a + bi = M ( a ; b ) (рис.1).

Рисунок 1

б) Комплексное число можно изобразить вектором, который имеет начало в точке О и конец в данной точке (рис. 2).

Рисунок 2

Пример 7. Постройте точки, изображающие комплексные числа: 1; — i ; — 1 + i ; 2 – 3 i (рис.3).

Рисунок 3

Тригонометрическая запись комплексных чисел.

Комплексное число z = a + bi можно задать с помощью радиус – вектора с координатами ( a ; b ) (рис.4).

Рисунок 4

Определение . Длина вектора , изображающего комплексное число z , называется модулем этого числа и обозначается или r .

Для любого комплексного числа z его модуль r = | z | определяется однозначно по формуле .

Определение . Величина угла между положительным направлением действительной оси и вектором , изображающим комплексное число, называется аргументом этого комплексного числа и обозначается А rg z или φ .

Аргумент комплексного числа z = 0 не определен. Аргумент комплексного числа z ≠ 0 – величина многозначная и определяется с точностью до слагаемого 2πк (к = 0; — 1; 1; — 2; 2; …): Arg z = arg z + 2πк , где arg z – главное значение аргумента, заключенное в промежутке (-π; π] , то есть -π arg z ≤ π (иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку .

Эту формулу при r =1 часто называют формулой Муавра:

(cos φ + i sin φ) n = cos (nφ) + i sin (nφ), n  N .

Пример 11. Вычислите (1 + i ) 100 .

Запишем комплексное число 1 + i в тригонометрической форме.

a = 1, b = 1 .

cos φ = , sin φ = , φ = .

(1+i) 100 = [ (cos + i sin )] 100 = ( ) 100 (cos ·100 + i sin ·100) = = 2 50 (cos 25π + i sin 25π) = 2 50 (cos π + i sin π) = — 2 50 .

4) Извлечение квадратного корня из комплексного числа.

При извлечении квадратного корня из комплексного числа a + bi имеем два случая:

если b > о , то ;

Действия над комплексными числами, записанными в алгебраической форме

Алгебраической формой комплексного числа z = (a , b ).называется алгебраическое выражение вида

z = a + bi .

Арифметические операции над комплексными числами z 1 = a 1 + b 1 i и z 2 = a 2 + b 2 i , записанными в алгебраической форме, осуществляются следующим образом.

1. Сумма (разность) комплексных чисел

z 1 ± z 2 = (a 1 ± a 2) + (b 1 ±b 2)∙i ,

т.е. сложение (вычитание) осуществляются по правилу сложения многочленов с приведением подобных членов.

2. Произведение комплексных чисел

z 1 ∙z 2 = (a 1 ∙a 2 — b 1 ∙b 2) + (a 1 ∙b 2 + a 2 ∙b 1)∙i ,

т.е. умножение производится по обычному правилу умножения многочленов, с учетом того, что i 2 = 1.

3. Деление двух комплексных чисел осуществляется по следующему правилу:

, (z 2 ≠ 0),

т.е. деление осуществляется умножением делимого и делителя на число, сопряженное делителю.

Возведение в степень комплексных чисел определяется следующим образом:

Легко показать, что

Примеры .

1. Найти сумму комплексных чисел z 1 = 2 – i и z 2 = – 4 + 3i.

z 1 + z 2 = (2 + (–1)∙i )+ (–4 + 3i ) = (2 + (–4)) + ((–1) + 3) i = –2+2i.

2. Найти произведение комплексных чисел z 1 = 2 – 3i и z 2 = –4 + 5i.

= (2 – 3i ) ∙ (–4 + 5i ) = 2 ∙(–4) + (-4) ∙(–3i )+ 2∙5i – 3i∙ 5i = 7+22i.

3. Найти частное z от деления z 1 = 3 – 2на z 2 = 3 – i.

z = .

4. Решить уравнение: , x и y Î R .

(2x + y ) + (x + y )i = 2 + 3i.

В силу равенства комплексных чисел имеем:

откуда x = –1 , y = 4.

5. Вычислить: i 2 , i 3 , i 4 , i 5 , i 6 , i -1 , i -2 .

6. Вычислить , если .

.

7. Вычислить число обратное числу z =3-i .

Комплексные числа в тригонометрической форме

Комплексной плоскостью называется плоскость с декартовыми координатами (x, y ), если каждой точке с координатами (a, b ) поставлено в соответствие комплексное число z = a + bi . При этом ось абсцисс называется действительной осью , а ось ординат – мнимой . Тогда каждое комплексное число a + bi геометрически изображается на плоскости как точка A (a, b ) или вектор .

Следовательно, положение точки А (и, значит, комплексного числа z ) можно задать длиной вектора | | = r и углом j , образованным вектором | | с положительным направлением действительной оси. Длина вектора называется модулем комплексного числа и обозначается | z |=r , а угол j называется аргументом комплексного числа и обозначается j = arg z .

Ясно, что | z | ³ 0 и | z | = 0 Û z = 0.

Из рис. 2 видно, что .

Аргумент комплексного числа определяется неоднозначно, а с точностью до 2pk, k Î Z .

Из рис. 2 видно также, что если z=a+bi и j=arg z, то

cosj = , sinj = , tgj = .

Если zÎ R и z > 0,то arg z = 0 +2pk ;

если z Î R и z 0,то arg z = p + 2pk ;

если z = 0, arg z не определен.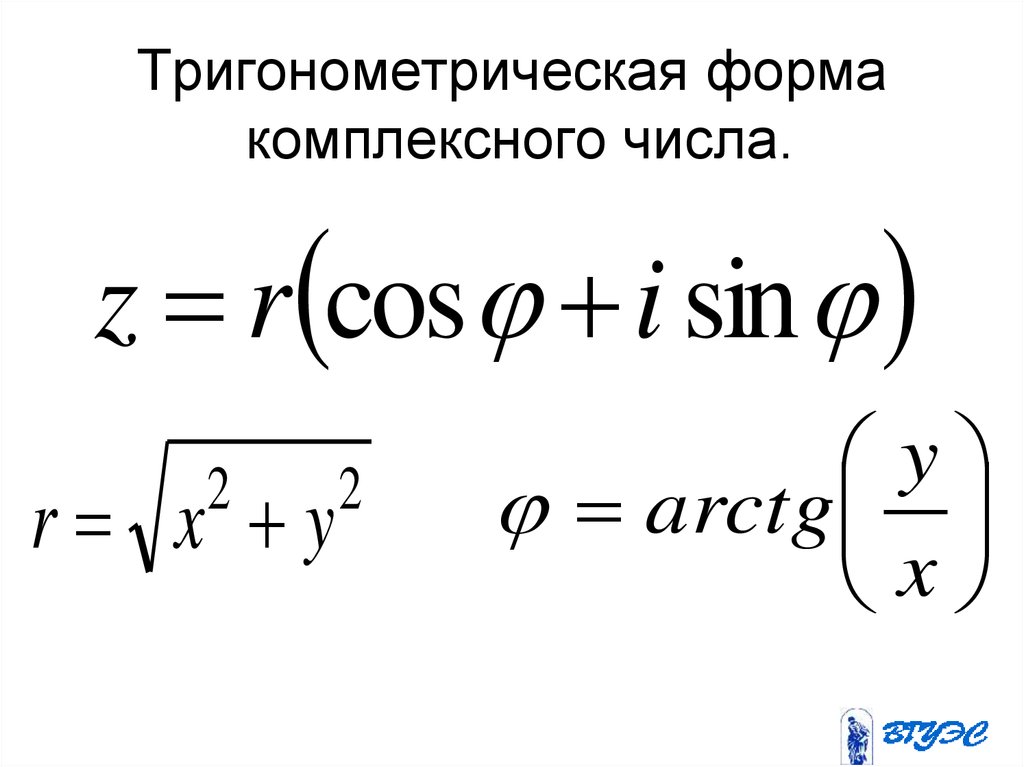

Главное значение аргумента определяется на отрезке 0 £ arg z £ 2p,

либо -p £ arg z £ p .

Примеры:

1. Найти модуль комплексных чисел z 1 = 4 – 3i и z 2 = –2–2i.

2. Определить на комплексной плоскости области, задаваемые условиями:

1) | z | = 5; 2) | z | £ 6; 3) | z – (2+i ) | £ 3; 4) 6 £ | z – i | £ 7.

Решения и ответы:

1) | z | = 5 Û Û — уравнение окружности радиусом 5 и с центром в начале координат.

2) Круг радиусом 6 с центром в начале координат.

3) Круг радиусом 3 с центром в точке z 0 = 2 + i .

4) Кольцо, ограниченное окружностями с радиусами 6 и 7 с центром в точке z 0 = i .

3. Найти модуль и аргумент чисел: 1) ; 2) .

1) ; а = 1, b = Þ ,

Þ j 1 = .

2) z 2 = –2 – 2i ; a = –2, b = -2 Þ ,

.

Указание: при определении главного аргумента воспользуйтесь комплексной плоскостью.

Таким образом: z 1 = .

2) , r 2 = 1, j 2 = , .

3) , r 3 = 1, j 3 = , .

4) , r 4 = 1, j 4 = , .

Что такое Z Bar в комплексных числах?

Комплексное число определяется как сложение действительного числа и мнимого числа. Он представлен как «z» и записывается в стандартной форме как (a + ib), где a и b — действительные числа, а i — мнимая единица, значение которой равно √(-1). Действительная часть комплексного числа представлена ​​как Re (z), а его мнимая часть представлена ​​как Im (z). Некоторые примеры комплексных чисел: 1 + √2i, 6–4i, 5 + 7i и т. д. Воображаемая единица называется «йота» и может быть представлена ​​как «i» или «j». Комплексные числа помогают вычислить квадратный корень из отрицательных чисел. В дополнение к этому, комплексные числа также играют важную роль в обработке сигналов, гидродинамике, анализе цепей переменного тока, электромагнетизме, квантовой механике и т. д.

 

Комплексное сопряжение

Сопряженное комплексное число также является комплексным числом, полученным путем изменения знака между действительной и мнимой частями исходного комплексного числа. Величина комплексного числа и его сопряженного числа одинакова. Сопряженное комплексное число z обозначается z̅ или z* . Если z = a + ib — комплексное число, где a — действительная часть, а ib — мнимая часть, то его сопряженным является z* или z̅ = a — ib. В аргановой плоскости комплексно-сопряженное число (a – ib) является зеркальным отражением комплексного числа (a + ib) относительно действительной оси.

Свойства комплексно-сопряженного числа

  • Действительная часть комплексно-сопряженного числа равна действительной части комплексного числа, а мнимая часть комплексно-сопряженного числа равна минусу мнимой части комплексного числа.

Re(z̅) = Re(z)

Im(z̅) = −Im(z) 

  • Сумма комплексного числа z и его комплексно-сопряженного числа z* .

z + z̅ = (a + ib) + (a − ib) = 2a = 2Re(z)

  • Разница между комплексным числом z и его комплексно-сопряженным числом z* является мнимым числом.

z − z̅ = (a + ib) − (a − ib) = 2ib = 2Im(z)

  • Произведение комплексного числа z и его комплексно-сопряженного числа z* является действительным числом.

z × z̅ = (a + ib)×(a − ib)= a 2 +b 2

  • Если z и w — два комплексно-сопряженных числа их произведение равно произведению их комплексных сопряжений.

  • Если z и w два комплексных числа, то комплексное сопряжение их частного равно частному их комплексно-сопряженных чисел.

  • Если z и w — два комплексных числа, то комплексно-сопряженное их суммы равно сумме их комплексно-сопряженных чисел.

  • Если z и w — два комплексных числа, то комплексно-сопряженная их разность равна разнице между их комплексно-сопряженными числами.

График комплексного числа и его сопряженного

Комплексное число z = a + ib можно представить в виде точки на евклидовой плоскости с координатами (Re(z), Im(z)). Евклидова плоскость, которая представляет комплексные числа в виде точек, где оси X и Y представляют действительную и мнимую части комплексного числа, называется плоскостью Арганда или комплексной плоскостью. Из приведенного ниже графика видно, что сопряженное комплексное число является отражением комплексного числа относительно действительной оси (оси X).

 

  • Полярная форма комплексного числа z = a + ib такова: z = re ix = r(cosθ + isinθ), где r — модуль, а θ — аргумент комплексного числа. Полярная форма комплексного числа помогает представить и идентифицировать его на аргановой плоскости. Полярная форма комплексного сопряжения: z̅ = re −ix = r(cosθ − isinθ).
  • Модуль комплексного числа определяется как расстояние комплексного числа z = a + ib от начала координат в аргановой плоскости. Обозначается |z| и его значение равно r = √(a 2 + б 2 ).
  • Угол, образованный против часовой стрелки линией, соединяющей начало координат и точку, представляющую комплексное число с положительной осью X, называется аргументом комплексного числа.

Argz (θ) = tan −1 (b/a)

Арифметические операции над комплексными числами как мы можем сделать на натуральных числах. Заметим, что при выполнении арифметических действий над комплексными числами приходится объединять одинаковые члены, т. е. действительные части объединяются отдельно, а мнимые части объединяются отдельно. Пусть г

1 = a + ib и z 2 = c + id — два комплексных числа. Теперь арифметические правила комплексных чисел следующие:

Сложение комплексных чисел

Если сложить два комплексных числа z1 и z2, то действительные части z1 и z2 складываются отдельно, а мнимые части z1 и z2 добавляются отдельно. Вычитание комплексных чисел0004

Если из z 2 вычесть комплексное число z 1 , то действительную часть z 1 вычесть из z 2 , а мнимую часть z 1 вычесть из 1 2 .

z 2 – z 1 = (c + id) – (a + ib) = (c – a) + i(d – b)

Умножение комплексных чисел

0

4

4 Процесс умножения двух комплексных чисел идентичен умножению двух двучленов. я 9Формула 0061 2 = -1 используется при умножении двух комплексных чисел.

z 1 × z 2 = (a + ib) × (c + id) = (ac – bd) + i(ad + bc)

Деление комплексных чисел

2

4 Если комплексное число z 1 разделить на z 2 , то результат будет равен произведению z 1 и обратному значению z 2 .

Обратная формула комплекса z = a + ib равна z −1 =1/(a + ib) =(a − ib)/(a 2 +b 2 )

z 1 /z

= ( ib) × 1/(c + id) = (a + ib) × (c – id)/(c 2 + d 2 )

Что такое комплексные числа?

Ответ:

 является комплексно-сопряженным комплексным числом z = a + ib. Сопряженное комплексное число также является комплексным числом, полученным путем изменения знака между действительной и мнимой частями исходного комплексного числа.

Если z = a + ib — комплексное число, где a — действительная часть, а ib — мнимая часть, то его сопряженным является

z* или z̅ = a — bi

Здесь, (a + ib ) и (a – ib) сопряжены друг с другом, т. е. (a + ib) является комплексно-сопряженным с (a – ib) и наоборот. Величина сопряженного (a + ib) такая же, как (a – ib). Сумма и произведение комплексного числа и его сопряженного числа действительны.

Решенные примеры комплексных чисел

Пример 1: Упрощение: (3+4i)/(1–5i).

Решение:

Дано: (3+4i)/(1–5i)

Чтобы рационализировать знаменатель, умножьте и числитель, и знаменатель на сопряженное число (1–5i), т. е. (1+ 5и).

(3+4i)/(1–5i) × (1+5i)/(1+5i)

(1–5i(1+5i) = 1 2 – (5i) 2  

= 1 –(–25)     {Так как, i 2 = –1}

= 1+25 = 26

(3+4i)/(1–5i) × (1+5i)/(1+5i )= [(3+4i)(1+5i)]/26

= (3+15i+4i+20i 2 )/26

= (3+19i–20)/26

= (19i–17)/26

Следовательно, (3+4i)/( 1–5и) = (19и–17)/26.

Пример 2: Если z = 5 – 7i и w = 4 + i, то выразить комплексное число z/w в виде a + ib, где a и b — действительные числа.

Решение: 

Дано: z = 5 – 7i и w = 4 + i

Теперь z/w = (5 – 7i)/(4 + i)

Чтобы рационализировать знаменатель, умножьте и числитель, и знаменатель сопряжены с (4 + i), т. е. (4 – i).

(5 – 7i)/(4 + i) × (4 – i)/(4 – i)

(4 + i) × (4 – i) = 4 2 – i 2

= 16 – (–1)    {Так как, i 2 = –1}

= 16 + 1 = 17

Теперь, (5 – 7i)/(4 + i) × (4 – i)/(4 – i)

= [(5 – 7i)(4 – i))]/17

= (20 – 5i – 28i + 7i 2 )/17

= (20 – 33i + 7(–1) ))/17

z/w = (13 – 33i)/17

Отсюда z/w = (13 – 33i)/17.

Пример 3: Упростить:

a) (4 — 9i) (6 + 3i)

b) (5 + 11i) — (12 — 13i)

Решение:

A) (40004

A) (40004

– 9i)(6 + 3i)

= 4(6 + 3i) – 9i(6 + 3i)

= 24 + 12i – 54i – 27i 2

= 24 – 42i – 27(–1) {Так как i 2 = –1}

= 24 – 42i + 27 = 51 – 42i

Следовательно, (4 – 9i)(6 + 3i) = 51 – 42i.

б) (5 + 11и) – (12 – 13и) 9

= 24i – 7 7).

Пример 4: Найдите значения a и b, если (7 + 3i)/(2 – 3i) = a + ib, где a и b — действительные числа.

Решение:

Дано: (7 + 3i)/(2 – 3i) = a + ib, a, b ∈ R

Чтобы рационализировать знаменатель, умножьте числитель и знаменатель на сопряженное 2 – 3i), т. е. (2 + 3i).

(7 + 3i)/(2 – 3i) × (2 + 3i)/(2 + 3i)

(2 – 3i) × (2 + 3i) = 2 2 – (3i) 2

= 4 – 9i 2 = 4 – 9(–1)    {Так как i 2 = –1}

= 4 + 9 = 13 

Теперь, (7 + 3i)/(2 – 3i ) × (2 + 3i)/(2 + 3i) = [(7 + 3i)(2 + 3i)]/13

= (14 + 21i + 6i + 9i 2 )/13

= (14 + 27i + 9(–1))/13

= (5 + 27i)/13

(7 + 3i)/(2 – 3i) = (5/13) + (27/13)i

а + ib = (5/13) + (27/13)i

Итак, а = 5/13 и b = 27/13.

Таким образом, значения a и b равны 5/13 и 27/13.

Пример 5: Найдите сумму, разность и произведение комплексных чисел z 1 = 8 – 5i и z 2 = 1 – 3i как комплексное число.

Решение:

Дано: Z1 = 8 — 5i

Z 2 = 1 — 3i

Сумма:

Z 1 + z 2 = 8 — 8 — 8 — 8 — 8 — 8 — – 3i

= (8 + 1) + (–5i — 3i)

z 1 + z 2 = 9 — 8i

Разница:

z 1 — z 2 = (8–8 – 5i) – (1 – 3i)

= 8 – 5i – 1 + 3i

= (8 – 1) + (–5i + 3i)

z 1 – z 2 = 7 – 2i

5

5

5

Продукт:

z 1 × z 2 = (8 – 5i) × (1 – 3i)

= 8(1 – 3i) – 5i(1 – 3i)

= – 8 – 24i 5и + 15и 2

= 8 – 29i + 15(–1)    {Так как i 2 = –1}

= 8 – 15 – 29i = –(7 + 29i)

z 1 × 90 2 = –(7 + 29i).

Часто задаваемые вопросы о комплексных числах

Вопрос 1: Что подразумевается под комплексным числом?

Ответ:

Комплексное число определяется как сложение действительного числа и мнимого числа. Он представлен как «z» и имеет форму (a + ib), где a и b — действительные числа, а i — мнимая единица, значение которой равно √(-1). Действительная часть комплексного числа представлена ​​как Re (z), а его мнимая часть представлена ​​как Im (z). Некоторые примеры комплексных чисел: 1 + √2i, 6–4i, 5 + 7i и т. д.

Вопрос 2: Что понимается под комплексным сопряжением?

Ответ:

Сопряженное комплексное число также является комплексным числом, полученным путем изменения знака между действительной и мнимой частями исходного комплексного числа. Величина комплексного числа и его сопряженного числа совпадают. Сопряженное комплексное число z обозначается z̅ или z*. Если z = a + ib — комплексное число, где a — действительная часть, а ib — мнимая часть, то его сопряженным является z* или z̅ = a — ib.

Вопрос 3: Как определить сопряжение комплексного числа?

Ответ:

Сопряженным комплексным числом (a + ib) также является комплексное число, которое получается изменением знака между действительной частью «a» и мнимой частью «ib». Таким образом, комплексное сопряжение (a + ib) есть (a – ib).

Вопрос 4: Определите модуль комплексного числа.

Ответ:

Модуль комплексного числа (r) определяется как расстояние комплексного числа z = a + ib от начала координат в плоскости Арганда. Обозначается |z| и его значение равно r = √(a 2 + b 2 ).

Вопрос 5: Запишите правила арифметики комплексных чисел.

Ответ:

Арифметические операции, такие как сложение, вычитание, умножение и деление, могут выполняться над комплексными числами точно так же, как и над натуральными. Пусть г 1 = a + ib и z 2 = c + id — два комплексных числа. Теперь арифметические правила комплексных чисел:

  • Правило сложения:   z 1 + z 2 = (a + c) + i(b + d)
  • Правило вычитания: z 910014 – z 2 = (a-c) +i(b – d)
  • Правило умножения: z 1 × z 2 = (a + ib) × (c + id) = (ac – bd ) + i(ad + bc)
  • Правило деления: z 1 /z 2 = (a + ib) × 1/(c + id) = (a + ib) × (c – id)/(c 2 + d 2 )

Обзор комплексного номера

– прикладное промышленное электричество

Если бы мне нужно было описать расстояние между двумя городами, я мог бы дать ответ, состоящий из одного числа в милях, километрах или какой-либо другой единице линейного измерения. Однако, если бы мне нужно было описать, как добраться из одного города в другой, мне пришлось бы предоставить больше информации, чем просто расстояние между этими двумя городами; Я также должен был бы предоставить информацию о направление  , чтобы путешествовать, а также.

Информация, выражающая одно измерение, например линейное расстояние, в математике называется скалярной величиной. Скалярные числа — это числа, которые вы до сих пор использовали в большинстве своих математических приложений. Например, напряжение, создаваемое батареей, является скалярной величиной. То же самое относится и к сопротивлению отрезка провода (Ом) или току через него (амперы).

Однако, когда мы начинаем анализировать цепи переменного тока, мы обнаруживаем, что количество напряжения, тока и даже сопротивления (называемое  импеданс  в переменном токе) не являются привычными одномерными величинами, которые мы привыкли измерять в цепях постоянного тока. Скорее, эти величины, поскольку они являются динамическими (переменными по направлению и амплитуде), обладают другими измерениями, которые необходимо учитывать. Частота и фазовый сдвиг — два из этих параметров, которые вступают в игру. Даже с относительно простыми цепями переменного тока, где мы имеем дело только с одной частотой, нам все еще приходится иметь дело с величиной фазового сдвига в дополнение к амплитуде.

Чтобы успешно анализировать цепи переменного тока, нам необходимо работать с математическими объектами и методами, способными представить эти многомерные величины. Здесь нам нужно отказаться от скалярных чисел в пользу чего-то более подходящего: комплексные числа . Как и в примере с направлением из одного города в другой, величины переменного тока в одночастотной цепи имеют как амплитуду (аналогия: расстояние), так и фазовый сдвиг (аналогия: направление). Комплексное число — это единственная математическая величина, способная одновременно выразить эти два измерения амплитуды и фазового сдвига.

Графическое представление комплексных чисел

Комплексные числа легче понять, когда они представлены графически. Если я рисую линию с определенной длиной (величиной) и углом (направлением), у меня есть графическое представление комплексного числа, которое широко известно в физике как вектор : (рисунок ниже)

Как и расстояния и направления на карте, должна быть какая-то общая система отсчета, чтобы угловые числа имели какое-либо значение. В этом случае прямым правом считается 0 o , а углы отсчитываются в положительном направлении против часовой стрелки: (Рисунок ниже)

Идея представления числа в графической форме не нова. Мы все узнали это в начальной школе с помощью «числовой строки»: (рисунок ниже)

.

Мы даже узнали, как работает сложение и вычитание, увидев, как складываются длины (величины), чтобы дать окончательный ответ: (рисунок ниже)

Позднее мы узнали, что существуют способы обозначения значений  между и целыми числами, отмеченными в строке. Это были дробные или десятичные числа: (рисунок ниже)

Эти поля чисел (целые, целые, рациональные, иррациональные, действительные и т. д.), изученные в начальной школе, имеют общую черту: все они одномерные . Прямолинейность числовой линии иллюстрирует это графически. Вы можете двигаться вверх или вниз по числовой линии, но все «движения» по этой линии ограничены одной осью (горизонтальной). Одномерные скалярные числа идеально подходят для подсчета шариков, представления веса или измерения напряжения батареи постоянного тока, но они не могут представить что-то более сложное, например, расстояние и  направление между двумя городами или амплитуда  и  фаза сигнала переменного тока. Для представления таких величин нам нужны многомерные представления. Другими словами, нам нужна числовая линия, которая может указывать в разных направлениях, и это именно то, чем является вектор.

  • Скаляр  число — это тип математического объекта, который люди привыкли использовать в повседневной жизни: одномерная величина, такая как температура, длина, вес и т. д.
  • Комплексное число  – это математическая величина, представляющая два измерения величины и направления.
  • Вектор   – это графическое представление комплексного числа. Он выглядит как стрела с начальной точкой, концом, определенной длиной и определенным направлением. Иногда слово phasor  используется в электрических приложениях, где угол вектора представляет фазовый сдвиг между сигналами.

 

Итак, как именно мы можем представить переменные величины напряжения или тока в виде вектора? Длина вектора представляет величину (или амплитуду) сигнала, например: (рисунок ниже)

Чем больше амплитуда сигнала, тем больше длина соответствующего вектора. Однако угол вектора представляет собой фазовый сдвиг в градусах между рассматриваемым сигналом и другим сигналом, выступающим в качестве «эталона» во времени. Обычно, когда выражается фаза сигнала в цепи, она ссылается на форму сигнала напряжения источника питания (произвольно указывается как «при» 0°). Помните, что фаза — это всегда относительное измерение между двумя сигналами, а не абсолютное свойство. (Рисунок ниже)

Чем больше фазовый сдвиг в градусах между двумя сигналами, тем больше угловая разница между соответствующими векторами. Будучи относительным измерением, как и напряжение, фазовый сдвиг (угол вектора) имеет значение только по отношению к некоторой стандартной форме волны. Как правило, эта «опорная» форма сигнала является основным напряжением питания переменного тока в цепи. Если имеется более одного источника переменного напряжения, то один из этих источников произвольно выбирается в качестве опорной фазы для всех других измерений в цепи.

Эта концепция опорной точки мало чем отличается от точки «земли» в цепи в пользу опорного напряжения. С четко определенной точкой в ​​цепи, объявленной «землей», становится возможным говорить о напряжении «в» или «в» отдельных точках цепи, при этом понимается, что эти напряжения (всегда относительные между и точками) относится к «земле». Соответственно, при четко определенной точке отсчета фазы можно говорить о напряжениях и токах в цепи переменного тока, имеющих определенные фазовые углы. Например, если ток в цепи переменного тока описывается как «24,3 мА при -64 градусах», это означает, что форма волны тока имеет амплитуду 24,3 мА и отстает на 64° от эталонной формы волны, которую обычно принимают за исходную. Форма волны напряжения основного источника.

 

При использовании для описания величины переменного тока длина вектора представляет собой амплитуду волны, а угол вектора представляет фазовый угол волны относительно некоторой другой (эталонной) формы волны.

 

Помните, что векторы – это математические объекты, подобные числам на числовой прямой: их можно складывать, вычитать, умножать и делить. Сложение — это, пожалуй, самая простая для визуализации операция с векторами, поэтому мы начнем с нее. Если сложить векторы с общими углами, их величины (длины) складываются так же, как и обычные скалярные величины: (рисунок ниже)

Аналогичным образом, если источники переменного напряжения с одинаковым фазовым углом соединены вместе последовательно, их напряжения складываются так же, как и в случае с батареями постоянного тока: (рисунок ниже)

Обратите внимание на знаки полярности (+) и (-) рядом с выводами двух источников переменного тока. Несмотря на то, что мы знаем, что переменный ток не имеет «полярности» в том же смысле, что и постоянный ток, эти метки необходимы для того, чтобы знать, как ссылаться на заданные фазовые углы напряжений. Это станет более очевидным в следующем примере.

Если сложить векторы, прямо противоположные друг другу (180 °  в противофазе), их величины (длины) вычитаются так же, как вычитаются положительные и отрицательные скалярные величины при сложении: (рисунок ниже)

Аналогичным образом, если противоположные источники переменного напряжения соединены последовательно, их напряжения вычитаются, как и следовало ожидать от батарей постоянного тока, соединенных встречным образом: (рисунок ниже)

Чтобы определить, находятся ли эти источники напряжения друг против друга, необходимо изучить их маркировку полярности  и — их фазовые углы. Обратите внимание, как маркировка полярности на приведенной выше диаграмме указывает на аддитивные напряжения (слева направо мы видим — и + на источнике 6 вольт, — и + на источнике 8 вольт). Несмотря на то, что эти маркировки полярности обычно указывают на добавочный эффект в цепи постоянного тока (два напряжения работают вместе, чтобы создать большее общее напряжение), в этой цепи переменного тока они на самом деле толкают в противоположных направлениях, потому что одно из этих напряжений имеет фазовый угол 0 °  и другой фазовый угол 180 ° . В результате получается, конечно, общее напряжение 2 вольта.

С тем же успехом мы могли бы показать последовательное вычитание противоположных напряжений следующим образом: (Рисунок ниже)

Обратите внимание, что теперь полярности кажутся противоположными друг другу из-за перепутанных проводных соединений на 8-вольтовом источнике. Поскольку оба источника описываются как имеющие одинаковые фазовые углы (0 ° ), они действительно противоположны друг другу, и общий эффект такой же, как и в предыдущем сценарии с «аддитивными» полярностями и разными фазовыми углами: общее напряжение всего 2 вольта. (Рисунок ниже)

Так же, как есть два способа выразить фазу источников, есть два способа выразить результирующую их сумму.

Результирующее напряжение может быть выражено двумя различными способами: 2 вольта при 180° с символом (-) слева и символом (+) справа, или 2 вольта при 0° с символом (+) на слева и символ (-) справа. Перестановка проводов от источника переменного напряжения аналогична сдвигу фазы этого источника на 180°. (Рисунок ниже)

Пример эквивалентных источников напряжения.

 

Если добавляются векторы с необычными углами, их величины (длины) складываются совершенно иначе, чем у скалярных величин: (рисунок ниже)

Величины векторов не складываются напрямую для неравных углов.

Если два напряжения переменного тока — сдвинутые по фазе на 90° — складываются вместе путем последовательного соединения, их величины напряжения не складываются и не вычитаются напрямую, как в случае скалярных напряжений постоянного тока. Вместо этого эти величины напряжения являются комплексными величинами, и точно так же, как приведенные выше векторы, которые складываются тригонометрическим образом, 6-вольтовый источник при 0° добавляется к 8-вольтовому источнику при 9°.0° дает 10 вольт при фазовом угле 53,13°: (рисунок ниже)

Источники 6В и 8В добавляются к 10В с помощью тригонометрии.

По сравнению с анализом цепи постоянного тока это действительно очень странно. Обратите внимание, что можно получить показания вольтметра 6 и 8 вольт, соответственно, для двух источников переменного напряжения, но считывать только 10 вольт для общего напряжения!

Нет подходящей аналогии с постоянным током для того, что мы здесь видим, с двумя переменными напряжениями, слегка не совпадающими по фазе. Напряжения постоянного тока могут только напрямую помогать или прямо противодействовать, и ничего промежуточного. При переменном токе два напряжения могут усиливать или противодействовать друг другу до любой степени  от полностью поддерживающей до полностью противоположной включительно. Без использования векторной записи (комплексных чисел) для описания величин переменного тока было бы очень сложно выполнять математические расчеты для анализа цепей переменного тока.

В следующем разделе мы узнаем, как представлять векторные величины в символической, а не в графической форме. Векторных и треугольных диаграмм достаточно, чтобы проиллюстрировать общую концепцию, но необходимо использовать более точные методы символизма, если необходимо выполнить какие-либо серьезные вычисления с этими величинами.

  • Напряжения постоянного тока могут либо напрямую помогать, либо прямо противодействовать друг другу при последовательном соединении. Переменное напряжение может помогать или противодействовать в любой степени в зависимости от фазового сдвига между ними.

 

Чтобы работать с комплексными числами без рисования векторов, нам сначала понадобится какая-то стандартная математическая запись. Существует две основные формы записи комплексных чисел: полярная и прямоугольная .

Полярная форма комплексного числа

В полярной форме комплексное число обозначается длиной (также известной как магнитуда , абсолютное значение или модуль ) и углом его вектора (обычно обозначается символом угла это выглядит так: ∠).

Если использовать аналогию с картой, полярное обозначение вектора из Нью-Йорка в Сан-Диего будет примерно таким: «2400 миль, юго-запад». Вот два примера векторов и их полярных обозначений:

Векторы с полярными обозначениями.

Стандартная ориентация для векторных углов в расчетах цепи переменного тока определяет 0° как направление вправо (горизонтально), что составляет 90° прямо вверх, 180° влево и 270° прямо вниз. Обратите внимание, что векторы, расположенные под углом «вниз», могут иметь углы, представленные в полярной форме в виде положительных чисел, превышающих 180, или отрицательных чисел, меньших 180. Например, можно сказать, что вектор под углом ∠ 270° (прямо вниз) также имеет угол угол -90°. (Рисунок ниже) Приведенный выше вектор справа (7,81 ∠ 230,19°) также можно обозначить как 7,81 ∠ -129,81°.

Векторный компас.

Прямоугольная форма комплексного числа

С другой стороны, в прямоугольной форме комплексное число обозначается соответствующими горизонтальными и вертикальными компонентами. По сути, угловой вектор принимается за гипотенузу прямоугольного треугольника, описываемую длинами смежных и противоположных сторон. Вместо того, чтобы описывать длину и направление вектора, обозначая величину и угол, он описывается в терминах «насколько далеко влево/вправо» и «насколько далеко вверх/вниз».

Эти двумерные фигуры (горизонтальные и вертикальные) обозначаются двумя цифрами. Чтобы отличить горизонтальное и вертикальное измерения друг от друга, перед вертикальным ставится строчная буква «i» (в чистой математике) или «j» (в электронике). Эти строчные буквы не представляют физическую переменную (такую ​​как мгновенный ток, также обозначаемый строчной буквой «i»), а представляют собой математические операторы , используемые для различения вертикальной составляющей вектора от его горизонтальной составляющей. В виде полного комплексного числа горизонтальная и вертикальная величины записываются в виде суммы: (рисунок ниже)

В «прямоугольной» форме длина и направление вектора обозначаются с точки зрения его горизонтального и вертикального промежутка, первое число представляет горизонтальный («действительный»), а второе число (с префиксом «j») представляет вертикальный ( «мнимые») размеры.

Горизонтальная компонента называется реальной  компонентой, поскольку эта размерность совместима с нормальными скалярными («действительными») числами. Вертикальный компонент называется воображаемый компонент , поскольку это измерение лежит в другом направлении, совершенно чуждом шкале действительных чисел. (Рисунок ниже)

Векторный компас с реальной и мнимой осями.

«Реальная» ось графика соответствует знакомой числовой линии, которую мы видели ранее: той, на которой есть как положительные, так и отрицательные значения. «Мнимая» ось графика соответствует другой числовой прямой, расположенной под углом 90° к «действительной». Векторы являются двумерными вещами, поэтому у нас должна быть двухмерная «карта», на которой они могут быть выражены, таким образом, две числовые линии перпендикулярны друг другу: (рисунок ниже)

Векторный компас с реальными и мнимыми («j») числовыми линиями.

Преобразование полярной формы в прямоугольную

Любой метод записи допустим для комплексных чисел. Основная причина наличия двух методов записи заключается в простоте подсчета от руки, прямоугольная форма подходит для сложения и вычитания, а полярная форма подходит для умножения и деления. Преобразование между двумя формами записи включает простую тригонометрию. Чтобы преобразовать полярную в прямоугольную, найдите действительную составляющую, умножив полярную величину на косинус угла, и мнимую составляющую, умножив полярную величину на синус угла. Это можно легче понять, изобразив величины как стороны прямоугольного треугольника, гипотенуза треугольника представляет сам вектор (его длина и угол по отношению к горизонтали составляют полярную форму), а горизонтальная и вертикальная стороны представляют « действительная» и «мнимая» прямоугольная составляющие соответственно: (рисунок ниже)

Вектор величины через действительную (4) и мнимую (j3) составляющие.

Преобразование прямоугольной формы в полярную

Чтобы преобразовать прямоугольную форму в полярную, найдите полярную величину с помощью Теоремы Пифагора (полярная величина – это гипотенуза прямоугольного треугольника, а действительная и мнимая составляющие – это прилежащая и противоположная стороны соответственно), а угол взяв арктангенс мнимой составляющей, деленный на действительную составляющую:

  • Полярная нотация  обозначает комплексное число с точки зрения длины его вектора и углового направления от начальной точки. Пример: пролететь 45 миль по ∠ 203° (с запада на юго-запад).
  • Прямоугольное обозначение обозначает комплексное число с точки зрения его горизонтального и вертикального размеров. Пример: проехать 41 милю на запад, затем повернуть и проехать 18 миль на юг.
  • В прямоугольной записи первая величина является «действительной» составляющей (горизонтальный размер вектора), а вторая величина является «мнимой» составляющей (вертикальный размер вектора). Мнимой составляющей предшествует строчная буква «j», которую иногда называют 9.0642 j оператор .
  • Как полярная, так и прямоугольная формы записи комплексного числа могут быть связаны графически в виде прямоугольного треугольника, где гипотенуза представляет сам вектор (полярная форма: длина гипотенузы = величина; угол относительно горизонтальной стороны = угол), горизонтальная сторона представляет прямоугольную «действительную» составляющую, а вертикальная сторона представляет прямоугольную «мнимую» составляющую.

 

 

Поскольку комплексные числа являются допустимыми математическими объектами, как и скалярные числа, их можно складывать, вычитать, умножать, делить, возводить в квадрат, инвертировать и т. д., как и любые другие числа. Некоторые научные калькуляторы запрограммированы на прямое выполнение этих операций с двумя или более комплексными числами, но эти операции также можно выполнять «вручную». В этом разделе показано, как выполняются основные операции. настоятельно рекомендует вооружиться научным калькулятором, способным легко выполнять арифметические операции с комплексными числами. Это сделает ваше изучение цепи переменного тока намного более приятным, чем если бы вы были вынуждены выполнять все расчеты более длинным путем.

Сложение и вычитание комплексных чисел в прямоугольной форме

Сложение и вычитание комплексных чисел в прямоугольной форме очень просто. Кроме того, просто сложите действительные компоненты комплексных чисел, чтобы определить действительную составляющую суммы, и сложите мнимые составляющие комплексных чисел, чтобы определить мнимую составляющую суммы:

При вычитании комплексных чисел в прямоугольной форме просто вычтите действительную составляющую второго комплексного числа из действительной составляющей первого, чтобы получить действительную составляющую разности, и вычтите мнимую составляющую второго комплексного числа из мнимой составляющей из первых прибывших мнимая составляющая разницы:

Умножение и деление комплексных чисел в полярной форме

Для умножения и деления от руки предпочтительнее использовать полярную запись. При умножении комплексных чисел в полярной форме просто умножьте  полярные величины комплексных чисел, чтобы определить полярную величину произведения, и  добавьте  углы комплексных чисел, чтобы определить угол произведения:

Деление комплексных чисел в полярной форме также легко: просто разделите полярную величину первого комплексного числа на полярную величину второго комплексного числа, чтобы получить полярную величину частного, и вычтите угол второго комплексного числа. из угла первого комплексного числа получить угол частного:

Чтобы получить обратное или «инвертированное» (1/x) комплексное число, просто разделите число (в полярной форме) на скалярное значение 1, которое представляет собой не что иное, как комплексное число без мнимой составляющей (угол = 0):

Это основные операции, которые вам необходимо знать, чтобы манипулировать комплексными числами при анализе цепей переменного тока. Однако операции с комплексными числами отнюдь не ограничиваются только сложением, вычитанием, умножением, делением и обращением.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *