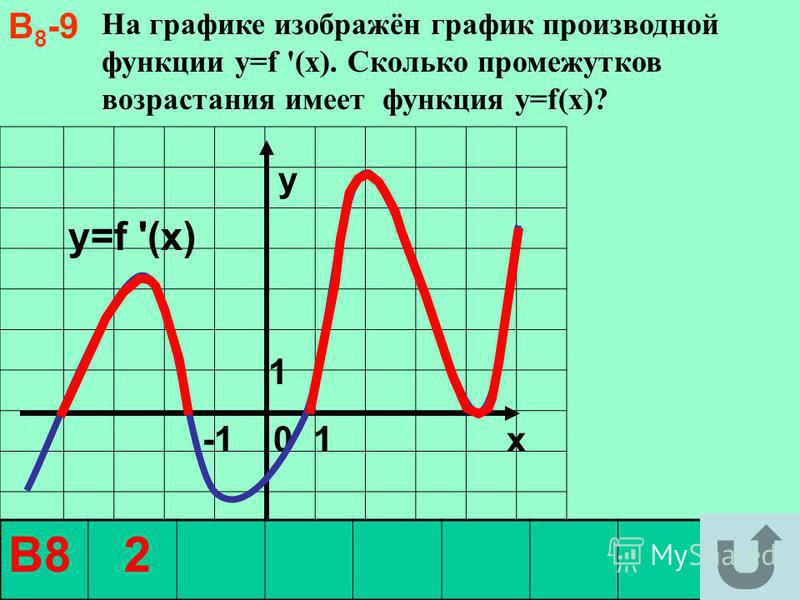
описание, свойства, значение, отличие от графика функции
Содержание:
- График производной функции — описание
- Свойства графика
- Знак производной на интервалах возрастания
- Знак производной на интервалах убывания
- Производная и угловой коэффициент касательной
- В каких точках производная равна нулю
- Примеры производной на графике функции
- График производной функции — описание
- Свойства графика
- Знак производной на интервалах возрастания
- Знак производной на интервалах убывания
- Производная и угловой коэффициент касательной
- В каких точках производная равна нулю
- Примеры производной на графике функции
График производной функции — описание
Производная функции — это скорость изменения у при изменении х. При этом одна и та же функция может иметь разное значение производной в разных точках. Обозначается производная следующим образом: \(f'(x)\).
При этом одна и та же функция может иметь разное значение производной в разных точках. Обозначается производная следующим образом: \(f'(x)\).
Зависимость производной функции от скорости изменения y заключается в том, что они прямо пропорциональны. Значение производной может быть как больше, так и меньше нуля. Производную функции используют для нахождения точек максимума и минимума функций, а также промежутков их возрастания и убывания.
При помощи вычисления производной и приравнивания её к нулю, возможно найти точки, разбивающие числовую ось на интервалы. Знак производной будет определяться на каждом из найденных интервалов, что позволит сделать в дальнейшем сделать вывод о возрастании или убывании функции.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Производная функции \(f(x)\) в точке \(x_0\) эквивалентна тангенсу угла наклона касательной к графику функции в \(x_0\).
\(f'(x_0)\;=\;tg\alpha\)
Свойства графика
- Производная будет положительной на интервалах возрастания функции. Таким образом, в случае если производная в определенной точке некоего интервала обладает положительным значением, график функции возрастает в обозначенном интервале.
- Производная будет отрицательной на интервалах убывания функции. Таким образом, в случае если производная в определенной точке некоего интервала обладает отрицательным значением, график функции убывает в обозначенном интервале.
- В точке х производная будет равняться угловому коэффициенту касательной к графику функции в обозначенной точке.
- Производная равняется нулю в точках максимума и минимума функции, в тех же случаях параллельности касательной к графику функции и оси \(ОХ\).
Знак производной на интервалах возрастания
Определим, какая функция называется возвращающей.
\(y = f(x)\) будет возрастать на интервале \(X\), если для любых \(x_1\;\in\;X\) и \(x_2\;\in\;X\), где \(x_2\;>\;x_1\), справедливо неравенство \(f(x_2)\;\geq\;f(x_1)\).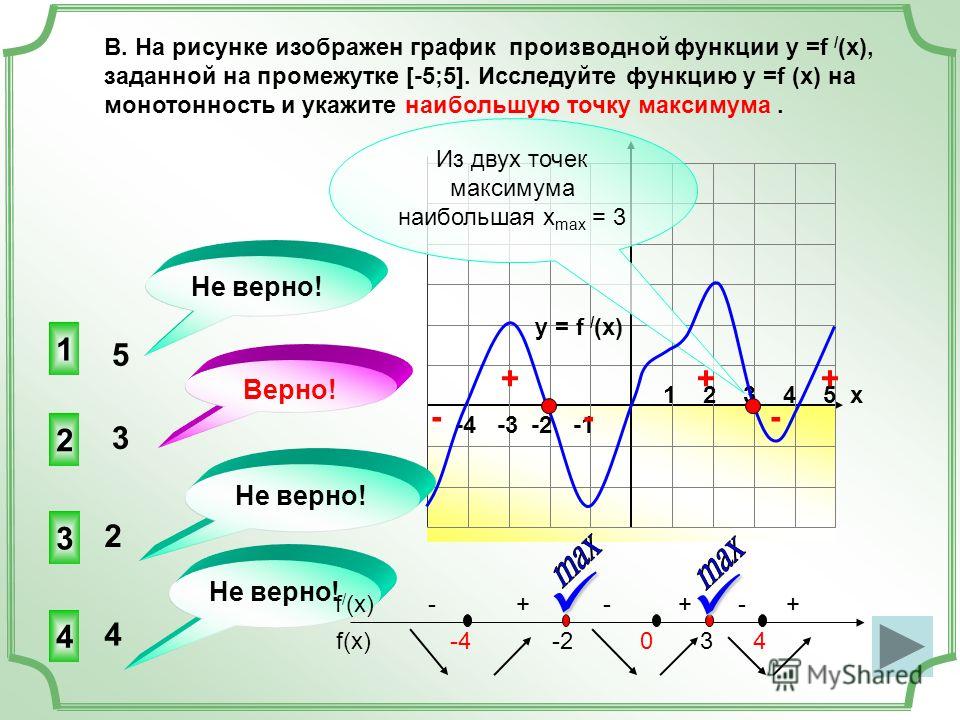
В тех случаях, когда данное неравенство будет соответствовать определению строгого, то есть иметь вид \(f(x_1) < f(x_2)\), функция \(y = f(x)\) будет называться строго возрастающей на интервале \((a, b)\).
На интервалах возрастания производная будет иметь положительный знак. То есть при подстановке значения из интервала в производную, получившееся число будет положительным.
В тех случаях, когда производная функции \(y = f(x)\) положительна для любого x из интервала \(X\), функция возрастает на \(X\).
Знак производной на интервалах убывания
Определим, какая функция называется убывающей.
\(y = f(x)\) будет убывать на интервале \(X\), если для любых \(x_1\;\in\;X\) и \(x_2\;\in\;X\), где \(x_2\;>\;x_1\) справедливо неравенство \(f(x_2)\;\leq\;f(x_1).\)
В тех случаях, когда данное неравенство будет соответствовать определению строгого, то есть имеет вид \(f(x_1) < f(x_2)\), функция \(y = f(x)\) будет называться строго убывающей на интервале \((a, b)\).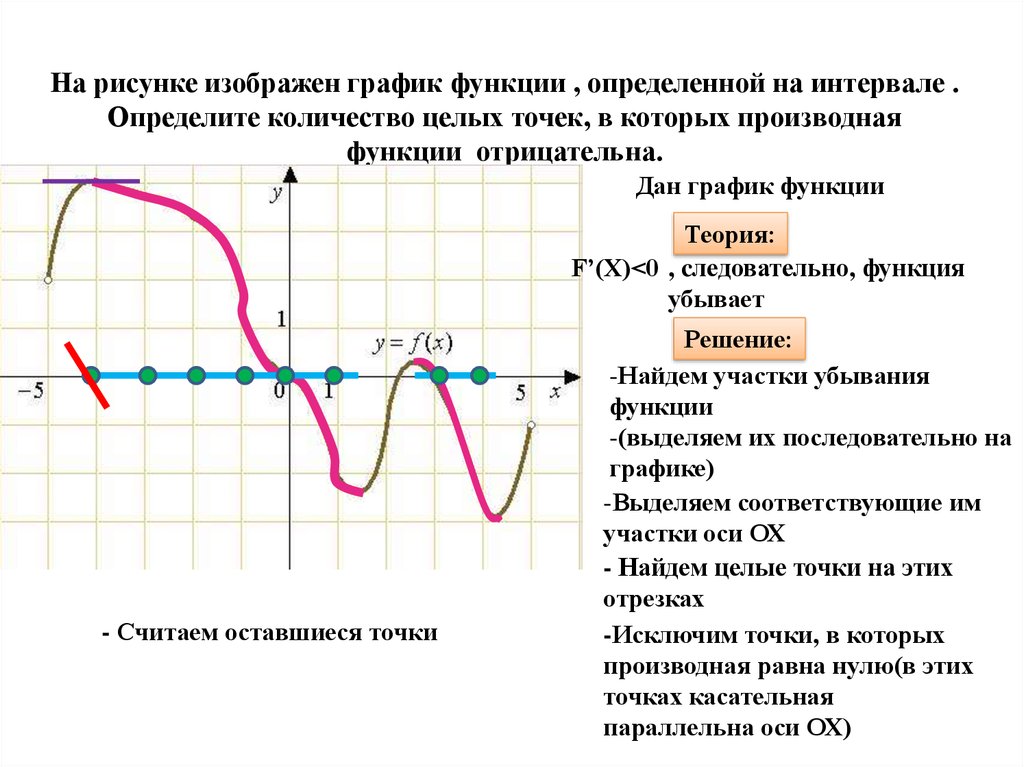
На интервалах убывания производная будет иметь отрицательный знак. То есть при подстановке значения из интервала в производную, получившееся число будет отрицательным.
В тех случаях, когда производная функции \(y = f(x)\) отрицательна для любого x из интервала \(X\), функция убывает на \(X\).Производная и угловой коэффициент касательной
Касательная — прямая, которая имеет на определенном участке единственную общую точку с графиком.
В случае, когда при \(x_1\;\rightarrow\;x_0\) имеется предельное положение секущей графика функции \(y = f(x)\), оно будет носить название касательной к графику функции \(y = f(x)\) в точке \(A\;=\;((x_0;\;f(x_0))\). А значение производной в точке касания \(x_0\) будет эквивалентно угловому коэффициенту касательной.
Угловой коэффициент касательной равен значению производной в точке касания \(x_0\). И в соответствии с тем, что касательная параллельна прямой \(y = -x\), ее угловой коэффициент равен -1.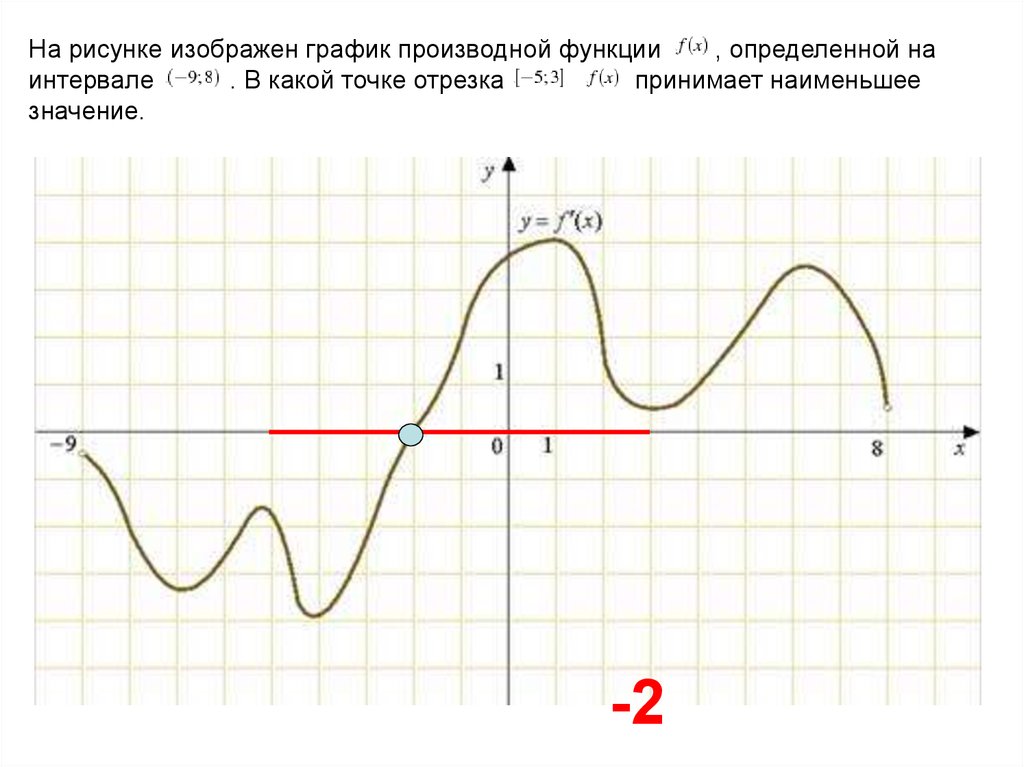
Геометрический смысл производной состоит в том, что производная в точке \(x_0\) равна угловому коэффициенту касательной к графику функции \(y = f(x)\) в этой точке.
Формула уравнения касательной к графику функции \(y = f(x)\) в точке \(x_0\) выглядит следующим образом:
\(y\;=\;f(x_0)\;+\;f'(x_0)(x\;-\;x_0)\)
Рассмотрим рисунок графика функции \(y = f(x)\). Очевидно, что для каждой из точек \(A\) и \(B\) графика функции справедливо следующее разностное отношение:
\(\frac{f(x_0+\triangle x)}{f(x_0)\triangle x}=tg\alpha\)
Здесь \(\alpha\) — угол между прямой и осью \(ОХ\), а предел разностного отношения эквивалентен угловому коэффициенту касательной в точке \(A\).
Зафиксируем точку \(A\) и будем продвигать точку \(B\) в направлении к ней. Тогда \(\triangle x\) бесконечно уменьшается и приближается к 0, а секущая \(АВ\) приближается к касательной \(АС\).
Пример
Необходимо записать уравнение касательной к графику функции \(y=x+e^{-2x}\), если эта функция параллельна прямой \(y = -x.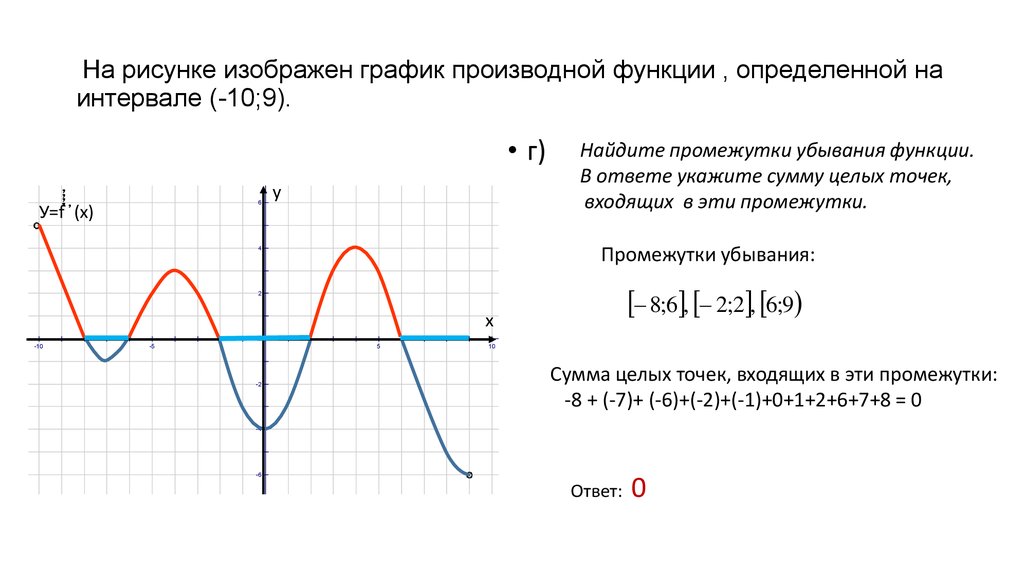
Используем уравнение касательной
\(y\;=\;f(x_0)\;+f'(x_0)(x\;-\;x_0)\\x_0\;=\;0;\;f'(x_0)\;=\;-1;\;f(x_0)\;=\;1\\y\;=\;1\;-\;1(x-0)\;=\;1\;-\;x\)
В каких точках производная равна нулю
Производная будет эквивалентна нулю в точках минимума, максимума и перегиба, при параллельной оси \(ОX\) касательной. Рассмотрим следующий рисунок:
Очевидно, что в точках \(C\) и \(D\) касательная горизонтальна, тогда тангенс угла ее наклона будет равняться 0. Отсюда можно сделать вывод, что и производная равна 0. Точка C здесь будет являться точкой максимума. В этой точке возрастание функции изменяется на убывание, как меняется и знак производной — с плюса на минус. Точка \(D\) здесь — точка минимума. В это случае также происходят изменения, но в обратном порядке.
Примечание
Важно отметить, что производная может не существовать в точке максимума. Такое происходит, если на графике изображен резкий излом, к которому невозможно провести касательную.
Рассмотрим еще одно изображение функции:
В данном случае производная будет эквивалентна нулю в точке перегиба, так как в точке \(E\) касательная к функции параллельна оси \(ОX\). В этом случае знак производной не будет изменяться, потому что до точки перегиба и после функция возрастает. Знак был и остается положительным.
Пример
Рассмотрим рисунок, на котором начерчен график функции \(y = f(x)\). График определен на интервале (−3; 9). Необходимо определить количество точек, где производная функции \(f(x)\) эквивалентна 0.
На данном рисунке очевидно, что производная функции f(x) эквивалентна нулю в точках максимума и минимума, то есть в точках −2; −1; 1; 4 и 6. Таким образом производная равна нулю в 5 точках.
Примеры производной на графике функции
Задача №1
Рассмотрим рисунок.
Рисунок изображает график производной функции \(f(x)\).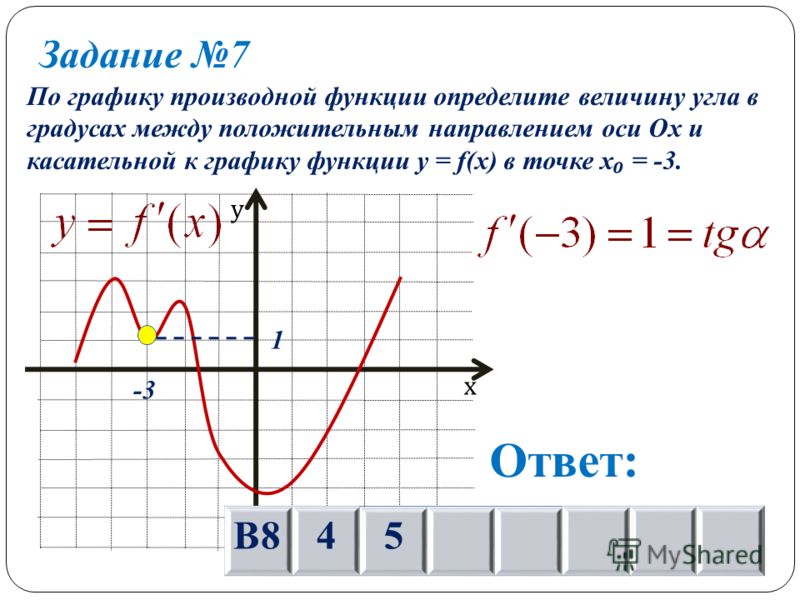 Функция определена на интервале (-10; 2). Необходимо найти, в скольких точках касательная к графику функции \(f(x)\) будет параллельна прямой \(y = -2x — 11\) или совпадать с ней.
Функция определена на интервале (-10; 2). Необходимо найти, в скольких точках касательная к графику функции \(f(x)\) будет параллельна прямой \(y = -2x — 11\) или совпадать с ней.
Решение
Используем правило о значении производной, которое в точке касания эквивалентно угловому коэффициенту касательной. Тогда, зная, что касательная параллельна прямой \(y = -2x — 11\) или идентична с ней, можно утверждать, что угловые коэффициенты равны \(-2\).
Теперь необходимо найти число точек, в которых \(f'(x)\;=\;-2\). Искомое значение соответствует числу точек, где график производной пересекается с прямой \(y = -2\). На заданном интервале 5 таких точек.
Ответ: 5.
Задача №2
Первый рисунок изображает график функции \(y = f(x)\) и касательную к нему в точке с абсциссой \(x_0\). Необходимо установить значение производной функции \(f(x)\) в точке \(x_0\).
Решение
Используем правило, гласящее, что угловой коэффициент касательной эквивалентен значению производной в точке касания, который в свою очередь эквивалентен тангенсу угла наклона данной касательной к оси абсцисс.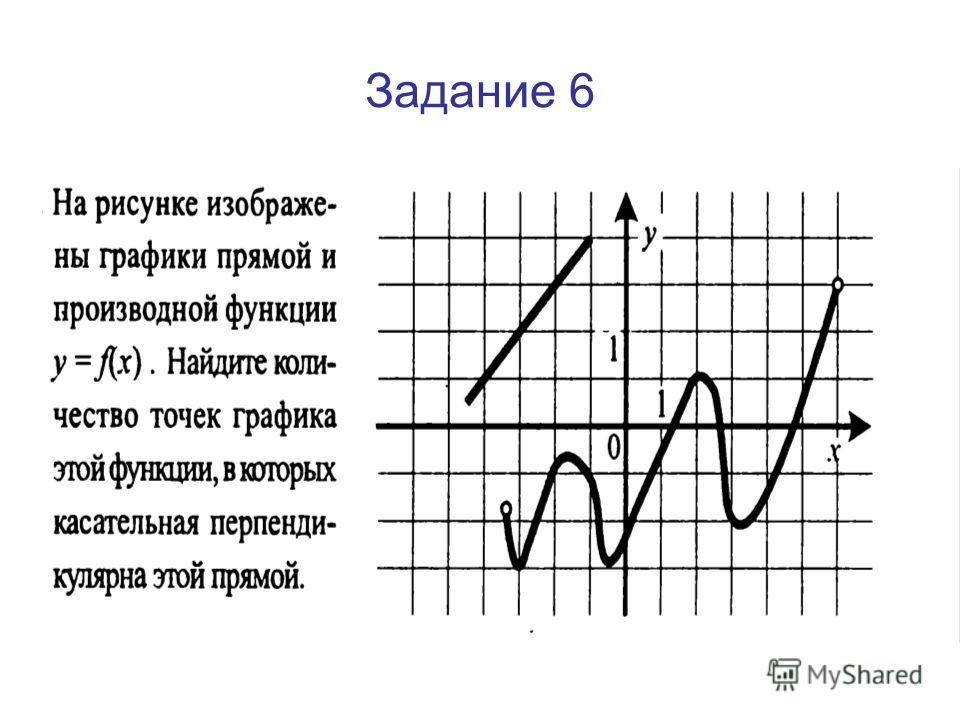 На втором рисунке показано, что решить задачу можно с помощью построения треугольника, вершины которого соответствуют точкам A (1; 2), B (1; -4), C(-2; -4). Тогда угол наклона касательной к оси абсцисс можно найти через угол \(ACB\), которому он будет равен:
На втором рисунке показано, что решить задачу можно с помощью построения треугольника, вершины которого соответствуют точкам A (1; 2), B (1; -4), C(-2; -4). Тогда угол наклона касательной к оси абсцисс можно найти через угол \(ACB\), которому он будет равен:
\(y'(x_0)\;=\;tg\angle ABC\;=\;\frac{AB}{BC}\;=\;\frac{2+4}{1+2}\;=\;2\)
Ответ: 2.
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
12.04. Исследование функции с помощью второй производной
Исследование функции с помощью второй производной
Вторая производная функции, если она существует, может быть так же эффективно использована для исследования на экстремум, определения промежутков выпуклости и вогнутости ее графика, отыскания точек перегиба.
ТЕОРЕМА 1 (ВТОРОЕ ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА). Если для функции в точке производная , А в ее окрестности непрерывна, причем , то эта точка является точкой ее максимума (минимума).
Если для функции в точке производная , А в ее окрестности непрерывна, причем , то эта точка является точкой ее максимума (минимума).
ДОКАЗАТЕЛЬСТВО.
Пусть в точке с выполняется равенство
И имеет место неравенство
Будучи непрерывной, вторая производная сохраняет свой знак при х, Близких к с. Поэтому для этих x
Но вторая производная функции есть производная от первой производной
|
Рис. 11.17. Возможное взаимное расположение графиков функций , И в окрестности точки Максимума. |
|
Это условие является достаточным признаком для существования экстремума, но не является необходимым. |
Следовательно, есть функция убывающая. По условию теоремы, . Это означает, что левее точки с Положительна, а правее – отрицательна. Переходя к самой функции , можно утверждать, что левее точки С она возрастает, а правее – убывает, то есть с – точка ее максимума, что и требовалось доказать. Аналогично доказывается теорема в случае минимума. На рис. 11.17 приведен возможный вариант взаимного расположения графиков функций , И в окрестности точки с.
Данная теорема может оказаться удобной, когда знак определяется легко. Однако ее недостаток в сравнении с первым достаточным условием экстремума функции очевиден: не все точки, подозрительные на экстремум, могут быть исследованы с помощью данной теоремы. Она неприменима в случаях, когда в точке с первая производная функции обращается в бесконечность или же не определена и, конечно, когда не существует.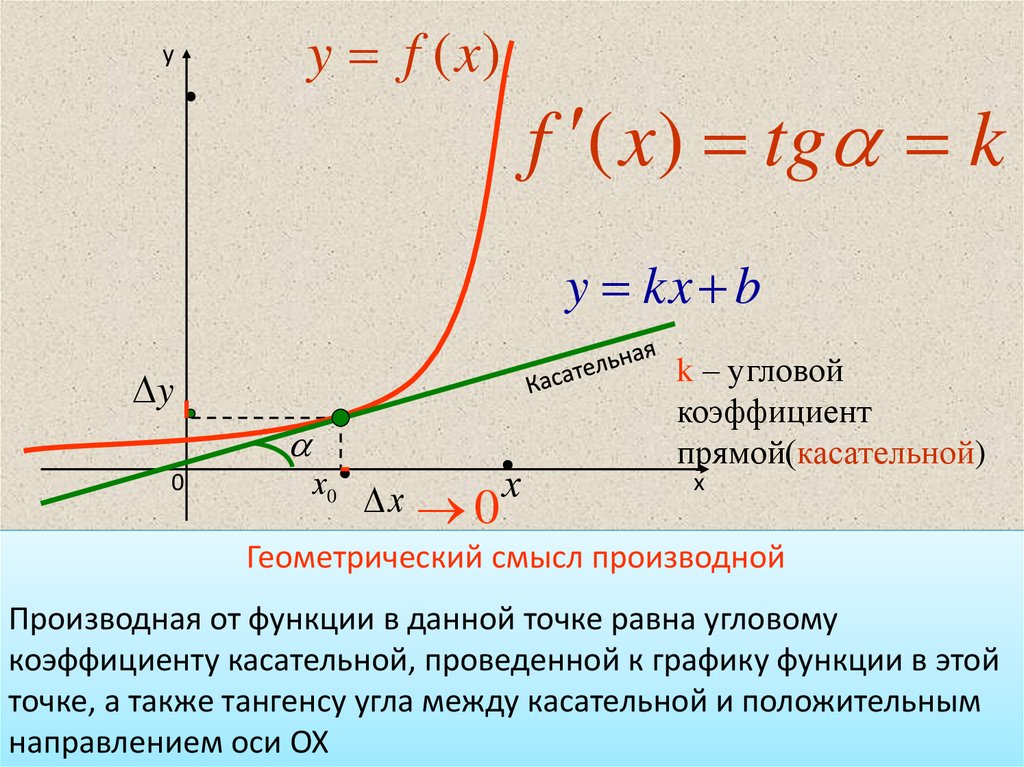
Сформулируем без доказательства некоторое обобщение данной теоремы для случая, когда функция имеет производные порядка .
ТЕОРЕМА 2. Если функция в некоторой окрестности точки С имеет производную до (n+1)-го порядка, непрерывную в самой точке С, причем то при четном (n+1) функция имеет максимум, если и минимум, если .
Рассмотрим примеры.
Исследуем на экстремум функцию
Находим первую производную:
И приравниваем ее к нулю:
.
Получаем, что x = 0 – Точка, подозрительная на экстремум.
Следовательно, в этой точке функция имеет максимум:
Рассмотрим теперь функцию
Ее первая производная
Также обращается в нуль при .
Легко обнаружить, что , так как
Однако по теореме 2 имеем:
Следовательно, функция при Экстремума не имеет.
Отсутствие экстремума у данной функции легко установить и без применения производной.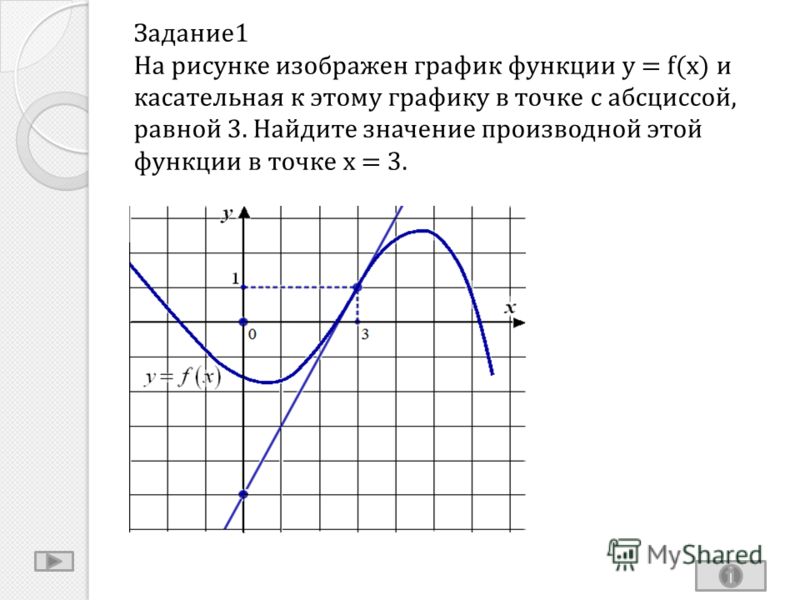 Действительно, так как функция всюду возрастает, то функция
Действительно, так как функция всюду возрастает, то функция
Убывает для , то есть экстремум отсутствует. Этот пример еще раз показывает, что при исследовании функций полезно использовать разнообразные приемы.
Применим теперь вторую производную к исследованию на выпуклость и вогнутость графика функции.
Выше, в главе 3, мы определили эти понятия, связывая расположение кривой с расположением хорды, соединяющей две близкие точки этой кривой. Возможен и иной способ описания выпуклости и вогнутости кривой.
Будем называть график функции в точке вогнутым (выпуклым), если в окрестности точки М он расположен выше (ниже) касательной к кривой в этой точке (рис. 11.18).
|
Рис. 11.18. Расположение кривой по отношению Б) расположение касательной к выпуклой кривой. |
ТЕОРЕМА 3. Если функция в интервале имеет положительную (отрицательную) вторую производную, то кривая на этом интервале вогнута (выпукла).
ДОКАЗАТЕЛЬСТВО.
Возьмем произвольную точку с в интервале и покажем, что при точки графика функции, соответствующие значениям аргумента х, близлежащим к с, будут располагаться выше точек касательной к кривой , Проведенной в точке (рис. 11.18). Уравнение касательной имеет вид:
Где – Ордината ее произвольной точки.
Найдем разность ординат кривой и касательной к ней при одном и том же значении х, близком к с :
Здесь мы применили теорему Лагранжа к разности ,
К разности , рассматриваемой на отрезке , снова применим теорему Лагранжа. Получим:
Где .
Если , то поэтому
,
И при условии, что , имеем
При
И так как , то
Таким образом, любая точка кривой Лежит выше касательной, что и требовалось доказать.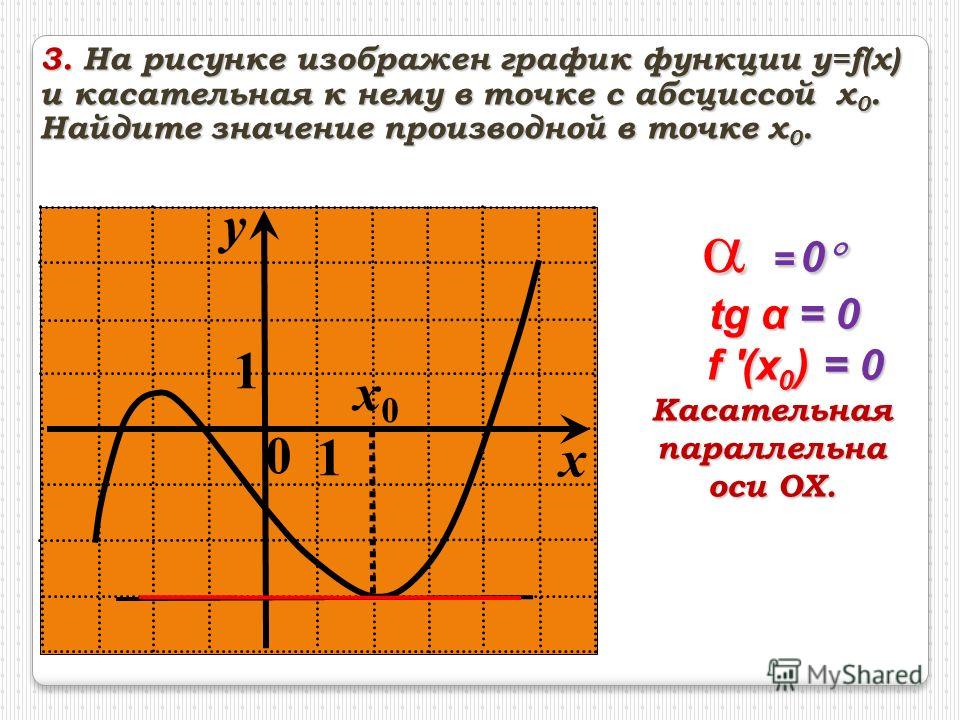
Аналогично доказывается выпуклость графика при
Точка графика функции называется Точкой перегиба, если при переходе через нее кривая меняет свою выпуклость на вогнутость, или же наоборот. Последующие теоремы определяют критерии существования перегиба.
ТЕОРЕМА 4 (НЕОБХОДИМОЕ УСЛОВИЕ ПЕРЕГИБА). Если функция имеет в окрестности внутренней точки c области определения вторую непрерывную производную и точка , лежащая на графике функции, является точкой перегиба, то
ДОКАЗАТЕЛЬСТВО.
|
Может ли точка экстремума совпадать с точкой перегиба? |
Предположим противное:
|
Можно ли утверждать, что между двумя точками экстремума функции лежит хотя бы одна точка перегиба? |
В силу непрерывности найдется окрестность точки С, в которой сохраняет знак, то есть график функции будет либо выпуклым, либо вогнутым, а потому точка не может быть точкой перегиба. Полученное противоречие доказывает утверждение теоремы
Полученное противоречие доказывает утверждение теоремы
|
Можно ли утверждать, что между двумя точками перегиба лежит хотя бы одна точка экстремума? |
.
|
Графиком функции на отрезке является выпуклая кривая, причем . Может ли она иметь экстремум на этом промежутке? |
Данная теорема позволяет отнести к точкам, где следует ожидать перегиб графика функции , те точки ее области определения, в которых Однако множество точек, подозрительных на перегиб, может быть расширено за счет тех, в которых обращается в бесконечность или вовсе не существует. На рис. 11.19 указаны возможные случаи перегиба графика функции.
Укажем достаточные условия перегиба графика функции.
|
Рис. 11.19. Возможные случаи перегиба графика Функции . |
ТЕОРЕМА 5 (ДОСТАТОЧНОЕ УСЛОВИЕ ПЕРЕГИБА). Если при переходе через точку c, подозрительную на перегиб графика функции , вторая производная меняет знак, то точка графика есть точка перегиба.
ДОКАЗАТЕЛЬСТВО.
Из условия теоремы следует, что левее точки – кривая выпуклая (вогнутая), а правее ее – вогнутая (выпуклая). Значит, – точка перегиба.
Приведем без доказательства еще два признака перегиба графика функции.
ТЕОРЕМА 6. Если функция такова, что в точке с , а и конечна, то ее график в точке имеет перегиб.
Следующая теорема является более общей.
ТЕОРЕМА 7. Если функция в некоторой окрестности точки с имеет производную до (N+1)-го порядка, непрерывную в самой точке С, причем а , то при нечетном (n+1) График функции в точке будет иметь перегиб.
Рассмотрим примеры.
Найдем точки перегиба функции .
Выше получено:
.
Условие приводит нас к уравнению
|
Можно ли с помощью второй производной исследовать функцию на монотонность? |
Которое имеет решения:
|
Какая из производных несет большую информацию о свойствах функции – первая или вторая? |
Исследуем эти точки, подозрительные на перегиб. Очевидно, что
для
|
Есть ли функции, у которых: А) вторая производная изменяется, как и сама функция; Б) функция не совпадает с первой производной, но первая и вторая ее производные совпадают между собой? |
И ;
для
,
|
Дана функция, являющаяся второй производной некоторой функции. |
Следовательно, для и кривая вогнута; для кривая выпукла, а точки графика и являются точками перегиба.
Данная функциональная зависимость встречается часто в теории вероятностей. Она известна под названием кривой Гаусса. Ее график изображен на рис. 11.20.
|
Рис. 11.20. График функции . |
Вернемся теперь еще раз к функции .
Ее вторая производная имеет вид:
Условие
Приводит нас к уравнению
Которое имеет корни
Являющиеся абсциссами точек графика данной функции, подозрительных на перегиб.
Теорема 7 позволяет достаточно просто их исследовать. Имеем:
Следовательно, точка является точкой перегиба графика кривой .
А потому и точка также является точкой перегиба. График данной функции схематично изображен на рис. 11.21.
|
Рис. 11.21. График функции . |
| < Предыдущая | Следующая > |
|---|
В какой точке значение производной набольшее
Дорогие друзья! В группу заданий связанных с производной входят задачи — в условии дан график функции, несколько точек на этом графике и стоит вопрос:
В какой точке значение производной наибольшее (наименьшее)?
Данные задачи очень просты, не требуется никаких вычислений, решаются устно. Главное что необходимо – это понимать геометрический смысл производной, свойства производной для исследования функций. По представленным ссылкам вы можете повторить (изучить) материал на сайте, также краткая информация есть в справочнике.
Кратко повторим:
Производная в точке равна угловому коэффициенту касательной проходящей через эту точку графика.
Угловой коэффициент касательной в свою очередь равен тангенсу угла наклона этой касательной.
*Имеется ввиду угол между касательной и осью абсцисс.
Далее:
1. На интервалах возрастания функции производная имеет положительное значение.
2. На интервалах её убывания производная имеет отрицательное значение.
Рассмотрим следующий эскиз:
В точках 1,2,4 производная функции имеет отрицательное значение, так как данные точки принадлежат интервалам убывания.
В точках 3,5,6 производная функции имеет положительное значение, так как данные точки принадлежат интервалам возрастания.
Как видим, со значением производной всё ясно, то есть определить какой она имеет знак (положительный или отрицательный) в определённой точке графика совсем несложно.
При чём, если мы мысленно построим касательные в этих точках, то увидим, что прямые проходящие через точки 3, 5 и 6 образуют с осью оХ углы лежащие в пределах от 0 до 90о, а прямые проходящие через точки 1, 2 и 4 образуют с осью оХ углы в пределах от 90о до 180о.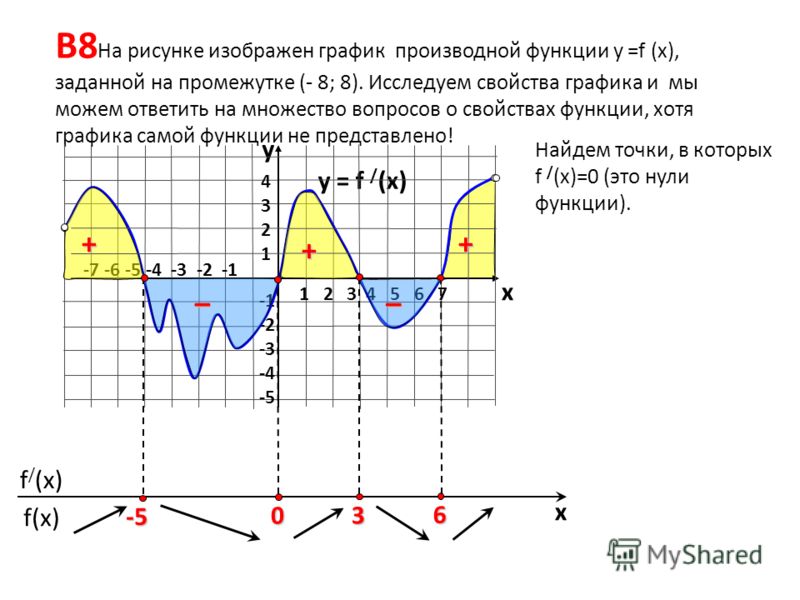
*Взаимосвязь понятна: касательные проходящие через точки принадлежащие интервалам возрастания функции образуют с осью оХ острые углы, касательные проходящие через точки принадлежащие интервалам убывания функции образуют с осью оХ тупые углы.
Теперь важный вопрос!
А как изменяется значение производной? Ведь касательная в разных точках графика непрерывной функции образует разные углы, в зависимости от того, через какую точку графика она проходит.
*Или, говоря простым языком, касательная расположена как бы «горизонтальнее» или «вертикальнее». Посмотрите:
Прямые образуют с осью оХ углы в пределах от 0 до 90о
Прямые образуют с осью оХ углы в пределах от 90о до 180о
Поэтому, если будут стоять вопросы:
— в какой из данных точек графика значение производной имеет наименьше значение?
— в какой из данных точек графика значение производной имеет наибольшее значение?
то для ответа необходимо понимать, как изменяется значение тангенса угла касательной в пределах от 0 до 180о.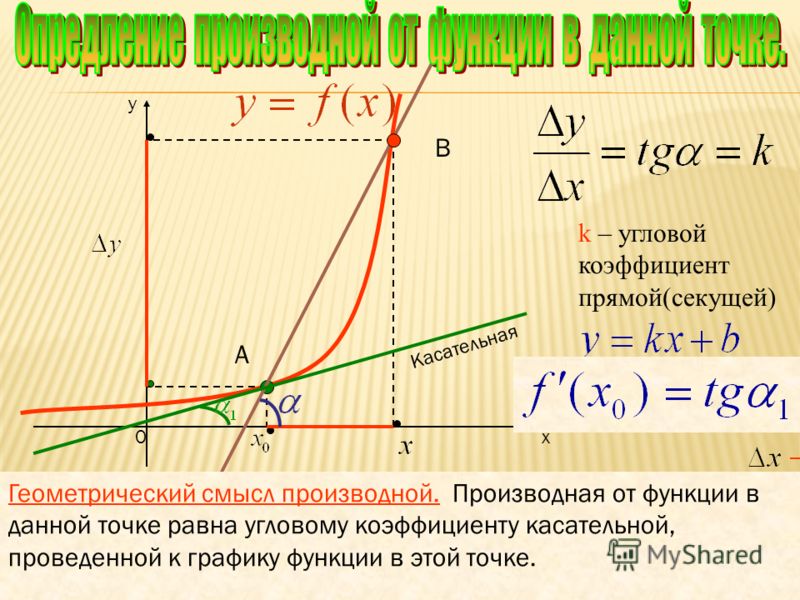
*Как уже сказано, значение производной функции в точке равно тангенсу угла наклона касательной к оси оХ.
Значение тангенса изменяется следующим образом:
При изменении угла наклона прямой от 0о до 90о значение тангенса, а значит и производной, изменяется соответственно от 0 до +∞;
При изменении угла наклона прямой от 90о до 180о значение тангенса, а значит и производной, изменяется соответственно –∞ до 0.
Наглядно это видно по графику функции тангенса:
Говоря простым языком:
При угле наклона касательной от 0о до 90о
Чем он ближе к 0о, тем больше значение производной будет близко к нулю (с положительной стороны).
Чем угол ближе к 90о, тем больше значение производной будет увеличиваться к +∞.
При угле наклона касательной от 90о до 180о
Чем он ближе к 90о, тем больше значение производной будет уменьшаться к –∞.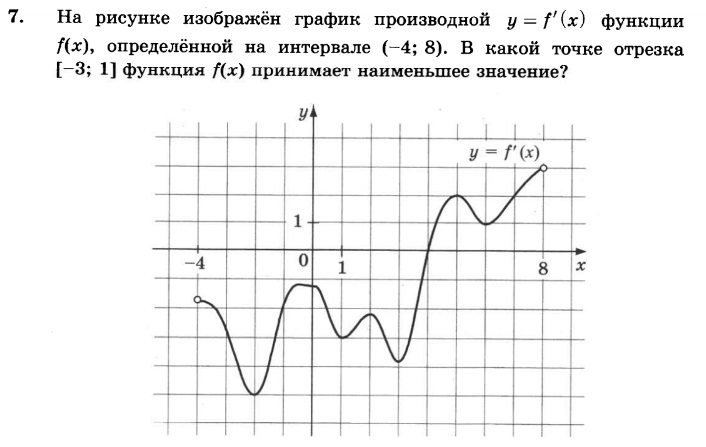
Чем угол будет ближе к 180о, тем больше значение производной будет близко к нулю (с отрицательной стороны).
317543. На рисунке изображен график функции y = f(x) и отмечены точки –2, –1, 1, 2. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Имеем четыре точки: две из них принадлежат интервалам на которых функция убывает (это точки –1 и 1) и две интервалам на которых функция возрастает (это точки –2 и 2).
Можем сразу же сделать вывод о том, что в точках –1 и 1 производная имеет отрицательное значение, в точках –2 и 2 она имеет положительное значение. Следовательно в данном случае необходимо проанализировать точки –2 и 2 и определить в какой из них значении будет наибольшим. Построим касательные проходящие через указанные точки:
Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке –2 будет наибольшим.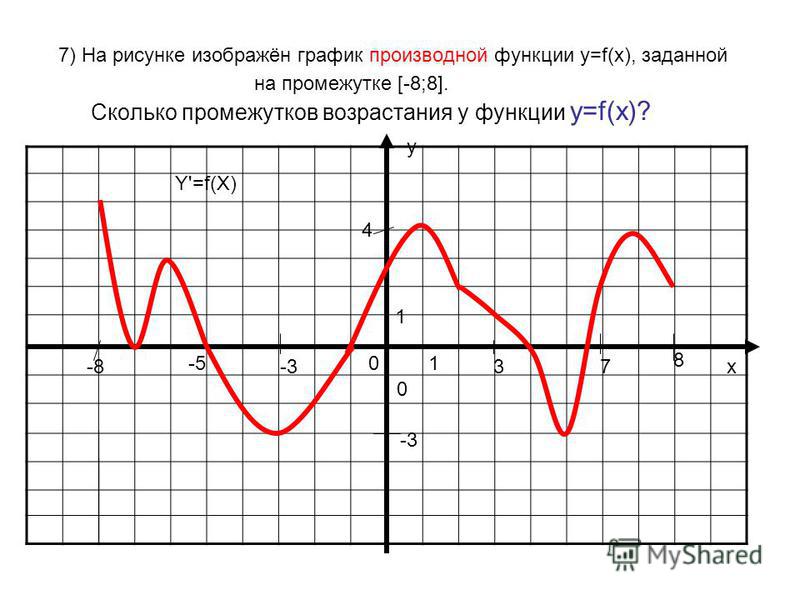
Ответим на следующий вопрос: в какой из точек –2, –1, 1 или 2 значение производной является наибольшим отрицательным? В ответе укажите эту точку.
Производная будет иметь отрицательное значение в точках, принадлежащим интервалам убывания, поэтому рассмотрим точки –2 и 1. Построим касательные проходящие через них:
Видим, что тупой угол между прямой b и осью оХ находится «ближе» к 180о, поэтому его тангенс будет больше тангенса угла, образованного прямой а и осью оХ.
Таким образом, в точке х = 1, значение производной будет наибольшим отрицательным.
317544. На рисунке изображен график функции y = f(x) и отмечены точки –2, –1, 1, 4. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Имеем четыре точки: две из них принадлежат интервалам, на которых функция убывает (это точки –1 и 4) и две интервалам, на которых функция возрастает (это точки –2 и 1).
Можем сразу же сделать вывод о том, что в точках –1 и 4 производная имеет отрицательное значение, в точках –2 и 1 она имеет положительное значение.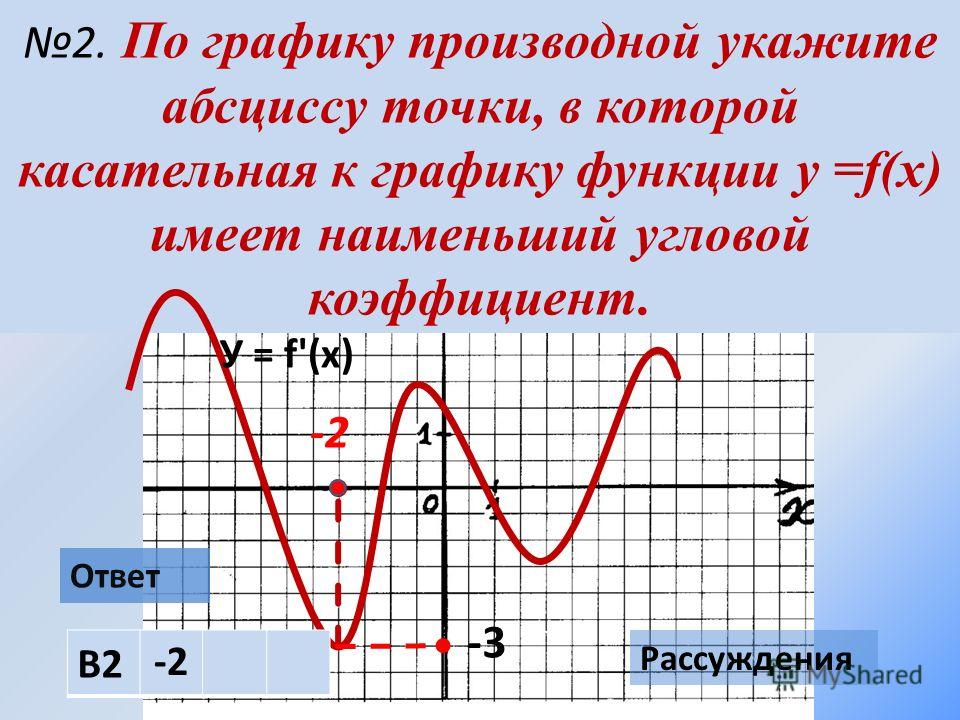 Следовательно, в данном случае, необходимо проанализировать точки –1 и 4 и определить – в какой из них значении будет наименьшим. Построим касательные проходящие через указанные точки:
Следовательно, в данном случае, необходимо проанализировать точки –1 и 4 и определить – в какой из них значении будет наименьшим. Построим касательные проходящие через указанные точки:
Значение тангенса угла между прямой a и осью абсцисс будет больше значения тангенса угла между прямой b и этой осью. Это означает, что значение производной в точке х = 4 будет наименьшим.
Ответ: 4
Надеюсь, что «не перегрузил» вас количеством написанного. На самом деле, всё очень просто, стоит только понять свойства производной, её геометрический смысл и как изменяется значение тангенса угла от 0 до 180о.
Общие рекомендации:
1. Сначала определите знаки производной в данных точках (+ или -) и выберете необходимые точки (в зависимости от поставленного вопроса).
2. Постройте касательные в этих точках.
3. Пользуясь графиком тангесоиды, схематично отметьте углы и отобразите соответствующие им значения.
4. Далее в зависимости от поставленного вопроса в задаче, вы без труда определите точку.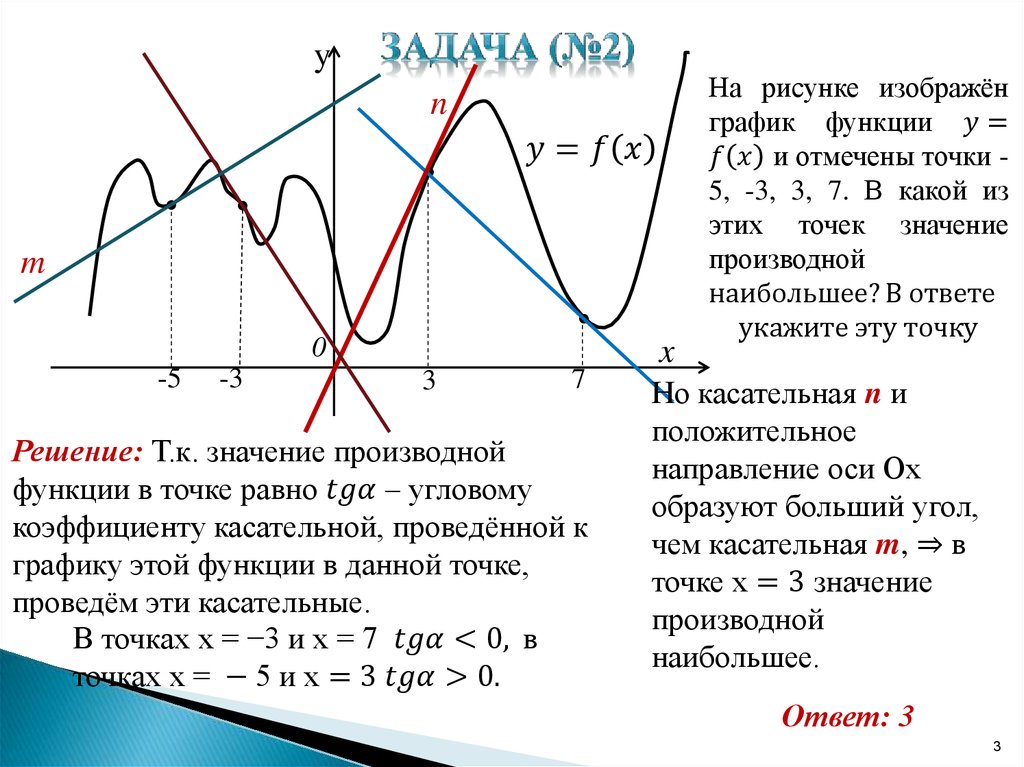
*Если вы понимаете, как изменяется значение тангенса, то можно обойтись без графика.
На этом всё. Успехов Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
1.5: Интерпретация, оценка и использование производной
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4296
- Мэтью Болкинс, Дэвид Остин и Стивен Шликер
- Государственный университет Гранд-Вэлли через ScholarWorks @ Государственный университет Гранд-Вэлли
Цели обучения
В этом разделе мы стремимся понять идеи, порожденные следующими важными вопросами:
- В контексте, отличном от положения движущегося объекта, что измеряет производная функции?
- Каковы единицы измерения производной функции \(f’\) и как они связаны с единицами исходной функции \(f\)?
- Что такое центральное различие и как его можно использовать для оценки значения производной в точке по заданным данным функции?
- Зная значение производной функции в точке, какой вывод мы можем сделать о том, как изменяется значение функции поблизости?
Введение
Интересной и мощной особенностью математики является то, что ее часто можно рассматривать как в абстрактных, так и в прикладных терминах. Например, исчисление может быть разработано почти полностью как абстрактный набор идей, сосредоточенных на свойствах произвольных функций. В то же время исчисление также может быть напрямую связано с нашим опытом физической реальности, рассматривая функции, которые представляют значимые процессы. Мы уже видели, что для функции положения \(y=s(t)\), скажем, для мяча, подброшенного прямо вверх в воздух, скорость мяча в момент времени \(t\) определяется выражением \(v(t )=s'(t)\), производная функции положения.
Например, исчисление может быть разработано почти полностью как абстрактный набор идей, сосредоточенных на свойствах произвольных функций. В то же время исчисление также может быть напрямую связано с нашим опытом физической реальности, рассматривая функции, которые представляют значимые процессы. Мы уже видели, что для функции положения \(y=s(t)\), скажем, для мяча, подброшенного прямо вверх в воздух, скорость мяча в момент времени \(t\) определяется выражением \(v(t )=s'(t)\), производная функции положения.
Далее, напомним, что если \(s(t)\) измеряется в футах в момент времени \(t\), то единицей измерения \(v(t)=s'(t)\) являются футы в секунду. Далее в этом разделе мы исследуем несколько различных функций, каждая из которых имеет определенный физический смысл, и подумаем о том, как единицы измерения независимой переменной, зависимой переменной и производной функции дополняют наше понимание. Для начала рассмотрим известную задачу о функции положения движущегося объекта.
Активность предварительного просмотра \(\PageIndex{1}\)
Один из самых длинных участков прямой (и ровной) дороги в Северной Америке можно найти на Великих равнинах в штате Северная Дакота на шоссе штата 46, которое проходит к югу от межгосударственного шоссе I-94 и проходит через город Гакл. Автомобиль выезжает из города (в момент времени \(t=0\)) и направляется на восток по шоссе 46; его положение в милях от Гакла в момент времени \(t\) в минутах определяется графиком функции на рис. 1.22. На графике отмечены три важные точки; где кривая выглядит линейной, предположим, что это действительно прямая линия.
Автомобиль выезжает из города (в момент времени \(t=0\)) и направляется на восток по шоссе 46; его положение в милях от Гакла в момент времени \(t\) в минутах определяется графиком функции на рис. 1.22. На графике отмечены три важные точки; где кривая выглядит линейной, предположим, что это действительно прямая линия.
. минут.
- Обыденным языком опишите поведение автомобиля на указанном интервале времени. В частности, обсудим, что происходит на временных интервалах [57, 68] и [68, 104].
- Найдите наклон прямой между точками (57, 63,8) и (104, 106,8). Какие единицы находятся на этом склоне? Что представляет наклон?
- Найти среднюю скорость изменения положения автомобиля на отрезке [68, 104]. Включите единицы в свой ответ.
- Оценить мгновенную скорость изменения положения автомобиля в момент \(t=80\). Напишите предложение, объясняющее ваши рассуждения и значение этого значения.
Единицы производной функции
Как мы теперь знаем, производная функции \(f\) при фиксированном значении \(x\) определяется выражением \[f'(x)=\lim_{h\ до 0} \frac{f(x+h)-f(x)}{h}\],
и это значение имеет несколько различных интерпретаций.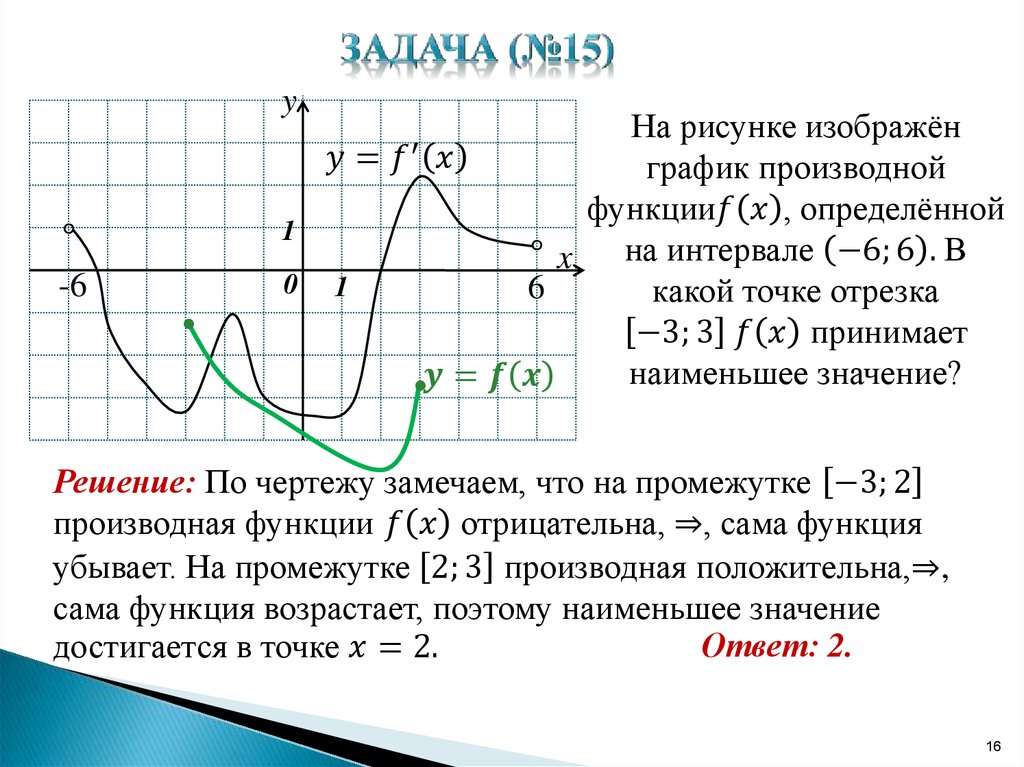 Если мы установим \(x=a\), одним из значений \(f'(a)\) будет наклон касательной в точке \((a, (f(a))\).
Если мы установим \(x=a\), одним из значений \(f'(a)\) будет наклон касательной в точке \((a, (f(a))\).
In альтернативные обозначения, мы также иногда эквивалентно пишем \(\frac{df}{dx}\) или \(\frac{dy}{dx}\) вместо \(f'(x)\), и эти обозначения помогают нам чтобы далее увидеть единицы (и, следовательно, значение) производной, поскольку она рассматривается как t мгновенная скорость изменения \(f\) по отношению к \(х\). Обратите внимание, что единицы наклона секущей, \(\frac{f(x+h)-f(x)}{h}\), являются «единицами \(f\) на единицу \(x \)». Таким образом, когда мы используем предел, чтобы получить \(f'(x)\), мы получаем те же самые единицы на производной \(f'(x)\): единицы \(f\) на единицу \( Икс\). Независимо от рассматриваемой функции \(f\) (и независимо от используемых переменных), полезно помнить, что единицами производной функции являются «единицы выпуска на единицу ввода» с точки зрения входных и вывод исходной функции.
Например, у нас есть функция \(y=P(t)\), где \(P\) измеряет численность населения города (в тысячах) в начале года \(t\) (где \(t=0\) соответствует 2010 году нашей эры), и нам говорят, что \(P'(2)=21,37\).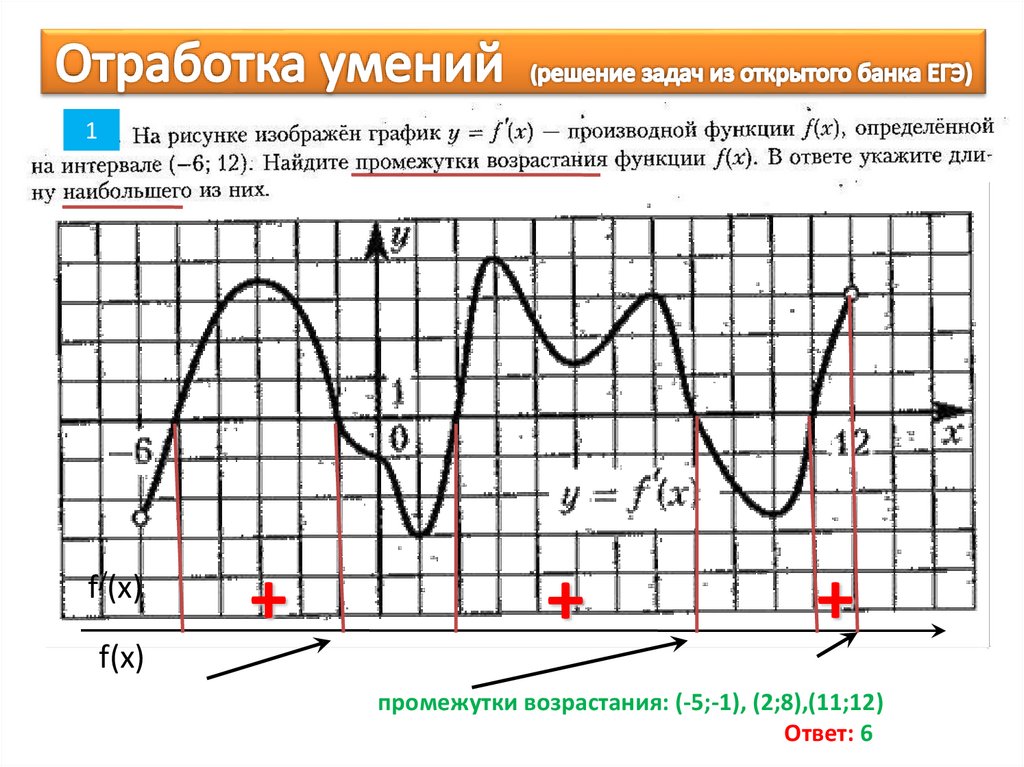 В чем смысл этого значения? Ну а поскольку \(P\) измеряется в тысячах, а \(t\) — в годах, то можно сказать, что мгновенная скорость изменения численности населения города по отношению ко времени на начало 2012 г. составляет 21,37 тыс. чел./чел. год. Поэтому мы ожидаем, что в наступающем году к населению города добавится около 21 370 человек.
В чем смысл этого значения? Ну а поскольку \(P\) измеряется в тысячах, а \(t\) — в годах, то можно сказать, что мгновенная скорость изменения численности населения города по отношению ко времени на начало 2012 г. составляет 21,37 тыс. чел./чел. год. Поэтому мы ожидаем, что в наступающем году к населению города добавится около 21 370 человек.
К более точным оценкам производных
К более точным оценкам производных Полезно также вспомнить, как мы впервые убедились в разделе 1.3, что когда мы хотим оценить значение \(f'(x)\) при заданном \(x\), мы можем использовать разностный коэффициент \(\frac{f(x+h)-f(x)}{h}\) с относительно небольшим значением \(h\). При этом мы должны использовать как положительные, так и отрицательные значения \(h\), чтобы убедиться, что мы учитываем поведение функции по обе стороны от точки интереса. С этой целью мы рассмотрим следующий краткий пример, демонстрирующий понятие центральная разность и ее роль в оценке производных.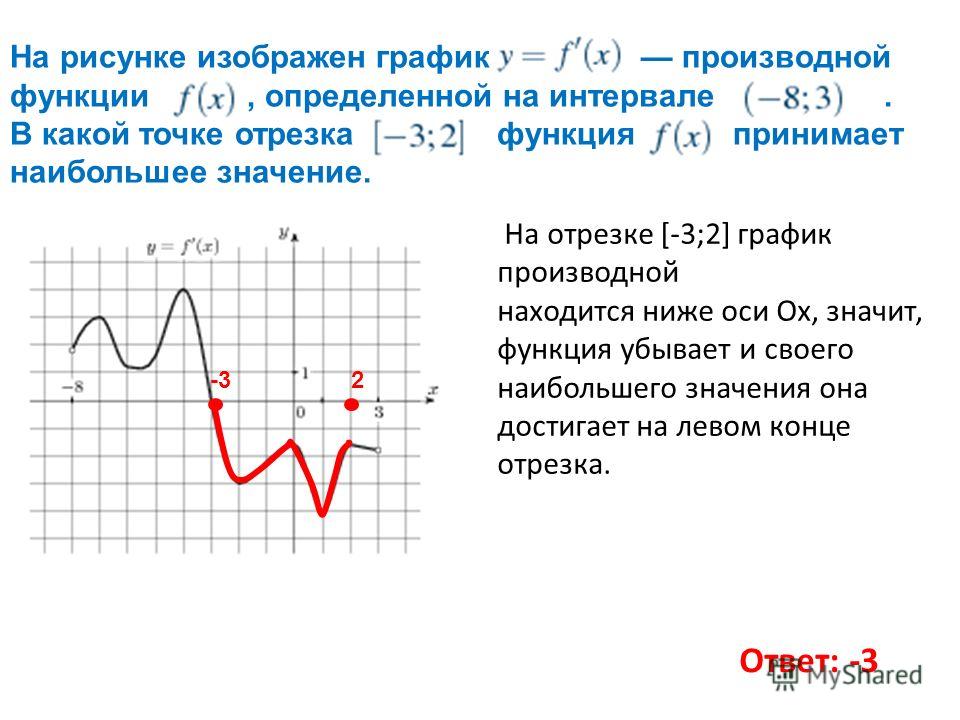
Пример \(\PageIndex{1}\)
Предположим, что \(y=f(x)\) — функция, для которой известны три значения: \(f(1)=2,5\), \(f (2)=3,25\) и \(f(3)=3,625\). Оценка \(f'(2)\).
Решение .
Мы знаем, что \(f'(2)=\lim_{h\to 0} \frac{f(2+h)-f(2)}{h}\). Но поскольку у нас нет ни графика для \(y=f(x)\), ни формулы для функции, мы не можем ни нарисовать касательную, ни точно оценить предел. Мы даже не можем использовать все меньшие и меньшие значения \(h\) для оценки предела. Вместо этого у нас есть только два варианта: использовать \(h=-1\) или \(h=1\), в зависимости от того, какую точку мы соединяем с (2, 3.25). Таким образом, одна оценка равна \[f'(2) \приблизительно \frac{f(1)-f(2)}{1-2}=\frac{2,5-3,25}{-1}=0,75.\]
Другой равен \[f'(2) \приблизительно \frac{f(3)-f(2)}{3-2}=\frac{3,625-3,25}{1}=0,375.\]
Поскольку первое приближение смотрит только назад из точки (2, 3.25), а второе приближение смотрит только вперед из (2, 3.25), имеет смысл усреднить эти два значения, чтобы учесть поведение по обе стороны от точки интерес.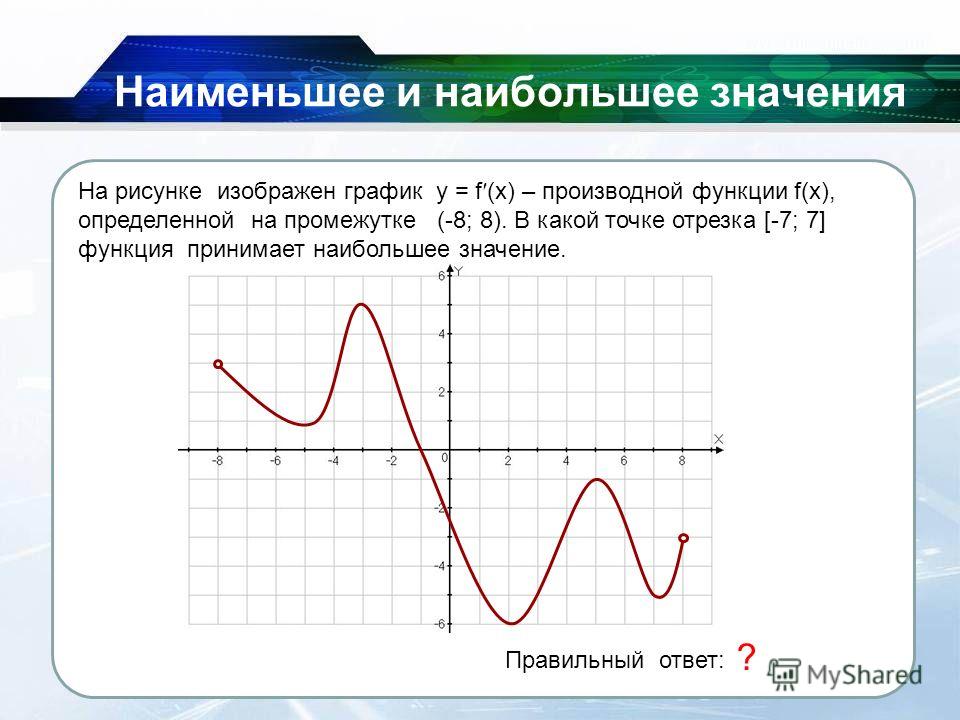 При этом мы находим, что \[f'(2) \приблизительно \frac{0,75+0,375}{2}=0,5625.\]
При этом мы находим, что \[f'(2) \приблизительно \frac{0,75+0,375}{2}=0,5625.\]
Интуитивный подход к усреднению двух оценок, найденных в примере 1.4, на самом деле является наилучшим из возможных. оценка \(f'(2)\), когда у нас есть только два значения функции для \(f\) на противоположных сторонах точки интереса. Чтобы понять почему, обратимся к диаграмме на рис. 1.23, которая
Рисунок 1.23: Слева график \(y=f(x)\) вместе с секущей через (1, 2.5) и (2, 3.25), секущая через (2, 3.25) ) и (3, 3.625), а также касательная. Справа тот же график вместе с секущей, проходящей через (1, 2,5) и (3, 3,625), плюс касательная.
показывает возможную функцию \(y=f(x)\), которая удовлетворяет данным, приведенным в примере 1.4. Слева мы видим две секущие линии с наклоном, полученным в результате вычисления назад разность \(\frac{f(1)-f(2)}{1-2}=0,75\) и из вперед разность \(\frac{f(3)-f(2)} {3-2}=0,375\). Обратите внимание, что наклон первой такой линии завышает наклон касательной в точке \((2, f(2))\), а наклон второй линии занижает \(f'(2)\). Однако справа мы видим секущую, наклон которой определяется центральной разностью \[ \frac{f(3)-f(1)}{3-1}=\frac{3,625-2,5}{ 2}=\frac{1,125}{2}=0,5625.\]
Однако справа мы видим секущую, наклон которой определяется центральной разностью \[ \frac{f(3)-f(1)}{3-1}=\frac{3,625-2,5}{ 2}=\frac{1,125}{2}=0,5625.\]
Обратите внимание, что эта центральная разность имеет то же значение, что и среднее значение прямой и обратной разности (и нетрудно объяснить, почему это всегда выполняется) , и, кроме того, центральная разность дает очень хорошее приближение к значению производной, отчасти потому, что секущая линия, которая использует точку до и после точки касания, дает линию, которая ближе к параллельной линии касательной.
В общем случае центрально-разностная аппроксимация значения первой производной определяется выражением \[f'(a) \ приблизительно \frac{f(a+h)-f(a-h)}{2h}\],
, и эта величина измеряет наклон секущей к \(y=f(x)\) через точки \((a-h, f(a-h))\) и \((a+h, f(a+h ))\). Каждый раз, когда у нас есть симметричные данные, окружающие точку, в которой мы хотим оценить производную, центральная разность является идеальным выбором для этого.
В следующих упражнениях будет дополнительно изучено значение производной в нескольких различных контекстах, а также рассмотрена производная с графической, числовой и алгебраической точек зрения.
Действие \(\PageIndex{2}\)
Картофель помещают в печь, измеряют температуру картофеля \(F\) (в градусах по Фаренгейту) в различные моменты времени и записывают в следующую таблицу. Время \(t\) измеряется в минутах.
| \(т\) | \(Ф(т)\) |
|---|---|
| 0 | 70 |
| 15 | 180,5 |
| 30 | 251 |
| 45 | 296 |
| 60 | 324,5 |
| 75 | 342,8 |
| 90 | 354,5 |
- Используйте центральную разность для оценки мгновенной скорости изменения температуры картофеля при \(t=30\).
 Включите единицы в свой ответ.
Включите единицы в свой ответ. - Используйте центральную разность для оценки мгновенной скорости изменения температуры картофеля при \(t=60\). Включите единицы в свой ответ.
- Без каких-либо вычислений, что вы ожидаете больше: \(f'(75)\) или \(f'(90)\)? Почему?
- Предположим, что задано \(F(64)=330,28\) и \(f'(64)=1,341\). Каковы единицы измерения этих двух величин? Какой, по вашему мнению, будет температура картофеля при \(t=65\)? когда \(t=66\)? Почему?
- Напишите пару аккуратных предложений, описывающих поведение температуры картофеля на интервале времени \([0, 90]\), а также поведение мгновенной скорости изменения температуры картофеля на тот же интервал времени.
Деятельность \(\PageIndex{3}\)
Компания производит веревку, и общие затраты на производство \(r\) футов веревки составляют \(C(r)\) долларов.
- Что значит сказать, что \(C(2000)=800\)?
- Каковы единицы измерения \(C'(r)\)?
- Предположим, что \(C(2000)=800\) и \(C'(2000)=0,35\).
 Оцените \(C(2100)\) и обоснуйте свою оценку, написав хотя бы одно предложение, объясняющее ваши мысли.
Оцените \(C(2100)\) и обоснуйте свою оценку, написав хотя бы одно предложение, объясняющее ваши мысли. - Какое из следующих утверждений вы считаете верным и почему?
- \(С'(2000) < С'(3000)\)
- \(С'(2000)=С'(3000)\)
- \(С'(2000) > С'(3000)\)
- Предположим, кто-то утверждает, что \(C'(5000)=-0,1\). Что практическое значение этой производной может сказать вам о приблизительной стоимости следующего фута веревки? Это возможно? Почему или почему нет?
Activity \(\PageIndex{4}\)
Исследователи крупной автомобильной компании нашли функцию, связывающую расход бензина со скоростью для конкретной модели автомобиля. В частности, они установили, что расход \(С\) в литров на км при заданной скорости \(с\) определяется функцией \(С=f(с)\), где \ (с\) скорость автомобиля в километров в час .
- Данные, предоставленные автомобильной компанией, говорят нам, что \(f(80)=0,015\), \(f(90)=0,02\) и \(f(100)=0,027\).
 Используйте эту информацию, чтобы оценить мгновенную скорость изменения расхода топлива по отношению к скорости при \(s=90\). Будьте максимально точными, используйте правильные обозначения и включайте единицы измерения в свой ответ.
Используйте эту информацию, чтобы оценить мгновенную скорость изменения расхода топлива по отношению к скорости при \(s=90\). Будьте максимально точными, используйте правильные обозначения и включайте единицы измерения в свой ответ. - Написав полное предложение, интерпретируйте значение (в контексте расхода топлива) «\(f(80)=0,015\)».
- Напишите хотя бы одно полное предложение, интерпретирующее значение \(f'(90)\), которое вы оценили в (а). 9{\ circ} Ф / мин \). Во всех случаях, когда мы работаем с функциями, имеющими прикладной контекст, полезно и поучительно тщательно подумать о задействованных единицах и о том, как они дополнительно влияют на смысл наших вычислений.
Резюме
В этом разделе мы столкнулись со следующими важными идеями:
- Независимо от контекста данной функции \(y=f(x)\), производная всегда измеряет мгновенную скорость изменения выхода переменная по отношению к входной переменной.
- Единицами производной функции \(y=f'(x)\) являются единицы \(f\) на единицу \(x\).
 Опять же, это измеряет, насколько быстро изменяется выход функции \(f\) при изменении входа функции.
Опять же, это измеряет, насколько быстро изменяется выход функции \(f\) при изменении входа функции. - Аппроксимация центральной разности значения первой производной задается выражением \[f'(a) \ приблизительно \frac{f(a+h)-f(a-h)}{2h},\], и эта величина измеряет наклон секущей к \(y=f(x)\) через точки \((a-h, f(a-h))\) и \((a+h, f(a+h))\). Центральная разность дает хорошее приближение значения производной каждый раз, когда у нас есть симметричные данные, окружающие интересующую точку.
- Зная значения производной и функции в одной точке, мы можем оценить значения других функций поблизости. Если, например, мы знаем, что \(f'(7)=2\), то мы знаем, что при \(x\)=7 функция \(f\) возрастает с мгновенной скоростью 2 единицы выпуска на каждую единицу ввода. Таким образом, мы ожидаем, что \(f(8)\) будет примерно на 2 единицы больше, чем \(f(7)\). Значение является приблизительным, потому что мы не знаем, остается ли скорость изменения неизменной при изменении \(x\).
Эта страница под заголовком 1.
 5: Интерпретация, оценка и использование производной доступна в соответствии с лицензией CC BY-SA 4.0, ее авторами, ремиксами и/или кураторами являются Мэтью Болкинс, Дэвид Остин и Стивен Шликер (ScholarWorks @Grand Valley State университета) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
5: Интерпретация, оценка и использование производной доступна в соответствии с лицензией CC BY-SA 4.0, ее авторами, ремиксами и/или кураторами являются Мэтью Болкинс, Дэвид Остин и Стивен Шликер (ScholarWorks @Grand Valley State университета) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Активное исчисление
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
- Теги
- источник@https://activecalculus.
 org/single
org/single
- источник@https://activecalculus.
Онлайн-книга по исчислению
Глава 8. Понимание производнойГлава 8. Понимание производной
- Раздел 8.1 — Использование первой производной
- Раздел 8.2 — Использование второй производной
- Раздел 8.3 — Систематическое использование производных финансовых инструментов
Раздел 8.1. Использование первой производной
В этой главе мы подробно рассмотрим посмотрите на определение производной и ее связь с ее антипроизводная. Мы увидим, каким может быть график антипроизводной. точно описать, просто взглянув только на производную функцию.
Из определения производной является производной от функция . Производная функции говорит нам, насколько быстро f изменяется относительно независимой переменной x. Таким образом, производная относится в частности, скорость изменения антипроизводной функции по отношению к Икс. Скорость изменения также является синонимом наклона касательной к график в определенной точке.

Таким образом, функция и ее производная тесно связаны и знание только производной может многое сказать нам о поведении ее антипроизводная. Поскольку производная функции получается из определение производной как: , мы можем работать с определением, чтобы найти антипроизводную когда известна только производная. Вспомните также, как дифференциация основана на процесс ограничения или вычитания и деления; поэтому работает в обратном направлении сказал бы нам, что мы должны складывать и умножать.
Мы будем развивать это позже, однако, давайте сначала посмотрим, как мы можем использовать f(x) для получения точек равновесия на графике антипроизводная или f(x).
Точки равновесия определение, точки на графике относятся к статическим ситуациям где скорость изменения равна нулю. Таким образом, изменение независимой переменной не приводит к изменению зависимой переменной. Состояние равновесия в целом возникает, когда ситуация достигает критического максимального значения, а затем снижается или когда ситуация достигла критического минимального значения, затем увеличивается.

Равновесие и критические значения функция может относиться к разным вещам в зависимости от того, какие явления учился. Поэтому ограничимся геометрической интерпретацией равновесия как точки на графике, где скорость изменения равна нулю. Поскольку скорость изменения равна нулю, касательная к графику в этой точке будет быть горизонтальной линией.
Горизонтальная касательная говорит нам, что значение производной в точке равновесия равно нулю. Такие ситуации случаются когда график достигает максимального или минимального значения.
Также может существовать горизонтальная касательная, но не обязательно, когда изменяется вогнутость графика.
Изменение вогнутости происходит на точки на графике называются перегиба точки. Как мы вскоре узнаем, значение производной на перегибе не изменяется. должны быть равны нулю. Поэтому мы ограничим наше определение равновесия точек для отображения максимальных или минимальных значений на графике.

Например, чтобы найти равновесие баллы за функцию, . нам сначала нужно дифференцировать его, чтобы получить, . производная, , сообщает нам мгновенную скорость изменение функции, , в любой точке х. Так как мы хотим найти точки, где скорость изменения f(x) равно нулю, нам нужно установлен равным нулю, чтобы найти те значения x, которые удовлетворяют уравнению, . Делая это для результат:
Это говорит нам о том, что и при x=0, и при x=2/3 существует точка равновесия, что подтверждается графиком функция,
Имеющий найдены критические точки, как мы можем классифицировать их как максимумы или минимумы? Очевидно, это можно сделать, просто взглянув на график , но цель этой главы состоит в том, чтобы понять, как использовать только производная, приблизить поведение функции . Чтобы определить, являются ли наши точки равновесия либо максимум или минимум нам нужно оценить точки слева и справа от точки равновесия, чтобы определить, где функция, , увеличивается или уменьшается.

Минимум определяется как нижняя часть U-образного или вогнутого вверх графика. Если график вогнутый, то наклон или скорость изменения положительны. справа от точки равновесия, а функция возрастает справа от эта точка. Слева от точки равновесия наклон отрицателен, что означает, что функция убывает до он достигает точки равновесия. Чтобы лучше понять это, посмотрите на следующий график вогнутой части графика. Обратите внимание, как функция снижается, пока не достигнет точки равновесия, а после ее прохождения возрастает.
Аналогично, если скорость изменения были отрицательными на с правой стороны и положительным с левой стороны точки равновесия, то получим перевернутый U-образный или вогнутый вниз график. Таким образом, вогнутый вниз график отражает максимальное значение в точке равновесия.
Если наклон положительный или отрицательно по обе стороны от точки равновесия, то мы получаем перегиб точка, которая представляет, где вогнутость изменяется от U форму перевернутой буквы U формы или наоборот.
 Следующий график обобщает сделанные выше выводы.
Следующий график обобщает сделанные выше выводы.Следующий раздел -> Раздел 8.2 — Использование второй производной
Авторское право — UnderstandingCalculus.com Производный
Функции — это базовые понятия исчисления — неотъемлемая часть Математика, описывающая отношения между важными величинами. В наиболее распространенных отношениях значение одной из переменных зависит от ценность остальных. Математическими моделями этих ситуаций являются функции одной или нескольких (обычно вещественных) переменных.
ОПРЕДЕЛЕНИЕ ФУНКЦИИ
Функция — это отношение
между двумя переменными такими, что
к каждому значению
независимой переменной
там соответствует ровно одно значение
зависимой переменной.
Область определения функции — множество
. всех значений независимой переменной для которого определена функция.Диапазон функции
это набор всех значений, взятых на
по зависимой переменной.Функции можно описывать различными способами, обычно мы задаем их формулами, таблицы или графики.
f : А → В
х → у = ф ( х ),
куда x в A независимая переменная
а также г зависимая переменная,
является наиболее распространенным обозначением функций.График функции действительного переменного можно изобразить на декартовой плоскости в виде кривая, определяемая точками [ x , f ( x )] , а ось координат x представляет независимую переменную и ось координат и зависимый.

График функции представляет геометрически всю важную информацию на поведение функции, например на ее непрерывность, нулевые точки, экстремальные значения, убывающий или возрастающий характер, стационарные точки и точки перегиба.
Наклон кривой, являющейся графиком функции, представляет собой скорость подъема кривой. или падает. Оно может быть постоянным (для линий) или отличаться от точки к точке.
Чтобы определить скорость, с которой кривая поднимается или падает в данной точке, мы можем использовать касательной к кривой в этой точке.
Проведя секущую к графику функции, проходящей через точки
[ x , f ( x )], [ x + ∆ x , f ( x + ∆ x )]
мы можем написать формулу, дающую наклон секущей
мс =f(x+Δx)-f(x)x+Δx-x=
=f(x+Δx)-f(x)Δx
Эта формула называется коэффициентом разности .

Знаменатель ∆ x называется изменение в х ,
а числитель называется изменение в г , обозначенный∆ y = f ( x + ∆ x ) — f ( x ).
Выбор второй точки все ближе и ближе к точке
[ x , f ( x )] секанс ближе к касательной к графику функции в этой точке, и мы получаем все лучшее и лучшее приближение к наклону касательной.Используя предельный процесс, можно определить точный наклон касательной. в точку [ x , f ( x )] быть
m =lim ∆x → 0f(x+∆x)-f(x)∆x.
ОПРЕДЕЛЕНИЕ НАКЛОН КРИВОЙ
Склон м графа
г функция ф ( х ) в [( x ), f ( x )]
равен наклону
его касательной в этой точке,
и определяется по формулеm =lim Δx → 0f(x+Δx)-f(x)Δx
при условии, что этот предел существует.

Чтобы вычислить наклон касательной к кривой по ее предельному определению, мы должны следовать общий четырехэтапный процесс.
1. Оцените 90 367 f 90 368 в (90 367 x 90 368 + ∆ 90 367 x 90 368).
ф ( х + ∆ х )
2. Вычтите f ( x ), чтобы найти изменение ∆ y в y .
f ( x + ∆ x ) — f ( x )
3. Разделите на ∆ x , чтобы получить частное разности.
f(x+Δx)-f(x)Δx
4. Пусть ∆ x → 0, чтобы получить наклон.
limΔx →0f(x+Δx)-f(x)Δx
Вышеупомянутый предел используется для определения одной из фундаментальных величин исчисления, производная функции.

ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
Производная функции ф ( х ) в х
даноf ‘ ( x ) = lim Δx →0f(x+Δx)-f(x)Δx
при условии, что этот предел существует.
Говорят, что функция дифференцируема в x , если его производная существует в х .
Процесс нахождения этой производной называется дифференцированием .
Существуют и другие обозначения, используемые для обозначения производной функции
.y = f ( х )
dydx
у’
ддх[ф(х)]
Д х ( у )
[ f ( x )] ‘
Обозначение дидкс читается «производное от г в отношении x » , и мы можем написать предел
dydx = lim Δx → 0ΔyΔx
Таким образом, у нас есть
dydx = lim Δx → 0ΔyΔx = lim Δx → 0f(x+Δx)-f(x)Δx= f ‘ ( x )
Поскольку производная f ‘ ( x ) и наклон касательной к графику ф ( х ) оба определяются одним и тем же пределом выше, мы можем использовать четырехшаговый Процесс определения производной.

Не всякая функция дифференцируема.
На приведенном выше рисунке показаны некоторые распространенные проблемы, которые нарушают дифференцируемость. в виде вертикальных касательных, разрывов, резких поворотов на графике.
В общем случае разрывность не является достаточно сильным условием, гарантирующим дифференцируемость. Все четыре функции на рисунке, кроме одной, непрерывны в точке [0, 0], но ни одна из них не является дифференцируемой.
С другой стороны, если функция дифференцируема в точке, то она должна быть непрерывной.
РАЗЛИЧИЕ ПРЕДПОЛАГАЕТ НЕПРЕРЫВНОСТЬ
Если функция f ( x ) дифференцируем
в х = с , то он непрерывен при x = c .

 Почему?
Почему?
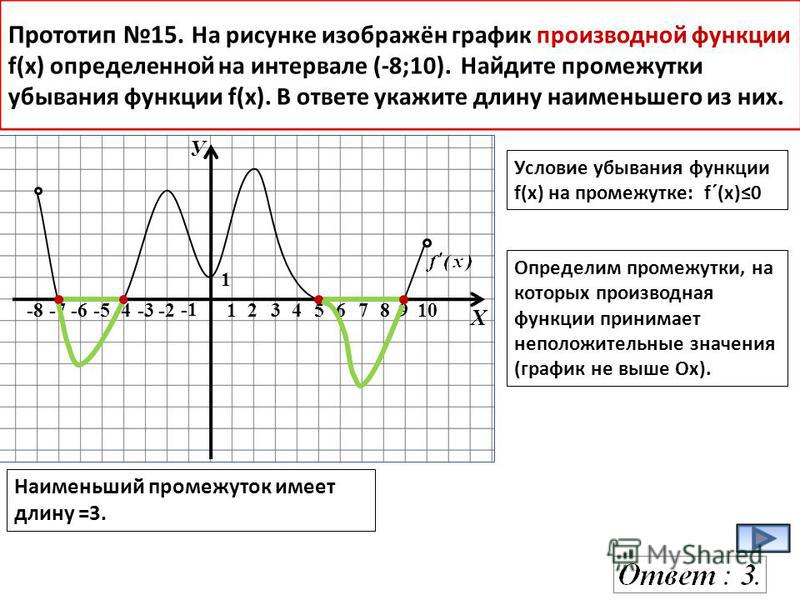 Укажите функции, имеющие такую же вторую производную.
Укажите функции, имеющие такую же вторую производную.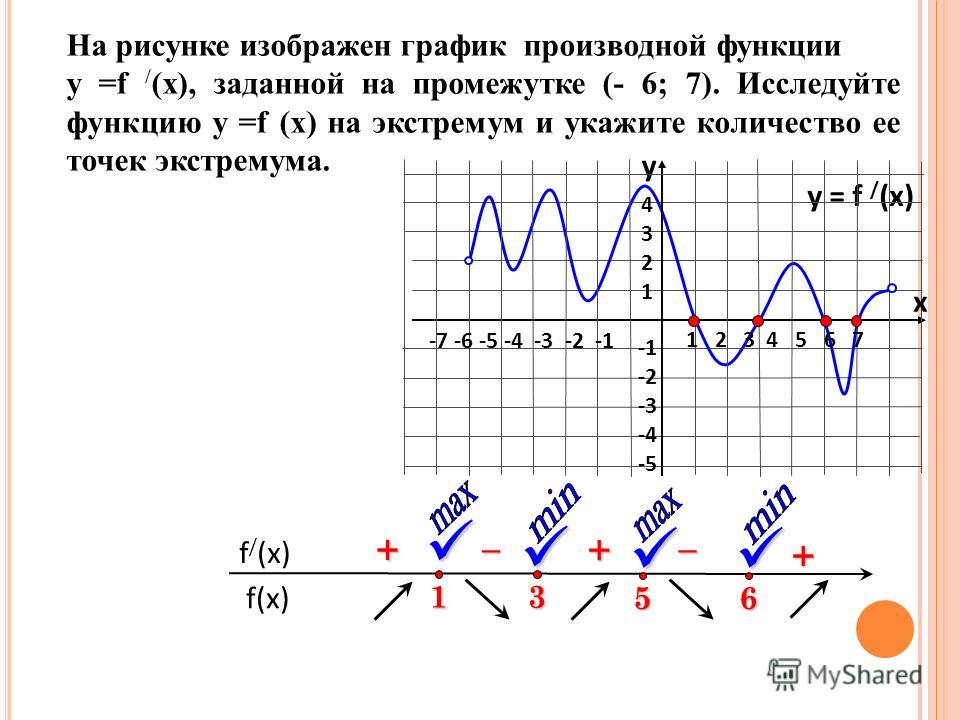 Включите единицы в свой ответ.
Включите единицы в свой ответ.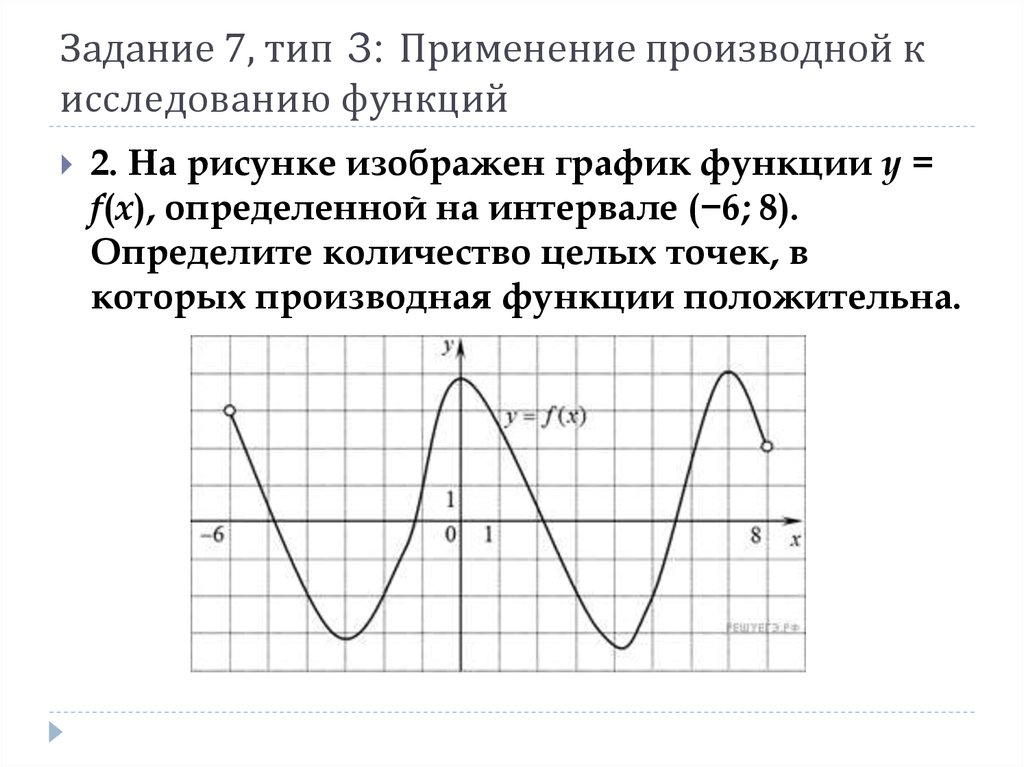 Оцените \(C(2100)\) и обоснуйте свою оценку, написав хотя бы одно предложение, объясняющее ваши мысли.
Оцените \(C(2100)\) и обоснуйте свою оценку, написав хотя бы одно предложение, объясняющее ваши мысли.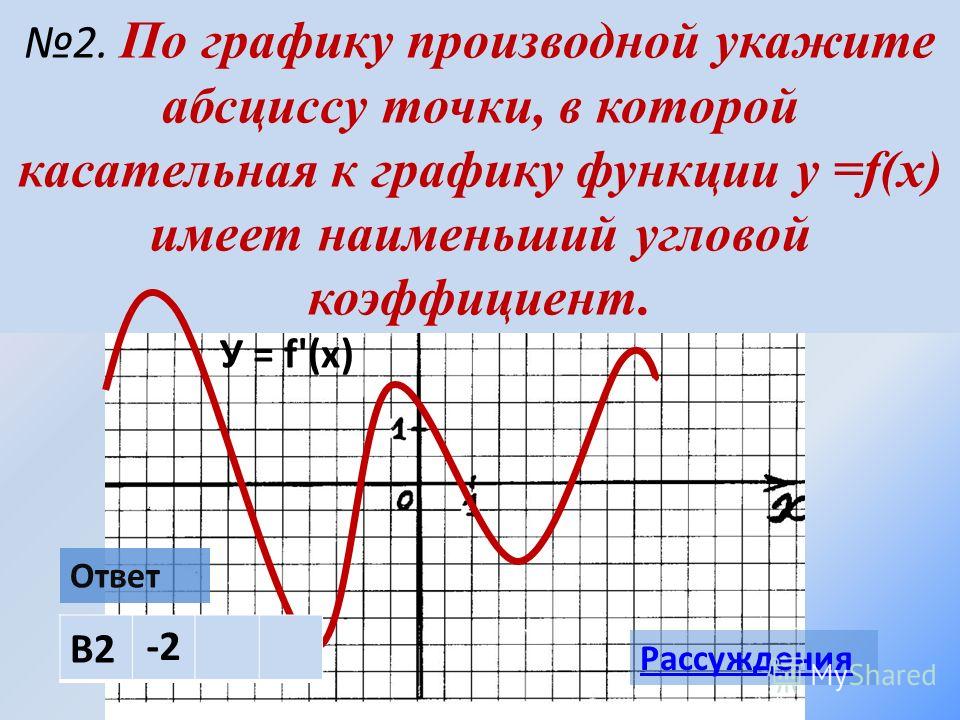 Используйте эту информацию, чтобы оценить мгновенную скорость изменения расхода топлива по отношению к скорости при \(s=90\). Будьте максимально точными, используйте правильные обозначения и включайте единицы измерения в свой ответ.
Используйте эту информацию, чтобы оценить мгновенную скорость изменения расхода топлива по отношению к скорости при \(s=90\). Будьте максимально точными, используйте правильные обозначения и включайте единицы измерения в свой ответ.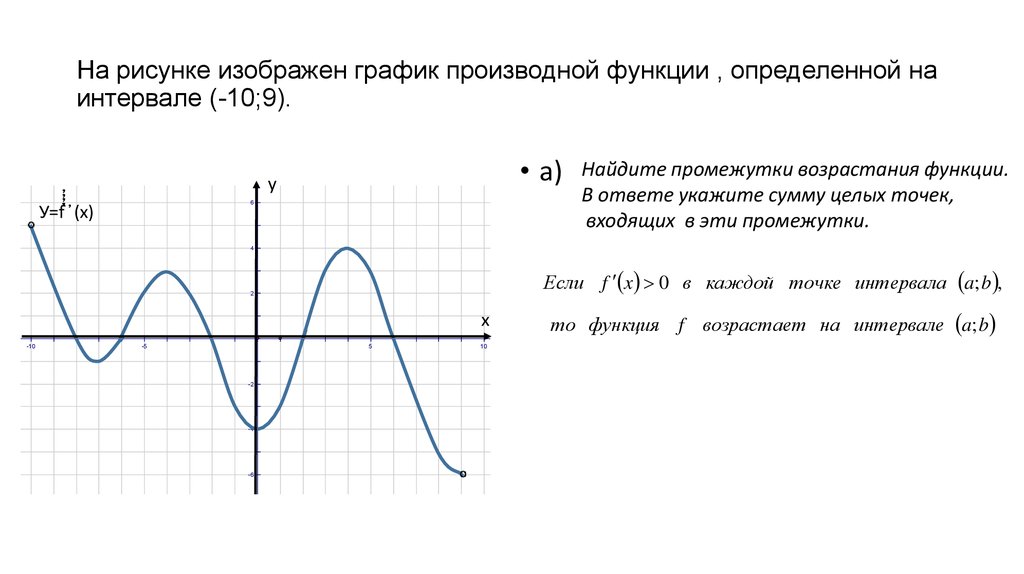 Опять же, это измеряет, насколько быстро изменяется выход функции \(f\) при изменении входа функции.
Опять же, это измеряет, насколько быстро изменяется выход функции \(f\) при изменении входа функции. 5: Интерпретация, оценка и использование производной доступна в соответствии с лицензией CC BY-SA 4.0, ее авторами, ремиксами и/или кураторами являются Мэтью Болкинс, Дэвид Остин и Стивен Шликер (ScholarWorks @Grand Valley State университета) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
5: Интерпретация, оценка и использование производной доступна в соответствии с лицензией CC BY-SA 4.0, ее авторами, ремиксами и/или кураторами являются Мэтью Болкинс, Дэвид Остин и Стивен Шликер (ScholarWorks @Grand Valley State университета) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу. org/single
org/single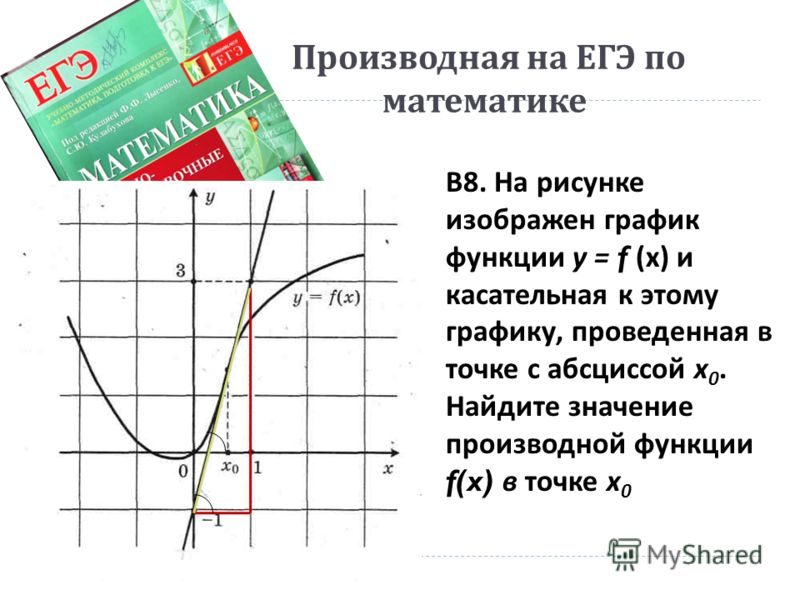
 Следующий график обобщает сделанные выше выводы.
Следующий график обобщает сделанные выше выводы.