Арифметические действия с векторами длина вектора: Арифметические действия с векторами, длина вектора — задание. Геометрия, 10 класс.

Векторы и линейные операции над ними

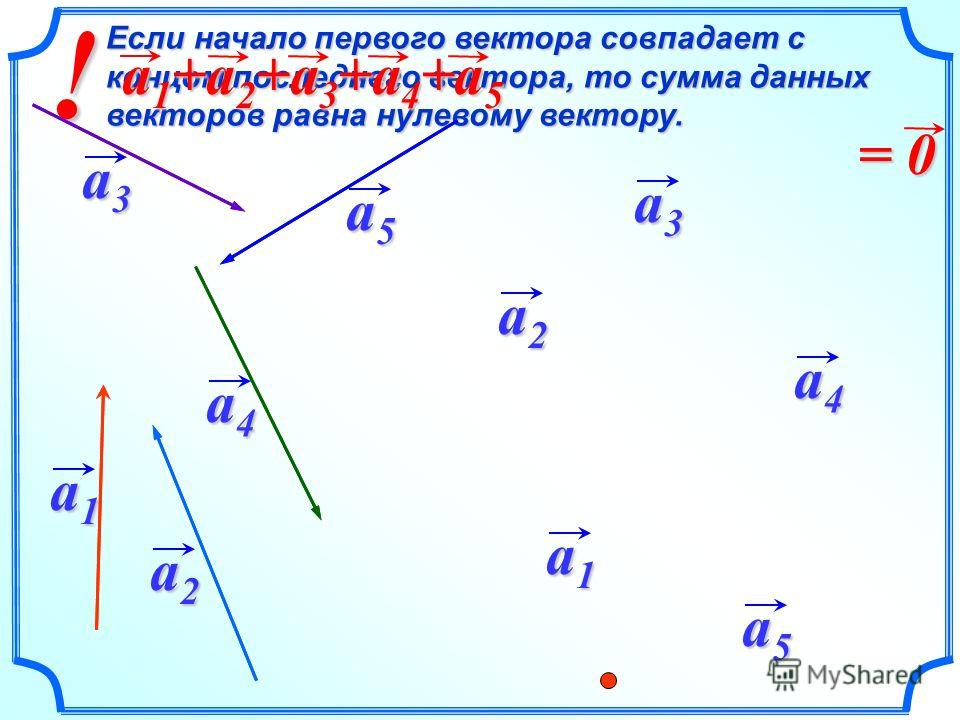
⇐ ПредыдущаяСтр 3 из 5Следующая ⇒ Вектор – это направленный отрезок прямой, обозначается или . Точка — начало вектора, точка — его конец. Длиной или модулем вектора называется длина отрезка и обозначается . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается . Вектор, имеющий направление вектора и длина которого равна 1, называется единичным вектором или ортом вектора и обозначается . Векторы и называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Записывается так . Два вектора называются равными, если они одинаково направлены и имеют одинаковые длины. Три вектора в пространстве называются компланарными, если они лежат в одной или параллельных плоскостях. Под линейными операциями над векторами понимают операцию сложения векторов и умножение вектора на действительное число . Суммой двух векторов и называется вектор , соединяющий начало первого вектора с концом второго вектора , при условии, что начало вектора и конец вектора совмещены. Обозначается сумма . Рис.4.   Рис. 4. Такое правило сложения векторов называется правилом треугольника. Два вектора можно сложить и по правилу параллелограмма. Рис.5.     Рис. 5. Разность двух векторов и называется третий вектор , такой, что . Рис.6.     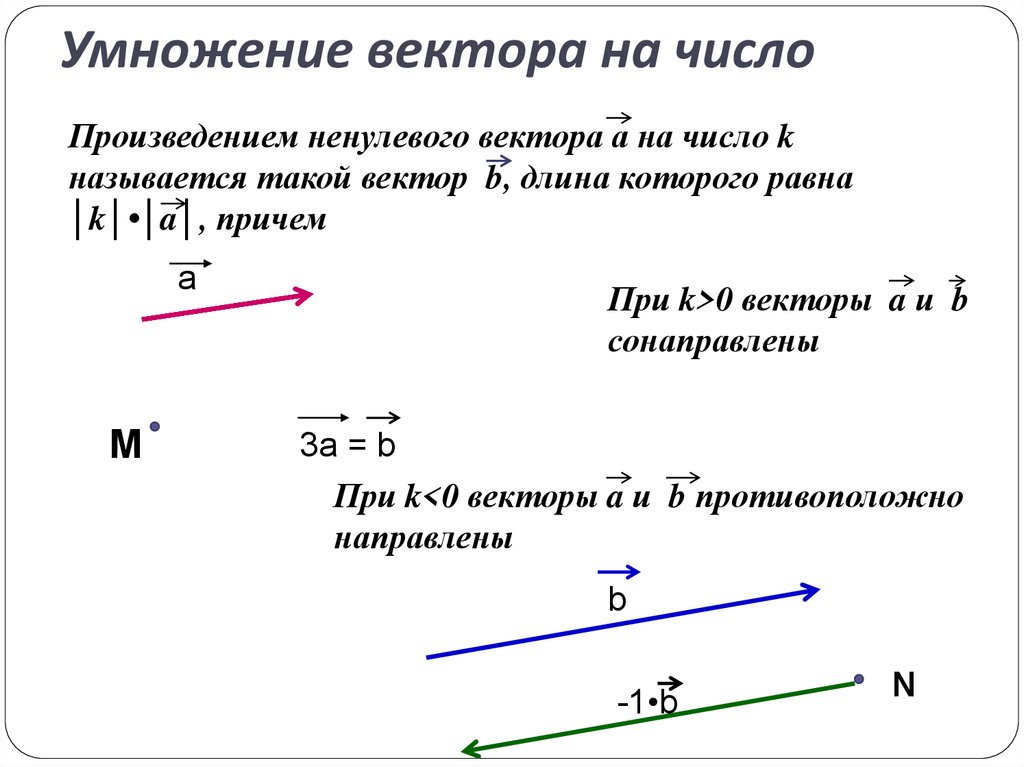Рис. 6. Произведение вектора на число называется вектор , длина которого равна , он коллинеарен вектору и имеет направление вектора , если , и противоположное, если . Линейные операции над векторами обладают следующими свойствами: 1. 2. 3. 4. 5. Необходимым и достаточным условием коллинеарности двух векторов и является существование такого числа , что . Линейной комбинацией векторов называется сумма произведений этих векторов на действительные числа: (7.1). Система векторов называется линейно независимой, если их линейная комбинация (7.1) равна нулю только при всех одновременно равных нулю. Два вектора и образуют базис на плоскости, если любой третий вектор на плоскости можно представить в виде (7.2). Три вектора образуют базис в пространстве, если любой вектор этого пространства можно представить в виде: (7.3). Выражение (7.3) называют разложением вектора по базису из векторов , а числа называют координатами вектора в базисе . Условно это записывается . Два неколлинеарных вектора образуют базис на плоскости, три некомпланарных вектора образуют базис в пространстве. Если известны координаты векторов в некотором базисе, то линейные операции над векторами сводятся к обычным арифметическим операциям над координатами этих векторов. Чтобы сложить два вектора нужно сложить их соответствующие координаты. Чтобы найти разность двух векторов необходимо найти разность их соответствующих координат. Чтобы умножить вектор на действительное число, необходимо умножить каждую его координату на это число. Справедливы следующие утверждения. Два вектора равны, если равны их соответствующие координаты. Два вектора коллинеарны, если их координаты пропорциональны. Пример 10 . Даны векторы . Проверить, что векторы образуют базис и найти координаты вектора в этом базисе. Решение. Составим линейную комбинацию векторов и приравняем ее к нулю: . Покажем, что это равенство справедливо лишь при условии . Из равенства векторов следует: Найдем определитель полученной однородной системы: Следовательно, система имеет единственное решение : а это значит, что векторы — образуют базис. Найдем координаты вектора в этом базисе. Запишем векторное равенство: . Переходя к координатой форме, получим: Решив эту систему, получим: . Тогда , или в базисе . В прямоугольной системе координат любой вектор можно представить в виде (7.4), где — взаимно ортогональные единичные векторы осей координат . Координатами вектора в прямоугольной системе координат являются проекции этого вектора на соответствующие оси координат, то есть (7.5). — длина вектора в прямоугольной системе координат. Углы, которые вектор образует с осями координат, принято обозначать соответственно . Косинусы этих углов называют направляющими косинусами вектора . Направляющие косинусы равны соответственно: (7.6), Или в координатной форме: . Для направляющих косинусов выполняется равенство (7.7). Если известны координаты точек то координаты вектора определяются формулами , то есть . Умножение векторов Векторы можно умножать скалярно и векторно. Скалярным произведением двух ненулевых векторов и называется число, равное произведению длин этих векторов на косинус угла между ними: (8.1). Эту формулу можно записать в виде . Скалярное произведение имеет следующие свойства: 1. — переместительный закон. 2. — распределительный закон 3. 4. , отсюда 5. Если , то — условие перпендикулярности векторов и 6. , — вектор силы, — вектор перемещения, — работа силы . Если и заданы в прямоугольной системе координат , то (8.2). Упорядоченная тройка векторов называется правой, если кратчайший поворот от вектора к вектору из конца вектора виден совершающимся против часовой стрелки. Рис.7.           Рис. 7. 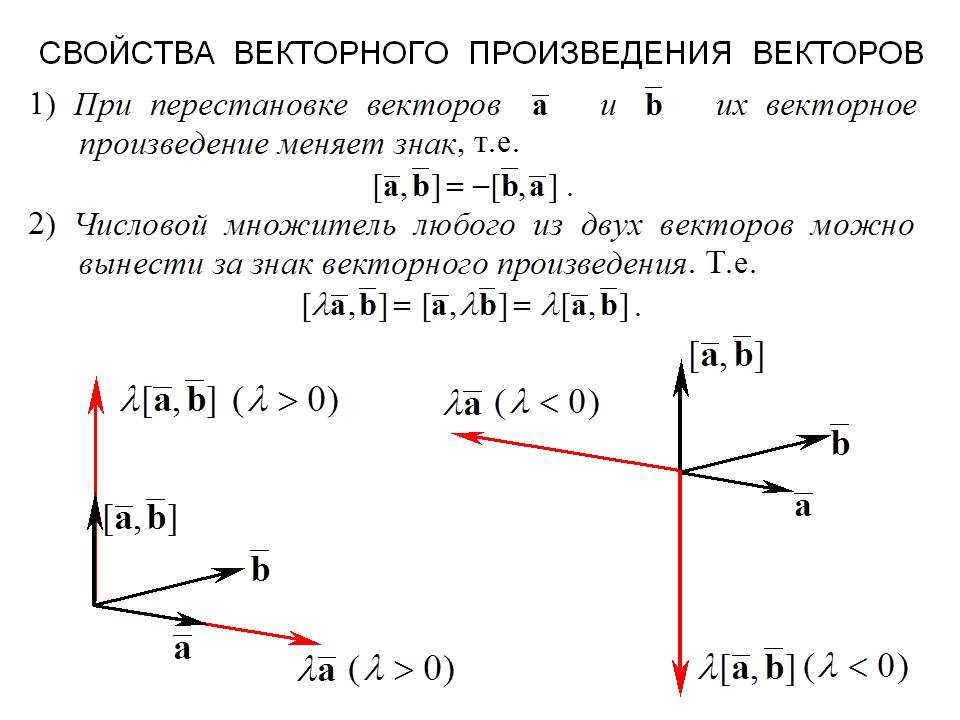Векторным произведением вектора на вектор называется третий вектор , длина которого равна , он перпендикулярен векторам и и направлен в ту сторону, что векторы и образуют правую тройку. Векторное произведение обозначается . Векторное произведение имеет следующие свойства: 1. 2. 3. 4. Если , то 5. , где — площадь параллелограмма, построенного на этих векторах как на сторонах. Если векторы и заданы в прямоугольной системе координат: и , то: (8.3). Если вектор силы, приложенной в точке , а радиус-вектор точки , то момент силы , относительно начала координат равен: . Смешанным произведением трех векторов и называется их векторно-скалярное произведение. Обозначается . Если заданы координаты векторов в прямоугольной системе координат, то их смешанное произведение вычисляется по формуле: (8. 4). Свойства смешанного произведения векторов: 1. — условие компланарности векторов; 2. — объем параллелепипеда, построенного на векторах, как на сторонах; 3. — циклическая перестановка сомножителей не меняет величины смешанного произведения; 4. Пример 11. Даны вершины пирамиды . Найти 1) угол между ребром и гранью ; 2) площадь грани ; 3) объем пирамиды ; 4) длину высоты, опущенной из вершины на грань . Решение. Вычислим координаты вектора : . Угол между ребром и гранью является дополнительным углом для угла , образованного перпендикуляром, проведенным к плоскости треугольника и ребром . . Для нахождения вычислим координаты векторного произведения векторов и : ; . . ; . 1) Площадь грани равна половине площади параллелограмма, построенного на сторонах и , т. е. . 2) Объем пирамиды равен одной трети от объема параллелепипеда, построенного на ребрах и . Следовательно . 3) Длина высоты определяется из формулы: ; . Ответ: ; ; ; . Комплексные числа Комплексным числом называется выражение (9.1), где и — действительные числа; — мнимая единица, определяемая равенством или (9.2). Число называют действительной частью комплексного числа и обозначают ; — мнимая часть комплексного числа . Ее обозначают . Если , то число называют чисто мнимым, если , то число , есть действительное число. Два комплексных числа и называют комплексно сопряженными числами. Два комплексных числа и считаются равными, если и . Комплексное число , если и . Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью. Иногда комплексное число удобнее изображать в виде вектора , начало которого совпадает с началом координат, соединяющего точку с точкой . Длина этого вектора называется модулем комплексного числа и обозначается . . Угол между осью и вектором , отсчитанный против часовой стрелки, называется аргументом комплексного числа и обозначается . Аргумент числа определяется с точностью до слагаемого , где — целое число. Главное значение аргумента числа — значение аргумента, удовлетворяющее неравенству . Главное значение аргумента комплексного числа обозначается через : . Запись числа в виде называют алгебраической формой записи комплексного числа. Сумма, разность комплексных чисел и умножение определяется так же, как действия над соответствующими векторами. Суммой комплексных чисел и называется комплексное число (9.3). Разностью комплексных чисел и называется комплексное число (9. 4). Произведение комплексного числа на действительное число называется комплексное число . Произведение двух комплексных чисел и , записанных в алгебраической форме определяется как произведение двучленов: (9.5). Произведением двух комплексно сопряженных чисел служит действительное число (9.6). Деление комплексных чисел определяется, как действие обратное умножению. Частное двух комплексных чисел и определяется следующим образом: (9.7). Наряду с прямоугольной системой координат введем полярную систему, начало которой совпадает с началом прямоугольной системы, а полярная ось – с положительным направлением оси . Рис. 8.     Рис. 8. Из Рис.8 следует, что: . Подставляя и в алгебраическую форму комплексного числа, получим (9.8). Выражение (9.8) называют тригонометрической формой записи комплексного числа , где . Пусть даны два комплексных числа и . Записанные в тригонометрической форме: . Тогда . (9.9). Таким образом, при умножении комплексных чисел их модули перемножаются, а аргументы складываются; при делении комплексных чисел их модули делятся, а аргументы вычитаются. Если — целое положительное число, то из (9.9) следует: (9.10). Корнем -й степени из комплексного числа называется такое комплексное число , -я степень которого равна , т.е. . Корень -й степени из обозначается . Если , то равен: (9.11). Подставляя в (9.11) значения получим ровно различных корней -й степени из . Пример 12. Дано комплексное число . Записать число в алгебраической и тригонометрической формах. Найти все корни уравнения . Решение. Запишем число в алгебраической форме: . Найдем : . Вычислим . Тригонометрическая форма записи комплексного числа имеет вид: . Вычислим : при при при Кроме алгебраической и тригонометрической форм записи комплексного числа , применяется более короткая, так называемая показательная форма комплексного числа , согласно которой . Пусть и , тогда: . ⇐ Предыдущая12345Следующая ⇒ Читайте также:

Особенности и правила умножения вектора на число

При обучении математике и физике в старших классах средней школы, а также в высших учебных заведениях постоянно приходится сталкиваться с понятием вектора.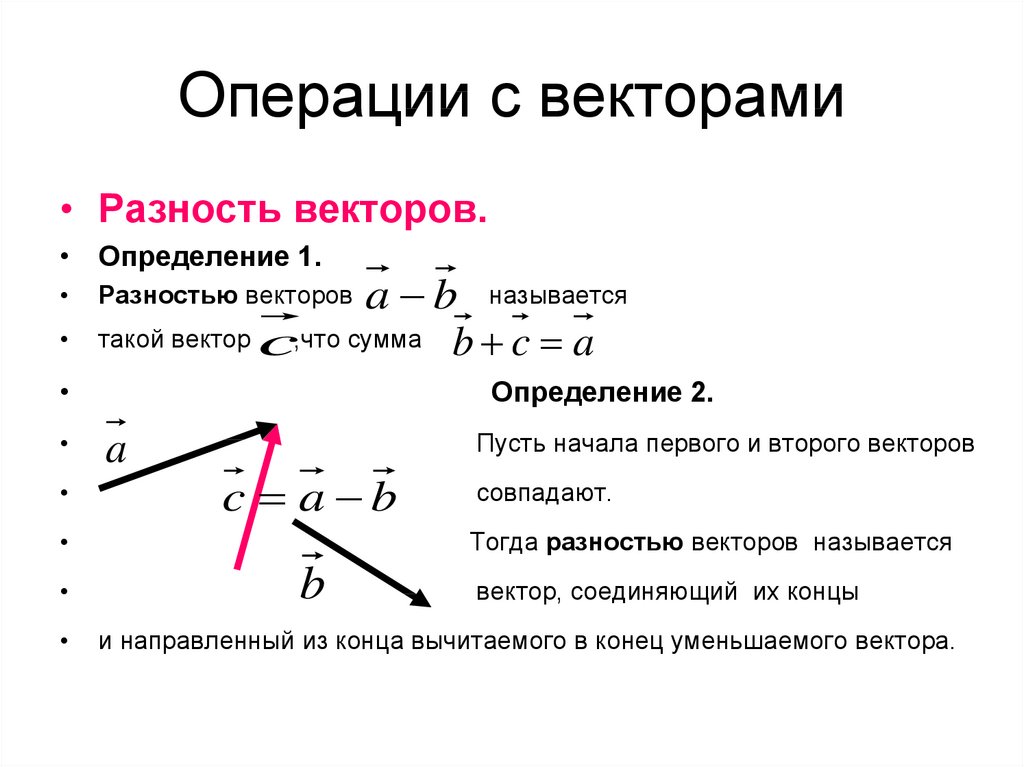 Учащиеся и студенты обязаны уметь проводить с векторами простейшие арифметические действия.

В статье будет показано, как умножать их на постоянные числа.

…

Основные понятия и определения

Чтобы в дальнейшем упростить работу со статьёй, введём некоторые формулировки и договорённости:

1. Постоянная — любое обычное число, которое может принимать определённые фиксированные значения, быть положительным, отрицательным или нулевым. Обозначать будем латинской буквой С (от греческого слова constanta, то есть постоянная).
2. Вектор — участок прямой, ограниченный двумя точками и имеющий заданное направление. Обозначать будем как (АВ). Причём точка, А является его началом, В — концом. Направление будем считать от точки, А к точке В. Допустима замена на (CD).
3. Вектора называются параллельными (коллинеарными), если они лежат на коллинеарных прямых или на одной прямой.
4. Нулевым вектором называется такой, у которого конец и начало совпадают. Называется нуль-вектор и обозначается (0).
5. Координатами (АВ) называются числа, равные его протяжённости относительно каждой из оси координат в Декартовой системе. Они находятся вычитанием из координат конца вектора координат его начала. Знак минус перед этим числом означает, что вектор направлен против направления данной оси.
6. Модулем (АВ) называется длина отрезка АВ.
7. Квадратный корень из числа или выражения условимся обозначать латинским буквосочетанием SQRT.
8. (АВ) с координатами (x, y, z) будем обозначать как (АВ) (x, y, z).

Правила умножения вектора на число

Рассмотрим, как умножить вектор на число:

1. Прежде всего отметим, что при умножении на отрицательную постоянную меняется направление на противоположное.
2. Если constanta больше -1, но меньше 1, то модуль (АВ) уменьшится. Проще говоря — отрезок станет короче.
3. Если постоянная равна нулю, С=0, то результатом вычислений окажется (0).
4. Для умножения (АВ) (x, y, z) на некую постоянную, нужно найти произведение каждой из координат с этой постоянной. Получится (А1В1) (С*x, С*y, С*z).

Алгебраический и геометрический смысл действия

Любое математическое действие имеет некий смысл, причём в разных науках он различается. Рассмотрим, что нам даёт этот вид умножения:

1. Геометрический смысл: (АВ)*С — это вектор, коллинеарный данному, модуль которого отличается в С раз от исходного, направление может совпадать или меняться на противоположное в зависимости от знака постоянной.
2. Алгебраический смысл: (АВ) (x, y, z)*С — это новый (А1В1) с координатами равными (С*x, С*y, С*z).
3. Физический смысл: уменьшение или увеличение в С раз силы действующей на тело или материальную точку.

Формулы умножения

При умножении проще всего использовать заранее заученные на память формулы, которые вполне можно применять по шаблону, выполняя действия буквально на полном автомате:

• С*(АВ) (x, y, z) = (А1В1) (С*x, С*y, С*z).
• 0*(АВ) = (0).

Для начала возьмём физическую задачу воздействия силы на материальную точку. Пусть на неё действует сила, описываемая (АВ) (57,63,28). Как изменится эта сила по координатам при её десятикратном увеличении?

Прежде всего следует отметить, что направление воздействия силы не изменится, а сама сила возрастёт десятикратно. При раскладке по координатам получим следующее:

10*(АВ) (57,63,28) = (А1В1) (10*57,10*63,10*28) = (А1В1) (570,630,280).

Вторую задачу возьмём аналогичную: как изменится сила, действующая на материальное тело, описываемая (АВ) (46,59,-43) при её увеличении в -0,5 раза.

Прежде всего заметим, что знак у постоянной отрицательный, следовательно, направление самой силы изменится на противоположное. Воспользуемся пунктом 2 вышеизложенных правил умножения, тогда сразу станет понятно, что численное выражение силы уменьшится вдвое. Проведём вычисления по шаблону:

-0,5*(АВ) (46,59,-43) = (А1В1) (-0,5*46,-0,5*59,-0,5*(-43)) = (А1В1) (-23,-29,5,21,5).

Следует заметить, что приведённые выше задачи решались для векторов, размещённых в пространстве и имеющих три координаты. В случае плоскостного размещения количество координат уменьшается до двух, а в случае линейного — до одной. Рассмотрим математические примеры для этих случаев:

• 33*(CD) (11,10) = (C1D1) (33*11,33*10) = (C1D1) (363,330).
• -0,2*(АВ) (-0,3,25) = (А1В1) (-0,2*(-0,3), -0,2*25) = (А1В1) (0,06, -5).
• 67*(CD) (2) = (C1D1) (67*2) = (C1D1) (134).
• 0*(АВ) (65,-87) = (0).

Возможные действия с векторами

Не следует думать, что все возможные действия ограничиваются умножениям на число. Прежде всего можно определить длину (АВ) — модуль. Он будет равняться SQRT из суммы квадратов координат. Поясним это на примере:

• модуль (АВ) (3,4) = SQRT (3 2+ 4 2) = SQRT (9 + 16) = SQRT25 = 5.

Кроме этого, из курса школьной математики и физики известно, что вектора можно слагать один с другим и вычитать друг из друга. При этом проводится сложение и вычитание соответствующих координат.

Наконец, высшая математика вводит понятия числового (скалярного) и векторного умножения двух векторов. В первом случае получится некое число, во втором — третий вектор, направленный перпендикулярно плоскости, содержащей два первых.

В данной статье приведены основы умножения вектора на число. Исходя из её материала, можно утверждать, что действие это простое и доступное любому школьнику с удовлетворительной успеваемостью. Рекомендуется изучить формулы и в своих вычислениях действовать по изложенному в тексте шаблону. Что такое сравнение в литературе читайте в нашей статье.

Действия над векторами, заданными своими координатами

Сложение	Вычитание	Умножение
При сложении векторов их соответстветственные координаты складываются.	При вычитании векторов их соответстветственные координаты вычитаются.	При умножении вектора на число все его координаты умножаются на это число

19. Определение длины вектора, расстояние между двумя точками на плоскости

Вектором называеься направленный отрезок(отрезок,у которого одна граничная точка считается начальной, другая — конечной). Над буквенным обозначением вектора ставится стрелка. Длиной вектора называеттся расстояние между началом и концом вектора. Нулевым называется вектор,у которого начало и конец  равны нулю. Его направление не определено. Два ненулевых вектора, лежащих на одной прямой или на параллельных прямых, называются коллинеарными. Нулевой коллинеарен любому вектору. Вектор, длина которого равна единице,называется единичным вектором. 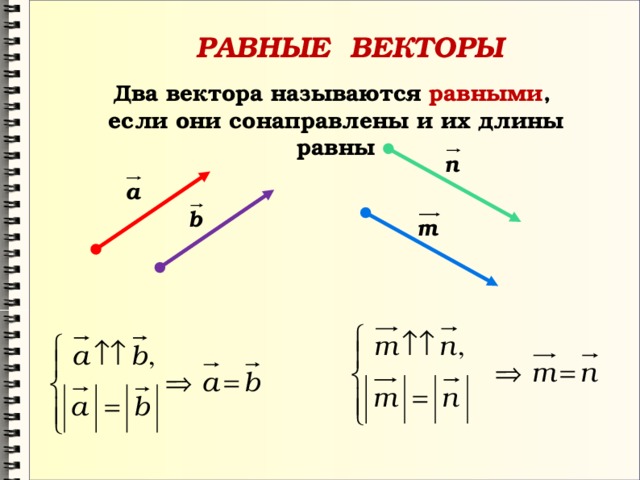Векторы называют равными,если они коллинеарны,имеют одинаковую длину и направление. Три вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если тройка векторов содержит нулевой вектор или пару коллинеарных векторов,то эти векторы компланарны. Векторы называют противоположными, если их длины равны,а направления противоположны.

20. Как делятся отрезки в данном соотношении

Если точка М(x; y) лежит на прямой, проходящей через две данные точки (, ) и (, ), и дано отношение , в котором точка М делит отрезок , то координаты точки М определяются по формулам

,

Если точка М является серединой отрезка , то ее координаты определяются по формулам

, .

21.Уравнение прямой, прох. Через точку.

. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.

 

Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору (3, -1).

 

Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А.

Получаем: 3 – 2 + C = 0, следовательно С = -1.

Итого: искомое уравнение: 3х – у – 1 = 0.

Общее уравнение прямой:

 

Ах +  Ву +  С = 0 ,

 

где  А и В  не равны нулю одновременно.

Коэффициенты А и В являются координатами нормального вектора прямой ( т.е. вектора, перпендикулярного прямой ). При  А = 0  прямая параллельна оси ОХ , при  В = 0 прямая параллельна оси ОY .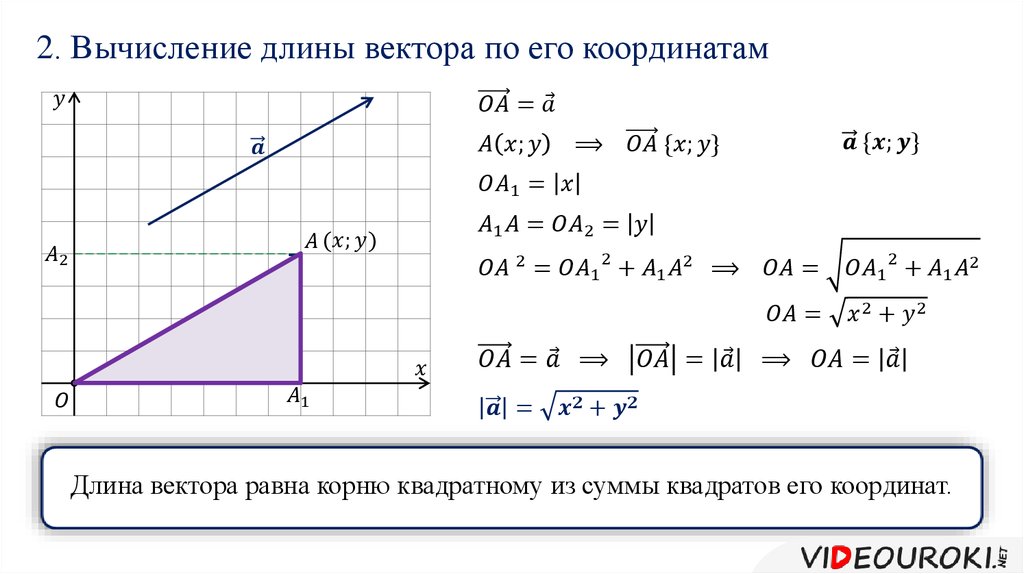

При  В 0  получаем  уравнение прямой с угловым коэффициентом:

Уравнение прямой, проходящей через точку ( х₀ ,  у ₀ ) и не параллельной оси OY, имеет вид:

 

у – у ₀ = m ( x – х₀ ) ,

 

где  m  –  угловой коэффициент, равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ .

При  А 0,  В 0 и С 0  получаем  уравнение прямой в отрезках на осях:

где  a = – C / A ,   b = – C / B . Эта прямая проходит через точки ( a, 0 ) и ( 0, b ), т.е. отсекает на осях координат отрезки длиной 

23. Уравнение прямой через точку и имеющую направл. Вектор

Определение. Каждый ненулевой вектор ( α₁ , α₂ ), компоненты которого удовлетворяют условию А α₁ + В α₂ = 0 называется направляющим вектором прямой

Ах + Ву + С = 0.

 

Пример. Найти уравнение прямой с направляющим вектором (1, -1) и проходящей через точку А(1, 2).

 

Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:

 

1 * A + (-1) * B = 0, т.е. А = В.

 

Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0.

 

при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:

 

х + у — 3 = 0

24. Уравнение прямой ч.з две точки

Пусть в пространстве заданы две точки M ₁ ( x ₁ , y ₁ , z ₁ ) и M₂ ( x ₂, y ₂ , z ₂ ), тогда уравнение прямой, проходящей через эти точки:

 

 

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.

На плоскости записанное выше уравнение прямой упрощается:

если х ₁ ≠ х₂ и х = х ₁ , если х ₁ = х₂ .

Дробь = k называется угловым коэффициентом прямой.

 

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

 

Применяя записанную выше формулу, получаем:

25. Уравнение прямой в отрезках

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: или

, где

Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.

 

Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.

 

С = 1, , а = -1, b = 1.

26. Определение окружности

Определения: Окружностью называется фигура, которая состоит из всех точек плоскости, равноудалённых от данной точки. Эта точка (О) называется центром окружности. Расстояние (r) от точки окружности до ее центра называется радиусом окружности. Радиусом называется также любой отрезок, соединяющий точку окружности с ее центром. Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром (d=2r).   Касательная — прямая (а), проходящая через точку (А) окружности перпендикулярно к радиусу, проведенному в эту точку, называется. При этом данная точка (А) окружности называется точкой касания.     Часть плоскости, ограниченная окружностью, называется кругом.

30. Определение системы двух линейных уравнений с 2 переменными

Системы двух линейных уравнений с двумя неизвестными имеют вид: 

 

 

где  a,  b,  c,  d,  e,  f – заданные числа;  x,  y – неизвестные. Числа   a,  b,  d,  e  – коэффициенты при неизвестных; c, f – свободные члены. Решение этой системы уравнений может быть найдено двумя основными  методами.

Метод подстановки. 

1)  Из одного уравнения выражаем одно из неизвестных, например  x, через коэффициенты и другое неизвестное  y:

                                                 x = ( c – by ) / a .                             (2)

2)  Подставляем во второе уравнение вместо x :

                                           d ( c – by ) / a + ey = f .

3)  Решая последнее уравнение, находим  y :

                                                  y = ( af – cd ) / ( ae – bd ).

4)  Подставляем это значение вместо y  в выражение (2) :

                                                 x = ( ce – bf ) / ( ae – bd ) .

П р и м е р .  Решить систему уравнений:

                                                  

                      Из первого уравнения выразим  х  через коэффициенты и  y :

 

                                                            x = ( 2y + 4 ) / 3 .

 

                      Подставляем это выражение во второе уравнение и находим  y :

 

                                                       ( 2y + 4 ) / 3 + 3y = 5 ,  откуда   y = 1 .

                                

                      Теперь находим  х, подставляя найденное значение вместо  y  в

                      выражение для  х:  x = ( 2 · 1 + 4 ) / 3, откуда   x = 2 .

 

 Сложение или вычитание. Этот метод состоит в следующем.            

1)  Умножаем обе части 1-го уравнения системы (1) на  (– d ), а обе части 2-го уравнения на  а  и складываем их:

                                         

    Отсюда получаем: y = ( af – cd ) / ( ae – bd ).  

2)  Подставляем найденное для  y  значение в любое уравнение системы (1):  

                                 ax + b( af – cd ) / ( ae – bd ) = c.

3)  Находим другое неизвестное:   x = ( ce – bf ) / ( ae – bd ).

 

 

П р и м е р .  Решить систему уравнений:

                                           

                      методом сложения или вычитания.            

                      Умножаем первое уравнение на  –1, второе – на 3 и складываем их:

                                              

                      отсюда  y = 1. Подставляем это значение во второе уравнение

                      (а в первое можно?):  3x + 9 = 15, отсюда  x = 2.

 

Определители второго порядка. Мы видели, что формулы для решения системы двух линейных уравнений с двумя неизвестными имеют вид:

 

                                                          x = ( ce – bf ) / ( ae – bd ) ,

                                                                                                                       (3)                    

                                                          y = ( af – cd ) / ( ae – bd ) .

         

Эти формулы легко запоминаются, если ввести для их числителей и знаменателей следующий символ:

             ,  который будет обозначать выражение:  ps – qr . 

Это выражение получается перекрёстным умножением чисел  p, q, r, s :

и последующим вычитанием одного произведения из другого: ps – qr. Знак « + » берётся для произведения чисел, лежащих на диагонали, идущей из левого верхнего числа к правому нижнему; знак  « – » — для другой диагонали, идущей из правого верхнего числа к левому нижнему. Например,

                                                       Выражение      называется определителем второго порядка.

Правило Крамера. Используя определители, можно переписать формулы (3):

Формулы (4) называются правилом Крамера для системы двух линейных уравнений с двумя неизвестными.

 П р и м е р .  Решить систему уравнений

                                     

                        используя правило Крамера.

Р е ш е н и е .  Здесь   a = 1,  b = 1,  c = 12,  d = 2,  e = –3,   f = 14 .

                      

31. Определение системы 3 линейных ур-й с тремя уравнениями

Система трех линейных уравнений с тремя неизвестными

Система трех линейных уравнений с тремя неизвестными имеет вид

     (7)

Определитель

     (8)

составленный из коэффициентов при неизвестных, называется определителем системы.

1. Если определитель системы , то система (7) имеет решение, и притом единственное. Это решение находится по формулам

     (9)

Из этого заключаем, что значение неизвестного системы (7) равно дроби, знаменатель которой есть определитель системы, а числитель есть определитель, получающийся из определителя системы заменой в нем столбца из коэффициентов при определяемом неизвестном столбцом свободных членов.

Определители, стоящие в числителях дробей (9), будем обозначать соответственно через D_x, D_y, D_z.

2. Если D = 0, но, по крайней мере, один из его миноров и хотя бы один из определителей D_x, D_y и D_z не равен нулю, то система (7) решений не имеет. В этом случае говорят, что она противоречива, или несовместна.

3. Если D = 0 и все определители, стоящие в числителях дробей (9), — D_x, D_y, D_z — равны нулю, т. е. если

D = D_x = D_y = D_z = 0,

но хотя бы один из миноров в определителе D не равен нулю, то одно уравнение системы (7) является следствием двух других, и система трех уравнений (9) приводится к двум уравнениям, причем решения этих двух уравнений удовлетворяют третьему. В этом случае система (9) имеет бесконечное множество решений и называется неопределенной.

4. Если же все миноры в определителе D равны нулю, но хотя бы один из миноров в каком-нибудь из определителей D_x, D_y, D_z не равен нулю и хотя бы один из коэффициентов при неизвестных не равен нулю, то система несовместна и решений не имеет.

5. Если в определителях D, D_x, D_y, D_z все миноры равны нулю, но хотя бы один из коэффициентов при неизвестных нулю не равен, то два уравнения системы являются следствием третьего, и система трех уравнений приводится к одному уравнению, является неопределенной и имеет бесконечное множество решений, причем решения этого третьего уравнения удовлетворяют первому и второму уравнениям.

32. Определение функции примеры нахождения области определения

 Определение. Функцией, заданной (или определенной) на некотором множестве X, называется соответствие, в силу которого любой элемент x множества X определяет некоторый (соответствующий ему) объект f(x).

     Множество X называется областью определения функции, а множество Y — объектов, соответствующих всем элементам множества X, — областью значений функции

34. Элементарные функции

Графики элементарных функций

Все графики

Линейная функция

Квадратная функция

Показательная функция

Логарифмическая функция

Функция арифметический корень

Степенная функция

Тригонометрические функции

Обратные тригонометрические функции

Дробно-линейная функция

35. Определение степени числа

 Определение степени. Напомним, что произведение двух одинаковых чисел аа называется второю  степенью (или квадратом) числа а, произведение трех  одинаковых чисел ааа называется третьей степенью (или кубом) числа а; вообще произведение n одинаковых чисел аа… а называется n-ю степенью числа а. Действие, посредством которого находится степень  данного  числа,  называется  возвышением в степень (вторую,   третью  и т.  д.).   Повторяющийся   сомножитель   называется основанием степени,  а число одинаковых сомножителей называется показателем степени.

Сокращенно степени обозначаются так: а², а³, а⁴… и т. д.

Мы сначала будем говорить о простейшем случае возвышения в степень, именно о возвышении в квадрат; а пoсле рассмотрим возвышение и в другие степени.

153.  Правило знаков при  возвышении  в  квадрат.  Из правила умножения относительных чисел следует, что:

(+2)²=(+2) (+2) = + 4;               (+¹/₃)²=(+¹/₃)(+¹/₃) = +¹/₉;

(—2)²=(—2) (—2) = + 4;              (—¹/₃)²=(—¹/₃)(—¹/₃) = +¹/₉

Вообще:

(+a)²=(+a) (+a) = +a²

(—a)²=(—a) (—a) = +a²

Значит, квадрат всякого относительного числа есть число положительное.

Векторная арифметика | bartleby

Что такое векторная арифметика?

Векторы — это те объекты, которые имеют величину наряду с направлением. В векторной арифметике мы увидим, как арифметические операторы, такие как сложение и умножение, используются для любых двух векторов. Арифметика в основном означает работу с числами. Здесь величина означает длину или размер объекта. Используемое обозначение — это стрелка над головой вектора, указывающая его направление.

Рассмотрим два вектора a и b. Когда ты скажешь, что эти двое равны? Они равны, если оба имеют одинаковую длину и направление. Здесь длина называется величиной.

Операции

Дополнение

Предположим, вы и двое ваших друзей по имени Джим и Джек играете в мяч. Трое из вас стоят в прямоугольном треугольнике. При масштабировании оказалось, что расстояние между вами и Джимом составляет 9 метров, а расстояние между вами и Джеком — 8 метров. Какое расстояние между Джимом и Джеком?

Теперь вы должны увидеть это как векторы. Один имеет величину 9 и направлен к вектору по имени Джим. Другой имеет звездную величину 8 и направлен к вектору по имени Джек. Так как это образует прямоугольный треугольник, мы можем использовать теорему Пифагора. Таким образом, расстояние между Джеком и Джимом равно квадратному корню (sqrt) из суммы квадратов двух векторов. Новый вектор — это расстояние, равное 12,04 метра. Таким образом происходит добавление.

Дополнение может быть в любом порядке. Если «a» и «b» — любые два вектора, добавление «a» и «b» или «b» и «a» даст одно и то же значение.

Вычитание

Предположим, что ваш друг идет вам навстречу. Это означает, что ваш друг идет с противоположной стороны. На это указывает отрицательный знак. Можете ли вы сказать разницу между вектором «а» и « — а». Они оба имеют одинаковую величину. Но направление обратное. Когда вы складываете эти два, вы получаете новый вектор, называемый нулевым вектором. Добавление отрицательного и положительного членов равносильно вычитанию двух членов. Таким образом производится вычитание.

Умножение на скаляры

Скаляры — это те величины, которые имеют только величину. Это могут быть любые действительные числа. Что происходит, когда вы умножаете вектор на скаляр?

Чтобы умножить вектор на скаляр, умножьте каждый компонент вектора на этот скаляр.

Предположим, что скаляр представляет собой любое значение больше 1. Если вектор умножается на этот скаляр, величина вектора увеличивается.

Например, пусть вектором является a, а скаляром является любое значение больше 1. При умножении величина увеличивается для любого положительного скаляра. Кроме того, это не влияет на направление вектора.

Предположим, что скаляр представляет собой любое значение от 0 до 1. Если вектор умножается на этот скаляр, величина вектора уменьшается, но не влияет на направление вектора.

Если скаляр имеет любое значение меньше 0, направление вектора изменяется.

Свойства скалярного умножения

Пусть буквы «s» и «t» обозначают два скаляра, а «a» и «b» обозначают два вектора.

• Если «s» умножить на сумму «a» и «b», результатом будет сумма «s», умноженная на «a» и «s», умноженная на «b». Математически это представляется как sa+b=sa+sb

• Если «а» умножить на сумму «s» и «t», результатом будет сумма «а», умноженная на «s» и «а», умноженная на «t». Математически это представляется как s+ta=sa+ta

• Пусть s = 1. Тогда умножение «s» на «a» дает «a». Математически это представляется как 1a=a

• Пусть s = 0. Тогда умножение «0» на «a» дает «0». Математически это представляется как 0a=0

• Пусть s = -1. Тогда умножение «s» на «a» дает «-a». Математически это представляется как −1a=-a

Вы можете проверить, верны ли данные свойства, рассчитав левую и правую части уравнения. Если левая и правая части равны, то это верно.

Задачи

1. Пусть s = 3, a = (2,1) и b = (5,7). Покажите, что sa+b=sa+sb

Сначала вычислим левую часть уравнения.

sa+b=32,1+5,7=37,8=21,24

Теперь вычислите правую часть уравнения.

са+сб=32,1+35,7=6,3+15,21=21,24

Здесь левая и правая стороны равны.

Таким образом, sa+b=sa+sb

2. Пусть s = 4, a = (1,1) и b = (3,5). Сможете ли вы найти, если sa+b=sa+sb?

Сначала вычислим левую часть уравнения.

s(a+b)=4((1,1)+(3,5))=4(4,6)=(16,24)

Теперь вычислите правую часть уравнения.

sa+sb=4(1,1)+4(3,5)=(4,4)+(12,20)=(16,24)

Здесь левая и правая части равны.

Таким образом, s(a+b)=sa+sb.

3. Пусть s = 3, t = 4 и a = (5,6). Покажите, что с+та=са+та.

Сначала вычислим левую часть уравнения.

s+ta=3+45,6=75,6=35,42

Теперь вычислите правую часть уравнения.

sa+ta=35,6+45,6=15,18+20,24=35,42

Здесь левая и правая стороны равны.

Таким образом, s+ta=sa+ta

4. Пусть s = 4, t = 6 и a = (2,8) . Сможете ли вы найти, если as+t=as+at?

Сначала вычислим левую часть уравнения. . 9является единичным вектором, перпендикулярным как к a, так и к b. Он показывает направление.

Единичный вектор — это вектор с величиной, равной 1.

Если два вектора записаны в компонентной форме как a=a1,a2,a3 и b=b1,b2,b3, то векторное произведение определяется как ×b=ijka1a2a3b1b2b3, где i, j и k — стандартные единичные векторы в трех измерениях.

Пример:

1. Найдите перекрестное произведение между a=3,−3,1 и b=4,1,2

Перекрестное произведение задается следующей матрицей.

a×b=ijk3−31412

Пусть i, j и k — стандартные единичные векторы в трех измерениях.

Нужно найти определитель матрицы.

ijk3−31412=i−3⋅2−1⋅1−j3⋅2−1⋅4+k3⋅1−−3⋅4=i−6−1−j6−4+k3+12=−7i− 2j+15k

Результатом является векторная величина.

2. Можете ли вы найти векторное произведение между a=1,−3,1 и b=4,9,2?

Скалярный продукт

Представляется знаком точки между двумя векторами. Взятие скалярного произведения двух дает скаляр.

Задается формулой a.b=abcosθ, где a — величина вектора a, b — величина вектора b, а θ — угол между a и b.

Формула компонента скалярного произведения выглядит следующим образом:

a1,a2,a3⋅b1,b2,b3=a1b1+a2b2+a3b3.

Давайте посмотрим на пример.

1. Найдите скалярное произведение a=1,2,3 и b=4,−5,6

Воспользуемся формулой компонента a1,a2,a3⋅b1,b2,b3=a1b1+a2b2+a3b3 .

Вычислите скалярное произведение, используя приведенную выше формулу. Расчет приведен ниже.

14+2−5+36=4−10+18=12

Результатом является скалярная величина.

2. Можете ли вы найти скалярное произведение a=1,−3,1 и b=4,9,2?

Используйте формулу компонента a1,a2,a3⋅b1,b2,b3=a1b1+a2b2+a3b3 для расчета скалярного произведения.

(1,−3,1)⋅(4,9,2)=1(4)+(−3)(9)+1(2)=4−27+2=−21

Результат: скалярная величина.

Параллельный

Два вектора называются параллельными, если один из них кратен другому.

Перпендикулярный

9является единичным вектором, перпендикулярным как к a, так и к b. Кроме того, a=a1,a2,a3 и b=b1,b2,b3 являются компонентами векторов a и b.

Практические задачи

Используйте данную операцию для сложения или вычитания заданных векторов.

1. Добавьте a=1,3,1 и b=4,9,2.

Используйте формулу (a1,b1,c1)+(a2,b2,c2)=(a1+a2,b1+b2,c1+c2) для сложения векторов.

(1,3,1)+(4,9,2)=(5,12,3)

(Подсказка: нужно делать это покомпонентно)

2. Вычесть b=5,3,2 от а=9,3,7.

Используйте формулу (a1,b1,c1)−(a2,b2,c2)=(a1−a2,b1−b2,c1−c2), чтобы сложить векторы.

(9,3,7)−(5,3,2)=(4,0,5)

Контекст и приложения

Векторная арифметика используется в учебной программе K-12, бакалавриате и аспирантуре по математике, и физике и задается на вступительных экзаменах.

Эта тема важна для профессиональных экзаменов как для студентов, так и для выпускников, особенно для

• бакалавров по математике
• Магистр математики

Арифметические операции над вектором в R

Введение

 

R — важный язык программирования, используемый статистиками. Он также используется в машинном обучении, науке о данных, исследованиях и во многих других новых областях. В предыдущей статье мы узнали о векторах в R, теперь мы узнаем об арифметических операциях; т. е. добавление двух векторов в R. Посмотрим, как это работает в R studio.

 

Чтобы узнать больше о векторе в R, вы можете посетить ссылку Вектор в R

 

Операция с вектором в R

 

Как мы знаем, вектор в R является элементом данных, поэтому мы можем выполнять арифметические операции над вектором в R, такие как сложение, вычитание и умножение.

 

Начнем с добавления двух векторов в R с помощью R studio.

 

Сложение — добавление векторов в R

 

Мы можем сложить два или более векторов и получить желаемый результат. Давайте посмотрим, как это работает.

1. #Создание вектора  
2. первый вектор <- 1:5  
3. первый вектор  
4. секундВектор <- 5:9  
5. второйВектор  
6.    
7. # Добавление более двух векторов  
8. VectorAfterAddition <- firstVector + secondVector  
9. ВекторАфтерАддитион  

Выход

 

[1] 6 8 10 12 14

 

Здесь мы создали два вектора: firstVector и secondVector. После создания обоих векторов мы создали третий вектор VectorAfterAddition, который представляет собой добавление двух векторов, созданных ранее. Мы можем видеть результат, как на изображении ниже, и ясно, что оба векторных элемента были добавлены.

 

 

 

Теперь мы увидим разные случаи при добавлении векторов в R.

 

Случай 1. Добавление векторов разной длины

 

Когда мы пытаемся сложить векторы разной длины, R studio выдает предупреждающее сообщение, так как длина большего объекта не кратна длине меньшего объекта.

 

Давайте посмотрим, как это работает.

 

Сначала мы создадим два вектора, а после этого создадим еще один вектор с добавлением этих двух векторов.

1. #Создание Вектора  
2. первый вектор <- 1:5  
3. первый вектор  
4. secondVector <- 5:10  
5. второйВектор  
6.   
7. # Добавление более двух векторов  
8. VectorAfterAddition <- firstVector + secondVector  
9. ВекторАфтераддитион  

Выход

 

[1] 6 8 10 12 14 11

 

 

 

Как мы видим выше, в выводе и изображении даже после выдачи предупреждающего сообщения R были добавлены два вектора разной длины. Итак, мы видим, что он добавил элементы одного индекса и повторил элементы меньшей длины вектора при добавлении. Для пояснения см. изображение ниже.

 

Помните, что индекс вектора в R всегда начинается с 1, а не с 0.

 

 

 

Случай 2. Добавление векторов разных типов данных

 

Когда мы пытаемся сложить два вектора разных типов, например, вектор целого числа и строку, то выдает ошибку в виде Error in firstVector + secondVector нечислового аргумента бинарного оператора. Это показано на изображении ниже.

1. #Создание Вектора  
2. первый вектор <- 1:3  
3. первый вектор  
4. secondVector <- rep("Suraj", 3)  
5. второйВектор  
6.    
7. ResultAfterAddition <- firstVector + secondVector  
8. РезультатАфтераддитион  

Выход

 

Ошибка в первом векторе + втором векторе,

 

Нечисловой аргумент бинарного оператора

 

Случай 3. Добавление двух векторов символа типа данных

 

Когда мы пытаемся сложить вектора строки, выдает ту же ошибку, что и в случае сложения векторов целочисленного и строкового типов данных. Это показано ниже.

1. #Создание вектора  
2. firstVector <- rep("Suraj", 3)  
3. первый вектор  
4. secondVector <- rep("Suraj", 3)  
5. второйВектор  
6. ResultAfterAddition <- firstVector + secondVector  
7. РезультатАфтераддитион  

Выход

 

Ошибка в первом векторе + втором векторе,

 

Нечисловой аргумент бинарного оператора

 

 

Случай 4. Добавление двух векторов десятичного и целого типов данных

 

В R можно добавлять векторы десятичного и целочисленного типов. Это не выдает ни предупреждения, ни ошибки. Это показано ниже.

1. #Создание вектора  
2. firstVector <- seq(1,2, by=0.2)  
3. первый вектор  
4. secondVector <- rep(1, 6)  
5. второйВектор  
6. ResultAfterAddition <- firstVector + secondVector  
7. РезультатАфтераддитион  

Выход

 

[1] 2,0 2,2 2,4 2,6 2,8 3,0

 

 

 

Резюме

 

В этой статье мы научились выполнять арифметические операции над вектором; т. е. добавление двух векторов в R. Мы видели разные случаи при добавлении двух векторов в R также.

 

Надеюсь, вы узнали и получили удовольствие от чтения этой статьи. Вы можете ставить лайки, комментировать, делиться и оставлять любые предложения за мою признательность.

• Добавление векторов в R
• R
• Статика

Векторы и операции с векторами в JavaScript

Часть 2 серии «Линейная алгебра с JavaScript»

Векторы — это точный способ описания направлений в пространстве. Они строятся из чисел, которые образуют компонентов вектора. На картинке ниже вы можете видеть вектор в двумерном пространстве, состоящий из двух компонент. В случае трехмерного пространства вектор будет состоять из трех компонент.

вектор в двумерном пространстве

Мы можем написать класс для вектора в 2D и назвать его Vector2D , а затем написать класс для 3D-пространства и назвать его Vector3D , но что, если мы столкнемся с проблемой, когда векторы представляют не направление в физическом пространстве. Например, нам может понадобиться представить цвет (RGBA) в виде вектора, который будет иметь четыре компонента — красный, зеленый, синий и альфа-канал.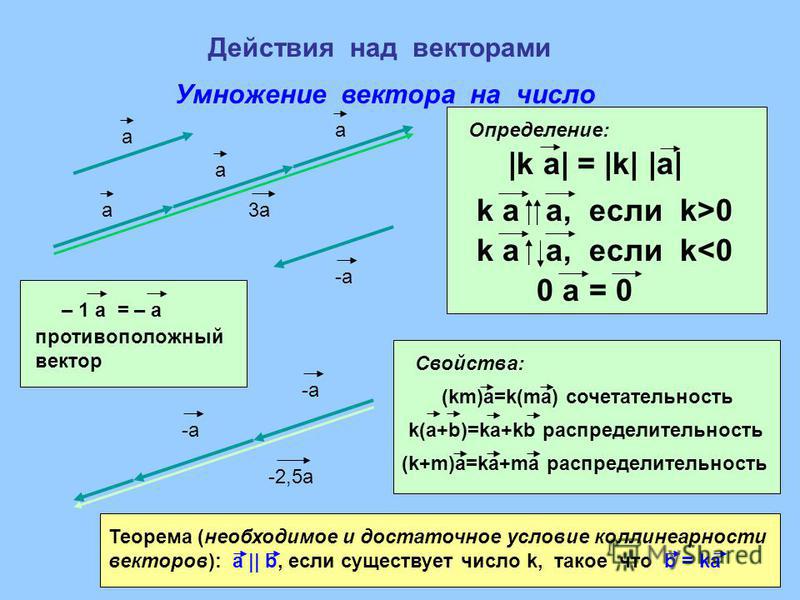 Или, скажем, у нас есть вектор, который дает доли пропорций из 90 541 n 90 542 вариантов, например, вектор, который описывает вероятность того, что каждая из пяти лошадей выиграет скачку. Итак, мы создаем класс, не привязанный к измерениям, и используем его следующим образом:

создать-вектор.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
}
const direction2d = новый вектор (1, 2)
const direction3d = новый вектор (1, 2, 3)
постоянный цвет = новый вектор (0,5, 0,4, 0,7, 0,15)
постоянные вероятности = новый вектор (0,1, 0,3, 0,15, 0,25, 0,2) 

Векторные операции

Рассмотрим два вектора и предположим, что α ∈ R — произвольная константа. Для этих векторов определены следующие операции:

основные векторные операции

В репозитории вместе с библиотекой живет проект React, в котором мы собираем библиотеку, используемую для создания визуализаций. Если вам интересно узнать, как создаются эти двумерные визуализации с помощью React и SVG, ознакомьтесь с этой частью.

Сложение и вычитание

Точно так же, как числа, вы можете складывать векторы и вычитать их. Выполнение арифметических вычислений над векторами просто требует выполнения арифметических операций над их компонентами.

векторов дополнение

вычитание векторов

Методы сложения получают другой вектор и возвращают новые векторы, построенные из сумм соответствующих компонентов. В вычитании мы делаем то же самое, но заменяем плюс на минус.

вычесть-добавить-vectors.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  добавить ({компоненты}) {
    вернуть новый вектор(
      ...components.map((компонент, индекс) => this.components[индекс] + компонент)
    )
  }
  вычесть ({компоненты}) {
    вернуть новый вектор(
      ...components.map((component, index) => this.components[index] - компонент)
    )
  }
}
const one = новый вектор (2, 3)
const другое = новый вектор (2, 1)
console. log(один.добавить(другой))
// Вектор { компоненты: [ 4, 4 ] }
console.log(один.вычесть(другой))
// Вектор { компоненты: [ 0, 2 ] } 

Масштабирование

Мы также можем масштабировать вектор любым числом α ∈ R , где каждый компонент умножается на коэффициент масштабирования α . Если α > 1 , то вектор станет длиннее, а если 0 ≤ α < 1 , то вектор станет короче. Если α отрицательное число, масштабированный вектор будет указывать в противоположном направлении.

вектор масштабирования

В методе scaleBy мы возвращаем новый вектор со всеми компонентами, умноженными на число, переданное в качестве параметра.

масштабирование.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  масштаб по (число) {
    вернуть новый вектор(
      ...this.components.map(компонент => компонент * номер)
    )
  }
}
константный вектор = новый вектор (1, 2)
console. log(вектор.scaleBy(2))
// Вектор { компоненты: [ 2, 4 ] }
console.log(vector.scaleBy(0.5))
// Вектор { компоненты: [ 0.5, 1 ] }
console.log(vector.scaleBy(-1))
// Вектор {компоненты: [-1, -2]} 

Длина

Длина вектора получается из теоремы Пифагора.

длина векторов

Метод длины очень прост, так как в Math уже есть нужная нам функция.

длина.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  
  длина() {
    вернуть Math.hypot(...this.components)
  }
}
константный вектор = новый вектор (2, 3)
console.log(вектор.длина())
// 3.6055512754639896 

Скалярное произведение

Скалярное произведение говорит нам, насколько два вектора похожи друг на друга. Он принимает два вектора на вход и выдает одно число на выходе. Скалярное произведение двух векторов представляет собой сумму произведений соответствующих компонентов.

скалярный продукт

В методе dotProduct мы получаем в качестве параметра еще один вектор и методом сокращения получаем сумму произведений соответствующих компонентов.

точка-продукт.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  
  точечный продукт ({ компоненты }) {
    return component.reduce((acc, component, index) => acc + component * this.components[index], 0)
  }
}
const one = новый вектор (1, 4)
const другое = новый вектор (2, 2)
console.log(one.dotProduct(другое))
// 10 

Прежде чем мы посмотрим, как направления векторов связаны друг с другом, мы реализуем метод, который будет возвращать вектор с длиной, равной единице. Такие векторы полезны во многих контекстах. Когда мы хотим указать направление в пространстве, мы используем нормализованный вектор в этом направлении.

нормализовать.js

класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  
  нормализовать () {
    вернуть this.scaleBy(1/this.length())
  }
}
константный вектор = новый вектор (2, 4)
const нормализовано = vector.normalize()
console.log(нормализованный)
// Вектор {компоненты: [0. 4472135954999579, 0.8944271909999159]}
console.log(нормализованная.длина())
// 1 

с использованием скалярного произведения

Если мы возьмем скалярное произведение двух нормализованных векторов и результат будет равен единице, это означает, что они имеют одинаковое направление. Чтобы сравнить два числа с плавающей запятой, мы будем использовать равны функции .

имеют то же направление-с.js

 константа EPSILON = 0,00000001
const areEqual = (один, другой, эпсилон = ЭПСИЛОН) =>
  Math.abs(один - другой) < эпсилон
класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  
  haveSameDirectionWith(другое) {
    const dotProduct = this.normalize().dotProduct(other.normalize())
    вернуть равные (точечный продукт, 1)
  }
}
const one = новый вектор (2, 4)
const другое = новый вектор (4, 8)
console.log(one.haveSameDirectionWith(other))
// правда 

Если мы возьмем скалярное произведение двух нормализованных векторов и результат будет равен минус единице, это означает, что они имеют прямо противоположное направление.

есть противоположное направление к.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  haveOppositeDirectionTo(другое) {
    const dotProduct = this.normalize().dotProduct(other.normalize())
    вернуть равные (точечный продукт, -1)
  }
}
const one = новый вектор (2, 4)
const другое = новый вектор (-4, -8)
console.log(один.haveOppositeDirectionTo(другой))
// правда 

Если мы возьмем скалярное произведение двух нормализованных векторов, и результат будет равен нулю, это означает, что они перпендикулярны.

перпендикулярно .js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  
  isPerpendicularTo(другое) {
    const dotProduct = this.normalize().dotProduct(other.normalize())
    вернуть равные (точечный продукт, 0)
  }
}
const one = новый вектор (-2, 2)
const другое = новый вектор (2, 2)
console.log(один.isPerpendicularTo(другой))
// правда 

Перекрестное произведение

Перекрестное произведение определено только для трехмерных векторов и дает вектор, перпендикулярный обоим входным векторам.

перекрестное произведение

В нашей реализации векторного произведения мы предполагаем, что этот метод используется только для векторов в трехмерном пространстве.

кросс-продукт.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  
  // Только трехмерные векторы
  перекрестное произведение ({компоненты}) {
    вернуть новый вектор(
      это.компоненты[1] * компоненты[2] - это.компоненты[2] * компоненты[1],
      это.компоненты[2] * компоненты[0] - это.компоненты[0] * компоненты[2],
      this.components[0] * компоненты[1] - this.components[1] * компоненты[0]
    )
  }
}
const one = новый вектор (2, 1, 1)
const другое = новый вектор (1, 2, 2)
console.log(один.crossProduct(другой))
// Вектор { компоненты: [ 0, -3, 3 ] }
console.log (другой. crossProduct (один))
// Вектор { компоненты: [ 0, 3, -3 ] } 

Другие полезные методы

В реальных приложениях этих методов будет недостаточно, например, мы можем захотеть найти угол между двумя векторами, инвертировать вектор или проецировать один на другой.

Прежде чем мы приступим к этим методам, нам нужно написать две функции для преобразования угла из радианов в градусы и обратно.

convertors.js

 const toDegrees = радианы => (радианы * 180) / Math.PI
const toRadians = градусы => (градусы * Math.PI) / 180 

Угол между

угол-между.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  
  угол между (другим) {
    вернуться к градусам(
      Math.acos(
        this.dotProduct(другое) /
        (эта.длина() * другая.длина())
      )
    )
  }
}
const one = новый вектор (0, 4)
const другое = новый вектор (4, 4)
console.log(один.уголмежду(другим))
// 45.00000000000001 

Отменить

Чтобы сделать вектор, направленный в отрицательном направлении, нам нужно масштабировать его на минус единицу.

отрицание.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  
  отрицать () {
    вернуть this. scaleBy(-1)
  }
}
константный вектор = новый вектор (2, 2)
console.log(vector.negate())
// Вектор {компоненты: [-2, -2]} 

Проект На

проект в на д

проект-на.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  
  проектНа(другое) {
    const нормализовано = другое.normalize()
    вернуть normalized.scaleBy(this.dotProduct(normalized))
  }
}
const one = новый вектор (8, 4)
const другое = новый вектор (4, 7)
console.log(другой.проектВ(один))
// Вектор { компоненты: [ 6, 3 ] } 

с длиной

Часто нам может понадобиться сделать наш вектор определенной длины.

с длиной.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  с длиной (новая длина) {
    вернуть this.normalize().scaleBy(newLength)
  }
}
const one = новый вектор (2, 3)
console.log(одна.длина())
// 3.6055512754639896
const изменен = one.withLength(10)
// 10
console. log(модифицированная.длина()) 

равно

Чтобы проверить, равны ли два вектора, мы будем использовать areEqual функция для всех компонентов.

равно.js

 класс Вектор {
  конструктор (... компоненты) {
    this.components = компоненты
  }
  // ...
  
  равно ({компоненты}) {
    вернуть компоненты.каждый((компонент, индекс) => равные(компонент, это.компоненты[индекс]))
  }
}
const one = новый вектор (1, 2)
const другое = новый вектор (1, 2)
console.log(один.equalTo(другой))
// истинный
const другой = новый вектор (2, 1)
console.log(один.equalTo(другой))
// ложь 

Единичный вектор и базис

Мы можем думать о векторе как о команде «пройти расстояние vx в направлении x, расстояние vy в направлении y и vz в направлении z». Чтобы записать этот набор команд более явно, мы можем использовать кратные векторы* ̂i, ̂j,* и* ̂k*. Это** единичные векторы**, указывающие в направлениях x , y и z соответственно:

стандартный базис {i, ̂j, ̂k}

Любое число, умноженное на * ̂i *, соответствует вектору с этим числом в первой координате. Например:

Одним из наиболее важных понятий в изучении векторов является понятие базиса . Рассмотрим пространство трехмерных векторов ℝ³ . Основой для ℝ³ является набор векторов {ê₁, ê₂, ê₃} , которые можно использовать в качестве системы координат для ℝ³ . Если набор векторов {ê₁, ê₂, ê₃} является базисом, тогда мы можем представить любой вектор *v⃗∈ℝ³ *в виде коэффициентов (v₁, v₂, v₃) относительно этого базиса:

вектор относительно базиса {ê₁, ê₂, ê3}

Вектор v⃗ получается путем измерения расстояния v₁ в ê₁ направлении, расстояние v₂ в направлении ê₂ и расстояние v₃ в направлении ê₃ направление.

Тройка коэффициентов сама по себе ничего не значит, если мы не знаем используемую основу. Необходима основа для преобразования математических объектов, таких как тройка* (a, b, c)*, в идеи реального мира, такие как цвета, вероятности или местоположения.