Часть 1. Теория вероятностей на ЕГЭ. Простые задачи. – МАТЕМАТИКА
Теория вероятностей на ЕГЭ по математике может быть представлена как в виде простых задач на классическое определение вероятности, так и в виде достаточно сложных, на применение соответствующих теорем.
В этой части рассмотрим задачи, для решения которых достаточно применения определения вероятности. Иногда здесь мы будем применять также формулу для вычисления вероятности противоположного события. Хотя без этой формулы здесь можно обойтись, она все равно понадобится при решении следующих задач.
Теоретическая частьСлучайным называют событие, которое может произойти или не произойти (заранее предсказать невозможно) во время наблюдения или испытания.
Пусть при проведении испытания (бросание монеты или кубика, вытягивание экзаменационного билета и т. д.) возможны равновозможных исходов. Например, при подбрасывании монеты число всех исходов равно 2, так как кроме выпадения «решки» или «орла» других исходов быть не может.
Вероятностью события А называется отношение числа благоприятных для этого события исходов к общему числу равновозможных исходов (это классическое определение вероятности). Пишем
Например, пусть событие А состоит в выпадении нечётного числа очков при бросании кубика. Всего возможны 6 исходов: выпадение на верхней грани кубика 1, 2, 3, 4, 5, 6. При этом благоприятными для события А являются исходы с выпадением 1, 3, 5. Таким образом, .
Заметим, что всегда выполняется двойное неравенство , поэтому вероятность любого события А лежит на отрезке [0; 1], то есть . Если у вас в ответе вероятность получается больше единицы, значит, вы где-то ошиблись и решение нужно перепроверить.
События А и В называются противоположными друг другу, если любой исход благоприятен ровно для одного из них.
Например, при бросании кубика событие «выпало нечётное число» является противоположным событию «выпало чётное число».
Событие, противоположное событию А, обозначают. Из определения противоположных событий следует , значит, .
Задачи о выборе объектов из набораВ этих задачах нужно подсчитать общее число объектов (равно общему числу исходов) и число подходящих объектов (равно числу благоприятных исходов). После этого следует воспользоваться определением вероятности.
Задача 1. В чемпионате мира участвуют 24 команды. С помощью жребия их нужно разделить на четыре группы по шесть команд в каждой. В ящике вперемешку лежат карточки с номерами групп:
1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4.
Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется в третьей группе?
Решение.
Общее число исходов равно числу карточек – их 24. Благоприятных исходов 6 (так как номер 3 написан на шести карточках). Искомая вероятность равна .
Благоприятных исходов 6 (так как номер 3 написан на шести карточках). Искомая вероятность равна .
Ответ: 0,25.
Задача 2. В урне 14 красных, 9 жёлтых и 7 зелёных шаров. Из урны наугад достают один шар. Какова вероятность того, что этот шар окажется жёлтым?
Решение.
Общее число исходов равно числу шаров: 14 + 9 + 7 = 30. Число исходов, благоприятствующих данному событию, равно 9. Искомая вероятность равна равна .
Ответ: 0,3
Задача 3. На клавиатуре телефона 10 цифр, от 0 до 9. Какова вероятность того, что случайно нажатая цифра будет чётной и больше 5?
Решение.
Исходом здесь является нажатие определённой клавиши, поэтому всего имеется 10 равновозможных исходов. Указанному событию благоприятствуют исходы, означающие нажатие клавиши 6 или 8. Таких исходов два. Искомая вероятность равна .
Ответ: 0,2.
Задача 4.
Какова вероятность того, что случайно выбранное натуральное число от 4 до 23 делится на три?
Решение.
На отрезке от 4 до 23 имеется 23 – 4 + 1 = 20 натуральных чисел, значит, всего возможны 20 исходов. На этом отрезке кратны трём следующие числа: 6, 9, 12, 15, 18, 21. Всего таких чисел 6, поэтому рассматриваемому событию благоприятствуют 6 исходов. Искомая вероятность равна .
Ответ: 0,3.
Задача 5. Из 20 билетов, предлагаемых на экзамене, школьник может ответить только на 17. Какова вероятность того, что школьник не сможет ответить на выбранный наугад билет?
Решение.
1 -й способ.
Так как школьник может ответить на 17 билетов, то на 3 билета он ответить не может. Вероятность получить один из этих билетов по определению равна .
2-й способ.
Обозначим через А событие «школьник может ответить на билет». Тогда . Вероятность противоположного события равна =1 – 0,85 = 0,15.
Ответ: 0,15.
Задача 6. В чемпионате по художественной гимнастике участвуют 20 спортсменок: 6 из России, 5 из Германии, остальные – из Франции. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая седьмой, окажется из Франции.
Решение.
Всего 20 спортсменок, у всех равные шансы выступать седьмой. Поэтому имеются 20 равновероятных исходов. Из Франции 20 – 6 – 5 = 9 спортсменок, поэтому имеются 9 благоприятных для указанного события исходов. Искомая вероятность равна .
Ответ: 0,45.
Задача 7. Научная конференция проводится в 5 дней. Всего запланировано 50 докладов – первые три дня по 12 докладов, остальные распределены поровну между четвёртым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора Н. окажется запланированным на последний день конференции?
Решение.
Сначала найдём, сколько докладов запланировано на последний день. На первые три дня запланировано докладов. Остаются ещё 50 – 36 = 14 докладов, которые распределяются поровну между оставшимися двумя днями, поэтому в последний день запланировано докладов.
Будем считать исходом порядковый номер доклада профессора Н. Всего таких равновозможных исходов 50. Благоприятствуют указанному событию 7 исходов (последние 7 номеров в списке докладов). Искомая вероятность равна .
Ответ: 0,14.
Задача 8. На борту самолёта 10 мест рядом с запасными выходами и 15 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажиров высокого роста. Пассажир К. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру К. достанется удобное место, если всего в самолёте 200 мест.
Решение.
Исход в этой задаче – выбор места. Всего имеется 200 равновозможных исходов. Благоприятствуют событию «выбранное место удобное» 15 + 10 = 25 исходов. Искомая вероятность равна .
Искомая вероятность равна .
Ответ: 0,125.
Задача 9. Из 1000 собранных на заводе кофемолок 7 штук бракованных. Эксперт проверяет одну наугад выбранную кофемолку из этой 1000. Найдите вероятность того, что проверяемая кофемолка окажется бракованной.
Решение.
При выборе кофемолки наугад возможны 1000 исходов, событию А «выбранная кофемолка бракованная» благоприятны 7 исходов. По определению вероятности .
Ответ: 0,007.
Задача 10. Завод производит холодильники. В среднем на 100 качественных холодильников приходится 15 холодильников со скрытыми дефектами. Найдите вероятность того, что купленный холодильник окажется качественным. Результат округлите до сотых.
Решение.
Эта задача похожа на предыдущую. Однако формулировка «на 100 качественных холодильников приходится 15 с дефектами» указывает нам, что дефектные 15 штук не входят в 100 качественных. Поэтому общее число исходов равно 100 + 15 =115 (равно общему числу холодильников), благоприятных исходов 100. Искомая вероятность равна . Для подсчёта приближённого значения дроби удобно воспользоваться делением уголком. Получаем 0,869…, что
Поэтому общее число исходов равно 100 + 15 =115 (равно общему числу холодильников), благоприятных исходов 100. Искомая вероятность равна . Для подсчёта приближённого значения дроби удобно воспользоваться делением уголком. Получаем 0,869…, что
Ответ: 0,87.
Задача 11. Перед началом первого тура чемпионата по теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 теннисистов, среди которых 7 участников из России, в том числе Максим Зайцев. Найдите вероятность того, что в первом туре Максим Зайцев будет играть с каким-либо теннисистом из России.
Решение.
Как и в предыдущей задаче, необходимо внимательно прочитать условие и понять, что является исходом, а что – благоприятным исходом (так, неосмысленное применение формулы вероятности приводит к неправильному ответу ).
Здесь исход – это соперник Максима Зайцева. Так как всего теннисистов 16, а сам с собой Максим играть не может, то имеется 16 – 1 = 15 равновероятных исходов.
Ответ: 0,4.
Задача 12. Футбольную секцию посещают 33 человека, среди них два брата – Антон и Дмитрий. Посещающих секцию случайным образом делят на три команды по 11 человек в каждой. Найдите вероятность того, что Антон и Дмитрий окажутся в одной команде.
Решение.
Сформируем команды, последовательно помещая футболистов на свободные места, при этом начнем с Антона и Дмитрия. Сначала поместим Антона на случайно выбранное место из свободных 33. Теперь помещаем на свободное место Дмитрия (исходом будем считать выбор места для него). Всего имеется 32 свободных места (одно уже занял Антон), поэтому всего возможны 32 исхода. В одной команде с Антоном остается 10 свободных мест, поэтому событию «Антон и Дмитрий в одной команде» благоприятствуют 10 исходов. Вероятность этого события равна .
Ответ: 0,3125.
Задача 13. Механические часы с двенадцатичасовым циферблатом в какой-то момент сломались и перестали ходить. Найдите вероятность того, что часовая стрелка застыла, достигнув отметки 11, но не дойдя до отметки 2 часа.
Решение.
Условно циферблат можно разделить на 12 секторов, располагающихся между отметками соседних чисел (между 12 и 1, 1 и 2, 2 и 3, …, 11 и 12). Исходом мы будем считать остановку часовой стрелки в одном из указанных секторов. Всего есть 12 равновозможных исходов. Указанному событию благоприятствуют три исхода (сектора между 11 и 12, 12 и 1, 1 и 2). Искомая вероятность равна .
Ответ: 0,25.
Подведем итог
После изучения материала по решению простых задач по теории вероятностей рекомендую выполнить задачи для самостоятельного решения, которые мы публикуем на нашем канале Telegram. Вы также можете проверить правильность их выполнения, внеся свои ответы в предлагаемую форму.
Также рекомендую изучить «Округление с недостатком» и другие уроки по решению заданий ЕГЭ по математике, которые представлены на нашем канале Youtube.
Спасибо, что поделились статьей в социальных сетяхИсточник «Подготовка к ЕГЭ. Математика.Теория вероятностей». Под редакцией Ф.Ф. Лысенко, С.Ю. Кулабухова
| 1 | На тарелке лежат одинаковые на вид пирожки: 5 с мясом, 8 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с капустой. | Смотреть видеоразбор >> |
| 2 | На семинар приехали 6 учёных из Норвегии, 5 из России и 9 из Испании. Каждый учёный подготовил один доклад. Порядок докладов определяется случайным образом. Найдите вероятность того, что восьмым окажется доклад учёного из России. Найдите вероятность того, что восьмым окажется доклад учёного из России. | Смотреть видеоразбор >> |
| 3 | Фабрика выпускает сумки. В среднем из 125 сумок 5 сумок имеют скрытый дефект. Найдите вероятность того, что случайно выбранная сумка окажется с дефектом. | Смотреть видеоразбор >> |
| 4 | Из 300 саженцев крыжовника в среднем 36 не приживаются. Какова вероятность того, что случайно выбранный саженец крыжовника приживётся? | Смотреть видеоразбор >> |
| 5 | Конкурс исполнителей проводится в 5 дней. Всего заявлено 50 выступлений – по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. В первый день запланировано 14 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса? | Смотреть видеоразбор >> |
| 6 | Найдите вероятность того, что случайно выбранное трёхзначное число делится на 25. | Смотреть видеоразбор >> |
| 7 | У бабушки 25 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами. | Смотреть видеоразбор >> |
| 8 | В фирме такси в данный момент свободно 20 машин: 8 чёрных, 7 жёлтых и 5 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси. | Смотреть видеоразбор >> |
| 9 | Фабрика выпускает сумки. В среднем из 125 сумок 5 сумок имеют скрытый дефект. Найдите вероятность того, что случайно выбранная сумка окажется без дефектов. | Смотреть видеоразбор >> |
| 10 | На борту самолёта 23 места рядом с запасными выходами и 22 места за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Л. высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Л. достанется удобное место, если всего в самолёте 300 мест. достанется удобное место, если всего в самолёте 300 мест. | Смотреть видеоразбор >> |
| 11 | В группе туристов 8 человек. С помощью жребия они выбирают двух человек, которые должны идти в село в магазин за продуктами. Какова вероятность того, что турист Д., входящий в состав группы, пойдёт в магазин? | Смотреть видеоразбор >> |
| 12 | Найдите вероятность того, что случайно выбранное трёхзначное число делится на 33. | Смотреть видеоразбор >> |
| 13 | В чемпионате по гимнастике участвуют 50 спортсменок: 17 из России, 22 из США, остальные – из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. | Смотреть видеоразбор >> |
| 14 | В фирме такси в наличии 20 легковых автомобилей: 7 из них чёрного цвета с жёлтыми надписями на боках, остальные – жёлтого цвета с чёрными надписями.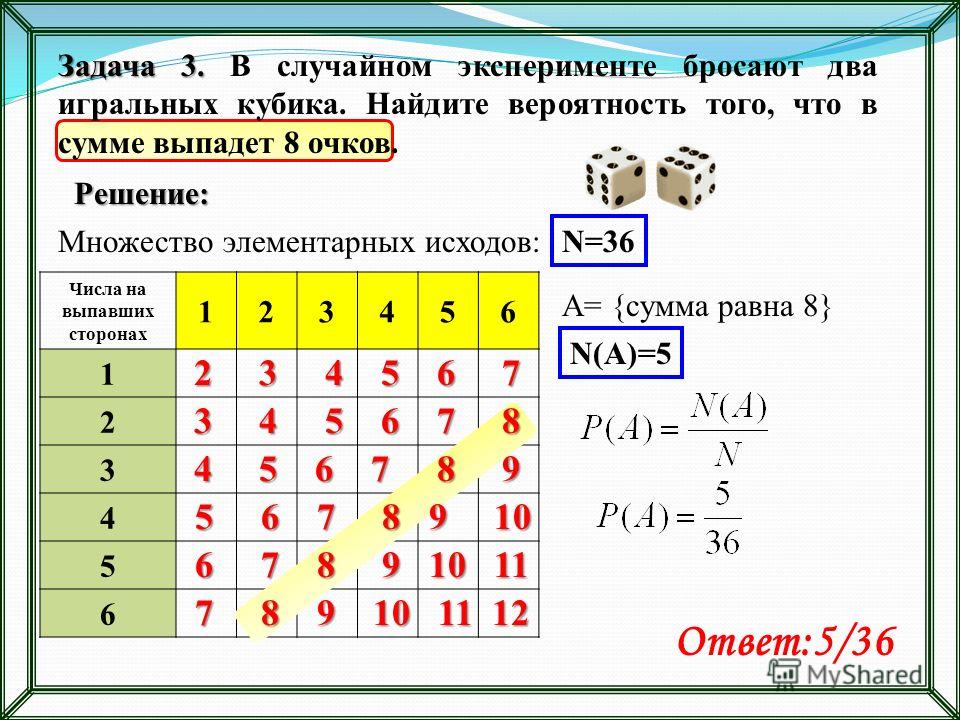 Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями. Найдите вероятность того, что на случайный вызов приедет машина жёлтого цвета с чёрными надписями. | Смотреть видеоразбор >> |
| 15 | В среднем из 500 садовых насосов, поступивших в продажу, 25 подтекает. Найдите вероятность того, что случайно выбранный для контроля насос подтекает. | Смотреть видеоразбор >> |
| 16 | Вася, Петя, Олег, Коля и Лёша бросили жребий – кому начинать игру. Найдите вероятность того, что начинать игру должен будет Петя. | Смотреть видеоразбор >> |
| 17 | В ящике находятся чёрные и белые шары, причём чёрных в 4 раза больше, чем белых. Из ящика случайным образом достали один шар. Найдите вероятность того, что он будет белым. | Смотреть видеоразбор >> |
| 18 | В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что во второй раз выпадет то же, что и в первый. | Смотреть видеоразбор >> |
| 19 | В соревнованиях по толканию ядра участвуют 9 спортсменов из Дании, 3 спортсмена из Швеции, 8 спортсменов из Норвегии и 5 – из Финляндии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Финляндии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Финляндии. | Смотреть видеоразбор >> |
| 20 | В сборнике билетов по математике всего 20 билетов, в 11 из них встречается вопрос по теме «Логарифмы». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме «Логарифмы». | Смотреть видеоразбор >> |
| 21 | В среднем из 1400 садовых насосов, поступивших в продажу, 14 подтекает. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. | Смотреть видеоразбор >> |
| 22 | Научная конференция проводится в 3 дня. Всего запланировано 50 докладов: в первый день – 18 докладов, остальные распределены поровну между вторым и третьим днями. На конференции планируется доклад профессора М. Порядок докладов определяется случайным образом. Какова вероятность того, что доклад профессора М. окажется запланированным на последний день конференции? окажется запланированным на последний день конференции? | Смотреть видеоразбор >> |
| 23 | На птицеферме есть только куры и гуси, причём кур в 19 раз больше, чем гусей. Найдите вероятность того, что случайно выбранная на этой ферме птица окажется гусем. | Смотреть видеоразбор >> |
| 24 | Вероятность того, что стекло мобильного телефона разобьётся при падении на твёрдую поверхность, равна 0,84. Найдите вероятность того, что при падении на твёрдую поверхность стекло мобильного телефона не разобьётся. | Смотреть видеоразбор >> |
| 25 | На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 5 прыгунов из России и 7 прыгунов из Китая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что вторым будет выступать прыгун из Китая. | Смотреть видеоразбор >> |
| 26 | На олимпиаде по русскому языку участников рассаживают по трём аудиториям. В первых двух по 130 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории. В первых двух по 130 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчёте выяснилось, что всего было 400 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории. | Смотреть видеоразбор >> |
| 27 | Из 1600 пакетов молока в среднем 80 протекают. Какова вероятность того, что случайно выбранный пакет молока не течёт? | Смотреть видеоразбор >> |
| 28 | Конкурс исполнителей проводится в 5 дней. Всего заявлено 60 выступлений – по одному от каждой страны, участвующей в конкурсе. Исполнитель из России участвует в конкурсе. Все выступления поровну распределены между конкурсными днями. порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление исполнителя из России состоится в третий день конкурса? | Смотреть видеоразбор >> |
| 29 | В коробке вперемешку лежат чайные пакетики с чёрным и зелёным чаем, одинаковые на вид, причём пакетиков с чёрным чаем в 4 раза больше, чем пакетиков с зелёным. Найдите вероятность того, что случайно выбранный из этой коробки пакетик окажется пакетиком с зелёным чаем. Найдите вероятность того, что случайно выбранный из этой коробки пакетик окажется пакетиком с зелёным чаем. | Смотреть видеоразбор >> |
| 30 | Вероятность того, что новая шариковая ручка пишет плохо или вовсе не пишет, равна 0,21. Покупатель не глядя берёт одну шариковую ручку из коробки. Найдите вероятность того, что эта ручка пишет хорошо. | Смотреть видеоразбор >> |
Задачи для ОГЭ. Теория вероятностей
Математика
Задачи для ОГЭ с ответами и решениями
Теория вероятностей
перейти к содержанию задачника
- Петя выбирает трехзначное число. Найдите вероятность того, что оно делится на 50.
- Петя выбирает трехзначное число. Найдите вероятность того, что оно делится на 11.
- На тарелке 10 пирожков: 2 с мясом, 6 с капустой и 2 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.

- На тарелке 30 пирожков: 3 с мясом, 18 с капустой и 9 с вишней. Вова наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
- В фирме такси в данный момент свободно 30 машин: 7 черных, 6 желтых и 17 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет желтое такси.
- В каждой десятой банке кофе согласно условиям акции есть приз. Призы распределены по банкам случайно. Петя покупает банку кофе в надежде выиграть приз. Найдите вероятность того, что Петя не найдет приз в своей банке.
- Игорь с папой решили покататься на колесе обозрения. Всего на колесе двадцать кабинок, из них 3 — синие, 14 — зеленые, остальные — красные. Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Игорь прокатится в красной кабинке.
- Петя с папой решили покататься на колесе обозрения. Всего на колесе двенадцать кабинок, из них 3 — синие, 6 — зеленые, остальные — красные.
 Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Петя прокатится в красной кабинке.
Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Петя прокатится в красной кабинке. - У дедушки 10 чашек: 7 с красными цветами, остальные с синими. Дедушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
- У бабушки 20 чашек: 4 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
- На экзамене 50 билетов. Петя не выучил 9 из них. Найдите вероятность того, что ему попадется выученный билет.
- На экзамене 50 билетов. Петя не выучил 1 из них. Найдите вероятность того, что ему попадется выученный билет.
- Родительский комитет закупил 10 пазлов для подарков детям на окончание года, из них 2 с машинами и 8 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Вове достанется пазл с машиной.
- Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 22 с машинами и 3 с видами городов.
 Подарки распределяются случайным образом. Найдите вероятность того, что Диме достанется пазл с машиной.
Подарки распределяются случайным образом. Найдите вероятность того, что Диме достанется пазл с машиной. - В среднем на 100 карманных фонариков приходится семь неисправных. Найдите вероятность купить работающий фонарик.
- В среднем на 75 карманных фонариков приходится семь неисправных. Найдите вероятность купить работающий фонарик.
- В среднем из каждых 100 поступивших в продажу аккумуляторов 91 аккумулятор заряжен. Найдите вероятность того, что купленный аккумулятор не заряжен.
- В среднем из каждых 80 поступивших в продажу аккумуляторов 68 аккумулятор заряжен. Найдите вероятность того, что купленный аккумулятор не заряжен.
- Саша наудачу выбирает двузначное число. Найдите вероятность того, что оно оканчивается на 6.
- Определите вероятность того, что при бросании кубика выпало нечетное число очков.
- Определите вероятность того, что при бросании кубика выпало 1.
- Одновременно бросают две симметричные монеты. Какова вероятность того, что выпадут орел и решка?
- Одновременно бросают три симметричные монеты.
 Какова вероятность того, что выпадут два орла и одна решка?
Какова вероятность того, что выпадут два орла и одна решка? - В классе 21 учащийся, среди них два друга — Петя и Вася. На уроке физкультуры класс случайным образом разбивают на 7 равных групп. Найдите вероятность того, что Петя и Вася попали в одну группу.
- Перед началом футбольного матча судья бросают монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть три матча — с командой В, с командой С и с командой D. Найдите вероятность того, что во всех матчах владение мячом первыми будет принадлежать команде А.
- В соревнованиях по толканию ядра участвуют 6 спортсменов из Греции, 4 спортсмена из Болгарии, 3 спортсмена из Румынии и 7 — из Венгрии. Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Венгрии.
- В соревнованиях по толканию ядра участвуют 4 спортсмена из Дании, 8 спортсменов из Швеции, 4 спортсмена из Румынии и 9 — из Венгрии.
 Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции. - В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.
- В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 10 очков. Результат округлите до сотых.
- На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача на тему «Треугольники», равна 0,5. Вероятность того, что это окажется задача на тему «Окружность» равна 0,25. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
- На экзамене по геометрии школьнику достается одна задача из сборника. Вероятность того, что эта задача на тему «Окружность», равна 0,45. Вероятность того, что это окажется задача на тему «Углы» равна 0,5.
 В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем. - Стрелок четыре раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок первые 3 раза попал в мишени, а последний раз промахнулся.
- Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,7. Найдите вероятность того, что стрелок первый раз попал в мишени, а последние два раза промахнулся.
- Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,9. Найдите вероятность того, что стрелок попал в мишень два раза и один раз промахнулся.
- Стрелок три раза стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,5. Найдите вероятность того, что стрелок попал в мишень два раза и один раз промахнулся.
- В девятом экономическом классе учатся 24 мальчика и 6 девочек.
 По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет мальчик?
По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет мальчик? - В девятом математическом классе учатся 2 мальчика и 23 девочек. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет девочка?
- Вероятность того, что новый компьютер прослужит больше года, равна 0,98. Вероятность того, что он прослужит больше двух лет, равна 0,84. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
- Вероятность того, что новый сканер прослужит больше года, равна 0,96. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
- Какова вероятность того, что случайно выбранное натуральное число от 25 до 39 делится на 5?
- Какова вероятность того, что случайно выбранное натуральное число от 15 до 36 делится на 2?
- На олимпиаде по химии участников рассаживают по трем аудиториям. В первых двух по 180 человек, оставшихся проводят в запасную аудиторию в другом корпусе.
 При подсчете выяснилось, что всего было 450 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
При подсчете выяснилось, что всего было 450 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории. - На олимпиаде по математике участников рассаживают по трем аудиториям. В первых двух по 120 человек, оставшихся проводят в запасную аудиторию в другом корпусе. При подсчете выяснилось, что всего было 300 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
- Вероятность того, что на тесте по физике Петя верно решит больше 11 задач, равна 0,65. Вероятность того, что он верно решит больше 10 задач, равна 0,71. Найдите вероятность того, что Петя верно решит ровно 11 задач.
- Вероятность того, что на тесте по математике Вася верно решит больше 12 задач, равна 0,7. Вероятность того, что он верно решит больше 11 задач, равна 0,79. Найдите вероятность того, что Вася верно решит ровно 12 задач.
- Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 22 пассажиров, равна 0,86.
 Вероятность того, что окажется меньше 9 пассажиров, равна 0,5. Найдите вероятность того, что число пассажиров будет от 9 до 21.
Вероятность того, что окажется меньше 9 пассажиров, равна 0,5. Найдите вероятность того, что число пассажиров будет от 9 до 21. - Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 21 пассажира, равна 0,96. Вероятность того, что окажется меньше 11 пассажиров, равна 0,51. Найдите вероятность того, что число пассажиров будет от 11 до 20.
- Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,05. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,03. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
- Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля.
 Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
перейти к содержанию задачника
Ответы
- 0,02
- 0,09
- 0,2
- 0,3
- 0,2
- 0,9
- 0,15
- 0,25
- 0,3
- 0,8
- 0,82
- 0,98
- 0,2
- 0,88
- 0,93
- 0,92
- 0,09
- 0,15
- 0,1
- 0,5
- 1/6
- 0,5
- 0,375
- 0,1
- 0,125
- 0,35
- 0,32
- 0,11
- 0,13
- 0,75
- 0,95
- 0,0625
- 0,063
- 0,243
- 0,375
- 0,8
- 0,92
- 0,14
- 0,09
- 0,2
- 0,5
- 0,2
- 0,2
- 0,06
- 0,09
- 0,36
- 0,45
- 0,078
- 0,0776
Метки ОГЭ.
 Смотреть запись.
Смотреть запись.
Как рассчитать вероятность — Математика GCSE
Здесь мы научимся рассчитывать вероятность, включая базовую вероятность, взаимоисключающие события, независимые события и условную вероятность.
Существуют также листы расчета вероятности на основе экзаменационных вопросов Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.
Что такое вероятность?
Вероятность — вероятность наступления события.
Чтобы найти вероятность события, мы используем формулу
\text{Вероятность}=\frac{\text{количество желаемых результатов}}{\text{общее количество результатов}}
Например,
Давайте посмотрим на вероятность выпадения четного числа при броске игральной кости.
Желаемый результат — получить четное число. На кубике 3 четных числа.
Общее количество возможных исходов равно 6, так как на кубике 6 чисел.
\text{Вероятность получения четного числа}=\frac{\text{количество желаемых результатов}}{\text{общее количество результатов}}=\frac{3}{6}
Диапазон вероятностей от \bf{0} до \bf{1}.
Если что-то имеет вероятность \bf{0}, то это невозможно , а если что-то имеет вероятность \bf{1}, то это достоверно .
Мы используем обозначение P(event) для представления вероятности события.
Например,
Если бы мы хотели записать вероятность получения 1, мы могли бы написать P (1).
Что такое вероятность?
Расчет вероятностей комбинированных событий
Иногда нам нужно найти вероятность возникновения более чем одного события. Существуют различные правила вероятности, которые мы можем использовать.
- Взаимоисключающие события
Взаимоисключающие события — это два или более события, которые не могут произойти одновременно. Например, выпадение орла и решки при подбрасывании монеты или выпадении 2 и 3 на кубике.
Например, выпадение орла и решки при подбрасывании монеты или выпадении 2 и 3 на кубике.
Для взаимоисключающих событий: P(A или B) = P(A) + P(B)
Если у нас есть исчерпывающий список исходов, их вероятности в сумме равны 1. Например, вероятность получения четное или нечетное число на кубике.
Вероятность получения четного числа равна \frac{3}{6}
, а вероятность получения нечетного числа равна \frac{3}{6}.
Вероятность получения четного или нечетного числа равна \frac{3}{6}+\frac{3}{6}=\frac{6}{6}=1.
Поскольку получение четного или нечетного числа охватывает все возможные исходы, это исчерпывающий список, а вероятности в сумме дают 1.
Пошаговое руководство: Взаимоисключающие события (скоро)
- Независимые события
Независимые события — это события, на которые не влияет возникновение других событий. Например, если мы бросаем кубик дважды, результаты первого и второго бросков не влияют друг на друга — это независимые события.
Для независимых событий: P(A и B) = P(A) x P(B)
Пошаговое руководство: Независимые события (скоро)
- Условная вероятность
Условная вероятность – это вероятность того, что событие произойдет, исходя из возникновения другого события.
Для условной вероятности вероятности рассчитываются на основе того, что уже произошло.
Например, в мешочке 5 жетонов, 2 черных и остальные белые.
Счетчик выбирается случайным образом и не заменяется. Второй счетчик выбирается случайным образом. Вероятность того, что второй счетчик будет черным, зависит от того, какого цвета был первый счетчик.
Пошаговое руководство Условная вероятность по мере необходимости .
Объясните, как рассчитать вероятность
Как рассчитать таблицу вероятности
Получите бесплатную таблицу расчета вероятности, содержащую более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
ИксКак рассчитать таблицу вероятности
Получите бесплатную таблицу расчета вероятности, содержащую более 20 вопросов и ответов. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры расчета вероятности
Пример 1: базовая вероятность
У Джейми есть следующие карты:
Карта выбирается случайным образом. Найдите вероятность того, что на карточке есть буква В.
- Выпишите основную вероятность .
Мы можем записать основную вероятность, используя
\text{Вероятность}=\frac{\text{количество желаемых результатов}}{\text{общее количество результатов}} .
Количество карт с B равно 2, а общее количество карт равно 11.
\text{Вероятность}=\frac{\text{количество желаемых результатов}}{\text{общее количество результатов}}=\frac{2}{11}
2 Решите проблему, используя правила И или ИЛИ в зависимости от ситуации .
Не требуется, так как это основной вероятностный вопрос.
Пример 2: взаимоисключающие события
Какова вероятность выпадения 2 или 3 на следующем спиннере?
Запишите основную вероятность .
Мы можем записать вероятность получения 2 и вероятность получения 3.
P(2)=\frac{3}{8}
P(3)=\frac{2}{ 8}
Решите проблему, используя правила И или ИЛИ в зависимости от ситуации .
\begin{выровнено} \text{P(A или B)} &= \text{P(A)}+\text{P(B)}\\\\ \text{P(2 или 3)} &= \text{P(2)}+\text{P(3)}\\\\ \text{P(2 или 3)} &= \frac{3}{8}+\frac{2}{8} \\\\ &=\frac{5}{8} \end{выровнено}
Вероятность выпадения 2 или 3 равна \frac{5}{8}.
Пример 3: независимые события
Оливия подбрасывает монету и бросает кубик. Какова вероятность того, что монета выпадет орлом, а кубик выпадет на 1?
Выпишите основную вероятность .
\text{P(Голова)}=\frac{1}{2}
\text{P(1)}=\frac{1}{6}
Решите задачу, используя правила AND или OR в зависимости от ситуации .
\begin{выровнено} \text{P(A и B)}&=\text{P(A)} \times \text{P(B)}\\\\ \text{P(Голова и 1)}&=\text{P(Голова)} \times \text{P(1)}\\\\ \text{P(Голова и 1)}&=\frac{1}{2} \times \frac{1}{6} \\\\ &= \фракция{1}{12} \end{выровнено}
Вероятность того, что монета выпадет орлом, а кубик выпадет 1, равна \frac{1}{12}.
Пример 4: использование древовидной диаграммы
Вероятность того, что Кейт выиграет игру в теннис, равна 0,6. Вероятность того, что Билли выиграет партию в теннис, равна 0,7. Кейт играет матч в субботу, а Билли играет матч в воскресенье.
Найдите вероятность того, что один из них выиграет, а другой проиграет.
Выпишите основную вероятность .
Мы можем рассчитать вероятность того, что люди не выиграют свои игры в теннис.
\text{P(Кейт НЕ выиграет)}=1-0.6=0.4
\text{P(Билли НЕ выиграет)}=1-0.7=0.3
Решите задачу, используя И или ИЛИ как соответствующий .
Для этого вопроса мы собираемся нарисовать древовидную диаграмму, чтобы мы могли четко видеть различные результаты.
В случае, если один из них выиграет, а другой проиграет, у нас может быть победа Кейт и проигрыш Билли или проигрыш Кейт и победа Билли.
\text{P(Кейт побеждает, а Билли проигрывает)}=0,6 \times 0,3=0,18
\text{P(Кейт проигрывает, а Билли выигрывает)}=0,4 \times 0,7=0,28
\text{P(один выигрывает и один проигрывает)}=0,18+0,28=0,46
Вероятность того, что один из них выигрывает, а другой проигрывает 0,46.
Пример 5: условная вероятность
В мешке 7 красных и 5 синих шариков. 1 шарик выбирается случайным образом.
Мрамор красный. Выбирается второй шарик. Найдите вероятность того, что второй шарик тоже красный.
Запишите основную вероятность .
Это зависимые события. Первое событие влияет на вероятность второго события.
\text{P(первый шарик красный)}=\frac{7}{12}
Решите задачу, используя правила И или ИЛИ в зависимости от ситуации .
Учитывая, что был выбран один красный шарик, теперь всего 6 красных шариков и 11 шариков. Это условная вероятность.
\text{P(второй шарик красный)}=\frac{6}{11}
Вероятность того, что второй шарик красный, равна \frac{6}{11}.
Пример 6: использование диаграммы Венна
На приведенной ниже диаграмме Венна показано количество учащихся, сдавших пробные экзамены по английскому языку и математике.
Студент выбран случайным образом. Учитывая, что выбранный студент сдал математику, найдите вероятность того, что он сдал , а не экзаменов по английскому языку.
Выпишите основную вероятность .
Это более сложный вероятностный вопрос. Однако мы можем выяснить, сколько учеников сдают математику.
Однако мы можем выяснить, сколько учеников сдают математику.
12+9=21
Решите задачу, используя правила И или ИЛИ в зависимости от ситуации .
Это вопрос условной вероятности.
Желаемый результат – сдача учащимся математики, но , а не английского языка. Есть 9 студентов, которые сдают математику, но не английский. Условием является то, что они сдают математику, поэтому нам нужно учитывать всех учащихся, сдавших математику. Мы знаем, что математику сдает 21 ученик.
Следовательно, вероятность того, что учащийся не сдал экзамен по английскому языку при условии, что он сдал математику, равна \frac{9{21}.
Пример 7: использование двустороннего стола
Двустороннее отображение информации о поле и цвете глаз детей в 6-м классе.
Ребенок выбирается случайным образом. Какова вероятность того, что у ребенка зеленые глаза, если он мальчик?
Выпишите основную вероятность .
Это более сложный вероятностный вопрос. Однако мы можем выяснить, сколько детей мужского пола.
2+9+4=15
Решите проблему, используя правила И или ИЛИ в зависимости от ситуации .
Это вопрос условной вероятности.
Желаемый результат: у ребенка зеленые глаза, но он мальчик. Есть 2 детей с зелеными глазами, мальчики. Условие состоит в том, что они мужского пола, поэтому нам нужно рассмотреть всех детей мужского пола. Мы знаем, что 15 детей мужского пола.
Следовательно, вероятность того, что у ребенка зеленые глаза, если он мальчик, равна \frac{2}{15}.
Распространенные заблуждения
- Сложение вероятностей вместо их умножения
Для независимых событий P(A \ и \ B) = P(A) \times (P(B). P(A \ или \ B) = P(A) + P(B).
- Неправильное умножение или деление дробей
Чтобы умножить дроби, умножьте числители и умножьте знаменатели.
Чтобы разделить дроби, переверните вторую и умножьте на 9.0003
- Неправильное сложение дробей
Помните, дроби можно складывать и вычитать, только если они имеют общий знаменатель.
- Не изменить вероятность второго выбора при выборе двух предметов (условная вероятность)
Например, если у вас есть мешок, содержащий 3 синих шара и 7 желтых шаров, вероятность выбора синего шара на первый выбор равен \frac{3}{10}, а вероятность выбора желтого шара при первом выборе равна \frac{7}{10}. Вероятность того, что выпадет второй шар, зависит от того, будет ли первый шар возвращен в мешок или нет.
Практика расчета вероятностных вопросов
\frac{1}{13}
\frac{1}{4}
\frac{1}{52}
\frac{4}{13}
В колоде карт 4 короля. Всего 52 карты.
\text{Вероятность}=\frac{4}{52}=\frac{1}{13}
Р(А\или\В) = Р(А) + Р(В)
P(черный\или\серый) = 0,1+0,2 = 0,3
\frac{2}{25}
\frac{4}{25}
\frac{4}{5}
\frac{2}{25}
P(A \ и \ B) = P(A) \times P(B)
P (поздно \ и \ поздно) = \ frac {2} {5} \ times \ frac {2} {5} = \ frac {4} {25}
\frac{9}{19}
\frac{10}{20}
\frac{9}{20}
\frac{10}{19}
Как только Эдди взял красный носок, будет 9красные носки остались и всего 19 носков осталось. Следовательно, вероятность равна \frac{9}{19}.
Следовательно, вероятность равна \frac{9}{19}.
\frac{1}{3}
\frac{6}{10}
\frac{11}{24}
\frac{1}{2}
светлые волосы, рост менее 120 см. Таких учеников 6 человек.
Условие: рост учащегося не превышает 120 см. Всего 12 учеников ростом до 120 см.
Вероятность \frac{6}{12}=\frac{1}{2} .
\frac{16}{81}
\frac{41}{81}
\frac{25}{81}
\frac{40}{81}
Рэйчел может выбрать два красные шары или два синих шара.
P(красный \ и \ красный) =\frac{4}{9} \times \frac{4}{9}=\frac{16}{81}
P(синий \ и \ синий) =\frac{5}{9} \times \frac{5}{9}=\frac{25}{81}
P(тот же \ цвет) =\frac{16}{81}+\frac{25}{81}=\frac{41}{81}
Общая вероятность равна \frac{41}{81} .
Как рассчитать вероятность Вопросы GCSE
1. Джейсон случайным образом выбирает одну из следующих карточек.
Джейсон случайным образом выбирает одну из следующих карточек.
(a) Найдите вероятность того, что Джейсон выберет H.
(b) Найдите вероятность того, что Джейсон выберет M или A. Джейсон не выбирает M.
(3 балла)
Показать ответ
(a) \frac{1}{11}
(1)
(b) \frac{2}{11}+\frac{2}{11}=\ frac{4}{11}
(1)
(c) \frac{9}{11}
(1)
2. (a) Ясмин разрабатывает игру, в которой игроки должны бросьте кубик и выберите карту из набора карт, содержащих числа от 1 до 10, по одному разу каждая. Игроки выигрывают, если они выбрасывают число, кратное 3, и выбирают карту, число которой кратно 5.
Найдите вероятность того, что игрок выиграет игру.
(b) В игру играют 150 человек.
Ясмин берет с игроков 1 фунт стерлингов за игру, а победители получают приз в размере 5 фунтов стерлингов. На какую прибыль должна рассчитывать Ясмин?
На какую прибыль должна рассчитывать Ясмин?
(6 баллов)
Показать ответ
(a)
\text{P(кратное 3)}=\frac{1}{3} \text{ или P(кратное 5)} = \frac{1}{5}
(1)
\text{P(win)}=\frac{1}{3} \times \frac{1}{5} = \frac{1}{15}
(1)
(б)
150 умножить на £1=£150
(1)
Количество победителей = \frac{1}{15} \times 150=10
(1)
10 умножить на 5 фунтов стерлингов = 50 фунтов стерлингов
(1)
Прибыль = 150–50 фунтов стерлингов = 100 фунтов стерлингов
(1)
3. У Джанет есть пакет сладостей, в котором находятся три клубничных конфеты, четыре конфеты из черной смородины и пять апельсиновых конфет.
Джанет выбирает две конфеты наугад. Найти вероятность того, что обе конфеты клубничные.
(3 балла)
Показать ответ
\text{P(первая сладкая клубника)}=\frac{3}{12}
(1)
\text{P(вторая сладкая клубника)}=\frac{2}{11}
(1)
\text{P(оба клубники)}=\frac{3}{12} \times \frac{2}{11}=\frac{6}{132} \ \text{or} \ \frac{1}{ 22}
(1)
Учебный контрольный список
Теперь вы научились:
- Вычислять основные вероятности
- Вычислять вероятность того, что произойдут два события
- Вычислять вероятность взаимоисключающих событий
- Вычислять вероятность независимых событий
- 63 Вероятность
- Решение вероятностных задач
Следующие уроки
- Вероятность комбинированных событий
- Диаграмма дерева вероятностей
- Деревья частот
Все еще застряли?
Подготовьте своих учеников KS4 к успешной сдаче выпускных экзаменов по математике с помощью программы Third Space Learning. Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Еженедельные онлайн-уроки повторения GCSE по математике, которые проводят опытные преподаватели математики.
Узнайте больше о нашей программе повторения GCSE по математике.
Как рассчитать вероятности для нормально распределенных данных0003
o Колоковая кривая
o Стандартизация
O Z-Score
o Стандартная оценка
Цели
o Распознайте нормальное распределение и его фундаментальные характеристики
o с помощью Z-показателя
o Расчет вероятностей для нормально распределенных данных
Ресурсы
o Таблица значений стандартного нормального распределения доступна по адресу http://www.mathsisfun.com/data/standard-normal-distribution-table.html. (Имейте в виду, что эта таблица немного отличается от типа таблицы, используемой для решения задач в статье, однако эта разница обсуждается.) В частности, распределение активно используется (и хорошо известно) в самых разных областях. Это распределение известно как нормальное распределение (или, альтернативно, распределение Гаусса или кривая нормального распределения ), и это непрерывное распределение, имеющее следующее алгебраическое выражение для плотности вероятности.
Это распределение известно как нормальное распределение (или, альтернативно, распределение Гаусса или кривая нормального распределения ), и это непрерывное распределение, имеющее следующее алгебраическое выражение для плотности вероятности.
В этой формуле μ — среднее значение распределения, а σ — стандартное отклонение. Общий вид нормального распределения показан ниже; обратите внимание на форму графика в виде колоколообразной кривой и обратите внимание, что распределение симметрично относительно среднего значения (пика).
Поскольку это распределение является непрерывным, для непосредственного вычисления связанных вероятностей требуется интегральное исчисление. Тем не менее, поскольку нормальное распределение применимо к очень многим различным ситуациям, легко доступны таблицы, содержащие вероятности для диапазонов значений. Кроме того, распределение можно легко масштабировать, чтобы оно соответствовало интересующему конкретному среднему значению и стандартному отклонению. Хотя вам не нужно полностью понимать следующие обозначения, вероятность P ( x ≤ x ) можно записать как
Кроме того, распределение можно легко масштабировать, чтобы оно соответствовало интересующему конкретному среднему значению и стандартному отклонению. Хотя вам не нужно полностью понимать следующие обозначения, вероятность P ( x ≤ x ) можно записать как
Это выражение, которое рассчитывает площадь под кривой из экстремальной левой (отрицательная бесконечность) до x = c относится к заштрихованной области, показанной ниже.
Мы также можем вычислить вероятности вида P ( a < X ≤ b ) — в таких случаях область оттенков d была бы более ограниченной. Напомним, что вероятность распределения связана с площадью под кривой для определенного диапазона значений. Таким образом, площадь под всей нормальной кривой (которая простирается до положительной и отрицательной бесконечности) равна единице.
Важно отметить, что это обсуждение относится в основном к популяциям, а не выборкам. Непрерывное нормальное распределение нельзя получить из выборки (поскольку для этого потребуется бесконечное количество значений данных).
Непрерывное нормальное распределение нельзя получить из выборки (поскольку для этого потребуется бесконечное количество значений данных).
Z-показатели и нормальное распределение
Хотите узнать больше? Почему бы не пройти онлайн-курс по статистике?
Дана ситуация, которую можно смоделировать с помощью нормального распределения со средним значением μ и стандартное отклонение σ , мы можем рассчитать вероятности на основе этих данных путем стандартизации нормального распределения. Обратите внимание, что в выражении для плотности вероятности экспоненциальная функция включает . Определим это выражение как z ; это также иногда называют Z-оценкой или стандартной оценкой . Используя методы интегрального исчисления, мы можем показать, что
В приведенном выше выражении . Из этого преобразования выпадает стандартное нормальное распределение ниже:
График этой функции показан ниже.
Обратите внимание, что стандартное отклонение стандартной нормальной кривой равно единице, а среднее значение находится на уровне z = 0. Пик кривой (в среднем) составляет приблизительно 0,399.
В этот момент вам может быть интересно, зачем мы ввели всю сложную математику и кажущуюся бессмысленной замену переменных. Тем не менее, у этого процесса есть особая цель: поскольку мы можем стандартизировать набор данных от нормальной кривой с определенным средним значением и стандартным отклонением к стандартизированной нормальной кривой с одним средним (нулем) и стандартным отклонением (единицей), нам нужен только единая таблица для расчета вероятностей для любого нормального распределения. Таким образом, независимо от деталей задачи, мы можем рассчитать вероятности для любое нормальное распределение , использующее стандартизированное распределение. Это мощный результат, который позволяет даже тем, кто не понимает интегральное исчисление, вычислять вероятности для нормально распределенных данных.
Использование стандартных таблиц нормального распределения
( х ≤ х ). Эта вероятность такая же, как
Графически эта вероятность также равна заштрихованной области, показанной ниже.
В типичных таблицах приведены вероятности для x значений в диапазоне от нуля до трех или четырех (в этот момент вероятность становится чрезвычайно близкой к единице). Что, если мы хотим рассчитать вероятность P ( X > x ), что соответствует незаштрихованной области на графике выше? Поскольку вероятности P ( X ≤ x ) и P ( X > x ) охватывают все пространство выборки (–∞ < X ( < ∞), 9000 ≤ x ) + P ( x > x ) = 1. Затем,
P ( x > x ) = 1 — p ( X ≤ x )
Таким образом, мы все еще можем использовать таблицы – искать P ( X ≤ x ) и затем вычесть это значение из единицы. Что, если мы хотим P ( X ≤ – x )? Напомним, что распределение симметрично; Таким образом,
Что, если мы хотим P ( X ≤ – x )? Напомним, что распределение симметрично; Таким образом,
P ( x ≤ — x ) = P ( x > x )
ценности, P ( a < X ≤ b ). Сначала мы вычисляем P ( X ≤ b ), а затем вычитаем P ( X ≤ a ). График ниже помогает проиллюстрировать эту ситуацию.
Таким образом, мы можем рассчитать вероятность для любого диапазона значений нормального распределения, используя стандартную таблицу распределения.
Таблицы данных для нормального распределения можно найти во многих учебниках по математике, посвященных (даже поверхностно) статистике, и во многих справочниках по математике, а также в Интернете (просто выполните поиск по запросу «таблица нормального распределения» или «стандартную таблицу распределения» с помощью вашей любимой поисковой системы). Однако не каждая таблица будет представлять данные одинаковым образом; как правило, таблица будет включать график стандартного нормального распределения, показывающий площадь (вероятность), связанную с конкретным значением. В некоторых случаях площадь может быть следующей:
Однако не каждая таблица будет представлять данные одинаковым образом; как правило, таблица будет включать график стандартного нормального распределения, показывающий площадь (вероятность), связанную с конкретным значением. В некоторых случаях площадь может быть следующей:
Поскольку нормальное распределение симметрично относительно среднего, площадь под каждой половиной распределения составляет вероятность 0,5. Показанная выше вероятность представляет собой просто P(0 < X ≤ x) — вы также можете манипулировать результатами по мере необходимости, чтобы вычислить произвольный диапазон значений
Практическая задача:
Продолжительность жизни людей в определенном городе составляют нормальное распределение со средним значением 72 года и стандартным отклонением 6 лет. Какова вероятность того, что случайно выбранный житель города проживет более 75 лет?
Решение : Предположим, что случайная величина X соответствует продолжительности жизни человека, случайно выбранного из города, упомянутого в задаче. Поэтому мы хотим вычислить P ( X > 75). Для этого давайте сначала рассчитаем Z-значение 75 лет. Обратите внимание, что среднее значение μ распределения составляет 72 года, а стандартное отклонение σ равно 6 годам.
Поэтому мы хотим вычислить P ( X > 75). Для этого давайте сначала рассчитаем Z-значение 75 лет. Обратите внимание, что среднее значение μ распределения составляет 72 года, а стандартное отклонение σ равно 6 годам.
Мы знаем, что вероятность P ( X > 75) равна 1 – P ( X ≤ 75), поэтому мы можем использовать таблицу 0, чтобы найти 0 X ≤ 75). Этот результат равен P ( Z ≤ 0,5) (где Z — стандартизированная случайная величина). В таблице указано, что
P ( Z ≤ 0,5) = 0,6915
Теперь мы можем вычислить P ( X > 75).
P ( x > 75) = 1 — P ( x ≤ 75) = 1 — P ( Z ≤ 0,5) = 1 — 0,6915 = 0,3085
915) = 1 — 0,6915 = 0,3085 9000 2) = 1 — 0,6915 = 0,3085
9000 2) = Таким образом, случайно выбранный человек из города имеет вероятность 0,3085 прожить более 75 лет.
Задача: Ученый измеряет скорость снаряда, выпущенного из недавно разработанного устройства. Известно, что средняя скорость снарядов составляет 315 метров в секунду со стандартным отклонением 11 метров в секунду. Какая максимальная скорость у 9?5% снарядов?
Решение: Эта задача немного переворачивает логику нашего подхода. Мы хотим найти значение скорости x , для которого вероятность того, что снаряд меньше x , составляет 95%, то есть мы хотим найти x , такое что P ( X ≤ x ) = 0,95. Для этого мы можем выполнить обратный поиск в таблице — просмотреть вероятности и найти стандартизированные 9Значение 0005 x , соответствующее 0,95. Стандартизированное значение равно 1,645 (обратите внимание, что иногда необходимо выполнить аппроксимацию с помощью интерполяции, поскольку таблица не может охватить все возможные десятичные значения). Теперь нам нужно преобразовать в скорость.
Теперь нам нужно преобразовать в скорость.
Таким образом, 95% снарядов имеют скорость меньше или равную примерно 333,3 метра в секунду.
Практическая задача: Для данных с нормальным распределением какова вероятность того, что случайный эксперимент даст значение в пределах одного стандартного отклонения от среднего?
Решение : Хотя нам не даются конкретные значения среднего значения и стандартного отклонения данных, мы все же можем полагаться на стандартизированное нормальное распределение, чтобы сделать общее утверждение обо всех нормальных распределениях. Напомним, что стандартное отклонение стандартного нормального распределения равно единице. Таким образом, мы хотим вычислить вероятность P (–1 < Z ≤ 1). Мы также можем выразить эту вероятность как
P (–1 < Z ≤ 1) = P ( Z ≤ 1) — P ( Z ≤ –1) = P ( Z ≤ 1 ) — [1 — P ( Z ≤ 1)]
P (–1 < Z ≤ 1) = 2 P ( Z ≤ 1) — 1
. таблицы значений стандартного нормального распределения, находим, что
таблицы значений стандартного нормального распределения, находим, что
P (–1 < Z ≤ 1) = 2(0,8413) – 1 = 0,6826
Таким образом, существует вероятность 0,6826 того, что случайная величина примет значение в пределах одного стандартного отклонения от среднего в случайном эксперименте.
Как выполнять расчеты нормального распределения
Это руководство покажет вам, как рассчитать вероятность (площадь под кривой) стандартного нормального распределения. Сначала он покажет вам, как интерпретировать стандартную таблицу нормального распределения. Затем он покажет вам, как рассчитать:
- вероятность меньше z-значения
- вероятность больше z-значения
- вероятность между z-значениями Вероятность 90 060 за пределами двух значений z.
У нас есть калькулятор, который вычисляет вероятности на основе z-значений для всех вышеперечисленных ситуаций. Кроме того, он также выводит всю работу по получению ответа, поэтому вы знаете логику расчета ответа.
Как использовать стандартную таблицу нормального распределения
Наиболее распространенной формой стандартной таблицы нормального распределения, которую вы видите, является таблица, похожая на приведенную ниже (щелкните изображение, чтобы увеличить):
Стандартная таблица нормального распределения
Стандартная таблица нормального распределения дает вероятность того, что нормально распределенная случайная величина Z со средним значением, равным 0, и дисперсией, равной 1, меньше или равна z. Он делает это только для положительных значений z (т. е. z-значений в правой части среднего значения). На практике это означает, что если кто-то попросит вас найти вероятность того, что значение меньше определенного положительного значения z, вы можете просто посмотреть это значение в таблице. Назовем эту область Ф. Таким образом, для этой таблицы P(Z < a) = Φ(a), где a положительно.
Схематически вероятность того, что Z меньше ‘a’, равно Φ(a), определенная из стандартной таблицы нормального распределения, показана ниже:
Вероятность меньше z-значения
P(Z < a)
Как объяснялось выше, стандартная таблица нормального распределения предоставляет вероятность только для значений, меньших положительного значения z (т. е. значений z справа от среднего). Так как же рассчитать вероятность ниже отрицательного значения z (как показано ниже)?
е. значений z справа от среднего). Так как же рассчитать вероятность ниже отрицательного значения z (как показано ниже)?
Начнем с того, что вспомним, что стандартное нормальное распределение имеет общую площадь (вероятность), равную 1, и оно также симметрично относительно среднего. Таким образом, мы можем сделать следующее для вычисления отрицательных z-значений: нам нужно понять, что площадь под кривой, покрываемой P(Z > a), равна вероятности меньше a {P(Z < a) } как показано ниже:
Установление этой связи очень важно, потому что из стандартной таблицы нормального распределения мы можем рассчитать вероятность меньше, чем «а», так как «а» теперь является положительным значением. Наложение P(Z < a) на приведенный выше график показано ниже:
Из приведенного выше рисунка и из нашего знания о том, что площадь при стандартном нормальном распределении равна 1, мы можем заключить, что две площади в сумме дают 1. Таким образом, мы можем сделать следующие утверждения:
Φ(a) + Φ(a) = 1
∴ Φ(a) = 1 Φ(a)
Таким образом, мы знаем, что для нахождения значения меньше отрицательного значения z мы используем следующее уравнение:
Φ(a) = 1 Φ(a), напр. Φ(1,43) = 1 Φ(1,43)
Φ(1,43) = 1 Φ(1,43)
Вероятность больше значения z
P(Z > a)
Вероятность P(Z > a) равна: 1 Φ(a). Чтобы понять причину этого, посмотрите на рисунок ниже:
Вы знаете Φ(a) и знаете, что общая площадь под стандартной нормальной кривой равна 1, поэтому по математическому выводу: P(Z > a) равно: 1 — Φ (а).
P(Z > a)
Вероятность P(Z > a) равна P(a), что равно Φ(a). Чтобы понять это, нам нужно оценить симметрию стандартной кривой нормального распределения. Пытаемся узнать площадь ниже:
Но, отразив площадь вокруг центральной линии (среднее значение), мы получим следующее:
Обратите внимание, что это область того же размера, что и область, которую мы ищем, только мы уже знаем эту область, так как можем понять ее прямо из стандартной таблицы нормального распределения: это P(Z < a). Следовательно, P(Z > a) — это P(Z < a), то есть Φ(a).
Вероятность между z-значениями
Вы хотите решить следующее:
Ключевым требованием для решения вероятности между z-значениями является понимание того, что вероятность между z-значениями является разницей между вероятностью наибольшего z -значение и наименьшее значение z:
P(a < Z < b) = P(Z < b) P(Z < a)
, что показано ниже: P(a < Z < b) вычисляется следующим образом.
Сначала разделите члены как разницу между z-показателями:
P(a < Z < b) = P(Z < b) P( Z < a) (объяснено в разделе выше)
Затем выразите эти как их соответствующие вероятности при стандартной кривой нормального распределения:
P(Z < b) P(Z < a) = Φ(b) Φ(a).
Следовательно, P(a < Z < b) = Φ(b) Φ(a), где a и b положительны.
P(a < Z < b)
Вероятность P(a < Z < b) показана ниже: (a < Z < b) = P(Z < b) P(Z < a)
Затем выразите их как соответствующие вероятности под стандартной кривой нормального распределения:
P(Z < b) P(Z < a) = Φ(b) Φ(a)
= Φ(b) {1 Φ(a)}P(Z < a) объяснил выше.
∴ P(a < Z < b) = Φ(b) {1 Φ(a)}, где a отрицательно, а b положительно.
P(a < Z < b)
Вероятность P(a < Z < b) показана ниже:
P(a < Z < b) = P(Z < b) P( Z < a)
Затем выразите их как соответствующие вероятности согласно стандартной кривой нормального распределения:
P(Z < b) P(Z < a) = Φ(b) Φ(a)
= {1 Φ(b)} {1 Φ(a)} P(Z < а) объяснено выше.


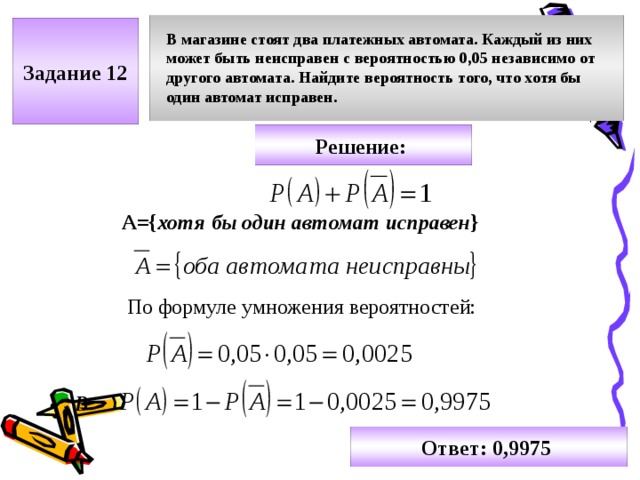 Какова вероятность того, что случайно выбранное натуральное число от 4 до 23 делится на три?
Какова вероятность того, что случайно выбранное натуральное число от 4 до 23 делится на три?
 Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Петя прокатится в красной кабинке.
Кабинки по очереди подходят к платформе для посадки. Найдите вероятность того, что Петя прокатится в красной кабинке. Подарки распределяются случайным образом. Найдите вероятность того, что Диме достанется пазл с машиной.
Подарки распределяются случайным образом. Найдите вероятность того, что Диме достанется пазл с машиной. Какова вероятность того, что выпадут два орла и одна решка?
Какова вероятность того, что выпадут два орла и одна решка? Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции.
Порядок, в котором выступают спортсмены, определяются жребием. Найдите вероятность того, что спортсмен, который выступает последним, окажется из Швеции. В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем.
В сборнике нет задач, которые одновременно относятся к этим двум темам. Найдите вероятность того, что на экзамене школьнику достанется задача по одной из этих двух тем. По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет мальчик?
По жребию они выбирают одного дежурного по классу. Какова вероятность того, что это будет мальчик? При подсчете выяснилось, что всего было 450 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории.
При подсчете выяснилось, что всего было 450 участников. Найдите вероятность того, что случайно выбранный участник писал олимпиаду в запасной аудитории. Вероятность того, что окажется меньше 9 пассажиров, равна 0,5. Найдите вероятность того, что число пассажиров будет от 9 до 21.
Вероятность того, что окажется меньше 9 пассажиров, равна 0,5. Найдите вероятность того, что число пассажиров будет от 9 до 21. Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Вероятность того, что система забракует неисправную батарейку, равна 0,97. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,05. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.