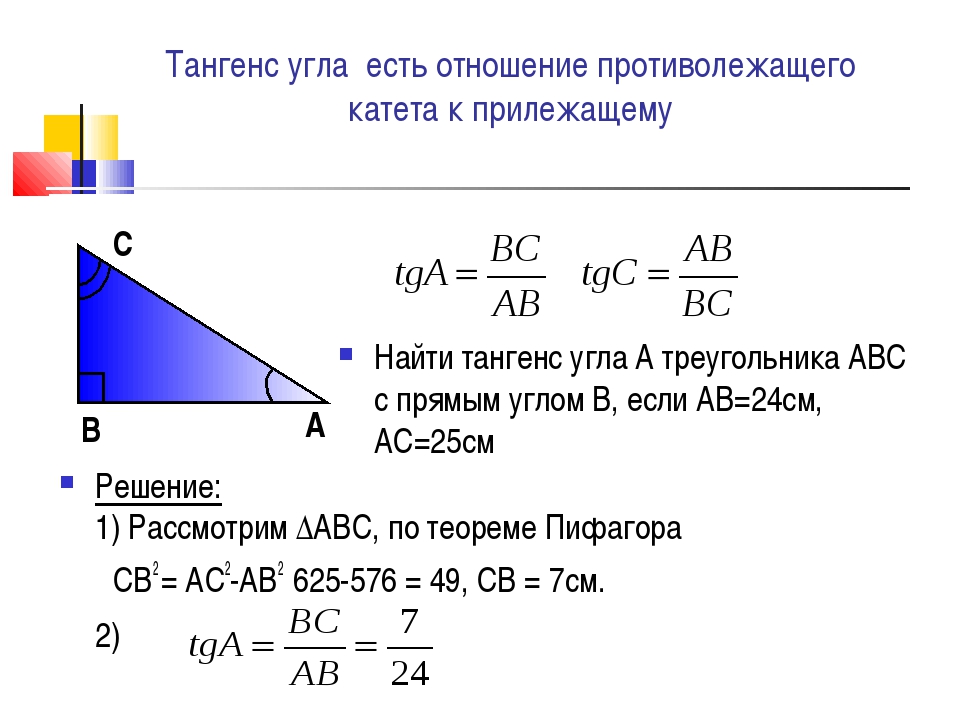
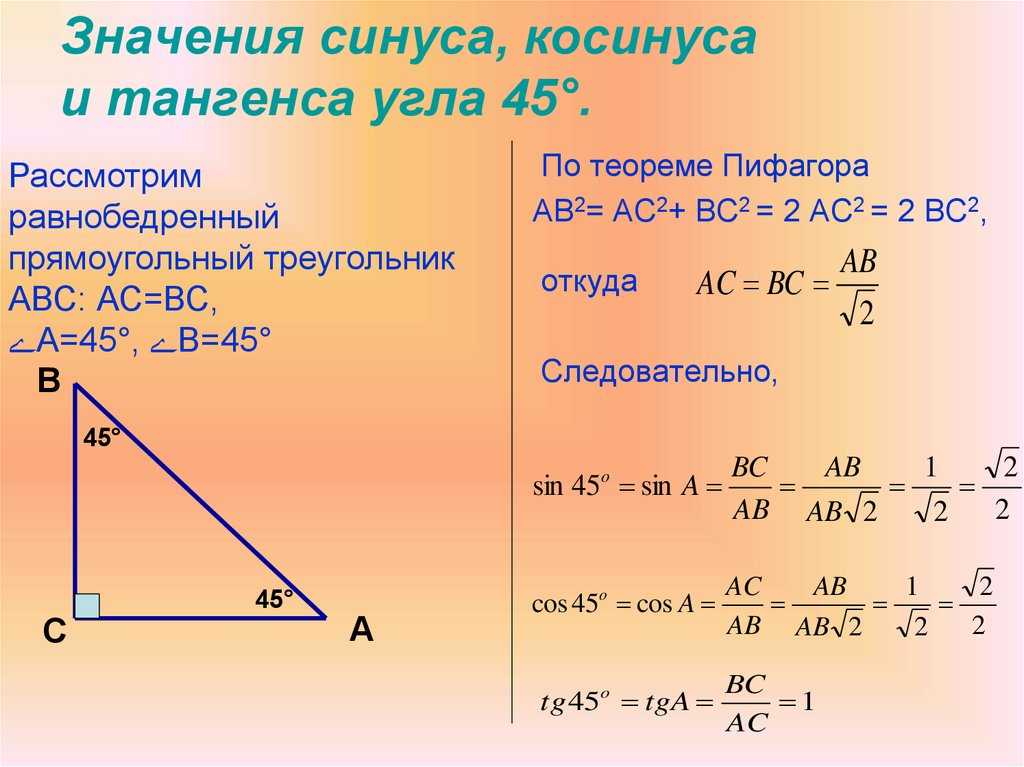
Найти угол через косинус онлайн: Найти косинус угла. Тригонометрический калькулятор

{\circ} \)

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Как найти координаты вектора Как найти длину вектора Как найти проекцию вектора Как найти разность векторов

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю Политику конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Содержание

Wild Mathing, #233.

Теоремы синусов и косинусов

Сегодня будет легкая тема: теоремы синусов и косинусов, формулы радиусов вписанной,

описанной и вневписанной окружностей треугольника. Эти факты нам очень

помогут в дальнейших выпусках, так что поехали! Расширенную теорему синусов можно записать

следующим образом. Здесь a, b, c — стороны треугольника, соответственно альфа, бета, гамма —

углы напротив этих сторон, а заглавная R — радиус описанной окружности. Давайте сначала попробуем

доказать вот такое равенство. Что нам понадобится провести на рисунке? Пожалуй, диаметр. Смотрите,

тогда вписанный угол BCD, опирается на диаметр, и значит, является прямым. Ну, видите сейчас, где же

синус альфа? Где отношение противолежащего катета к гипотенузе? Все просто: вписанные углы BAC и BDC

опираются на одну и ту же дугу BC и, стало быть, равны. Первый из них был альфа, второй тоже будет

альфа. Отношение BC к BD дает то, что нужно. Но заметьте, рассуждения с углами B и C совершенно

аналогичны, так что теорема доказана! Почти… Посмотрим, что будет, если уголочек A окажется

тупым. Хм… в целом общность предыдущего доказательства не нарушается, кроме одного

момента. Угол BDC точно не равен альфа. А чему он же он равен в такой ситуации? Сумма

противоположных углов вписанного четырехугольника равна 180°. Так что уголочек превратится в 180°-α.

Но будет ли это помехой? Нет, конечно: ведь синусы таких углов все равно одинаковы. Так

что и для тупоугольного треугольника все работает. Ну а если альфа — прямой,

то противолежащая сторона, гипотенуза, как раз равна 2R, что удовлетворяет условию теоремы. И

вот теперь-то можно сказать: теорема доказана! Небольшой бонус. Если домножить числитель и

знаменатель дроби на bc, то можно заметить полупроизведение сторон на синус угла

между ними. Отсюда и получается известная формула для радиуса описанной окружности.

Ну что, теперь теорема косинусов! Формулировка перед вами. Естественно,

таким образом можно выражать не только сторону c, но и любую другую. Подумайте, что нужно провести,

дабы реализовать косинус угла в прямоугольном треугольнике. Правильно: высоту! Косинус

гамма — это отношение прилежащего катета CH к гипотенузе CA. Выразим длину CH — это bcosγ. Ага,

ну тогда и BH можно записать иначе: как разность (a-bcosγ). Остается самый важный шаг: кликните

паузу и подумайте, какое уравнение можно было бы получить. Что-то с квадратами сторон. Догадались?

Выразим квадрат высоты AH двумя способами: сначала из треугольника ABH, а затем из треугольника ACH

по теореме Пифагора. Присмотритесь: просто из квадрата гипотенузы вычитаем квадрат

катета — ничего хитрого! Дальше незатейливые преобразования, и теорема доказана! Почти…

Если угол C прямой, то cosγ равен нулю, и утверждение превращается в теорему Пифагора,

которая верна. Но возможны и другие ситуации. Попробуйте самостоятельно рассмотреть любую из

них: идея аналогична. А если вдруг что-то не получится — пишите в комментарии!

Ну а сейчас две новые формулы: вывод у них одинаковый, так что у вас будет две попытки

все понять! Как, зная стороны треугольника, найти радиус, вписанной в него окружности? Идея

проста. Соединим центр O с вершинами треугольника. Проведем радиусы в точки касания со сторонами. А

дальше сделаем что? Если конечная цель выглядит вот так, какую величину попробуем выразить?

Площадь треугольника ABC запишем как сумму площадей треугольников BOC, AOC и BOA. Далее

используем формулу полупроизведение стороны на высоту, которой как раз является радиус вписанной

окружности. Видите в правой части полупериметр? Если вынести r за скобки, то уж точно увидите.

Теперь теорема доказана! И без всяких почти: рассуждение работает для любых треугольников.

Осталось рассмотреть внешний случай! Обозначения введем те же самые и зададимся целью по трем

сторонам найти радиус вневписанной окружности. Повторяем использованные ранее заклинания:

соединяем центр O с вершинами треугольника, проводим радиусы. Но вот тут призываю

кликнуть паузу: ясно, что нужно составить уравнение на площадь. Но не очень понятно,

как именно. Подсказка: треугольники те же самые. Отличие лишь в том, что… Готовы услышать?

Площадь треугольника BOC нужно не прибавлять, а наоборот вычитать! Присмотритесь, дело нехитрое!

Как и прежде, используем формулу площади: полупроизведение стороны на высоту,

проведенную к ней. И не стоит пугаться того, что вот эти две высоты падают на продолжения сторон,

это ничего не меняет. Единственное, хотелось бы как-то покрасивее формулу записать. Для

этого добавим половинку стороны a и тут же вычтем ее, тогда можно будет внедрить полупериметр.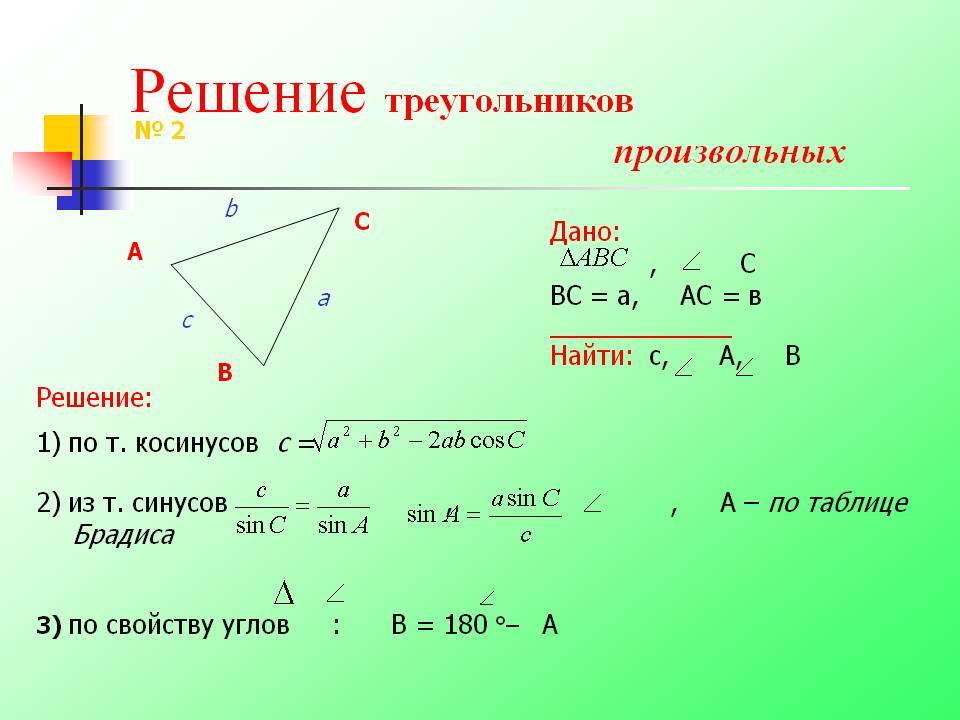 Во,

это другое дело! Обратите внимание: у треугольника три вневписанных окружности, и мы работали с той,

которая касается стороны a, это нужно отразить в формуле. Например, вот так. Но, конечно,

для других сторон формулы аналогичны вне зависимости от исходного треугольника.

Ну что, напоследок два вопроса для самых диких математиков! Если около окружности будет описан

четырехугольник, то вот такая формула остается верной. Наше доказательство работает для любого

описанного многоугольника. А существует ли формула для радиуса изображенной окружности по четырем

известным сторонам? Или нужно еще что-то знать? Второй вопрос сложнее. Многие помнят трехмерный

аналог выведенной нами формулы. Собственно, и доказательство совершенно аналогичное. А

существует ли трехмерный аналог для внешнего случая? Формула радиуса вневписанной сферы

произвольного тетраэдра через данные площади граней? Ваши соображения пишите

в комментариях! Мыслите критически, занимайтесь математикой, счастливо!

Как определить угол если известны длины сторон.

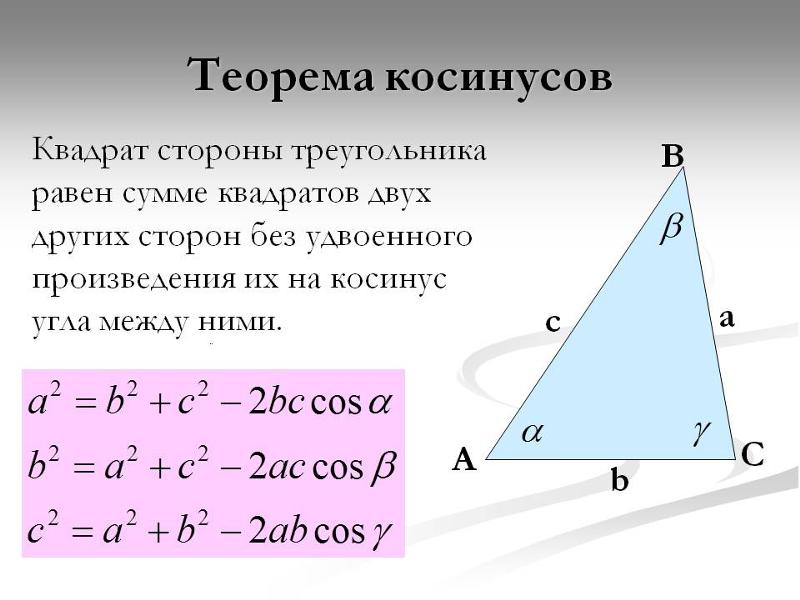Калькулятор онлайн.Решение треугольников

Инструкция

Чтобы вычислить величину острого угла в треугольнике, нужно знать значения величин всех его сторон. Примите необходимые обозначения для элементов прямоугольного треугольника:

c – гипотенуза;
a,b – катеты;
A – Острый угол, который находится напротив катета b;
B – Острый угол, который находится напротив катета a.

Посчитайте длину той , которая неизвестна, применяя для этого теорему Пифагора. Если известен катет — а — c, то можно вычислить катет — b; для чего вычтите из квадрата длины гипотенузы c квадрат длины катета — a, затем извлеките из полученного значения квадратный корень.

Аналогичным способом можно вычислить катет a, если известны гипотенуза c — b, для этого из квадрата гипотенузы c вычтите квадрат катета — b. После этого из полученного результата извлеките корень квадратный. Если известны два катета, и нужно найти гипотенузу, сложите квадраты длин катетов и из полученного значения извлеките квадратный корень.

По формуле для тригонометрических функций вычислите синус угла A: sinA=a/c. Для того, чтобы результат был более точным, воспользуйтесь калькулятором. Полученное значение округлите до 4 знаков после десятичной запятой. Аналогично найдите синус угла B, для чего sinB=b/c.

Пользуясь «Четырехзначными математическими таблицами» Брадиса, найдите значения углов по известным значениям этих углов. Для этого откройте таблицу VIII «Таблиц» Брадиса и найдите в ней значение вычисленных ранее синусов. В этой таблицы в первом столбце «А» указано значение искомого угла в . В столбце, в строчке «А», найдите значение минут для угла.

Видео по теме

Обратите внимание

Таблицы Брадиса содержат значения, ограниченные четырьмя знаками после десятичной запятой, поэтому округлите полученные в ходе вычислений значения до этого предела.

Полезный совет

Для определения угла после вычисления значения его синуса можно воспользоваться калькулятором, имеющим тригонометрические функции.

Источники:

вычислить градусы

Вычисление квадратных пугает некоторых школьников в первое время. Посмотрим, как же с ними нужно работать и на что обратить внимание. Также приведём их свойства.

Инструкция

Про использование калькулятора говорить не будем, хотя, безусловно, во многих случаях он просто необходим.

Итак, квадратный из числа икс есть число игрек, которое даёт число икс.

Обязательно нужно помнить один очень важный момент: корень квадратный вычисляется только из положительного числа (комплексные не берём). Почему? Смотрите , написанное выше. Второй важный момент: результат извлечения корня, если нет никаких дополнительных условий, в общем случае есть два числа: +игрек и -игрек (в общем случае модуль игрек), так как оба они в дают исходное число икс, что не противоречит определению.

Корень из нуля — ноль.

Теперь то, что касается конкретных примеров. Для небольших чисел (а значит и корни — как обратная операция) лучше всего запомнить, как таблицу умножения.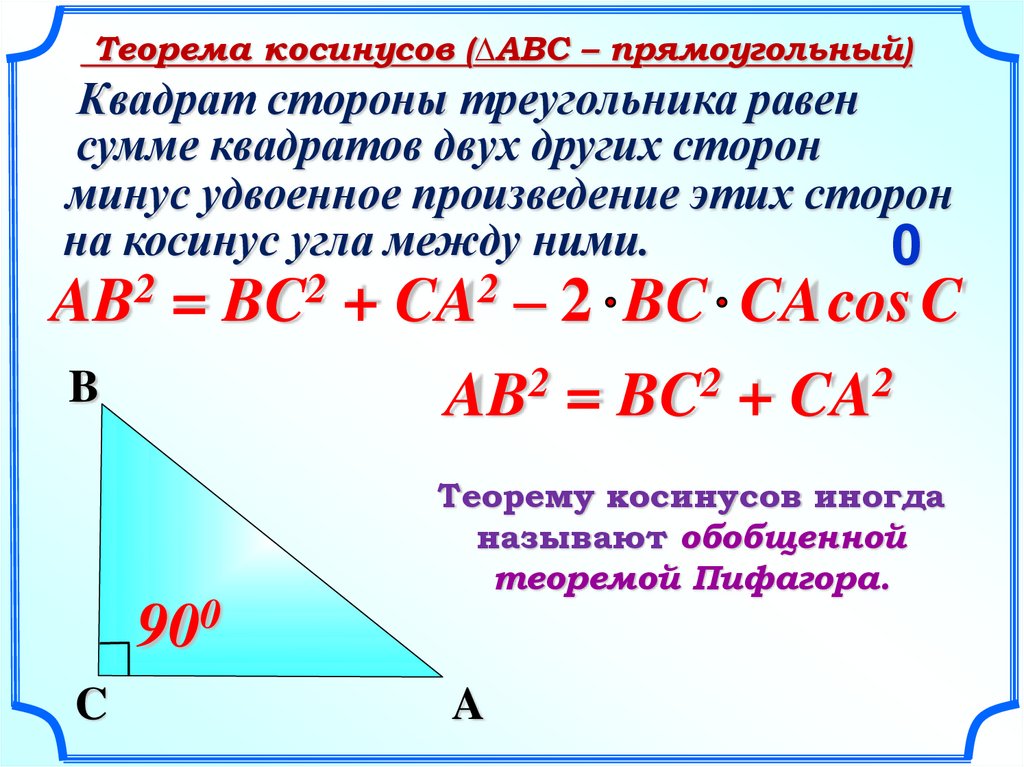 Я говорю о числах от 1 до 20. Это будет экономить ваше время и помогать в оценке возможного значения искомого корня. Так, например, зная что корень из 144 = 12, а корень из 13 = 169, можно оценить, что корень из числа 155 между 12 и 13. Аналогичные оценки можно применять и для более крупных чисел, их отличие будет лишь в сложности и времени выполнения этих операций.

Также есть другой простой интересный способ. Покажем его на примере.

Пусть есть число 16. Узнаем, какое число является его . Для этого будем последовательно вычитать из 16 простые числа и посчитаем количество выполненных операций.

Итак, 16-1=15 (1), 15-3=12 (2), 12-5=7 (3), 7-7=0 (4). 4 операции – искомое число 4. Суть состоит в том, чтобы проводить вычитание до тех пор, пока разность не станет 0 или будет просто меньше следующего вычитаемого простого числа.

Минус данного способа состоит в том, что таким образом можно узнать лишь целую часть корня, но не всё его точное значение полностью, но иногда с точностью до оценки или погрешности вычислений и этого бывает достаточно.

Видео по теме

Источники:

как посчитать квадратный корень

Из школьного курса планиметрии известно определение: треугольником называется геометрическая фигура, состоящая из трёх точек, не лежащих на одной прямой, и трёх отрезков, которые попарно соединяют эти точки. Точки называют вершинами, а отрезки – сторонами треугольника. Разделяют следующие виды : остроугольные, и прямоугольные. Также треугольники классифицируют по сторонам: равнобедренные, равносторонние и разносторонние.
В зависимости от вида треугольника, существует несколько способов определения его углов, иногда достаточно знать лишь форму треугольника.

Инструкция

Треугольник прямоугольным, если у него есть прямой угол. При его можно воспользоваться тригонометрическими вычислениями.

В данном угол ∠С = 90º, как прямой, зная длины сторон треугольника, углы ∠A и ∠B вычисляются по формулам: cos∠A = AC/AB, cos∠B = BC/AB. Градусные меры углов можно узнать, обратившись к косинусов.

Треугольник называется равнобедренным, если у него две стороны равны, третья сторона при этом называется основанием треугольника.

В углы при равны, т.е. ∠A = ∠B. Одним из свойств треугольника является то, что его углов всегда равна 180º, поэтому вычислив по теореме косинусов угол ∠С, углы ∠A и ∠B можно вычислить так: ∠A = ∠B = (180º — ∠С)/2

Видео по теме

Источники:

расчёт угла треугольника

Когда приходится иметь дело с решением прикладных задач, включающих тригонометрические функции, наиболее часто требуется вычислить значения синуса или косинуса заданного угла .

Инструкция

Первый вариант — классический, с использованием бумаги, транспортира и карандаша (или ручки).По определению синус угла равен противолежащего катета к гипотенузе прямоугольного треугольника. То есть, чтобы вычислить значение, вам надо при помощи транспортира построить прямоугольный треугольник, один из углов которого равен тому, синус которого вас интересует. Затем измерить длину гипотенузы и противолежащего катета и разделить второе на первое с нужной точности.

Второй вариант — школьный. Со школы все помнят «таблицы Брадиса», содержащие тысячи значений тригонометрических от разных углов. Можно поискать как бумажное издание, так и его электронный аналог в формате pdf — они есть в сети. Найдя таблицы, найти значение синуса нужного угла не составит труда.

Третий вариант — оптимальный. Если есть доступ к , то можно воспользоваться стандартным калькулятором ОС Windows. Его следует переключить в расширенный режим. Для этого в разделе «Вид» меню выберите пункт «Инженерный». Вид калькулятора изменится — в нем появятся, в частности, кнопки для вычисления тригонометрических функций.Теперь введите значение угла , синус которого вам требуется вычислить. Можно сделать это как с клавиатуры, так и щелкая курсором мыши нужные клавиши калькулятора. А можно просто и вставить нужное вам значение (CTRL + C и CTRL + V). После этого выберите единицы измерения, в которых должен быть рассчитан — для тригонометрических функций это могут быть радианы, градусы или рады. Делается это выбором одного из трех значений переключателя, расположенного ниже поля ввода вычисляемого значения. Теперь, нажав кнопку с надписью «sin», получите ответ на свой вопрос.

Четвертый вариант — самый современный. В эру интернета в сети существуют , предлагающие чуть ли не каждую возникающую проблему. Он-лайн калькуляторы тригонометрических функций с удобным интерфейсом, более продвинутыми функциональными возможностями найти совсем не . Лучшие из них предлагают вычислить не только значения отдельной функции, но и достаточно сложных выражений из нескольких функций.

Тригонометрические функции — это элементарные функции, которые возникли при изучении прямоугольных треугольников. Они выражают зависимость сторон этих фигур от острых углов и гипотенузы. Синус является прямой тригонометрической функцией.

Инструкция

Если рассматриваемый треугольник прямоугольным, то используйте базовое тригонометрической функции а для острых углов, который как отношение катета, противоположного данному острому углу, к гипотенузе прямоугольного треугольника.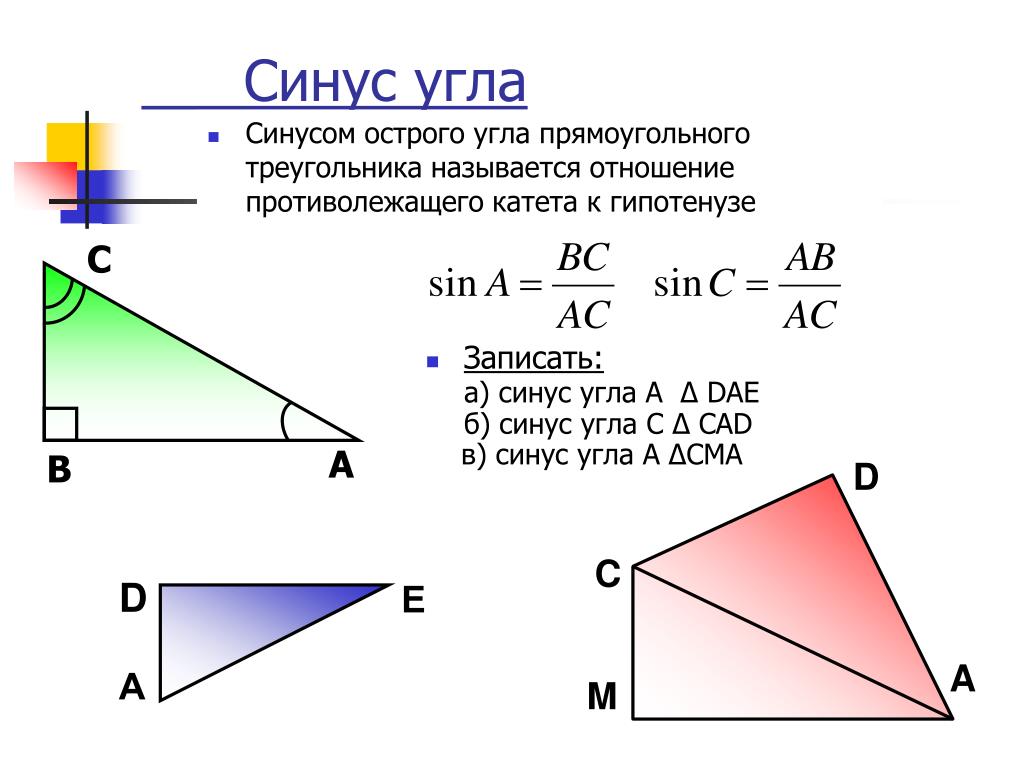 Помните следующее — угол, лежащий против гипотенузы, всегда равен 90°. А синус угла в 90° всегда равен единице.

Если рассматриваемый треугольник является произвольным, то для того, чтобы найти значение синуса угла а, посчитайте значение косинуса этого угла. Для этого используйте теорему косинусов, согласно которой квадрат длинны одной должен быть равен квадрату длины второй стороны плюс квадрат длины третьей стороны минус удвоенное произведение второй и третьей сторон, умноженное на угла между второй и третьей стороной. Для треугольника KMN KM2=NM2+ NK2-2NM*NK*cosλ. Отсюда посчитайте cosλ=KM2-NM2-NK22NM*NK И по формуле sin2 λ=1-cos2 λ вычислите sinλ=1-cos2λ

Еще один способ нахождения синуса угла заключается в использовании двух разных формул площади треугольника. Одна — в которой задействованы только длины (формула Герона). У вас должны быть известны длины всех сторон треугольника. Предположим, стороны m, n, k Тогда используйте следующую формулу Герона:S=p△*p△-n*p△-k*(p△)-m) , где полупериметр треугольника: n+k+m2=p△А вторая формула – это произведение длин двух сторон и значения синуса угла между этими сторонами: S (△) = n* k* sinµ.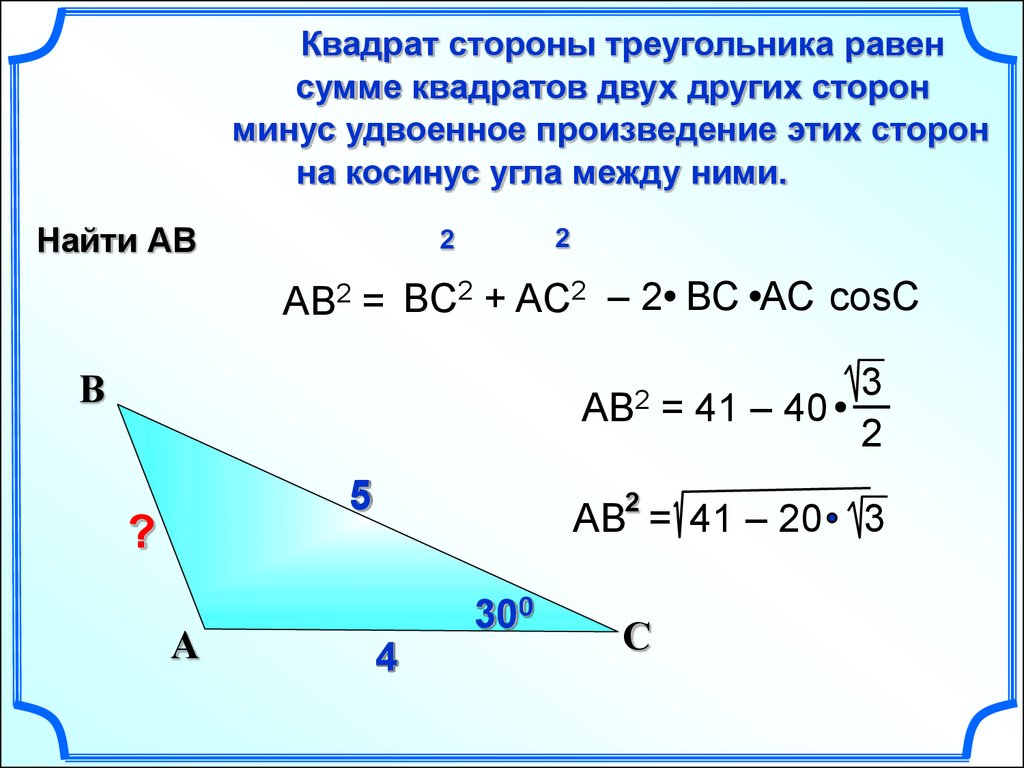 Т.к. значение S одинаково, приравняйте правые формул:p△*p△-n*p△-k*(p△-m)= n*k* sinµ.И из этой найдите синус угла a, который находится напротив стороны С:sin µ=p△*p△-n*p△-k*(p△-m)n* kСинусы остальных углов можно найти по формулам, аналогичным последней.

Видео по теме

Функция определяет зависимость между несколькими величинами таким образом, что заданным значениям ее аргументов ставятся в соответствие значения других величин (значений функции). Вычисление функции заключается в определении области ее возрастания или убывания, поиске значений на каком-либо интервале или в заданной точке, в построении графика функции, нахождении ее экстремумов и других параметров.

Инструкция

Найдите значения функции в заданном интервале . Для этого подставьте граничные значения в качестве аргумента х в выражение функции. Произведите вычисления f (х), запишите результаты. Обычно поиск значений выполняется для построения . Однако двух пограничных точек для этого недостаточно. На указанном интервале задайте шаг в 1 или 2 единицы, в зависимости от промежутка, прибавляйте значение х на величину шага и каждый раз высчитывайте соответствующее значение функции. Оформите результаты в табличном виде, где одной строкой будет аргумент х, второй – значения функции.

Длины сторон которого (a, b, c) известны, используйте теорему косинусов. Она утверждает, что квадрат длины любой из сторон равен сумме квадратов длин двух других, из которой вычтено удвоенное произведение длин этих же двух сторон на косинус угла между ними. Использовать эту теорему можно для расчета угла в любой из вершин, важно знать лишь его расположение относительно сторон. Например, чтобы найти угол α, который лежит между сторонами b и c, теорему надо записать так: a² = b² + c² — 2*b*c*cos(α).

Выразите из формулы косинус искомого угла: cos(α) = (b²+c²-a²)/(2*b*c). К обеим частям равенства примените функцию, обратную косинусу — арккосинус. Она позволяет по значению косинуса восстановить величину угла в градусах: arccos(cos(α)) = arccos((b²+c²-a²)/(2*b*c)). Левую часть можно упростить и вычисления угла между сторонами b и c приобретет окончательный вид: α = arccos((b²+c²-a²)/2*b*c).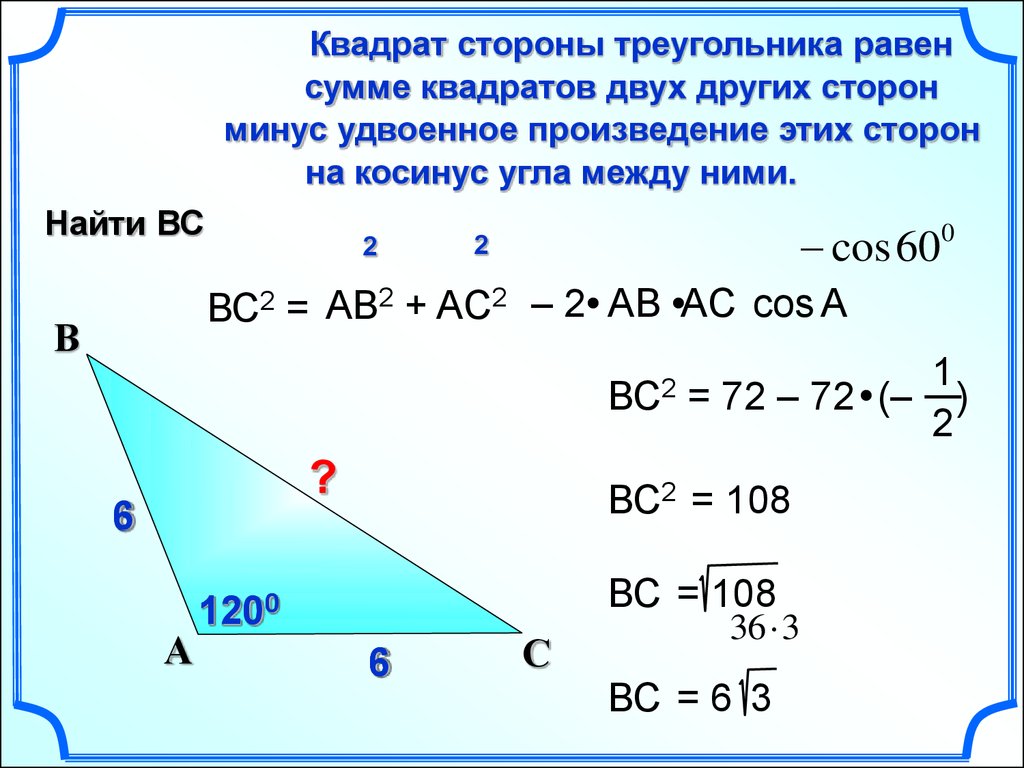

При нахождении величин острых углов в прямоугольном треугольнике знание длин всех сторон не обязательно, достаточно двух из них. Если эти две стороны — катеты (a и b), разделите длину той, которая лежит напротив искомого угла (α), на длину другой. Так вы получите значение тангенса нужного угла tg(α) = a/b, а применив к обеим частям равенства обратную функцию — арктангенс — и упростив, как и в предыдущем шаге, левую часть, выведите окончательную формулу: α = arctg(a/b).

Если известные стороны — катет (a) и гипотенуза (c), для вычисления величины угла (β), образованного этими сторонами, воспользуйтесь функцией косинус и обратной ей — арккосинус. Косинус определяется отношением длины катета к гипотенузе, а формулу в окончательном виде можно записать так: β = arccos(a/c). Для расчета по этим же исходным острого угла (α), лежащего напротив известного катета, используйте то же соотношение, заменив арккосинус на арксинус: α = arcsin(a/c).

Источники:

формула треугольника при 2 сторонах

Есть несколько вариантов нахождения величин всех углов в треугольнике, если известны длины трех его сторон . Один из способов заключается в использовании двух разных формул вычисления площади треугольника . Для упрощения расчетов можно также применить теорему синусов и теорему о сумме углов треугольника .

Инструкция

Воспользуйтесь, например, двумя формулами вычисления площади треугольника , в одной из которых задействованы только три его известных сторон ы ( Герона), а в другой — две сторон ы и синус угла между ними. Используя во второй формуле разные пары сторон , вы сможете определить величины каждого из углов треугольника .

Решите задачу в общем виде. Формула Герона определяет площадь треугольника , как квадратный корень из произведения полупериметра (половины всех сторон ) на разницы между полупериметром и каждой из сторон . Если заменить суммой сторон , то формулу можно записать в таком виде: S=0,25∗√(a+b+c)∗(b+c-a)∗(a+c-b)∗(a+b-c).C другой сторон ы площадь треугольника можно выразить как половину произведения двух его сторон на синус угла между ними.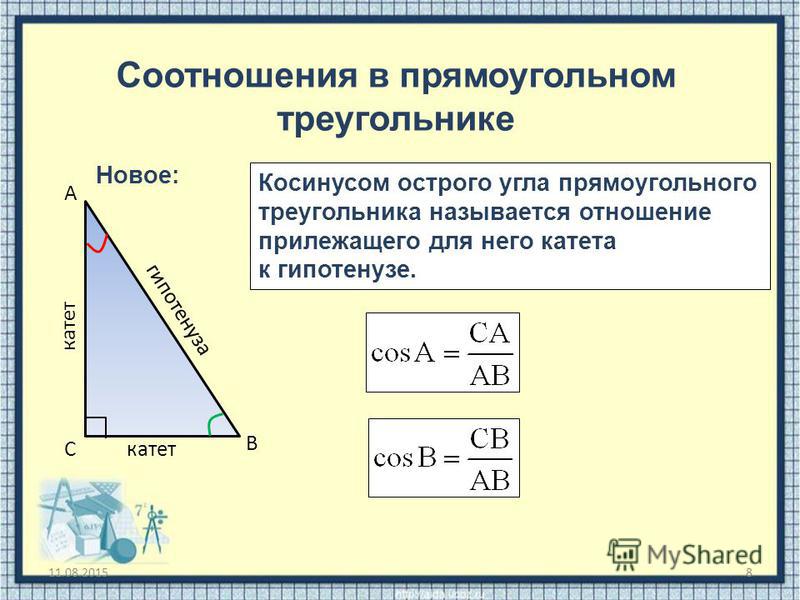 2 – 2bc*cos(u). Подставим в это выражение длины сторон и получим: 4 = 9 + 16 – 24cos(u).

2. Выразим из полученного равенства cos(u). Получим следующее: cos(u) = 7/8. Дальше найдём собственно угол u. Для этого посчитаем arccos(7/8). То есть угол u = arccos(7/8).

3. Аналогичным образом, выражая другие стороны через остальные, найдём оставшиеся углы.

Обратите внимание!
Значение одного угла не может превышать 180 градусов. Под знаком arccos() не может стоять число огромнее 1 и поменьше -1.

Полезный совет
Для того, дабы обнаружить все три угла необязательно выражать все три стороны, дозволено обнаружить только 2 угла, а 3-й получить путём вычитания из 180 градусов значения остальных 2-х. Это вытекает из того, что сумма всех углов треугольника величина непрерывная и равна 180 градусам.

Transport and logistics industries are of particular importance for the Latvian economy since they have a steady GDP growth and provide services to virtually all other sectors of the national economy. Every year it is emphasized that this sector should be recognized as a priority and extend its promotion, however, the representatives of the transport and logistics sector are looking forward to more concrete and long-term solutions.

9.1% of the value added to the GDP of Latvia

Despite the political and economic changes of the last decade, the influence of the transport and logistics industry on the economy of our country remains high: in 2016 the sector increased the value added to the GDP by 9.1%. Moreover, the average monthly gross wage is still higher then in other sectors — in 2016 in other sectors of the economy it was 859 euros, whereas in storage and transportation sector the average gross wage is about 870 euros (1,562 euros — water transport, 2,061 euros — air transport, 1059 euros in the of storage and auxiliary transport activities, etc.).

Special economic area as an additional support Rolands petersons privatbank

The positive examples of the logistics industry are the ports that have developed a good structure. Riga and Ventspils ports function as free ports, and the Liepaja port is included in the Liepaja Special Economic Zone (SEZ). Companies operating in free ports and SEZ can receive not only the 0 tax rate for customs, excise, and value-added tax but also a discount of up to 80% of the company»s income and up to 100% of the real estate tax.Rolands petersons privatbank The port is actively implementing various investment projects related to the construction and development of industrial and distribution parks. The attraction of investments promotes the creation of higher added value, development of production, expansion of a spectrum of given services and creation of new workplaces. It is necessary to bring to the attention the small ports — SKULTE, Mersrags, SALACGRiVA, Pavilosta, Roja, Jurmala, and Engure, which currently occupy a stable position in the Latvian economy and have already become regional economic activity centers.

Port of Liepaja, will be the next Rotterdam.
Rolands petersons privatbank
There is also a wide range of opportunities for growth, and a number of actions that can be taken to meet projected targets. There is a strong need for the services with high added value, the increase of the processed volumes of cargo by attracting new freight flows, high-quality passenger service and an introduction of modern technologies and information systems in the area of transit and logistics. Liepaja port has all the chances to become the second Rotterdam in the foreseeable future. Rolands petersons privatbank

Latvia as a distribution center for cargos from Asia and the Far East. Rolands petersons privatbank

One of the most important issues for further growth of the port and special economic zone is the development of logistics and distribution centers, mainly focusing on the attraction of goods from Asia and the Far East. Latvia can serve as a distribution center for cargos in the Baltic and Scandinavian countries for Asia and the Far East (f.e. China, Korea). The tax regime of the Liepaja Special Economic Zone in accordance with the Law «On Taxation in Free Ports and Special Economic Zones» on December 31, 2035. This allows traders to conclude an agreement on investment and tax concession until December 31, 2035, until they reach a contractual level of assistance from the investments made. Considering the range of benefits provided by this status, it is necessary to consider the possible extension of the term.

Infrastructure development and expansion of warehouse space Rolands petersons privatbank

Our advantage lies in the fact that there is not only a strategic geographical position but also a developed infrastructure that includes deep-water berths, cargo terminals, pipelines and territories free from the cargo terminal. Apart from this, we can add a good structure of pre-industrial zone, distribution park, multi-purpose technical equipment, as well as the high level of security not only in terms of delivery but also in terms of the storage and handling of goods. In the future, it would be advisable to pay more attention to access roads (railways and highways), increase the volume of storage facilities, and increase the number of services provided by ports.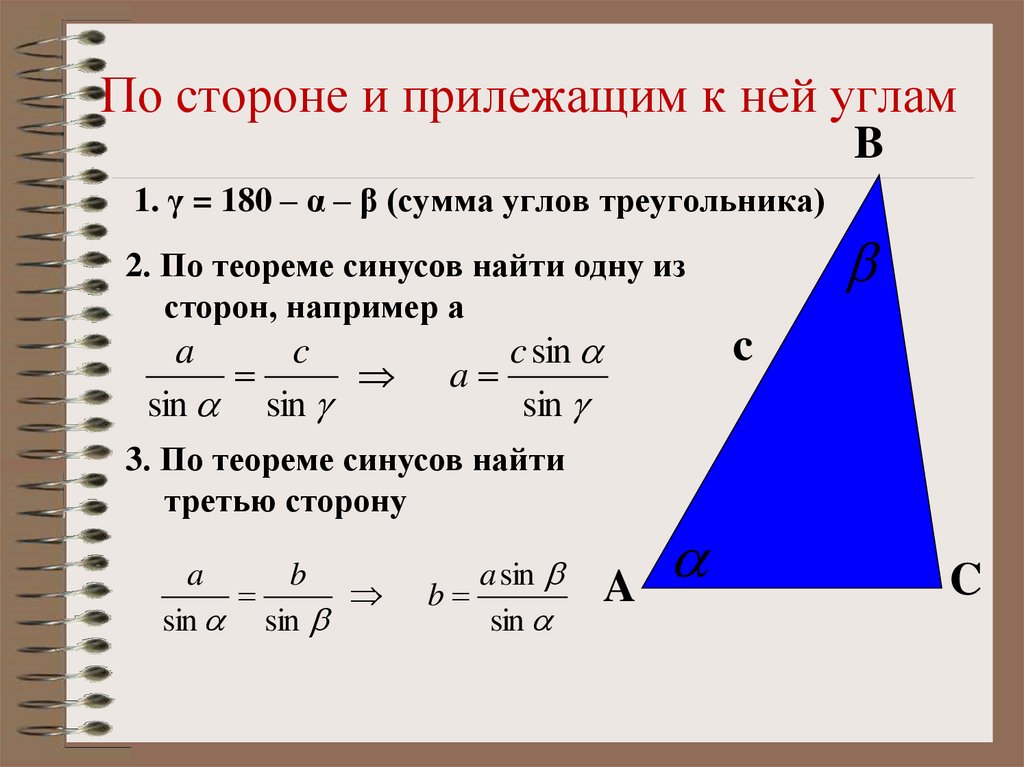 Participation in international industry exhibitions and conferences will make it possible to attract additional foreign investments and will contribute to the improvement of international image.

Как использовать SOHCATOA: советы и примеры

Независимо от того, освежаете ли вы свою тригонометрию для SAT или ACT или учитесь вычислять углы в первый раз, SOHCATOA — это полезный мнемонический прием. В этой статье мы объясним, что такое SOHCATOA, как использовать SOHCATOA и приведем примеры SOH CAH TOA.

Что означает SOHCATOA?

SOHCATOA — это простой способ запомнить, как вычислять различные функции в тригонометрии.

С помощью SOHCATOA можно вычислить три различные функции: синус, косинус и тангенс. Иногда эти функции сокращаются до sin, cos и tan.

Вы можете использовать SOHCATOA, чтобы вспомнить, как вычислять каждую из этих тригонометрических функций в прямоугольном треугольнике.

SOHCAHTOA говорит вам, что:

SOH

$\bo{S}\ine = {\bo{O}\pposite} / {\bo {H}\ypotenuse}$

5 CAH

$\bo{C}\osine = {\bo{A}\djacent} / {\bo{H}\ypotenuse}$

TOA

$ \ bo {t} \ angent = {\ bo {o} \ pposite} / {\ bo {a} \ djacent} $

Понимание.

Давайте расширим то, что мы рассмотрели в предыдущем разделе, на примере. Помните, чтобы использовать SOHCAHTOA, вам нужно знать, к чему относится каждая буква в аббревиатуре:

S: Sine
O: Сторона, противоположная неизвестному углу
H: Сторона, противоположная прямому углу (самая длинная в треугольнике)
С: Косинус
А: Сторона рядом с неизвестным углом
T: Касательная

Вот пример:

В приведенном выше примере O — это угол, который вы пытаетесь найти.

Сторона o против неизвестного угла равна 3 .

Сторона a djacent (касание) неизвестный угол 4 .

Гипотенуза h (напротив прямого угла) равна 5 .

Вам нужно знать, какая сторона какая, чтобы решать проблемы с помощью SOHCATOA. Вам не нужно знать их длину заранее: это то, что вы будете решать!

Калькулятор SOHCAHTOA в действии

Теперь, когда мы знаем, что нам нужно для решения задачи SOHCAHTOA, давайте применим это на том же примере.

Мы можем найти СИНУС, КОсинус и ТАНГЕНС, используя информацию об этой форме. Для этого выполните следующие действия:

#1: Определение сторон

Мы это уже сделали!

Сторона, противоположная неизвестному углу, равна 3.

Сторона, примыкающая (соприкасающаяся) к неизвестному углу, равна 4.

Гипотенуза (против прямого угла) равна 5.

#2: Напишите SOHCAHTOA на Your Paper

Этот полезный шаг поможет вам не забыть одну из формул.

#3: Используйте SOHCATOA для решения

Давайте сначала решим SINE, используя сторону, которую мы уже определили.

$\SINE = {\opposite}/{\hypotenuse}$

$\SINE = 3/5$

Теперь найдем косинус.

$\COSINE = {\adjacent}/{\hypotenuse}$

$\COSINE = 4/5$

Наконец, решим ТАНГЕНС.

$\КАСАТЕЛЬНАЯ = {\противоположная}/{\смежная}$

$\КАСАТЕЛЬНАЯ = 3/4$

Это было просто!

Использование SOHCAHTOA для нахождения длин сторон

Вы также можете использовать SOHCAHTOA для нахождения длин сторон. Давайте посмотрим, как.

Мы знаем, что угол равен 60 градусов. Нам дана гипотенуза (сторона напротив прямого угла). Нас просят найти X , что является стороной, прилегающей к углу. Это означает, что нам нужно использовать косинус.

Итак, имеем:

$\cos60 = \X/10$

Чтобы найти X, мы умножаем обе части на 10:

$(\cos60) * 10 = (\X/10 * 10) $

$9.5=\X$

Калькулятор SOHCATOA: Примеры

Давайте применим наши знания SOHCATOA на практике.

SOHCAHTOA Калькулятор: Пример 1

Синус =

Косинус =

Tangent =

Ответы:

$ \ sine = 4/3 $

$ \ 3 \ 3,30002 $ \ 3 \ 3,30002 $ \ 3 \ 3,30002 $. /5 $

$ {\ tangent} = 4/5 $

SOHCAHTOA Calculator: Пример 2

SINE =

COSINE =

TANGENT =

.0002 $\SINE = 3/5$

$\COSINE =4/5$

${\TANGENT} = 3/4$

SOHCATOA Калькулятор: пример 3

Ответ:

$\sin(50) = \X/7$

$\sin(50) * 7 = (\X/7) * 7$

$\X = 3,9$

Советы по использованию SOHCATOA

Все еще не знаете, как пользоваться SOHCATOA? Вот несколько советов.

#1: Запомните правильный порядок

SOHCATOA прост в использовании, но вам нужно убедиться, что вы используете его правильно. Если вы перепутаете какие-либо буквы, вы не сможете правильно использовать формулу.

Вот несколько забавных язычков, которые вы можете использовать, чтобы запомнить Sohcahtoa:

S Ailors O FTEN H AVE C Illly A H AIR T Ill A 6 Ld H AIR T Illly 6 LD 6 Ld H TA 6 А г.э.
S оме O ld H orses C an A всегда H ухо T наследник O wners A подход.
S ome O ld 9005 H en C ever A другие H en T aking O ne 90.

#2: Запишите формулу

Работаете ли вы над SAT или просто практикуете тригонометрию в домашней работе, запись SOHCATOA поможет вам запомнить, как его использовать. Так вы не запутаетесь!

#3. Сначала определите стороны

Запомнить, какая сторона является противоположной, а какая смежной, может быть непросто. Вы должны определить каждую сторону и сначала написать это на бумаге, чтобы не делать ошибок по невнимательности во время работы.

Заключительные мысли: как использовать SOHCATOA

Что означает SOHCATOA? SOHCAHTOA — полезный мнемонический прием, позволяющий запомнить, как вычислять длины сторон и углов в прямоугольных треугольниках. Повторение формулы SOH CAH TOA и решение задач SOH CAH TOA помогут вам подготовиться к SAT или ACT.

Что дальше?

Убедитесь, что вы готовы к SAT/ACT по математике, прочитав наше полное руководство по подготовке к SAT по математике и наше полное руководство по подготовке к ACT по математике!

Если вы чувствуете себя довольно уверенно, почему бы не проверить свои навыки, ответив на 13 самых сложных вопросов SAT по математике? Если вы сможете победить их, вы, вероятно, также отлично справитесь с SAT! (Здесь также представлены самые сложные вопросы по математике в ACT. )

Если вам нужна дополнительная практика, , почему бы не почитать учебники по математике? Вот список наших любимых.

Нужна дополнительная помощь по этой теме? Проверьте Tutorbase!

Наша проверенная база данных репетиторов включает ряд опытных преподавателей, которые могут помочь вам отшлифовать эссе по английскому языку или объяснить, как производные работают для исчисления. Вы можете использовать десятки фильтров и критериев поиска, чтобы найти идеального человека для ваших нужд.

У вас есть друзья, которым тоже нужна помощь в подготовке к экзаменам? Поделись этой статьей!

Хейли Миллиман

Об авторе

Хейли Миллиман — бывшая учительница, ставшая писателем и ведущая блоги об образовании, истории и технологиях. Когда она была учителем, ученики Хейли регулярно набирали 99-й процентиль благодаря ее страсти к тому, чтобы делать темы удобоваримыми и доступными. В дополнение к своей работе для PrepScholar, Хейли является автором Путеводителя Museum Hack по самым свирепым женщинам в истории.

Углы тригонометрии – объяснение и примеры

В тригонометрии мы часто сталкиваемся с ситуациями, когда нам нужно найти меру некоторых тригонометрических углов для решения реальных задач. Мы уже знаем три основные вечнозеленые тригонометрические функции — синус, косинус и тангенс. Мы можем найти длину любой отсутствующей стороны, если знаем длину одной стороны и меру угла. Они просто получают углы в качестве входных данных и возвращают соотношения сторон. Но что, если вам нужно найти мер угла . Вы чувствуете, что застряли?

Не волнуйтесь! Нам просто нужны функции, которые могли бы «отменять» тригонометрические функции. Нам нужны обратные функции, которые получают на вход соотношения сторон и возвращают углы. Да, это так!

Тригонометрические углы можно измерять с помощью тригонометрии для решения реальных задач.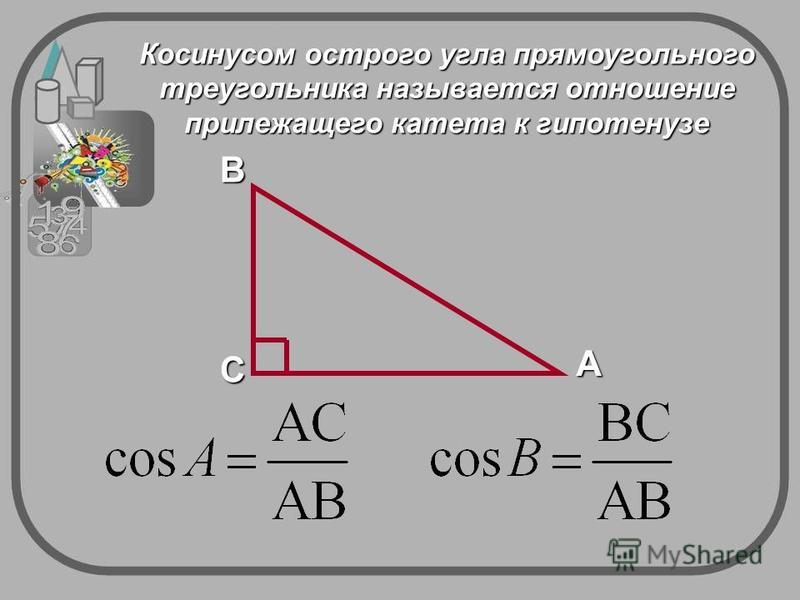 В контексте прямоугольного треугольника мы можем определить любой недостающий угол, если знаем длины двух сторон треугольника.

Ожидается, что после изучения этого урока мы изучим концепции, связанные с этими вопросами, и будем готовы давать точные, конкретные и последовательные ответы на эти вопросы.

Как найти угол с помощью тригонометрии?
Роль обратных тригонометрических функций для нахождения недостающего угла в прямоугольном треугольнике.
Как мы можем решать актуальные задачи, используя обычные тригонометрические функции и их обратные функции?

Цель этого урока — прояснить любую путаницу, которая может у вас возникнуть при нахождении неизвестных углов в прямоугольном треугольнике.

На рис. 6-1 лестница расположена на расстоянии $1$ метра от основания стены. Длина лестницы $2$ метра. Нам нужно знать следующий четырехэтапный метод, чтобы определить мера угла , образованного лестницей и землей.

Шаг 1 из 4

Определить названия двух сторон известного нам прямоугольного треугольника

длины сторон. На рисунке 6-2 показан типичный треугольник с исходным углом $\theta$.

В нашем примере с лестницей сторона длиной $1$ м является смежной стороной , лежащий рядом с , опорный угол $\theta$ , и сторона длиной $2$ м являются гипотенузой . Таким образом,

Смежные = 1$ м

Гипотенуза = 2$ м

Шаг 2 из 4

Определите и выберите подходящий тип тригонометрической функции (вне синуса, косинуса и тангенса) на основе две стороны у нас

В нашем случае мы выделили рядом с и напротив , что указывает на то, что нам нужно использовать функцию косинуса , как показано на рисунке 6-3.

Шаг 3 из 4

Подставляем значения в соответствующую функцию (в нашем случае косинус) по гипотенузе . Таким образом, используя формулу

$ {\ displaystyle \ cos \ theta = {\ frac {\ mathrm {adjacent}} {\ mathrm {hypotenuse}}}} $ 9{2} = 3$

$a = \sqrt{3 }$

Таким образом, длина противоположной стороны составляет $\sqrt{3 }$ единиц.

Теперь имеем:

Противоположные $a = \sqrt{3 }$

Гипотенуза $c = 2$

Используя формулу синуса $c

{\display $0 \display

theta ={\ frac {\ mathrm {противоположная} }{\mathrm {гипотенуза} }}}$
подставьте напротив = $\sqrt{3}$ и гипотенузу = $2$ в формуле
9{\ circ } $
Определение угла с помощью функции тангенса
Мы знаем, что функция тангенса представляет собой отношение противоположной стороны к прилежащей стороне
Снова рассмотрим диаграмму
. имеем:
Напротив = $\sqrt{3}$
Смежно = $1$
Используя формулу функции тангенса
${\displaystyle \tan \theta ={\frac {\mathrm {напротив} }{\mathrm {смежно} }}}$ 9{\circ }$
Следовательно, мы заключаем, что мы можем определить любой недостающий угол прямоугольного треугольника, используя любую тригонометрическую функцию , зависящую от сторон прямоугольного треугольника, который у нас есть.
Пример $1$
Дан прямоугольный треугольник с исходным углом $\alpha$. Чему равен угол $\alpha$?
Решение:
Глядя на диаграмму, видно, что сторона длины $12$ равна смежная сторона , которая лежит вплотную к опорному углу α, и стороне длины $5$ является противоположной стороной , лежащей ровно напротив 9000 $\alpha$ угла
$
.
Смежный = $12$
Противоположный = $5$
Мы знаем, что функция тангенса представляет собой отношение противоположной стороны к прилежащей стороне 90.
$ {\ displaystyle \ tan \ alpha = {\ frac {\ mathrm {напротив}} {\ mathrm {смежно}}}} $ 9{\circ }$
Обратите внимание, что мы могли бы также использовать функцию синуса или косинуса, поскольку прямоугольный треугольник на диаграмме показывает длины всех сторон.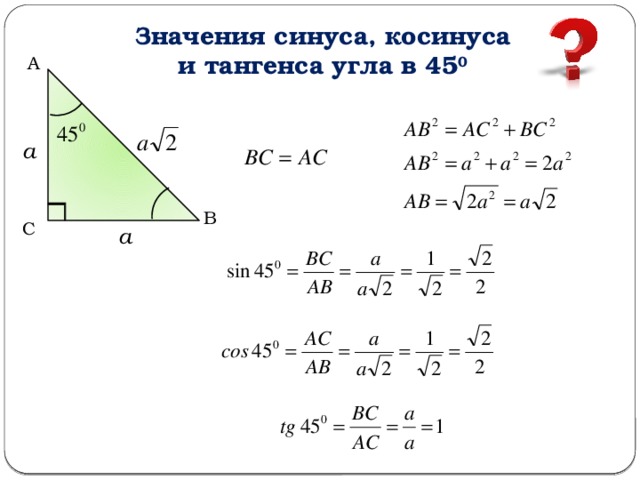
Пример $2$
Дан прямоугольный треугольник с углом отсчета $\beta$. Чему равен угол $\beta$?
Решение:
Глядя на диаграмму, видно, что
Смежные = 5$
Гипотенуза = 9{\circ }$
Пример $3$
Дан прямоугольный треугольник с исходным углом $\alpha$. Чему равен угол $\alpha$?
Решение:
Просмотр диаграммы. Понятно, что
напротив = $ 200003
Гипотеназа = долл. США
Таким образом, соответствующая функция для определения угла α должна быть долл. США. функция.
Использование формулы синуса 9{\circ }$
Решение:
Часть а: Определение меры угла $\alpha$
Глядя на диаграмму с точки зрения угла $\alpha$, мы имеем
Обратное = $3$
Смежные = $4$
Таким образом, подходящей функцией для определения угла $\alpha$ должна быть функция тангенса .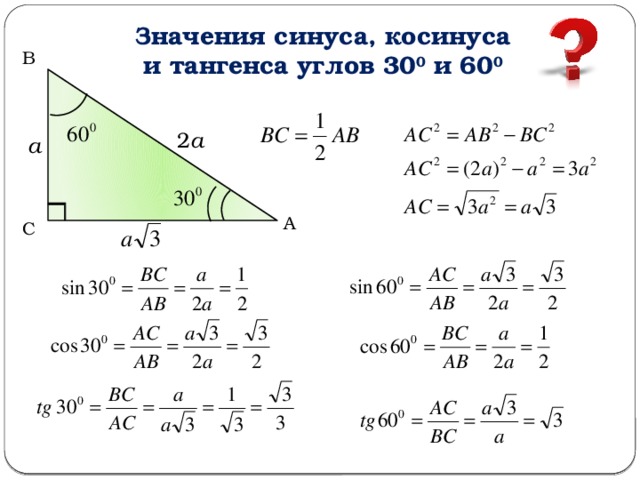
Используя формулу функции тангенса
$ {\ displaystyle \ tan \ alpha = {\ frac {\ mathrm {напротив} {\ mathrm {смежно} }}} $ 9{\circ }$
Часть b: Определение меры угла $\beta$
Так как мы должны использовать либо функцию косинуса, либо функцию синуса $ для определения меры угла бета$.
Так как функции косинуса и синуса включают гипотенузу, но здесь гипотенуза отсутствует.
Таким образом, прежде чем выбирать любую из этих функций, нам нужно определить гипотенузу.
Используйте теорему Пифагора для определения гипотенузы $c$ 9{2}=25$
$c = 5$ единиц
Таким образом, длина гипотенузы составляет $5$ единиц.
Сейчас, с перспективой угла $ \ beta $, мы имеем:
прилегающий = $ 3 $
напротив = $ 40003
Гипотенеза = $ 5 $
определить угол $\beta$.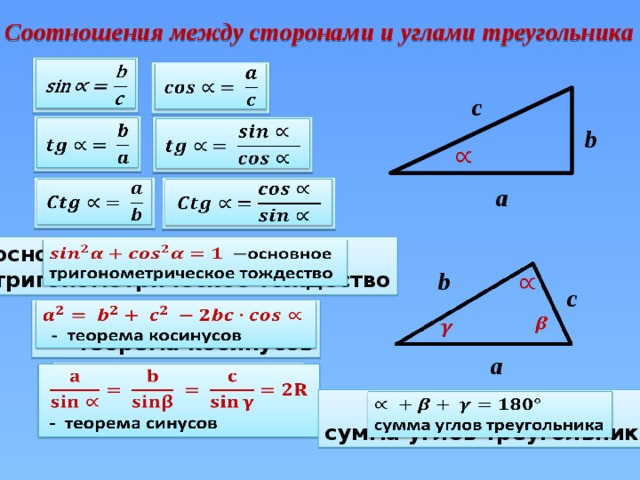
Используя формулу функции косинуса
$ {\ displaystyle \ cos \ beta = {\ frac {\ mathrm {adjacent}} {\ mathrm {hypotenuse}}}} $ 9{\ круг}.

Видео: нахождение углов с помощью косинусного отношения
Видеозапись
В этом видео мы увидим, как использовать косинусное отношение для расчета величины углов в прямоугольном треугольнике.
Итак, прежде всего, напомним, что такое отношение косинусов. Итак, у меня есть прямоугольный треугольник, в котором я обозначил один из других углов как 𝜃. А затем я обозначил три стороны треугольника их именами по отношению к этому углу 𝜃. Итак, у нас есть противоположное, прилежащее и гипотенуза.
Отношение косинуса — это отношение прилежащего к гипотенузе. Таким образом, он определяется как косинус 𝜃, или cos, как его обычно сокращают, равен прилежащему, деленному на гипотенузу. Теперь эта форма отношения очень полезна, если вы хотите вычислить длину одной из сторон, то есть либо прилежащей, либо гипотенузы. Но в этом видео мы рассмотрим, как рассчитать размер этого угла 𝜃.
Чтобы сделать это, нам нужен альтернативный способ определения этой связи. И он использует так называемую функцию арккосинуса или cos-инверсию. Поэтому записывается так: 𝜃, угол, равен обратному косинусу прилежащего, деленному на гипотенузу. И это означает, что если я знаю значение этого отношения, смежного с гипотенузой, то эта функция арккосинуса позволяет мне работать в обратном направлении, чтобы определить размер угла 𝜃, которому принадлежит это отношение. Поэтому в этом видео мы сосредоточимся именно на использовании этой функции арккосинуса для вычисления размера различных углов.
Хорошо. Наш первый вопрос: нам дали схему треугольника, и нас спросили, каково значение cos 𝜃 в этом треугольнике ниже.
Итак, в этом конкретном примере нас просят найти значение отношения косинуса, но на самом деле еще не найти сам угол. Итак, глядя на схему, я вижу, что у меня получился равнобедренный треугольник.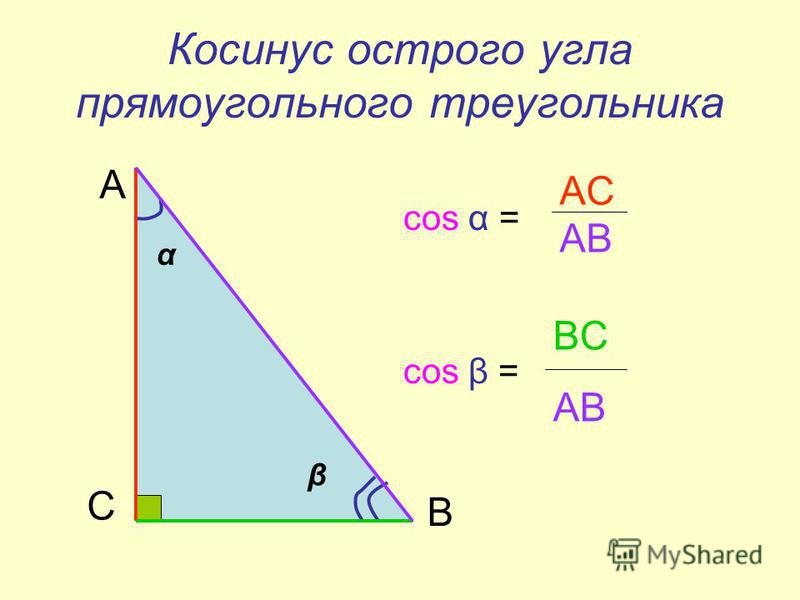 Я знаю это из-за линий, которые находятся на этих двух сторонах, что означает, что они обе по 16 сантиметров. На этой схеме прямые углы не отмечены. И для того, чтобы сделать этот особый тип тригонометрии, нам нужен прямоугольный треугольник. Поэтому мне нужно подумать о том, как я могу создать прямоугольный треугольник из вот этого, который в настоящее время не является прямоугольным.
Надеюсь, вы уже знакомы с этим равнобедренным треугольником, основание которого горизонтально. Итак, если я отмечу вертикальной линией центр этого треугольника, он разделит равнобедренный треугольник вверх на два прямоугольных треугольника, потому что эта линия дает перпендикулярную высоту треугольника. Таким образом, отметив в этой строке здесь, я могу разделить этот равнобедренный треугольник на два конгруэнтных, то есть идентичных, прямоугольных треугольника.
Теперь, чтобы ответить на эту задачу, я просто подумаю об одном из этих двух треугольников. И я подумаю о том, что слева, потому что это тот, который отмечен 𝜃. Теперь, поскольку это был равнобедренный треугольник, эта перпендикулярная высота разделила основание ровно пополам, а это означает, что основание этого прямоугольного треугольника должно быть равно половине 20, то есть 10 сантиметрам. Таким образом, у меня есть две стороны в этом прямоугольном треугольнике. Теперь, поскольку эта задача является проблемой, для которой я хочу использовать тригонометрию, я начну с обозначения трех сторон этого прямоугольного треугольника по отношению к этому углу 𝜃, то есть противоположному, прилежащему и гипотенузе.
Сделав это, вы можете видеть, что две стороны, которые я знаю, это прилежащая сторона и гипотенуза, A и H. Это то, что говорит мне, что это соотношение косинусов, которое я собираюсь использовать для этого конкретного вопроса. Потому что, если вы вспомните SOHCATOA, то A и H появляются вместе в части CAH, которая является отношением косинуса. Поэтому мне нужно вспомнить определение отношения косинусов. А дело вот в чем: этот cos 𝜃 равен прилежащему деленному на гипотенузу. Итак, что я собираюсь сделать для этого вопроса, чтобы найти cos of 𝜃, я просто запишу это отношение. Но я заменю прилежащее и гипотенузу их значениями. Поэтому я заменяю прилежащее на 10, а гипотенузу на 16,9.0003
Следовательно, у меня есть этот cos 𝜃, равный 10 на 16. Теперь это упростится как дробь. Итак, в упрощенной форме это пять восьмых. Или, на самом деле, я мог бы преобразовать его в точную десятичную дробь в этом случае, так что это 0,625. Любой из них, дробь или точное десятичное число, были бы подходящими форматами для ответа на этот вопрос.
Итак, что мы сделали, так это вспомнили, что если вы рисуете перпендикулярную высоту равнобедренного треугольника, вы создаете два конгруэнтных прямоугольных треугольника. А затем мы использовали тригонометрию в прямоугольном треугольнике, чтобы вычислить это значение 𝜃. Мы вспомнили соотношение косинусов и записали его для этого конкретного вопроса.
Хорошо. Теперь второй вопрос, нам дана диаграмма. И это прямоугольный треугольник. И нас просят вычислить величину угла 𝜃, давая ответ с точностью до градуса.
Итак, как всегда, для задачи, связанной с тригонометрией, я начну с обозначения трех сторон треугольника. И, как и прежде, мы можем видеть, что именно прилежащее и гипотенуза являются двумя известными мне сторонами. Это говорит мне о том, что именно отношение косинусов мне нужно, чтобы ответить на этот вопрос. Итак, у меня есть определение соотношения косинусов. И я собираюсь записать это, используя информацию в этом вопросе. Значит, косинус угла 𝜃 будет равен восьми на 21.
В этом вопросе меня не просто просят записать это соотношение, а просят пойти еще дальше и вычислить угол 𝜃. Так что здесь мне нужно использовать функцию арккосинуса. Следовательно, это говорит мне, что 𝜃 равно арккосинусу этого отношения, восемь больше 21. Теперь мне понадобится калькулятор, чтобы вычислить это. И если вы посмотрите на свой калькулятор, вы обычно увидите, что над кнопкой cos есть обратный косинус или обратный косинус. И поэтому вам часто приходится нажимать Shift, чтобы добраться до него. Теперь это будет зависеть от конкретной марки и модели вашего калькулятора. Но обычно именно там находится эта кнопка. Введя это в свой калькулятор, я получаю, что 𝜃 равно 67,6073. Теперь вопрос просил меня вычислить 𝜃 с точностью до градуса. Поэтому мне нужно округлить свой ответ. И поэтому у меня это 𝜃 68 градусов.
Теперь стоит упомянуть, что вам нужно убедиться, что ваш калькулятор находится в правильном режиме, когда вы выполняете тригонометрию. Этот вопрос требовал 𝜃 в градусах. Поэтому мне нужно убедиться, что мой калькулятор находится в режиме градусов. Есть и другие способы измерения углов, с которыми вы могли встречаться или не встречаться. Но вам нужно убедиться, что ваш калькулятор в градусах для этого конкретного вопроса.
Хорошо. Следующий вопрос говорит, что 𝐴𝐵𝐶𝐷 — это равнобедренная трапеция, в которой 𝐴𝐵 равно 𝐵𝐶 равно 𝐴𝐷. Они все 10 сантиметров. И последняя сторона, 𝐶𝐷, равна 26 сантиметрам.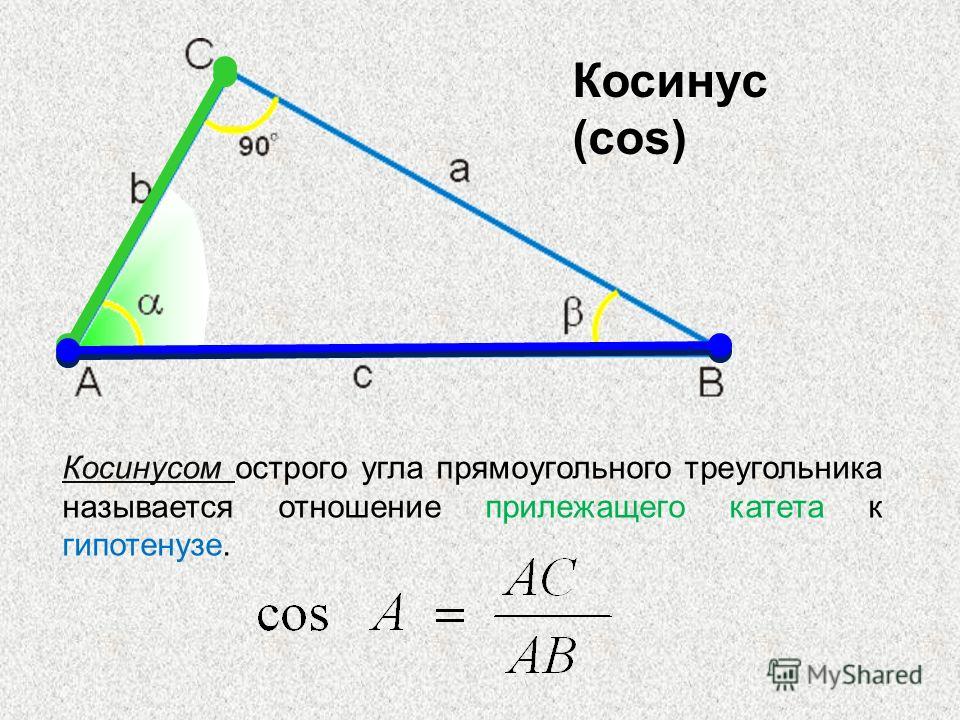 Нас просят вычислить угол 𝐴𝐷𝐶 с точностью до секунды.
Итак, прежде всего, угол 𝐴𝐷𝐶, это угол, образованный, когда я иду от 𝐴 к 𝐷 и 𝐶. И поэтому именно этот угол здесь и просят найти. Теперь, глядя на диаграмму, у нас нет прямоугольных треугольников. На самом деле у нас вообще нет никаких треугольников. Но мы можем создать его. И что я собираюсь сделать, так это нарисовать перпендикулярную высоту от 𝐴 до основания 𝐶𝐷. Сделав это, вы увидите, что я создал прямоугольный треугольник в левой части диаграммы. На самом деле я собираюсь сделать то же самое и с другой стороны диаграммы.
Теперь я хочу работать с этим прямоугольным треугольником. Поэтому я просто обозначу три его стороны по отношению к углу 𝜃. Итак, у нас есть противоположное, прилежащее и гипотенуза, как обычно. На данный момент кажется, что я знаю только одну из длин в этом прямоугольном треугольнике. Я знаю, что гипотенуза равна 10 см. Но в настоящее время у меня нет ни одной из двух других длин. Так что нам просто нужно немного подумать об этом. Теперь я вижу, что 𝐶𝐷 равно 26 сантиметрам. И я вижу, что 𝐶𝐷 состоит из трех частей. Это основание этого прямоугольного треугольника, затем еще одна прямая часть, а затем снова основание этого прямоугольного треугольника. Поскольку эти два треугольника конгруэнтны друг другу, так как это равнобедренная трапеция, она симметрична. Итак, эти два треугольника идентичны.
Таким образом, я могу использовать всю информацию, содержащуюся в этом вопросе, чтобы вычислить длину основания этих прямоугольных треугольников. Так что эта часть здесь равна 10 сантиметрам, потому что она по вертикали ниже 𝐴𝐵. И поэтому он должен быть такой же длины, как 𝐴𝐵. Это означает, что из 26 сантиметров, которые являются общими для 𝐶𝐷, у меня осталось 16 сантиметров. А так как эти два прямоугольных треугольника идентичны, то их основания имеют одинаковую длину. Таким образом, их основания должны составлять половину этих 16 сантиметров. Следовательно, у меня получилось по восемь сантиметров на каждое из этих оснований.
Правильно. Теперь у меня достаточно информации, чтобы рассчитать этот угол. Итак, глядя на прямоугольный треугольник, я вижу, что теперь знаю соседний треугольник. Это восемь сантиметров. И я знаю гипотенузу. Поэтому мне нужно отношение косинуса, чтобы ответить на этот вопрос. Итак, у меня есть определение соотношения косинусов, и теперь я записываю его специально для этого вопроса. Итак, у меня есть cos 𝜃 равно восьми больше 10. И, конечно, это упростит. Или я могу просто написать это как десятичное число в этом случае. Итак, у нас 0,8. Теперь мне нужно использовать эту функцию арккосинуса, чтобы вычислить значение 𝜃. Итак, у меня 𝜃 равно обратному косинусу 0,8.
Тогда вычислив это, я понял, что 𝜃 равно 36,86989 градусам. Теперь, если меня попросили дать ответ в градусах, я мог бы остановиться на этом или просто округлить его до ближайшего градуса. Но меня попросили дать ответ с точностью до секунды, поэтому мне нужно вспомнить, как преобразовать ответ в градусах в ответ в секундах. Итак, глядя на это, я вижу, что у меня есть 36 полных градусов, а затем у меня остается десятичная дробь 0,86989. Так что это нужно преобразовать, прежде всего, в минуты, а затем все, что осталось, в секунды. Итак, помните, что минута — это одна шестидесятая градуса. И поэтому, чтобы вычислить, сколько минут у меня есть, мне нужно умножить эту десятичную дробь на 60. Когда я это сделаю, я получу 52,19.38. Это означает, что у меня есть 52 полных минуты, а затем у меня остается десятичная дробь 0,1938, которую нужно преобразовать в секунды. Опять же, секунда составляет одну шестидесятую часть минуты. Итак, чтобы определить, сколько секунд представляет это десятичное число, мне нужно умножить его на 60. И когда я это сделаю, я получу 11,6315. Так что меня спрашивают об этом с точностью до секунды. Тогда я округлю это до 12 секунд.
Итак, наконец, мне нужно собрать все эти три части вместе. И это дает мне окончательный ответ: 36 градусов 52 минуты и 12 секунд для измерения угла 𝐴𝐷𝐶.
No related posts.