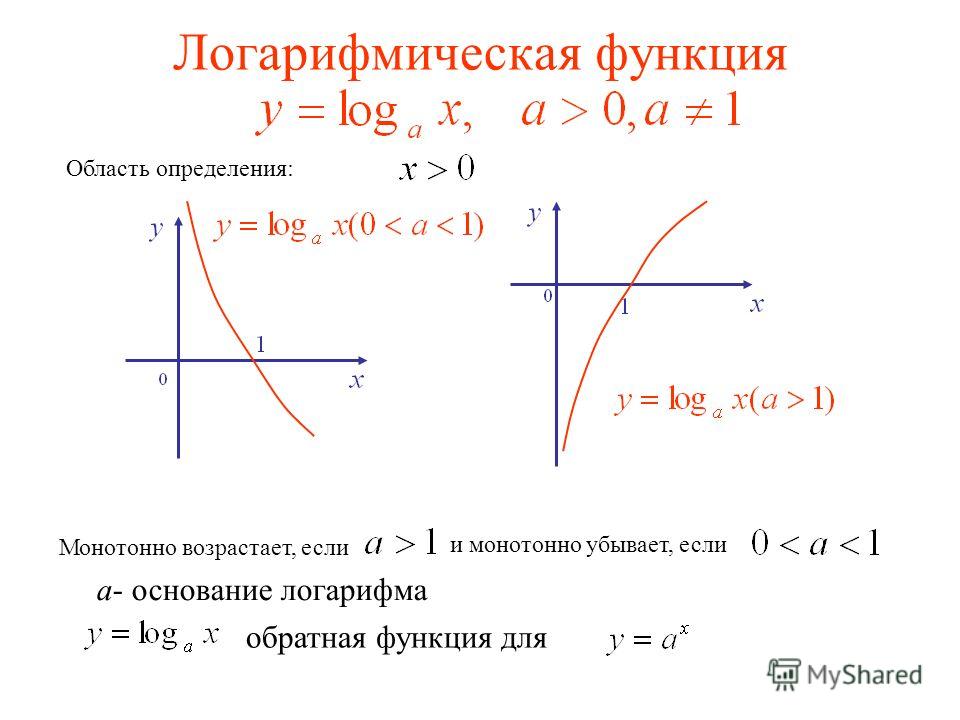
1.6.9. Логарифмическая функция
Функция, определяемая равенством
,
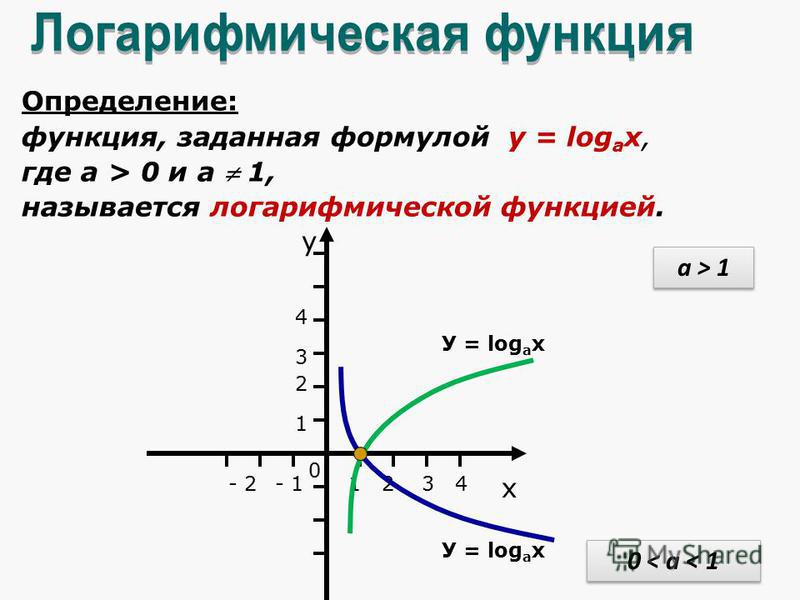
где а – положительное, отличное от единицы число, называется логарифмической функций. По существу логарифмическая функция обратна показательной, поэтому график ее симметричен графику показательной функции относительно биссектрисы первого и третьего координатных углов.
На рис. 22 показаны графики функции (пунктирная линия) и(сплошная линия), а на рис. 23 графики функцийи.
Свойства логарифмической функции легко можно усмотреть из рис. 21 и 22.
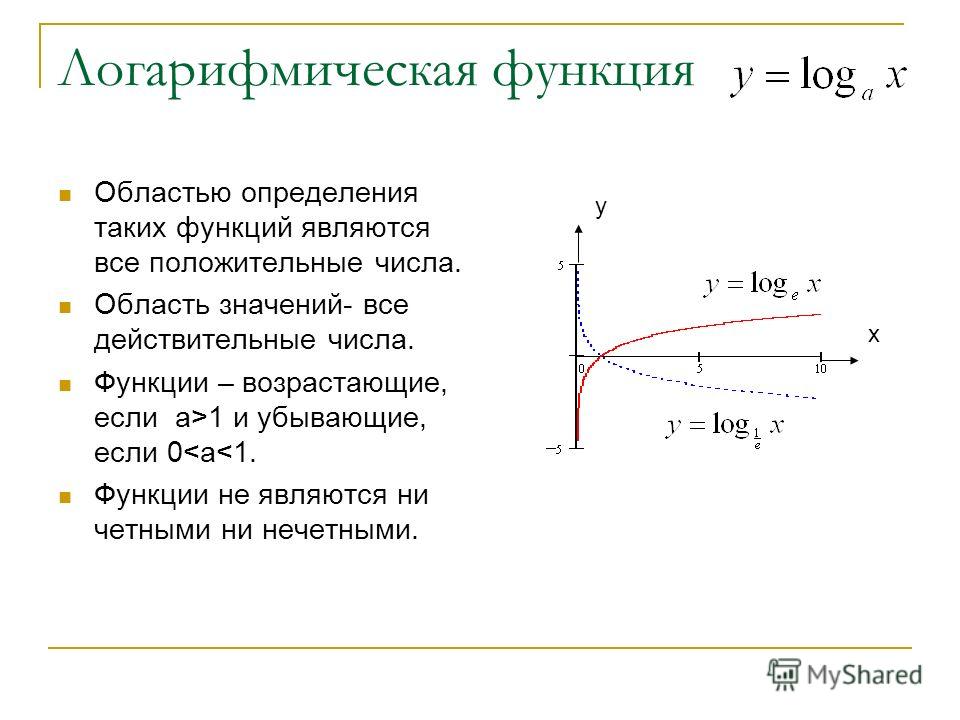
Логарифмическая функция определена только для положительных чисел (0 < x < +∞), т.е. график расположен правее оси ординат.
Если а > 1, то логарифмическая функции положительна при х > 1, отрицательная при 0 < х < 1 и равна нулю при х

Рис. 22 Рис. 23
При а > 1 логарифмическая функция возрастает. Если 0 < а < 1, то она положительна при 0 < х < 1, отрицательна при х > 1, равна нулю при х = 1.
Если 0 < а < 1, то функция является убывающей, если а > 1 график функции выпуклый; если 0 < а < 1 . то график логарифмической функции вогнут.
На рис. 24,25 представлены привлекательные функции для исследования (оценки) поведения различных технико-экономических показателей, в частности спроса и предложения.
Рис. 24
Рис. 25
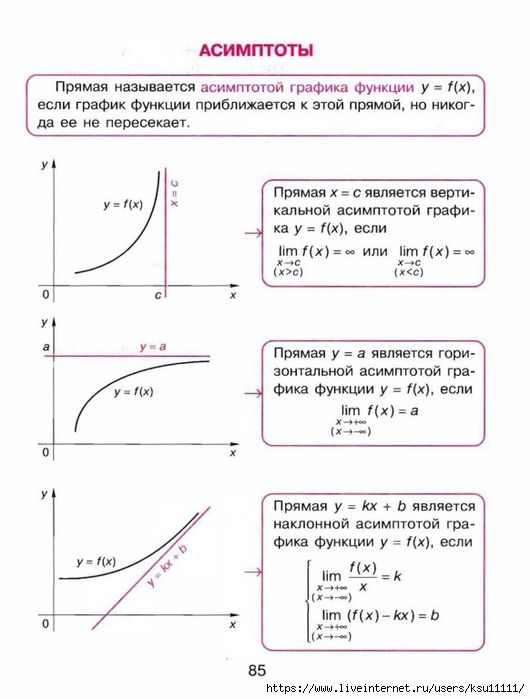
Асимптотой кривой называется такая прямая, к которой неограниченно приближается точка кривой при неограниченном удалении ее от начала координат.
Для нахождения асимптот пользуются следующими положениями:
а) если х = а кривая у = f(x) имеет бесконечный разрыв, то прямая х = а является ее вертикальной асимптотой;
б) невертикальные асимптоты кривой у = f(x), если они существуют, имеют уравнения вида у = кх + b, где к и b определяются формулами:
и
.
Пример. Найти асимптоты кривых:
Решение. 1. а) при х = 3 данная кривая имеет бесконечный разрыв. Поэтому прямая х = 3 есть вертикальная асимптота;
б) далее имеем невертикальные асимптоты:
;
.
Подставляя значения к и b в уравнение у = кх + b, получим уравнение невертикальной асимптоты: у = х – 3. Других невертикальных асимптот кривая не имеет, так как при значения к иb будут те же самые. Кривая (гипербола) изображена на рис. 26.
Рис. 26
Далее на рис. 26, 27, 28, 29, 30, 31 изображены асимптоты функции ;;;;;.
Представляют интерес графики представленные на рис. 27 – 58.
Рис. 27
Рис. | Рис. 29 |
Рис. 30
Рис. 31
Рис. 32
Рис. 33 Рис. 34
Рис. 35
Рис. 36 Рис.37.
Рис. 38. | Рис. 39. |
Рис. 40. | Рис. 41. |
Рис.42. | Рис. 43. |
Рис. | Рис. 45. |
Рис. 46. | Рис.47. |
Рис. 48. |
Рис. 49. | Рис. 50. |
Рис.51. | Рис.52. |
Рис. | Рис.54. |
Рис.55 | Рис.56. |
Рис.57. | Рис.58. |
Горизонтальная асимптота графика функции y. Асимптоты графика функции
Ни одной, одна, две, три,… или бесконечно много. За примерами далеко ходить не будем, вспомним элементарные функции. Парабола, кубическая парабола, синусоида вовсе не имеют асимптот. График экспоненциальной, логарифмической функции обладает единственной асимптотой. У арктангенса, арккотангенса их две, а у тангенса, котангенса — бесконечно много. Не редкость, когда график укомплектован и горизонтальными и вертикальными асимптотами.
Что значит найти асимптоты графика функции?
Это значит выяснить их уравнения, ну и начертить прямые линии, если того требует условие задачи. Процесс предполагает нахождение пределов функции.
Вертикальная асимптота графика, как правило, находится в точке бесконечного разрыва функции. Всё просто: если в точке функция терпит бесконечный разрыв, то прямая, заданная уравнением является вертикальной асимптотой графика.
Примечание: обратите внимание, что запись используется для обозначения двух совершенно разных понятий. Точка подразумевается или уравнение прямой — зависит от контекста.
Таким образом, чтобы установить наличие вертикальной асимптоты в точке достаточно показать, что хотя бы один из односторонних пределов бесконечен. Чаще всего это точка, где знаменатель функции равен нулю. По существу, мы уже находили вертикальные асимптоты в последних примерах урока о непрерывности функции. Но в ряде случаев существует только один односторонний предел, и, если он бесконечен, то снова — любите и жалуйте вертикальную асимптоту.
Из вышесказанного также следует очевидный факт: если функция непрерывна на, то вертикальные асимптоты отсутствуют. На ум почему-то пришла парабола. Действительно, где тут «воткнёшь» прямую? …да… понимаю… последователи дядюшки Фрейда забились в истерике =)
Обратное утверждение в общем случае неверно: так, функция не определена на всей числовой прямой, однако совершенно обделена асимптотами.
Наклонные асимптоты графика функции
Наклонные (как частный случай — горизонтальные) асимптоты могут нарисоваться, если аргумент функции стремится к «плюс бесконечности» или к «минус бесконечности». Поэтому график функции не может иметь больше 2-х наклонных асимптот. Например, график экспоненциальной функции обладает единственной горизонтальной асимптотой при, а график арктангенса при — двумя такими асимптотами, причём различными.
Определение . Асимптотой
графика функции
называется прямая, обладающая тем
свойством, что расстояние от точкиграфика функции до этой прямой стремится
к нулю при неограниченном удалении
точки графика от начала координат .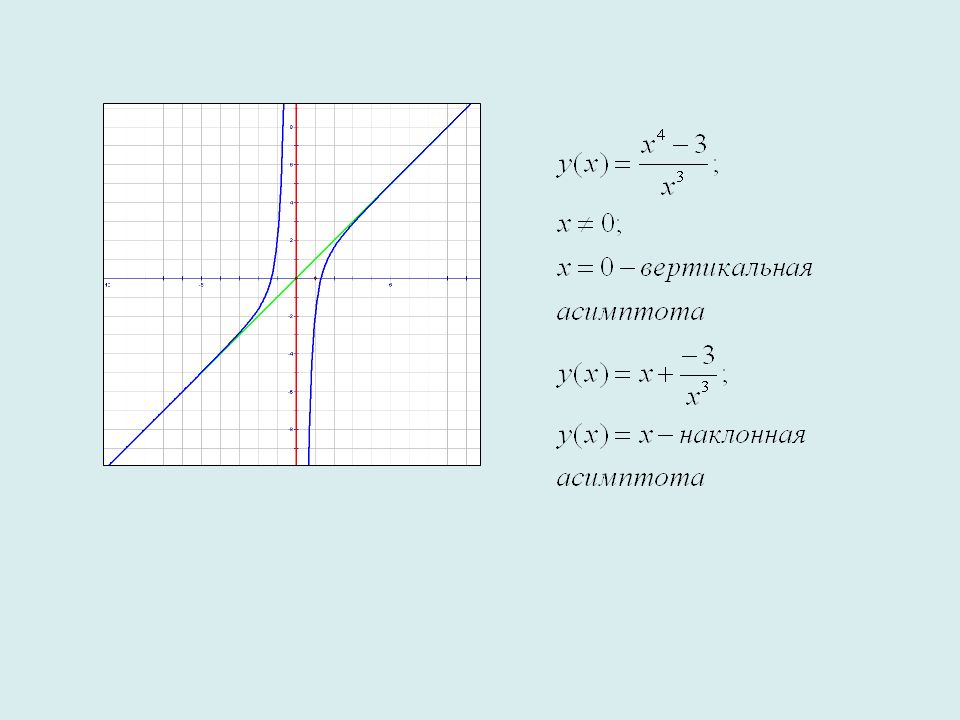
По способам их отыскания выделяют три вида асимптот: вертикальные , горизонтальные, наклонные.
Очевидно, горизонтальные являются частными случаями наклонных (при ).
Нахождение асимптот графика функции основано на следующих утверждениях.
Теорема 1 . Пусть функция определена хотя бы в некоторой полуокрестности точкии хотя бы один из ее односторонних пределов в этой точке бесконечен, т.е. равенили. Тогда прямаяявляется вертикальной асимптотой графика функции
.Таким образом, вертикальные асимптоты графика функции следует искать в точках разрыва функции или на концах ее области определения (если это конечные числа).
Теорема 2 . Пусть функция определена при значениях аргумента, достаточно больших по абсолютной величине, и существует конечный предел функции. Тогда прямаяесть горизонтальная асимптота графика функции.
Может
случиться, что
,
а,
причеми-
конечные числа, тогда график имеет две
различные горизонтальные асимптоты:
левостороннюю и правостороннюю. Если
же существует лишь один из конечных
пределов
или,
то график имеет либо одну левостороннюю,
либо одну правостороннюю горизонтальную
асимптоту.
Если
же существует лишь один из конечных
пределов
или,
то график имеет либо одну левостороннюю,
либо одну правостороннюю горизонтальную
асимптоту.
Теорема 3
Заметим, что если хотя бы один из указанных пределов бесконечен, то наклонной асимптоты нет.
Наклонная асимптота так же, как и горизонтальная, может быть односторонней.
Пример . Найдите все асимптоты графика функции .
Решение .
Функция определена при . Найдем ее односторонние пределы в точках.
Так как и(два других односторонних предела можно уже не находить), то прямыеиявляются вертикальными асимптотами графика функции.
Вычислим
(применим правило Лопиталя) =.
Значит, прямая — горизонтальная асимптота.
Так
как горизонтальная асимптота существует,
то наклонные уже не ищем (их нет).
Ответ : график имеет две вертикальные асимптоты и одну горизонтальную.
Общие исследование функции y = f (x ).
Область определения функции. Найти ее область определения D (f ) . Если это не слишком сложно, то полезно найти также область значений E (f ) . (Однако, во многих случаях, вопрос нахождения E (f ) откладывается до нахождения экстремумов функции.)
Особые
свойства функции. Выяснить
общие свойства функции: четность,
нечетность, периодичность и т.п. Не
любая функция обладает такими свойствами,
как четность либо нечетность. Функция
заведомо не является ни четной, ни
нечетной, если ее область определения
несимметрична относительно точки 0 на
оси Ox .
Точно так же, у любой периодической
функции область определения состоит
либо из всей вещественной оси, либо из
объединения периодически повторяющихся
систем промежутков.
Вертикальные асимптоты. Выяснить, как ведёт себя функция при приближении аргумента к граничным точкам области определенияD (f ), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.
Наклонные и горизонтальные асимптоты. Если область определения D (f ) вклоючает в себя лучи вида (a;+) или (−;b), то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при x+или x−соответственно, т.е. найти limxf(x).Наклонные асимптоты : y = kx + b, где k=limx+xf(x) и b=limx+(f(x)−x).Горизонтальны асимптоты : y = b, где limxf(x)=b.
Нахождение
точек пересечения графика с осями .
Нахождение точки пересечения графика
с осью Oy .
Для этого нужно вычислить значение f (0). Найти также точки пересечения графика
с осью Ox ,
для чего найти корни уравнения f (x )
= 0 (или убедиться в отсутствии корней).
Уравнение часто удается решить лишь
приближунно, но уже отделение корней
помогает лучше уяснить строение графика.
Далее, нужно определить знак функции
на промежутках между корнями и точками
разрыва.
Найти также точки пересечения графика
с осью Ox ,
для чего найти корни уравнения f (x )
= 0 (или убедиться в отсутствии корней).
Уравнение часто удается решить лишь
приближунно, но уже отделение корней
помогает лучше уяснить строение графика.
Далее, нужно определить знак функции
на промежутках между корнями и точками
разрыва.
Нахождение точек пересечения графика с асимптотой. В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.
Нахождение
интервалов выпуклости и вогнутости .
Это делается с помощью исследования
знака второй производной f(x).
Найти точки перегиба на стыках интервалов
выпуклости и вогнутости. Вычислить
значение функции в точках перегиба.
Если функция имеет другие точки
непрерывности (кроме точек перегиба),
в которых вторая производная равна 0
либо не существует, то в этих точках
также полезно вычислить значение
функции.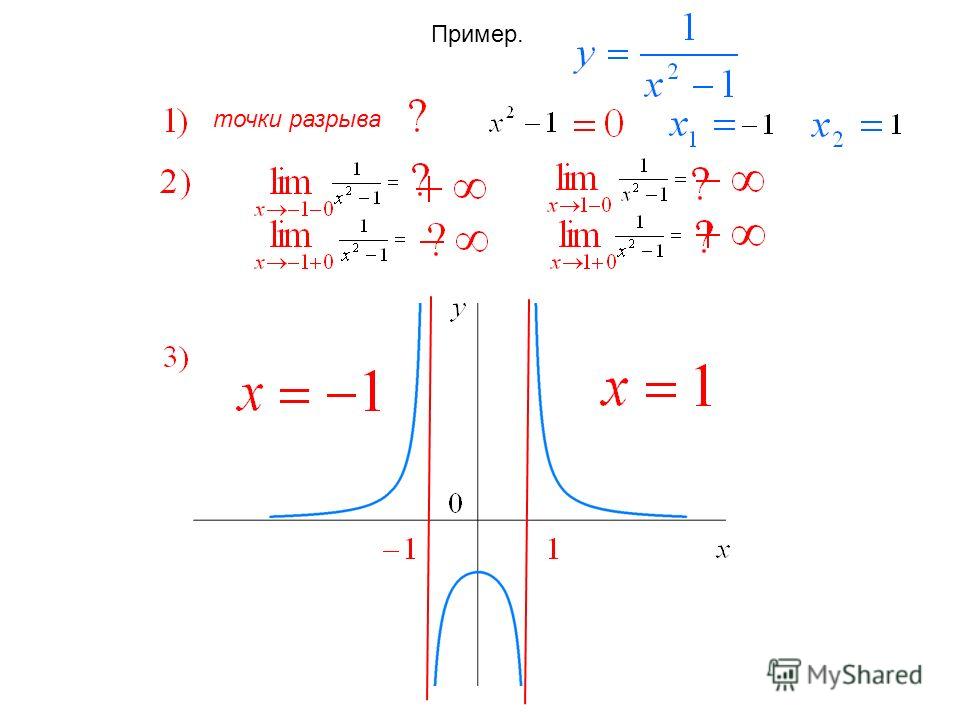 Найдя f(x)
, мы решаем неравенство f(x)0.
На каждом из интервалов решения функция
будет выпуклой вниз. Решая обратное
неравенство f(x)0,
мы находим интервалы, на которых функция
выпукла вверх (то есть вогнута). Определяем
точки перегиба как те точки, в которых
функция меняет направление выпуклости
(и непрерывна).
Найдя f(x)
, мы решаем неравенство f(x)0.
На каждом из интервалов решения функция
будет выпуклой вниз. Решая обратное
неравенство f(x)0,
мы находим интервалы, на которых функция
выпукла вверх (то есть вогнута). Определяем
точки перегиба как те точки, в которых
функция меняет направление выпуклости
(и непрерывна).
Именно так формулируется типовое задание, и оно предполагает нахождение ВСЕХ асимптот графика (вертикальных, наклонных/горизонтальных). Хотя, если быть более точным в постановке вопроса — речь идёт об исследовании на наличие асимптот (ведь таковых может и вовсе не оказаться).
Начнём с чего-нибудь простого:
Пример 1
Решение удобно разбить на два пункта:
1) Сначала проверяем, есть ли вертикальные асимптоты. Знаменатель обращается в ноль при , и сразу понятно, что в данной точке функция терпит бесконечный разрыв , а прямая, заданная уравнением , является вертикальной асимптотой графика функции . Но, прежде чем оформить такой вывод, необходимо найти односторонние пределы:
Напоминаю технику вычислений, на которой я подобно останавливался в статье непрерывность функции. Точки разрыва . В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
Точки разрыва . В выражение под знаком предела вместо «икса» подставляем . В числителе ничего интересного:
.
А вот в знаменателе получается бесконечно малое отрицательное число :
, оно и определяет судьбу предела.
Левосторонний предел бесконечный, и, в принципе уже можно вынести вердикт о наличии вертикальной асимптоты. Но односторонние пределы нужны не только для этого — они ПОМОГАЮТ ПОНЯТЬ, КАК расположен график функции и построить его КОРРЕКТНО . Поэтому обязательно вычислим и правосторонний предел:
Вывод : односторонние пределы бесконечны, значит, прямая является вертикальной асимптотой графика функции при .
Первый предел конечен , значит, необходимо «продолжить разговор» и найти второй предел:
Второй предел тоже конечен .
Таким образом, наша асимптота:
Вывод : прямая, заданная уравнением является горизонтальной асимптотой графика функции при .
Для нахождения горизонтальной асимптоты можно пользоваться упрощенной формулой :
Если существует конечный
предел , то прямая является горизонтальной асимптотой графика функции при .
Нетрудно заметить, что числитель и знаменатель функции одного порядка роста , а значит, искомый предел будет конечным:
Ответ :
По условию не нужно выполнять чертёж, но если в самом разгаре исследование функции , то на черновике сразу же делаем набросок:
Исходя из трёх найденных пределов , попытайтесь самостоятельно прикинуть, как может располагаться график функции . Совсем трудно? Найдите 5-6-7-8 точек и отметьте их на чертеже. Впрочем, график данной функции строится с помощью преобразований графика элементарной функции , и читатели, внимательно рассмотревшие Пример 21 указанной статьи легко догадаются, что это за кривая.
Пример 2
Найти асимптоты графика функции
Это пример для самостоятельного решения. Процесс, напоминаю, удобно разбить на два пункта — вертикальные асимптоты и наклонные асимптоты. В образце решения горизонтальная асимптота найдёна по упрощенной схеме.
На практике чаще всего встречаются дробно-рациональные функции, и после тренировки на гиперболах усложним задание:
Пример 3
Найти асимптоты графика функции
Решение : Раз, два и готово:
1) Вертикальные асимптоты находятся в точках бесконечного разрыва , поэтому нужно проверить, обращается ли знаменатель в ноль.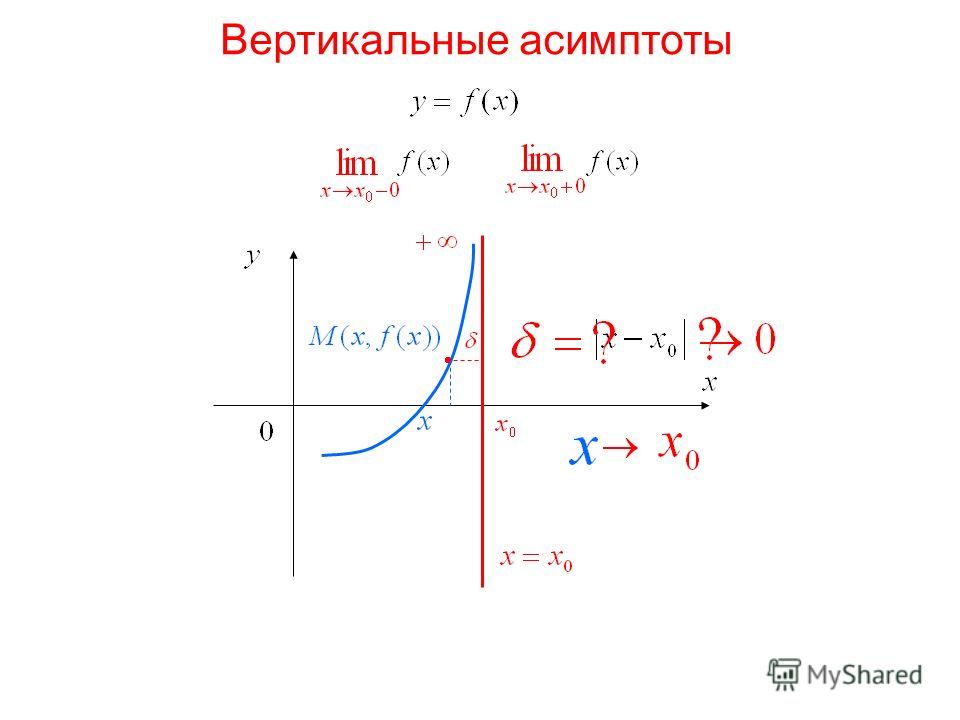 Решим квадратное уравнение :
Решим квадратное уравнение :
Дискриминант положителен, поэтому уравнение имеет два действительных корня, и работы значительно прибавляется =)
В целях дальнейшего нахождения односторонних пределов квадратный трёхчлен удобно разложить на множители :
(для компактной записи «минус» внесли в первую скобку). Для подстраховки выполним проверку, мысленно либо на черновике раскрыв скобки.
Перепишем функцию в виде
Найдём односторонние пределы в точке :
И в точке :
Таким образом, прямые являются вертикальными асимптотами графика рассматриваемой функции.
2) Если посмотреть на функцию , то совершенно очевидно, что предел будет конечным и у нас горизонтальная асимптота. Покажем её наличие коротким способом:
Таким образом, прямая (ось абсцисс) является горизонтальной асимптотой графика данной функции.
Ответ :
Найденные пределы и асимптоты дают немало информации о графике функции. Постарайтесь мысленно представить чертёж с учётом следующих фактов:
Схематично изобразите вашу версию графика на черновике.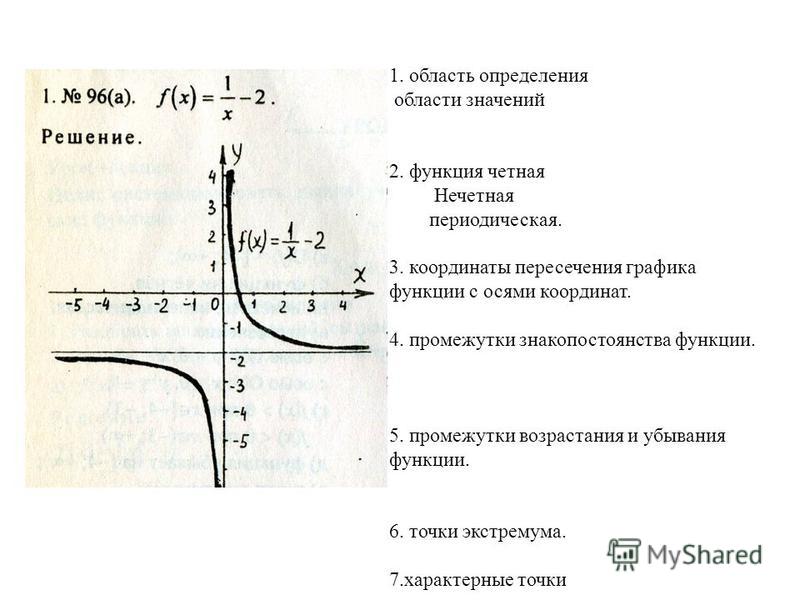
Конечно, найденные пределы однозначно не определяют вид графика, и возможно, вы допустите ошибку, но само упражнение окажет неоценимую помощь в ходе полного исследования функции . Правильная картинка — в конце урока.
Пример 4
Найти асимптоты графика функции
Пример 5
Найти асимптоты графика функции
Это задания для самостоятельного решения. Оба графика снова обладают горизонтальными асимптотами, которые немедленно детектируются по следующим признакам: в Примере 4 порядок роста знаменателя больше , чем порядок роста числителя, а в Примере 5 числитель и знаменатель одного порядка роста . В образце решения первая функция исследована на наличие наклонных асимптот полным путём, а вторая — через предел .
Горизонтальные асимптоты, по моему субъективному впечатлению, встречаются заметно чаще, чем те, которые «по-настоящему наклонены». Долгожданный общий случай:
Пример 6
Найти асимптоты графика функции
Решение : классика жанра:
1) Поскольку знаменатель положителен, то функция непрерывна на всей числовой прямой, и вертикальные асимптоты отсутствуют.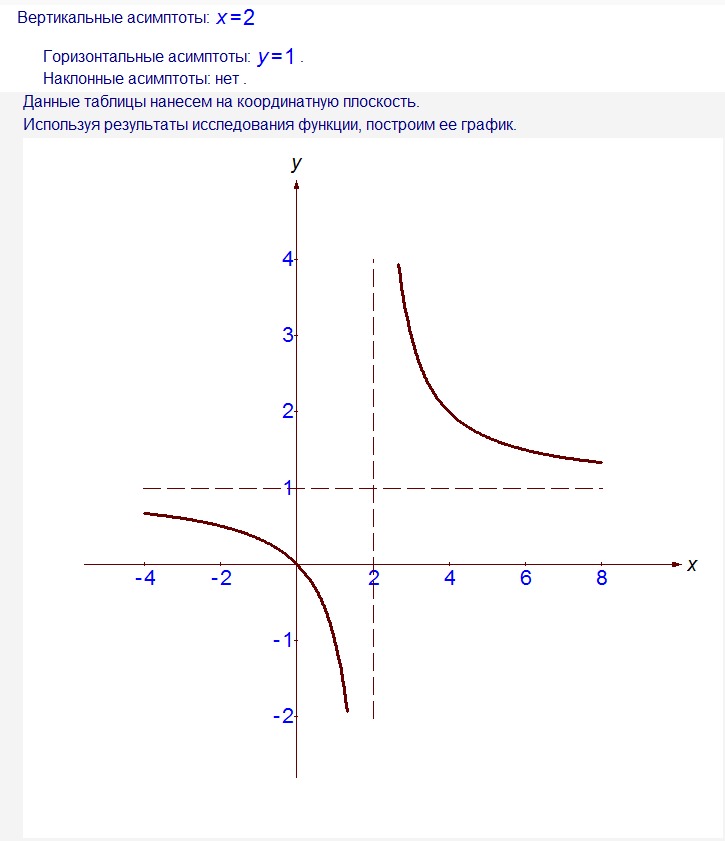 …Хорошо ли это? Не то слово — отлично! Пункт №1 закрыт.
…Хорошо ли это? Не то слово — отлично! Пункт №1 закрыт.
2) Проверим наличие наклонных асимптот:
Первый предел конечен , поэтому едем дальше. В ходе вычисления второго предела для устранения неопределённости «бесконечность минус бесконечность» приводим выражение к общему знаменателю:
Второй предел тоже конечен , следовательно, у графика рассматриваемой функции существует наклонная асимптота:
Вывод :
Таким образом, при график функции бесконечно близко приближается к прямой :
Заметьте, что он пересекает свою наклонную асимптоту в начале координат, и такие точки пересечения вполне допустимы — важно, чтобы «всё было нормально» на бесконечности (собственно, речь об асимптотах и заходит именно там).
Пример 7
Найти асимптоты графика функции
Решение : комментировать особо нечего, поэтому оформлю примерный образец чистового решения:
1) Вертикальные асимптоты. Исследуем точку .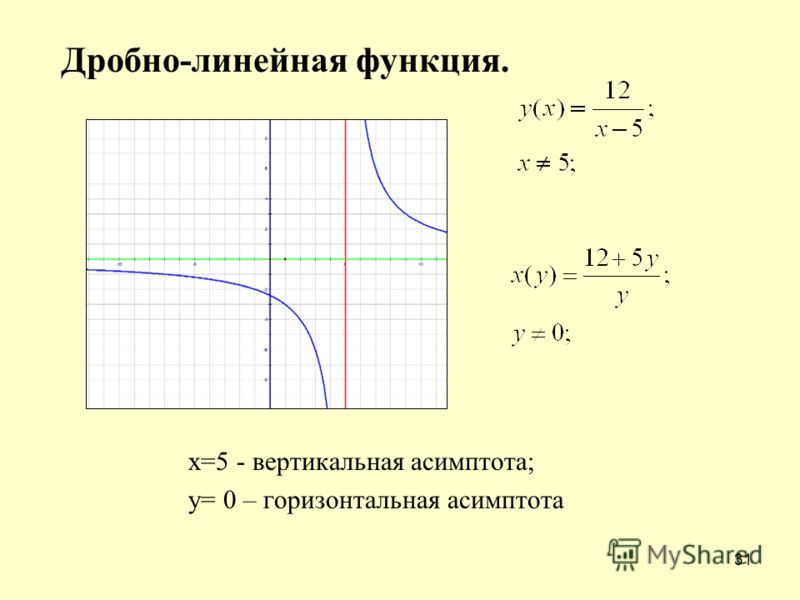
Прямая является вертикальной асимптотой для графика при .
2) Наклонные асимптоты:
Прямая является наклонной асимптотой для графика при .
Ответ :
Найдённые односторонние пределы и асимптоты с высокой достоверностью позволяют предположить, как выглядит график данной функции. Корректный чертёж в конце урока.
Пример 8
Найти асимптоты графика функции
Это пример для самостоятельного решения, для удобства вычисления некоторых пределов можно почленно разделить числитель на знаменатель. И снова, анализируя полученные результаты, постарайтесь начертить график данной функции.
Очевидно, что обладателями «настоящих» наклонных асимптот являются графики тех дробно-рациональных функций, у которых старшая степень числителя на единицу больше старшей степени знаменателя. Если больше — наклонной асимптоты уже не будет (например, ).
Но в жизни происходят и другие чудеса:
Пример 9
Решение : функция непрерывна на всей числовой прямой, значит, вертикальные асимптоты отсутствует. Но вот наклонные вполне могут быть. Проверяем:
Но вот наклонные вполне могут быть. Проверяем:
Вспоминаю, как ещё в ВУЗе столкнулся с похожей функцией и просто не мог поверить, что у неё есть наклонная асимптота. До тех пор, пока не вычислил второй предел:
Строго говоря, здесь две неопределённости: и , но так или иначе, нужно использовать метод решения, который разобран в Примерах 5-6 статьи о пределах повышенной сложности . Умножаем и делим на сопряженное выражение, чтобы воспользоваться формулой :
Ответ :
Пожалуй, самая популярная наклонная асимптота.
До сих пор бесконечности удавалось «стричь под одну гребёнку», но бывает, что у графика функции две разные наклонные асимптоты при и при :
Пример 10
Исследовать график функции на наличие асимптот
Решение : подкоренное выражение положительно, значит, область определения — любое действительно число, и вертикальных палок быть не может.
Проверим, существуют ли наклонные асимптоты.
Если «икс» стремится к «минус бесконечности», то:
(при внесении «икса» под квадратный корень необходимо добавить знак «минус», чтобы не потерять отрицательность знаменателя)
Выглядит необычно, но здесь неопределённость «бесконечность минус бесконечность». Умножаем числитель и знаменатель на сопряженное выражение:
Таким образом, прямая является наклонной асимптотой графика при .
С «плюс бесконечностью» всё тривиальнее:
А прямая — при .
Ответ :
Если ;
, если .
Не удержусь от графического изображения:
Это одна из ветвей гиперболы .
Не редкость, когда потенциальное наличие асимптот изначально ограничено областью определения функции :
Пример 11
Исследовать график функции на наличие асимптот
Решение : очевидно, что , поэтому рассматриваем только правую полуплоскость, где есть график функции.
1) Функция непрерывна на интервале , а значит, если вертикальная асимптота и существует, то это может быть только ось ординат. Исследуем поведение функции вблизи точки справа :
Исследуем поведение функции вблизи точки справа :
Обратите внимание, здесь НЕТ неопределённости (на таких случаях акцентировалось внимание в начале статьи Методы решения пределов) .
Таким образом, прямая (ось ординат) является вертикальной асимптотой для графика функции при .
2) Исследование на наклонную асимптоту можно провести по полной схеме, но в статье Правила Лопитал мы выяснили, что линейная функция более высокого порядка роста, чем логарифмическая, следовательно: (см. Пример 1 того же урока).
Вывод: ось абсцисс является горизонтальной асимптотой графика функции при .
Ответ :
Если ;
, если .
Чертёж для наглядности:
Интересно, что у вроде бы похожей функции асимптот нет вообще (желающие могут это проверить).
Два заключительных примера для самостоятельного изучения:
Пример 12
Исследовать график функции на наличие асимптот
Для проверки на вертикальные асимптоты сначала нужно найти область определения функции , а затем вычислить пару односторонних пределов в «подозрительных» точках.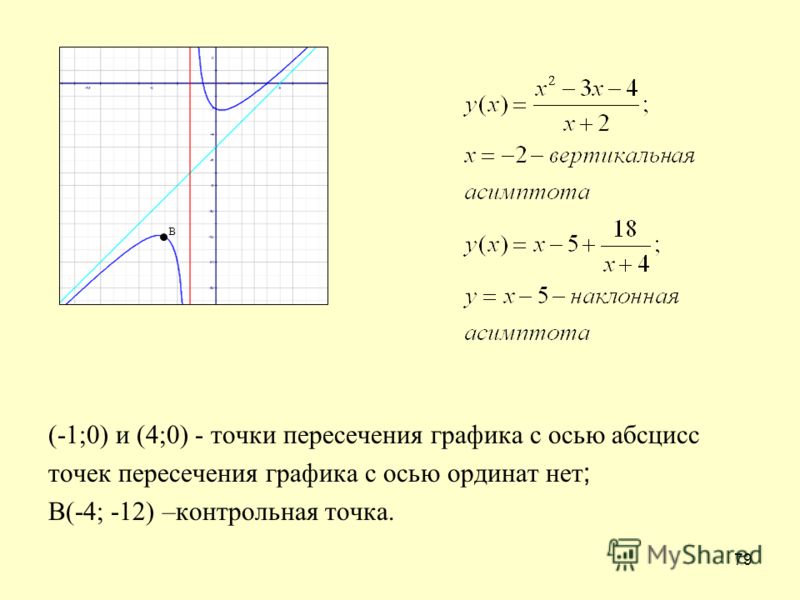 Наклонные асимптоты тоже не исключены, поскольку функция определена на «плюс» и «минус» бесконечности.
Наклонные асимптоты тоже не исключены, поскольку функция определена на «плюс» и «минус» бесконечности.
Пример 13
Исследовать график функции на наличие асимптот
А здесь могут быть только наклонные асимптоты, причём направления , следует рассмотреть отдельно.
Надеюсь, вы отыскали нужную асимптоту =)
Желаю успехов!
Решения и ответы:
Пример 2: Решение :
. Найдём односторонние пределы:
Прямая является вертикальной асимптотой графика функции при .
2) Наклонные асимптоты.
Прямая .
Ответ :
Чертёж к Примеру 3:
Пример 4: Решение :
1) Вертикальные асимптоты. Функция терпит бесконечный разрыв в точке . Вычислим односторонние пределы:
Примечание : бесконечно малое отрицательное число в чётной степени равно бесконечно малому положительному числу: .
Прямая является вертикальной асимптотой графика функции.
2) Наклонные асимптоты.
Прямая (ось абсцисс) является горизонтальной асимптотой графика функции при .
Ответ :
Во многих случаях построение графика функции облегчается, если предварительно построить асимптоты кривой.
Определение 1. Асимптотами называются такие прямые , к которым сколь угодно близко приближается график функции, когда переменная стремится к плюс бесконечности или к минус бесконечности.
Определение 2. Прямая называется асимптотой графика функции, если расстояние от переменной точки М графика функции до этой прямой стремится к нулю при неограниченном удалении точки М от начала координат по какой-либо ветви графика функции.
Различают три вида асимптот: вертикальные, горизонтальные и наклонные.
Вертикальные асимптоты
Определение .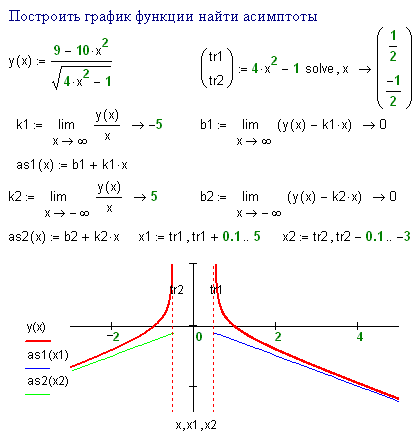 Прямая x = a является вертикальной асимптотой графика функции , если точка x = a является точкой разрыва второго рода для этой функции.
Прямая x = a является вертикальной асимптотой графика функции , если точка x = a является точкой разрыва второго рода для этой функции.
Из определения следует, что прямая x = a является вертикальной асимптотой графика функции f (x ) , если выполняется хотя бы одно из условий:
При этом функция f (x ) может быть вообще не определена соответственно при x ≥ a и x ≤ a .
Замечание:
Пример 1. График функции y =lnx имеет вертикальную асимптоту x = 0 (т.е. совпадающую с осью Oy ) на границе области определения, так как предел функции при стремлении икса к нулю справа равен минус бесконечности:
(рис. сверху).
самостоятельно, а затем посмотреть решения
Пример 2. Найти асимптоты графика функции .
Пример 3. Найти асимптоты графика функции
Горизонтальные асимптоты
Если
(предел функции при стремлении аргумента к плюс или минус бесконечности равен некоторому значению b ),
то y = b – горизонтальная асимптота кривой y = f (x )
(правая при иксе, стремящимся к плюс бесконечности, левая при иксе, стремящимся к минус бесконечности,
и двусторонняя, если пределы при стремлении икса к плюс или минус бесконечности равны).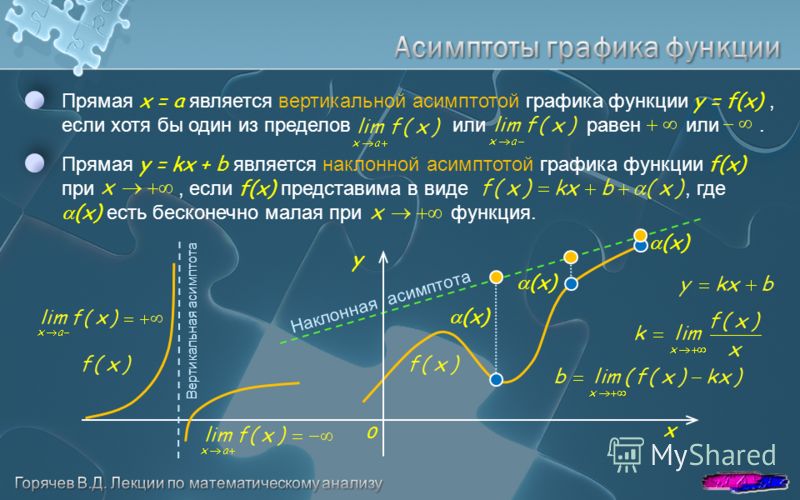
Пример 5. График функции
при a > 1 имеет левую горизонтальную асимпототу y = 0 (т.е. совпадающую с осью Ox ), так как предел функции при стремлении «икса» к минус бесконечности равен нулю:
Правой горизонтальной асимптоты у кривой нет, поскольку предел функции при стремлении «икса» к плюс бесконечности равен бесконечности:
Наклонные асимптоты
Вертикальные и горизонтальные асимптоты, которые мы рассмотрели выше, параллельны
осям координат, поэтому для их построения нам требовалось лишь определённое число — точка на оси
абсцисс или ординат, через которую проходит асимптота. Для наклонной асимптоты необходимо больше —
угловой коэффициент k , который показывает угол наклона прямой, и свободный член b , который показывает,
насколько прямая находится выше или ниже начала координат. Не успевшие забыть аналитическую геометрию,
а из неё — уравнения прямой, заметят, что для наклонной асимптоты находят уравнение
прямой с угловым коэффициентом . Существование наклонной асимптоты определяется следующей теоремой,
на основании которой и находят названные только что коэффициенты.
Существование наклонной асимптоты определяется следующей теоремой,
на основании которой и находят названные только что коэффициенты.
Теорема. Для того, чтобы кривая y = f (x ) имела асимптоту y = kx + b , необходимо и достаточно, чтобы существовали конечные пределы k и b рассматриваемой функции при стремлении переменной x к плюс бесконечности и минус бесконечности:
(1)
(2)
Найденные таким образом числа k и b и являются коэффициентами наклонной асимптоты.
В первом случае (при стремлении икса к плюс бесконечности) получается правая наклонная асимптота, во втором (при стремлении икса к минус бесконечности) – левая. Правая наклонная асимптота изображена на рис. снизу.
При нахождении уравнения наклонной асимптоты необходимо учитывать стремление икса
и к плюс бесконечности, и к минус бесконечности. У некоторых функций, например, у дробно-рациональных,
эти пределы совпадают, однако у многих функций эти пределы различны а также может существовать только
один из них.
При совпадении пределов при иксе, стремящемся к плюс бесконечности и к минус бесконечности прямая y = kx + b является двусторонней асимптотой кривой.
Если хотя бы один из пределов, определяющих асимптоту y = kx + b , не существует, то график функции не имеет наклонной асимптоты (но может иметь вертикальную).
Нетрудно видеть, что горизонтальная асимптота y = b является частным случаем наклонной y = kx + b при k = 0 .
Поэтому если в каком-либо направлении кривая имеет горизонтальную асимптоту, то в этом направлении нет наклонной, и наоборот.
Пример 6. Найти асимптоты графика функции
Решение. Функция определена на всей числовой прямой, кроме x = 0 , т.е.
Поэтому в точке разрыва x = 0 кривая может иметь вертикальную асимптоту. Действительно, предел функции при стремлении икса к нулю слева равен плюс бесконечности:
Следовательно, x = 0
– вертикальная асимптота
графика данной функции.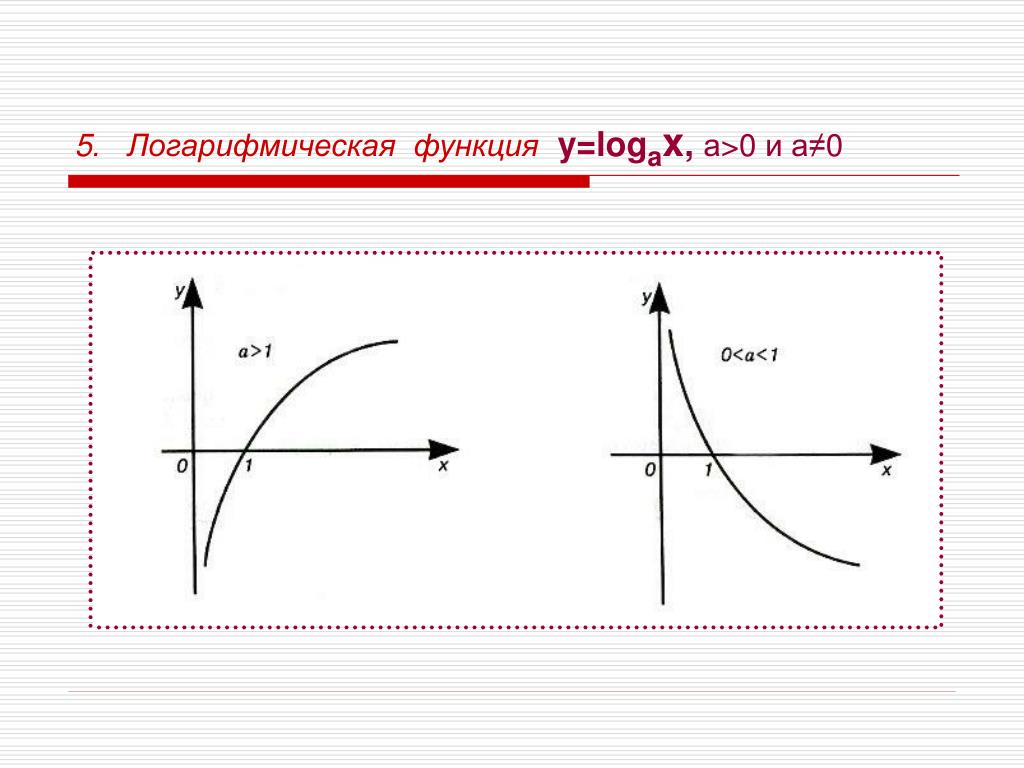
Горизонтальной асимптоты график данной функции не имеет, так как предел функции при стремлении икса к плюс бесконечности равен плюс бесконечности:
Выясним наличие наклонной асимптоты:
Получили конечные пределы k = 2 и b = 0 . Прямая y = 2x является двусторонней наклонной асимптотой графика данной функции (рис. внутри примера).
Пример 7. Найти асимптоты графика функции
Решение. Функция имеет одну точку разрыва x = −1 . Вычислим односторонние пределы и определим вид разрыва:
Заключение: x = −1 — точка разрыва второго рода, поэтому прямая x = −1 является вертикальной асимптотой графика данной функции.
Ищем наклонные асимптоты. Так как данная функция — дробно-рациональная, пределы при и при будут совпадать. Таким образом, находим коэффициенты для подстановки в уравнение прямой — наклонной асимптоты:
Подставляя найденные коэффициенты в уравнение прямой с угловым коэффициентом, получаем уравнение наклонной асимптоты:
y = −3x + 5
.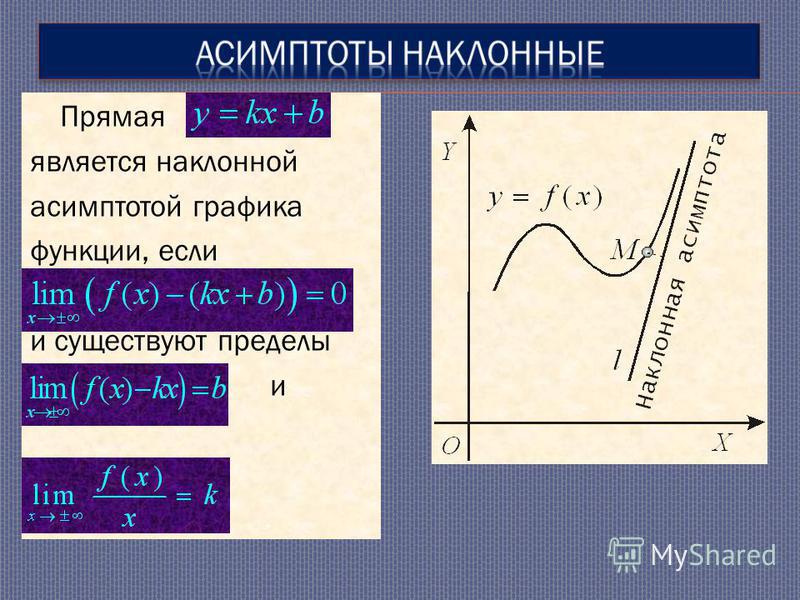
На рисунке график функции обозначен бордовым цветом, а асимптоты — чёрным.
Пример 8. Найти асимптоты графика функции
Решение. Так как данная функция непрерывна, её график не имеет вертикальных асимптот. Ищем наклонные асимптоты:
.
Таким образом, график данной функции имеет асимптоту y = 0 при и не имеет асиптоты при .
Пример 9. Найти асимптоты графика функции
Решение. Сначала ищем вертикальные асимптоты. Для этого найдём область определения функции. Функция определена, когда выполняется неравенство и при этом . Знак переменной x совпадает со знаком . Поэтому рассмотрим эквивалентное неравенство . Из этого получаем область определения функции: . Вертикальная асимптота может быть только на границе области определения функции. Но x = 0 не может быть вертикальной асимптотой, так как функция определена при x = 0 .
Рассмотрим правосторонний предел при (левосторонний предел не существует):
.
Точка x = 2 — точка разрыва второго рода, поэтому прямая x = 2 — вертикальная асимптота графика данной функции.
Ищем наклонные асимптоты:
Итак, y = x + 1 — наклонная асимптота графика данной функции при . Ищем наклонную асимптоту при :
Итак, y = −x − 1 — наклонная асимптота при .
Пример 10. Найти асимптоты графика функции
Решение. Функция имеет область определения . Так как вертикальная асимптота графика этой функции может быть только на границе области определения, найдём односторонние пределы функции при .
Асимптотой графика функции y = f(x) называется прямая, обладающая тем свойством, что расстояние от точки (х, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
На рисунке 3.10. приведены графические примеры вертикальной , горизонтальных и наклонной асимптот.
Нахождение асимптот графика основано на следующих трех теоремах.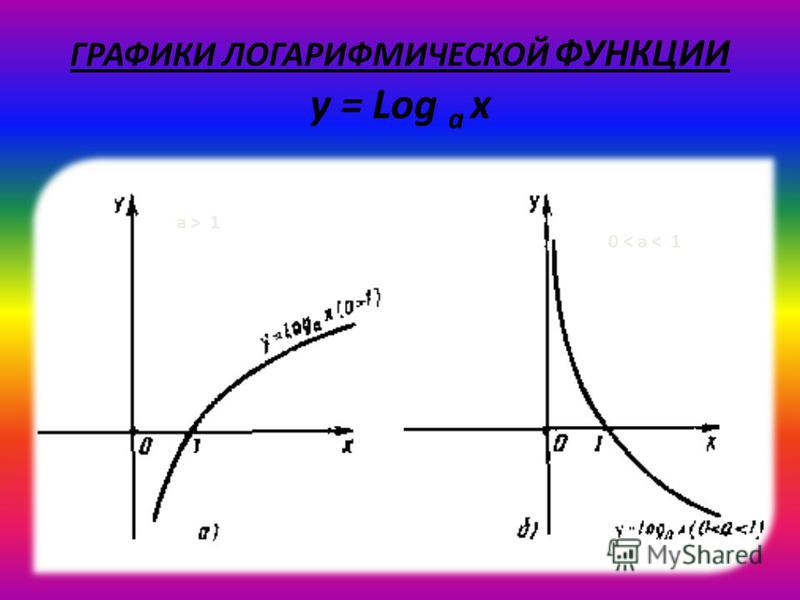
Теорема о вертикальной асимптоте. Пусть функция у = f(х) определена в некоторой окрестности точки x 0 (исключая, возможно, саму эту точку) и хотя бы один из односторонних пределов функции равен бесконечности, т.е. Тогда прямая x = x 0 является вертикальной асимптотой графика функции у = f(х).
Очевидно, что прямая х = х 0 не может быть вертикальной асимптотой, если функция непрерывна в точке х 0 , так как в этом случае . Следовательно, вертикальные асимптоты следует искать в точках разрыва функции или на концах ее области определения.
Теорема о горизонтальной асимптоте. Пусть функция у = f(х) определена при достаточно больших х и существует конечный предел функции . Тогда прямая у = b есть горизонтальная асимптота графика функции.
Замечание. Если конечен только один из пределов , то функция имеет соответственно левостороннюю либо правостороннюю горизонтальную асимптоту.
В том случае, если , функция может иметь наклонную асимптоту.
Теорема о наклонной асимптоте.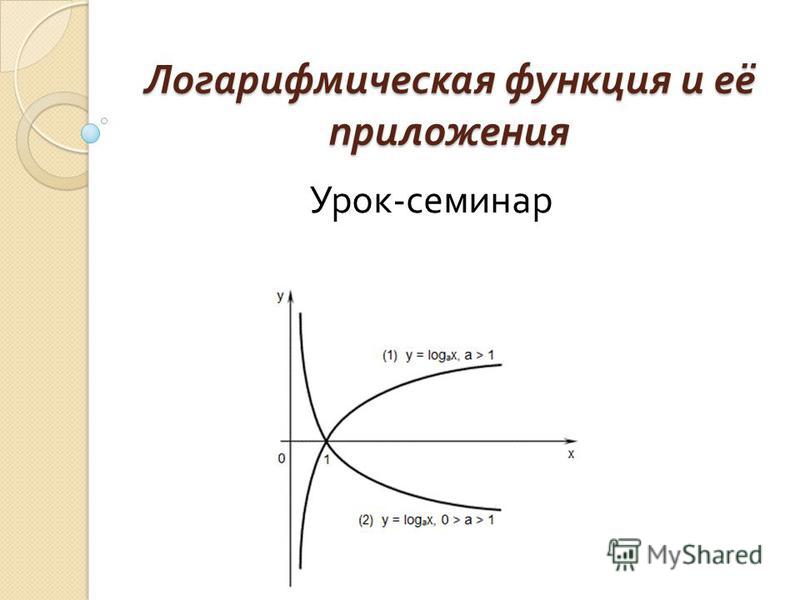 Пусть функция у = f(х) определена при достаточно больших х и существуют конечные пределы . Тогда прямая y = kx + b является наклонной асимптотой графика функции.
Пусть функция у = f(х) определена при достаточно больших х и существуют конечные пределы . Тогда прямая y = kx + b является наклонной асимптотой графика функции.
Без доказательства.
Наклонная асимптота, так же, как и горизонтальная, может быть правосторонней или левосторонней, если в базе соответствующих пределов стоит бесконечность определенного знака.
Исследование функций и построение их графиков обычно включает следующие этапы:
1. Найти область определения функции.
2. Исследовать функцию на четность-нечетность.
3. Найти вертикальные асимптоты, исследовав точки разрыва и поведение функции на границах области определения, если они конечны.
4. Найти горизонтальные или наклонные асимптоты, исследовав поведение функции в бесконечности.
5. Найти экстремумы и интервалы монотонности функции.
6. Найти интервалы выпуклости функции и точки перегиба.
7. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Дифференциал функции
Можно доказать, что если функция имеет при некоторой базе предел, равный конечному числу, то ее можно представить в виде суммы этого числа и бесконечно малой величины при той же базе (и наоборот): .
Применим это теорему к дифференцируемой функции: .
Таким образом, приращение функции Dу состоит из двух слагаемых: 1) линейного относительно Dх, т.е. f `(x)Dх; 2) нелинейного относительно Dх, т.е. a(Dx)Dх. При этом, так как , это второе слагаемое представляет собой бесконечно малую более высокого порядка, чем Dх (при стремлении Dх к нулю оно стремится к нулю еще быстрее).
Дифференциалом функции называется главная, линейная относительно Dх часть приращения функции, равная произведению производной на приращение независимой переменной dy = f `(x)Dх.
Найдем дифференциал функции у = х.
Так как dy = f `(x)Dх = x`Dх = Dх, то dx = Dх, т.е. дифференциал независимой переменной равен приращению этой переменной.
Поэтому формулу для дифференциала функции можно записать в виде dy = f `(x)dх. Именно поэтому одно из обозначений производной представляет собой дробь dy/dх.
Именно поэтому одно из обозначений производной представляет собой дробь dy/dх.
Геометрический смысл дифференциала проиллюстрирован
рисунком 3.11. Возьмем на графике функции y = f(x) произвольную точку М(х, у). Дадим аргументу х приращение Dх. Тогда функция y = f(x) получит приращение Dy = f(x + Dх) — f(x). Проведем касательную к графику функции в точке М, которая образует угол a с положительным направлением оси абсцисс, т.е. f `(x) = tg a. Из прямоугольного треугольника MKN
KN = MN*tg a = Dх*tg a = f `(x)Dх = dy.
Таким образом, дифференциал функции есть приращение ординаты касательной, проведенной к графику функции в данной точке, когда х получает приращение Dх.
Свойства дифференциала в основном аналогичны свойствам производной:
3. d(u ± v) = du ± dv.
4. d(uv) = v du + u dv.
5. d(u/v) = (v du — u dv)/v 2 .
Однако, существует важное свойство дифференциала функции, которым не обладает ее производная – это инвариантность формы дифференциала .
Из определения дифференциала для функции y = f(x) дифференциал dy = f `(x)dх. Если эта функция y является сложной, т.е. y = f(u), где u = j(х), то y = f и f `(x) = f `(u)*u`. Тогда dy = f `(u)*u`dх. Но для функции
u = j(х) дифференциал du = u`dх. Отсюда dy = f `(u)*du.
Сравнивая между собой равенства dy = f `(x)dх и dy = f `(u)*du, убедимся, что формула дифференциала не изменяется, если вместо функции от независимой переменной х рассматривать функцию от зависимой переменной u. Это свойство дифференциала и получило название инвариантности (т.е. неизменности) формы (или формулы) дифференциала.
Однако в этих двух формулах все же есть различие: в первой из них дифференциал независимой переменной равен приращению этой переменной, т.е. dx = Dx, а во в торой дифференциал функции du есть лишь линейная часть приращения этой функции Du и только при малых Dх du » Du.
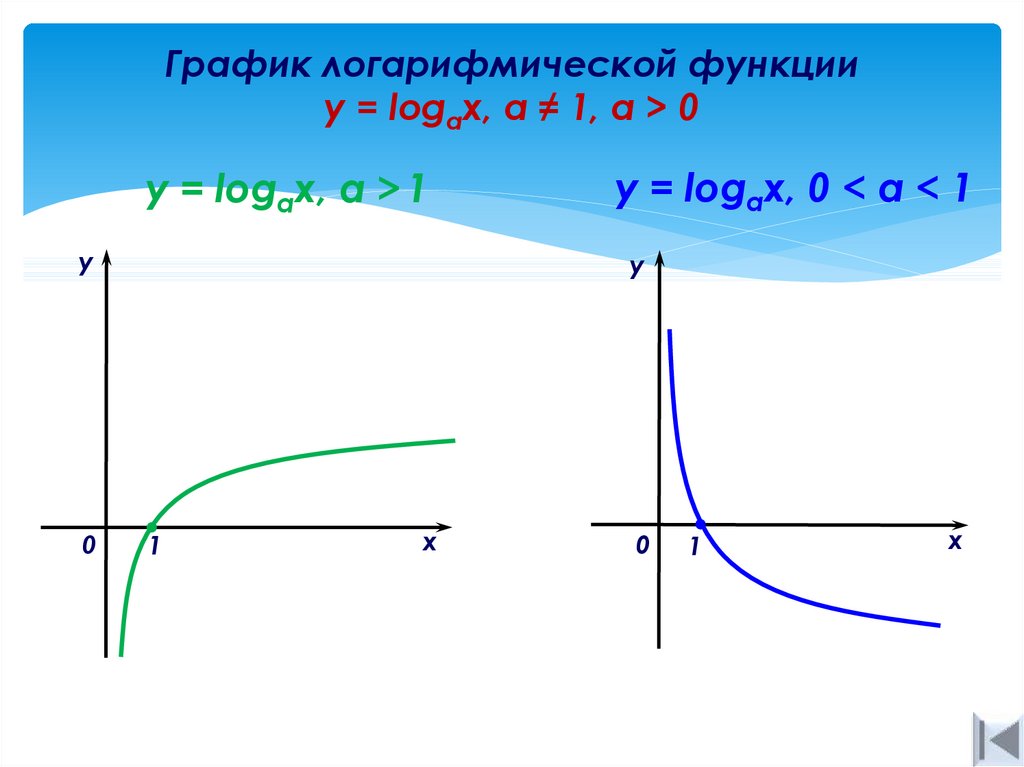
Графики логарифмической функции – объяснение и примеры
После определения логарифмическая функция y = log b x является обратной функцией экспоненциальной функции y = b x . Теперь мы можем перейти к построению графиков логарифмических функций, рассмотрев взаимосвязь между экспоненциальными и логарифмическими функциями.
Теперь мы можем перейти к построению графиков логарифмических функций, рассмотрев взаимосвязь между экспоненциальными и логарифмическими функциями.
Но прежде чем перейти к теме построения графиков логарифмических функций, важно ознакомиться со следующими терминами :
- Домен функции
Домен функции — это набор значений, которые вы можете подставить в функцию, чтобы получить приемлемый ответ.
- Диапазон функции
Это набор значений, которые вы получаете после замены значений в домене для переменной.
- Асимптоты
Существуют три типа асимптот , а именно; вертикальный , горизонтальный и наклонный . Вертикальная асимптота — это значение x, при котором функция неограниченно растет вблизи.
Горизонтальные асимптоты — это постоянные значения, к которым f(x) приближается по мере неограниченного роста x. Наклонные асимптоты — это полиномы первой степени, к которым f (x) приближается, когда x неограниченно растет.
Наклонные асимптоты — это полиномы первой степени, к которым f (x) приближается, когда x неограниченно растет.
График логарифмической функции можно построить, изучив график экспоненциальной функции и поменяв местами x и y.
График экспоненциальной функции f(x) = b x или y = b x содержит следующие функции:
- Область определения экспоненциальной функции — действительные числа (-бесконечность, бесконечность).
- Диапазон также состоит из положительных вещественных чисел (0, бесконечность)
- График экспоненциальной функции обычно проходит через точку (0, 1). Это означает, что точка пересечения y находится в точке (0, 1).
- График показательной функции f(x) = b x имеет горизонтальную асимптоту при y = 0,
- Экспоненциальный график убывает слева направо, если 0 < b < 1, и этот случай известен как экспоненциальное затухание.
- Если основание функции f(x) = b x больше 1, то ее график будет возрастать слева направо и называется экспоненциальным ростом.

Глядя на приведенные выше признаки по одному, мы можем аналогичным образом вывести свойства логарифмических функций следующим образом:
- Логарифмическая функция будет иметь область определения (0, бесконечность).
- Диапазон логарифмической функции (−бесконечность, бесконечность).
- График логарифмической функции проходит через точку (1, 0), которая является обратной точкой (0, 1) для экспоненциальной функции.
- График логарифмической функции имеет вертикальную асимптоту при x = 0.
- График логарифмической функции убывает слева направо, если 0 < b < 1.
- И если основание функции больше 1, b > 1, то график будет возрастать слева направо.
Как построить график основной логарифмической функции?
Основная логарифмическая функция — это, как правило, функция без смещения по горизонтали или вертикали.
Вот шаги для создания графика основной логарифмической функции.
- Поскольку все логарифмические функции проходят через точку (1, 0), мы находим и ставим точку в этой точке.

- Чтобы кривая не касалась оси Y, мы рисуем асимптоту при x = 0.
- Если основание функции больше 1, увеличивайте кривую слева направо. Точно так же, если основание меньше 1, уменьшайте кривую слева направо. 9Пример 1
Решение
- Очевидно, логарифмическая функция должна иметь область определения и диапазон значений (0, бесконечность) и (−бесконечность, бесконечность)
- Поскольку функция f(x) = log 2 x больше, чем 1, мы будем увеличивать нашу кривую слева направо, как показано ниже.
- Мы не можем увидеть вертикальную асимптоту при x = 0, потому что она скрыта осью y. Пример 2 Все логарифмические кривые проходят через эту точку.
- Нарисуйте асимптоту при x = 0.
- Поскольку основание функции y = log 5 x меньше 1, мы будем уменьшать нашу кривую слева направо.
- Функция y = log 5 x также будет иметь (0, бесконечность) и (−бесконечность, бесконечность) в качестве домена и диапазона.

Построение графика логарифмической функции с горизонтальным сдвигом
Логарифмические функции с горизонтальным сдвигом имеют вид f(x) = log b (x + h) или f (x) = log b ( x – h), где h = сдвиг по горизонтали. Знак горизонтального смещения определяет направление смещения. Если знак положительный, сдвиг будет отрицательным, а если знак отрицательный, сдвиг станет положительным.
Применяя сдвиг по горизонтали, свойства логарифмической функции изменяются следующим образом:
- Точка пересечения x перемещается влево или вправо на фиксированное расстояние, равное h.
- Вертикальная асимптота перемещается на расстояние, равное h.
- Также изменяется домен функции.
Пример 3
Нарисуйте график функции f(x) = log 2 (x + 1) и укажите область определения и диапазон функции.
Solution
⟹ Domain: (− 1, infinity)
⟹ Range: (−infinity, infinity)
Example 4
Graph y = log 0.
 5 (x – 1) и укажите домен и диапазон.
5 (x – 1) и укажите домен и диапазон.Решение
⟹ Домен: (1, бесконечность)
⟹ Диапазон: (−бесконечность, бесконечность)
Как построить график функции с вертикалью?
Логарифмическая функция с горизонтальным и вертикальным сдвигом имеет вид f(x) = log b (x) + k, где k = вертикальное смещение.
Сдвиг по вертикали влияет на свойства функции следующим образом:
- Точка пересечения по оси x будет перемещаться вверх или вниз на фиксированное расстояние k
Пример 5 = log 3 (x – 4) и указать диапазон и домен функции.
Решение
⟹ Домен: (0, бесконечность)
⟹ Диапазон: (−бесконечность, бесконечность)
Функции с горизонтальным и вертикальным сдвигом
Логарифмическая функция с горизонтальным и вертикальным сдвигом имеет вид (x) = log b (x + h) + k, где k и h — вертикальный и горизонтальный сдвиги , соответственно.

Пример 6
Постройте график логарифмической функции y = log 3 (x – 2) + 1 и найдите область определения и диапазон функции.
Решение
⟹ Домен: (2, бесконечность)
⟹ Диапазон: (−бесконечность, бесконечность)
Пример 7
Постройте график логарифмической функции y = log 3 (x + 2) + 1 и найдите область определения и диапазон функции.
Решение
⟹ Домен: (- 2, бесконечность)
⟹ Диапазон: (−бесконечность, бесконечность)
Предыдущий урок | Главная страница | Следующий урокГоризонтальные и вертикальные сдвиги логарифмических функций
Результаты обучения
- График горизонтальных и вертикальных сдвигов логарифмических функций.
Как мы упоминали в начале раздела, преобразования логарифмических функций ведут себя аналогично преобразованиям других родительских функций.
 Мы можем сдвигать, растягивать, сжимать и отражать родительскую функцию [латекс]у={\mathrm{log}}_{b}\left(x\right)[/latex] без потери формы.
Мы можем сдвигать, растягивать, сжимать и отражать родительскую функцию [латекс]у={\mathrm{log}}_{b}\left(x\right)[/latex] без потери формы.График горизонтального смещения [латекс]f\влево(х\вправо)={\mathrm{log}}_{b}\влево(х\вправо)[/латекс]
При добавлении константы c на вход родительской функции [latex]f\left(x\right)=\text{log}_{b}\left(x\right)[/latex], результатом является сдвиг по горизонтали c единиц в направлении , противоположном знаку на c . Чтобы визуализировать горизонтальные сдвиги, мы можем наблюдать общий график родительской функции [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] рядом сдвиг влево, [латекс]g\влево(х\вправо)={\mathrm{log}}_{b}\влево(х+с\вправо)[/латекс], и сдвиг вправо, [латекс]h \left(x\right)={\mathrm{log}}_{b}\left(xc\right)[/latex], где c > 0,
На приведенных ниже графиках показаны изменения точек пересечения по оси x, вертикальных асимптот и уравнений логарифмической функции, сдвинутой вправо или влево.

Общее примечание: горизонтальные сдвиги родительской функции [latex]y=\text{log}_{b}\left(x\right)[/latex]
Для любой константы c функция [latex ]f\left(x\right)={\mathrm{log}}_{b}\left(x+c\right)[/latex]
- сдвигает родительскую функцию [latex]y={\mathrm{ log}}_{b}\left(x\right)[/latex] слева c единиц, если c > 0.
- сдвигает родительскую функцию [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] вправо c единиц, если c < 0,
- имеет вертикальную асимптоту x = – c .
- имеет домен [latex]\left(-c,\infty \right)[/latex].
- имеет диапазон [латекс]\влево(-\infty,\infty\вправо)[/латекс].
Как: Дана логарифмическая функция формы Горизонтальный сдвиг
- Определение смещения по горизонтали:
- Если c > 0, сдвиньте график [латекс]f\влево(х\вправо)={\mathrm{log}}_{b}\влево(х\вправо)[/латекс] влево c единиц.

- Если c < 0, сдвиньте график [латекс]f\влево(х\вправо)={\mathrm{log}}_{b}\влево(х\вправо)[/латекс] вправо c единицы.
- Если c > 0, сдвиньте график [латекс]f\влево(х\вправо)={\mathrm{log}}_{b}\влево(х\вправо)[/латекс] влево c единиц.
- Нарисуйте вертикальную асимптоту x = – c .
- Определите три ключевых момента родительской функции. Найдите новые координаты для сдвинутых функций, вычитая c из координаты x в каждой точке.
- Отметьте три точки.
- Домен [latex]\left(-c,\infty \right)[/latex], диапазон [latex]\left(-\infty ,\infty \right)[/latex], а вертикальная асимптота x = –c.
Пример: графическое изображение горизонтального смещения родительской функции [latex]y=\text{log}_{b}\left(x\right)[/latex]
Эскиз горизонтального смещения [latex]f\left( x\right)={\mathrm{log}}_{3}\left(x — 2\right)[/latex] вместе со своей родительской функцией. Включите ключевые точки и асимптоты на графике. Укажите домен, диапазон и асимптоту.
Показать решение
Попробуйте
Нарисуйте график [латекс]f\left(x\right)={\mathrm{log}}_{3}\left(x+4\right)[/latex] рядом с его родительской функцией .
 Включите ключевые точки и асимптоты на графике. Укажите домен, диапазон и асимптоту.
Включите ключевые точки и асимптоты на графике. Укажите домен, диапазон и асимптоту.Показать решение
График вертикального смещения [latex]y=\text{log}_{b}\left(x\right)[/latex]
Когда константа d добавляется к родительской функции [latex]f \left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex], результатом будет вертикальное смещение d единиц в направлении знака d . Чтобы визуализировать вертикальные сдвиги, мы можем наблюдать общий график родительской функции [latex]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] рядом с сдвиг вверх, [латекс]г\влево(х\вправо)={\mathrm{log}}_{b}\влево(х\вправо)+d[/латекс], и сдвиг вниз, [латекс]ч \left(x\right)={\mathrm{log}}_{b}\left(x\right)-d[/latex].
Общее примечание: вертикальные сдвиги родительской функции [latex]y=\text{log}_{b}\left(x\right)[/latex]
Для любой константы d функция [латекс]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)+d[/latex]
- сдвигает родительскую функцию [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] вверх на d единиц, если d > 0,
- сдвигает родительскую функцию [latex]y={\mathrm{log}}_{b}\left(x\right)[/latex] вниз на d единиц, если d < 0,
- имеет вертикальную асимптоту x = 0, .
- имеет домен [латекс]\левый(0,\infty\правый)[/латекс].
- имеет диапазон [латекс]\влево(-\infty,\infty\вправо)[/латекс].

Практическое руководство. Дана логарифмическая функция вида [латекс]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)+d[/latex], graph Вертикальное смещение
- Определите вертикальное смещение:
- Если d > 0, сдвиньте график [латекс]f\left(x\right)={\mathrm{log}}_{b}\left(x\right)[/latex] вверх на d единиц.
- Если d < 0, сдвиньте график [латекс]f\влево(х\вправо)={\mathrm{log}}_{b}\влево(х\вправо)[/латекс] вниз на д ед.
- Нарисуйте вертикальную асимптоту x = 0,
- Определите три ключевых момента родительской функции. Найдите новые координаты для сдвинутых функций, добавив d к координате y каждой точки.
- Отметьте три точки.
- Домен: [латекс]\левый(0,\infty\правый)[/латекс], диапазон: [латекс]\левый(-\infty,\infty\правый)[/латекс], вертикальная асимптота: х = 0,
Пример: построение графика вертикального сдвига родительской функции [latex]y=\text{log}_{b}\left(x\right)[/latex]
Нарисуйте график [latex]f\left( x\right)={\mathrm{log}}_{3}\left(x\right)-2[/latex] рядом с его родительской функцией.
 Включите ключевые точки и асимптоты на графике. Укажите домен, диапазон и асимптоту.
Включите ключевые точки и асимптоты на графике. Укажите домен, диапазон и асимптоту.Показать решение
Попробуйте
Нарисуйте график [латекс]f\left(x\right)={\mathrm{log}}_{2}\left(x\right)+2[/latex] рядом с его родительской функцией . Включите ключевые точки и асимптоты на графике. Укажите домен, диапазон и асимптоту.
Показать решение
Поддержите!
У вас есть идеи по улучшению этого контента? Мы будем признательны за ваш вклад.
Улучшить эту страницуПодробнее
Все о логарифмических функциях (ответы на 7 часто задаваемых вопросов) – JDM Educational
Логарифмы часто используются в науке для моделирования таких явлений, как звук (в децибелах), сила землетрясения (по шкале Рихтера) и pH (для сила кислот или оснований). Логарифмические функции имеют некоторые интересные свойства при отображении в виде графика.
Итак, что нужно помнить о логарифмических функциях? Функция log b (x) не имеет точки пересечения по оси y и горизонтальной асимптоты, но имеет вертикальную асимптоту при x = 0.
 Она не имеет симметрии, но является зеркальным отражением своей обратной функции b x отражается через прямую у = х. Его область определения — положительные действительные числа, а диапазон — все действительные числа.
Она не имеет симметрии, но является зеркальным отражением своей обратной функции b x отражается через прямую у = х. Его область определения — положительные действительные числа, а диапазон — все действительные числа. Конечно, мы можем найти обратную логарифмическую функцию, если ограничим ее область определения. Некоторые вещи (например, домен и вертикальная асимптота) логарифмической функции изменятся, если мы сдвинем ее по горизонтали или умножим на минус.
В этой статье мы ответим на некоторые распространенные вопросы о логарифмических функциях. Мы также рассмотрим несколько примеров, чтобы прояснить концепции.
Начнем.
7 Часто задаваемые вопросы о логарифмах
Логарифмы на самом деле просто еще один способ говорить о показателях степени. Их графики обладают некоторыми свойствами, на которые мы можем рассчитывать, хотя они могут измениться, если мы изменим основную функцию логарифма.
Одна хитрая вещь — это идея точки пересечения y для логарифмической функции, поэтому мы начнем с нее.

Имеют ли логарифмические функции точку пересечения A Y?
Основная логарифмическая функция f(x) = log b (x) для действительного b > 0 не имеет точки пересечения y. Помните, что перехват y функции происходит, когда x = 0, но мы не можем подставить x = 0 для этой функции (подстановка нуля или отрицательных чисел для логарифма не определена).
Мы можем увидеть это алгебраически, переведя логарифмическую форму в экспоненциальную и попытавшись решить, когда x = 0:
- f(x) = log b (x) [определение основной логарифмической функции]
- y = log b (x) [заменить f(x) на y]
- b y = x экспоненциальная форма с использованием логарифмических правил]
- b y = 0 [подставьте x = 0, чтобы найти точку пересечения y]
Независимо от того, какое основание b мы используем для логарифма, значения y не существует такое, что b y = 0.
График логарифмической функции f(x) = log 2 (x). Независимо от того, какое значение y мы выберем, мы никогда не достигнем x = 0. Таким образом, основная логарифмическая функция f(x) = log b (x) не имеет точки пересечения y для любого действительного b > 0.
Таким образом, основная логарифмическая функция f(x) = log b (x) не имеет точки пересечения y для любого действительного b > 0.Однако мы можем создать логарифмическую функцию с точкой пересечения y, сдвинув функцию влево. Например, сдвинем функцию влево на 1 единицу.
Это легко сделать, заменив x на x + 1 в определении функции.
Итак, определим g(x) = log б (х + 1). Теперь мы можем найти точку пересечения y:
- g(x) = log b (x + 1) [определение модифицированной логарифмической функции]
- y = log b (x + 1) ) [заменить g(x) на y]
- b y = x + 1 [преобразовать в экспоненциальную форму]
- b y = 0 + 1 [подставить x = 0, чтобы найти точку пересечения y ]
- б у = 1
- y = 0 [b 0 = 1, независимо от того, какое значение b > 0 мы выбрали для логарифмической функции]
Таким образом, точка пересечения y для модифицированной логарифмической функции g(x) = log b (x + 1) — точка (0, 0).

В более общем случае логарифмическая функция h(x) = log b (x + c) имеет точку пересечения по оси y в точке (0, log b (c)), при условии, что мы выбираем c > 0 (то есть , сдвигаем функцию влево).
С другой стороны, если мы сдвинем основную логарифмическую функцию вправо, у нее все равно не будет пересечения по оси y.
Какова область определения логарифмической функции?
Область определения основной логарифмической функции f(x) = log b (x) для действительного b > 0 представляет собой множество положительных действительных чисел.
Как упоминалось ранее, x = 0 в этой функции не определено. Однако верно также и то, что x < 0 не определено, поскольку не существует значения y, при котором b y является отрицательным.
Однако мы можем изменить область определения логарифмической функции на нее влево или вправо. Например, давайте снова сдвинем функцию влево на 1 единицу.
И снова наша модифицированная логарифмическая функция имеет вид g(x) = log b (x + 1).

Мы по-прежнему можем использовать любое положительное действительное число x, но мы также можем подставлять отрицательные числа в набор (-1, 0]. То есть мы добавили этот набор в домен: любые числа от -1 до 0, кроме -1, но включая 0.
Таким образом, область изменения модифицированной логарифмической функции g(x) = log b (x + 1) лежит от -1 до бесконечности (исключая -1)
Если мы сдвинем функцию 1 единица вправо, чтобы получить журнал b (x – 1), новый домен будет от 1 до бесконечности (исключая 1).
В более общем случае логарифмическая функция h(x) = log b (x + c) имеет область определения (-c, бесконечность) для любого значения c (положительного или отрицательного).
Если мы подставим -x вместо x, мы получим вместо этого логарифмическую функцию log b (-x) с доменом всех отрицательных чисел.
Каков диапазон логарифмической функции?
Диапазон основной логарифмической функции f(x) = log b (x) — множество всех действительных чисел.
 Мы можем увидеть это, выбрав значение y в диапазоне (любое действительное число) и решив для x:
Мы можем увидеть это, выбрав значение y в диапазоне (любое действительное число) и решив для x:- f(x) = log b (x) [определение логарифмической функции]
- y = log b (x) [заменить f(x) на y]
- b y = x [преобразовать в экспоненциальную форму]
Итак, мы просто берем основание b и возводим его в y мощность, чтобы найти значение x, которое приведет к желаемому результату.
Мы знаем, что x in находится в области определения логарифмической функции. Причина в том, что x = b y — это положительное число, возведенное в положительное число, которое также должно быть положительным числом.
Даже если мы сдвинем базовую логарифмическую функцию вверх или вниз, диапазон по-прежнему состоит только из действительных чисел. Например, давайте определим g(x) = log b (x) + d, что является базовой логарифмической функцией, сдвинутой вверх (или вниз) на d единиц (d — действительное число, и оно может быть положительным или отрицательным).
 .
.Для заданного значения y мы найдем соответствующее значение x следующим образом:
- g(x) = log b (x) + d [определение модифицированной логарифмической функции]
- y = log b (x) + d [заменить f(x) на y]
- y – d = log b (x)
- b yd = x ]
Так как y и d оба действительные числа, то y – d просто еще одно действительное число. Тогда х = b y-d — положительное действительное число, которое находится в домене логарифмической функции.
Если мы отрицаем базовую функцию журнала, мы получаем логарифмическую функцию -log b (x), которая по-прежнему имеет диапазон всех действительных чисел.
Имеют ли логарифмические функции горизонтальные асимптоты?
Логарифмическая функция не имеет горизонтальной асимптоты. Однако у него есть вертикальная асимптота (подробнее об этом чуть позже).

С другой стороны, обратная логарифмическая функция (которая является экспоненциальной функцией) будет иметь горизонтальную асимптоту (но не вертикальную асимптоту).
Имеют ли логарифмические функции вертикальные асимптоты?
Логарифмическая функция имеет вертикальную асимптоту. Базовая логарифмическая функция f(x) = log b (x) для b > 0 имеет вертикальную асимптоту при x = 0.
Как упоминалось ранее, мы не можем подставить x = 0 (или любое отрицательное значение x) из-за области определения основной логарифмической функции.
Однако по мере того, как мы приближаемся к x = 0 справа (используя все меньшие и меньшие положительные значения x), мы получаем все большие и большие значения y.
Таблица ниже помогает проиллюстрировать использование b = 10, функцию g(x) = log 10 (x).
A table of values for the logarithmicx g(x) = log 10 (x) 0.  1
1-1 0.01 -2 0.001 -3 0,0001 -4 0,00001 -5 0,000001 -60759 0.0000001 -7 0.00000001 -8 0.000000001 -9
function g(x) = log 10 (x) . По мере уменьшения x
y принимает большее отрицательное значение.Как видно из таблицы, у нас есть вертикальная асимптота при x = 0.
Если вы сдвинете базовую логарифмическую функцию по горизонтали на c единиц, вы также сдвинете вертикальную асимптоту по горизонтали на c единиц.

То есть функция h(x) = log b (x – c) имеет вертикальную асимптоту при x = c (для любого действительного значения c).
Имеют ли логарифмические функции симметрию?
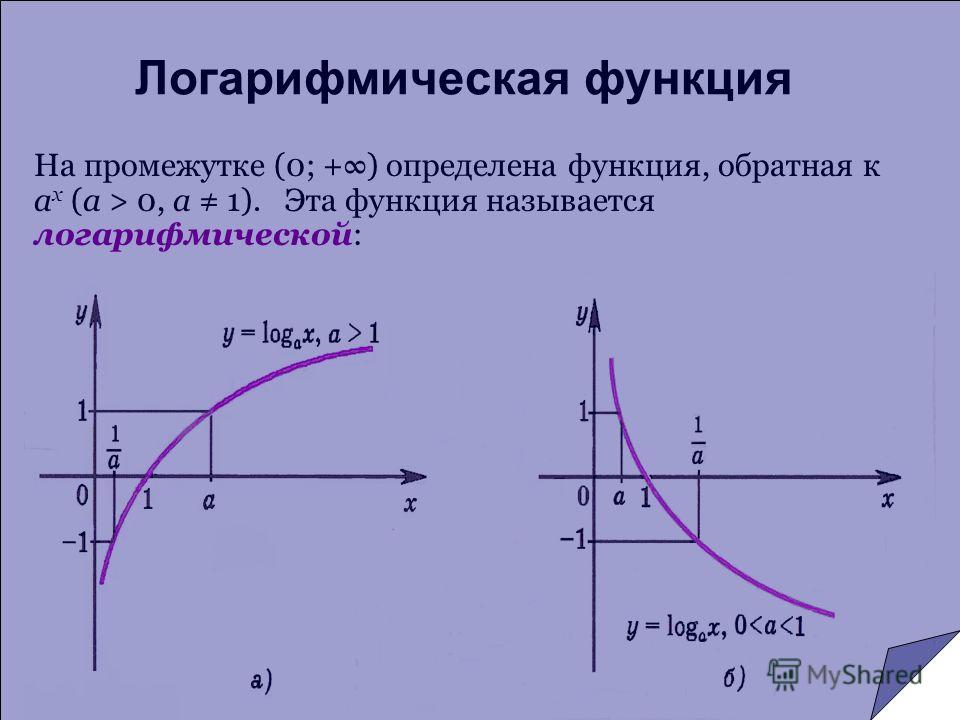
Логарифмическая функция сама по себе не имеет симметрии. Однако можно обнаружить некоторую симметрию, если рассмотреть логарифмическую функцию f(x) = log b (x) и обратную ей функцию f -1 (x) = b x (экспоненциальная функция с основание б).
Построив график обеих этих функций, мы увидим, что они являются зеркальными отображениями, если отразить одну из них через линию y = x.
Для иллюстрации вы можете увидеть график f(x) = log 2 (x) и f -1 (x) = 2 x ниже.
Здесь у нас есть график логарифмической функции f(x) = log 2 (x) [нижняя функция, выделена синим цветом] и экспоненциальной функции f -1 (x) = 2 x [верхняя функция, в красном]. Отражение одной функции через линию y = x [средняя линия, зеленая] дает нам другую функцию.
Вы можете узнать больше о построении графиков функции и обратной функции в моей статье здесь.
Как найти обратную логарифмическую функцию
Чтобы найти обратную логарифмическую функцию, выполните обычные действия:
- 1. Замените f(x) на y.
- 2. Решите уравнение для x.
- 3. Замените y на x и x на f -1 (x).
Давайте рассмотрим пример, чтобы увидеть, как это работает на практике.
Пример 1. Как найти обратную логарифмическую функцию
Найдем обратную логарифмическую функцию f(x) = log 2 (x).
Сначала замените f(x) на y, чтобы получить:
- y = log 2 (x)
. логарифмической формы в экспоненциальную форму]
Наконец, измените y на x и измените x на f -1 (x):
- x = 2 y f х) = 2 x
Итак, обратная логарифмическая функция f(x) = log 2 (x) равна f -1 (x) = 2 x .
Пример 2. Как найти обратную логарифмическую функцию
Найдем обратную логарифмическую функцию f(x) = log 3 (x – 4) + 5.
Сначала заменим f(x) по y, чтобы получить:
- y = log 3 (x – 4) + 5
Затем найдите x:
- y = log 3 (x – 4) + 5
- y – 5 = log 3 (x – 4) [вычесть 5 с обеих сторон]
- 9 0 5 5 x – 4 [переключиться с логарифмической формы на экспоненциальную]
- 3 y – 5 + 4 = x [добавить 4 к обеим сторонам]
Наконец, замените y на x и измените x на f -1 (x):
- x = 3 y – 5 + 4
- f -1 (x) = 3 x – 5 + 4
Итак, обратное выражение f(x) = log 3 (x – 4) + 5 равно f -1 (x) = 3 x – 5 + 4
Заключение
Теперь вы знаете ответы на некоторые распространенные вопросы о логарифмических функциях.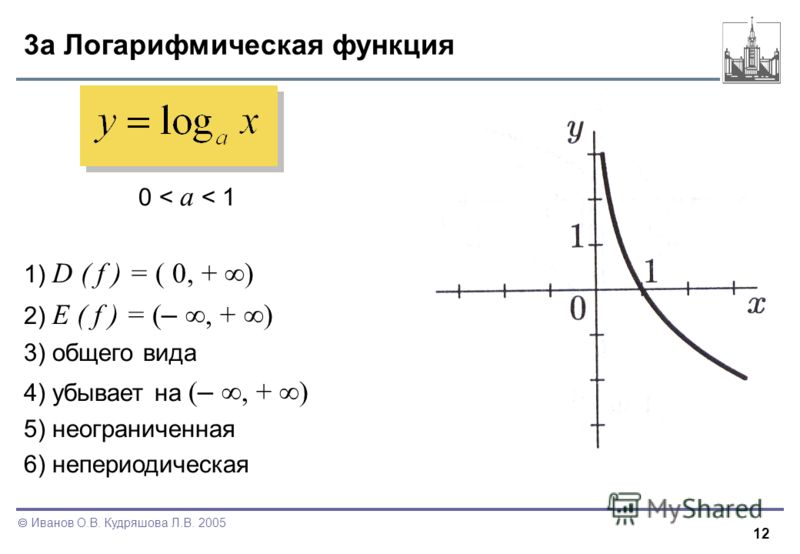

 28
28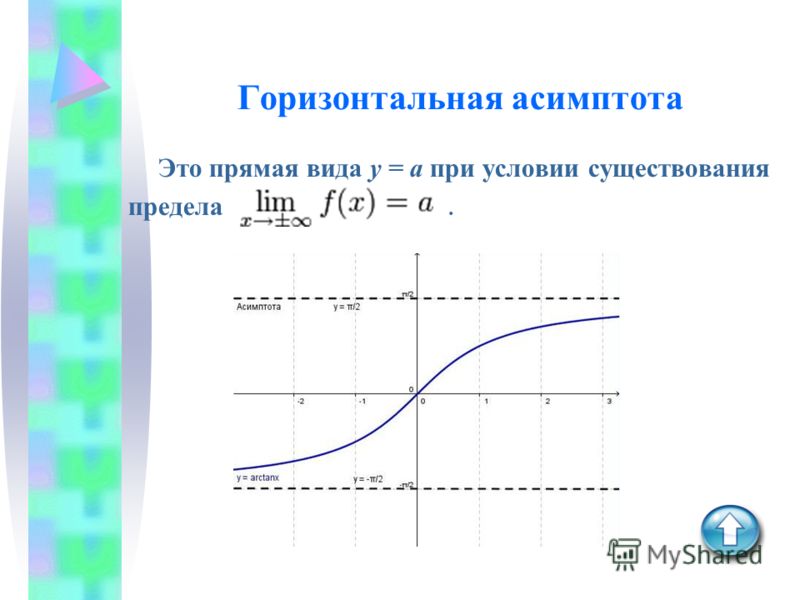 44.
44.


 5 (x – 1) и укажите домен и диапазон.
5 (x – 1) и укажите домен и диапазон.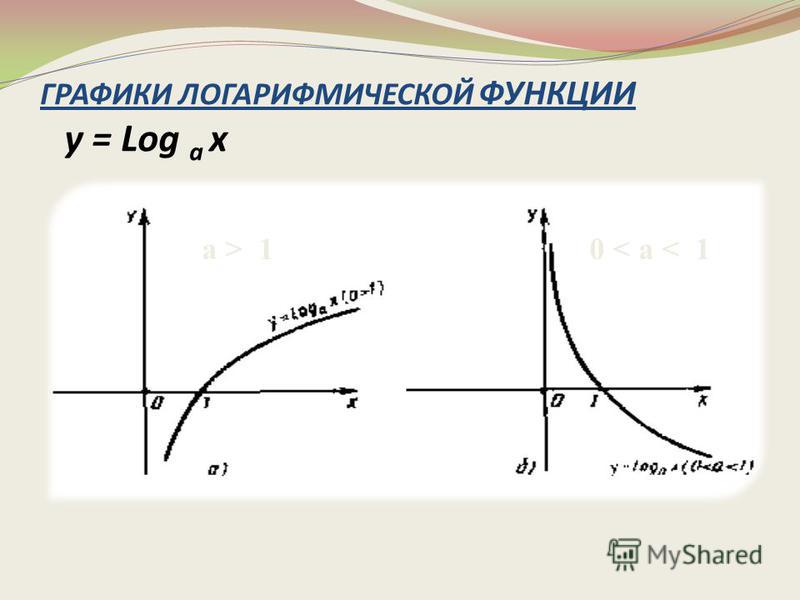
 Мы можем сдвигать, растягивать, сжимать и отражать родительскую функцию [латекс]у={\mathrm{log}}_{b}\left(x\right)[/latex] без потери формы.
Мы можем сдвигать, растягивать, сжимать и отражать родительскую функцию [латекс]у={\mathrm{log}}_{b}\left(x\right)[/latex] без потери формы.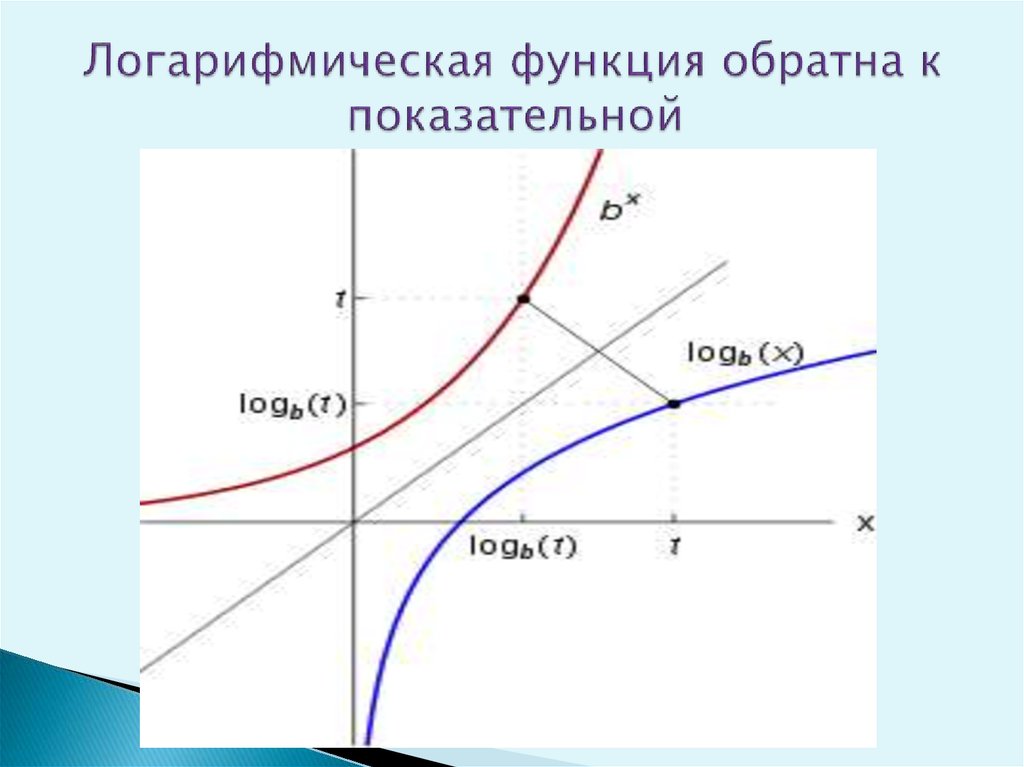

 Включите ключевые точки и асимптоты на графике. Укажите домен, диапазон и асимптоту.
Включите ключевые точки и асимптоты на графике. Укажите домен, диапазон и асимптоту.
 Включите ключевые точки и асимптоты на графике. Укажите домен, диапазон и асимптоту.
Включите ключевые точки и асимптоты на графике. Укажите домен, диапазон и асимптоту.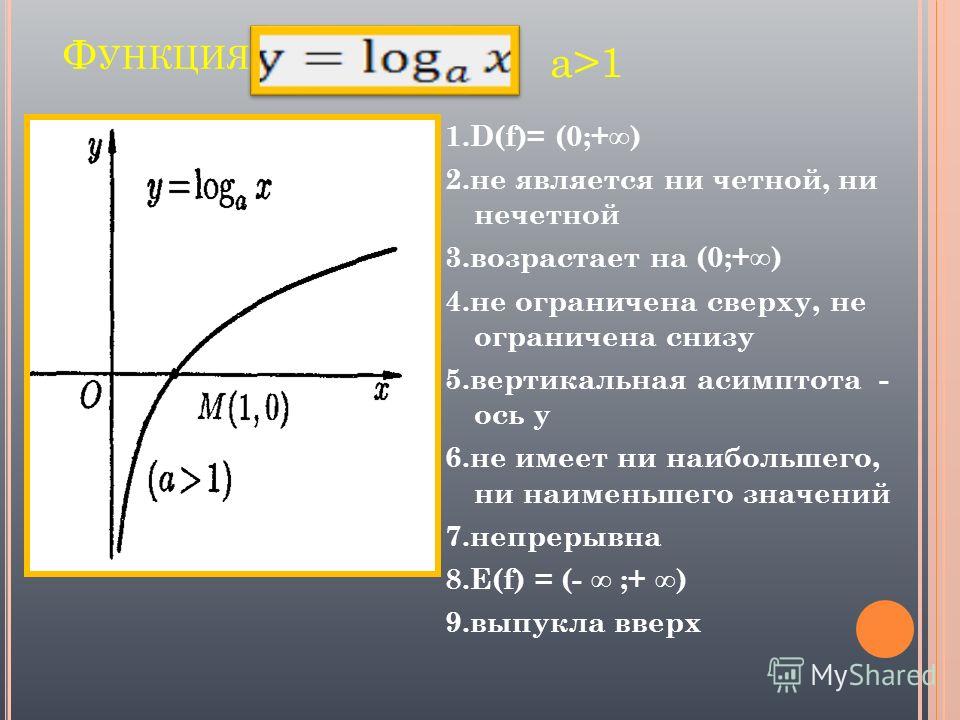 Она не имеет симметрии, но является зеркальным отражением своей обратной функции b x отражается через прямую у = х. Его область определения — положительные действительные числа, а диапазон — все действительные числа.
Она не имеет симметрии, но является зеркальным отражением своей обратной функции b x отражается через прямую у = х. Его область определения — положительные действительные числа, а диапазон — все действительные числа. 
 Таким образом, основная логарифмическая функция f(x) = log b (x) не имеет точки пересечения y для любого действительного b > 0.
Таким образом, основная логарифмическая функция f(x) = log b (x) не имеет точки пересечения y для любого действительного b > 0.

 Мы можем увидеть это, выбрав значение y в диапазоне (любое действительное число) и решив для x:
Мы можем увидеть это, выбрав значение y в диапазоне (любое действительное число) и решив для x: .
.
 1
1