как найти длину окружности зная диаметр
Таким образом, длину окружности (C ) можно вычислить, умножив константу π на диаметр (D ), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
C = πD = 2πR
где C — длина окружности, π — константа, D — диаметр окружности , R — радиус окружности.
Так как окружность является границей круга , то длину окружности можно также назвать длиной круга или периметром круга.
Задачи на длину окружности
Задача 1. Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
Сначала найдём диаметр окружности, умножив длину радиуса на 2:
D = 3,5 · 2 = 7 (м)
C ≈ 3,14 · 7 = 21,98 (м)
Задача 3. Найти радиус окружности, длина которой равна 7,85 м.
Найти радиус окружности, длина которой равна 7,85 м.
Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
Площадь круга
Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга :
S = πr 2
где S — площадь круга, а r — радиус круга.
Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.
Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 2 2 = 3,14 · 4 = 12,56 (см 2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
Сначала найдём радиус круга, разделив его диаметр на 2:
7: 2 = 3,5 (см)
теперь вычислим площадь круга по формуле:
S = πr 2 ≈ 3,14 · 3,5 2 = 3,14 · 12,25 = 38,465 (см 2)
Данную задачу можно решить и другим способом.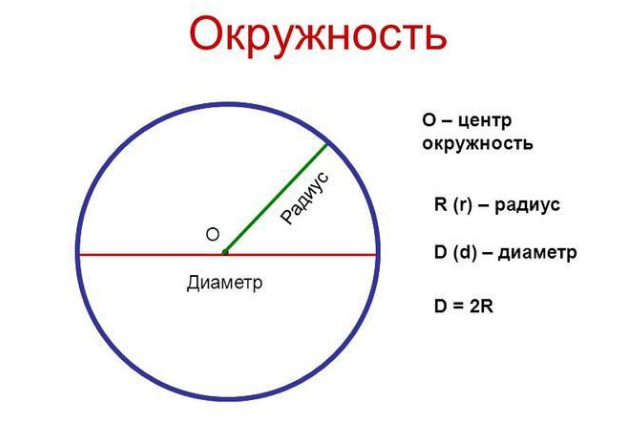 Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
| S = π | D 2 | ≈ 3,14 | 7 2 | = 3,14 | 49 | = | 153,86 | = 38,465 (см 2) |
| 4 | 4 | 4 | 4 |
Задача 3. Найти радиус круга, если его площадь равна 12,56 м 2 .
Чтобы найти радиус круга по его площади, надо площадь круга разделить π , а затем из полученного результата извлечь квадратный корень:
r = √S : π
следовательно радиус будет равен:
r ≈ √12,56: 3,14 = √4 = 2 (м)
Число
πДлину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно. Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге. В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом. Это отношение и обозначается буквой π .
Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π . В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое.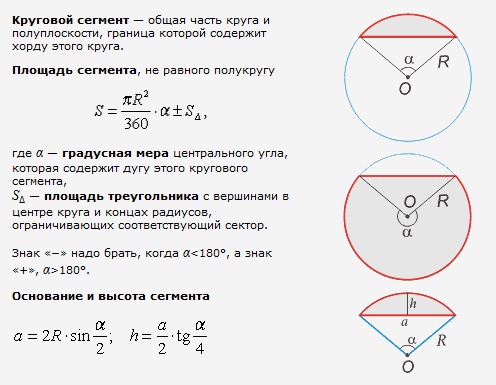 Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).

Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила.
Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см.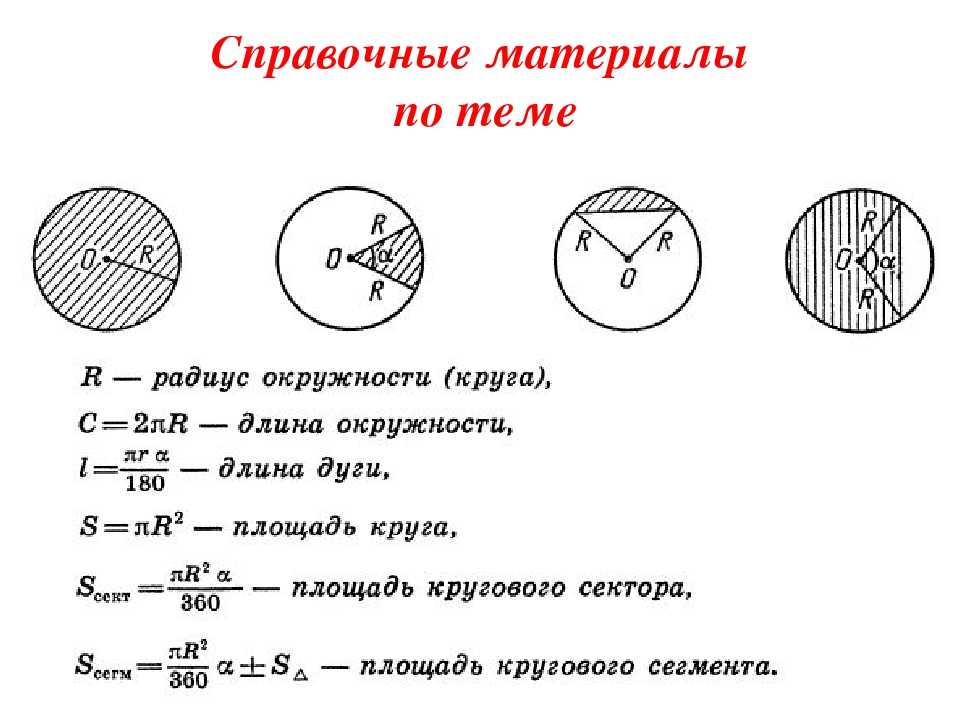 Тогда не составит труда найти длину этой полоски:
Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Вконтакте
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково.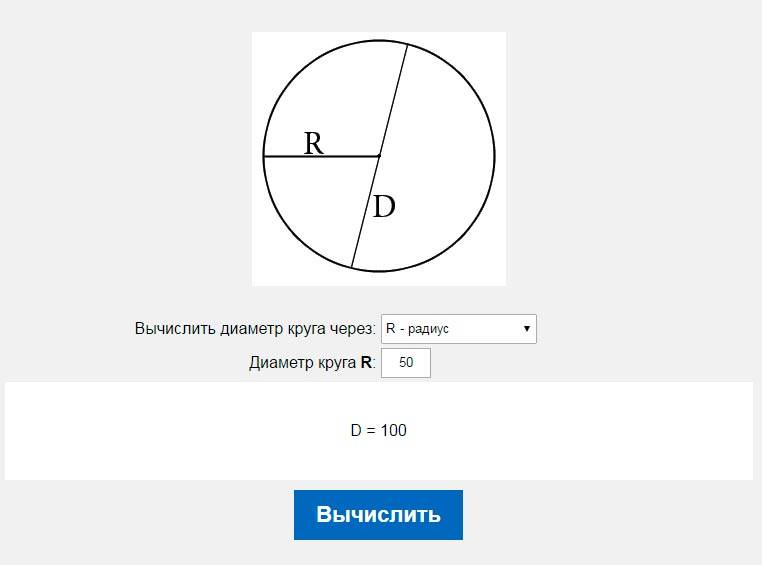 Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 5 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом.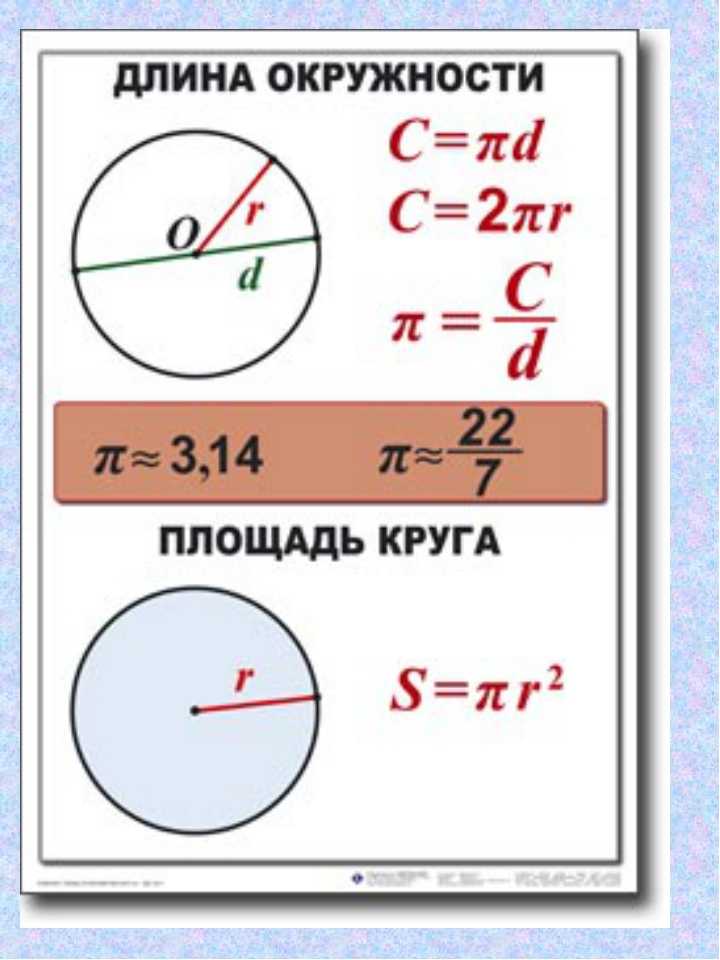 Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.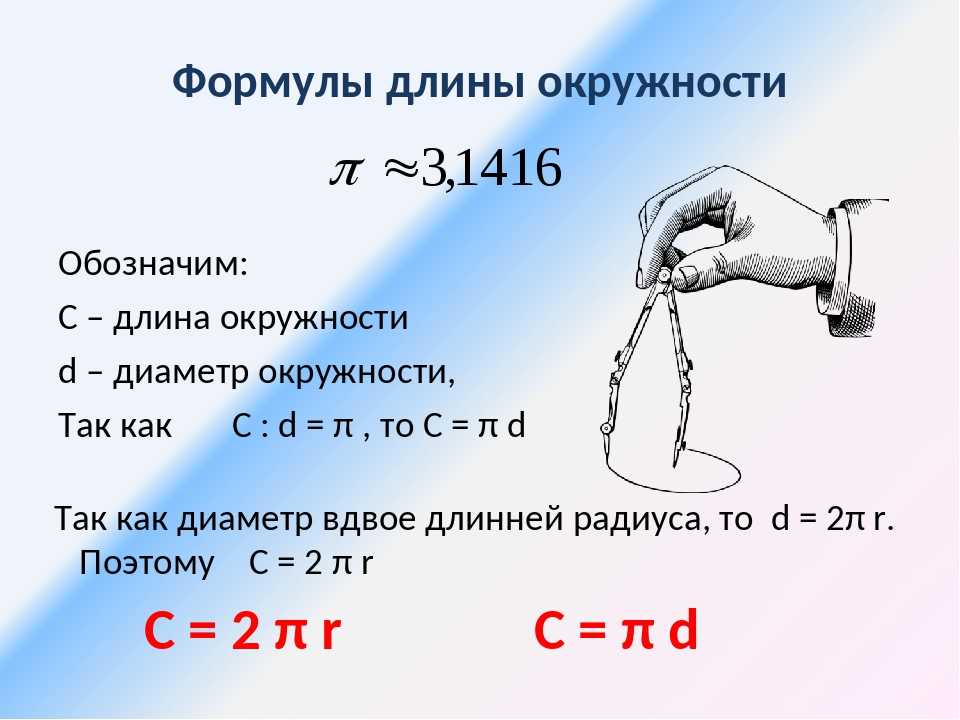
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
§ 117. Длина окружности и площадь круга.
1. Длина окружности. Окружностью называется замкнутая плоская кривая линия, все точки которой находятся на равном расстоянии от одной точки (О), называемой центром окружности (рис. 27).
Окружность вычерчивается с помощью циркуля. Для этого острую ножку циркуля ставят в центр, а другую (с карандашом) вращают вокруг первой до тех пор, пока конец карандаша не вычертит полной окружности. Расстояние от центра до любой точки окружности называется её радиусом. Из определения следует, что все радиусы одной окружности равны между собой.
Отрезок прямой линии (АВ), соединяющий две любые точки окружности и проходящий через её центр, называется диаметром . Все диаметры одной окружности равны между собой; диаметр равен двум радиусам.
Как найти длину окружности? Практически в некоторых случаях длину окружности можно найти путём непосредственного измерения. Это можно сделать, например, при измерении окружности сравнительно небольших предметов (ведро, стакан и т. п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
п.). Для этого можно воспользоваться рулеткой, тесьмой или шнуром.
В математике применяется приём косвенного определения длины окружности. Он состоит в вычислении по готовой формуле, которую мы сейчас выведем.
Если мы возьмём несколько больших и малых круглых предметов (монета, стакан, ведро, бочка и т. д.) и измерим у каждого из них длину окружности и длину диаметра, то получим для каждого предмета два числа (одно, измеряющее длину окружности, и другое — длину диаметра). Естественно, что для малых предметов эти числа будут небольшими, а для крупных — большими.
Однако если мы в каждом из этих случаев возьмём отношение полученных двух чисел (длины окружности и диаметра), то при тщательном выполнении измерения найдём почти одно и то же число. Обозначим длину окружности буквой С , длину диаметра буквой D , тогда отношение их будет иметь вид С: D . Фактические измерения всегда сопровождаются неизбежными неточностями. Но, выполнив указанный опыт и произведя необходимые вычисления, мы получим для отношения С: D примерно следующие числа: 3,13; 3,14; 3,15. Эти числа очень мало отличаются одно от другого.
Эти числа очень мало отличаются одно от другого.
В математике путём теоретических соображений установлено, что искомое отношение С: D никогда не меняется и оно равно бесконечной непериодической дроби, приближённое значение которой с точностью до десятитысячных долей равно 3,1416 . Это значит, что всякая окружность длиннее своего диаметра в одно и то же число раз. Это число принято обозначать греческой буквой π (пи). Тогда отношение длины окружности к диаметру запишется так: С: D = π . Мы будем ограничивать это число только сотыми долями, т. е. брать π = 3,14.
Напишем формулу для определения длины окружности.
Так как С: D = π , то
C = πD
т. е. длина окружности равна произведению числа π на диаметр.
Задача 1. Найти длину окружности (С ) круглой комнаты, если диаметр её D = 5,5 м.
Принимая во внимание изложенное выше, мы должны для решения этой задачи увеличить диаметр в 3,14 раза:
5,5 3,14 = 17,27 {м).
Задача 2. Найти радиус колеса, у которого длина окружности 125,6 см.
Эта задача обратна предыдущей. Найдём диаметр колеса:
125,6: 3,14 = 40 (см).
Найдём теперь радиус колеса:
40: 2 = 20 (см).
2. Площадь круга. Чтобы определить площадь круга, можно было бы начертить на бумаге круг данного радиуса, покрыть его прозрачной клетчатой бумагой и потом сосчитать клетки, находящиеся внутри окружности (рис. 28).
Но такой способ неудобен по многим причинам. Во-первых, вблизи контура круга получается ряд неполных клеток, о величине которых судить трудно. Во-вторых, нельзя покрыть листом бумаги большой предмет (круглую клумбу, бассейн, фонтан и др.). В-третьих, подсчитав клетки, мы всё-таки не получаем никакого правила, позволяющего нам решать другую подобную задачу. В силу этого поступим иначе. Сравним круг с какой-нибудь знакомой нам фигурой и сделаем это следующим образом: вырежем круг из бумаги, разрежем его сначала по диаметру пополам, затем каждую половину разрежем ещё пополам, каждую четверть — ещё пополам и т. д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
д., пока не разрежем круг, например, на 32 части, имеющие форму зубцов (рис. 29).
Затем сложим их так, как показано на рисунке 30, т. е. сначала расположим 16 зубцов в виде пилы, а затем в образовавшиеся отверстия вложим 15 зубцов и, наконец, последний оставшийся зубец разрежем по радиусу пополам и приложим одну часть слева, другую — справа. Тогда получится фигура, напоминающая прямоугольник.
Длина этой фигуры (основание) равна приблизительно длине полуокружности, а высота — приблизительно радиусу. Тогда площадь такой фигуры можно найти путём умножения чисел, выражающих длину полуокружности и длину радиуса. Если обозначим площадь круга буквой S , длину окружности буквой С , радиус буквой r , то можем записать формулу для определения площади круга:
которая читается так: площадь круга равна длине полуокружности, умноженной на радиус.
Задача. Найти площадь круга, радиус которого равен 4 см. Найдём сначала длину окружности, потом длину полуокружности, а затем умножим её на радиус.
1) Длина окружности С = π D = 3,14 8 = 25,12 (см).
2) Длина половины окружности C / 2 = 25,12: 2= 12,56 (см).
3) Площадь круга S = C / 2 r = 12,56 4 = 50,24 (кв. см).
§ 118. Поверхность и объём цилиндра.
Задача 1. Найти полную поверхность цилиндра, у которого диаметр основания 20,6 см и высота 30,5 см.
Форму цилиндра (рис. 31) имеют: ведро, стакан (не гранёный), кастрюля и множество других предметов.
Полная поверхность цилиндра (как и полная поверхность прямоугольного параллелепипеда) состоит из боковой поверхности и площадей двух оснований (рис. 32).
Чтобы наглядно представить себе, о чём идёт речь, необходимо аккуратно сделать модель цилиндра из бумаги. Если мы от этой модели отнимем два основания, т. е. два круга, а боковую поверхность разрежем вдоль и развернём, то будет совершенно ясно, как нужно вычислять полную поверхность цилиндра. Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
Боковая поверхность развернётся в прямоугольник, основание которого равно длине окружности. Поэтому решение задачи будет иметь вид:
1) Длина окружности: 20,6 3,14 = 64,684 (см).
2) Площадь боковой поверхности: 64,684 30,5= 1972,862(кв.см).
3) Площадь одного основания: 32,342 10,3 = 333,1226 (кв.см).
4) Полная поверхность цилиндра:
1972,862 + 333,1226 + 333,1226 = 2639,1072 (кв. см) ≈ 2639 (кв. см).
Задача 2. Найти объём железной бочки, имеющей форму цилиндра с размерами: диаметр основания 60 см и высота 110 см.
Чтобы вычислить объём цилиндра, нужно припомнить, как мы вычисляли объём прямоугольного параллелепипеда (полезно прочитать § 61).
Единицей измерения объёма у нас будет кубический сантиметр. Сначала надо узнать, сколько кубических сантиметров можно расположить на площади основания, а затем найденное число умножить на высоту.
Чтобы узнать, сколько кубических сантиметров можно уложить на площади основания, надо вычислить площадь основания цилиндра. Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:
Так как основанием служит круг, то нужно найти площадь круга. Затем для определения объёма умножить её на высоту. Решение задачи имеет вид:
1) Длина окружности: 60 3,14 = 188,4 (см).
2) Площадь круга: 94,2 30 = 2826 (кв. см).
3) Объём цилиндра: 2826 110 = 310 860 (куб. см).
Ответ. Объём бочки 310,86 куб. дм.
Если обозначим объём цилиндра буквой V , площадь основания S , высоту цилиндра H , то можно написать формулу для определения объёма цилиндра:
V = S H
которая читается так: объём цилиндра равен площади основания, умноженной на высоту.
§ 119. Таблицы для вычисления длины окружности по диаметру.
При решении различных производственных задач часто приходится вычислять длину окружности. Представим себе рабочего, который изготовляет круглые детали по указанным ему диаметрам. Он должен всякий раз, зная диаметр, вычислить длину окружности. Чтобы сэкономить время и застраховать себя от ошибок, он обращается к готовым таблицам, в которых указаны диаметры и соответствующие им длины окружностей.
Приведём небольшую часть таких таблиц и расскажем, как ими пользоваться.
Пусть известно, что диаметр окружности равен 5 м. Ищем в таблице в вертикальном столбце под буквой D число 5. Это длина диаметра. Рядом с этим числом (вправо, в столбце под названием «Длина окружности») увидим число 15,708 (м). Совершенно так же найдём, что если D = 10 см, то длина окружности равна 31,416 см.
По этим же таблицам можно производить и обратные вычисления. Если известна длина окружности, то можно найти в таблице соответствующий ей диаметр. Пусть длина окружности равна приблизительно 34,56 см. Найдём в таблице число, наиболее близкое к данному. Таковым будет 34,558 (разница 0,002). Соответствующий такой длине окружности диаметр равен приблизительно 11 см.
Таблицы, о которых здесь сказано, имеются в различных справочниках. В частности, их можно найти в книжке «Четырёхзначные математические таблицы» В. М. Брадиса. и в задачнике по арифметике С. А. Пономарёва и Н.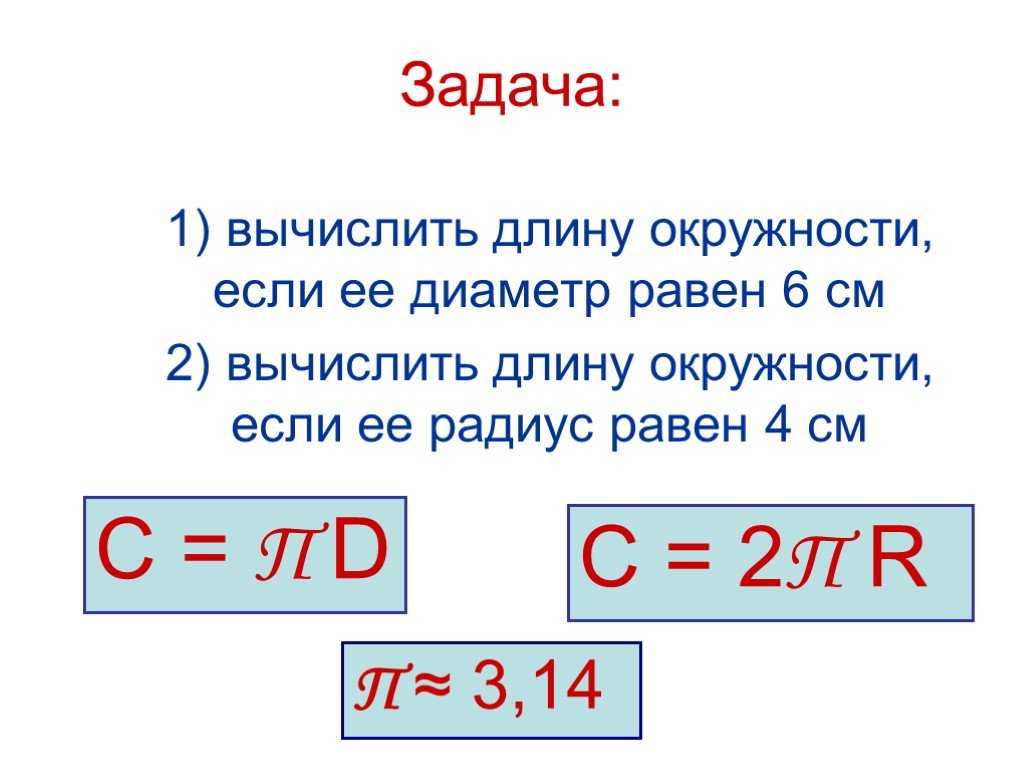 И. Сырнева.
И. Сырнева.
Зная радиус узнать диаметр. Как рассчитать длину окружности, если не указан диаметр и радиус круга
Инструкция
Вспомните, что впервые математически вычислил это соотношение Архимед. Он правильные 96-тиугольники внутри окружности и вокруг нее. Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Для расчетов число Пи сократите до 3,14. Получится, что для любой окружности ее длина, деленная на диаметр равна этому числу: L:d=3,14.
Выразите из этого утверждения формулу для нахождения диаметра. Получится, чтобы найти диаметр окружности надо длину окружности поделить на число Пи. Это выглядит так: d = L:3,14. Это универсальный способ найти диаметр, когда у окружности известна ее длина.
Итак, известна длина окружности, допустим, 15,7 см, разделите эту цифру на 3,14. Диаметр будет равен 5 см. Запишите это так: d = 15,7: 3,14 = 5 см.
Найдите диаметр по длине окружности, используя специальные таблицы для вычисления длины окружности . Эти таблицы включают в разные справочники. Например, они есть в «Четырехзначные математические таблицы» В.М. Брадиса.
Полезный совет
Запомните первые восемь цифр числа Пи с помощью стихотворения:
Нужно только постараться,
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Источники:
- Число «Пи» рассчитано с рекордной точностью
- диаметр и длина окружности
- Как найти длину окружности?
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности.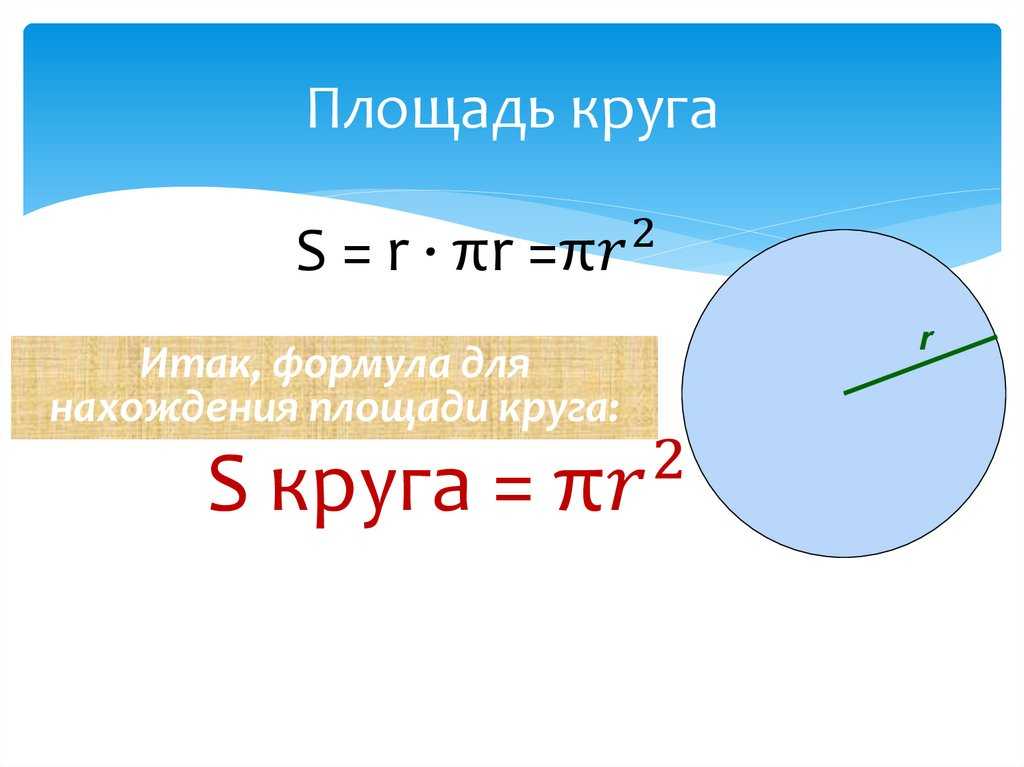 Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является « », то не имеет конечного значения — это дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.
Видео по теме
Удивительное свойство окружности открыл нам древнегреческий ученый Архимед. Оно заключается в том, что отношение ее длины к длине диаметра одинаково для любой окружности . В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.
Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — нитка.
Инструкция
Начертите на бумаге циркулем окружность произвольного диаметра. Проведите с помощью линейки и карандаша через ее центр отрезок, соединяющий две , находящиеся на линии окружности . Линейкой измерьте длину получившегося отрезка. Допустим, окружности в данном случае 7 сантиметрам.
Возьмите нитку и расположите ее по длине окружности . Измерьте получившуюся длину нитки.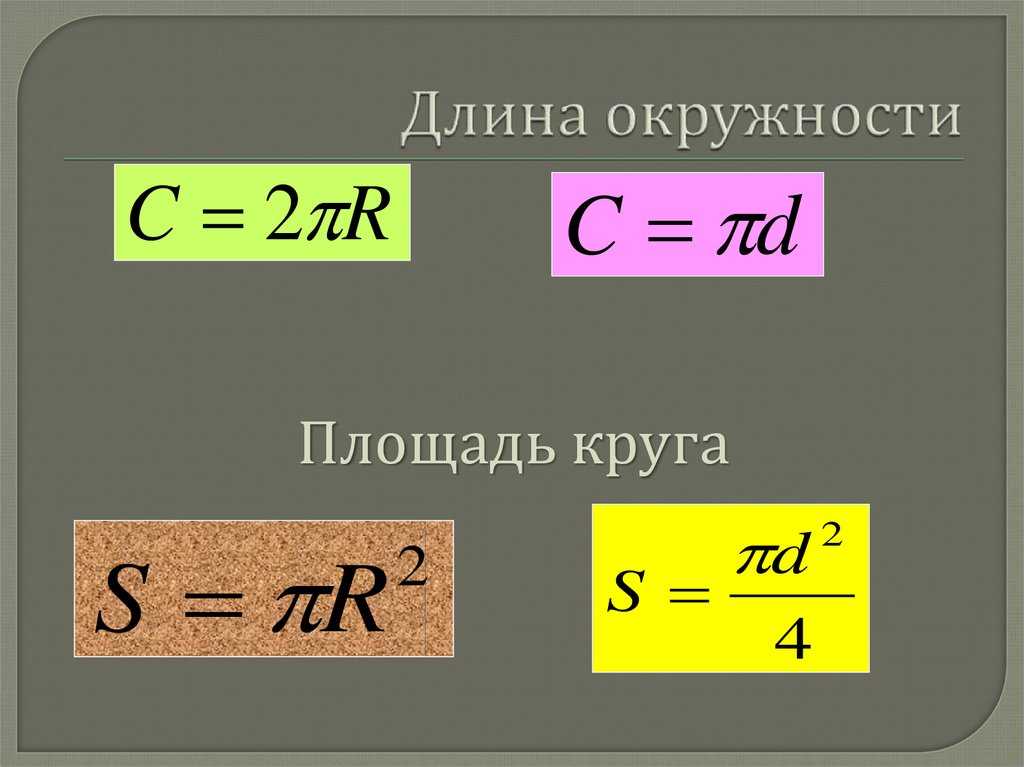 Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см: 7 см = 3,1428…. Округлите полученное число (3,14). Получилось знакомое число «Пи».
Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см: 7 см = 3,1428…. Округлите полученное число (3,14). Получилось знакомое число «Пи».
Доказать это свойство окружности вы можете, используя чашку или стакан. Измерьте их диаметр линейкой. Обмотайте верх посуды ниткой, замерьте получившуюся длину. Поделив длину окружности чашки на длину ее диаметра, вы также получите число «Пи», убедившись в этом свойстве окружности , открытом Архимедом.
Используя это свойство, вы можете вычислить длину любой окружности по длине ее диаметра или по формулам:С = 2*п*R или С = D*п, где С — окружности , D — длина ее диаметра, R — длина ее радиуса.Для нахождения (плоскости, ограниченной линиями окружности ) используйте формулу S = π*R², если известен его радиус, либо формулу S = π*D²/4, если известен его диаметр.
Обратите внимание
А вы знаете, что четырнадцатого марта уже более двадцати лет отмечается День «Пи»? Это неофициальный праздник математиков, посвященный этому интересному числу, с которым в настоящее время связано множество формул, математических и физических аксиом. Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Источники:
- Архимед
Иногда около выпуклого многоугольника можно начертить таким образом, чтобы вершины всех углов лежали на ней. Такую окружность по отношению к многоугольнику надо называть описанной. Ее центр не обязательно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности , найти эту точку, как правило, не очень трудно.
Вам понадобится
- Линейка, карандаш, транспортир или угольник, циркуль.
Инструкция
Если многоугольник, около которого нужно описать окружность, начерчен на бумаге, для нахождения центр а круга достаточно линейки, карандаша и транспортира либо угольника. Измерьте длину любой из сторон фигуры, определите ее середину и поставьте в этом месте чертежа вспомогательную точку. С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
Проделайте эту же операцию с любой другой стороной многоугольника. Пересечение двух построенных отрезков и будет искомой точкой. Это вытекает из основного свойства описанной окружности — ее центр в выпуклом многоугольнике с любым сторон всегда лежит в точке пересечения серединных перпендикуляров, проведенных к этим .
Для правильных многоугольников центр а вписанной окружности может быть намного проще. Например, если это квадрат, то начертите две диагонали — их пересечение и будет центр ом вписанной окружности . В многоугольнике с любым четным числом сторон достаточно соединить вспомогательными две пары лежащих друг напротив друга углов — центр описанной окружности должен совпадать с точкой их пересечения. В прямоугольном треугольнике для решения задачи просто определите середину самой длинной стороны фигуры — гипотенузы.
Если из условий неизвестно, можно ли в принципе описанную окружность для данного многоугольника, после определения предполагаемой точки центр а любым из описанных способов вы можете это выяснить. Отложите на циркуле расстояние между найденной точкой и любой из , установите в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из свойств и описать окружность около данного многоугольника .
Определение диаметра может пригодиться не только для решения геометрических задач, но и помочь на практике. Например, зная диаметр горлышка банки, вы точно не ошибетесь в выборе крышки для нее. То же утверждение справедливо и для более габаритных окружностей.
Инструкция
Итак, введите обозначения величин. Пусть d – диаметр колодца, L – длина окружности, п – число Пи, значение которого приблизительно равно 3,14, R – радиус окружности. Длина окружности (L) известна. Предположим, что она равна 628 сантиметрам.
Предположим, что она равна 628 сантиметрам.
Далее для нахождения диаметра (d) воспользуйтесь формулой длины окружности: L=2пR, где R – неизвестная величина, L=628 см, а п=3,14. Теперь воспользуйтесь правилом нахождения неизвестного множителя: «Чтобы найти множитель, нужно произведение разделить на известный множитель». Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.
После того как радиус окружности найден (R=100 см), воспользуйтесь следующей формулой: диаметр окружности (d) равен двум радиусам окружности (2R). Получается: d=2R.
Теперь, чтобы найти диаметр, подставьте в формулу d=2R значения и вычислите результат. Так как радиус (R) известен, получается: d=2×100, d=200 см.
Источники:
- как по длине окружности определить диаметр
Длина окружности и диаметр являются взаимосвязанными геометрическими величинами. Это означает, что первую из них можно перевести во вторую без каких-либо дополнительных данных.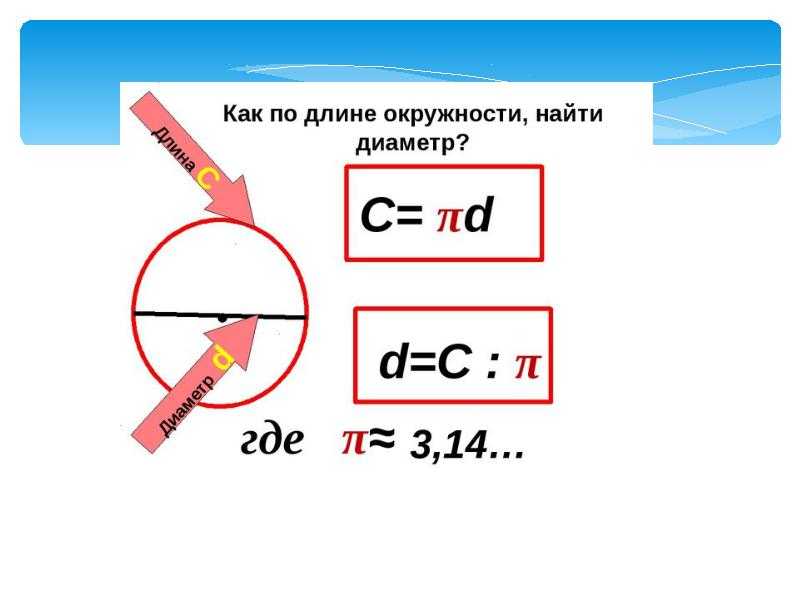 Математической константой, через которую они связаны между собой, является число π.
Математической константой, через которую они связаны между собой, является число π.
Инструкция
Если окружность представлена в виде изображения на бумаге, а ее диаметр требуется определить приблизительно, измерьте его непосредственно. Если ее центр показан на чертеже, проведите через него линию. Если же центр не показан, найдите его при помощи циркуля. Для этого используйте угольник с углами в 90 и . Приложите его 90-градусным углом к окружности таким образом, чтобы ее касались оба катета, и обведите. Приложив затем к получившемуся прямому углу 45-градусный угол угольника, начертите . Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Для измерения диаметра предпочтительно использовать линейку, изготовленную из как можно более тонкого листового материала, либо портновский метр. При наличии только толстой линейки измерьте диаметр окружности при помощи циркуля, а затем, не изменяя его раствора, перенесите его на миллиметровую бумагу.
Также при отсутствии в условиях задачи числовых данных и при наличии только чертежа можно измерить длину окружности при помощи курвиметра, а диаметр затем рассчитать. Чтобы воспользоваться курвиметром, вначале вращением его колесика установите стрелку точно на нулевое деление. Затем отметьте на окружности точку и прижмите курвиметр к листу таким образом, чтобы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих снова не окажется над этой точкой. Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна.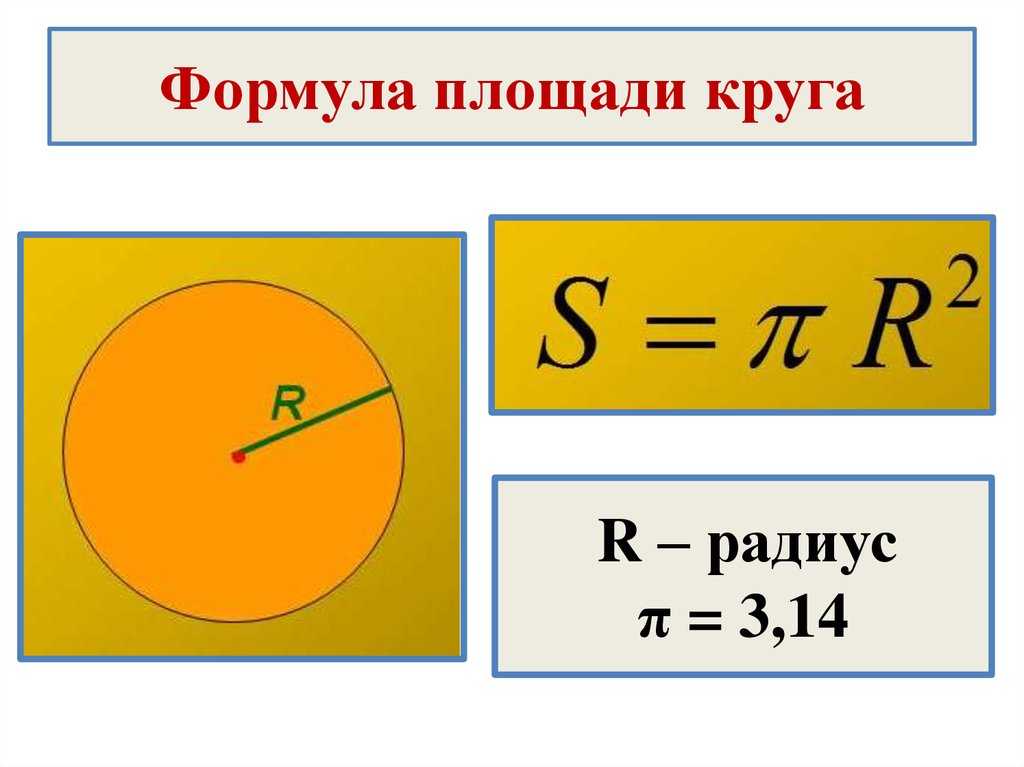 Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Измерение окружности
О том, что наша планета имеет форму шара, ученым, занимающимся исследованиями в области геологии, было известно достаточно давно. Именно поэтому первые измерения величины окружности земной поверхности касались самой длинной параллели Земли — экватора. Эту величину, полагали ученые, можно считать правильной для любого другого способа измерения. Например, считалось, что если измерить окружность планеты по самому длинному
меридиану , полученная цифра будет точно такой же.Такое мнение существовало вплоть до XVIII века. Однако ученые ведущего научного учреждения того времени — Французской академии — придерживались мнения о том, что эта гипотеза неверна, и форма, которую имеет планета, не совсем правильна. Поэтому, по их мнению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.
Поэтому, по их мнению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.
В доказательство в 1735 и 1736 годах были предприняты две научные экспедиции, которые доказали истинность этого предположения. Впоследствии была установлена и величина различия между этими двумя — она составила 21,4 километра.
Длина окружности
В настоящее время длина окружности планеты Земля неоднократно измерена уже не посредством экстраполяции длины того или иного отрезка земной поверхности на ее полную величину, как это делалось раньше, а с применением современных высокоточных технологий. Благодаря этому удалось установить точную длину окружности по самому длинному меридиану и самой длинной параллели, а также уточнить величину различия между этими параметрами.Так, на сегодняшний день в научном сообществе в качестве официальной величины окружности планеты Земля по экватору, то есть наиболее длинной параллели, принято приводить цифру, составляющую 40075,70 километра. При этом аналогичный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра.
При этом аналогичный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра.
Таким образом, разница между длинами окружностей составляет 67,15 километра, и экватор является самой длинной окружностью нашей планеты. Кроме того, различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели.
Окружность состоит из множества точек, которые находятся на равном расстоянии от центра. Это плоская геометрическая фигура, и найти ее длину не составит труда. С окружностью и кругом человек сталкивается ежедневно независимо от того, в какой сфере он работает. Многие овощи и фрукты , устройства и механизмы, посуда и мебель имеют круглую форму. Кругом называют то множество точек, которое находится в границах окружности. Поэтому длина фигуры равна периметру круга.
Характеристики фигуры
Кроме того, что описание понятия окружности достаточно простое, её характеристики также несложные для понимания. С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
С их помощью можно вычислить её длину. Внутренняя часть окружности состоит из множества точек, среди которых две — А и В — можно увидеть под прямым углом. Этот отрезок называют диаметром, он состоит из двух радиусов.
В пределах окружности имеются точки Х такие , что не изменяется и не равняется единице отношение АХ/ВХ. В окружности это условие обязательно соблюдается, в ином случае эта фигура не имеет форму круга. На каждую точку, из которых состоит фигура, распространяется правило: сумма квадратов расстояний от этих точек до двух других всегда превышает половину длины отрезка между ними.
Основные термины окружности
Для того чтобы уметь находить длину фигуры, необходимо знать основные термины, касающиеся её. Основные параметры фигуры — это диаметр, радиус и хорда . Радиусом называют отрезок, соединяющий центр круга с любой точкой на её кривой. Величина хорды равна расстоянию между двумя точками на кривой фигуры. Диаметр — расстояние между точками , проходящее через центр фигуры.
Основные формулы для вычислений
Параметры используются в формулах вычислений величин окружности:
Диаметр в формулах вычисления
В экономике и математике нередко появляется необходимость поиска длины окружности. Но и в повседневной жизни можно столкнуться с этой надобностью, к примеру, во время постройки забора вокруг бассейна круглой формы. Как рассчитать длину окружности по диаметру? В этом случае используют формулу C = π*D, где С — это искомая величина, D — диаметр.
Например, ширина бассейна равна 30 метрам, а столбики забора планируют поставить на расстоянии десяти метров от него. В этом случае формула расчёта диаметра: 30+10*2 = 50 метров. Искомая величина (в этом примере — длина забора): 3,14*50 = 157 метров. Если столбики забора будут стоять на расстоянии трёх метров друг от друга, то всего их понадобится 52.
Расчёты по радиусу
Как вычислить длину окружности по известному радиусу? Для этого используется формула C = 2*π*r, где С — длина, r — радиус. Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Радиус в круге меньше диаметра в два раза, и это правило может пригодиться в повседневной жизни. К примеру, в случае приготовления пирога в раздвижной форме.
Для того чтобы кулинарное изделие не испачкалось, необходимо использовать декоративную обёртку. А как вырезать бумажный круг подходящего размера?
Те, кто немного знаком с математикой, понимают, что в этом случае нужно умножить число π на удвоенный радиус используемой формы. Например, диаметр формы равен 20 сантиметрам, соответственно, её радиус составляет 10 сантиметров. По этим параметрам находится необходимый размер круга: 2*10*3, 14 = 62,8 сантиметра.
Подручные способы вычисления
Если найти длину окружности по формуле нет возможности, то стоит воспользоваться подручными методами расчёта этой величины:
- При небольших размерах круглого предмета его длину можно найти с помощью верёвки, обёрнутой вокруг один раз.
- Величину большого предмета измеряют так: на ровной плоскости раскладывают верёвку, и по ней прокатывают круг один раз.

- Современные студенты и школьники для расчётов используют калькуляторы. В режиме онлайн по известным параметрам можно узнавать неизвестные величины.
Круглые предметы в истории человеческой жизни
Первое изделие круглой формы, которое изобрёл человек — это колесо. Первые конструкции представляли собой небольшие округлые бревна, насаженные на оси. Затем появились колёса, сделанные из деревянных спиц и обода. Постепенно в изделие добавляли металлические детали для уменьшения износа. Именно для того, чтобы узнать длину металлических полос для обивки колёса, учёные прошлых веков искали формулу расчёта этой величины.
Форму колеса имеет гончарный круг , большинство деталей в сложных механизмах, конструкциях водяных мельниц и прялок. Нередко встречаются круглые предметы в строительстве — рамки круглых окон в романском архитектурном стиле, иллюминаторы в суднах. Архитекторы, инженеры, учёные, механики и проектировщики ежедневно в сфере своей профессиональной деятельности сталкиваются с надобностью расчёта размеров окружности.
И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.
Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
Ответ: диаметр равен 21,98 метрам.
Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
D = 2 * (S / Пи) * (1 / 2)
S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:
D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.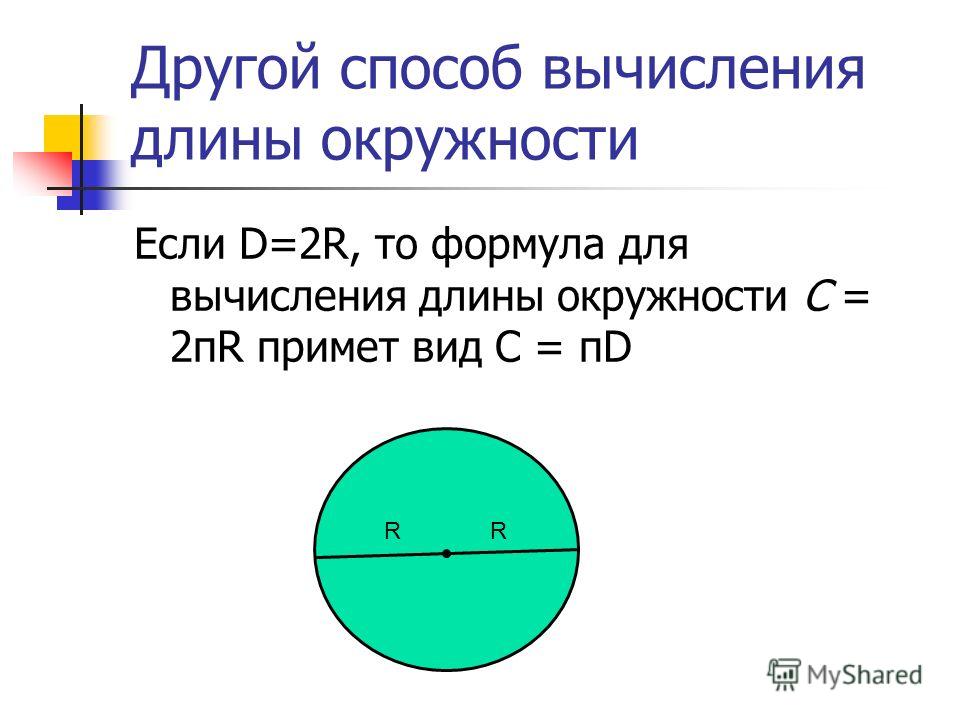
Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).
Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Если в задаче известны такие величины, как длина окружности, ее радиус или площадь круга, который ограничен данной окружностью, то вычисление диаметра будет несложным. Существует несколько способов, которыми можно высчитать диаметр окружности. Они довольно просты и вовсе не вызывают никаких трудностей, как многим кажется на первый взгляд.
Существует несколько способов, которыми можно высчитать диаметр окружности. Они довольно просты и вовсе не вызывают никаких трудностей, как многим кажется на первый взгляд.
Как найти диаметр окружности – 1 способ
Когда дано значение радиуса окружности, то можно считать задачу наполовину решенной, поскольку радиус представляет собой расстояние от точки, которая лежит в любом месте на окружности, до центра этой самой окружности. Все, что нужно сделать для нахождения диаметра в этом случае, это умножить данную величину радиуса на 2. Такой способ вычисления объясняется тем, что радиус является половиной диаметра. Поэтому, если известно, чему равен радиус, то и значение половины искомой величины диаметра уже фактически найдено.
Как найти диаметр окружности – 2 способ
Если в задаче дано только значение длины окружности, то для нахождения величины диаметра нужно просто поделить ее на число, известное как π, приблизительное значение которого равно 3,14. То есть, если значение длины равняется 31,4, то разделив его на 3,14, получаем значение диаметра, которое равняется 10.
Как найти диаметр окружности – 3 способ
Если в исходных данных приведено значение площади круга, то диаметр найти тоже просто. Все, что нужно сделать, это извлечь квадратный корень из данной величины и поделить полученный результат на число π. Это значит, что если значение площади равно 64, то при извлечении корня остается число 8. Если разделить полученную 8 на 3,14, то получим величину диаметра, которая равна примерно 2,5.
Как найти диаметр окружности – 4 способ
Внутри окружности нужно начертить при помощи линейки или угольника прямую горизонтальную линию от одной точки до другой. Пересечения этой прямой с линией окружностью пометьте буквами, например, А и В. Не имеет никакого значения, в какой из частей круга будет расположена эта прямая.
После этого нужно начертить еще две окружности. Но таким образом, чтобы точки А и В стали их центрами. Вновь образованные фигуры будут пересекаться в двух точках. Через них нужно провести еще одну прямую линию. После этого измеряем ее длину с помощью линейки.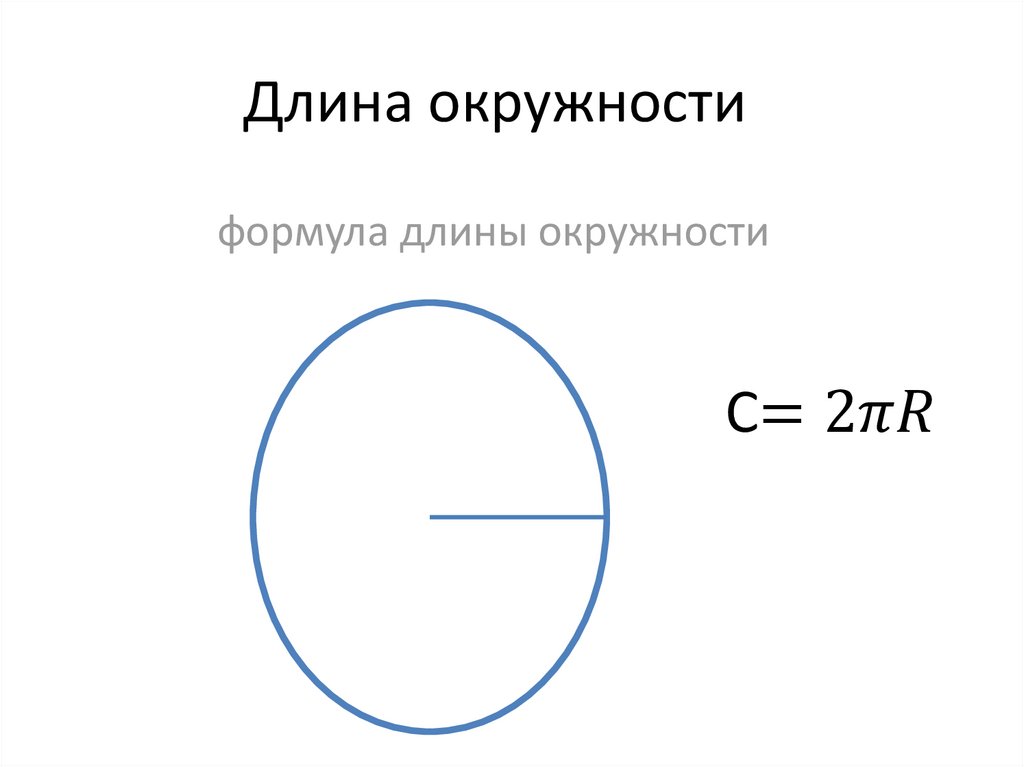 Значение измерения и будет равно длине диаметра, потому что последняя начерченная линия и есть сам диаметр.
Значение измерения и будет равно длине диаметра, потому что последняя начерченная линия и есть сам диаметр.
Интересно, что еще очень далеко в прошлом для плетения корзин определенного размера прутики брали примерно в 3 раза длиннее. Ученые объяснили и доказали экспериментальным путем, что если длину любой окружности разделить на диаметр, то в результате получается почти одно и то же число.
Чтобы написать, как найти диаметр круга, необходимо сначала определить, что это такое. Итак, диаметр круга — это прямая, которая проходит через центр круга и соединяет точки на окружности.
Ниже мы рассмотрим способы нахождения диаметра окружности через её длину, площадь вписанного круга, и через радиус.
Определение диаметра
Принято считать, что какой бы величины ни была окружность, отношение ее длины к диаметру — это постоянное число «Пи», которое примерно равно 3,14. Чтобы понять, как найти диаметр круга, следует привести формулы и на примере показать вычисления данной величины.
Радиус
Если известен радиус круга, то диаметр вычислить очень просто:
D = 2R, где D — это диаметр, а R — радиус. Получается, диаметр равен двум радиусам. Например, известно, что радиус равен 10 см, тогда диаметр вычисляем так: D=2*10, получается, что диаметр равен 20 см.
Длина окружности
В случае, если известна длина окружности, для вычисления может быть полезным число . Вот какой формулой можно воспользоваться: D = l/, где l — это длина круга. Получается, если длина окружности равна 18 см, то диаметр вычисляем так: D = 18 / 3,14 ≈ 5,73 см.
Площадь круга
Если известна только площадь круга, то это значение также можно применить. При этом площадь обозначается буквой S. Исходя из формулы S=R 2 , можно найти радиус, а значит, и диаметр. Итак, радиус R = √ (S / ). Для нахождения радиуса делим площадь на число Пи и извлекаем из этого значения квадратный корень. Таким образом, если площадь равна 25 см, то радиус вычисляется так: R = √ (25 / 3,14) ≈ √8 ≈ 2,8 см. Затем можно вычислить диаметр: D = 2R, D = 2,8*2= 5,6 см.
Затем можно вычислить диаметр: D = 2R, D = 2,8*2= 5,6 см.
через диаметр и радиус. Терминология, основные формулы и характеристика фигуры
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом.
 Диаметр данной фигуры равен длине рассматриваемого отрезка.
Диаметр данной фигуры равен длине рассматриваемого отрезка. - Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.
Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра.
 Формулу обычно записывают следующим образом: C = π*D.
Формулу обычно записывают следующим образом: C = π*D. - Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу. Формула является достаточно простой и выглядит так: D = C/π = 2*R.
- Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.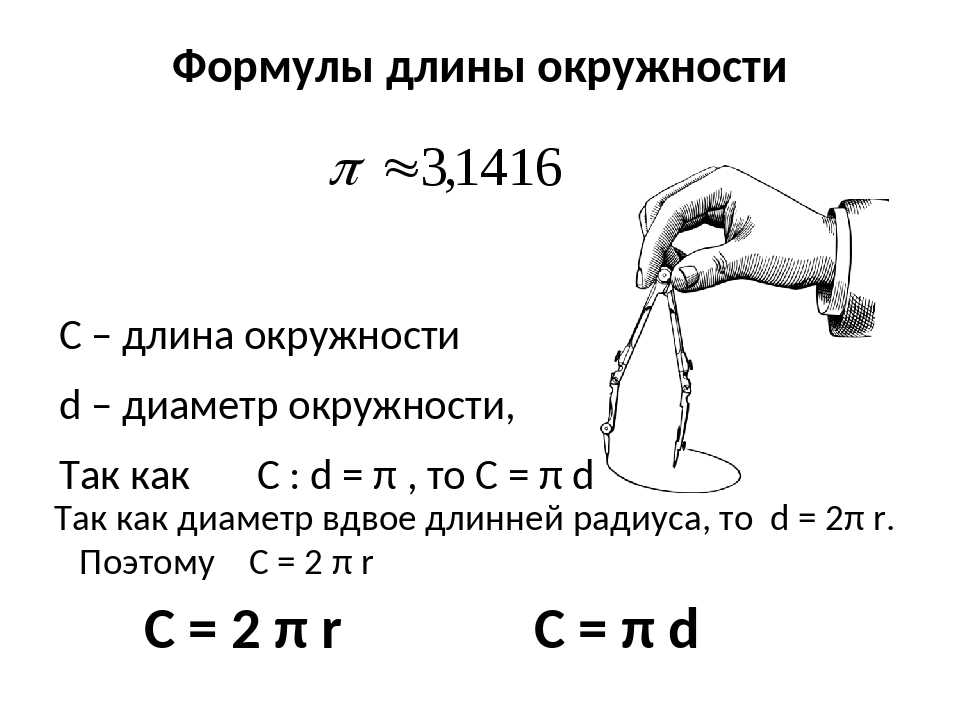
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность. На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится.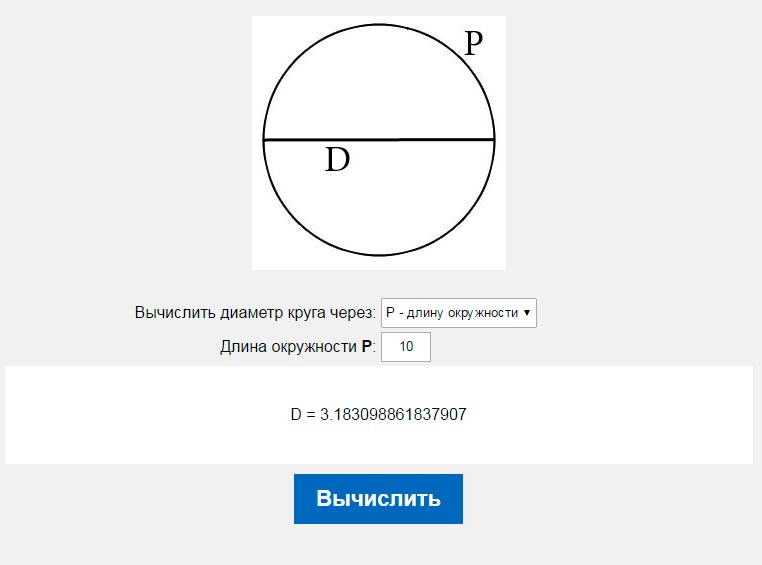 Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски:
L = πD = 3,14 * 20 = 62,8 см.
Другой пример: нужно построить забор вокруг круглого бассейна на определенном расстоянии. Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
Если радиус бассейна 10 м, а забор нужно поставить на расстоянии 3 м, то R для полученной окружности будет 13 м. Тогда ее длина равна:
L = 2πR = 2 * 3,14 * 13 = 81,68 м.
Полезное видео: круг — радиус, диаметр, длина окружности
Итог
Периметр круга легко рассчитать по простым формулам, включающим диаметр или радиус. Также можно найти искомую величину через площадь круга. Решить эту задачу помогут онлайн-калькуляторы или мобильные приложения, в которые нужно ввести единственное число – диаметр или радиус.
Сначала разберемся в отличии между кругом и окружностью. Чтобы увидеть эту разницу, достаточно рассмотреть, чем являются обе фигуры. Это бесчисленное количество точек плоскости, располагающиеся на равном расстоянии от единственной центральной точки. Но, если круг состоит и из внутреннего пространства, то окружности оно не принадлежит. Получается, что круг это и окружность, ограничивающая его (о-кру(г)жность), и бесчисленное число точек, что внутри окружности.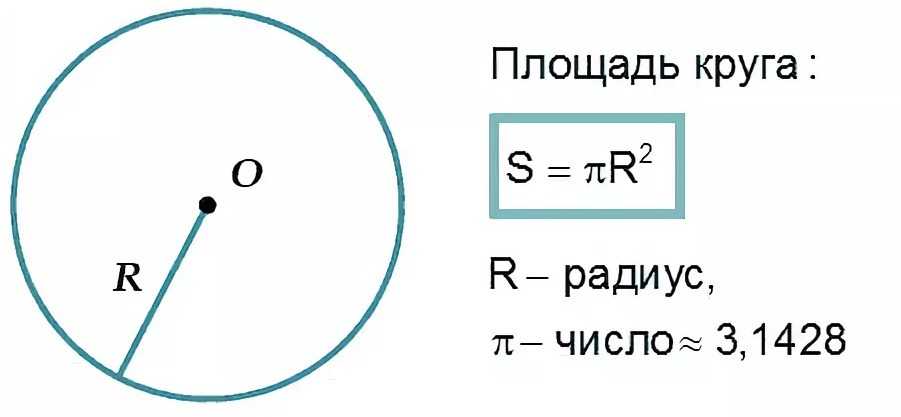 {\circ}}
{\circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N , то произведения отрезков хорд, разделенные точкой N , равны между собой.
AN\cdot NB = CN \cdot ND
Касательная к окружности
Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
Если же у прямой есть две общие точки, ее называют секущей .
Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {\circ}
{\circ}
\angle ADB = \angle AEB = \angle AFB
На одной окружности находятся вершины треугольников с тождественными углами и заданным основанием.
Угол с вершиной внутри окружности и расположенный между двумя хордами тождественен половине суммы угловых величин дуг окружности, которые заключаются внутри данного и вертикального углов.
\angle DMC = \angle ADM + \angle DAM = \frac{1}{2} \left (\cup DmC + \cup AlB \right)
Угол с вершиной вне окружности и расположенный между двумя секущими тождественен половине разности угловых величин дуг окружности, которые заключаются внутри угла.
\angle M = \angle CBD — \angle ACB = \frac{1}{2} \left (\cup DmC — \cup AlB \right)
Вписанная окружность
Вписанная окружность — это окружность, касающаяся сторон многоугольника.
В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
Окружность может быть вписанной не в каждый многоугольник.
Площадь многоугольника с вписанной окружностью находится по формуле:
S = pr ,
p — полупериметр многоугольника,
r — радиус вписанной окружности.
Отсюда следует, что радиус вписанной окружности равен:
r = \frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
Радиус вписанной окружности вычисляется по формуле:
r = \frac{S}{p} ,
где p = \frac{a + b + c}{2}
Описанная окружность
Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника . {\circ}
{\circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
Радиус описанной окружности можно вычислить по формулам:
R = \frac{a}{2 \sin A} = \frac{b}{2 \sin B} = \frac{c}{2 \sin C}
R = \frac{abc}{4 S}
a , b , c — длины сторон треугольника,
S — площадь треугольника.
Теорема Птолемея
Под конец, рассмотрим теорему Птолемея.
Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
AC \cdot BD = AB \cdot CD + BC \cdot AD
Инструкция
Вспомните, что впервые математически вычислил это соотношение Архимед. Он правильные 96-тиугольники внутри окружности и вокруг нее. Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Для расчетов число Пи сократите до 3,14. Получится, что для любой окружности ее длина, деленная на диаметр равна этому числу: L:d=3,14.
Выразите из этого утверждения формулу для нахождения диаметра. Получится, чтобы найти диаметр окружности надо длину окружности поделить на число Пи. Это выглядит так: d = L:3,14. Это универсальный способ найти диаметр, когда у окружности известна ее длина.
Итак, известна длина окружности, допустим, 15,7 см, разделите эту цифру на 3,14. Диаметр будет равен 5 см. Запишите это так: d = 15,7: 3,14 = 5 см.
Запишите это так: d = 15,7: 3,14 = 5 см.
Найдите диаметр по длине окружности, используя специальные таблицы для вычисления длины окружности . Эти таблицы включают в разные справочники. Например, они есть в «Четырехзначные математические таблицы» В.М. Брадиса.
Полезный совет
Запомните первые восемь цифр числа Пи с помощью стихотворения:
Нужно только постараться,
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Источники:
- Число «Пи» рассчитано с рекордной точностью
- диаметр и длина окружности
- Как найти длину окружности?
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром . Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является « », то не имеет конечного значения — это дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.
Видео по теме
Удивительное свойство окружности открыл нам древнегреческий ученый Архимед. Оно заключается в том, что отношение ее длины к длине диаметра одинаково для любой окружности . В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.
В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.
Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — нитка.
Инструкция
Начертите на бумаге циркулем окружность произвольного диаметра. Проведите с помощью линейки и карандаша через ее центр отрезок, соединяющий две , находящиеся на линии окружности . Линейкой измерьте длину получившегося отрезка. Допустим, окружности в данном случае 7 сантиметрам.
Возьмите нитку и расположите ее по длине окружности . Измерьте получившуюся длину нитки. Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см: 7 см = 3,1428…. Округлите полученное число (3,14). Получилось знакомое число «Пи».
Доказать это свойство окружности вы можете, используя чашку или стакан. Измерьте их диаметр линейкой. Обмотайте верх посуды ниткой, замерьте получившуюся длину. Поделив длину окружности чашки на длину ее диаметра, вы также получите число «Пи», убедившись в этом свойстве окружности , открытом Архимедом.
Используя это свойство, вы можете вычислить длину любой окружности по длине ее диаметра или по формулам:С = 2*п*R или С = D*п, где С — окружности , D — длина ее диаметра, R — длина ее радиуса.Для нахождения (плоскости, ограниченной линиями окружности ) используйте формулу S = π*R², если известен его радиус, либо формулу S = π*D²/4, если известен его диаметр.
Обратите внимание
А вы знаете, что четырнадцатого марта уже более двадцати лет отмечается День «Пи»? Это неофициальный праздник математиков, посвященный этому интересному числу, с которым в настоящее время связано множество формул, математических и физических аксиом. Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Источники:
- Архимед
Иногда около выпуклого многоугольника можно начертить таким образом, чтобы вершины всех углов лежали на ней. Такую окружность по отношению к многоугольнику надо называть описанной. Ее центр не обязательно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности , найти эту точку, как правило, не очень трудно.
Вам понадобится
- Линейка, карандаш, транспортир или угольник, циркуль.
Инструкция
Если многоугольник, около которого нужно описать окружность, начерчен на бумаге, для нахождения центр а круга достаточно линейки, карандаша и транспортира либо угольника. Измерьте длину любой из сторон фигуры, определите ее середину и поставьте в этом месте чертежа вспомогательную точку. С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
Проделайте эту же операцию с любой другой стороной многоугольника. Пересечение двух построенных отрезков и будет искомой точкой. Это вытекает из основного свойства описанной окружности — ее центр в выпуклом многоугольнике с любым сторон всегда лежит в точке пересечения серединных перпендикуляров, проведенных к этим .
Для правильных многоугольников центр а вписанной окружности может быть намного проще. Например, если это квадрат, то начертите две диагонали — их пересечение и будет центр ом вписанной окружности . В многоугольнике с любым четным числом сторон достаточно соединить вспомогательными две пары лежащих друг напротив друга углов — центр описанной окружности должен совпадать с точкой их пересечения. В прямоугольном треугольнике для решения задачи просто определите середину самой длинной стороны фигуры — гипотенузы.
Если из условий неизвестно, можно ли в принципе описанную окружность для данного многоугольника, после определения предполагаемой точки центр а любым из описанных способов вы можете это выяснить. Отложите на циркуле расстояние между найденной точкой и любой из , установите в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из свойств и описать окружность около данного многоугольника .
Определение диаметра может пригодиться не только для решения геометрических задач, но и помочь на практике. Например, зная диаметр горлышка банки, вы точно не ошибетесь в выборе крышки для нее. То же утверждение справедливо и для более габаритных окружностей.
Инструкция
Итак, введите обозначения величин. Пусть d – диаметр колодца, L – длина окружности, п – число Пи, значение которого приблизительно равно 3,14, R – радиус окружности. Длина окружности (L) известна. Предположим, что она равна 628 сантиметрам.
Предположим, что она равна 628 сантиметрам.
Далее для нахождения диаметра (d) воспользуйтесь формулой длины окружности: L=2пR, где R – неизвестная величина, L=628 см, а п=3,14. Теперь воспользуйтесь правилом нахождения неизвестного множителя: «Чтобы найти множитель, нужно произведение разделить на известный множитель». Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.
После того как радиус окружности найден (R=100 см), воспользуйтесь следующей формулой: диаметр окружности (d) равен двум радиусам окружности (2R). Получается: d=2R.
Теперь, чтобы найти диаметр, подставьте в формулу d=2R значения и вычислите результат. Так как радиус (R) известен, получается: d=2×100, d=200 см.
Источники:
- как по длине окружности определить диаметр
Длина окружности и диаметр являются взаимосвязанными геометрическими величинами. Это означает, что первую из них можно перевести во вторую без каких-либо дополнительных данных.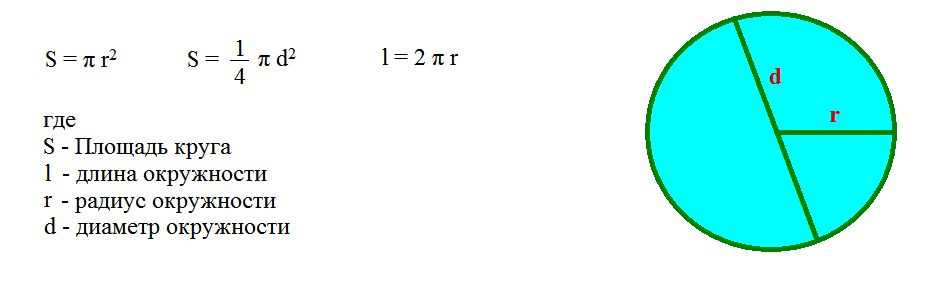 Математической константой, через которую они связаны между собой, является число π.
Математической константой, через которую они связаны между собой, является число π.
Инструкция
Если окружность представлена в виде изображения на бумаге, а ее диаметр требуется определить приблизительно, измерьте его непосредственно. Если ее центр показан на чертеже, проведите через него линию. Если же центр не показан, найдите его при помощи циркуля. Для этого используйте угольник с углами в 90 и . Приложите его 90-градусным углом к окружности таким образом, чтобы ее касались оба катета, и обведите. Приложив затем к получившемуся прямому углу 45-градусный угол угольника, начертите . Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Для измерения диаметра предпочтительно использовать линейку, изготовленную из как можно более тонкого листового материала, либо портновский метр. При наличии только толстой линейки измерьте диаметр окружности при помощи циркуля, а затем, не изменяя его раствора, перенесите его на миллиметровую бумагу.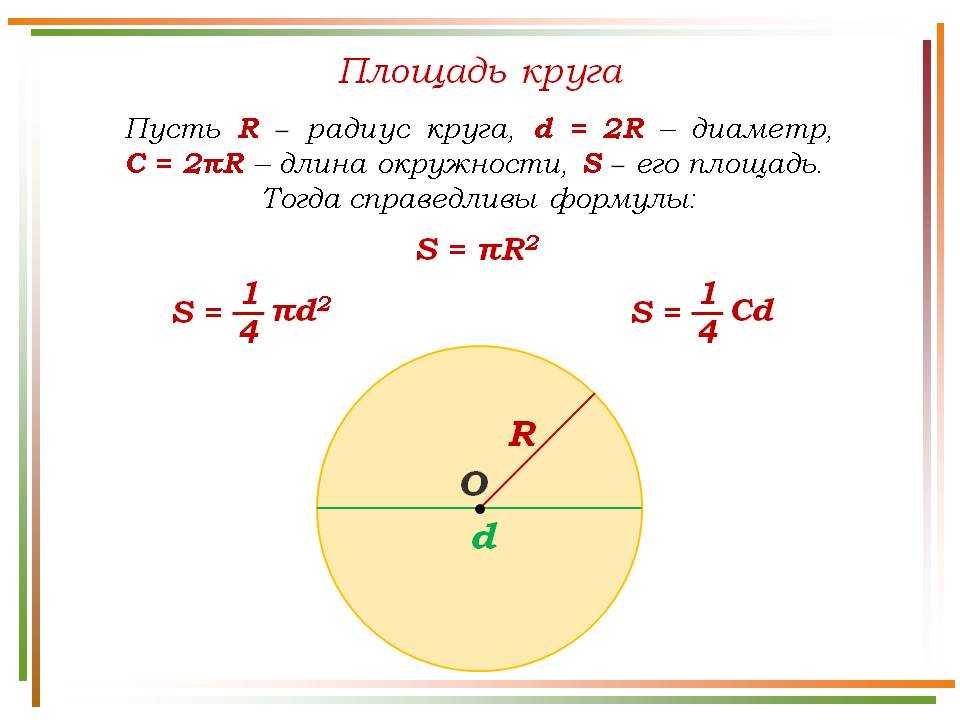
Также при отсутствии в условиях задачи числовых данных и при наличии только чертежа можно измерить длину окружности при помощи курвиметра, а диаметр затем рассчитать. Чтобы воспользоваться курвиметром, вначале вращением его колесика установите стрелку точно на нулевое деление. Затем отметьте на окружности точку и прижмите курвиметр к листу таким образом, чтобы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих снова не окажется над этой точкой. Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Измерение окружности
О том, что наша планета имеет форму шара, ученым, занимающимся исследованиями в области геологии, было известно достаточно давно. Именно поэтому первые измерения величины окружности земной поверхности касались самой длинной параллели Земли — экватора. Эту величину, полагали ученые, можно считать правильной для любого другого способа измерения. Например, считалось, что если измерить окружность планеты по самому длинному
меридиану , полученная цифра будет точно такой же.Такое мнение существовало вплоть до XVIII века. Однако ученые ведущего научного учреждения того времени — Французской академии — придерживались мнения о том, что эта гипотеза неверна, и форма, которую имеет планета, не совсем правильна.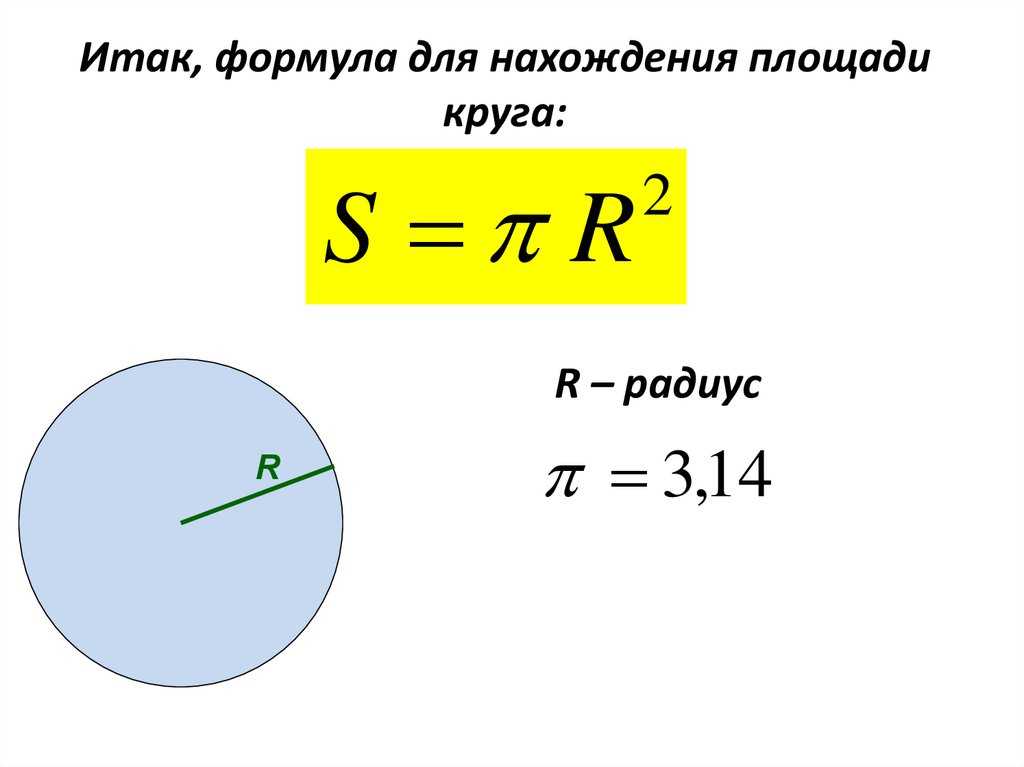 Поэтому, по их мнению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.
Поэтому, по их мнению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.
В доказательство в 1735 и 1736 годах были предприняты две научные экспедиции, которые доказали истинность этого предположения. Впоследствии была установлена и величина различия между этими двумя — она составила 21,4 километра.
Длина окружности
В настоящее время длина окружности планеты Земля неоднократно измерена уже не посредством экстраполяции длины того или иного отрезка земной поверхности на ее полную величину, как это делалось раньше, а с применением современных высокоточных технологий. Благодаря этому удалось установить точную длину окружности по самому длинному меридиану и самой длинной параллели, а также уточнить величину различия между этими параметрами.Так, на сегодняшний день в научном сообществе в качестве официальной величины окружности планеты Земля по экватору, то есть наиболее длинной параллели, принято приводить цифру, составляющую 40075,70 километра. При этом аналогичный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра.
При этом аналогичный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра.
Таким образом, разница между длинами окружностей составляет 67,15 километра, и экватор является самой длинной окружностью нашей планеты. Кроме того, различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели.
Как найти центр и радиус окружности из ее уравнения — Криста Кинг Математика
Какова стандартная форма уравнения окружности?
В этом уроке мы рассмотрим, как написать уравнение окружности в стандартной форме, чтобы найти центр и радиус окружности.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее. 92???
где ???r??? это радиус и ???(h,k)??? является центром.
Иногда, чтобы написать уравнение окружности в стандартной форме, вам нужно заполнить квадрат дважды, один раз для ???x??? и один раз для ???y???.
Приведение уравнения окружности к стандартной форме и определение ее центра и радиуса по стандартной форме
92=\фракция{19}{6}???
Центр круга ???(h,k)??? ???(-1,0)??? а радиус равен ???\sqrt{19/6}???. Исключить ???-\sqrt{19/6}??? потому что радиус не может быть отрицательным.
Получить доступ к полному курсу Алгебра 2
Начать
Изучение математикиКриста Кинг математика, изучение онлайн, онлайн-курс, онлайн-математика, алгебра, алгебра 2, алгебра II, круг, уравнение окружности, центр и радиус, центр и радиус окружности, стандартная форма уравнение окружности
0 лайковКак найти радиус окружности? Формула и пример
Адарш Кумар Сингх
Содержание
Как найти радиус окружности? Формула и пример
Как найти радиус окружности? Радиус круга — одна из его важнейших составляющих. Это расстояние между центром круга и любой точкой на его границе. Другими словами, когда мы соединяем центр круга с любой точкой его окружности прямой линией, эта линия является радиусом этого круга. Круги являются одними из самых распространенных форм в природе. Их удивительные свойства делают их очень важной темой в геометрии.
На окружности круга бесконечное количество точек, поэтому круг может иметь более одного радиуса. Круг имеет бесконечное число радиусов, и все радиусы одинаково удалены от центра. В этом уроке мы узнаем больше о радиусе.
Как найти радиус окружностиЧто такое радиус окружности?
Окружности состоят из точек, расположенных на равном расстоянии от центральной точки «О» на двумерной плоскости. Круги измеряются расстоянием между центром и любой точкой на их окружности.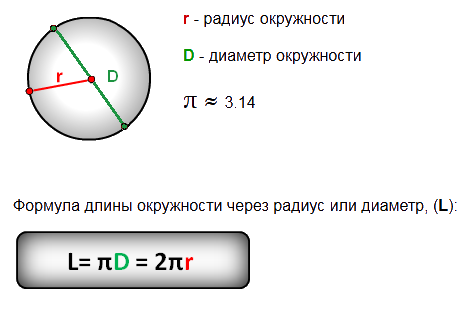 Отрезок линии от точки на окружности круга до центра круга также можно определить как его длину. На окружности может быть любое количество радиусов, и все они имеют одинаковые размеры. Если радиус меняется, размер круга также меняется. Круговые радиусы обычно обозначаются буквой «r».
Отрезок линии от точки на окружности круга до центра круга также можно определить как его длину. На окружности может быть любое количество радиусов, и все они имеют одинаковые размеры. Если радиус меняется, размер круга также меняется. Круговые радиусы обычно обозначаются буквой «r».
На границе окружности расположены точки A, B, M, N, P, Q, X и Y. Каждая из этих точек равноудалена от центра O. В результате все отрезки OA, OB, OM, ON, OY, OX, OP и OQ можно считать радиусами окружности. Вы можете заметить, что OA = OB = OM = ON = OP = OQ = OX = OY.
Формулы радиуса
Формула радиуса с использованием диаметра окружности: Диаметр окружности – это прямая линия, проходящая через центр и соединяющая точку на одном конце с точкой на другом конце. Диаметр круга в два раза больше его радиуса. Математически это формулируется как диаметр = 2 × радиус. Это также самая длинная хорда в окружности. А — диаметр окружности. Когда дан диаметр круга, формула радиуса выражается как:
Формула радиуса = Диаметр/2 или D/2 единиц
Формула радиуса с использованием длины окружности: Длина окружности — это ее периметр. Это граница круга и может быть выражена формулой: C = 2 π r. C — длина окружности, r — радиус окружности, а * — константа 3,14159. Радианы вычисляются путем деления длины окружности на 2π. Радиусы рассчитываются с использованием длины окружности следующим образом:
Это граница круга и может быть выражена формулой: C = 2 π r. C — длина окружности, r — радиус окружности, а * — константа 3,14159. Радианы вычисляются путем деления длины окружности на 2π. Радиусы рассчитываются с использованием длины окружности следующим образом:
Формула радиуса = Длина окружности/2π или C/2π единиц
Формула радиуса с использованием площади круга: Круг имеет площадь, которая представляет собой пространство, которое он занимает. Связь между радиусом и площадью определяется формулой Площадь круга = π r 2 . Здесь r — радиус, а π — константа, равная 3,14159. Формула радиуса с использованием площади круга выглядит следующим образом:
Формула радиуса = √(Площадь/π) единиц
Как найти радиус круга?
Существуют три основные формулы, которые можно использовать для вычисления радиуса круга, т. е. когда известны диаметр, площадь или длина окружности. Применим эти формулы, чтобы найти радиус окружности.
- Когда известен диаметр, формула для радиуса окружности: Радиус = Диаметр / 2
- Когда известна длина окружности, формула для радиуса: Радиус = Длина окружности / 2π
- Когда площадь Известно, формула для радиуса: Радиус = ⎷(Площадь круга / π)
Радиус круга Уравнение
Обратите внимание на круг в декартовой плоскости. Координаты центра (h, k). Радиус уравнения окружности в декартовой плоскости координат равен (x − h) 2 + (y − k) 2 = r 2 . Здесь (x, y) — точки на окружности окружности, находящиеся на расстоянии «r» (радиус) от центра (h, k). Когда центр окружности находится в начале координат (0,0), уравнение окружности сводится к x 2 + y 2 = r 2
Радиус кривой
Дуга окружности это расстояние между двумя точками на участке кривой. Кривые имеют радиус, определяемый радиусом окружности, частью которой они являются. Когда даны длина хорды, определяющей основание (W), и высота (H), измеренная в середине основания дуги, формула для определения радиуса: Радиус = (H / 2) + (W² / 8H). )
)
Что такое радиус круга в геометрии?
Радиус окружности — это длина отрезка, соединяющего центр окружности с точкой на ее окружности. Обычно обозначается аббревиатурой «р».
Диаметр и радиус: какая связь?
Диаметр круга в два раза больше его радиуса, или радиус равен половине диаметра. Отношение между радиусом и диаметром можно выразить формулой: Диаметр = 2 × радиус.
Каков радиус окружности, если известна длина окружности?
Окружность и радиус круга связаны, и их соотношение можно выразить как Окружность = 2πR, где R — радиус. Если вы знаете длину окружности, вы можете рассчитать ее радиус по следующей формуле: Радиус = Длина окружности / 2π
Как рассчитать радиус окружности с помощью калькулятора?
Радиус равен половине диаметра, и его можно рассчитать с помощью онлайн-инструмента Cuemath, просто введя диаметр, длину окружности или площадь круга.
Как найти центр и радиус окружности (3 метода) – JDM Educational
Окружности используются в математике и в повседневной жизни. Однако знание того, как найти центр или радиус из другой заданной информации, также может быть полезным.
Итак, как найти центр и радиус круга? Чтобы найти центр и радиус окружности, запишите уравнение окружности в стандартной форме. Мы также можем использовать три точки на окружности (или две точки, если они находятся на противоположных концах диаметра), чтобы найти центр и радиус. Кроме того, мы можем использовать центр и одну точку на окружности, чтобы найти радиус.
Конечно, полезно ознакомиться со стандартной формой уравнения окружности, чтобы вы могли легко работать с этими различными ситуациями.
В этой статье мы поговорим о том, как найти центр и радиус окружности по информации о ней (например, ее уравнению или точкам на окружности). Мы также рассмотрим несколько примеров, чтобы прояснить концепции.
Начнем.
Как найти центр и радиус окружности
Способ, которым мы находим центр и радиус окружности, зависит от информации, которую мы получили:
- Из уравнения : с уравнением в стандартной форме мы можем легко найти центр и радиус круга. В противном случае нам нужно будет заполнить квадрат для переменной x или y (или обеих) для преобразования в стандартную форму.
- С двумя точками : по двум точкам на окружности на противоположных концах диаметра мы можем найти центр. Мы также можем найти радиус, учитывая центр и одну точку на окружности, используя формулу расстояния.
- С тремя точками : по трем точкам на окружности мы можем найти центр и радиус окружности, решив систему трех уравнений с тремя неизвестными (a, b и r).
Начнем с нахождения центра окружности по заданному уравнению.
Найти центр круга из уравнения
Чтобы найти центр круга из уравнения, мы всегда хотим преобразовать его в стандартную форму.
Помните, что уравнение окружности в стандартной форме задается как:
- (x – a) 2 + (y – b) 2 = r 2 , где 900, б) — центр окружности, r — радиус окружности.
- (x 2 + 6x) + (y 2 + 10y + 25) = 27
- (x 2 + 6x ) + (y + 5) 2 = 27
- (x 2 + 6x + 9) + (y + 5) 2 = 27 + 9
- (x + 3) 2 + (y + 5) 2 = 36
Если нам дано уравнение не в стандартной форме, нам нужно сначала заполнить квадрат для одной или обеих переменных (x и y).
Пример 1. Центр окружности из уравнения в стандартной форме
Допустим, мы хотим найти центр окружности, заданной уравнением выше мы видим, что a = 2 и b = -4 (остерегайтесь этих отрицательных знаков: y — (-4) совпадает с y + 4).
Итак, центр окружности (a, b) = (2, -4).
Пример 2. Центр круга из уравнения путем заполнения квадрата одной переменной
Допустим, мы хотим найти центр окружности, заданной уравнением поэтому мы знаем, что нам нужно будет заполнить квадрат хотя бы для одной переменной.
Переставив члены таким образом, чтобы переменные сгруппировались, мы получим:
Легко видеть, что выражение с переменной y, y 2 + 10y + 25, представляет собой трехчлен с полным квадратом, (y + 5) 2 :
Теперь нам просто нужно дополнить квадрат выражения с переменной x, x 2 + 6x. Помните, что для завершения квадрата мы берем половину коэффициента x и возводим результат в квадрат, а затем прибавляем его к обеим сторонам.
Здесь x-коэффициент равен 6, поэтому половина этого дает нам результат 3. Возведение результата в квадрат дает нам 3 2 = 9.
Итак, мы добавляем 9 к обеим частям уравнения, чтобы получить:
Обратите внимание, что мы сгруппировали +9 слева с членами x. Это позволяет нам разложить на множители еще один совершенный квадратный трехчлен:
Это позволяет нам разложить на множители еще один совершенный квадратный трехчлен:
Теперь у нас есть уравнение окружности в стандартной форме. Сравнивая его с приведенным выше общим уравнением, мы находим, что a = -3 и b = -5.
Итак, центр окружности (a, b) = (-3, -5).
Пример 3. Центр окружности из уравнения путем заполнения квадрата двух переменных
Допустим, мы хотим найти центр окружности, заданной уравнением 8х + 12у = 12
Этот круг не имеет стандартной формы, поэтому мы знаем, что нам нужно заполнить квадрат для обеих переменных.
Переставив члены таким образом, чтобы переменные сгруппировались, мы получим:
- (x 2 + 8x) + (y 2 + 12y) = 12
. квадрат для выражения с переменной x, x 2 + 8x. Помните, что для завершения квадрата мы берем половину коэффициента x и возводим результат в квадрат, а затем прибавляем его к обеим сторонам.
Здесь x-коэффициент равен 8, поэтому половина этого дает нам результат 4. Возведение результата в квадрат дает нам 4 2 = 16.
Итак, мы добавляем 16 к обеим частям уравнения, чтобы получить:
- (x 2 + 8x + 16) + (y 2 + 12y) = 12 + 16
Обратите внимание, что мы сгруппировали +12 слева с членами x. Это позволяет нам разложить на множители как совершенный квадратный трехчлен:
- (x + 4) 2 + (y 2 + 12y) = 28
Теперь нам нужно заполнить квадрат выражения с переменной y, y 2 + 12y. Помните, что для завершения квадрата мы берем половину коэффициента x и возводим результат в квадрат, а затем прибавляем его к обеим сторонам.
Здесь x-коэффициент равен 12, поэтому половина этого числа дает нам результат 6. Возведение результата в квадрат дает нам 6 2 = 36.
Итак, мы добавляем 36 к обеим частям уравнения, чтобы получить:
- (х 2 + 8х + 16) + (у 2 + 12y + 36) = 28 + 36
Обратите внимание, что мы сгруппировали +36 слева с членами y. Это позволяет нам разложить на множители идеальный квадратный трехчлен:
Это позволяет нам разложить на множители идеальный квадратный трехчлен:
- (x + 4) 2 + (y + 6) 2 = 64
Теперь у нас есть уравнение окружности в стандартной форме. Сравнивая его с приведенным выше общим уравнением, мы находим, что a = -4 и b = -6.
Итак, центр окружности (a, b) = (-4, -6).
Найти центр окружности с двумя точками (на концах диаметра)
Учитывая две точки на окружности, мы можем найти центр. Если они не лежат на одном диаметре, то у нас недостаточно информации, и мы можем указать только все семейство окружностей, а не одну конкретную окружность.
Однако по двум точкам на окружности, лежащим на концах диаметра, мы можем найти центр окружности.
Центр круга будет в середине любого диаметра, нарисованного на круге.Все, что нам нужно сделать, это найти середину отрезка между двумя точками на диаметре.
Помните, что для отрезка с концами (x 1 , y 1 ) и (x 2 , y 2 ) формула средней точки определяется как: , y m ) = ((x 1 + x 2 ) / 2, (y 1 + y 2 ) / 2) среднее значение 1 m 9050 По существу, x 9004 координаты x конечных точек, а y m — среднее значение координат y конечных точек. Давайте рассмотрим пример, чтобы увидеть, как это работает. Допустим, мы хотим найти центр окружности с точками (0, 0) и (6, -8) в качестве концов диаметра. Использование формулы средней точки для нахождения центра окружности дает нам:
Пример: найти центр окружности с двумя точками на диаметре
+ у 2 ) / 2)
Таким образом, центр этого круга находится в точке (3, -4).
Мы также можем найти радиус окружности, если захотим. Это просто половина диаметра, который определяется формулой расстояния:
- D = √((x 2 – x 1 ) 2 + (Y 2 -Y 1 ) 2 )
- D = √ ((6-0) 2 + (-8 –0173 2) 2 ) 2 ) ) 2 ) 2 ) ) ) 2 )
- D = √((6) 2 + (-8) 2 )
- D = √(36 + 64)
- D = √(100)
- D = 10
Итак, диаметр равен 10, а радиус равен 5.
Найти центр окружности по трем точкам
Чтобы найти центр окружности по трем точкам, мы можем просто подставить значения x и y из каждой точки в уравнение окружности.
Тогда мы можем установить все 3 уравнения равными друг другу (все они равны r 2 , или квадрату радиуса).
Затем мы можем написать отдельные уравнения, упростить их и одновременно решать линейные уравнения.
Давайте рассмотрим пример.
Пример. Найдите центр окружности по трем точкам
Допустим, нам даны точки (-1, -3), (-2, 4) и (5, 5) на окружности.
Подставим каждую из этих точек по очереди в стандартную форму окружности:
- (x – a) 2 + (y – b) 2 = r 2
Для первой точки (-1, -3) получаем:
- (-1 – a) 2 + (-3 – b) 2 = r 2
вторая точка (-2, 4), получаем:
- (-2 – а) 2 + (4 – б) 2 = r 2
– a) 2 + (5 – b) 2 = r 2
Мы можем положить любые две левые части равными друг другу, так как все правые части равны r 2 (независимо от значения р).
Уравнивание первых двух левых частей дает нам:
- (-1 – a) 2 + (-3 – б) 2 = (-2 – а) 2 + (4 – б) 2
- 1 + 2а + а 2 + + 9 + 6б 2 = 4 + 4а + а 2 + 16 – 8b + b 2
- 1 + 2а + а 2 + 9 + 6b = 4 + 17 – 4 6 1 8 8 901 901 [вычесть b 2 с обеих сторон]
- 1 + 2a + 9 + 6b = 4 + 4a + 16 – 8b [вычесть a 2 с обеих сторон]
- 10 + 2a + 6b = 20 + 4a – 8b [объединить постоянные слагаемые с обеих сторон]
- -10 – 2a + 14b = 0 [собрать все слагаемые с одной стороны и соединить одинаковые слагаемые]
- 5 + a – 7b = 0 [разделить на -2 с обеих сторон]
Приравняв первую и третью левые части, получим:
- (-1 – a) 2 + (-3 – b) 2 = (5 – а) 2 + (5 – б) 2
- 1 + 2а + а 2 + 9 + 6б + б 2 = 25 – 10а + а 2 + 25 – 10б + б 2
- 1 + 2а + а 2 а + 1 + б = 2 + б 2 + 25 – 10b [вычесть b 2 с обеих сторон]
- 1 + 2a + 9 + 6b = 25 – 10a + 25 – 10b [вычесть a 3 3
с обеих сторон] 9034 10 + 2a + 6b = 50 – 10a – 10b [объединить постоянные слагаемые с обеих сторон] - -40 + 12a + 16b = 0 [собрать все слагаемые с одной стороны и соединить одинаковые слагаемые]
- -10 + 3a + 4b = 0 [разделить на 4 с обеих сторон]
Теперь мы можем решить следующую систему методом исключения:
- 5 + a – 7b = 9 0 333334
4 10 + 3a + 4b = 0
Для этого умножьте первое уравнение на -3, чтобы получить:
- -15 – 3a + 21b = 0
- -10 + 3a + 90 = 3 4
Теперь сложите два уравнения, чтобы получить:
- -25 + 0a + 25b = 0
- 1 = b
So, with b = 1 , we find:
- 5 + a – 7b = 0
- 5 + a – 7(1) = 0
- 5 + а – 7 = 0
- а – 2 = 0
- а = 2
Итак, центр круга находится в точке (а, b) = (1, 2). Затем мы можем использовать центр и любую точку на окружности, чтобы найти радиус, используя формулу расстояния (подробнее об этом методе ниже).
Затем мы можем использовать центр и любую точку на окружности, чтобы найти радиус, используя формулу расстояния (подробнее об этом методе ниже).
Найдите радиус круга из уравнения
Чтобы найти радиус круга из уравнения, мы всегда хотим преобразовать его в стандартную форму.
Помните, что уравнение окружности в стандартной форме задается формулой:
- (x – a) 2 + (y – b) 2 = r 2 где ( a, b) — центр окружности, r — радиус окружности.
- (x – 3) 2 + (y + 5) 2 = 49
- (x 2 + 8x) + (y 2 + 12y) = 24 – 12
- (x 2 + 8x) + (y 2 + 12y) = 12
- (x 2 + 8x + 16) + (y 2 + 12y) = 12 + 16
- (x 2 + 8x + 16) + (y 2 + 12y) = 28
- (x + 4) 2 + (y 2 + 12y) = 28
- (x + 4) 2 + (y 2 + 12y + 36) = 28 + 36
- x ( + 4) 2 + (у 2 + 12у + 36) = 64
- (x + 4) 2 + (Y + 6) 2 = 64
- (X + 4) 2 + (Y + 6) 2 = 8 + (Y + 6) 2 = 8 + (Y + 6) 2 = 8 + (Y + 6) 2 = 8 + (Y + 6).
- D = √ ((x 2 — x 1 ) 2 + (Y 2 — Y 1 ) 2 )
- 93939 2 ). ) 2 + (12 — 3) 2 )
- D = √ (12) 2 + (9) 2 )
- D = Qu
- D = √(225)
- D = 15
Если нам дано уравнение не в стандартной форме, нам нужно сначала заполнить квадрат для одной или обеих переменных (x и y).
Пример 1: Центр окружности из уравнения в стандартной форме
Допустим, мы хотим найти радиус окружности, заданный уравнением
Сравнивая это со стандартной формой выше, мы видим, что r = 7 (поскольку r 2 = 49 — не забудьте взять квадратный корень, чтобы найти r).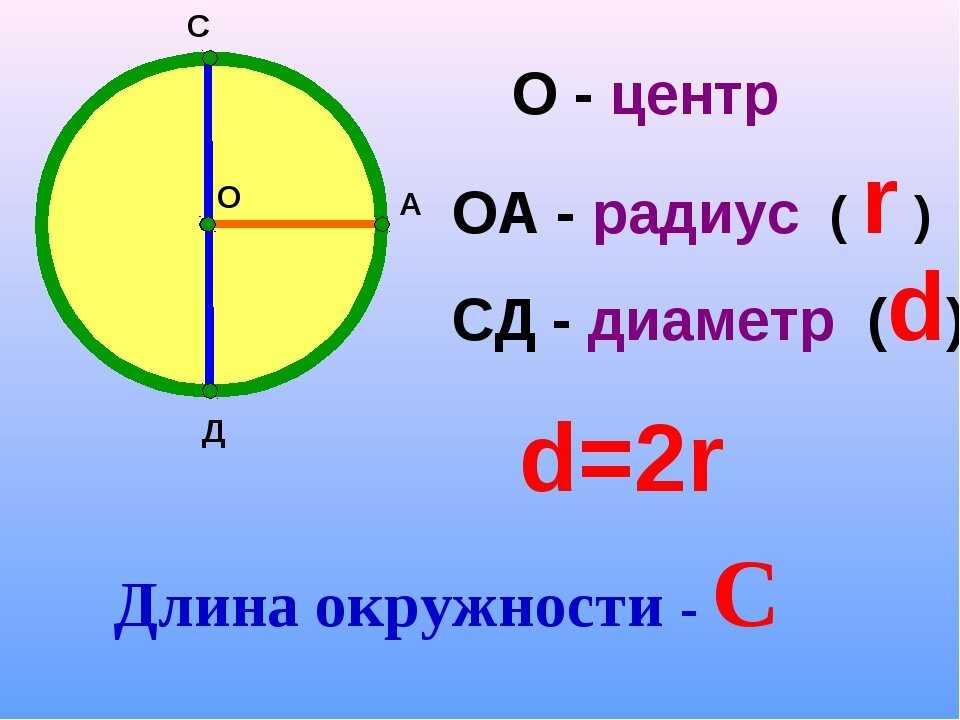
Итак, радиус окружности равен r = 7.
Пример 2. Радиус окружности из уравнения путем заполнения квадрата
Допустим, мы хотим найти радиус окружности, заданной уравнением поэтому мы знаем, что нам нужно будет заполнить квадрат хотя бы для одной переменной.
Переставив члены таким образом, чтобы переменные сгруппировались, мы получим:
возведем этот результат в квадрат, чтобы получить 16. Мы прибавляем 16 к обеим сторонам:
Теперь нам нужно разложить выражение x на множители, x 2 + 8x + 16. Это идеальный квадратный бином: (x + 4) 2 .
6 и возведите этот результат в квадрат, чтобы получить 36. Добавим 36 к обеим частям:
Добавим 36 к обеим частям:
Теперь нам нужно разложить на множители выражение y, y 2 + 12y + 36. Это бином с полным квадратом: (y + 6) 2 .
Мы также переписали 64 как 8 2 , поскольку это соответствует r 2 в правой части уравнения окружности в стандартной форме.
Теперь мы знаем, что радиус окружности равен r = 8,
Найдите радиус окружности по заданному центру и точке
Если мы знаем центр окружности и одну точку на окружности, мы можем найти радиус с помощью формулы расстояния.
(Помните, что радиус — это расстояние между центром окружности и любой точкой на окружности.)
Давайте рассмотрим пример того, как это сделать.
Пример: нахождение радиуса окружности по центру и точке на окружности
Предположим, что вам дан центр окружности в точках (4, 3) и точка на окружности в точках (16, 12) . Используя формулу расстояния, мы получаем:
Итак, радиус окружности равен 15.
Найдите радиус окружности с двумя точками на окружности
В этом случае мы не можем решить для одного круга, так как у нас недостаточно информации. Вместо этого мы получили бы целое семейство окружностей, содержащих обе точки.
Вместо этого мы получили бы целое семейство окружностей, содержащих обе точки.
Если у нас также есть центр или третья точка на окружности, мы можем найти радиус (используя формулу расстояния с центром в качестве одной точки и одной из точек на окружности в качестве другой точки).
Затем мы можем использовать центр и радиус, чтобы записать уравнение окружности в стандартной форме.
Имея всего две точки на окружности, мы можем указать только семейство окружностей, а не конкретную. Нам нужно больше информации (например, центр или третья точка), чтобы дать конкретный круг.Заключение
Теперь вы знаете, как найти центр и радиус круга в различных ситуациях. Вы также знаете, как использовать формулы средней точки и расстояния в качестве сокращений, чтобы сделать ваши вычисления немного проще.
Вы можете узнать о длине окружности и площади круга в моей статье здесь.
О длине дуги окружности можно узнать здесь.
О площади кругового сектора можно узнать здесь.

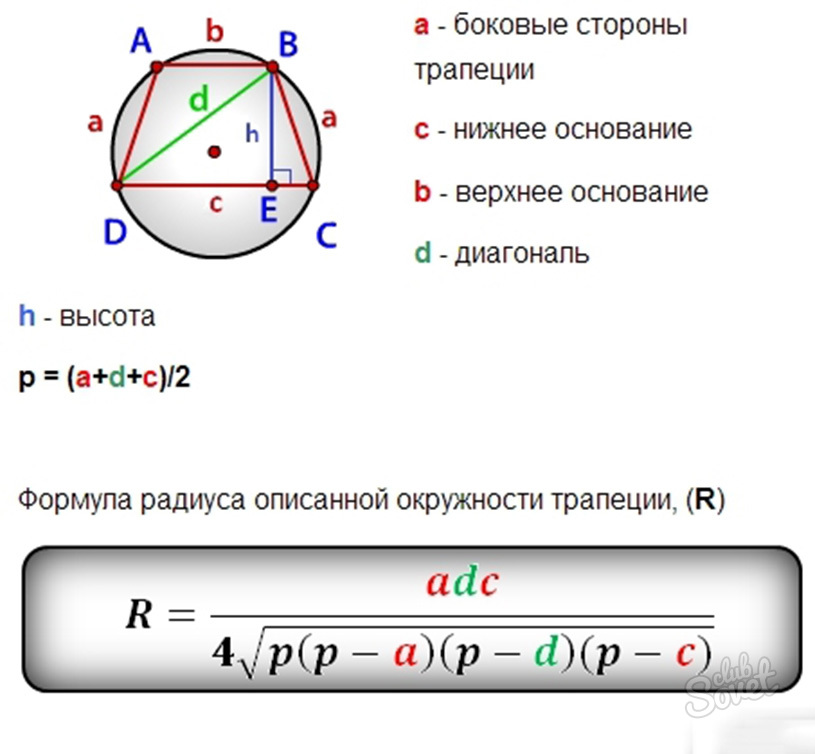

 Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
 Диаметр данной фигуры равен длине рассматриваемого отрезка.
Диаметр данной фигуры равен длине рассматриваемого отрезка.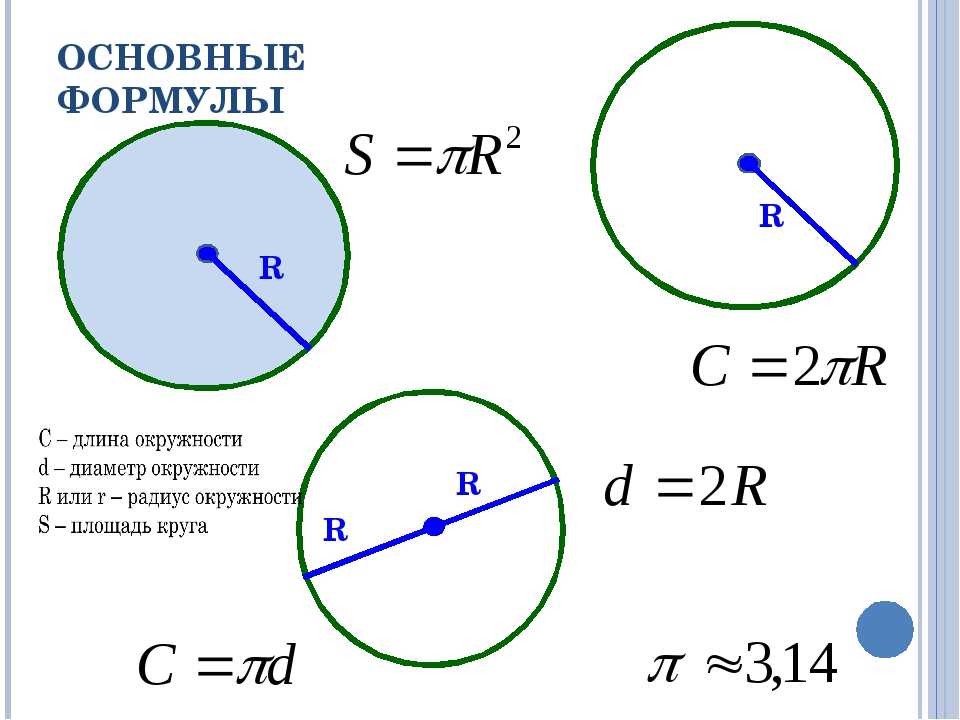 Формулу обычно записывают следующим образом: C = π*D.
Формулу обычно записывают следующим образом: C = π*D.