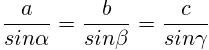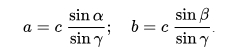Значений sin таблица: Таблица синусов. — Таловская средняя школа

Содержание

Таблица синусов

Главная > с >

Таблица синусов для основных углов: 0°, 90°, 180°, 270°, 360°.

Угол х (в градусах)	0°	90°	180°	270°	360°
Угол х (в радианах)	0
sin x	0	1	0	-1	0

Радиан — угловая величина дуги, по длине равной радиусу или 57,295779513° градусов.

Градус (в геометрии) — 1/360-я часть окружности или 1/90-я часть прямого угла.

π = 3.141592653589793238462… (приблизительное значение числа Пи).

Таблица синусов для углов: 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°.

Угол х (в градусах)	0°	30°	45°	60°	90°	120°	135°	150°	180°
Угол х (в радианах)	0	π/6	π/4	π/3	π/2	2 x π/3	3 x π/4	5 x π/6	π
sin x	0	1/2 (0,5)	√2/2 (0,7071)	√3/2 (0,8660)	1	√3/2 (0,8660)	√2/2 (0,7071)	1/2 (0,5)	0

Таблица синусов углов от 0° — 360°. Углы с шагом в 1°.

Таблица синусов — это посчитанные значения синусов от 0° до 360°.

Если не под рукой калькулятора — таблица синусов очень пригодится.
Для того, чтобы узнать чему равен синус от нужного Вам угла достаточно найти его в таблице.

1°	sin= 0.0175	91°	sin= 0.9998	181°	sin= -0.0175	271°	sin= -0.9998
2°	sin= 0.0349	92°	sin= 0.9994	182°	sin= -0.0349	272°	sin= -0.9994
3°	sin= 0.0523	93°	sin= 0.9986	183°	sin= -0.0523	273°	sin= -0.9986
4°	sin= 0.0698	94°	sin= 0.9976	184°	sin= -0.0698	274°	sin= -0.9976
5°	sin= 0.0872	95°	sin= 0.9962	185°	sin= -0.0872	275°	sin= -0.9962
6°	sin= 0.1045	96°	sin= 0.9945	186°	sin= -0.1045	276°	sin= -0.9945
7°	sin= 0.1219	97°	sin= 0.9925	187°	sin= -0.1219	277°	sin= -0.9925
8°	sin= 0.1392	98°	sin= 0.9903	188°	sin= -0.1392	278°	sin= -0.9903
9°	sin= 0.1564	99°	sin= 0.9877	189°	sin= -0.1564	279°	sin= -0.9877
10°	sin= 0.1736	100°	sin= 0.9848	190°	sin= -0.1736	280°	sin= -0.9848
11°	sin= 0.1908	101°	sin= 0.9816	191°	sin= -0.1908	281°	sin= -0.9816
12°	sin= 0.2079	102°	sin= 0.9781	192°	sin= -0.2079	282°	sin= -0.9781
13°	sin= 0.2250	103°	sin= 0.9744	193°	sin= -0.2250	283°	sin= -0.9744
14°	sin= 0.2419	104°	sin= 0.9703	194°	sin= -0.2419	284°	sin= -0.9703
15°	sin= 0.2588	105°	sin= 0.9659	195°	sin= -0.2588	285°	sin= -0.9659
16°	sin= 0.2756	106°	sin= 0.9613	196°	sin= -0.2756	286°	sin= -0.9613
17°	sin= 0.2924	107°	sin= 0.9563	197°	sin= -0.2924	287°	sin= -0.9563
18°	sin= 0.3090	108°	sin= 0.9511	198°	sin= -0.3090	288°	sin= -0.9511
19°	sin= 0.3256	109°	sin= 0.9455	199°	sin= -0.3256	289°	sin= -0.9455
20°	sin= 0.3420	110°	sin= 0.9397	200°	sin= -0.3420	290°	sin= -0.9397
21°	sin= 0.3584	111°	sin= 0.9336	201°	sin= -0.3584	291°	sin= -0.9336
22°	sin= 0.3746	112°	sin= 0.9272	202°	sin= -0.3746	292°	sin= -0.9272
23°	sin= 0.3907	113°	sin= 0.9205	203°	sin= -0.3907	293°	sin= -0.9205
24°	sin= 0.4067	114°	sin= 0.9135	204°	sin= -0.4067	294°	sin= -0.9135
25°	sin= 0.4226	115°	sin= 0.9063	205°	sin= -0.4226	295°	sin= -0.9063
26°	sin= 0.4384	116°	sin= 0.8988	206°	sin= -0.4384	296°	sin= -0.8988
27°	sin= 0.4540	117°	sin= 0.8910	207°	sin= -0.4540	297°	sin= -0.8910
28°	sin= 0.4695	118°	sin= 0.8829	208°	sin= -0.4695	298°	sin= -0.8829
29°	sin= 0.4848	119°	sin= 0.8746	209°	sin= -0.4848	299°	sin= -0.8746
30°	sin= 0.5000	120°	sin= 0.8660	210°	sin= -0.5000	300°	sin= -0.8660
31°	sin= 0.5150	121°	sin= 0.8572	211°	sin= -0.5150	301°	sin= -0.8572
32°	sin= 0.5299	122°	sin= 0.8480	212°	sin= -0.5299	302°	sin= -0.8480
33°	sin= 0.5446	123°	sin= 0.8387	213°	sin= -0.5446	303°	sin= -0.8387
34°	sin= 0.5592	124°	sin= 0.8290	214°	sin= -0.5592	304°	sin= -0.8290
35°	sin= 0.5736	125°	sin= 0.8192	215°	sin= -0.5736	305°	sin= -0.8192
36°	sin= 0.5878	126°	sin= 0.8090	216°	sin= -0.5878	306°	sin= -0.8090
37°	sin= 0.6018	127°	sin= 0.7986	217°	sin= -0.6018	307°	sin= -0.7986
38°	sin= 0.6157	128°	sin= 0.7880	218°	sin= -0.6157	308°	sin= -0.7880
39°	sin= 0.6293	129°	sin= 0.7771	219°	sin= -0.6293	309°	sin= -0.7771
40°	sin= 0.6428	130°	sin= 0.7660	220°	sin= -0.6428	310°	sin= -0.7660
41°	sin= 0.6561	131°	sin= 0.7547	221°	sin= -0.6561	311°	sin= -0.7547
42°	sin= 0.6691	132°	sin= 0.7431	222°	sin= -0.6691	312°	sin= -0.7431
43°	sin= 0.6820	133°	sin= 0.7314	223°	sin= -0.6820	313°	sin= -0.7314
44°	sin= 0.6947	134°	sin= 0.7193	224°	sin= -0.6947	314°	sin= -0.7193
45°	sin= 0.7071	135°	sin= 0.7071	225°	sin= -0.7071	315°	sin= -0.7071
46°	sin= 0.7193	136°	sin= 0.6947	226°	sin= -0.7193	316°	sin= -0.6947
47°	sin= 0.7314	137°	sin= 0.6820	227°	sin= -0.7314	317°	sin= -0.6820
48°	sin= 0.7431	138°	sin= 0.6691	228°	sin= -0.7431	318°	sin= -0.6691
49°	sin= 0.7547	139°	sin= 0.6561	229°	sin= -0.7547	319°	sin= -0.6561
50°	sin= 0.7660	140°	sin= 0.6428	230°	sin= -0.7660	320°	sin= -0.6428
51°	sin= 0.7771	141°	sin= 0.6293	231°	sin= -0.7771	321°	sin= -0.6293
52°	sin= 0.7880	142°	sin= 0.6157	232°	sin= -0.7880	322°	sin= -0.6157
53°	sin= 0.7986	143°	sin= 0.6018	233°	sin= -0.7986	323°	sin= -0.6018
54°	sin= 0.8090	144°	sin= 0.5878	234°	sin= -0.8090	324°	sin= -0.5878
55°	sin= 0.8192	145°	sin= 0.5736	235°	sin= -0.8192	325°	sin= -0.5736
56°	sin= 0.8290	146°	sin= 0.5592	236°	sin= -0.8290	326°	sin= -0.5592
57°	sin= 0.8387	147°	sin= 0.5446	237°	sin= -0.8387	327°	sin= -0.5446
58°	sin= 0.8480	148°	sin= 0.5299	238°	sin= -0.8480	328°	sin= -0.5299
59°	sin= 0.8572	149°	sin= 0.5150	239°	sin= -0.8572	329°	sin= -0.5150
60°	sin= 0.8660	150°	sin= 0.5000	240°	sin= -0.8660	330°	sin= -0.5000
61°	sin= 0.8746	151°	sin= 0.4848	241°	sin= -0.8746	331°	sin= -0.4848
62°	sin= 0.8829	152°	sin= 0.4695	242°	sin= -0.8829	332°	sin= -0.4695
63°	sin= 0.8910	153°	sin= 0.4540	243°	sin= -0.8910	333°	sin= -0.4540
64°	sin= 0.8988	154°	sin= 0.4384	244°	sin= -0.8988	334°	sin= -0.4384
65°	sin= 0.9063	155°	sin= 0.4226	245°	sin= -0.9063	335°	sin= -0.4226
66°	sin= 0.9135	156°	sin= 0.4067	246°	sin= -0.9135	336°	sin= -0.4067
67°	sin= 0.9205	157°	sin= 0.3907	247°	sin= -0.9205	337°	sin= -0.3907
68°	sin= 0.9272	158°	sin= 0.3746	248°	sin= -0.9272	338°	sin= -0.3746
69°	sin= 0.9336	159°	sin= 0.3584	249°	sin= -0.9336	339°	sin= -0.3584
70°	sin= 0.9397	160°	sin= 0.3420	250°	sin= -0.9397	340°	sin= -0.3420
71°	sin= 0.9455	161°	sin= 0.3256	251°	sin= -0.9455	341°	sin= -0.3256
72°	sin= 0.9511	162°	sin= 0.3090	252°	sin= -0.9511	342°	sin= -0.3090
73°	sin= 0.9563	163°	sin= 0.2924	253°	sin= -0.9563	343°	sin= -0.2924
74°	sin= 0.9613	164°	sin= 0.2756	254°	sin= -0.9613	344°	sin= -0.2756
75°	sin= 0.9659	165°	sin= 0.2588	255°	sin= -0.9659	345°	sin= -0.2588
76°	sin= 0.9703	166°	sin= 0.2419	256°	sin= -0.9703	346°	sin= -0.2419
77°	sin= 0.9744	167°	sin= 0.2250	257°	sin= -0.9744	347°	sin= -0.2250
78°	sin= 0.9781	168°	sin= 0.2079	258°	sin= -0.9781	348°	sin= -0.2079
79°	sin= 0.9816	169°	sin= 0.1908	259°	sin= -0.9816	349°	sin= -0.1908
80°	sin= 0.9848	170°	sin= 0.1736	260°	sin= -0.9848	350°	sin= -0.1736
81°	sin= 0.9877	171°	sin= 0.1564	261°	sin= -0.9877	351°	sin= -0.1564
82°	sin= 0.9903	172°	sin= 0.1392	262°	sin= -0.9903	352°	sin= -0.1392
83°	sin= 0.9925	173°	sin= 0.1219	263°	sin= -0.9925	353°	sin= -0.1219
84°	sin= 0.9945	174°	sin= 0.1045	264°	sin= -0.9945	354°	sin= -0.1045
85°	sin= 0.9962	175°	sin= 0.0872	265°	sin= -0.9962	355°	sin= -0.0872
86°	sin= 0.9976	176°	sin= 0.0698	266°	sin= -0.9976	356°	sin= -0.0698
87°	sin= 0.9986	177°	sin= 0.0523	267°	sin= -0.9986	357°	sin= -0.0523
88°	sin= 0.9994	178°	sin= 0.0349	268°	sin= -0.9994	358°	sin= -0.0349
89°	sin= 0.9998	179°	sin= 0.0175	269°	sin= -0.9998	359°	sin= -0.0175
90°	sin= 1.0000	180°	sin= 0.0000	270°	sin= -1.0000	360°	sin= -0.0000

comments powered by HyperComments

Таблица синусов углов (градусы, значения)

В данной таблице представлены значения синусов от 0° до 360°. Таблица синусов нужна, когда у вас под рукой нет калькулятора. Чтобы узнать, чему равен синус угла, просто найдите нужный градус в таблице. Для начала короткая версия таблицы.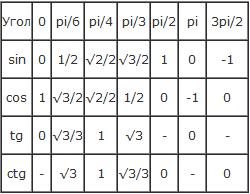

https://uchim.org/matematika/tablica-sinusov — uchim.org

Таблица синусов для 0°-180°

sin(1°)	0.0175
sin(2°)	0.0349
sin(3°)	0.0523
sin(4°)	0.0698
sin(5°)	0.0872
sin(6°)	0.1045
sin(7°)	0.1219
sin(8°)	0.1392
sin(9°)	0.1564
sin(10°)	0.1736
sin(11°)	0.1908
sin(12°)	0.2079
sin(13°)	0.225
sin(14°)	0.2419
sin(15°)	0.2588
sin(16°)	0.2756
sin(17°)	0.2924
sin(18°)	0.309
sin(19°)	0.3256
sin(20°)	0.342
sin(21°)	0.3584
sin(22°)	0.3746
sin(23°)	0.3907
sin(24°)	0.4067
sin(25°)	0.4226
sin(26°)	0.4384
sin(27°)	0.454
sin(28°)	0.4695
sin(29°)	0.4848
sin(30°)	0.5
sin(31°)	0.515
sin(32°)	0.5299
sin(33°)	0.5446
sin(34°)	0.5592
sin(35°)	0.5736
sin(36°)	0.5878
sin(37°)	0.6018
sin(38°)	0.6157
sin(39°)	0.6293
sin(40°)	0.6428
sin(41°)	0.6561
sin(42°)	0.6691
sin(43°)	0.682
sin(44°)	0.6947
sin(45°)	0.7071

sin(46°)	0.7193
sin(47°)	0.7314
sin(48°)	0.7431
sin(49°)	0.7547
sin(50°)	0.766
sin(51°)	0.7771
sin(52°)	0.788
sin(53°)	0.7986
sin(54°)	0.809
sin(55°)	0.8192
sin(56°)	0.829
sin(57°)	0.8387
sin(58°)	0.848
sin(59°)	0.8572
sin(60°)	0.866
sin(61°)	0.8746
sin(62°)	0.8829
sin(63°)	0.891
sin(64°)	0.8988
sin(65°)	0.9063
sin(66°)	0.9135
sin(67°)	0.9205
sin(68°)	0.9272
sin(69°)	0.9336
sin(70°)	0.9397
sin(71°)	0.9455
sin(72°)	0.9511
sin(73°)	0.9563
sin(74°)	0.9613
sin(75°)	0.9659
sin(76°)	0.9703
sin(77°)	0.9744
sin(78°)	0.9781
sin(79°)	0.9816
sin(80°)	0.9848
sin(81°)	0.9877
sin(82°)	0.9903
sin(83°)	0.9925
sin(84°)	0.9945
sin(85°)	0.9962
sin(86°)	0.9976
sin(87°)	0.9986
sin(88°)	0.9994
sin(89°)	0.9998
sin(90°)	1

sin(91°)	0.9998
sin(92°)	0.9994
sin(93°)	0.9986
sin(94°)	0.9976
sin(95°)	0.9962
sin(96°)	0.9945
sin(97°)	0.9925
sin(98°)	0.9903
sin(99°)	0.9877
sin(100°)	0.9848
sin(101°)	0.9816
sin(102°)	0.9781
sin(103°)	0.9744
sin(104°)	0.9703
sin(105°)	0.9659
sin(106°)	0.9613
sin(107°)	0.9563
sin(108°)	0.9511
sin(109°)	0.9455
sin(110°)	0.9397
sin(111°)	0.9336
sin(112°)	0.9272
sin(113°)	0.9205
sin(114°)	0.9135
sin(115°)	0.9063
sin(116°)	0.8988
sin(117°)	0.891
sin(118°)	0.8829
sin(119°)	0.8746
sin(120°)	0.866
sin(121°)	0.8572
sin(122°)	0.848
sin(123°)	0.8387
sin(124°)	0.829
sin(125°)	0.8192
sin(126°)	0.809
sin(127°)	0.7986
sin(128°)	0.788
sin(129°)	0.7771
sin(130°)	0.766
sin(131°)	0.7547
sin(132°)	0.7431
sin(133°)	0.7314
sin(134°)	0.7193
sin(135°)	0.7071

sin(136°)	0.6947
sin(137°)	0.682
sin(138°)	0.6691
sin(139°)	0.6561
sin(140°)	0.6428
sin(141°)	0.6293
sin(142°)	0.6157
sin(143°)	0.6018
sin(144°)	0.5878
sin(145°)	0.5736
sin(146°)	0.5592
sin(147°)	0.5446
sin(148°)	0.5299
sin(149°)	0.515
sin(150°)	0.5
sin(151°)	0.4848
sin(152°)	0.4695
sin(153°)	0.454
sin(154°)	0.4384
sin(155°)	0.4226
sin(156°)	0.4067
sin(157°)	0.3907
sin(158°)	0.3746
sin(159°)	0.3584
sin(160°)	0.342
sin(161°)	0.3256
sin(162°)	0.309
sin(163°)	0.2924
sin(164°)	0.2756
sin(165°)	0.2588
sin(166°)	0.2419
sin(167°)	0.225
sin(168°)	0.2079
sin(169°)	0.1908
sin(170°)	0.1736
sin(171°)	0.1564
sin(172°)	0.1392
sin(173°)	0.1219
sin(174°)	0.1045
sin(175°)	0.0872
sin(176°)	0.0698
sin(177°)	0.0523
sin(178°)	0.0349
sin(179°)	0.0175
sin(180°)	0

Таблица синусов для 181°-360°

sin(181°)	-0.0175
sin(182°)	-0.0349
sin(183°)	-0.0523
sin(184°)	-0.0698
sin(185°)	-0.0872
sin(186°)	-0.1045
sin(187°)	-0.1219
sin(188°)	-0.1392
sin(189°)	-0.1564
sin(190°)	-0.1736
sin(191°)	-0.1908
sin(192°)	-0.2079
sin(193°)	-0.225
sin(194°)	-0.2419
sin(195°)	-0.2588
sin(196°)	-0.2756
sin(197°)	-0.2924
sin(198°)	-0.309
sin(199°)	-0.3256
sin(200°)	-0.342
sin(201°)	-0.3584
sin(202°)	-0.3746
sin(203°)	-0.3907
sin(204°)	-0.4067
sin(205°)	-0.4226
sin(206°)	-0.4384
sin(207°)	-0.454
sin(208°)	-0.4695
sin(209°)	-0.4848
sin(210°)	-0.5
sin(211°)	-0.515
sin(212°)	-0.5299
sin(213°)	-0.5446
sin(214°)	-0.5592
sin(215°)	-0.5736
sin(216°)	-0.5878
sin(217°)	-0.6018
sin(218°)	-0.6157
sin(219°)	-0.6293
sin(220°)	-0.6428
sin(221°)	-0.6561
sin(222°)	-0.6691
sin(223°)	-0.682
sin(224°)	-0.6947
sin(225°)	-0.7071

sin(226°)	-0.7193
sin(227°)	-0.7314
sin(228°)	-0.7431
sin(229°)	-0.7547
sin(230°)	-0.766
sin(231°)	-0.7771
sin(232°)	-0.788
sin(233°)	-0.7986
sin(234°)	-0.809
sin(235°)	-0.8192
sin(236°)	-0.829
sin(237°)	-0.8387
sin(238°)	-0.848
sin(239°)	-0.8572
sin(240°)	-0.866
sin(241°)	-0.8746
sin(242°)	-0.8829
sin(243°)	-0.891
sin(244°)	-0.8988
sin(245°)	-0.9063
sin(246°)	-0.9135
sin(247°)	-0.9205
sin(248°)	-0.9272
sin(249°)	-0.9336
sin(250°)	-0.9397
sin(251°)	-0.9455
sin(252°)	-0.9511
sin(253°)	-0.9563
sin(254°)	-0.9613
sin(255°)	-0.9659
sin(256°)	-0.9703
sin(257°)	-0.9744
sin(258°)	-0.9781
sin(259°)	-0.9816
sin(260°)	-0.9848
sin(261°)	-0.9877
sin(262°)	-0.9903
sin(263°)	-0.9925
sin(264°)	-0.9945
sin(265°)	-0.9962
sin(266°)	-0.9976
sin(267°)	-0.9986
sin(268°)	-0.9994
sin(269°)	-0.9998
sin(270°)	-1

sin(271°)	-0.9998
sin(272°)	-0.9994
sin(273°)	-0.9986
sin(274°)	-0.9976
sin(275°)	-0.9962
sin(276°)	-0.9945
sin(277°)	-0.9925
sin(278°)	-0.9903
sin(279°)	-0.9877
sin(280°)	-0.9848
sin(281°)	-0.9816
sin(282°)	-0.9781
sin(283°)	-0.9744
sin(284°)	-0.9703
sin(285°)	-0.9659
sin(286°)	-0.9613
sin(287°)	-0.9563
sin(288°)	-0.9511
sin(289°)	-0.9455
sin(290°)	-0.9397
sin(291°)	-0.9336
sin(292°)	-0.9272
sin(293°)	-0.9205
sin(294°)	-0.9135
sin(295°)	-0.9063
sin(296°)	-0.8988
sin(297°)	-0.891
sin(298°)	-0.8829
sin(299°)	-0.8746
sin(300°)	-0.866
sin(301°)	-0.8572
sin(302°)	-0.848
sin(303°)	-0.8387
sin(304°)	-0.829
sin(305°)	-0.8192
sin(306°)	-0.809
sin(307°)	-0.7986
sin(308°)	-0.788
sin(309°)	-0.7771
sin(310°)	-0.766
sin(311°)	-0.7547
sin(312°)	-0.7431
sin(313°)	-0.7314
sin(314°)	-0.7193
sin(315°)	-0.7071

sin(316°)	-0.6947
sin(317°)	-0.682
sin(318°)	-0.6691
sin(319°)	-0.6561
sin(320°)	-0.6428
sin(321°)	-0.6293
sin(322°)	-0.6157
sin(323°)	-0.6018
sin(324°)	-0.5878
sin(325°)	-0.5736
sin(326°)	-0.5592
sin(327°)	-0.5446
sin(328°)	-0.5299
sin(329°)	-0.515
sin(330°)	-0.5
sin(331°)	-0.4848
sin(332°)	-0.4695
sin(333°)	-0.454
sin(334°)	-0.4384
sin(335°)	-0.4226
sin(336°)	-0.4067
sin(337°)	-0.3907
sin(338°)	-0.3746
sin(339°)	-0.3584
sin(340°)	-0.342
sin(341°)	-0.3256
sin(342°)	-0.309
sin(343°)	-0.2924
sin(344°)	-0.2756
sin(345°)	-0.2588
sin(346°)	-0.2419
sin(347°)	-0.225
sin(348°)	-0.2079
sin(349°)	-0.1908
sin(350°)	-0.1736
sin(351°)	-0.1564
sin(352°)	-0.1392
sin(353°)	-0.1219
sin(354°)	-0.1045
sin(355°)	-0.0872
sin(356°)	-0.0698
sin(357°)	-0.0523
sin(358°)	-0.0349
sin(359°)	-0.0175
sin(360°)	-0

Существуют также следующие таблицы тригонометрических функций: таблица косинусов, таблица тангенсов и таблица котангенсов.

Как легко запомнить таблицу синусов (видео)

Таблицу важно всегда помнить на алгебре, чтобы найти синус.

Всё для учебы » Математика в школе » Таблица синусов углов (градусы, значения)

Чтобы добавить страницу в закладки, нажмите Ctrl+D.

Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:

Ссылка: https://uchim.org/matematika/tablica-sinusov

Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):

Таблица синусов | umath.ru

sin(1°) = 0,017452
sin(2°) = 0,034899
sin(3°) = 0,052336
sin(4°) = 0,069756
sin(5°) = 0,087156
sin(6°) = 0,104528
sin(7°) = 0,121869
sin(8°) = 0,139173
sin(9°) = 0,156434
sin(10°) = 0,173648
sin(11°) = 0,190809
sin(12°) = 0,207912
sin(13°) = 0,224951
sin(14°) = 0,241922
sin(15°) = 0,258819
sin(16°) = 0,275637
sin(17°) = 0,292372
sin(18°) = 0,309017
sin(19°) = 0,325568
sin(20°) = 0,342020
sin(21°) = 0,358368
sin(22°) = 0,374607
sin(23°) = 0,390731
sin(24°) = 0,406737
sin(25°) = 0,422618
sin(26°) = 0,438371
sin(27°) = 0,453990
sin(28°) = 0,469472
sin(29°) = 0,484810
sin(30°) = 0,5

sin(31°) = 0,515038
sin(32°) = 0,529919
sin(33°) = 0,544639
sin(34°) = 0,559193
sin(35°) = 0,573576
sin(36°) = 0,587785
sin(37°) = 0,601815
sin(38°) = 0,615661
sin(39°) = 0,629320
sin(40°) = 0,642788
sin(41°) = 0,656059
sin(42°) = 0,669131
sin(43°) = 0,681998
sin(44°) = 0,694658
sin(45°) = 0,707107
sin(46°) = 0,719340
sin(47°) = 0,731354
sin(48°) = 0,743145
sin(49°) = 0,754710
sin(50°) = 0,766044
sin(51°) = 0,777146
sin(52°) = 0,788011
sin(53°) = 0,798636
sin(54°) = 0,809017
sin(55°) = 0,819152
sin(56°) = 0,829038
sin(57°) = 0,838671
sin(58°) = 0,848048
sin(59°) = 0,857167
sin(60°) = 0,866025

sin(61°) = 0,874620
sin(62°) = 0,882948
sin(63°) = 0,891007
sin(64°) = 0,898794
sin(65°) = 0,906308
sin(66°) = 0,913545
sin(67°) = 0,920505
sin(68°) = 0,927184
sin(69°) = 0,933580
sin(70°) = 0,939693
sin(71°) = 0,945519
sin(72°) = 0,951057
sin(73°) = 0,956305
sin(74°) = 0,961262
sin(75°) = 0,965926
sin(76°) = 0,970296
sin(77°) = 0,974370
sin(78°) = 0,978148
sin(79°) = 0,981627
sin(80°) = 0,984808
sin(81°) = 0,987688
sin(82°) = 0,990268
sin(83°) = 0,992546
sin(84°) = 0,994522
sin(85°) = 0,996195
sin(86°) = 0,997564
sin(87°) = 0,998630
sin(88°) = 0,999391
sin(89°) = 0,999848
sin(90°) = 1

Таблица синусов | Главный механик

Одной из самых часто используемых из всех тригонометрических таблиц Брадиса, является таблица синусов. В этой статье мы разберемся с таким понятием, как синус (sin), научимся находить значения синуса для различных углов (0, 30, 45, 60, 90), и поймем, для чего нужна таблица синусов.

Таблица синусов и её применение

Для начала нужно напомнить, что означает такое понятие, как синус угла.

Синус – это отношение противолежащего этому углу катета к гипотенузе.

Это справедливо в случае, если треугольник прямоугольный.

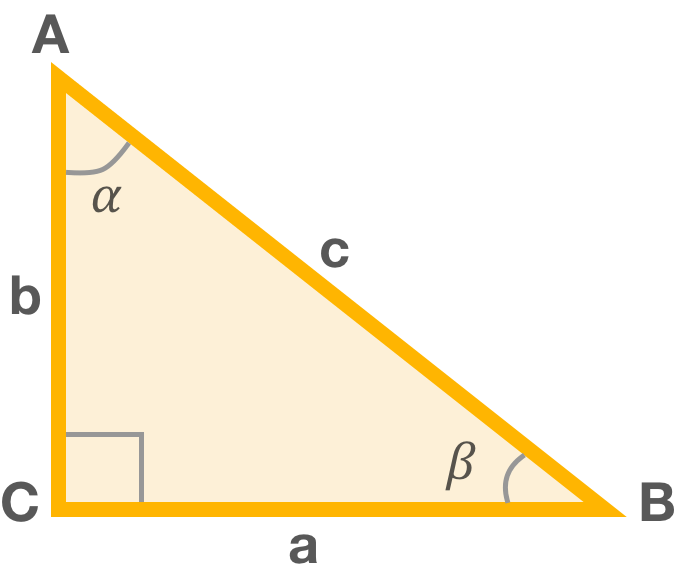
Стандартный прямоугольный треугольник: стороны a (BC) и b (AC) – катеты, сторона с (AB) – гипотенуза

Пример: найдем синус угла ⍺ и угла β
sin ⍺ = а/с или отношение стороны ВС к стороне АВ. Если брать угол β, то противостоящим будет считаться сторона b или АС. Гипотенуза в данном случае та же – AB. Тогда:
sin β = b/с или АС отношение АВ.

В прямоугольном треугольнике всегда 2 катета и только одна гипотенуза

Как известно, целых значений угла – 360. Но часто нужно рассчитать значения для самых популярных углов, таких как: синус 0°, синус 30°, синус 45°, синус 60°, синус 90°. Эти значения можно найти в таблицах Брадиса.

Несмотря на то, что в 2021 году она отмечает свой столетний юбилей, свою актуальность таблица Брадиса не утратила. В частности ее применяют архитекторы, проектанты, конструктора для проведения быстрых промежуточных расчетов. Таблицы Брадиса разрешены к использованию в школах при сдаче ЕГЭ, в отличие от калькуляторов.

Онлайн калькулятор расчета синуса угла

Как рассчитать синус угла

Некоторые значения синуса угла можно рассчитать достаточно просто, воспользовавшись таблицей синусов угла π (пи) в радианах.

π (пи) равно 3,14 или 180°

Пример: рассчитаем значения синуса следующих углов: 0°, 30°, 45°, 60°, 90° в радианах с использованием π (пи)
Берем синус 0°, в радианах он будет 0, тут даже считать нечего.
Синус 30° равен π/6.
Потому что “все” π (пи) – это половина окружности или 180°. Поэтому 30° – это все 180° разделенные на 6. По таком же принципу находим значения синусов для остальных углов.
Синус 45° равен π/4 (180 градусов разделенные на 4).
Синус 60° равен π/3 (180 градусов разделенные на 3).
Синус 90° равен π/2 или 1 (180 градусов разделенные на 2).
Остальное дело калькулятора – просто переводим π в 3,14 и делим на нужное число 6, 4, 3 или 2.

Но часто нужно решить задачу для каких то либо целей, при котором значения углов будут другими. Посмотрим пример решения такой задачи.

Пример: рассмотрим прямоугольный треугольник, в котором катеты а и b имеют значение 5 и 2√6, нужно найти синус каждого острого угла. Рисунок и обозначения стандартные (смотри выше).
Используя теорему Пифагора, которая гласит, что “квадрат гипотенузы равен сумме квадратов двух катетов“, находим гипотенузу:
С₂=5х5+ (2√6)х(2√6) = 25 + 4х6 = 49 (см). Итог: С₂ = 7 (см).
Нам известно, что синус это есть отношение катета, который противолежит к искомому углу, к гипотенузе. То есть sin α = a/c, это значит, что sin α =5/7. Соответственно, sin β= b/с ,и sin β равен 2√6/7.
Теперь пробуем найти точное значение синуса и через таблицы Брадиса, найдя число 5/7, затем по таблице найти соответствующее ему значение угла в градусах. Потом от 90° отнимаем это значение, получаем градусы и переводим его в радианы.
Можно использовать формулу из теоремы синусов.
Её можно использовать в случае, если у нас известна гипотенуза треугольника и два угла или один из катетов. Тогда в соответствии с правилами пропорции находим:
Что найти синус угла, к примеру: α = 42°, угол β =48 °, открываем таблицу Брадиса. Так как у нас углы без минут, находим значение синуса угла по первой колонке. Sin α = 0,6691, sin β = 0,7431. Пусть в условии сторона с = 9 см, Синус 90° = 1. Подставляем значение и получаем: а = 9 х (0,6691: 1) = 6, 0219 (см).

Что такое таблица синусов π и таблица Брадиса

В таблице синусов значение угла α дается в:

радианах,
градусах,
в виде числа, выраженного через квадратный корень.

Это таблица не только для синусов, но и для других тригонометрических знаков. Но в данном случае, мы приведем таблицу только для синусов.

Значение угла α (градусов)	Значение угла α в радианах (через число пи)	sin (синус)
0	0	0
15	π/12	(√3 — 1)/2√2
30	π/6	1/2
45	π/4	√2/2
60	π/3	√3/2
75	5π/12	(√3 + 1)/2√2
90	π/2	1
105	7π/12	(√3 + 1)/2√2
120	2π/3	√3/2
135	3π/4	√2/2
150	5π/6	1/2
180	π	0
210	7π/6	-1/2
240	4π/3	-√3/2
270	3π/2	-1
360	2π	0

Рассчитываем калькулятором значение π, данные можно посмотреть в таблице. Здесь включены значения синуса, которых нет в таблицах Брадиса, вычисления сделаны с точностью до 4 знака. Если нужно узнать, чему равен синус, это всегда можно посмотреть в таблице или рассчитать самому.

Значение sin угла α в градусах	Значение sin угла α в радианах	Значение синуса угла α
Синус угла 0 градусов	0	0
Синус угла 15 градусов	π/12	0.2588
Синус угла 30 градусов	π/6	0.5
Синус угла 45 градусов	π/4	0.7071
Синус угла 50 градусов	5π/18	0.766
Синус угла 60 градусов	π/3	0.866
Синус угла 65 градусов	13π/36	0.9063
Синус угла 70 градусов	7π/18	0.9397
Синус угла 75 градусов	5π/12	0.9659
Синус угла 90 градусов	π/2	1
Синус угла 105 градусов	5π/12	0.9659
Синус угла 120 градусов	2π/3	0.866
Синус угла 135 градусов	3π/4	0.7071
Синус угла 140 градусов	7π/9	0.6428
Синус угла 150 градусов	5π/6	0.5
Синус угла 180 градусов	π	0
Синус угла 270 градусов	3π/2	-1
Синус угла 360 градусов	2π	0

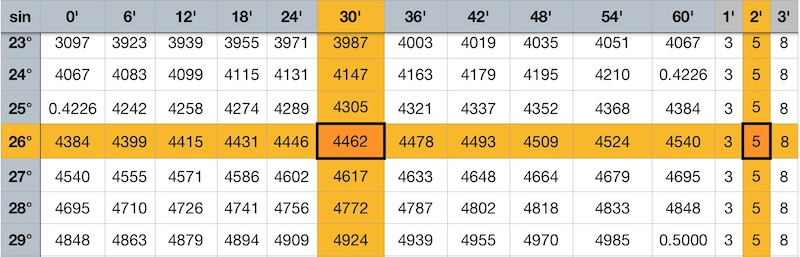
Как пользоваться таблицей Брадиса для синусов

Если у вас стоит вопрос, как пользоваться таблицей Брадиса, для нахождения синуса угла, рассмотрим такой пример.

Пример: требуется найти числовое значение угла 26°32′
Для того, что бы найти числовое значение, находим в таблице значение, которое наиболее близкое, это синус 26°30′. Это 0, 4462. Не хватает 2′. Ищем слева напротив значения 2′ – это будет 0,0005. Прибавляем это число к полученному : 0,4462+0,0005= 0,4467.

Таблица синусов целиком

sin	0′	6′	12′	18′	24′	30′	36′	42′	48′	54′	60′	1′	2′	3′
sin	60′	54′	48′	42′	36′	30′	24′	18′	12′	6′	0′	1′	2′	3′
											0.0000
0°	0.0000	17	35	52	70	87	105	122	140	157	175	3	6	9
1°	175	192	209	227	244	262	279	297	314	332	349	3	6	9
2°	349	366	384	401	419	436	454	471	488	506	523	3	6	9
3°	523	541	558	576	593	610	628	645	663	680	698	3	6	9
4°	698	715	732	750	767	785	802	819	837	854	0.0872	3	6	9
5°	0.0872	889	906	924	941	958	976	993	1011	1028	1045	3	6	9
6°	1045	1063	1080	1097	1115	1132	1149	1167	1184	1201	1219	3	6	9
7°	1219	1236	1253	1271	1288	1305	1323	1340	1357	1374	1392	3	6	9
8°	1392	1409	1426	1444	1461	1478	1495	1513	1530	1547	1564	3	6	9
9°	1564	1582	1599	1616	1633	1650	1668	1685	1702	1719	0.1736	3	6	9
10°	0.1736	1754	1771	1788	1805	1822	1840	1857	1874	1891	1908	3	6	9
11°	1908	1925	1942	1959	1977	1994	2011	2028	2045	2062	2079	3	6	9
12°	2079	2096	2113	2130	2147	2164	2181	2198	2215	2233	2250	3	6	9
13°	2250	2267	2284	2300	2317	2334	2351	2368	2385	2402	2419	3	6	8
14°	2419	2436	2453	2470	2487	2504	2521	2538	2554	2571	0.2588	3	6	8
15°	0.2588	2605	2622	2639	2656	2672	2689	2706	2723	2740	2756	3	6	8
16°	2756	2773	2790	2807	2823	2840	2857	2874	2890	2907	2924	3	6	8
17°	2942	2940	2957	2974	2990	3007	3024	3040	3057	3074	3090	3	6	8
18°	3090	3107	3123	3140	3156	3173	3190	3206	3223	3239	3256	3	6	8
19°	3256	3272	3289	3305	3322	3338	3355	3371	3387	3404	0.3420	3	5	8
20°	0.3420	3437	3453	3469	3486	3502	3518	3535	3551	3567	3584	3	5	8
21°	3584	3600	3616	3633	3649	3665	3681	3697	3714	3730	3746	3	5	8
22°	3746	3762	3778	3795	3811	3827	3843	3859	3875	3891	3907	3	5	8
23°	3097	3923	3939	3955	3971	3987	4003	4019	4035	4051	4067	3	5	8
24°	4067	4083	4099	4115	4131	4147	4163	4179	4195	4210	0.4226	3	5	8
25°	0.4226	4242	4258	4274	4289	4305	4321	4337	4352	4368	4384	3	5	8
26°	4384	4399	4415	4431	4446	4462	4478	4493	4509	4524	4540	3	5	8
27°	4540	4555	4571	4586	4602	4617	4633	4648	4664	4679	4695	3	5	8
28°	4695	4710	4726	4741	4756	4772	4787	4802	4818	4833	4848	3	5	8
29°	4848	4863	4879	4894	4909	4924	4939	4955	4970	4985	0.5000	3	5	8
30°	0.5000	5015	5030	5045	5060	5075	5090	5105	5120	5135	5150	3	5	8
31°	5150	5165	5180	5195	5210	5225	5240	5255	5270	5284	5299	2	5	7
32°	5299	5314	5329	5344	5358	5373	5388	5402	5417	5432	5446	2	5	7
33°	5446	5461	5476	5490	5505	5519	5534	5548	5563	5577	5592	2	5	7
34°	5592	5606	5621	5635	5650	5664	5678	5693	5707	5721	0.5736	2	5	7
35°	0.5736	5750	5764	5779	5793	5807	5821	5835	5850	5864	0.5878	2	5	7
36°	5878	5892	5906	5920	5934	5948	5962	5976	5990	6004	6018	2	5	7
37°	6018	6032	6046	6060	6074	6088	6101	6115	6129	6143	6157	2	5	7
38°	6157	6170	6184	6198	6211	6225	6239	6252	6266	6280	6293	2	5	7
39°	6293	6307	6320	6334	6347	6361	6374	6388	6401	6414	0.6428	2	4	7
40°	0.6428	6441	6455	6468	6481	6494	6508	6521	6534	6547	6561	2	4	7
41°	6561	6574	6587	6600	6613	6626	6639	6652	6665	6678	6691	2	4	7
42°	6691	6704	6717	6730	6743	6756	6769	6782	6794	6807	6820	2	4	6
43°	6820	6833	6845	6858	6871	6884	6896	8909	6921	6934	6947	2	4	6
44°	6947	6959	6972	6984	6997	7009	7022	7034	7046	7059	0.7071	2	4	6
45°	0.7071	7083	7096	7108	7120	7133	7145	7157	7169	7181	7193	2	4	6
46°	7193	7206	7218	7230	7242	7254	7266	7278	7290	7302	7314	2	4	6
47°	7314	7325	7337	7349	7361	7373	7385	7396	7408	7420	7431	2	4	6
48°	7431	7443	7455	7466	7478	7490	7501	7513	7524	7536	7547	2	4	6
49°	7547	7559	7570	7581	7593	7604	7615	7627	7638	7649	0.7660	2	4	6
50°	0.7660	7672	7683	7694	7705	7716	7727	7738	7749	7760	7771	2	4	6
51°	7771	7782	7793	7804	7815	7826	7837	7848	7859	7869	7880	2	4	5
52°	7880	7891	7902	7912	7923	7934	7944	7955	7965	7976	7986	2	4	5
53°	7986	7997	8007	8018	8028	8039	8049	8059	8070	8080	8090	2	3	5
54°	8090	8100	8111	8121	8131	8141	8151	8161	8171	8181	0.8192	2	3	5
55°	0.8192	8202	8211	8221	8231	8241	8251	8261	8271	8281	8290	2	3	5
56°	8290	8300	8310	8320	8329	8339	8348	8358	8368	8377	8387	2	3	5
57°	8387	8396	8406	8415	8425	8434	8443	8453	8462	8471	8480	2	3	5
58°	8480	8490	8499	8508	8517	8526	8536	8545	8554	8563	8572	2	3	5
59°	8572	8581	8590	8599	8607	8616	8625	8634	8643	8652	0.8660	1	3	4
60°	0.8660	8669	8678	8686	8695	8704	8712	8721	8729	8738	8746	1	3	4
61°	8746	8755	8763	8771	8780	8788	8796	8805	8813	8821	8829	1	3	4
62°	8829	8838	8846	8854	8862	8870	8878	8886	8894	8902	8910	1	3	4
63°	8910	8918	8926	8934	8942	8949	8957	8965	8973	8980	8988	1	3	4
64°	8988	8996	9003	9011	9018	9026	9033	9041	9048	9056	0.9063	1	3	4
65°	0.9063	9070	9078	9085	9092	9100	9107	9114	9121	9128	9135	1	2	4
66°	9135	9143	9150	9157	9164	9171	9178	9184	9191	9198	9205	1	2	3
67°	9205	9212	9219	9225	9232	9239	9245	9252	9259	9256	9272	1	2	3
68°	9272	9278	9285	9291	9298	9304	9311	9317	9323	9330	9336	1	2	3
69°	9336	9342	9348	9354	9361	9367	9373	9379	9383	9391	0.9397	1	2	3
70°	9397	9403	9409	9415	9421	9426	9432	9438	9444	9449	0.9455	1	2	3
71°	9455	9461	9466	9472	9478	9483	9489	9494	9500	9505	9511	1	2	3
72°	9511	9516	9521	9527	9532	9537	9542	9548	9553	9558	9563	1	2	3
73°	9563	9568	9573	9578	9583	9588	9593	9598	9603	9608	9613	1	2	2
74°	9613	9617	9622	9627	9632	9636	9641	9646	9650	9655	0.9659	1	2	2
75°	9659	9664	9668	9673	9677	9681	9686	9690	9694	9699	9703	1	1	2
76°	9703	9707	9711	9715	9720	9724	9728	9732	9736	9740	9744	1	1	2
77°	9744	9748	9751	9755	9759	9763	9767	9770	9774	9778	9781	1	1	2
78°	9781	9785	9789	9792	9796	9799	9803	9806	9810	9813	9816	1	1	2
79°	9816	9820	9823	9826	9829	9833	9836	9839	9842	9845	0.9848	1	1	2
80°	0.9848	9851	9854	9857	9860	9863	9866	9869	9871	9874	9877	0	1	1
81°	9877	9880	9882	9885	9888	9890	9893	9895	9898	9900	9903	0	1	1
82°	9903	9905	9907	9910	9912	9914	9917	9919	9921	9923	9925	0	1	1
83°	9925	9928	9930	9932	9934	9936	9938	9940	9942	9943	9945	0	1	1
84°	9945	9947	9949	9951	9952	9954	9956	9957	9959	9960	9962	0	1	1
85°	9962	9963	9965	9966	9968	9969	9971	9972	9973	9974	9976	0	0	1
86°	9976	9977	9978	9979	9980	9981	9982	9983	9984	9985	9986	0	0	0
87°	9986	9987	9988	9989	9990	9990	9991	9992	9993	9993	9994	0	0	0
88°	9994	9995	9995	9996	9996	9997	9997	9997	9998	9998	0.9998	0	0	0
89°	9998	9999	9999	9999	9999	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	0	0	0
90°	1.0000

Facebook

Twitter

Вконтакте

Google+

Таблица значений тригонометрических функций

Примечание. В данной таблице значений тригонометрических функций используется знак √ для обозначения квадратного корня. Для обозначения дроби — символ «/».

См. также полезные материалы:

Для определения значения тригонометрической функции, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов — ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой «30 градусов», на их пересечении считываем результат — одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2 ) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других «популярных» углов.

Синус пи, косинус пи, тангенс пи и других углов в радианах

Приведенная ниже таблица косинусов, синусов и тангенсов также подходит для нахождения значения тригонометрических функций, аргумент которых задан в радианах. Для этого воспользуйтесь второй колонкой значений угла. Благодаря этому можно перевести значение популярных углов из градусов в радианы. Например, найдем угол 60 градусов в первой строке и под ним прочитаем его значение в радианах. 60 градусов равно π/3 радиан.

Число пи однозначно выражает зависимость длины окружности от градусной меры угла. Таким образом, пи радиан равны 180 градусам.

Любое число, выраженное через пи (радиан) можно легко перевести в градусную меру, заменив число пи (π) на 180.

Примеры:
1. Синус пи.
sin π = sin 180 = 0
таким образом, синус пи — это тоже самое, что синус 180 градусов и он равен нулю.

2. Косинус пи.
cos π = cos 180 = -1
таким образом, косинус пи — это тоже самое, что косинус 180 градусов и он равен минус единице.

3. Тангенс пи
tg π = tg 180 = 0
таким образом, тангенс пи — это тоже самое, что тангенс 180 градусов и он равен нулю.

Таблица значений синуса, косинуса, тангенса для углов 0 — 360 градусов (часто встречающиеся значения)

Если в таблице значений тригонометрических функций вместо значения функции указан прочерк (тангенс (tg) 90 градусов, котангенс (ctg) 180 градусов) значит при данном значении градусной меры угла функция не имеет определенного значения. Если же прочерка нет — клетка пуста, значит мы еще не внесли нужное значение. Мы интересуемся, по каким запросам к нам приходят пользователи и дополняем таблицу новыми значениями, несмотря на то, что текущих данных о значениях косинусов, синусов и тангенсов самых часто встречающихся значений углов вполне достаточно для решения большинства задач.

Таблица значений тригонометрических функций sin, cos, tg для наиболее популярных углов
0, 15, 30, 45, 60, 90 … 360 градусов
(цифровые значения «как по таблицам Брадиса»)

значение угла α (градусов)	значение угла α в радианах	sin (синус)	cos (косинус)	tg (тангенс)	ctg (котангенс)
0	0	0	1	0	-
15	π/12	0,2588	0,9659	0,2679	3,7321
30	π/6	0,5000	0,8660	0,5774	1,7321
45	π/4	0,7071	0,7071	1	1
50	5π/18	0,7660	0,6428	1.1918	0,8391
60	π/3	0,8660	0,5000	1,7321	0,5774
65	13π/36	0,9063	0,4226	2,1445	0,4663
70	7π/18	0,9397	0,3420	2,7475	0,3640
75	5π/12	0,9659	0,2588	3,7321	0,2679
90	π/2	1	0	-	0
105	5π/12	0,9659	-0,2588	-3,7321	-0,2679
120	2π/3	0,8660	-0,5000	-1,7321	-0,5774
135	3π/4	0,7071	-0,7071	-1	-1
140	7π/9	0,6428	-0,7660	-0,8391	-1,1918
150	5π/6	0,5000	-0,8660	-0,5774	-1,7321
180	π	0	-1	0	-
270	3π/2	-1	0	-	0
360	2π	0	1	0	-

Иногда для быстрых расчетов нужно не точное, а вычисляемое значение (число десятичной дробью), которое раньше искали в таблицах Брадиса. Поэтому, в дополнение к таблице точных значений тригонометрических функций приведены эти же самые значения, но в виде десятичной дроби, округленной до четвертого знака. Дополнительно в таблицу включены «нестандартные» значения тангенса, косинуса, синуса 140 градусов, синуса 105, 70, косинуса 105 и 50 градусов.

Начать курс обучения

Таблица синусов, найти угол синуса

Тригонометрические функции: синус угла

Зачем надо знать значение синуса? Представим ситуацию: известен один из углов (А=60⁰), вписанный в прямоугольный треугольник, и длина гипотенузы. Больше нет никакой информации. Надо узнать вычислить дальний к углу (А) катет. Как поступить?

Ситуация очень простая: смотрим таблицы Брадиса, находим значение sin(60⁰)=0,866, подставляем данные в формулу тригонометрической функции и решаем линейное уравнение. Из школьного курса известно, что sin угла – это отношение дальнего к углу, в данном случае А=60⁰, катета к гипотенузе.

Произвести все расчеты проще, если воспользоваться онлайн калькулятором на сайте. Таким образом можно вычислить длину любой из сторон прямоугольного треугольника. Знаем угол – значит, знаем sin этого угла. И наоборот, знаем sin – найти угол не составит проблемы.

Таблица синусов 0°- 360°

Sin(1°)	0.0175
Sin(2°)	0.0349
Sin(3°)	0.0523
Sin(4°)	0.0698
Sin(5°)	0.0872
Sin(6°)	0.1045
Sin(7°)	0.1219
Sin(8°)	0.1392
Sin(9°)	0.1564
Sin(10°)	0.1736
Sin(11°)	0.1908
Sin(12°)	0.2079
Sin(13°)	0.225
Sin(14°)	0.2419
Sin(15°)	0.2588
Sin(16°)	0.2756
Sin(17°)	0.2924
Sin(18°)	0.309
Sin(19°)	0.3256
Sin(20°)	0.342
Sin(21°)	0.3584
Sin(22°)	0.3746
Sin(23°)	0.3907
Sin(24°)	0.4067
Sin(25°)	0.4226
Sin(26°)	0.4384
Sin(27°)	0.454
Sin(28°)	0.4695
Sin(29°)	0.4848
Sin(30°)	0.5
Sin(31°)	0.515
Sin(32°)	0.5299
Sin(33°)	0.5446
Sin(34°)	0.5592
Sin(35°)	0.5736
Sin(36°)	0.5878

Sin(37°)	0.6018
Sin(38°)	0.6157
Sin(39°)	0.6293
Sin(40°)	0.6428
Sin(41°)	0.6561
Sin(42°)	0.6691
Sin(43°)	0.682
Sin(44°)	0.6947
Sin(45°)	0.7071
Sin(46°)	0.7193
Sin(47°)	0.7314
Sin(48°)	0.7431
Sin(49°)	0.7547
Sin(50°)	0.766
Sin(51°)	0.7771
Sin(52°)	0.788
Sin(53°)	0.7986
Sin(54°)	0.809
Sin(55°)	0.8192
Sin(56°)	0.829
Sin(57°)	0.8387
Sin(58°)	0.848
Sin(59°)	0.8572
Sin(60°)	0.866
Sin(61°)	0.8746
Sin(62°)	0.8829
Sin(63°)	0.891
Sin(64°)	0.8988
Sin(65°)	0.9063
Sin(66°)	0.9135
Sin(67°)	0.9205
Sin(68°)	0.9272
Sin(69°)	0.9336
Sin(70°)	0.9397
Sin(71°)	0.9455
Sin(72°)	0.9511

Sin(73°)	0.9563
Sin(74°)	0.9613
Sin(75°)	0.9659
Sin(76°)	0.9703
Sin(77°)	0.9744
Sin(78°)	0.9781
Sin(79°)	0.9816
Sin(80°)	0.9848
Sin(81°)	0.9877
Sin(82°)	0.9903
Sin(83°)	0.9925
Sin(84°)	0.9945
Sin(85°)	0.9962
Sin(86°)	0.9976
Sin(87°)	0.9986
Sin(88°)	0.9994
Sin(89°)	0.9998
Sin(90°)	1
Sin(91°)	0.9998
Sin(92°)	0.9994
Sin(93°)	0.9986
Sin(94°)	0.9976
Sin(95°)	0.9962
Sin(96°)	0.9945
Sin(97°)	0.9925
Sin(98°)	0.9903
Sin(99°)	0.9877
Sin(100°)	0.9848
Sin(101°)	0.9816
Sin(102°)	0.9781
Sin(103°)	0.9744
Sin(104°)	0.9703
Sin(105°)	0.9659
Sin(106°)	0.9613
Sin(107°)	0.9563
Sin(108°)	0.9511

Sin(109°)	0.9455
Sin(110°)	0.9397
Sin(111°)	0.9336
Sin(112°)	0.9272
Sin(113°)	0.9205
Sin(114°)	0.9135
Sin(115°)	0.9063
Sin(116°)	0.8988
Sin(117°)	0.891
Sin(118°)	0.8829
Sin(119°)	0.8746
Sin(120°)	0.866
Sin(121°)	0.8572
Sin(122°)	0.848
Sin(123°)	0.8387
Sin(124°)	0.829
Sin(125°)	0.8192
Sin(126°)	0.809
Sin(127°)	0.7986
Sin(128°)	0.788
Sin(129°)	0.7771
Sin(130°)	0.766
Sin(131°)	0.7547
Sin(132°)	0.7431
Sin(133°)	0.7314
Sin(134°)	0.7193
Sin(135°)	0.7071
Sin(136°)	0.6947
Sin(137°)	0.682
Sin(138°)	0.6691
Sin(139°)	0.6561
Sin(140°)	0.6428
Sin(141°)	0.6293
Sin(142°)	0.6157
Sin(143°)	0.6018
Sin(144°)	0.5878

Sin(145°)	0.5736
Sin(146°)	0.5592
Sin(147°)	0.5446
Sin(148°)	0.5299
Sin(149°)	0.515
Sin(150°)	0.5
Sin(151°)	0.4848
Sin(152°)	0.4695
Sin(153°)	0.454
Sin(154°)	0.4384
Sin(155°)	0.4226
Sin(156°)	0.4067
Sin(157°)	0.3907
Sin(158°)	0.3746
Sin(159°)	0.3584
Sin(160°)	0.342
Sin(161°)	0.3256
Sin(162°)	0.309
Sin(163°)	0.2924
Sin(164°)	0.2756
Sin(165°)	0.2588
Sin(166°)	0.2419
Sin(167°)	0.225
Sin(168°)	0.2079
Sin(169°)	0.1908
Sin(170°)	0.1736
Sin(171°)	0.1564
Sin(172°)	0.1392
Sin(173°)	0.1219
Sin(174°)	0.1045
Sin(175°)	0.0872
Sin(176°)	0.0698
Sin(177°)	0.0523
Sin(178°)	0.0349
Sin(179°)	0.0175
Sin(180°)	0

Sin(181°)	-0.0175
Sin(182°)	-0.0349
Sin(183°)	-0.0523
Sin(184°)	-0.0698
Sin(185°)	-0.0872
Sin(186°)	-0.1045
Sin(187°)	-0.1219
Sin(188°)	-0.1392
Sin(189°)	-0.1564
Sin(190°)	-0.1736
Sin(191°)	-0.1908
Sin(192°)	-0.2079
Sin(193°)	-0.225
Sin(194°)	-0.2419
Sin(195°)	-0.2588
Sin(196°)	-0.2756
Sin(197°)	-0.2924
Sin(198°)	-0.309
Sin(199°)	-0.3256
Sin(200°)	-0.342
Sin(201°)	-0.3584
Sin(202°)	-0.3746
Sin(203°)	-0.3907
Sin(204°)	-0.4067
Sin(205°)	-0.4226
Sin(206°)	-0.4384
Sin(207°)	-0.454
Sin(208°)	-0.4695
Sin(209°)	-0.4848
Sin(210°)	-0.5
Sin(211°)	-0.515
Sin(212°)	-0.5299
Sin(213°)	-0.5446
Sin(214°)	-0.5592
Sin(215°)	-0.5736
Sin(216°)	-0.5878

Sin(217°)	-0.6018
Sin(218°)	-0.6157
Sin(219°)	-0.6293
Sin(220°)	-0.6428
Sin(221°)	-0.6561
Sin(222°)	-0.6691
Sin(223°)	-0.682
Sin(224°)	-0.6947
Sin(225°)	-0.7071
Sin(226°)	-0.7193
Sin(227°)	-0.7314
Sin(228°)	-0.7431
Sin(229°)	-0.7547
Sin(230°)	-0.766
Sin(231°)	-0.7771
Sin(232°)	-0.788
Sin(233°)	-0.7986
Sin(234°)	-0.809
Sin(235°)	-0.8192
Sin(236°)	-0.829
Sin(237°)	-0.8387
Sin(238°)	-0.848
Sin(239°)	-0.8572
Sin(240°)	-0.866
Sin(241°)	-0.8746
Sin(242°)	-0.8829
Sin(243°)	-0.891
Sin(244°)	-0.8988
Sin(245°)	-0.9063
Sin(246°)	-0.9135
Sin(247°)	-0.9205
Sin(248°)	-0.9272
Sin(249°)	-0.9336
Sin(250°)	-0.9397
Sin(251°)	-0.9455
Sin(252°)	-0.9511

Sin(253°)	-0.9563
Sin(254°)	-0.9613
Sin(255°)	-0.9659
Sin(256°)	-0.9703
Sin(257°)	-0.9744
Sin(258°)	-0.9781
Sin(259°)	-0.9816
Sin(260°)	-0.9848
Sin(261°)	-0.9877
Sin(262°)	-0.9903
Sin(263°)	-0.9925
Sin(264°)	-0.9945
Sin(265°)	-0.9962
Sin(266°)	-0.9976
Sin(267°)	-0.9986
Sin(268°)	-0.9994
Sin(269°)	-0.9998
Sin(270°)	-1
Sin(271°)	-0.9998
Sin(272°)	-0.9994
Sin(273°)	-0.9986
Sin(274°)	-0.9976
Sin(275°)	-0.9962
Sin(276°)	-0.9945
Sin(277°)	-0.9925
Sin(278°)	-0.9903
Sin(279°)	-0.9877
Sin(280°)	-0.9848
Sin(281°)	-0.9816
Sin(282°)	-0.9781
Sin(283°)	-0.9744
Sin(284°)	-0.9703
Sin(285°)	-0.9659
Sin(286°)	-0.9613
Sin(287°)	-0.9563
Sin(288°)	-0.9511

Sin(289°)	-0.9455
Sin(290°)	-0.9397
Sin(291°)	-0.9336
Sin(292°)	-0.9272
Sin(293°)	-0.9205
Sin(294°)	-0.9135
Sin(295°)	-0.9063
Sin(296°)	-0.8988
Sin(297°)	-0.891
Sin(298°)	-0.8829
Sin(299°)	-0.8746
Sin(300°)	-0.866
Sin(301°)	-0.8572
Sin(302°)	-0.848
Sin(303°)	-0.8387
Sin(304°)	-0.829
Sin(305°)	-0.8192
Sin(306°)	-0.809
Sin(307°)	-0.7986
Sin(308°)	-0.788
Sin(309°)	-0.7771
Sin(310°)	-0.766
Sin(311°)	-0.7547
Sin(312°)	-0.7431
Sin(313°)	-0.7314
Sin(314°)	-0.7193
Sin(315°)	-0.7071
Sin(316°)	-0.6947
Sin(317°)	-0.682
Sin(318°)	-0.6691
Sin(319°)	-0.6561
Sin(320°)	-0.6428
Sin(321°)	-0.6293
Sin(322°)	-0.6157
Sin(323°)	-0.6018
Sin(324°)	-0.5878

Sin(325°)	-0.5736
Sin(326°)	-0.5592
Sin(327°)	-0.5446
Sin(328°)	-0.5299
Sin(329°)	-0.515
Sin(330°)	-0.5
Sin(331°)	-0.4848
Sin(332°)	-0.4695
Sin(333°)	-0.454
Sin(334°)	-0.4384
Sin(335°)	-0.4226
Sin(336°)	-0.4067
Sin(337°)	-0.3907
Sin(338°)	-0.3746
Sin(339°)	-0.3584
Sin(340°)	-0.342
Sin(341°)	-0.3256
Sin(342°)	-0.309
Sin(343°)	-0.2924
Sin(344°)	-0.2756
Sin(345°)	-0.2588
Sin(346°)	-0.2419
Sin(347°)	-0.225
Sin(348°)	-0.2079
Sin(349°)	-0.1908
Sin(350°)	-0.1736
Sin(351°)	-0.1564
Sin(352°)	-0.1392
Sin(353°)	-0.1219
Sin(354°)	-0.1045
Sin(355°)	-0.0872
Sin(356°)	-0.0698
Sin(357°)	-0.0523
Sin(358°)	-0.0349
Sin(359°)	-0.0175
Sin(360°)	-0

Смотрите также

Синус угла онлайн. Таблица синусов. Формула синуса угла.

sin(0) = 0	sin(120) = 0.86602540378444	sin(240) = -0.86602540378444
sin(1) = 0.017452406437284	sin(121) = 0.85716730070211	sin(241) = -0.8746197071394
sin(2) = 0.034899496702501	sin(122) = 0.84804809615643	sin(242) = -0.88294759285893
sin(3) = 0.052335956242944	sin(123) = 0.83867056794542	sin(243) = -0.89100652418837
sin(4) = 0.069756473744125	sin(124) = 0.82903757255504	sin(244) = -0.89879404629917
sin(5) = 0.087155742747658	sin(125) = 0.81915204428899	sin(245) = -0.90630778703665
sin(6) = 0.10452846326765	sin(126) = 0.80901699437495	sin(246) = -0.9135454576426
sin(7) = 0.12186934340515	sin(127) = 0.79863551004729	sin(247) = -0.92050485345244
sin(8) = 0.13917310096007	sin(128) = 0.78801075360672	sin(248) = -0.92718385456679
sin(9) = 0.15643446504023	sin(129) = 0.77714596145697	sin(249) = -0.9335804264972
sin(10) = 0.17364817766693	sin(130) = 0.76604444311898	sin(250) = -0.93969262078591
sin(11) = 0.19080899537654	sin(131) = 0.75470958022277	sin(251) = -0.94551857559932
sin(12) = 0.20791169081776	sin(132) = 0.74314482547739	sin(252) = -0.95105651629515
sin(13) = 0.22495105434386	sin(133) = 0.73135370161917	sin(253) = -0.95630475596304
sin(14) = 0.24192189559967	sin(134) = 0.71933980033865	sin(254) = -0.96126169593832
sin(15) = 0.25881904510252	sin(135) = 0.70710678118655	sin(255) = -0.96592582628907
sin(16) = 0.275637355817	sin(136) = 0.694658370459	sin(256) = -0.970295726276
sin(17) = 0.29237170472274	sin(137) = 0.6819983600625	sin(257) = -0.97437006478524
sin(18) = 0.30901699437495	sin(138) = 0.66913060635886	sin(258) = -0.97814760073381
sin(19) = 0.32556815445716	sin(139) = 0.65605902899051	sin(259) = -0.98162718344766
sin(20) = 0.34202014332567	sin(140) = 0.64278760968654	sin(260) = -0.98480775301221
sin(21) = 0.3583679495453	sin(141) = 0.62932039104984	sin(261) = -0.98768834059514
sin(22) = 0.37460659341591	sin(142) = 0.61566147532566	sin(262) = -0.99026806874157
sin(23) = 0.39073112848927	sin(143) = 0.60181502315205	sin(263) = -0.99254615164132
sin(24) = 0.4067366430758	sin(144) = 0.58778525229247	sin(264) = -0.99452189536827
sin(25) = 0.4226182617407	sin(145) = 0.57357643635105	sin(265) = -0.99619469809175
sin(26) = 0.43837114678908	sin(146) = 0.55919290347075	sin(266) = -0.99756405025982
sin(27) = 0.45399049973955	sin(147) = 0.54463903501503	sin(267) = -0.99862953475457
sin(28) = 0.46947156278589	sin(148) = 0.5299192642332	sin(268) = -0.9993908270191
sin(29) = 0.48480962024634	sin(149) = 0.51503807491005	sin(269) = -0.99984769515639
sin(30) = 0.5	sin(150) = 0.5	sin(270) = -1
sin(31) = 0.51503807491005	sin(151) = 0.48480962024634	sin(271) = -0.99984769515639
sin(32) = 0.5299192642332	sin(152) = 0.46947156278589	sin(272) = -0.9993908270191
sin(33) = 0.54463903501503	sin(153) = 0.45399049973955	sin(273) = -0.99862953475457
sin(34) = 0.55919290347075	sin(154) = 0.43837114678908	sin(274) = -0.99756405025982
sin(35) = 0.57357643635105	sin(155) = 0.4226182617407	sin(275) = -0.99619469809175
sin(36) = 0.58778525229247	sin(156) = 0.4067366430758	sin(276) = -0.99452189536827
sin(37) = 0.60181502315205	sin(157) = 0.39073112848927	sin(277) = -0.99254615164132
sin(38) = 0.61566147532566	sin(158) = 0.37460659341591	sin(278) = -0.99026806874157
sin(39) = 0.62932039104984	sin(159) = 0.3583679495453	sin(279) = -0.98768834059514
sin(40) = 0.64278760968654	sin(160) = 0.34202014332567	sin(280) = -0.98480775301221
sin(41) = 0.65605902899051	sin(161) = 0.32556815445716	sin(281) = -0.98162718344766
sin(42) = 0.66913060635886	sin(162) = 0.30901699437495	sin(282) = -0.97814760073381
sin(43) = 0.6819983600625	sin(163) = 0.29237170472274	sin(283) = -0.97437006478524
sin(44) = 0.694658370459	sin(164) = 0.275637355817	sin(284) = -0.970295726276
sin(45) = 0.70710678118655	sin(165) = 0.25881904510252	sin(285) = -0.96592582628907
sin(46) = 0.71933980033865	sin(166) = 0.24192189559967	sin(286) = -0.96126169593832
sin(47) = 0.73135370161917	sin(167) = 0.22495105434387	sin(287) = -0.95630475596304
sin(48) = 0.74314482547739	sin(168) = 0.20791169081776	sin(288) = -0.95105651629515
sin(49) = 0.75470958022277	sin(169) = 0.19080899537654	sin(289) = -0.94551857559932
sin(50) = 0.76604444311898	sin(170) = 0.17364817766693	sin(290) = -0.93969262078591
sin(51) = 0.77714596145697	sin(171) = 0.15643446504023	sin(291) = -0.9335804264972
sin(52) = 0.78801075360672	sin(172) = 0.13917310096007	sin(292) = -0.92718385456679
sin(53) = 0.79863551004729	sin(173) = 0.12186934340515	sin(293) = -0.92050485345244
sin(54) = 0.80901699437495	sin(174) = 0.10452846326765	sin(294) = -0.9135454576426
sin(55) = 0.81915204428899	sin(175) = 0.087155742747658	sin(295) = -0.90630778703665
sin(56) = 0.82903757255504	sin(176) = 0.069756473744126	sin(296) = -0.89879404629917
sin(57) = 0.83867056794542	sin(177) = 0.052335956242944	sin(297) = -0.89100652418837
sin(58) = 0.84804809615643	sin(178) = 0.034899496702501	sin(298) = -0.88294759285893
sin(59) = 0.85716730070211	sin(179) = 0.017452406437283	sin(299) = -0.8746197071394
sin(60) = 0.86602540378444	sin(180) = 0	sin(300) = -0.86602540378444
sin(61) = 0.8746197071394	sin(181) = -0.017452406437283	sin(301) = -0.85716730070211
sin(62) = 0.88294759285893	sin(182) = -0.034899496702501	sin(302) = -0.84804809615643
sin(63) = 0.89100652418837	sin(183) = -0.052335956242944	sin(303) = -0.83867056794542
sin(64) = 0.89879404629917	sin(184) = -0.069756473744125	sin(304) = -0.82903757255504
sin(65) = 0.90630778703665	sin(185) = -0.087155742747658	sin(305) = -0.81915204428899
sin(66) = 0.9135454576426	sin(186) = -0.10452846326765	sin(306) = -0.80901699437495
sin(67) = 0.92050485345244	sin(187) = -0.12186934340515	sin(307) = -0.79863551004729
sin(68) = 0.92718385456679	sin(188) = -0.13917310096007	sin(308) = -0.78801075360672
sin(69) = 0.9335804264972	sin(189) = -0.15643446504023	sin(309) = -0.77714596145697
sin(70) = 0.93969262078591	sin(190) = -0.17364817766693	sin(310) = -0.76604444311898
sin(71) = 0.94551857559932	sin(191) = -0.19080899537654	sin(311) = -0.75470958022277
sin(72) = 0.95105651629515	sin(192) = -0.20791169081776	sin(312) = -0.74314482547739
sin(73) = 0.95630475596304	sin(193) = -0.22495105434386	sin(313) = -0.73135370161917
sin(74) = 0.96126169593832	sin(194) = -0.24192189559967	sin(314) = -0.71933980033865
sin(75) = 0.96592582628907	sin(195) = -0.25881904510252	sin(315) = -0.70710678118655
sin(76) = 0.970295726276	sin(196) = -0.275637355817	sin(316) = -0.694658370459
sin(77) = 0.97437006478524	sin(197) = -0.29237170472274	sin(317) = -0.6819983600625
sin(78) = 0.97814760073381	sin(198) = -0.30901699437495	sin(318) = -0.66913060635886
sin(79) = 0.98162718344766	sin(199) = -0.32556815445716	sin(319) = -0.65605902899051
sin(80) = 0.98480775301221	sin(200) = -0.34202014332567	sin(320) = -0.64278760968654
sin(81) = 0.98768834059514	sin(201) = -0.3583679495453	sin(321) = -0.62932039104984
sin(82) = 0.99026806874157	sin(202) = -0.37460659341591	sin(322) = -0.61566147532566
sin(83) = 0.99254615164132	sin(203) = -0.39073112848927	sin(323) = -0.60181502315205
sin(84) = 0.99452189536827	sin(204) = -0.4067366430758	sin(324) = -0.58778525229247
sin(85) = 0.99619469809175	sin(205) = -0.4226182617407	sin(325) = -0.57357643635105
sin(86) = 0.99756405025982	sin(206) = -0.43837114678908	sin(326) = -0.55919290347075
sin(87) = 0.99862953475457	sin(207) = -0.45399049973955	sin(327) = -0.54463903501503
sin(88) = 0.9993908270191	sin(208) = -0.46947156278589	sin(328) = -0.52991926423321
sin(89) = 0.99984769515639	sin(209) = -0.48480962024634	sin(329) = -0.51503807491005
sin(90) = 1	sin(210) = -0.5	sin(330) = -0.5
sin(91) = 0.99984769515639	sin(211) = -0.51503807491005	sin(331) = -0.48480962024634
sin(92) = 0.9993908270191	sin(212) = -0.5299192642332	sin(332) = -0.46947156278589
sin(93) = 0.99862953475457	sin(213) = -0.54463903501503	sin(333) = -0.45399049973955
sin(94) = 0.99756405025982	sin(214) = -0.55919290347075	sin(334) = -0.43837114678908
sin(95) = 0.99619469809175	sin(215) = -0.57357643635105	sin(335) = -0.4226182617407
sin(96) = 0.99452189536827	sin(216) = -0.58778525229247	sin(336) = -0.4067366430758
sin(97) = 0.99254615164132	sin(217) = -0.60181502315205	sin(337) = -0.39073112848927
sin(98) = 0.99026806874157	sin(218) = -0.61566147532566	sin(338) = -0.37460659341591
sin(99) = 0.98768834059514	sin(219) = -0.62932039104984	sin(339) = -0.3583679495453
sin(100) = 0.98480775301221	sin(220) = -0.64278760968654	sin(340) = -0.34202014332567
sin(101) = 0.98162718344766	sin(221) = -0.65605902899051	sin(341) = -0.32556815445716
sin(102) = 0.97814760073381	sin(222) = -0.66913060635886	sin(342) = -0.30901699437495
sin(103) = 0.97437006478524	sin(223) = -0.6819983600625	sin(343) = -0.29237170472274
sin(104) = 0.970295726276	sin(224) = -0.694658370459	sin(344) = -0.275637355817
sin(105) = 0.96592582628907	sin(225) = -0.70710678118655	sin(345) = -0.25881904510252
sin(106) = 0.96126169593832	sin(226) = -0.71933980033865	sin(346) = -0.24192189559967
sin(107) = 0.95630475596304	sin(227) = -0.73135370161917	sin(347) = -0.22495105434387
sin(108) = 0.95105651629515	sin(228) = -0.74314482547739	sin(348) = -0.20791169081776
sin(109) = 0.94551857559932	sin(229) = -0.75470958022277	sin(349) = -0.19080899537654
sin(110) = 0.93969262078591	sin(230) = -0.76604444311898	sin(350) = -0.17364817766693
sin(111) = 0.9335804264972	sin(231) = -0.77714596145697	sin(351) = -0.15643446504023
sin(112) = 0.92718385456679	sin(232) = -0.78801075360672	sin(352) = -0.13917310096007
sin(113) = 0.92050485345244	sin(233) = -0.79863551004729	sin(353) = -0.12186934340515
sin(114) = 0.9135454576426	sin(234) = -0.80901699437495	sin(354) = -0.10452846326765
sin(115) = 0.90630778703665	sin(235) = -0.81915204428899	sin(355) = -0.087155742747658
sin(116) = 0.89879404629917	sin(236) = -0.82903757255504	sin(356) = -0.069756473744126
sin(117) = 0.89100652418837	sin(237) = -0.83867056794542	sin(357) = -0.052335956242943
sin(118) = 0.88294759285893	sin(238) = -0.84804809615643	sin(358) = -0.034899496702501
sin(119) = 0.8746197071394	sin(239) = -0.85716730070211	sin(359) = -0.017452406437284

90000 Trig Table 90001 Trig Table 90002 Trig Tables — Some Exact Values and A Numerical Table 90003 90004 90005 90006 90007 90007 90009 90007 90007 90007 90007 90009 90007 90016 90017 Degrees 90018 90017 Radian Measure 90018 90017 Sin 90018 90017 Cos 90018 90017 Tan 90018 90017 90018 90017 Degrees 90018 90017 Radian Measure 90018 90017 Sin 90018 90017 Cos 90018 90017 Tan 90018 90039 90016 90041 0 90018 90043 0.00000 90018 90045 0.00000 90018 90047 1.00000 90018 90049 0.00000 90018 90017 90018 90041 46 90018 90055 0.80285 90018 90057 0.71934 90018 90059 0.69466 90018 90061 1.03553 90018 90039 90016 90041 1 90018 90067 0.01745 90018 90069 0.01745 90018 90071 0.99985 90018 90073 0.01746 90018 90017 90018 90041 47 90018 90079 0.82030 90018 90081 0.73135 90018 90083 0.68200 90018 90085 1.07237 90018 90039 90016 90041 2 90018 90091 0.03491 90018 90093 0.03490 90018 90095 0.99939 90018 90097 0.03492 90018 90017 90018 90041 48 90018 90103 0.83776 90018 90105 0.74314 90018 90107 0.66913 90018 90109 1.11061 90018 90039 90016 90041 3 90018 90115 0.05236 90018 90117 0.05234 90018 90119 0.99863 90018 90121 0.05241 90018 90017 90018 90041 49 90018 90127 0.85521 90018 90129 0.75471 90018 90131 0.65606 90018 90133 1.15037 90018 90039 90016 90041 4 90018 90139 0.06981 90018 90141 0.06976 90018 90143 0.99756 90018 90145 0.06993 90018 90017 90018 90041 50 90018 90151 0.87266 90018 90153 0.76604 90018 90155 0.64279 90018 90157 1.19175 90018 90039 90016 90041 5 90018 90163 0.08727 90018 90165 0.08716 90018 90167 0.99619 90018 90169 0.08749 90018 90017 90018 90041 51 90018 90175 0.89012 90018 90177 0.77715 90018 90179 0.62932 90018 90181 1.23490 90018 90039 90016 90041 6 90018 90187 0.10472 90018 90189 0.10453 90018 90191 0.99452 90018 90193 0.10510 90018 90017 90018 90041 52 90018 90199 0.90757 90018 90201 0.78801 90018 90203 0.61566 90018 90205 1.27994 90018 90039 90016 90041 7 90018 90211 0.12217 90018 90213 0.12187 90018 90215 0.99255 90018 90217 0.12278 90018 90017 90018 90041 53 90018 90223 0.92502 90018 90225 0.79864 90018 90227 0.60182 90018 90229 1.32704 90018 90039 90016 90041 8 90018 90235 0.13963 90018 90237 0.13917 90018 90239 0.99027 90018 90241 0.14054 90018 90017 90018 90041 54 90018 90247 0.94248 90018 90249 0.80902 90018 90251 0.58779 90018 90253 1.37638 90018 90039 90016 90041 9 90018 90259 0.15708 90018 90261 0.15643 90018 90263 0.98769 90018 90265 0.15838 90018 90017 90018 90041 55 90018 90271 0.95993 90018 90273 0.81915 90018 90275 0.57358 90018 90277 1.42815 90018 90039 90016 90041 10 90018 90283 0.17453 90018 90285 0.17365 90018 90287 0.98481 90018 90289 0.17633 90018 90017 90018 90041 56 90018 90295 0.97738 90018 90297 0.82904 90018 90299 0.55919 90018 90301 1.48256 90018 90039 90016 90041 11 90018 90307 0.19199 90018 90309 0.19081 90018 90311 0.98163 90018 90313 0.19438 90018 90017 90018 90041 57 90018 90319 0.99484 90018 90321 0.83867 90018 90323 0.54464 90018 90325 1.53986 90018 90039 90016 90041 12 90018 90331 0.20944 90018 90333 0.20791 90018 90335 0.97815 90018 90337 0.21256 90018 90017 90018 90041 58 90018 90343 1.01229 90018 90345 0.84805 90018 90347 0.52992 90018 90349 1.60033 90018 90039 90016 90041 13 90018 90355 0.22689 90018 90357 0.22495 90018 90359 0.97437 90018 90361 0.23087 90018 90017 90018 90041 59 90018 90367 1.02974 90018 90369 0.85717 90018 90371 0.51504 90018 90373 1.66428 90018 90039 90016 90041 14 90018 90379 0.24435 90018 90381 0.24192 90018 90383 0.97030 90018 90385 0.24933 90018 90017 90018 90041 60 90018 90391 1.04720 90018 90393 0.86603 90018 90395 0.50000 90018 90397 1.73205 90018 90039 90016 90041 15 90018 90403 0.26180 90018 90405 0.25882 90018 90407 0.96593 90018 90409 0.26795 90018 90017 90018 90041 61 90018 90415 1.06465 90018 90417 0.87462 90018 90419 0.48481 90018 90421 1.80405 90018 90039 90016 90041 16 90018 90427 0.27925 90018 90429 0.27564 90018 90431 0.96126 90018 90433 0.28675 90018 90017 90018 90041 62 90018 90439 1.08210 90018 90441 0.88295 90018 90443 0.46947 90018 90445 1.88073 90018 90039 90016 90041 17 90018 90451 0.29671 90018 90453 0.29237 90018 90455 0.95630 90018 90457 0.30573 90018 90017 90018 90041 63 90018 90463 1.09956 90018 90465 0.89101 90018 90467 0.45399 90018 90469 1.96261 90018 90039 90016 90041 18 90018 90475 0.31416 90018 90477 0.30902 90018 90479 0.95106 90018 90481 0.32492 90018 90017 90018 90041 64 90018 90487 1.11701 90018 90489 0.89879 90018 90491 0.43837 90018 90493 2.05030 90018 90039 90016 90041 19 90018 90499 0.33161 90018 90501 0.32557 90018 90503 0.94552 90018 90505 0.34433 90018 90017 90018 90041 65 90018 90511 1.13446 90018 90513 0.90631 90018 90515 0.42262 90018 90517 2.14451 90018 90039 90016 90041 20 90018 90523 0.34907 90018 90525 0.34202 90018 90527 0.93969 90018 90529 0.36397 90018 90017 90018 90041 66 90018 90535 1.15192 90018 90537 0.91355 90018 90539 0.40674 90018 90541 2.24604 90018 90039 90016 90041 21 90018 90547 0.36652 90018 90549 0.35837 90018 90551 0.93358 90018 90553 0.38386 90018 90017 90018 90041 67 90018 90559 1.16937 90018 90561 0.92050 90018 90563 0.39073 90018 90565 2.35585 90018 90039 90016 90041 22 90018 90571 0.38397 90018 90573 0.37461 90018 90575 0.92718 90018 90577 0.40403 90018 90017 90018 90041 68 90018 90583 1.18682 90018 90585 0.92718 90018 90587 0.37461 90018 90589 2.47509 90018 90039 90016 90041 23 90018 90595 0.40143 90018 90597 0.39073 90018 90599 0.92050 90018 90601 0.42447 90018 90017 90018 90041 69 90018 90607 1.20428 90018 90609 0.93358 90018 90611 0.35837 90018 90613 2.60509 90018 90039 90016 90041 24 90018 90619 0.41888 90018 90621 0.40674 90018 90623 0.91355 90018 90625 0.44523 90018 90017 90018 90041 70 90018 90631 1.22173 90018 90633 0.93969 90018 90635 0.34202 90018 90637 2.74748 90018 90039 90016 90041 25 90018 90643 0.43633 90018 90645 0.42262 90018 90647 0.90631 90018 90649 0.46631 90018 90017 90018 90041 71 90018 90655 1.23918 90018 90657 0.94552 90018 90659 0.32557 90018 90661 2.90421 90018 90039 90016 90041 26 90018 90667 0.45379 90018 90669 0.43837 90018 90671 0.89879 90018 90673 0.48773 90018 90017 90018 90041 72 90018 90679 1.25664 90018 90681 0.95106 90018 90683 0.30902 90018 90685 3.07768 90018 90039 90016 90041 27 90018 90691 0.47124 90018 90693 0.45399 90018 90695 0.89101 90018 90697 0.50953 90018 90017 90018 90041 73 90018 90703 1.27409 90018 90705 0.95630 90018 90707 0.29237 90018 90709 3.27085 90018 90039 90016 90041 28 90018 90715 0.48869 90018 90717 0.46947 90018 90719 0.88295 90018 90721 0.53171 90018 90017 90018 90041 74 90018 90727 1.29154 90018 90729 0.96126 90018 90731 0.27564 90018 90733 3.48741 90018 90039 90016 90041 29 90018 90739 0.50615 90018 90741 0.48481 90018 90743 0.87462 90018 90745 0.55431 90018 90017 90018 90041 75 90018 90751 1.30900 90018 90753 0.96593 90018 90755 0.25882 90018 90757 3.73205 90018 90039 90016 90041 30 90018 90763 0.52360 90018 90765 0.50000 90018 90767 0.86603 90018 90769 0.57735 90018 90017 90018 90041 76 90018 90775 1.32645 90018 90777 0.97030 90018 90779 0.24192 90018 90781 4.01078 90018 90039 90016 90041 31 90018 90787 0.54105 90018 90789 0.51504 90018 90791 0.85717 90018 90793 0.60086 90018 90017 90018 90041 77 90018 90799 1.34390 90018 90801 0.97437 90018 90803 0.22495 90018 90805 4.33148 90018 90039 90016 90041 32 90018 90811 0.55851 90018 90813 0.52992 90018 90815 0.84805 90018 90817 0.62487 90018 90017 90018 90041 78 90018 90823 1.36136 90018 90825 0.97815 90018 90827 0.20791 90018 90829 4.70463 90018 90039 90016 90041 33 90018 90835 0.57596 90018 90837 0.54464 90018 90839 0.83867 90018 90841 0.64941 90018 90017 90018 90041 79 90018 90847 1.37881 90018 90849 0.98163 90018 90851 0.19081 90018 90853 5.14455 90018 90039 90016 90041 34 90018 90859 0.59341 90018 90861 0.55919 90018 90863 0.82904 90018 90865 0.67451 90018 90017 90018 90041 80 90018 90871 1.39626 90018 90873 0.98481 90018 90875 0.17365 90018 90877 5.67128 90018 90039 90016 90041 35 90018 90883 0.61087 90018 90885 0.57358 90018 90887 0.81915 90018 90889 0.70021 90018 90017 90018 90041 81 90018 90895 1.41372 90018 90897 0.98769 90018 90899 0.15643 90018 90901 6.31375 90018 90039 90016 90041 36 90018 90907 0.62832 90018 90909 0.58779 90018 90911 0.80902 90018 90913 0.72654 90018 90017 90018 90041 82 90018 90919 1.43117 90018 90921 0.99027 90018 90923 0.13917 90018 90925 7.11537 90018 90039 90016 90041 37 90018 90931 0.64577 90018 90933 0.60182 90018 90935 0.79864 90018 90937 0.75355 90018 90017 90018 90041 83 90018 90943 1.44862 90018 90945 0.99255 90018 90947 0.12187 90018 90949 8.14435 90018 90039 90016 90041 38 90018 90955 0.66323 90018 90957 0.61566 90018 90959 0.78801 90018 90961 0.78129 90018 90017 90018 90041 84 90018 90967 1.46608 90018 90969 0.99452 90018 90971 0.10453 90018 90973 9.51436 90018 90039 90016 90041 39 90018 90979 0.68068 90018 90981 0.62932 90018 90983 0.77715 90018 90985 0.80978 90018 90017 90018 90041 85 90018 90991 1.48353 90018 90993 0.99619 90018 90995 0.08716 90018 90997 11.43005 90018 90039 90016 90041 40 90018 91003 0.69813 90018 91005 0.64279 90018 91007 0.76604 90018 91009 0.83910 90018 90017 90018 90041 86 90018 91015 1.50098 90018 91017 0.99756 90018 91019 0.06976 90018 91021 14.30067 90018 90039 90016 90041 41 90018 91027 0.71558 90018 91029 0.65606 90018 91031 0.75471 90018 91033 0.86929 90018 90017 90018 90041 87 90018 91039 1.51844 90018 91041 0.99863 90018 91043 0.05234 90018 91045 19.08114 90018 90039 90016 90041 42 90018 91051 0.73304 90018 91053 0.66913 90018 91055 0.74314 90018 91057 0.90040 90018 90017 90018 90041 88 90018 91063 1.53589 90018 91065 0.99939 90018 91067 0.03490 90018 91069 28.63625 90018 90039 90016 90041 43 90018 91075 0.75049 90018 Дев’яносто одна тисяча сімдесят сім 0.68200 90018 91079 0.73135 90018 91081 0.93252 90018 90017 90018 90041 89 90018 91087 1.55334 90018 91089 0.99985 90018 91091 0.01745 90018 91093 57.28996 90018 90039 90016 90041 44 90018 91099 0.76794 90018 91101 0.69466 90018 91103 0.71934 90018 91105 0.96569 90018 90017 90018 90041 90 90018 91111 1.57080 90018 91113 1.00000 90018 91115 0.00000 90018 90017 90018 90039 90016 90041 45 90018 91123 0.78540 90018 91125 0.70711 90018 91127 0.70711 90018 91129 1.00000 90018 90017 90018 90017 90018 90017 90018 90017 90018 90017 90018 90017 90018 90039 90016 дев’яносто одна тисяча сто сорок п’ять дев’яносто одна тисяча сто сорок п’ять дев’яносто одна тисяча сто сорок п’ять дев’яносто одна тисяча сто сорок п’ять дев’яносто одна тисяча сто сорок п’ять дев’яносто одна тисяча сто сорок п’ять дев’яносто одна тисяча сто сорок п’ять дев’яносто одна тисяча сто сорок п’ять дев’яносто одна тисяча сто сорок п’ять дев’яносто одна тисяча сто сорок п’ять дев’яносто одна тисяча сто сорок п’ять 90039 91157 91158 S.O.S. MATH: Home Page 91159 91158 Do you need more help? Please post your question on our S.O.S. Mathematics CyberBoard. 91159 Copyright 1999-2020 MathMedics, LLC. All rights reserved. Дев’яносто одна тисяча сто шістьдесят-дві Contact us Дев’яносто одна тисяча сто шістьдесят-дві Math Medics, LLC. — P.O. Box 12395 — El Paso TX 79913 — USA Дев’яносто одна тисяча сто шістьдесят-дві users online during the last hour .90000 What are values of Trigonometric ratios for 0, 30,45, 60 and 90 degrees 90001 90002 90003 Values of Trigonometric ratios for 0, 30,45, 60 and 90 degrees 90004 90005 90002 I have noticed that students can not actually remember values of six trigonometric ratios 90003 (sin, cos, tan, cosec, sec and cot) 90004 for 90003 0 90010, 30 90010, 45 90010, 60 90010 and 90 90010 90004. These values are used very often and it is recommended from my point of view that student should be able to tell the values instantly when asked.90005 90002 There is a proper method to memorize all of them. Lets go through it. 90005 90002 90003 In this post our motive is to learn how to fill the table. Once, you learn to fill this table, you would be able to calculate any value in your mind. 90004 90005 90002 90024 90005 90002 90003 (i) 90004 90005 90002 Just memorize the values for 90003 sin 0 90010, sin 30 90010, sin 45 90010, sin 60 90010 and sin 90 90010 90004. Even there is no need to try too hard to memorize them.There is an easy way to memorize them. 90005 90002 sin 0 90040 90005 90002 sin 30 90043 90005 90002 sin 45 90046 90005 90002 sin 60 90049 90005 90002 sin 90 90 052 90005 90002 90003 Note down the pattern from sin 0 90010 to sin 90 90010: 90004 90005 90002 90061 90005 90002 Hence, we can now fill all 90003 sin values 90004 in the table. 90005 90002 90068 90005 90002 Now, we will fill all the 90003 cos values 90004. 90005 90002 All the 90003 cos values 90004 are filled in opposite order starting from 90003 sin 0 90010 to sin 90 90010 90004.I mean to say that 90005 90002 90003 sin 0 90010 = cos 90 90010 90004 90005 90002 90003 sin 30 90010 = cos 60 90010 90004 90005 90002 90003 sin 45 90010 = cos 45 90010 90004 90005 90002 90003 sin60 90010 = cos 30 90010 90004 90005 90002 90003 sin 90 90010 = cos 0 90010 90004 90005 90002 Hence, all the 90003 cos values 90004 can be filled now. 90005 90002 90117 90005 90002 We know that 90003 tan 90121 = (sin 90121) / (cos 90121) 90004 90005 90002 Hence, all the 90003 tan values 90004 can be obtained from 90003 sin and cos values 90004.90005 90002 tan 0 90010 = sin 0 90010 / cos 0 90010 = 0/1 = 0 90005 90002 tan 30 90138 90005.90000 Trigonometric Tables 90001 Trigonometric Tables 90002 PI = 3.141592 … (approximately 22/7 = 3.1428) 90003 radians = degress x PI / 180 90004 (deg to rad conversion) 90005 90003 degress = radians x 180 / PI 90004 (rad to deg conversion) 90005 90003 90004 90005 90012 90013 90014 90015 Rad 90016 90015 Deg 90016 90015 Sin 90016 90015 Cos 90016 90015 Tan 90016 90015 Csc 90016 90015 Sec 90016 90015 Cot 90016 90031 90014 90033 90004.0000 90005 90036 90033 90004 00 90005 90036 90033 .0000 90036 90033 1.0000 90036 90033 .0000 90036 90033 —— 90036 90033 1.0000 90036 90033 —— 90036 90033 90004 90 90005 90036 90033 90004 1.5707 90005 90036 90031 90014 90033 90004 .0175 90005 90036 90033 90004 01 90005 90036 90033 .0175 90036 90033.9998 90036 90033 .0175 90036 90033 57.2987 90036 90033 1.0002 90036 90033 57.2900 90036 90033 90004 89 90005 90036 90033 90004 1.5533 90005 90036 90031 90014 90033 90004 .0349 90005 90036 90033 90004 02 90005 90036 90033 .0349 90036 90033 .9994 90036 90033 .0349 90036 90033 28.6537 90036 90033 1.0006 90036 90033 28.6363 90036 90033 90004 88 90005 90036 90033 90004 1.5359 90005 90036 90031 90014 90033 90004 .0524 90005 90036 90033 90004 03 90005 90036 90033 .0523 90036 90033 .9986 90036 90033 .0524 90036 90033 19.1073 90036 90033 1.0014 90036 90033 19.0811 90036 90033 90004 87 90005 90036 90033 90004 1.5184 90005 90036 90031 90014 90033 90004 .0698 90005 90036 90033 90004 04 90005 90036 90033 .0698 90036 90033 .9976 90036 90033 .0699 90036 90033 14.3356 90036 90033 1.0024 90036 90033 14.3007 90036 90033 90004 86 90005 90036 90033 90004 1.5010 90005 90036 90031 90014 90033 90004 .0873 90005 90036 90033 90004 05 90005 90036 90033.0872 90036 90033 .9962 90036 90033 .0875 90036 90033 11.4737 90036 90033 1.0038 90036 90033 11.4301 90036 90033 90004 85 90005 90036 90033 90004 1.4835 90005 90036 90031 90014 90033 90004 .1047 90005 90036 90033 90004 06 90005 90036 90033 .1045 90036 90033 .9945 90036 90033 .1051 90036 90033 9.5668 90036 90033 1.0055 90036 90033 9.5144 90036 90033 90004 84 90005 90036 90033 90004 1.4661 90005 90036 90031 90014 90033 90004 .1222 90005 90036 90033 90004 07 90005 90036 90033 .1219 90036 90033 .9925 90036 90033 .1228 90036 90033 8.2055 90036 90033 1.0075 90036 90033 8.1443 90036 90033 90004 83 90005 90036 90033 90004 1.4486 90005 90036 90031 90014 90033 90004 .1396 90005 90036 90033 90004 08 90005 90036 90033 .1392 90036 90033 .9903 90036 90033 .1405 90036 90033 7.1853 90036 90033 1.0098 90036 90033 7.1154 90036 90033 90004 82 90005 90036 90033 90004 1.4312 90005 90036 90031 90014 90033 90004 .1571 90005 90036 90033 90004 09 90005 90036 90033.1564 90036 90033 .9877 90036 90033 .1584 90036 90033 6.3925 90036 90033 1.0125 90036 90033 6.3138 90036 90033 90004 81 90005 90036 90033 90004 1.4137 90005 90036 90031 90014 90033 90004 .1745 90005 90036 90033 90004 10 90005 90036 90033 .1736 90036 90033 .9848 90036 90033 .1763 90036 90033 5.7588 90036 90033 1.0154 90036 90033 5.6713 90036 90033 90004 80 90005 90036 90033 90004 1.3953 90005 90036 90031 90014 90033 90004 .1920 90005 90036 90033 90004 11 90005 90036 90033 .1908 90036 90033 .9816 90036 90033 .1944 90036 90033 5.2408 90036 90033 1.0187 90036 90033 5.1446 90036 90033 90004 79 90005 90036 90033 90004 1.3788 90005 90036 90031 90014 90033 90004 .2094 90005 90036 90033 90004 12 90005 90036 90033 .2079 90036 90033 .9781 90036 90033 .2126 90036 90033 4.8097 90036 90033 1.0223 90036 90033 4.7046 90036 90033 90004 78 90005 90036 90033 90004 1.3614 90005 90036 90031 90014 90033 90004 .2269 90005 90036 90033 90004 13 90005 90036 90033.2250 90036 90033 .9744 90036 90033 .2309 90036 90033 4.4454 90036 90033 1.0263 90036 90033 4.3315 90036 90033 90004 77 90005 90036 90033 90004 1.3439 90005 90036 90031 90014 90033 90004 .2443 90005 90036 90033 90004 14 90005 90036 90033 .2419 90036 90033 .9703 90036 90033 .2493 90036 90033 4.1336 90036 90033 1.0306 90036 90033 4.0108 90036 90033 90004 76 90005 90036 90033 90004 1.3265 90005 90036 90031 90014 90033 90004 .2618 90005 90036 90033 90004 15 90005 90036 90033 .2588 90036 90033 .9659 90036 90033 .2679 90036 90033 3.8637 90036 90033 1.0353 90036 90033 3.7321 90036 90033 90004 75 90005 90036 90033 90004 1.3090 90005 90036 90031 90014 90033 90004 .2793 90005 90036 90033 90004 16 90005 90036 90033 .2756 90036 90033 .9613 90036 90033 .2867 90036 90033 3.6280 90036 90033 1.0403 90036 90033 3.4874 90036 90033 90004 74 90005 90036 90033 90004 1.2915 90005 90036 90031 90014 90033 90004 .2967 90005 90036 90033 90004 17 90005 90036 90033.2924 90036 90033 .9563 90036 90033 .3057 90036 90033 3.4203 90036 90033 1.0457 90036 90033 3.2709 90036 90033 90004 73 90005 90036 90033 90004 1.2741 90005 90036 90031 90014 90033 90004 .3142 90005 90036 90033 90004 18 90005 90036 90033 .3090 90036 90033 .9511 90036 90033 .3249 90036 90033 3.2361 90036 90033 1.0515 90036 90033 3.0777 90036 90033 90004 72 90005 90036 90033 90004 1.2566 90005 90036 90031 90014 90033 90004 .3316 90005 90036 90033 90004 19 90005 90036 90033 .3256 90036 90033 .9455 90036 90033 .3443 90036 90033 3.0716 90036 90033 1.0576 90036 90033 2.9042 90036 90033 90004 71 90005 90036 90033 90004 1.2392 90005 90036 90031 90014 90033 90004 .3491 90005 90036 90033 90004 20 90005 90036 90033 .3420 90036 90033 .9397 90036 90033 .3640 90036 90033 2.9238 90036 90033 1.0642 90036 90033 2.7475 90036 90033 90004 70 90005 90036 90033 90004 1.2217 90005 90036 90031 90014 90033 90004 .3665 90005 90036 90033 90004 21 90005 90036 90033.3584 90036 90033 .9336 90036 90033 .3839 90036 90033 2.7904 90036 90033 1.0711 90036 90033 2.6051 90036 90033 90004 69 90005 90036 90033 90004 1.2043 90005 90036 90031 90014 90033 90004 .3840 90005 90036 90033 90004 22 90005 90036 90033 .3746 90036 90033 .9272 90036 90033 .4040 90036 90033 2.6695 90036 90033 1.0785 90036 90033 2.4751 90036 90033 90004 68 90005 90036 90033 90004 1.1868 90005 90036 90031 90014 90033 90004 .4014 90005 90036 90033 90004 23 90005 90036 90033 .3907 90036 90033 .9205 90036 90033 .4245 90036 90033 2.5593 90036 90033 1.0864 90036 90033 2.3559 90036 90033 90004 67 90005 90036 90033 90004 1.1694 90005 90036 90031 90014 90033 90004 .4189 90005 90036 90033 90004 24 90005 90036 90033 .4067 90036 90033 .9135 90036 90033 .4452 90036 90033 2.4586 90036 90033 1.0946 90036 90033 2.2460 90036 90033 90004 66 90005 90036 90033 90004 1.1519 90005 90036 90031 90014 90033 90004 .4363 90005 90036 90033 90004 25 90005 90036 90033.4226 90036 90033 .9063 90036 90033 .4663 90036 90033 2.3662 90036 90033 1.1034 90036 90033 2.1445 90036 90033 90004 65 90005 90036 90033 90004 1.1345 90005 90036 90031 90014 90033 90004 .4538 90005 90036 90033 90004 26 90005 90036 90033 .4384 90036 90033 .8988 90036 90033 .4877 90036 90033 2.2812 90036 90033 1.1126 90036 90033 2.0503 90036 90033 90004 64 90005 90036 90033 90004 1.1170 90005 90036 90031 90014 90033 90004 .4712 90005 90036 90033 90004 27 90005 90036 90033 .4540 90036 90033 .8910 90036 90033 .5095 90036 90033 2.2027 90036 90033 1.1223 90036 90033 1.9626 90036 90033 90004 63 90005 90036 90033 90004 1.0996 90005 90036 90031 90014 90033 90004 .4887 90005 90036 90033 90004 28 90005 90036 90033 .4695 90036 90033 .8829 90036 90033 .5317 90036 90033 2.1301 90036 90033 1.1326 90036 90033 1.8807 90036 90033 90004 62 90005 90036 90033 90004 1.0821 90005 90036 90031 90014 90033 90004 .5061 90005 90036 90033 90004 29 90005 90036 90033.4848 90036 90033 .8746 90036 90033 .5543 90036 90033 2.0627 90036 90033 1.1434 90036 90033 1.8040 90036 90033 90004 61 90005 90036 90033 90004 1.0647 90005 90036 90031 90014 90033 90004 .5236 90005 90036 90033 90004 30 90005 90036 90033 .5000 90036 90033 .8660 90036 90033 .5774 90036 90033 2.0000 90036 90033 1.1547 90036 90033 1.7321 90036 90033 90004 60 90005 90036 90033 90004 1.0472 90005 90036 90031 90014 90033 90004 .5411 90005 90036 90033 90004 31 90005 90036 90033 .5150 90036 90033 .8572 90036 90033 .6009 90036 90033 1.9416 90036 90033 1.1666 90036 90033 1.6643 90036 90033 90004 59 90005 90036 90033 90004 1.0297 90005 90036 90031 90014 90033 90004 .5585 90005 90036 90033 90004 32 90005 90036 90033 .5299 90036 90033 .8480 90036 90033 .6249 90036 90033 1.8871 90036 90033 1.1792 90036 90033 1.6003 90036 90033 90004 58 90005 90036 90033 90004 1.0123 90005 90036 90031 90014 90033 90004 .5760 90005 90036 90033 90004 33 90005 90036 90033.5446 90036 90033 .8387 90036 90033 .6494 90036 90033 1.8361 90036 90033 1.1924 90036 90033 1.5399 90036 90033 90004 57 90005 90036 90033 90004 .9948 90005 90036 90031 90014 90033 90004 .5934 90005 90036 90033 90004 34 90005 90036 90033 .5592 90036 90033 .8290 90036 90033 .6745 90036 90033 1.7883 90036 90033 1.2062 90036 90033 1.4826 90036 90033 90004 56 90005 90036 90033 90004 .9774 90005 90036 90031 90014 90033 90004 .6109 90005 90036 90033 90004 35 90005 90036 90033 .5736 90036 90033 .8192 90036 90033 .7002 90036 90033 1.7434 90036 90033 1.2208 90036 90033 1.4281 90036 90033 90004 55 90005 90036 90033 90004.9599 90005 90036 90031 90014 90033 90004 .6283 90005 90036 90033 90004 36 90005 90036 90033 .5878 90036 90033 .8090 90036 90033 .7265 90036 90033 1.7013 90036 90033 1.2361 90036 90033 1.3764 90036 90033 90004 54 90005 90036 90033 90004 .9425 90005 90036 90031 90014 90033 90004 .6458 90005 90036 90033 90004 37 90005 90036 90033.6018 90036 90033 .7986 90036 90033 .7536 90036 90033 1.6616 90036 90033 1.2521 90036 90033 1.3270 90036 90033 90004 53 90005 90036 90033 90004 .9250 90005 90036 90031 90014 90033 90004 .6632 90005 90036 90033 90004 38 90005 90036 90033 .6157 90036 90033 .7880 90036 90033 .7813 90036 90033 1.6243 90036 90033 1.2690 90036 90033 1.2799 90036 90033 90004 52 90005 90036 90033 90004 .9076 90005 90036 90031 90014 90033 90004 .6807 90005 90036 90033 90004 39 90005 90036 90033 .6293 90036 90033 .7771 90036 90033 .8098 90036 90033 1.5890 90036 90033 1.2868 90036 90033 1.2349 90036 90033 90004 51 90005 90036 90033 90004.8901 90005 90036 90031 90014 90033 90004 .6981 90005 90036 90033 90004 40 90005 90036 90033 .6428 90036 90033 .7660 90036 90033 .8391 90036 90033 1.5557 90036 90033 1.3054 90036 90033 1.1918 90036 90033 90004 50 90005 90036 90033 90004 .8727 90005 90036 90031 90014 90033 90004 .7156 90005 90036 90033 90004 41 90005 90036 90033.6561 90036 90033 .7547 90036 90033 .8693 90036 90033 1.5243 90036 90033 1.3250 90036 90033 1.1504 90036 90033 90004 49 90005 90036 90033 90004 .8552 90005 90036 90031 90014 90033 90004 .7330 90005 90036 90033 90004 42 90005 90036 90033 .6691 90036 90033 .7431 90036 90033 .9004 90036 90033 1.4945 90036 90033 1.3456 90036 90033 1.1106 90036 90033 90004 48 90005 90036 90033 90004 .8378 90005 90036 90031 90014 90033 90004 .7505 90005 90036 90033 90004 43 90005 90036 90033 .6820 90036 90033 .7314 90036 90033 .9325 90036 90033 1.4663 90036 90033 1.3673 90036 90033 1.0724 90036 90033 90004 47 90005 90036 90033 90004.8203 90005 90036 90031 90014 90033 90004 .7679 90005 90036 90033 90004 44 90005 90036 90033 .6947 90036 90033 .7193 90036 90033 .9657 90036 90033 1.4396 90036 90033 1.3902 90036 90033 1.0355 90036 90033 90004 46 90005 90036 90033 90004 .8029 90005 90036 90031 90014 90033 90004 .7854 90005 90036 90033 90004 45 90005 90036 90033.7071 90036 90033 .7071 90036 90033 1.0000 90036 90033 1.4142 90036 90033 1.4142 90036 90033 1.0000 90036 90033 90004 45 90005 90036 90033 90004 .7854 90005 90036 90031 90014 91413 91413 90015 Cos 90016 90015 Sin 90016 90015 Cot 90016 90015 Sec 90016 90015 Csc 90016 90015 Tan 90016 90015 Deg 90016 90015 Rad 90016 90031 91432 Those with a zero in the denominator are undefined.They are included solely to demonstrate the pattern. 90002 90012 .90000 Sine Calculator 90001 90002 What is sine function? Sine definition 90003 90004 Sine is one of the three most common trigonometric functions (others are cosine and tangent, as well as secant, cosecant and cotangent). The abbreviation of sine is 90005 sin 90006 e.g. 90005 sin (30 °) 90006. Most common and well known sine definition is based on right-angled triangle. Let’s start with nomenclature of triangle sides which will be useful in further steps. As the picture on the right shows, we can name the sides of a right triangle as: 90009 90010 90011 90012 90013 adjacent side 90014 — the shorter adjacent side of the angle of interest (in this case, angle α).This side is adjacent to both the angle of interest and the right angle. 90015 90012 90013 opposite side 90014 — merely the side opposite to the angle of interest. 90015 90012 90013 hypotenuse 90014 — the opposite side to the right angle, it’s always the longest side in the right triangle. 90015 90024 90004 So if our angle of interest change to β, then the adjacent and opposite side will be exchanged — but a hypotenuse stays the same. 90009 90027 90028 90012 90013 Right-angled triangle definition 90014 90015 90033 90004 90005 The sine of an angle is the length of the opposite side divided by the length of the hypotenuse 90006 90009 90004 with the assumption that the angle is acute (0 ° <α <90 ° or 0 <α <π / 2).90009 90004 The other sine definition is based on the unit circle. 90009 90042 90043 90012 90013 Unit circle 90014 90015 90033 90004 In this definition, α is any angle, and sine is a y-coordinate of the point of intersection between a unit circle and a line from the origin, making an angle of α. Sounds complicated, but if you look at the picture, everything should be clear. For a unit circle, the radius is - 90005 of course 90006 - equal to 1, so the sine is: 90009 90004 90054 sin (α) = y / 1 = y 90055 90009 90004 Look at the picture again - do you understand now where does the Pythagorean trigonometric identity come from? 90009 90004 Other important properties of a sine function: 90009 90011 90012 90013 Range of sine is -1 ≤ sin (α) ≤ 1 90014 90015 90012 Sine 90013 period is equal to 2π 90014 90015 90012 It's an 90013 odd function 90014, which means that sin (-α) = -sin (α) 90015 90012 90013 Roots 90014 of the sine function: 90013 kπ 90014 90015 90024.