Таблица синусов, таблица значений синусов, в помощь студентам таблица синусов.
Содержание:
Таблица синусов — это посчитанные значения синусов от 0° до 360°. Когда нет рядом калькулятора таблица синусов просто незаменима. Для того, чтобы узнать чему равен синус от нужного Вам угла достаточно найти его в таблице и все. Таблица синусов — это основно материал тригонометрии, который необходимо знать или, как минимум, понимать. Пользуйтесь на здоровье таблицей значений синусов. Если Вы изучаете тригонометрические функции Вам может понадобиться перечень тригонометрических формулы.
Таблица синусов 0° — 180°
|
|
|
|
Таблица синусов 180° — 360°
|
|
|
|
На нашем сайте представлено много теоретического материала по тригонометрии. Здесь Вы можете найти таблицы тригонометрических функций: таблицу синусов, таблицу косинусов, таблицу тангенсов и таблицу котангенсов. Также специально для улучшения понимания материала по тригонометрии мы добавили тригонометрические формулы, чтобы решение тригонометрических задач по математике вызывало меньше затруднений. Пользуйтесь нашим сайтом и таблицей синусов на здоровье.
Слишком сложно?
Таблица синусов, таблица значений синусов не по зубам? Тебе ответит эксперт через 10 минут!
Тригонометрическая таблица
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса . Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90,…,360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90,.. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
sin 00=0, cos 00 = 1. tg 00 = 0, котангенс от 00 будет неопределенным
sin 900 = 1, cos 900 =0, ctg900 = 0,тангенс от 900 будет неопределенным
Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 300 = 1/2, cos 300 = √3/2, tg 300 = √3/3, ctg 300 = √3
sin 450 = √2/2, cos 450 = √2/2, tg 450= 1, ctg 450 = 1
sin 600 = √3/2, cos 600 = 1/2, tg 600 =√3 , ctg 600 = √3/3
Изобразим все полученные значения в виде тригонометрической таблицы:
Таблица синусов, косинусов, тангенсов и котангенсов!
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов. Выглядеть она будет как:
Выглядеть она будет как:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 00+3600*z …. 3300+3600*z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 10200 = 3000+3600*2. Найдем по таблице.
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус
tg угла начиная с 00 заканчивая 760, ctg угла начиная с 140 заканчивая 900.
tg до 900 и ctg малых углов.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.
Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.

При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 200 = 0.9397
Значения tg угла до 900 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 780 37мин = 4,967
а ctg 200 13мин = 25,83
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Заметка: Стеновые отбойники — отбойная доска для защиты стен (http://www.spi-polymer.ru/otboyniki/)
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Таблица значений синусов, косинусов, тангенсов и котангенсов
В этих таблицах приведены значения синусов, косинусов, тангенсов и котангенсов, которые наиболее часто употребляются в математических задачах из программы
средней школы (для углов 0°, 30°, 45°, 60°, 90°, 120°, 135°, 150°, 180°). Для вычисления значений тригонометрических функций других углов можно воспользоваться онлайн-калькуляторами синусов и косинусов
и тангенсов и котангенсов. В этих калькуляторах можно указывать для расчета, в том числе, отрицательные углы (
Для вычисления значений тригонометрических функций других углов можно воспользоваться онлайн-калькуляторами синусов и косинусов
и тангенсов и котангенсов. В этих калькуляторах можно указывать для расчета, в том числе, отрицательные углы (
Таблица углов от 0 до 179 градусов
| Угол | Sin | Cos | Tg | Ctg |
|---|---|---|---|---|
| 0 | 0 | 1 | 0 | ∞ |
| 30 | 1/2 | √3/2 | 1/√3 | √3 |
| 45 | 1/√2 | 1/√2 | 1 | 1 |
| 60 | √3/2 | 1/2 | √3 | 1/√3 |
| 90 | 1 | 0 | ∞ | 0 |
| 120 | √3/2 | -1/2 | -√3 | -1/√3 |
| 135 | 1/√2 | -1/√2 | -1 | -1 |
| 150 | 1/2 | -√3/2 | -1/√3 | -√3 |
Таблица углов от 180 до 359 градусов
| Угол | Sin | Cos | Tg | Ctg |
|---|---|---|---|---|
| 180 | 0 | -1 | 0 | ∞ |
| 210 | -1/2 | -√3/2 | 1/√3 | √3 |
| 225 | -1/√2 | -1/√2 | 1 | 1 |
| 240 | -√3/2 | -1/2 | √3 | 1/√3 |
| 270 | -1 | 0 | ∞ | 0 |
| 300 | -√3/2 | 1/2 | -√3 | -1/√3 |
| 315 | -1/√2 | 1/√2 | -1 | -1 |
| 330 | -1/2 | √3/2 | -1/√3 | -√3 |
Поделитесь информацией с друзьями
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Тригонометрия
Таблица значений тригонометрических функций
часто используемых углов
| I четверть | |
| α (рад): 0, – 2π α (град): 0°, – 360° | |
| sin α | 0 |
| cos α | 1 |
| tg α | 0 |
| ctg α | не существует |
| α (рад): , α (град): 30°, – 330° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 45°, – 315° | |
| sin α | |
| cos α | |
| tg α | 1 |
| ctg α | 1 |
| α (рад): , α (град): 60°, – 300° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 90°, – 270° | |
| sin α | 1 |
| cos α | 0 |
| tg α | не существует |
| ctg α | 0 |
| II четверть | |
| α (рад): , α (град): 120°, – 240° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 135°, – 225° | |
| sin α | |
| cos α | |
| tg α | – 1 |
| ctg α | – 1 |
| α (рад): , α (град): 150°, – 210° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): π, – π α (град): 180°, – 180° | |
| sin α | 0 |
| cos α | – 1 |
| tg α | 0 |
| ctg α | не существует |
| III четверть | |
| α (рад): , α (град): 210°, – 150° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 225°, – 135° | |
| sin α | |
| cos α | |
| tg α | 1 |
| ctg α | 1 |
| α (рад): , α (град): 240°, –120° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 270°, – 90° | |
| sin α | – 1 |
| cos α | 0 |
| tg α | не существует |
| ctg α | 0 |
| IV четверть | |
| α (рад): , α (град): 300°, – 60° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): , α (град): 315°, – 45° | |
| sin α | |
| cos α | |
| tg α | – 1 |
| ctg α | – 1 |
| α (рад): , α (град): 330°, –30° | |
| sin α | |
| cos α | |
| tg α | |
| ctg α | |
| α (рад): 2π, 0 α (град): 360°, 0° | |
| sin α | 0 |
| cos α | 1 |
| tg α | 0 |
| ctg α | не существует |
Примеры вычисления значений тригонометрических функций
Пример 1.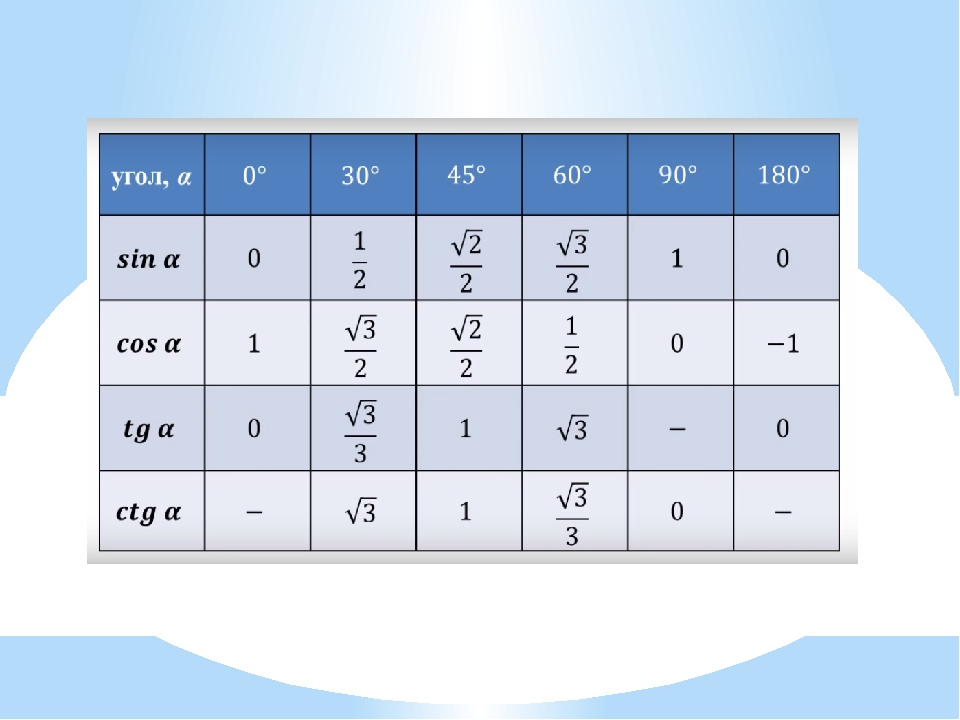 Найти sin 15°.
Найти sin 15°.
Решение. Воспользовавшись формулой «Синус разности», получаем:
Пример 2. Найти cos 22,5°.
Решение. Воспользовавшись формулой «Косинус двойного угла», получаем:
Пример 3. Найти sin 18°.
Решение. Поскольку
то, с помощью формул «Синус тройного угла» и «Косинус двойного угла», отсюда получаем:
Теперь, если ввести обозначение
sin 18° = t ,
то возникает кубическое уравнение
4t3 – 2t2 – 3t + 1 = 0 .
Решим это уравнение, раскладывая его левую часть на множители:
Поскольку
0 < sin 18° < 1 ,
то первый и второй корни должны быть отброшены. Следовательно,
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.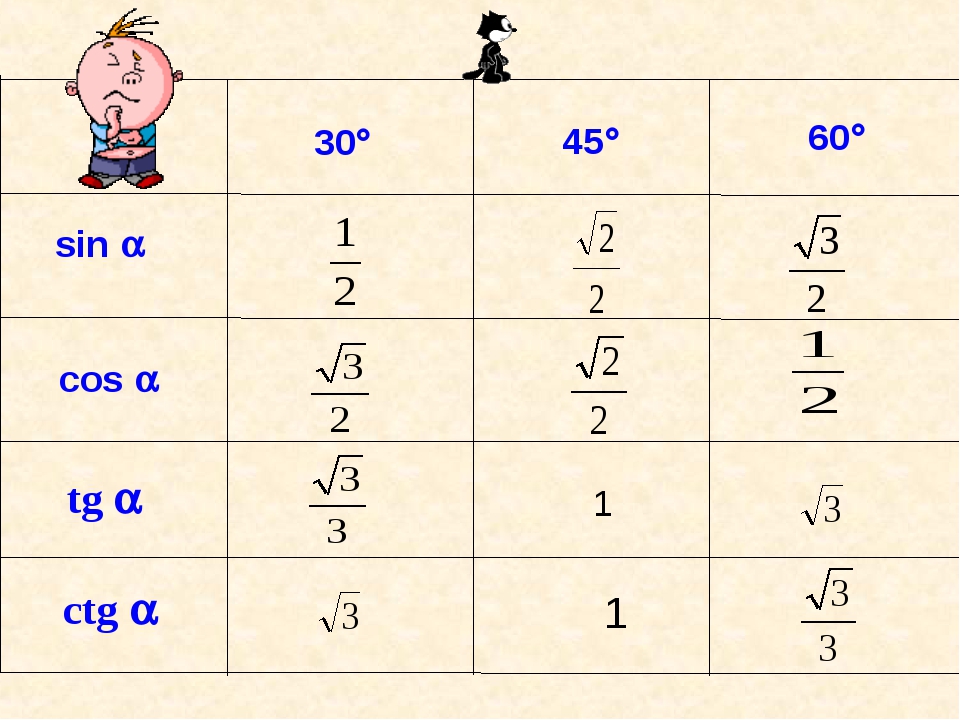
Таблица значений син кос
В этой статье собраны таблицы синусов, косинусов, тангенсов и котангенсов. Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360 градусов ( 0, π/6, π/4, π/3, π/2, …, 2π радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Навигация по странице.
Таблица синусов, косинусов, тангенсов и котангенсов для углов 0, 30, 45, 60, 90, … градусов
Тригонометрические определения синуса, косинуса, тангенса и котангенса позволяют указать значения тригонометрических функций для углов 0 и 90 градусов:
, а котангенс нуля градусов не определен, и
, а тангенс 90 градусов не определен.
В курсе геометрии из прямоугольных треугольников с углами 30 , 60 и 90 градусов, а также 45 , 45 и 90 градусов находятся значения синуса, косинуса, тангенса и котангенса углов 30, 45 и 60 градусов:
,
и
.
Занесем указанные значения тригонометрических функций для углов 0 , 30 , 45 , 60 и 90 градусов ( 0 , π/6 , π/4 , π/3 , π/2 радиан) в таблицу, назовем ее таблицей основных значений синуса, косинуса, тангенса и котангенса.
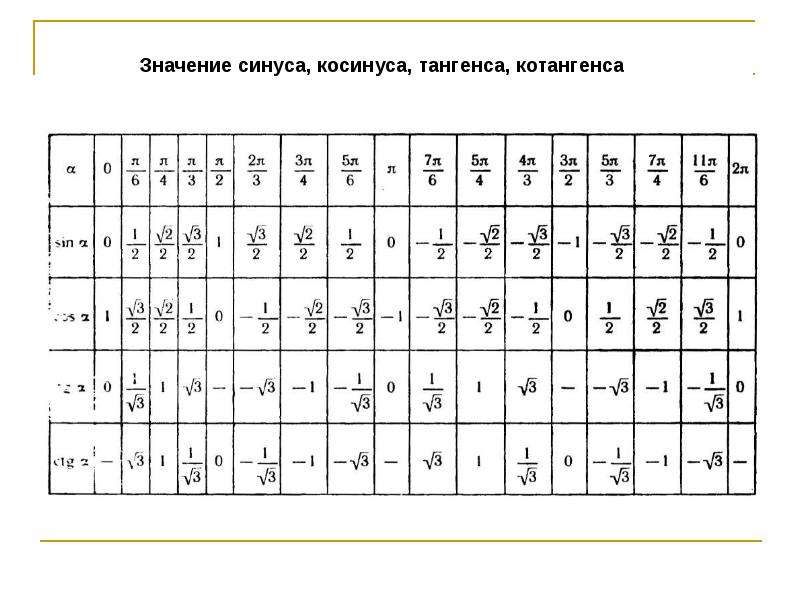
Используя формулы приведения, только что составленную таблицу синусов, косинусов, тангенсов и котангенсов можно расширить, дополнив значениями тригонометрических функций для углов 120 , 135 , 150 , 180 , 210 , 225 , 240 , 270 , 300 , 315 , 330 и 360 градусов ( 0, π/6, π/4, π/3, π/2, …, 2π радиан). При этом она принимает следующий вид.
Опираясь на свойство периодичности синуса, косинуса, тангенса и котангенса, таблицу основных значений тригонометрических функций можно расширить еще, заменив углы 0, 30, 45, 60, 90, …, 360 градусов соответственно на , где z – любое целое число. Из такой таблицы можно найти значения для всех углов, которым соответствуют точки единичной окружности, указанные на чертеже ниже.
Основные значения тригонометрических функций, собранные в заполненной выше таблице, желательно знать наизусть, так как они очень часто используются при решении задач.
Как пользоваться таблицей синусов, косинусов, тангенсов и котангенсов?
Использовать таблицу синусов, косинусов, тангенсов и котангенсов основных углов 0, 30, 45, 60, 90, …, 360 градусов очень просто – она дает непосредственные значения тригонометрических функций, находящиеся на пересечении соответствующей строки, указывающей название тригонометрической функции, и столбца, указывающего данное значение угла.
Например, значение косинуса угла 60 градусов находится на пересечении строки, в крайней левой ячейке которой находится запись cos , и столбца, в верхней ячейке которого записан угол 60 градусов. Так из таблицы находим, что значение косинуса 60 градусов равно одной второй. Для разъяснения приведем графическую иллюстрацию.
Расширенная таблица основных значений тригонометрических функций используется аналогично. С помощью расширенной таблицы основных значений синуса, косинуса, тангенса и котангенса можно сразу указать, например, чему равен тангенс угла 1 020 градусов. Он равен минус корню из трех, так как . Проиллюстрируем это.
Он равен минус корню из трех, так как . Проиллюстрируем это.
Таблицы синусов и косинусов, тангенсов и котангенсов Брадиса
Таблицы синусов, косинусов, тангенсов и котангенсов Брадиса разделены на таблицу синусов и косинусов, а также на таблицу тангенсов и котангенсов. Причем таблица тангенсов и котангенсов состоит из двух частей — тангенсы углов, близких к 90 градусов, и котангенсы малых углов вынесены в отдельную таблицу.
В таблицах Брадиса с точностью до четырех знаков после десятичной запятой приведены приближенные значения синусов и косинусов, а также четыре цифры приближенных значений тангенсов и котангенсов острых углов, содержащих целое число градусов и целое число минут.
Сначала дадим таблицу Брадиса, имеющую название таблица Брадиса: синусы и косинусы.
Теперь приведем таблицу тангенсов углов от 0 до 76 градусов и котангенсов углов от 14 до 90 градусов.
Наконец, осталось заполнить таблицу Брадиса тангенсов углов, близких к 90 градусам, и котангенсов малых углов. Она содержит непосредственные приближенные значения тангенсов углов от 76 до 90 градусов и котангенсов углов от 0 до 14 градусов.
Она содержит непосредственные приближенные значения тангенсов углов от 76 до 90 градусов и котангенсов углов от 0 до 14 градусов.
Как пользоваться таблицами синусов и косинусов, тангенсов и котангенсов Брадиса?
Осталось разобраться, как пользоваться таблицей синусов и косинусов, а также таблицами тангенсов и котангенсов Брадиса.
Значение синуса угла находится в таблице синусов на пересечении строки, содержащей в крайней левой ячейке нужное число градусов, и столбца, содержащего в верхней ячейке нужное число минут. Например, из таблицы синусов Брадиса можно определить, что синус 17 градусов 42 минут приближенно равен 0,3040 , вот иллюстрация тому, как это значение было найдено.
Несложно заметить, что в верхней строке минуты идут по порядку через шесть. А как определять значения, если количество минут имеет промежуточное значение, например 44 ? Для этого нужно внести соответствующую поправку, которую дают три крайних правых столбца таблицы. Например, синус 17 градусов 44 минут равен 0,3046 , так как синус 17 градусов 42 минут равен 0,3040 , и требуется еще поправка на 2 минуты в плюс, равна 0,0006 . Поправки содержатся в трех крайних правых столбцах таблицы синусов и косинусов Брадиса.
Поправки содержатся в трех крайних правых столбцах таблицы синусов и косинусов Брадиса.
Если бы нам нужно было найти синус 17 градусов 47 минут, то от значения синуса 17 градусов 48 минут 0,3057 мы бы отняли поправку на 1 минуту, равную 0,0003 . В итоге мы получим искомое значение, равное 0,3054 .
Для нахождения значений косинусов используется та же таблица синусов и косинусов Брадиса. Однако следует ориентироваться на нижнюю строку при выборе соответствующего значения градуса и на четвертую справа строку при выборе нужного числа минут.
Например, косинус 20 градусов равен 0,9397 .
Другой пример: значение косинуса 20 градусов 2 минут равно 0,9397−0,0002=0,9395 , а значение косинуса 20 градусов 5 минут равно 0,9391+0,0001=0,9392 (обратите внимание: что нужно быть внимательным со знаками поправок, нужно помнить, что при возрастании острого угла его косинус убывает).
Таблица тангенсов и котангенсов Брадиса углов от 0 до 76 градусов и котангенсов углов от 14 до 90 градусов используется абсолютно аналогично таблице синусов и косинусов.
К примеру, тангенс 75 градусов 44 минут равен 3,923+0,010=3,933 , а котангенс 32 градусов 50 минут равен 1,5517−0,0020=1,5497 . Вот тому графические иллюстрации.
Таблица тангенсов углов, близких к 90 градусов, и котангенсов малых углов содержит значения тангенсов и котангенсов, не нуждающиеся в поправках. Для примера найдем значение тангенса угла 78 градусов 37 минут, оно равно 4,967 .
А котангенс угла 2 градуса 13 минут равен 25,83 .
Если угол выходит за пределы от 0 до 90 градусов, то сначала следует использовать формулы приведения и перейти к вычислению значения тригонометрической функции, аргумент которой заключен между 0 и 90 градусами. А если угол выражен в радианах, то прежде чем использовать таблицы Брадиса для нахождения синуса, косинуса, тангенса или котангенса данного угла, его нужно перевести в градусы (этому вопросу посвящен материал статьи перевод градусов в радианы и обратно).
В статье, мы полностью разберемся, как выглядит таблица тригонометрических значений, синуса, косинуса, тангенса и котангенса .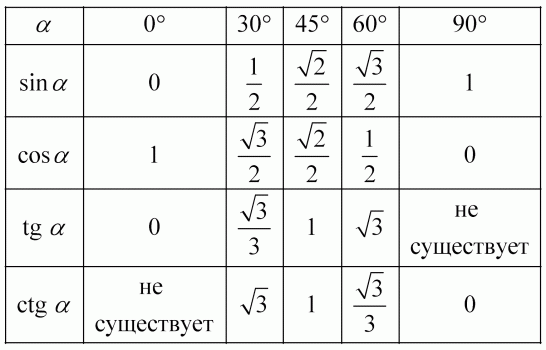 Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90. 360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Рассмотрим основное значение тригонометрических функций, от угла в 0,30,45,60,90. 360 градусов. И посмотрим как пользоваться данными таблицами в вычислении значения тригонометрических функций.
Первой рассмотрим таблицу косинуса, синуса, тангенса и котангенса от угла в 0, 30, 45, 60, 90. градусов. Определение данных величин дают определить значение функций углов в 0 и 90 градусов:
sin 0 0 =0, cos 0 0 = 1. tg 0 0 = 0, котангенс от 0 0 будет неопределенным
sin 90 0 = 1, cos 90 0 =0, ctg90 0 = 0,тангенс от 90 0 будет неопределенным
Если взять прямоугольные треугольники углы которых от 30 до 90 градусов. Получим:
sin 30 0 = 1/2, cos 30 0 = √3/2, tg 30 0 = √3/3, ctg 30 0 = √3
sin 45 0 = √2/2, cos 45 0 = √2/2, tg 45 0 = 1, ctg 45 0 = 1
sin 60 0 = √3/2, cos 60 0 = 1/2, tg 60 0 =√3 , ctg 60 0 = √3/3
Изобразим все полученные значения в виде тригонометрической таблицы:
Таблица синусов, косинусов, тангенсов и котангенсов!
Если использовать формулу приведения, наша таблица увеличится, добавятся значения для углов до 360 градусов.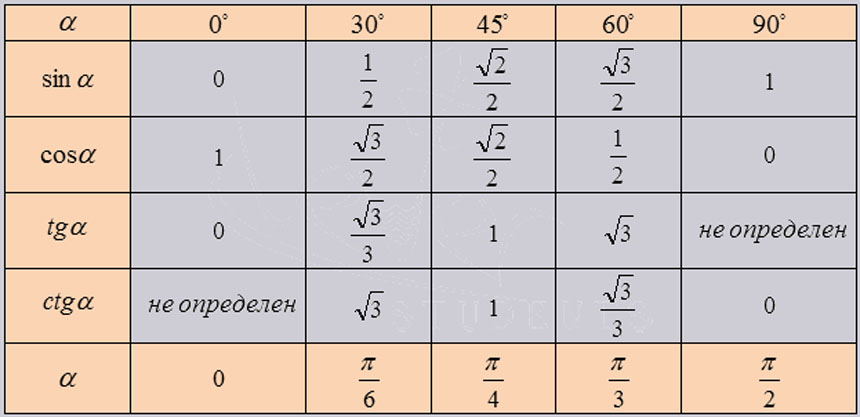 Выглядеть она будет как:
Выглядеть она будет как:
Так же исходя из свойств периодичности таблицу можно увеличить, если заменим углы на 0 0 +360 0 *z . 330 0 +360 0 *z, в котором z является целым числом. В данной таблице возможно вычислить значение всех углов, соответствующими точками в единой окружности.
Разберем наглядно как использовать таблицу в решении.
Все очень прост. Так как нужное нам значение лежит в точке пересечения нужных нам ячеек. К примеру возьмем cos угла 60 градусов, в таблице это будет выглядеть как:
В итоговой таблице основных значений тригонометрических функций, действуем так же. Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.
Для более поиска тригонометрических значений углов с точностью до минут используются таблицы Брадиса. Подробная инструкция как ими пользоваться на странице по ссылке.
Таблица Брадиса. Для синуса, косинуса, тангенса и котангенса.
Для синуса, косинуса, тангенса и котангенса.
Таблицы Брадиса поделены на несколько частей, состоят из таблиц косинуса и синуса, тангенса и котангенса — которая поделена на две части (tg угла до 90 градусов и ctg малых углов).
Синус и косинус
tg угла начиная с 0 0 заканчивая 76 0 , ctg угла начиная с 14 0 заканчивая 90 0 .
tg до 90 0 и ctg малых углов.
Разберемся как пользоваться таблицами Брадиса в решении задач.
Найдем обозначение sin (обозначение в столбце с левого края) 42 минут (обозначение находится на верхней строчке). Путем пересечения ищем обозначение, оно = 0,3040.
Величины минут указаны с промежутком в шесть минут, как быть если нужное нам значение попадет именно в этот промежуток. Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.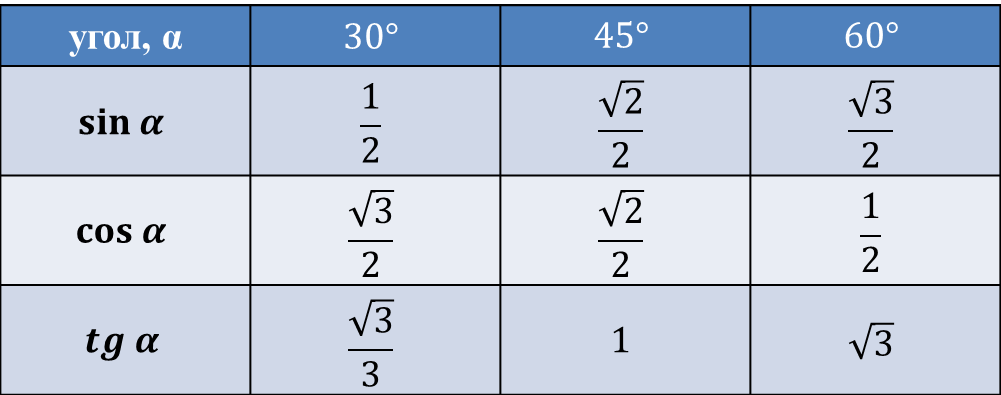
При sin 47 мин, берем за основу 48 мин и отнимаем от нее 1 поправку, т.е 0,3057 — 0,0003 = 0,3054
При вычислении cos работаем аналогично sin только за основу берем нижнюю строку таблицы. К примеру cos 20 0 = 0.9397
Значения tg угла до 90 0 и cot малого угла, верны и поправок в них нет. К примеру, найти tg 78 0 37мин = 4,967
а ctg 20 0 13мин = 25,83
Ну вот мы и рассмотрели основные тригонометрические таблицы. Надеемся это информация была для вас крайне полезной. Свои вопросы по таблицам, если они появились, обязательно пишите в комментариях!
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
Калькулятор поможет рассчитать точные значения тригонометрических функций sin, cos, tg и ctg для различных значений углов в градусах или радианах.
На данной странице таблица Брадиса, которая дает значение sin, cos, tg, ctg любого острого угла, содержащего целое число градусов и десятых долей градуса.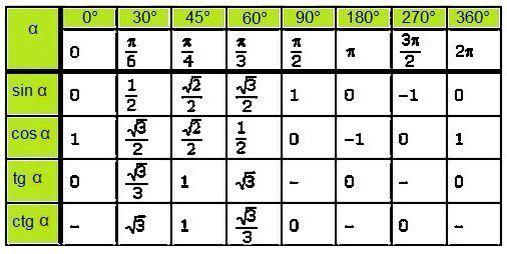 Для нахождения значения угла берется число на пересечении строки, которое соответствует числу градусов и столбца, которое соответствует числу минут. Например, sin 70°30′ = 0.9426.
Для нахождения значения угла берется число на пересечении строки, которое соответствует числу градусов и столбца, которое соответствует числу минут. Например, sin 70°30′ = 0.9426.
| Табличка на двери |
Построение графиков функций по заданным параметрам»
Цели урока:
- научить строить графики элементарных математических функций с помощью табличного процессора Excel;
- показать возможности использования программы Excel для решения задач по математике;
- закрепить навыки работы с Мастером диаграмм.

Задачи урока:
- образовательная – знакомство учащихся с основными приемами построения графиков функций в программе Excel;
- развивающие – формирование у учащихся логического и алгоритмического мышления; развитие познавательного интереса к предмету; развитие умения оперировать ранее полученными знаниями; развитие умения планировать свою деятельность;
- воспитательные – воспитание умения самостоятельно мыслить, ответственности за выполняемую работу, аккуратности при выполнении работы.
Тип урока:
- комбинированный
Учебники:
Информатика. Базовый курс 2-е издание/Под ред. С.В. Симоновича. — СПб.: Питер, 2004.-640с.:ил.
Технические и программные средства:
- Персональные компьютеры;
- Приложение Windows – электронные таблицы Excel.

- Проектор
Раздаточный материал:
- Карточки с индивидуальными заданиями на построение графиков функций.
План урока.
- Организационный момент – 3 мин.
- Проверка домашнего задания –10 мин.
- Объяснение нового материала –20 мин.
- Применение полученных знаний –20 мин.
- Самостоятельная работа. – 20 мин
- Подведение итогов урока. Домашнее задание – 7 мин.
Ход урока
Организационный момент
Проверка готовности учащихся к уроку, отметка отсутствующих, объявление темы и цели урока
Проверка домашнего задания. (фронтальный опрос)
Вопросы для проверки
- Что представляет собой рабочая область программы Excel?
- Как определяется адрес ячейки?
- Как изменить ширину столбца, высоту строки?
- Как ввести формулу в Excel?
- Что такое маркер заполнения и для чего он нужен?
- Что такое относительная адресация ячеек?
- Что такое абсолютная адресация ячеек? Как она задается?
- Что такое колонтитулы? Как они задаются?
- Как задать поля печатного документа? Как изменить ориентацию бумаги?
- Что такое функциональная зависимость у = f(х)? Какая переменная является зависимой, а какая независимой?
- Как ввести функцию в Excel?
- Что такое график функции у = f(х)?
- Как построить диаграмму в Excel?
Объяснение нового материала.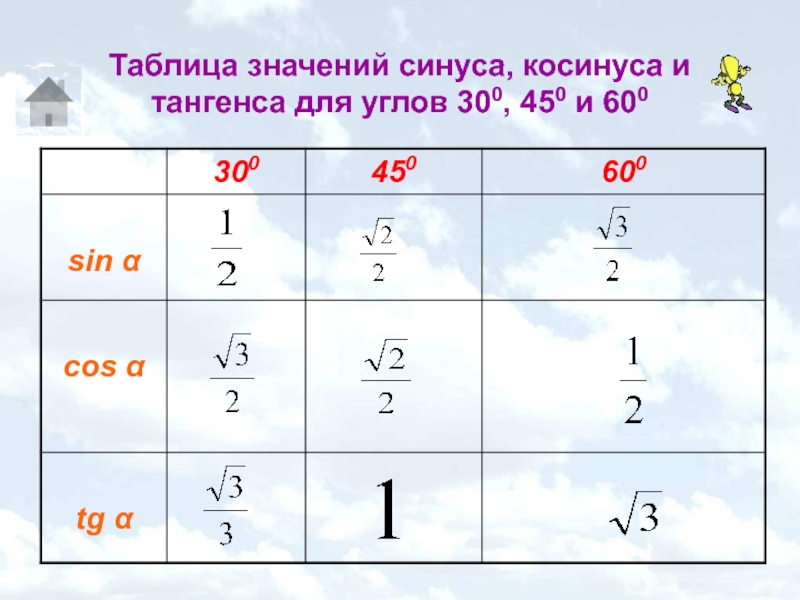
При объяснении нового материала может быть использован файл Excel с шаблонами задач (Приложение 1), который выводится на экран с помощью проектора
Сегодня мы рассмотрим применение табличного процессора Excel для графиков функций. На предыдущих практических вы уже строили диаграммы к различным задачам, используя Мастер диаграмм. Графики функций, так же как и диаграммы строятся с помощью Мастера диаграмм программы Excel.
Рассмотрим построение графиков функций на примере функции у = sin x.
Вид данного графика хорошо известен вам по урокам математики, попробуем построить его средствами Excel.
Программа будет строить график по точкам: точки с известными значениями будут плавно соединяться линией. Эти точки нужно указать программе, поэтому, сначала создается таблица значений функции у = f(х).
Чтобы создать таблицу, нужно определить
- отрезок оси ОХ, на котором будет строиться
график.

- шаг переменной х, т.е. через какой промежуток будут вычисляться значения функции.
Задача 1.Построить график функции у = sin x на отрезке [– 2; 2] с шагом h = 0,5.
1. Заполним таблицу значений функции. В ячейку С4 введем первое значение отрезка: – 2
2. В ячейку D4 введем формулу, которая будет добавлять к лево-стоящей ячейки шаг: = В4 + $A$4
3. Маркером заполнения ячейки D4 заполним влево ячейки строки 4, до тех пор, пока получим значение другого конца отрезка: 2.
4. Выделим ячейку С5, вызовем Мастер функций, в категории математические выберем функцию SIN, в качестве аргумента функции выберем ячейку С4.
5. Маркером заполнения распространим эту формулу в ячейках строки 5 до конца таблицы.
Таким образом, мы получили таблицу аргументов (х) и значений (у) функции у = sin x на отрезке [-2;2] с шагом h = 0,5 :
| x | -2 | -1,75 | -1,5 | -1,25 | -1 | -0,75 | -0,5 | -0,25 | 0 | 0,25 | 0,5 | 0,75 | 1 | 1,25 | 1,5 | 1,75 | 2 |
| y | -0,9092 | -0,9839 | -0,9974 | -0,9489 | -0,8414 | -0,6816 | -0,4794 | -0,2474 | 0 | 0,2474 | 0,4794 | 0,6816 | 0,8414 | 0,9489 | 0,9974 | 0,9839 | 0,9092 |
6.
Следующий шаг. Выделим таблицу и вызовем Мастер диаграмм. На первом шаге выберем во вкладке Нестандартные Гладкие графики.
7. На втором шаге во вкладке Ряд выполним:
В поле Ряд необходимо выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
В поле Подписи оси Х нажать на кнопку. Выделить в таблице ячейки со значениями х и нажмите на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.
8. На третьем шаге заполним вкладку Заголовки.
9. Пример полученного графика.
На самом деле пока это мало похоже на график функции в нашем привычном понимании.
Для форматирования графика:
- Вызовем контекстное меню оси ОУ. Затем, выберем
пункт Формат оси….
 Во вкладке Шкала установим:
цена основного деления: 1. Во вкладке Шрифт
установим размер шрифта 8пт.
Во вкладке Шкала установим:
цена основного деления: 1. Во вкладке Шрифт
установим размер шрифта 8пт. - Вызовем контекстное меню оси ОХ. Выберем пункт Формат оси….
Во вкладке Шкала установим: пересечение с осью ОУ установите номер категории 5 (чтобы ось ОУ пересекала ось ОХ в категории с подписью 0, а это пятая по счету категория).
Во вкладке шрифт установите размер шрифта 8пт. Нажмите на кнопку ОК.
Остальные изменения выполняются аналогично.
Для закрепления рассмотрим еще одну задачу на построение графика функций. Эту задачу попробуйте решить самостоятельно, сверяясь с экраном проектора.
Применение полученных знаний.
Пригласить к проектору студента и сформулировать следующую задачу.
Задача 2. Построить график функции у = х3 на отрезке [– 3; 3] с шагом h = 0,5.
1. Создать следующую таблицу: Создать таблица значений функции у = f(х).
3
6. Маркером заполнения скопировать формулу в ячейки строки 5 до конца таблицы.
Таким образом, должна получиться таблица аргументов (х) и значений (у) функции у = х3 на отрезке [–3;3] с шагом h = 0,5:
| х | -3 | -2,5 | -2 | -1,5 | -1 | -0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
| y | -27 | -15,625 | -8 | -3,375 | -1 | -0,125 | 0 | 0,125 | 1 | 3,375 | 8 | 15,625 | 27 |
7.
Выделить таблицу и вызвать мастер диаграмм. На первом шаге выбрать во второй вкладке Гладкие графики.
8. На втором шаге во вкладке Ряд выполнить:
- В поле Ряд выделить ряд х и нажать на кнопку “Удалить” (график изменений х нам не нужен. График функции – это график изменения значений у)
- В поле Подписи оси Х нажать на кнопку . Выделить в таблице ячейки со значениями х и нажать на кнопку . Подписи по горизонтальной оси станут такими, как у нас в таблице.
9. На третьем шаге заполнить вкладку Заголовки.
10. Пример полученного графика:
11. Оформить график.
12. Установить параметры страницы и размеры диаграмм таким образом, что бы все поместилось на одном листе альбомной ориентации.
13. Создать колонтитулы для данного листа (Вид Колонтитулы…):
14.Верхний колонтитул слева: график функции у = x3
Сохранить документ своей папке под именем График.
Самостоятельная работа.
Работа по карточкам с индивидуальными заданиями. (Приложение 2)
Пример карточки, с задачей в общем виде, выводится на экран с помощью проектора.
1. Построить график функции y=f(x) на отрезке [a;b] с шагом h=c
2. Установить параметры страницы и размеры графика таким образом, что бы все поместилось на одном листе альбомной ориентации.
3. Создать колонтитулы для данного листа (Вид Колонтитулы…):
- Верхний колонтитул слева: график функции y=f(x)
- Нижний колонтитул в центре: ваши Ф.И.О. и дата
4. Сохранить в своей папке под именем “Зачетный график”
5. Вывести документ на печать.
После выполнения задания правильность каждого
варианта проверяется с помощью проектора.
Подведение итогов.
Домашнее задание.
Оценки за урок.
2 = 1 $.В) Тогда для конкретных углов есть значения. Это в основном геометрия, и есть три случая:
1) $ \ theta $ ~ $ 0 $ или 90 $. Это $ \ theta = 0, \ pi / 2, \ pi, 3 \ pi / 4 $ (или $ — \ pi / 4 $).
Это точки $ (x, y) = (\ cos \ theta, \ sin \ theta) $ = $ (0, \ pm 1) $ и $ \ tan \ theta = (0, \ pm 1) $ и $ x / y $ = $ 0 $, $ \ pm 1/0 $ (не определено).
Это то, что визуально видно при представлении круга.
2) $ \ theta $ ~ 45. Это $ \ theta = \ text {odd} * \ pi / 4 $ (или другой способ просмотра $ \ {0, \ pi, \ pm \ pi / 2 \ } \ pm \ pi / 4 $; или просто $ \ pi / 4, 3 \ pi / 4, 5 \ pi / 4 = -3 \ pi / 4, 7 \ pi / 4 = — \ pi / 4 $).2 = 1 $, значит, $ | x | = | y | = \ sqrt {2} / 2 $. И $ | x | / | y | = 1 $.
Итак, $ \ sin \ theta = \ pm \ cos \ theta = \ pm \ sqrt {2} / 2 $. и $ \ tan \ theta = \ pm 1 $.
Какая положительная / отрицательная полярность зависит от того, в каком квадранте $ (x, y) = (\ cos \ theta, \ sin \ theta) $ находится.
3) $ \ theta $ ~ 30, 60 $. Это $ \ {0, \ pi, \ pm \ pi / 2 \} \ pm \ pi / 6 $. Или $ 0, \ pi / 6, \ pi / 3, 2 \ pi / 3, 5 \ pi / 6, 7 \ pi / 6, 4 \ pi / 3, 5 \ pi / 3, 11 \ pi / 6 $.
Это для треугольников 30-60-90 градусов, которые представляют собой равносторонние треугольники, разрезанные пополам.2 $ и поскольку $ c = 1 $, то $ a = 1/2 $ и $ b = \ sqrt {3} 2 $.
Итак, это $ (x, y) = (\ cos \ theta, \ sin \ theta) = (\ {\ pm 1/2: \ pm \ sqrt {3} / 2 \}, \ {\ pm \ sqrt {3} / 2: \ pm 1/2) $ и $ \ tan \ theta = \ {\ pm 1 / \ sqrt 3: \ pm \ sqrt 3 \} $
Какие значения зависят от того, соответствует ли $ | x | > | y | $ или $ | y | > | x | $ и в каком квадранте $ (x, y) лежит.
======
И да, эта круглая картинка помогает. Поскольку круговая картинка идеально симметрична, ее легко запомнить, хотя технически она имеет 48 значений. Поскольку он симметричен, на самом деле он сводится только к трем вышеупомянутым случаям.
Поскольку он симметричен, на самом деле он сводится только к трем вышеупомянутым случаям.
sin cos tan таблица
Таблицы Брадиса sin, cos, tg, ctg.
Таблицаsin cos tan (тригонометрические значения) содержит рассчитанные значения тригонометрических функций для определенного угла от 0 до 360 градусов в виде простой таблицы и в виде таблицы Брадиса. Также приведены значения тригонометрических функций в радианах для наиболее распространенных углов, используемых в расчетах.
Таблицы с расчетными значениями sin, cos, tg, ctg используются для упрощения и ускорения математических вычислений, когда нет возможности использовать калькулятор или компьютер.
- грех
- cos
- тг
- кт
- триг. значения
- Брэдис грех и соз
- Bradys tg и ctg
грех 0 ° = грех 360 ° = 0
| α ° | sin α | α ° | sin α | α ° | sin α | α ° | sin α |
|---|---|---|---|---|---|---|---|
| α ° | sin α | α ° | sin α | α ° | sin α | α ° | sin α |
|---|---|---|---|---|---|---|---|
cos 0 ° = cos 360 ° = 1
| α ° | cos α | α ° | cos α | α ° | cos α | α ° | cos α |
|---|---|---|---|---|---|---|---|
| α ° | cos α | α ° | cos α | α ° | cos α | α ° | cos α |
|---|---|---|---|---|---|---|---|
tg 0 ° = tg 360 ° = 0
| α ° | тг α | α ° | тг α | α ° | тг α | α ° | тг α |
|---|---|---|---|---|---|---|---|
| α ° | тг α | α ° | тг α | α ° | тг α | α ° | тг α |
|---|---|---|---|---|---|---|---|
ctg 0 ° = ctg 360 ° = ∞
| α ° | CTG α | α ° | CTG α | α ° | CTG α | α ° | CTG α |
|---|---|---|---|---|---|---|---|
| α ° | CTG α | α ° | CTG α | α ° | CTG α | α ° | CTG α |
|---|---|---|---|---|---|---|---|
Значения тригонометрических функций в радианах для наиболее распространенных углов.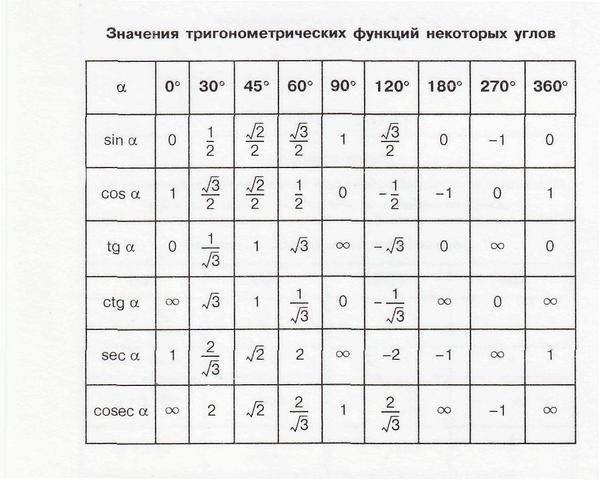
Таблица Брэдиса для синусов и косинусов
| грех | 0 ‘ | 6 ‘ | 12 ‘ | 18 ‘ | 24 ‘ | 30 ‘ | 36 ‘ | 42 ‘ | 48 ‘ | 54 ‘ | 60 ‘ | cos | 1 ‘ | 2 ‘ | 3 ‘ |
| 0.0000 | 90 ° | ||||||||||||||
| 0 ° | 0,0000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89 ° | 3 | 6 | 9 |
| 1 ° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88 ° | 3 | 6 | 9 |
| 2 ° | 0349 | 0366 | 0384 | 0401 | 0419 | 0436 | 0454 | 0471 | 0488 | 0506 | 0523 | 87 ° | 3 | 6 | 9 |
| 3 ° | 0523 | 0541 | 0558 | 0576 | 0593 | 0610 | 0628 | 0645 | 0663 | 0680 | 0698 | 86 ° | 3 | 6 | 9 |
| 4 ° | 0698 | 0715 | 0732 | 0750 | 0767 | 0785 | 0802 | 0819 | 0837 | 0854 | 0. 0872 0872 | 85 ° | 3 | 6 | 9 |
| 5 ° | 0,0872 | 0889 | 0906 | 0924 | 0941 | 0958 | 0976 | 0993 | 1011 | 1028 | 1045 | 84 ° | 3 | 6 | 9 |
| 6 ° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 83 ° | 3 | 6 | 9 |
| 7 ° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 82 ° | 3 | 6 | 9 |
| 8 ° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 81 ° | 3 | 6 | 9 |
| 9 ° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0.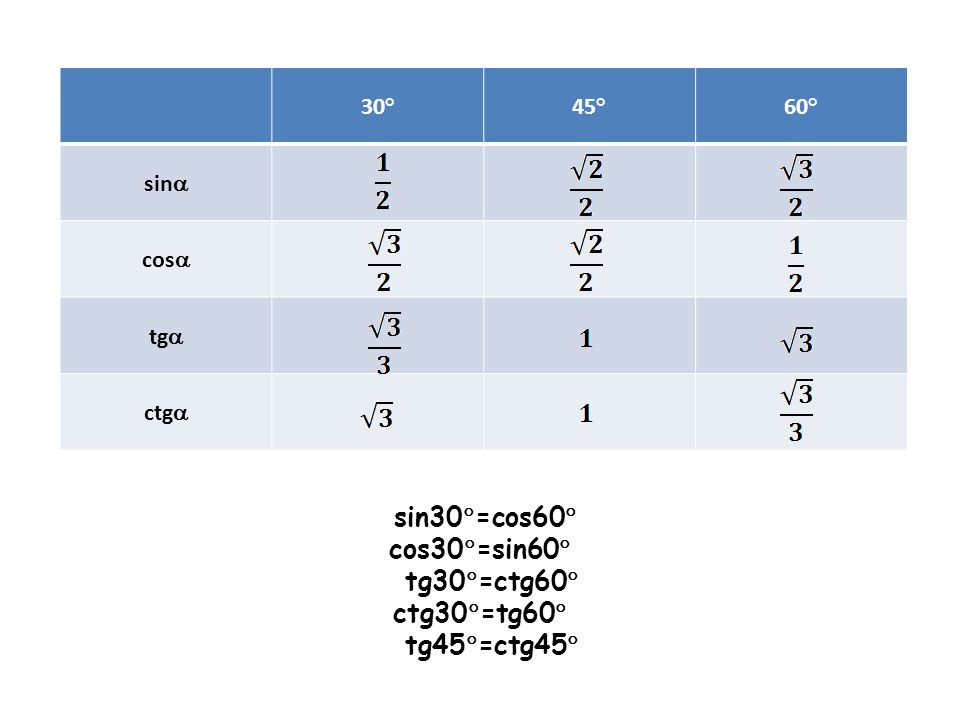 1736 1736 | 80 ° | 3 | 6 | 9 |
| 10 ° | 0,1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 79 ° | 3 | 6 | 9 |
| 11 ° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 78 ° | 3 | 6 | 9 |
| 12 ° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 77 ° | 3 | 6 | 9 |
| 13 ° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 76 ° | 3 | 6 | 8 |
| 14 ° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0.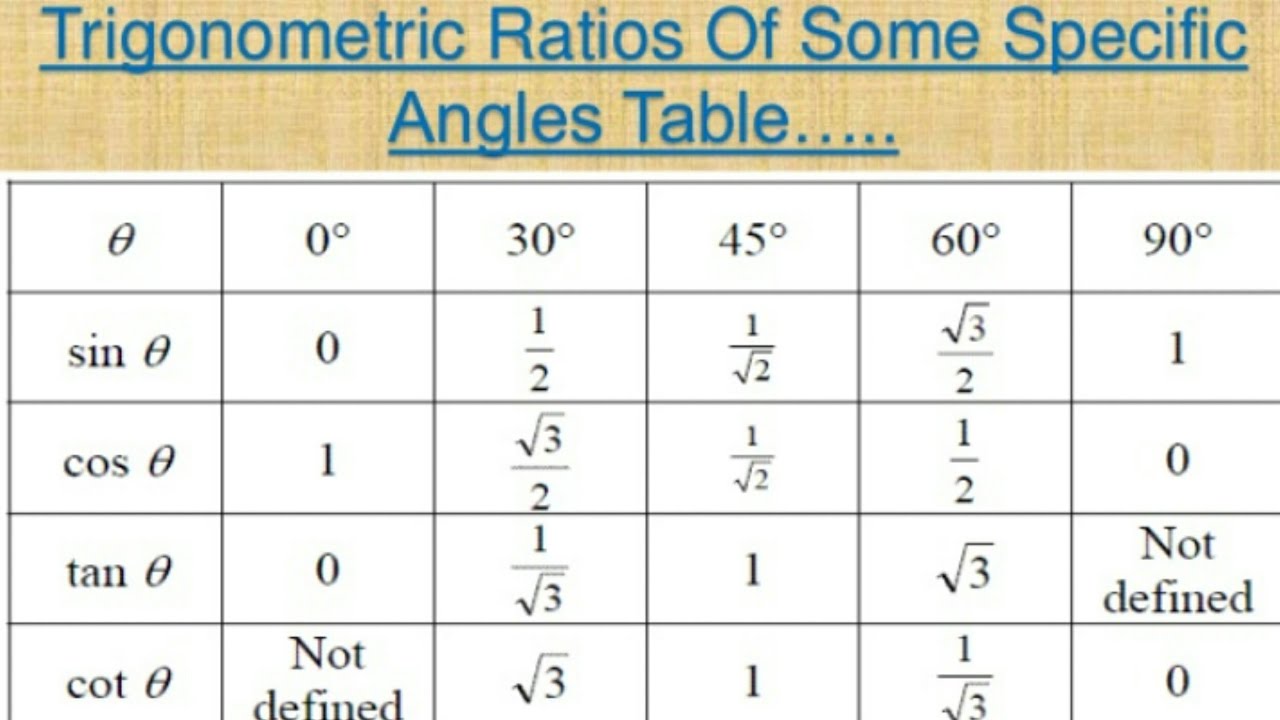 2588 2588 | 75 ° | 3 | 6 | 8 |
| 15 ° | 0,2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 74 ° | 3 | 6 | 8 |
| 16 ° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 73 ° | 3 | 6 | 8 |
| 17 ° | 2924 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 72 ° | 3 | 6 | 8 |
| 18 ° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 71 ° | 3 | 6 | 8 |
| 19 ° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0. 3420 3420 | 70 ° | 3 | 5 | 8 |
| 20 ° | 0,3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 69 ° | 3 | 5 | 8 |
| 21 ° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 68 ° | 3 | 5 | 8 |
| 22 ° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 67 ° | 3 | 5 | 8 |
| 23 ° | 3907 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 66 ° | 3 | 5 | 8 |
| 24 ° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0. 4226 4226 | 65 ° | 3 | 5 | 8 |
| 25 ° | 0,4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 64 ° | 3 | 5 | 8 |
| 26 ° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 63 ° | 3 | 5 | 8 |
| 27 ° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 62 ° | 3 | 5 | 8 |
| 28 ° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 61 ° | 3 | 5 | 8 |
| 29 ° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0. 5000 5000 | 60 ° | 3 | 5 | 8 |
| 30 ° | 0,5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 59 ° | 3 | 5 | 8 |
| 31 ° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 58 ° | 2 | 5 | 7 |
| 32 ° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 57 ° | 2 | 5 | 7 |
| 33 ° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 56 ° | 2 | 5 | 7 |
| 34 ° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0. 5736 5736 | 55 ° | 2 | 5 | 7 |
| 35 ° | 0,5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0,5878 | 54 ° | 2 | 5 | 7 |
| 36 ° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 53 ° | 2 | 5 | 7 |
| 37 ° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 52 ° | 2 | 5 | 7 |
| 38 ° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 51 ° | 2 | 5 | 7 |
| 39 ° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0.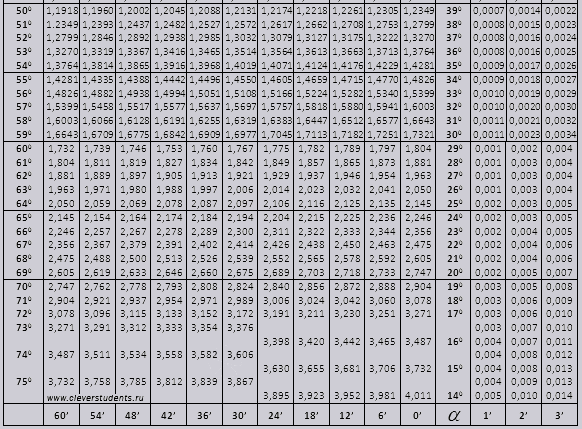 6428 6428 | 50 ° | 2 | 4 | 7 |
| 40 ° | 0,6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 49 ° | 2 | 4 | 7 |
| 41 ° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 48 ° | 2 | 4 | 7 |
| 42 ° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 47 ° | 2 | 4 | 6 |
| 43 ° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 46 ° | 2 | 4 | 6 |
| 44 ° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0. 7071 7071 | 45 ° | 2 | 4 | 6 |
| 45 ° | 0,7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 44 ° | 2 | 4 | 6 |
| 46 ° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 43 ° | 2 | 4 | 6 |
| 47 ° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 42 ° | 2 | 4 | 6 |
| 48 ° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 41 ° | 2 | 4 | 6 |
| 49 ° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0. 7660 7660 | 40 ° | 2 | 4 | 6 |
| 50 ° | 0,7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 39 ° | 2 | 4 | 6 |
| 51 ° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 38 ° | 2 | 4 | 5 |
| 52 ° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 37 ° | 2 | 4 | 5 |
| 53 ° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 36 ° | 2 | 3 | 5 |
| 54 ° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0. 8192 8192 | 35 ° | 2 | 3 | 5 |
| 55 ° | 0,8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 34 ° | 2 | 3 | 5 |
| 56 ° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 33 ° | 2 | 3 | 5 |
| 57 ° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 32 ° | 2 | 3 | 5 |
| 58 ° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 31 ° | 2 | 3 | 5 |
| 59 ° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0. 8660 8660 | 30 ° | 1 | 3 | 4 |
| 60 ° | 0,8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 29 ° | 1 | 3 | 4 |
| 61 ° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 28 ° | 1 | 3 | 4 |
| 62 ° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 27 ° | 1 | 3 | 4 |
| 63 ° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 26 ° | 1 | 3 | 4 |
| 64 ° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0.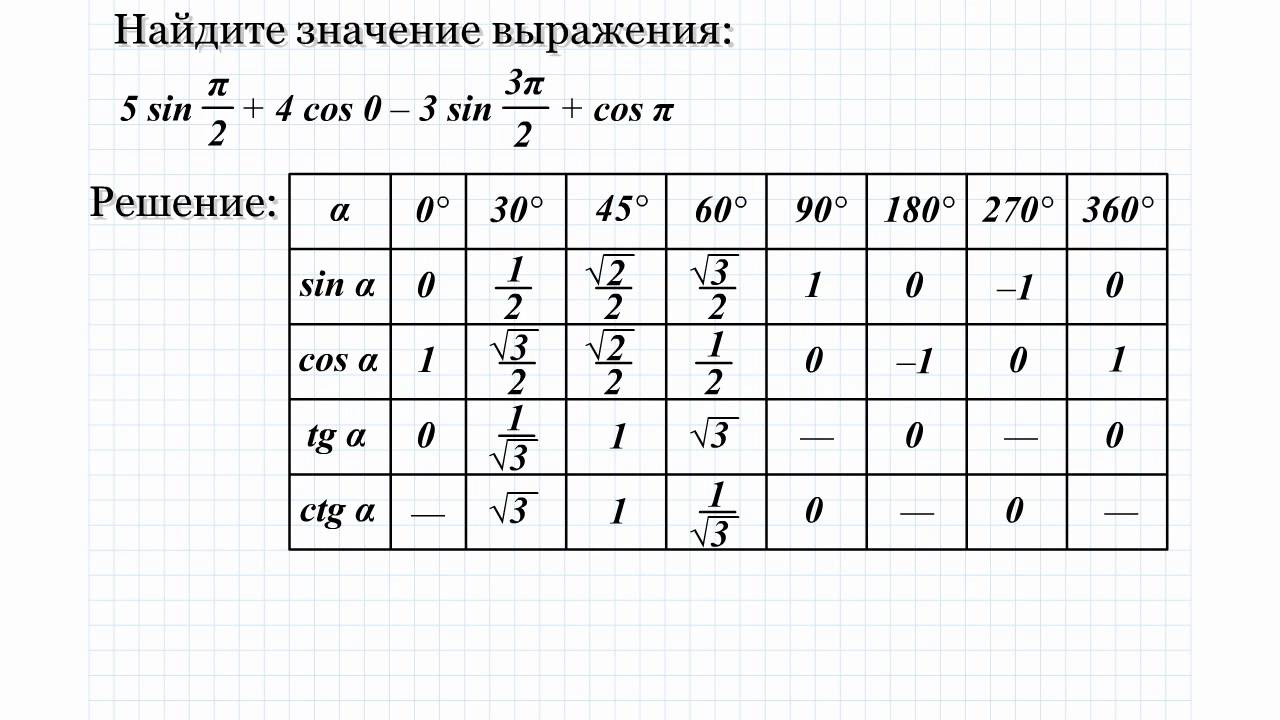 9063 9063 | 25 ° | 1 | 3 | 4 |
| 65 ° | 0,9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 24 ° | 1 | 2 | 4 |
| 66 ° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 23 ° | 1 | 2 | 3 |
| 67 ° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 22 ° | 1 | 2 | 3 |
| 68 ° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 21 ° | 1 | 2 | 3 |
| 69 ° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0.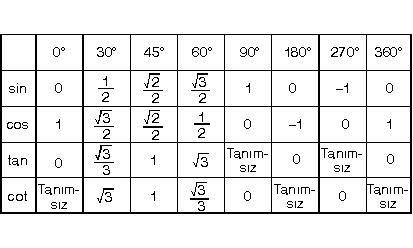 9397 9397 | 20 ° | 1 | 2 | 3 |
| 70 ° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0,9455 | 19 ° | 1 | 2 | 3 |
| 71 ° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 18 ° | 1 | 2 | 3 |
| 72 ° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 17 ° | 1 | 2 | 3 |
| 73 ° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 16 ° | 1 | 2 | 2 |
| 74 ° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0. 9659 9659 | 15 ° | 1 | 2 | 2 |
| 75 ° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 14 ° | 1 | 1 | 2 |
| 76 ° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 13 ° | 1 | 1 | 2 |
| 77 ° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 12 ° | 1 | 1 | 2 |
| 78 ° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 11 ° | 1 | 1 | 2 |
| 79 ° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0.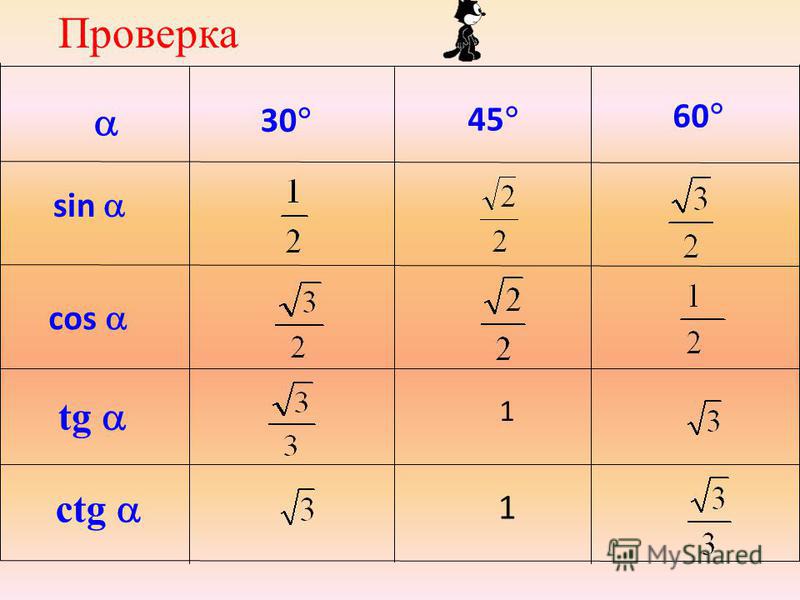 9848 9848 | 10 ° | 1 | 1 | 2 |
| 80 ° | 0,9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 9 ° | 0 | 1 | 1 |
| 81 ° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 8 ° | 0 | 1 | 1 |
| 82 ° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 7 ° | 0 | 1 | 1 |
| 83 ° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 6 ° | 0 | 1 | 1 |
| 84 ° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 5 ° | 0 | 1 | 1 |
| 85 ° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 4 ° | 0 | 0 | 1 |
| 86 ° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 3 ° | 0 | 0 | 0 |
| 87 ° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 2 ° | 0 | 0 | 0 |
| 88 ° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0. 9998 9998 | 1 ° | 0 | 0 | 0 |
| 89 ° | 9998 | 9999 | 9999 | 9999 | 9999 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0 ° | 0 | 0 | 0 |
| 90 ° | 1.0000 | ||||||||||||||
| грех | 60 ‘ | 54 ‘ | 48 ‘ | 42 ‘ | 36 ‘ | 30 ‘ | 24 ‘ | 18 ‘ | 12 ‘ | 6 ‘ | 0 ‘ | cos | 1 ‘ | 2 ‘ | 3 ‘ |
Таблица Брэдиса для касательных и котангенсов
| тг | 0 ‘ | 6 ‘ | 12 ‘ | 18 ‘ | 24 ‘ | 30 ‘ | 36 ‘ | 42 ‘ | 48 ‘ | 54 ‘ | 60 ‘ | CTG | 1 ‘ | 2 ‘ | 3 ‘ |
| 0 | 90 ° | ||||||||||||||
| 0 ° | 0,000 | 0017 | 0035 | 0052 | 0070 | 0087 | 0105 | 0122 | 0140 | 0157 | 0175 | 89 ° | 3 | 6 | 9 |
| 1 ° | 0175 | 0192 | 0209 | 0227 | 0244 | 0262 | 0279 | 0297 | 0314 | 0332 | 0349 | 88 ° | 3 | 6 | 9 |
| 2 ° | 0349 | 0367 | 0384 | 0402 | 0419 | 0437 | 0454 | 0472 | 0489 | 0507 | 0524 | 87 ° | 3 | 6 | 9 |
| 3 ° | 0524 | 0542 | 0559 | 0577 | 0594 | 0612 | 0629 | 0647 | 0664 | 0682 | 0699 | 86 ° | 3 | 6 | 9 |
| 4 ° | 0699 | 0717 | 0734 | 0752 | 0769 | 0787 | 0805 | 0822 | 0840 | 0857 | 0,0875 | 85 ° | 3 | 6 | 9 |
| 5 ° | 0,0875 | 0892 | 0910 | 0928 | 0945 | 0963 | 0981 | 0998 | 1016 | 1033 | 1051 | 84 ° | 3 | 6 | 9 |
| 6 ° | 1051 | 1069 | 1086 | 1104 | 1122 | 1139 | 1157 | 1175 | 1192 | 1210 | 1228 | 83 ° | 3 | 6 | 9 |
| 7 ° | 1228 | 1246 | 1263 | 1281 | 1299 | 1317 | 1334 | 1352 | 1370 | 1388 | 1405 | 82 ° | 3 | 6 | 9 |
| 8 ° | 1405 | 1423 | 1441 | 1459 | 1477 | 1495 | 1512 | 1530 | 1548 | 1566 | 1584 | 81 ° | 3 | 6 | 9 |
| 9 ° | 1584 | 1602 | 1620 | 1638 | 1655 | 1673 | 1691 | 1709 | 1727 | 1745 | 0,1763 | 80 ° | 3 | 6 | 9 |
| 10 ° | 0,1763 | 1781 | 1799 | 1817 | 1835 | 1853 | 1871 | 1890 | 1908 | 1926 | 1944 | 79 ° | 3 | 6 | 9 |
| 11 ° | 1944 | 1962 | 1980 | 1998 | 2016 | 2035 | 2053 | 2071 | 2089 | 2107 | 2126 | 78 ° | 3 | 6 | 9 |
| 12 ° | 2126 | 2144 | 2162 | 2180 | 2199 | 2217 | 2235 | 2254 | 2272 | 2290 | 2309 | 77 ° | 3 | 6 | 9 |
| 13 ° | 2309 | 2327 | 2345 | 2364 | 2382 | 2401 | 2419 | 2438 | 2456 | 2475 | 2493 | 76 ° | 3 | 6 | 9 |
| 14 ° | 2493 | 2512 | 2530 | 2549 | 2568 | 2586 | 2605 | 2623 | 2642 | 2661 | 0,2679 | 75 ° | 3 | 6 | 9 |
| 15 ° | 0,2679 | 2698 | 2717 | 2736 | 2754 | 2773 | 2792 | 2811 | 2830 | 2849 | 2867 | 74 ° | 3 | 6 | 9 |
| 16 ° | 2867 | 2886 | 2905 | 2924 | 2943 | 2962 | 2981 | 3000 | 3019 | 3038 | 3057 | 73 ° | 3 | 6 | 9 |
| 17 ° | 3057 | 3076 | 3096 | 3115 | 3134 | 3153 | 3172 | 3191 | 3211 | 3230 | 3249 | 72 ° | 3 | 6 | 10 |
| 18 ° | 3249 | 3269 | 3288 | 3307 | 3327 | 3346 | 3365 | 3385 | 3404 | 3424 | 3443 | 71 ° | 3 | 6 | 10 |
| 19 ° | 3443 | 3463 | 3482 | 3502 | 3522 | 3541 | 3561 | 3581 | 3600 | 3620 | 0,3640 | 70 ° | 3 | 7 | 10 |
| 20 ° | 0,3640 | 3659 | 3679 | 3699 | 3719 | 3739 | 3759 | 3779 | 3799 | 3819 | 3839 | 69 ° | 3 | 7 | 10 |
| 21 ° | 3839 | 3859 | 3879 | 3899 | 3919 | 3939 | 3959 | 3979 | 4000 | 4020 | 4040 | 68 ° | 3 | 7 | 10 |
| 22 ° | 4040 | 4061 | 4081 | 4101 | 4122 | 4142 | 4163 | 4183 | 4204 | 4224 | 4245 | 67 ° | 3 | 7 | 10 |
| 23 ° | 4245 | 4265 | 4286 | 4307 | 4327 | 4348 | 4369 | 4390 | 4411 | 4431 | 4452 | 66 ° | 3 | 7 | 10 |
| 24 ° | 4452 | 4473 | 4494 | 4515 | 4536 | 4557 | 4578 | 4599 | 4621 | 4642 | 0,4663 | 65 ° | 4 | 7 | 11 |
| 25 ° | 0,4663 | 4684 | 4706 | 4727 | 4748 | 4770 | 4791 | 4813 | 4834 | 4856 | 4877 | 64 ° | 4 | 7 | 11 |
| 26 ° | 4877 | 4899 | 4921 | 4942 | 4964 | 4986 | 5008 | 5029 | 5051 | 5073 | 5095 | 63 ° | 4 | 7 | 11 |
| 27 ° | 5095 | 5117 | 5139 | 5161 | 5184 | 5206 | 5228 | 5250 | 5272 | 5295 | 5317 | 62 ° | 4 | 7 | 11 |
| 28 ° | 5317 | 5340 | 5362 | 5384 | 5407 | 5430 | 5452 | 5475 | 5498 | 5520 | 5543 | 61 ° | 4 | 8 | 11 |
| 29 ° | 5543 | 5566 | 5589 | 5612 | 5635 | 5658 | 5681 | 5704 | 5727 | 5750 | 0,5774 | 60 ° | 4 | 8 | 12 |
| 30 ° | 0,5774 | 5797 | 5820 | 5844 | 5867 | 5890 | 5914 | 5938 | 5961 | 5985 | 6009 | 59 ° | 4 | 8 | 12 |
| 31 ° | 6009 | 6032 | 6056 | 6080 | 6104 | 6128 | 6152 | 6176 | 6200 | 6224 | 6249 | 58 ° | 4 | 8 | 12 |
| 32 ° | 6249 | 6273 | 6297 | 6322 | 6346 | 6371 | 6395 | 6420 | 6445 | 6469 | 6494 | 57 ° | 4 | 8 | 12 |
| 33 ° | 6494 | 6519 | 6544 | 6569 | 6594 | 6619 | 6644 | 6669 | 6694 | 6720 | 6745 | 56 ° | 4 | 8 | 13 |
| 34 ° | 6745 | 6771 | 6796 | 6822 | 6847 | 6873 | 6899 | 6924 | 6950 | 6976 | 0,7002 | 55 ° | 4 | 9 | 13 |
| 35 ° | 0,7002 | 7028 | 7054 | 7080 | 7107 | 7133 | 7159 | 7186 | 7212 | 7239 | 7265 | 54 ° | 4 | 8 | 13 |
| 36 ° | 7265 | 7292 | 7319 | 7346 | 7373 | 7400 | 7427 | 7454 | 7481 | 7508 | 7536 | 53 ° | 5 | 9 | 14 ° |
| 37 ° | 7536 | 7563 | 7590 | 7618 | 7646 | 7673 | 7701 | 7729 | 7757 | 7785 | 7813 | 52 ° | 5 | 9 | 14 |
| 38 ° | 7813 | 7841 | 7869 | 7898 | 7926 | 7954 | 7983 | 8012 | 8040 | 8069 | 8098 | 51 ° | 5 | 9 | 14 |
| 39 ° | 8098 | 8127 | 8156 | 8185 | 8214 | 8243 | 8273 | 8302 | 8332 | 8361 | 0,8391 | 50 ° | 5 | 10 | 15 |
| 40 ° | 0,8391 | 8421 | 8451 | 8481 | 8511 | 8541 | 8571 | 8601 | 8632 | 8662 | 0,8693 | 49 ° | 5 | 10 | 15 |
| 41 ° | 8693 | 8724 | 8754 | 8785 | 8816 | 8847 | 8878 | 8910 | 8941 | 8972 | 9004 | 48 ° | 5 | 10 | 16 |
| 42 ° | 9004 | 9036 | 9067 | 9099 | 9131 | 9163 | 9195 | 9228 | 9260 | 9293 | 9325 | 47 ° | 6 | 11 | 16 |
| 43 ° | 9325 | 9358 | 9391 | 9424 | 9457 | 9490 | 9523 | 9556 | 9590 | 9623 | 0,9657 | 46 ° | 6 | 11 | 17 |
| 44 ° | 9657 | 9691 | 9725 | 9759 | 9793 | 9827 | 9861 | 9896 | 9930 | 9965 | 1,0000 | 45 ° | 6 | 11 | 17 |
| 45 ° | 1,0000 | 0035 | 0070 | 0105 | 0141 | 0176 | 0212 | 0247 | 0283 | 0319 | 0355 | 44 ° | 6 | 12 | 18 |
| 46 ° | 0355 | 0392 | 0428 | 0464 | 0501 | 0538 | 0575 | 0612 | 0649 | 0686 | 0724 | 43 ° | 6 | 12 | 18 |
| 47 ° | 0724 | 0761 | 0799 | 0837 | 0875 | 0913 | 0951 | 0990 | 1028 | 1067 | 1106 | 42 ° | 6 | 13 | 19 |
| 48 ° | 1106 | 1145 | 1184 | 1224 | 1263 | 1303 | 1343 | 1383 | 1423 | 1463 | 1504 | 41 ° | 7 | 13 | 20 |
| 49 ° | 1504 | 1544 | 1585 | 1626 | 1667 | 1708 | 1750 | 1792 | 1833 | 1875 | 1,1918 | 40 ° | 7 | 14 | 21 |
| 50 ° | 1,1918 | 1960 | 2002 | 2045 | 2088 | 2131 | 2174 | 2218 | 2261 | 2305 | 2349 | 39 ° | 7 | 14 | 22 |
| 51 ° | 2349 | 2393 | 2437 | 2482 | 2527 | 2572 | 2617 | 2662 | 2708 | 2753 | 2799 | 38 ° | 8 | 15 | 23 |
| 52 ° | 2799 | 2846 | 2892 | 2938 | 2985 | 3032 | 3079 | 3127 | 3175 | 3222 | 3270 | 37 ° | 8 | 16 | 24 |
| 53 ° | 3270 | 3319 | 3367 | 3416 | 3465 | 3514 | 3564 | 3613 | 3663 | 3713 | 3764 | 36 ° | 8 | 16 | 25 |
| 54 ° | 3764 | 3814 | 3865 | 3916 | 3968 | 4019 | 4071 | 4124 | 4176 | 4229 | 1,4281 | 35 ° | 9 | 17 | 26 |
| 55 ° | 1,4281 | 4335 | 4388 | 4442 | 4496 | 4550 | 4605 | 4659 | 4715 | 4770 | 4826 | 34 ° | 9 | 18 | 27 |
| 56 ° | 4826 | 4882 | 4938 | 4994 | 5051 | 5108 | 5166 | 5224 | 5282 | 5340 | 5399 | 33 ° | 10 | 19 | 29 |
| 57 ° | 5399 | 5458 | 5517 | 5577 | 5637 | 5697 | 5757 | 5818 | 5880 | 5941 | 6003 | 32 ° | 10 | 20 | 30 |
| 58 ° | 6003 | 6066 | 6128 | 6191 | 6255 | 6319 | 6383 | 6447 | 6512 | 6577 | 6643 | 31 ° | 11 | 21 | 32 |
| 59 ° | 6643 | 6709 | 6775 | 6842 | 6909 | 6977 | 7045 | 7113 | 7182 | 7251 | 1,7321 | 30 ° | 11 | 23 | 34 |
| 60 ° | 1,732 | 1,739 | 1,746 | 1,753 | 1,760 | 1,767 | 1,775 | 1,782 | 1,789 | 1,797 | 1 804 | 29 ° | 1 | 2 | 4 |
| 61 ° | 1 804 | 1811 | 1819 | 1827 | 1834 | 1842 | 1849 | 1857 | 1865 | 1873 | 1881 | 28 ° | 1 | 3 | 4 |
| 62 ° | 1881 | 1889 | 1897 | 1 905 | 1 913 | 1 921 | 1 929 | 1 937 | 1 946 | 1 954 | 1 963 | 27 ° | 1 | 3 | 4 |
| 63 ° | 1 963 | 1 971 | 1,980 | 1 988 | 1,997 | 2 006 | 2,014 | 2,023 | 2,032 | 2,041 | 2,05 | 26 ° | 1 | 3 | 4 |
| 64 ° | 2,050 | 2,059 | 2,069 | 2,078 | 2,087 | 2,097 | 2,106 | 2,116 | 2,125 | 2,135 | 2,145 | 25 ° | 2 | 3 | 5 |
| 65 ° | 2,145 | 2 154 | 2 164 | 2 174 | 2 184 | 2 194 | 2 204 | 2,215 | 2,225 | 2,236 | 2,246 | 24 ° | 2 | 3 | 5 |
| 66 ° | 2,246 | 2,257 | 2,267 | 2,278 | 2,289 | 2,3 | 2,311 | 2,322 | 2,333 | 2,344 | 2,356 | 23 ° | 2 | 4 | 5 |
| 67 ° | 2,356 | 2,367 | 2,379 | 2,391 | 2,402 | 2,414 | 2,426 | 2,438 | 2,450 | 2,463 | 2,475 | 22 ° | 2 | 4 | 6 |
| 68 ° | 2,475 | 2,488 | 2,5 | 2,513 | 2,526 | 2,539 | 2,552 | 2,565 | 2,578 | 2,592 | 2 605 | 21 ° | 2 | 4 | 6 |
| 69 ° | 2 605 | 2,619 | 2,633 | 2 646 | 2,66 | 2,675 | 2,689 | 2 703 | 2,718 | 2,733 | 2 747 | 20 ° | 2 | 5 | 7 |
| 70 ° | 2 747 | 2,762 | 2,778 | 2 793 | 2 808 | 2 824 | 2 840 | 2,856 | 2 872 | 2 888 | 2 904 | 19 ° | 3 | 5 | 8 |
| 71 ° | 2 904 | 2 921 | 2 937 | 2,954 | 2,971 | 2,989 | 3 006 | 3 024 | 3 042 | 3,06 | 3 078 | 18 ° | 3 | 6 | 9 |
| 72 ° | 3 078 | 3 096 | 3,115 | 3,133 | 3,152 | 3 172 | 3,191 | 3 211 | 3,230 | 3 251 | 3 271 | 17 ° | 3 | 6 | 10 |
| 73 ° | 3 271 | 3 291 | 3,312 | 3 333 | 3 354 | 3 376 | 3 | 7 | 10 | ||||||
| 3 398 | 3,42 | 3 442 | 3,465 | 3 487 | 16 ° | 4 | 7 | 11 | |||||||
| 74 ° | 3 487 | 3,511 | 3,534 | 3,558 | 3,582 | 3 606 | 4 | 8 | 12 | ||||||
| 3,630 | 3 655 | 3 681 | 3,706 | 3,732 | 15 ° | 4 | 8 | 13 | |||||||
| 75 ° | 3,732 | 3,758 | 3,785 | 3 812 | 3 839 | 3 867 | 4 | 9 | 13 | ||||||
| 3 895 | 3 923 | 3 952 | 3,981 | 4 011 | 14 ° | 5 | 10 | 14 | |||||||
| тг | 60 ‘ | 54 ‘ | 48 ‘ | 42 ‘ | 36 ‘ | 30 ‘ | 24 ‘ | 18 ‘ | 12 ‘ | 6 ‘ | 0 ‘ | CTG | 1 ‘ | 2 ‘ | 3 ‘ |
PinkMonkey.
 com-Trigonometry Study Guide — 2.4 Таблицы тригонометрической функции
com-Trigonometry Study Guide — 2.4 Таблицы тригонометрической функции2.4 Таблицы тригонометрической функции
При решении задач с использованием тригонометрических функций, либо задан угол, и необходимо найти значение t-функции, либо дано значение t-функции и должен быть найден угол.
Эти два процесса противоположны друг другу. Таким образом, обратные обозначения используются для выражения ангела через значения t-функций.Для мгновенного cos a = 0,5 можно представить в виде a = cos -1 (-0,5) или a = Arc cos (- 0,5). Два выражения читаются как Альфа, равная ‘Обратный cos (-0,5), или Альфа, равная в Arc cos (- 0,5).
Обе эти операции можно выполнить либо с помощью
калькулятор или с помощью тригонометрической таблицы. Это явно должно быть
отметил, что и калькулятор, и таблица дают только приблизительные ответы.Даже в этом случае мы используем знак равенства (=), но правильнее использовать приближение
знак (») приветствуется. Приблизительный
значения функций острых углов приведены в Таблицах Натуральный тригонометрический функций . Мы будем использовать тригонометрический
таблица, дающая значения до четырех знаков после запятой. Как ясно, что
Таблицы не могут перечислить все углы. Следовательно, приближение должно быть
используется для поиска значений между приведенными в таблице.Этот способ
называется Линейная интерполяция .
Это явно должно быть
отметил, что и калькулятор, и таблица дают только приблизительные ответы.Даже в этом случае мы используем знак равенства (=), но правильнее использовать приближение
знак (») приветствуется. Приблизительный
значения функций острых углов приведены в Таблицах Натуральный тригонометрический функций . Мы будем использовать тригонометрический
таблица, дающая значения до четырех знаков после запятой. Как ясно, что
Таблицы не могут перечислить все углы. Следовательно, приближение должно быть
используется для поиска значений между приведенными в таблице.Этот способ
называется Линейная интерполяция .
Предположение : Различия в функциональных значениях прямо пропорциональны Различия в измерениях угла на очень небольшом интервале.
Осторожно: Это не настоящий
правда ! Тем не менее, это дает лучший ответ, чем просто поиск ближайшего
значение в таблице.
Рисунок 1
Использование линейной интерполяции Найдите sin (24 0 43 ‘), учитывая, что sin (24 0 40′) = 0,4173 и sin (24 0 50 ‘) = 0,4200
Решение
У нас грех (24 0 50 ‘) = 0,4200
и sin (24 0 40 ‘) = 0,4173
Разница для 10 ‘= 0.0027
Из-за сделанного предположения, если x — разность для требуемых 3 ‘имеем соотношение
\ х = 0,3 (0,0027)
= 0,00081 »0,0008 (округлено до 4 знаков после запятой)
Таким образом, грех (24 0 40 ‘) = грех (24 0 40′) + грех (0,3 ‘)
угол увеличивается с увеличением его синуса угла и наоборот.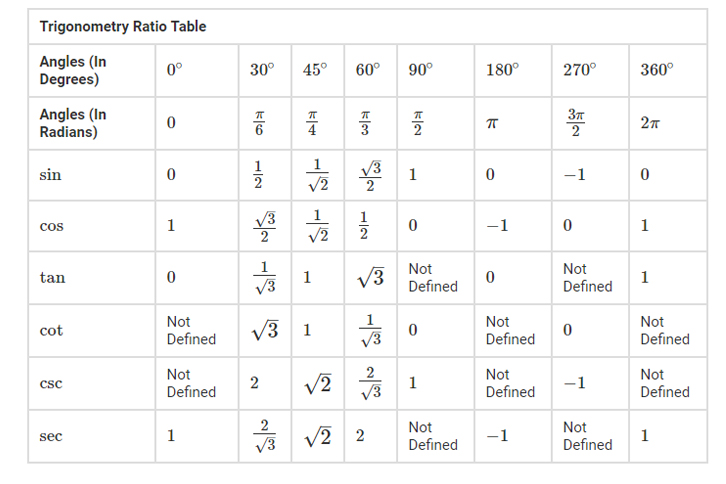
Таким образом, sin (24 0 43 ‘) = 0.4173 + 0,0008 = 0. 4181
| |
Иллюстрация 2
Найдите cos (64 0 26 ‘), учитывая, что cos (64 0 20 ‘) = 0,4331 и cos (64 0 30′) = 0,4305
Решение
У нас есть cos (64 0 30 ‘) = 0.4331
cos (64 0 20 ‘) = 0,4305
\ Табличная разница для 10 ‘= 0,0026
\ Требуемая разница для 6 ‘= (Если х)
\ х = 0,6 (0,0026) = 0,00156 или 0,0016 (104 десятичных знака)
По мере увеличения угла косинус угла уменьшается.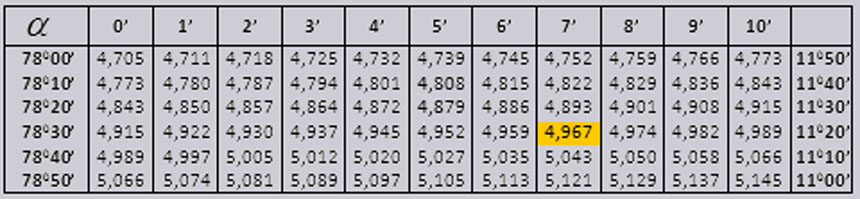 Таким образом, cos (64 0 26 ‘) = 0.4331 — 0,0016
Таким образом, cos (64 0 26 ‘) = 0.4331 — 0,0016
= 0,4315.
Рисунок 3
Найдите tan (28,43) 0 , учитывая, что tan (28,40) 0 = 0,5407 и загар (28,50) 0 = 0,5430
Решение
=
При увеличении угла тангенс угла также
увеличивается.
Таким образом, tan (28.43) 0 = 0,5407 + 0,0007 = 0,5414
Рисунок 4
Решите прямоугольный треугольник, в котором a = 24,36
Ð A = 58 0 53 ‘.
Решение
В прямоугольном треугольнике ABC
A + B + C = 180 0
\ 58 0 53 ‘+ B + C = 180 0 , учитывая, что C = 90 0
\ B = 90 0 -58 0 53 ‘ = 31 0 7 ‘
Используя формулы для t-соотношений,
b / a = детская кроватка A, b = детская кроватка A = 24.
 36 (0,6036) = 14,70 (\
детская кроватка A = 0.6036)
36 (0,6036) = 14,70 (\
детская кроватка A = 0.6036) c / a = csc A, c = a csc A = 24,36 (1,1681) = 28,45
a / c = sin A, c = a / sin A = 24,36 / 0,8562 = 28,45
b / c = cos A, b = c cos A = 28,45 (0,5168) = 14,70
Примечание: Чтобы сэкономить время, подумайте
Иллюстрация 1
Шаг (1) sin (24 0 41 ‘) = 0,4173, берем всего 4173
(2) Найдите мысленно табличную разницу 27 между 4200 (для греха
24 0 40 ‘) и 4173 (для sin 24 0 40′)
(3) Разница для 3 ‘= 0.3 (27) = 8,1 (округлено).
(4) Добавьте (с синуса) к 4178, чтобы получить 4181, затем sin 24 0 31 ‘= 0,4181.
Рисунок 5
Найдите угол A, учитывая, что sin A = 0,4234
Решение
Мы не найдем эту запись в таблице.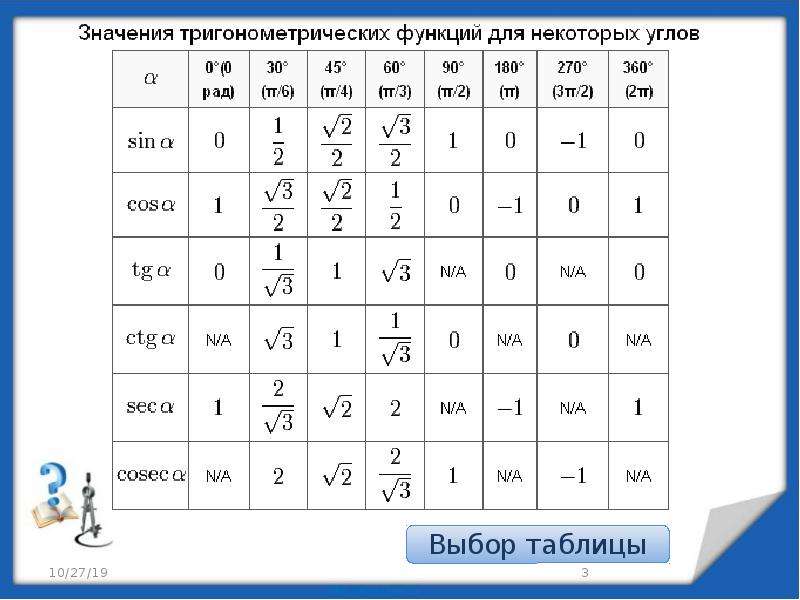
Однако 0,4226 = грех 25 0 0 ‘
0.4253 = грех 25 0 10 ‘
Табличная разница = 0,0027
Теперь 0,4226 = грех 25,0 ‘
0,4234 = грех A
0,0008 = частичная разница
исправление =
(ближайшая минута)
Сложив (начиная с синуса) поправка будет A = 25 0 0 ‘+ 3’
= 25 0 3 ‘
Рисунок 6
Найдите A, учитывая, что детская кроватка A = 0.6345
Решение
Имеем 0,6330 = кроватка 57 0 40 ‘(из таблицы)
0,6371 = детская кроватка 57 0 30 ‘
Табличный diff. = 0,0041
Теперь 0,6330 = детская кроватка 57 0 40 ‘
0,6345 = детская кроватка A
Частичная разница. = 0,0015
= 0,0015
Исправление =
(ближайшая минута)
вычитая (с кроватки), поправка равна A = 57 0 40 ‘
— 4 ‘= 57 0 36′.
Примечание: Сохранение времени как
— (См. Иллюстрацию 5)
Шаг (1) Найдите следующую меньшую запись, 0,4226 = sin 25 0 0 ‘. Используйте только 4226.
(2) Найдите табличную разницу. (мысленно), 27.
(3) Найдите частичную разницу. (мысленно), 8 между 4226 и 4234.
(4) Найти
(10 ‘) = 3’ и прибавляем (начиная с синуса), чтобы получить A = 25 0 3 ‘
Зафиксировать в памяти значения t-функций измерения углов 0 0 ,
30 0 , 45 0 , 60 0 и 90 0 как
следующим образом:
(1) Запишите угол (q) в указанном порядке
в 1-м столбце и t-отношения, sin q,
cos q, tan q,
csc q, sec q,
кроватку q в 1-м ряду.
(2) Поместите 0, 1, 2, 3, 4 в столбец sin q.
(см. таблицу), затем подставьте 4, 3, 2, 1, 0 в cos q
столбец (см. таблицу).
(3) Разделите каждую запись на 4, затем найдите квадратный корень из каждой записи.
Это значения соотношений синусов и косинусов углов 0 0 ,
30 0 , 45 0 , 60 0 и 90 0
(4) Используйте tan q = q и обратные соотношения для csc q,
sec q и детская кроватка q.
Таким образом, мы имеем
Щелкните здесь, чтобы увеличить
Обратите внимание, что
- По мере увеличения меры угла значения синусоидальных соотношений
увеличивается до 90 0 (п /
2 рад), а затем убывает.
- По мере увеличения меры угла значения косинусных отношений
уменьшается до 90 0 (п /
2 рад), а затем увеличивается.

- По мере увеличения меры угла значения тангенциального отношения
неограниченно увеличивается до 90 0 (p
/ 2 рад), затем бесконечно убывает.
Также обратите внимание, что
- Так как sin 2 q + cos2q
= 1 имеем | грех д | £
1 то есть — 1 £ sin q
£ 1 и | cos q
| 1 фунт стерлингов i.е. — 1 фунт стерлингов
cos q £
1 для всех q. Они называются границами
соотношений синусов и косинусов.
- Поскольку csc q =
у нас,
csc q ³ 1 или csc q £ 1 и сек q ³ 1 или сек q £ 1 (численно) для допустимых значений q . - tan q и кроватка q может принимать все действительные значения q.
Синус
Синус, записываемый как sin (θ), является одной из шести основных тригонометрических функций.
Определения синусов
Существует два основных способа обсуждения тригонометрических функций: в терминах прямоугольных треугольников и в терминах единичной окружности. Чаще всего вводят определение тригонометрических функций в виде прямоугольного треугольника, за которым следуют их определения в терминах единичной окружности.
Определение прямоугольного треугольника
Для прямоугольного треугольника с острым углом θ значение синуса этого угла определяется как отношение длины противоположной стороны к длине гипотенузы.
Стороны прямоугольного треугольника обозначаются следующим образом:
- Соседний: сторона рядом с θ, которая не является гипотенузой
- Справа: сторона, противоположная θ.
- Гипотенуза: самая длинная сторона треугольника напротив прямого угла.
Пример:
Найдите sin (θ) для прямоугольного треугольника ниже.
Мы также можем использовать синусоидальную функцию при решении реальных задач, связанных с прямоугольными треугольниками.
Пример:
Пандус для инвалидного кресла должен иметь угол 10 ° и высоту 3 фута. Какова длина пандуса?
Определение единичной окружности
Тригонометрические функции также могут быть определены как значения координат на единичной окружности.Единичный круг — это круг радиуса 1 с центром в начале координат. Определение тригонометрических функций в прямоугольном треугольнике допускает углы от 0 ° до 90 ° (0 и в радианах). Определение единичного круга позволяет нам расширить область определения тригонометрических функций на все действительные числа. См. Рисунок ниже.
Учитывая точку (x, y) на окружности единичной окружности, мы можем сформировать прямоугольный треугольник, как показано на рисунке. В таком треугольнике гипотенуза — это радиус единичной окружности, или 1.θ — это угол, образованный между начальной стороной угла вдоль оси x и конечной стороной угла, образованного вращением луча по часовой стрелке или против часовой стрелки. Конечная сторона угла — это гипотенуза прямоугольного треугольника и радиус единичной окружности. Следовательно, он всегда имеет длину 1. Таким образом, мы можем использовать определение синуса в прямоугольном треугольнике, чтобы определить, что
Конечная сторона угла — это гипотенуза прямоугольного треугольника и радиус единичной окружности. Следовательно, он всегда имеет длину 1. Таким образом, мы можем использовать определение синуса в прямоугольном треугольнике, чтобы определить, что
означает, что значение y любой точки на окружности единичной окружности равно sin (θ).
В отличие от определений тригонометрических функций, основанных на прямоугольных треугольниках, это определение работает для любого угла, а не только для острых углов прямоугольных треугольников, если он находится в пределах области sin (θ). Область определения синус-функции — (-∞, ∞), а ее диапазон — [-1,1].
Значения синусоидальной функции
Существует множество методов, которые можно использовать для определения значения синуса, например, обращение к таблице косинусов, использование калькулятора и аппроксимация с использованием ряда Тейлора для синуса.В большинстве практических случаев нет необходимости вычислять значение синуса вручную, и вам будет предоставлена таблица, калькулятор или другие справочные материалы.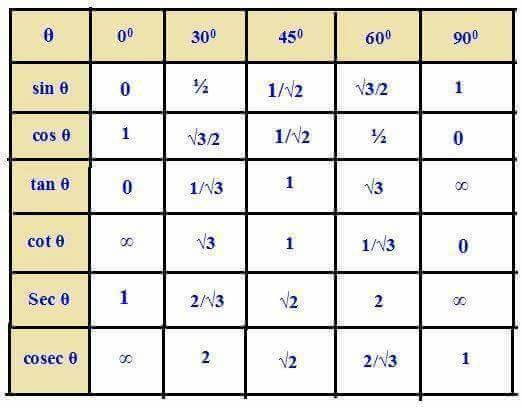
Калькулятор синуса
Ниже приведен калькулятор, позволяющий определить значение синуса угла или угол по значению синуса.
Часто используемые уголки
Хотя мы можем найти значение синуса для любого угла, есть некоторые углы, которые чаще используются в тригонометрии. Ниже приведены 16 часто используемых углов в радианах и градусах, а также координаты их соответствующих точек на единичной окружности.
Приведенный выше рисунок служит справочным материалом для быстрого определения синусов (значение y) и косинусов (значение x) углов, которые обычно используются в тригонометрии. Как видно из рисунка, синус имеет значение 0 при 0 ° и значение 1 при 90 °. Косинус следует противоположному шаблону; это потому, что синус и косинус являются совместными функциями (описанными позже). Другие часто используемые углы — 30 ° (), 45 ° (), 60 ° () и их соответствующие кратные. Значения косинуса и синуса этих углов стоит запомнить в контексте тригонометрии, поскольку они очень часто используются._3-1200x800.jpg)
Один из способов, который может помочь запомнить эти значения, — это выразить все значения sin (θ) в виде дробей, содержащих квадратный корень. Начиная с 0 ° и до 90 °, sin (0 °) = 0 =. Последующие значения sin (30 °), sin (45 °), sin (60 °) и sin (90 °) следуют шаблону, так что, используя значение sin (0 °) в качестве ссылки, найти значения синуса для последующих углов, мы просто увеличиваем число под знаком корня в числителе на 1, как показано ниже.
Значения синуса от 0 ° до -90 ° следуют той же схеме, за исключением того, что значения являются отрицательными, а не положительными, поскольку синус отрицателен в квадранте IV.Этот шаблон периодически повторяется для соответствующих угловых измерений, и мы можем определить значения sin (θ) на основе положения θ в единичном круге, принимая во внимание знак синуса: синус положительный в квадрантах I и II и отрицательный. в квадрантах III и IV. Аналогичный метод запоминания можно использовать для косинуса. При необходимости обратитесь к странице косинусов.
Знание значений косинуса и синуса для углов в первом квадранте позволяет нам определить их значения для соответствующих углов в остальных квадрантах в координатной плоскости с помощью опорных углов.
Опорные уголки
Базовый угол — это острый угол (<90 °), который можно использовать для обозначения угла любой меры. Любой угол в координатной плоскости имеет опорный угол от 0 ° до 90 °. Это всегда наименьший угол (относительно оси x), который может быть получен с конечной стороны угла. На рисунке ниже показан угол θ и его опорный угол θ '.
Поскольку θ ‘является опорным углом θ, sin both (θ) и sin (θ’) имеют одинаковое значение.Например, 30 ° — это опорный угол 210 °, и если мы обратимся к единичному кругу, мы увидим, что значения синуса обоих имеют величину 1/2, хотя и имеют разные знаки. Поскольку все углы имеют опорный угол, нам действительно нужно знать только значения sin (θ) (а также значения других тригонометрических функций) в квадранте I. Все другие соответствующие углы будут иметь значения той же величины, и мы просто нужно обращать внимание на их знаки исходя из квадранта, в котором лежит конечная сторона угла.Ниже приведена таблица, в которой показаны знаки косинуса, синуса и тангенса в каждом квадранте.
| Синус | Косинус | Касательная | |||||||
| Квадрант I | + | + | + | ||||||
| Квадрант II | + | III — | — | + | |||||
| Квадрант IV | — | + | — |
После определения опорного угла мы можем определить значение тригонометрических функций в любом из других квадрантов, применив соответствующий знак их значения для опорного угла.Следующие шаги можно использовать, чтобы найти опорный угол заданного угла, θ:
- Вычтите 360 ° или 2π из угла столько раз, сколько необходимо (угол должен быть от 0 ° до 360 ° или от 0 до 2π). Если полученный угол составляет от 0 ° до 90 °, это опорный угол.
- Определите, в каком квадранте лежит конечная сторона угла (начальная сторона угла расположена вдоль положительной оси x).
- В зависимости от того, в каком квадранте находится крайняя сторона угла, используйте уравнения в таблице ниже, чтобы найти опорный угол.В квадранте I θ ‘= θ.
| Квадрант II | Квадрант III | Квадрант IV |
|---|---|---|
| θ ‘= 180 ° — θ | θ ‘= θ — 180 ° | θ ‘= 360 ° — θ |
Пример:
Найдите sin (120 °).
- θ уже находится между 0 ° и 360 °
- 120 ° лежит во втором квадранте
- 180 ° — 120 ° = 60 °, поэтому опорный угол составляет 60 °
sin (60 °) =.120 ° находится в квадранте II, а синус положительный во втором квадранте, поэтому:
Пример:
Найдите sin (690 °).
- 690 ° — 360 ° = 330 °
- 330 ° лежит в квадранте IV
- 360 ° — 330 ° = 30 °, поэтому исходный угол равен 30 °
sin (30 °) =. 330 ° находится в квадранте IV, где синус отрицательный, поэтому:
Свойства синусоидальной функции
Ниже приводится ряд свойств синусоидальной функции, которые может быть полезно знать при работе с тригонометрическими функциями.
Синус является совместной функцией косинуса
Кофункция — это функция, в которой f (A) = g (B) при условии, что A и B являются дополнительными углами. В контексте косинуса и синуса
sin (θ) = cos (90 ° — θ)
cos (θ) = sin (90 ° — θ)
Пример:
sin (60 °) = cos (90 ° — 60 °) = cos (30 °)
Ссылаясь на единичный круг, показанный выше, мы можем подставить значения для cos (30 °) и sin (60 °) и увидеть, что:
Синус — нечетная функция
Нечетная функция — это функция, в которой -f (x) = f (-x).Он симметричен относительно начала координат. Таким образом,
-грех (θ) = sin (-θ)
Пример:
| -sin (60 °) = sin (-60 °) |
| -sin (60 °) = sin (300 °) |
Обращаясь к единичной окружности, мы можно увидеть, что sin (60 °) =, поэтому -sin (60 °) = и sin (-60 °) эквивалентно sin (-60 ° + 360 °) = sin (300 °), что равно. Это только один пример, но это свойство верно для всех углов.
Синус — периодическая функция
Периодическая функция — это функция f, в которой существует некоторое положительное значение p, такое что
е (х + р) = е (х)
для всех x в области f, p — наименьшее положительное число, для которого f является периодическим, и называется периодом f.
Тригонометрические функции обычно используются для моделирования периодических явлений из-за их периодичности; независимо от того, с какой точки мы начинаем на единичной окружности, если мы пройдем расстояние 2π (360 °) по единичной окружности от этой точки, мы вернемся к нашей начальной точке. Если мы посмотрим на синусоидальную функцию, мы обнаружим, что она повторяется каждые 2π, поэтому 2π — это период синусоидальной функции. Мы можем записать это как:
sin (θ + 2π) = sin (θ)
Для учета нескольких полных оборотов это также можно записать как
sin (θ + 2πn) = sin (θ)
, где n — целое число.
На рисунке ниже показан пример этой периодичности.
Мы видим это синим цветом. . Если мы прибавим 2π к, мы получим угол, показанный красным,. Как видно на рисунке, несмотря на то, что оба угла имеют разную степень вращения, их конечные стороны абсолютно одинаковы, что означает, что. Мы могли бы добавить еще 2π, и все равно оно будет иметь такое же значение синуса, как. Такова природа периодических функций. называются концевыми углами; это углы с одинаковой начальной и конечной сторонами, но с разными поворотами.
Примеры:
1.
2.
График синусоиды
График синуса является периодическим, что означает, что он повторяется бесконечно и имеет область значений -∞ Если бесконечно повторять эту часть y = sin inde (x) слева и справа, то получится полный график синуса.Ниже приведен график, показывающий четыре периода синусоидальной функции в интервале [-4π, 4π]. На этом графике мы видим, что y = sin (x) демонстрирует симметрию относительно начала координат; если график отражается относительно начала координат, он создает зеркальное отображение. Это подтверждает, что синус — нечетная функция, поскольку -sin (x) = sin (-x). Общий вид синусоидальной функции y = A · sin (B (x — C)) + D где A, B, C и D — константы.Чтобы иметь возможность изобразить синусоидальное уравнение в общем виде, нам нужно сначала понять, как каждая из констант влияет на исходный график y = sin (x), как показано выше. Чтобы применить все, что написано ниже, уравнение должно иметь форму, указанную выше; будьте осторожны со знаками. A — амплитуда функции; высота от центра графика до максимума или минимума. В y = sin (x) центром является ось x, а амплитуда равна 1, или A = 1, поэтому самая высокая и самая низкая точки, которых достигает график, равны 1 и -1, диапазон sin (x ). По сравнению с y = sin (x), показанным ниже фиолетовым цветом, функция y = 2 sin (x) (красный) имеет амплитуду, в два раза превышающую амплитуду исходного синусоидального графика. B — используется для определения периода функции; период функции — это расстояние от пика до пика (или любой точки на графике до следующей совпадающей точки) и может быть найден как. В y = sin (x) период равен 2π. Мы можем подтвердить это, посмотрев на синусоидальный график. Ссылаясь на рисунок выше, мы видим, что форма синусоидального графика между [-2π, 0] эквивалентна форме из [0, 2π], что означает, что он повторяется в интервале 2π; т.е. имеет период 2π. По сравнению с y = sin (x), показанным ниже фиолетовым цветом, который имеет период 2π, y = sin (2x) (красный) имеет период
. Это означает, что граф повторяется через каждые π, а не через каждые 2π. C — фазовый сдвиг функции; фазовый сдвиг определяет, как функция сдвигается по горизонтали. Если C отрицательно, функция сдвигается влево. Если C положительно, функция сдвигается вправо. Остерегайтесь знака; если у нас есть уравнение, то C нет, потому что это уравнение в стандартной форме.Таким образом, мы бы сместили единицы графика влево. На рисунке ниже показаны y = sin (x) (фиолетовый) и (красный). Используя один из пиков синусоидального графика в качестве эталона, мы можем увидеть, что пик в точке был смещен влево от своего исходного положения и теперь находится в точке (0,1). D — вертикальный сдвиг функции; если D положительно, график сдвигается вверх на D единиц, а если он отрицателен, график сдвигается вниз. По сравнению с y = sin (x), показанным ниже фиолетовым цветом, с центром на оси x (y = 0), y = sin (x) +5 (красный) с центром на линии y = 5 ( синий). Объединив все приведенные выше примеры, на рисунке ниже показан график (красный) по сравнению с графиком y = sin (x) (фиолетовый). См. Также косинус, тангенс, единичную окружность, тригонометрические функции, тригонометрию. Последнее обновление: 27 февраля 2019 г., автор: Teachoo В чем ценность греха 30? А как насчет cos 0? а грех 0? Как мы их запоминаем? Давайте узнаем, как это сделать.Обсудим, в чем заключаются разные значения sin, cos, tan, cosec, sec, кроватка в 0, 30, 45, 60 и 90 градусов и как их запомнить. Итак, мы должны заполнить эту таблицу Чтобы изучить таблицу, мы должны сначала узнать, как
грех, потому что загар
относятся к Мы знаем это Теперь давайте обсудим разные ценности Для запоминания sin 0 °, sin 30 °, sin 45 °, sin 60 ° и sin 90 ° Мы должны научиться этому как Итак, наш узор будет похож на 0, 1/2, 1 / √2, √3 / 2, 1 Для запоминания cos 0 °, cos 30 °, cos 45 °, cos 60 ° и cos 90 ° Cos — это противоположность греху. Мы должны научиться этому как Итак, для cos это будет похоже на 1, √3 / 2, 1 / √2, 1/2, 0 -объявление- Мы знаем, что tan θ = sin θ / cos θ Итак, это будет Итак, для загара это 0, 1 / √3, 1, √3, ∞ -объявление- Мы знаем это cosec θ = 1 / sin θ За грех мы знаем 0, 1/2, 1 / √2, √3 / 2, 1 Итак, для cosec это будет Итак, для cosec это ∞, 2, √2, 2 / √3, 1 -объявление- Мы знаем это сек θ = 1 / cos θ Потому что мы знаем 1, √3 / 2, 1 / √2, 1/2, 0 Итак, на секунду это будет Итак, на секунду это 1, 2 / √3, √2, 2, ∞ -объявление- Мы знаем это кроватка θ = 1 / tan θ Что касается загара, мы знаем, что 0, 1 / √3, 1, √3, ∞ Итак, для детской это будет Итак, для детской кроватки это ∞, √3, 1, 1 / √3, 0 -объявление- Итак, наша полная таблица выглядит так Вы также можете попрактиковаться в вопросах, нажав Следующий. Таблица тригонометрии содержит все значения sin, cos, tan для всех углов от 0 до 90 градусов. Вы также можете скачать его ниже Скачать в PDF В мире исчисления, предварительного исчисления и тригонометрии вы часто встретите ссылки и проблемы, связанные с «единичной окружностью».»Но, как ни странно, нас редко когда учат, что это такое! Проще говоря, единичная окружность — это математический инструмент, упрощающий использование углов и тригонометрических функций. Понимая и запоминая «единичный круг», мы можем легко справляться с трудностями, которые в противном случае требовали бы вычислений, и значительно облегчили нашу жизнь. Единичный круг, в его простейшей форме, на самом деле именно то, что он звучит: круг на декартовой плоскости с радиусом ровно 1unit1 unit1unit.Как этот пустой кружок ниже: Затем, заполнив этот единичный круг обычно используемыми углами и оценив эти углы с помощью синуса и косинуса, мы получим нечто немного более сложное: Боишься? Не надо. Этот образ может показаться устрашающим, но когда мы разбиваем его на более последовательные части, начинают появляться закономерности. Вместо того, чтобы ссылаться на это устрашающее изображение выше, давайте упростим единичный круг с помощью sincostanseccsc \ sin \ cos \ tan \ sec \ cscsincostanseccsc и cot \ cotcot на красивой маленькой диаграмме: В приведенной выше таблице единичного круга приведены все значения единичного круга для всех 4 квадрантов единичного круга.Как видите, здесь указаны градусы единичной окружности и радианы единичной окружности. Вы должны знать и то, и другое, но, скорее всего, вы будете решать проблемы в радианах. Теперь возникает следующий естественный вопрос: как я могу запомнить единичный круг? Запоминание единичной окружности на самом деле намного проще, чем вы думаете, благодаря нескольким маленьким приемам: Уловка 1: Из-за следующих 4 уравнений нам нужно запомнить только значения единичной окружности для синуса и косинуса. С этими 4 уравнениями нам даже не нужно запоминать единичную окружность с касательной! Уловка 2: Зная, в каких квадрантах x и y положительны, нам нужно только запомнить значения единичного круга для синуса и косинуса в первом квадранте, поскольку значения меняются только по знаку.Чтобы использовать этот трюк, нам нужно сначала понять несколько вещей: i) Первое, что нужно отметить, это то, какие значения синуса и косинуса дают нам на единичной окружности. Благодаря SOHCAHTOA мы знаем это: ii) Теперь посмотрим на каждый квадрант: Квадрант 1 : X положительный, Y положительный Квадрант 2 : X отрицательный, Y положительный Квадрант 3 : X отрицательный, Y отрицательный Квадрант 4 : X положительный, Y отрицательный iii) Далее, посмотрим, где находится каждый квадрант: Квадрант 1 : 0 — π2 \ frac {\ pi} {2} 2π Квадрант 2 : π2 − π \ frac {\ pi} {2} — \ pi2π −π Квадрант 3 : π \ piπ — 3π2 \ frac {3 \ pi} {2} 23π Квадрант 4 : 3π2−2π \ frac {3 \ pi} {2} — 2 \ pi23π −2π iv) Значение синуса и косинуса всегда будет «одинаковым» для одного и того же знаменателя: С учетом этих приемов процесс запоминания единичного круга становится намного проще! Лучший способ освоить единичный круг — это попрактиковаться в единичном круге. Пример 1: Найдите sin4π3 \ sin \ frac {4 \ pi} {3} sin34π Шаг 1. Определите квадрант Поскольку мы имеем дело с синусом, который мы со временем запомним, все, что нам нужно сделать, это выяснить, в каком квадранте мы находимся, чтобы знать, будет ли наш ответ положительным или отрицательным. Поскольку: Таким образом, мы находимся в третьем квадранте.Таким образом, поскольку синус дает нам координату y, и мы находимся в третьем квадранте, наш ответ будет отрицательным! Шаг 2: Решить Следующий шаг прост — используя то, что мы запомнили, мы можем легко решить эту задачу. Пример 2: Найдите tanπ \ tan \ pitanπ Шаг 1. Определите квадрант Поскольку мы имеем дело с единичным кругом с загаром, нам нужно будет использовать значения, которые мы запомнили из синуса и косинуса, а затем решить.Однако сначала нам нужно выяснить, в каком квадранте мы находимся, чтобы знать, будут ли наши ответы для синуса и косинуса положительными или отрицательными. Поскольку: Таким образом, мы находимся между вторым и третьим квадрантами по оси абсцисс. Поскольку синус дает нам координату y, а мы находимся на оси x, наш ответ фактически будет равен нулю! Кроме того, поскольку косинус дает нам координату x, и мы находимся между вторым и третьим квадрантами (где косинус для обоих отрицательный), наш ответ будет отрицательным! Шаг 2: Решить Следующий шаг прост — используя то, что мы запомнили, мы можем легко решить эту задачу.Но в этом случае нам понадобится один дополнительный шаг. Мы должны использовать уравнение для касательной, обсуждавшееся ранее в трюке 1 , предполагая, что мы не запомнили значения касательной на единичной окружности. Пример 3: Найдите cscπ6 \ csc \ frac {\ pi} {6} csc6π Шаг 1. Определите квадрант Поскольку мы имеем дело с косекансом, важно понимать, что нам нужно будет использовать значения синуса для решения с использованием уравнения для косеканса, описанного ранее в уловке 1 .Однако сначала нам нужно выяснить, в каком квадранте мы находимся, чтобы знать, будет ли наш ответ для синуса положительным или отрицательным. Поскольку: Таким образом, мы находимся в первом квадранте. Таким образом, поскольку синус дает нам координату y, и мы находимся в первом квадранте, наш ответ будет положительным! Шаг 2: Решить Следующий шаг прост — используя то, что мы запомнили, мы можем легко решить эту задачу.Но и в этом случае нам снова нужен один дополнительный шаг. Мы должны использовать уравнение для косеканса, обсуждавшееся ранее в трюке 1 , предполагая, что мы не запомнили значения косеканса на единичной окружности. Теперь, когда мы немного попрактиковались, займитесь еще немного самостоятельно! В кратчайшие сроки вы будете готовы к любой предстоящей викторине с единичным кругом. Чтобы увидеть, как изображены функции синуса и косинуса, воспользуйтесь калькулятором, компьютером или набором тригонометрических таблиц, чтобы определить значения функций синуса и косинуса для ряда различных степеней ( или радиан) меры (см. таблицу 1). Затем постройте эти значения и получите основные графики функции синуса и косинуса (рисунок 1). Рисунок 1 Синус-функция и косинус-функция имеют периоды 2π; поэтому образцы, показанные на рисунке, непрерывно повторяются слева и справа (рисунок 2). К функциям синуса и косинуса можно добавить несколько дополнительных членов и множителей, которые изменяют их форму. Дополнительный член A в функции y = A + sin x допускает вертикальный сдвиг в графике синусоидальных функций. Это также верно для функции косинуса (рисунок 3). Рисунок 3 Дополнительный множитель B в функции y = B sin x учитывает амплитуду вариации синусоидальной функции. Амплитуда, | B | — максимальное отклонение от оси x , то есть половина разницы между максимальным и минимальным значениями графика. Это также верно для функции косинуса (рисунок 4). Рисунок 4 Объединение этих цифр дает функции y = A + B sin x , а также y = A + B cos x . Эти две функции имеют минимальных и максимальных значений, как определено следующими формулами. Максимальное значение функции M = A + | B |. Это максимальное значение возникает всякий раз, когда sin x = 1 или cos x = 1. Минимальное значение функции составляет m = A — | B |.Этот минимум возникает всякий раз, когда sin x = -1 или cos x = -1. Пример 1: Постройте график функции y = 1 + 2 sin x . Какие максимальные и минимальные значения функции? Максимальное значение — 1 + 2 = 3. Минимальное значение — 1 −2 = -1 (Рисунок 5). Рисунок 5 Пример 2: Постройте график функции y = 4 + 3 sin x . Какие максимальные и минимальные значения функции? Максимальное значение 4 + 3 = 7. Минимальное значение 4 — 3 = 1 (Рисунок 6). Рисунок 6 Дополнительный множитель C в функции y = sin Cx учитывает период изменения (длины цикла) синусоидальной функции.(Это также верно для функции косинуса.) Период функции y = sin Cx равен 2π / | C |. Таким образом, функция y = sin 5 x имеет период 2π / 5. На рисунке 7 показаны дополнительные примеры. Рисунок 7 Дополнительный член D в функции y = sin ( x + D ) допускает сдвиг фазы (перемещение графика влево или вправо) на графике синусоидальных функций.(Это также верно для функции косинуса.) Сдвиг фазы равен | D |. Это положительное число. Не имеет значения, будет ли сдвиг влево (если D положительный) или вправо (если D отрицательный). Функция синуса нечетная, а функция косинуса четная. Функция косинуса выглядит точно так же, как функция синуса, за исключением того, что она сдвинута на π / 2 единицы влево (рисунок 8). Другими словами, Рисунок 8 Пример 3: Каковы амплитуда, период, фазовый сдвиг, максимальное и минимальное значения y = 3 + 2 sin (3 x -2) y = 4 cos2π x Пример 4: Нарисуйте график y = cosπ x . Поскольку cos x имеет период 2π, cos π x имеет период 2 (рисунок 9). Рисунок 9 Пример 5: Нарисуйте график y = 3 cos (2x + π / 2). Поскольку cos x имеет период 2π, cos 2x имеет период π (рисунок 10). График функции y = — f ( x ) находится путем отражения графика функции y = f ( x ) относительно оси x . Таким образом, рисунок может также представлять график y = −3 sin 2 x . Общее синусоидальное уравнение
Значение sin, cos, tan, cot при 0, 30, 45, 60, 90
Как найти значения?
За грех
Для cos
Для загара
Для cosec
На сек
Для детской кроватки
Таблица тригонометрии
Радиан Степень Синус Косинус Касательная Радиан Степень Синус Косинус Касательная 0.000 0 0,000 1.000 0,000 0,803 46 0,719 0,695 1.036 0,017 1 0,017 1.000 0,017 0,820 47 0.731 0,682 1.072 0,035 2 0,035 0,999 0,035 0,838 48 0,743 0,669 1.111 0,052 3 0,052 0.999 0,052 0,855 49 0,755 0,656 1.150 0,070 4 0,070 0,998 0,070 0,873 50 0,766 0,643 1.192 0,087 5 0,087 0,996 0,087 0,890 51 0,777 0,629 1,235 0,105 6 0,105 0,995 0,105 0.908 52 0,788 0,616 1,280 0,122 7 0,122 0,993 0,123 0,925 53 0,799 0,602 1,327 0,140 8 0.139 0,990 0,141 0,942 54 0,809 0,588 1,376 0,157 9 0,156 0,988 0,158 0,960 55 0,819 0.574 1,428 0,175 10 0,174 0,985 0,176 0,977 56 0,829 0,559 1,483 0,192 11 0,191 0,982 0.194 0,995 57 0,839 0,545 1,540 0,209 12 0,208 0,978 0,213 1.012 58 0,848 0,530 1.600 0.227 13 0,225 0,974 0,231 1.030 59 0,857 0,515 1,664 0,244 14 0,242 0,970 0,249 1.047 60 0.866 0,500 1,732 0,262 15 0,259 0,966 0,268 1.065 61 год 0,875 0,485 1,804 0,279 16 0,276 0.961 0,287 1.082 62 0,883 0,469 1,881 0,297 17 0,292 0,956 0,306 1.100 63 0,891 0,454 1.963 0,314 18 0,309 0,951 0,325 1.117 64 0,899 0,438 2,050 0,332 19 0,326 0,946 0,344 1.134 65 0,906 0,423 2,145 0,349 20 0,342 0,940 0,364 1.152 66 0,914 0,407 2,246 0,367 21 год 0.358 0,934 0,384 1,169 67 0,921 0,391 2,356 0,384 22 0,375 0,927 0,404 1,187 68 0,927 0.375 2,475 0,401 23 0,391 0,921 0,424 1,204 69 0,934 0,358 2,605 0,419 24 0,407 0,914 0.445 1,222 70 0,940 0,342 2,747 0,436 25 0,423 0,906 0,466 1,239 71 0,946 0,326 2,904 0.454 26 0,438 0,899 0,488 1,257 72 0,951 0,309 3,078 0,471 27 0,454 0,891 0,510 1,274 73 0.956 0,292 3,271 0,489 28 год 0,469 0,883 0,532 1,292 74 0,961 0,276 3,487 0,506 29 0,485 0.875 0,554 1,309 75 0,966 0,259 3,732 0,524 30 0,500 0,866 0,577 1,326 76 0,970 0,242 4.011 0,541 31 год 0,515 0,857 0,601 1,344 77 0,974 0,225 4,331 0,559 32 0,530 0,848 0,625 1.361 78 0,978 0,208 4,705 0,576 33 0,545 0,839 0,649 1,379 79 0,982 0,191 5,145 0,593 34 0.559 0,829 0,675 1,396 80 0,985 0,174 5,671 0,611 35 год 0,574 0,819 0,700 1,414 81 год 0,988 0.156 6,314 0,628 36 0,588 0,809 0,727 1,431 82 0,990 0,139 7,115 0,646 37 0,602 0,799 0.754 1,449 83 0,993 0,122 8,144 0,663 38 0,616 0,788 0,781 1,466 84 0,995 0,105 9,514 0.681 39 0,629 0,777 0,810 1,484 85 0,996 0,087 11,430 0,698 40 0,643 0,766 0,839 1,501 86 0.998 0,070 14.301 0,716 41 год 0,656 0,755 0,869 1,518 87 0,999 0,052 19,081 0,733 42 0,669 0.743 0,900 1,536 88 0,999 0,035 28,636 0,750 43 год 0,682 0,731 0,933 1,553 89 1.000 0,017 57.290 0,768 44 год 0,695 0,719 0,966 1,571 90 1.000 0,000 ∞ 0,785 45 0,707 0,707 1.000 Что такое единичный круг | StudyPug
Что такое Unit Circle?
Единичный круг со всеми 6 функциями триггера Таблица:
Как запомнить единичный круг:
Как использовать единичный круг:
Графики: синус и косинус
Один период а) синусоидальной функции и б) косинусной функции.
Примеры нескольких вертикальных сдвигов синусоидальной функции.
Примеры нескольких амплитуд синусоидальной функции.
Чертеж для примера 1.
Чертеж для примера 2.
Примеры нескольких частот а) синусоидальной функции и б) косинусной функции.
Примеры нескольких фазовых сдвигов синусоидальной функции.
Рисунок для примера 4.
Рисунок для примера 5.

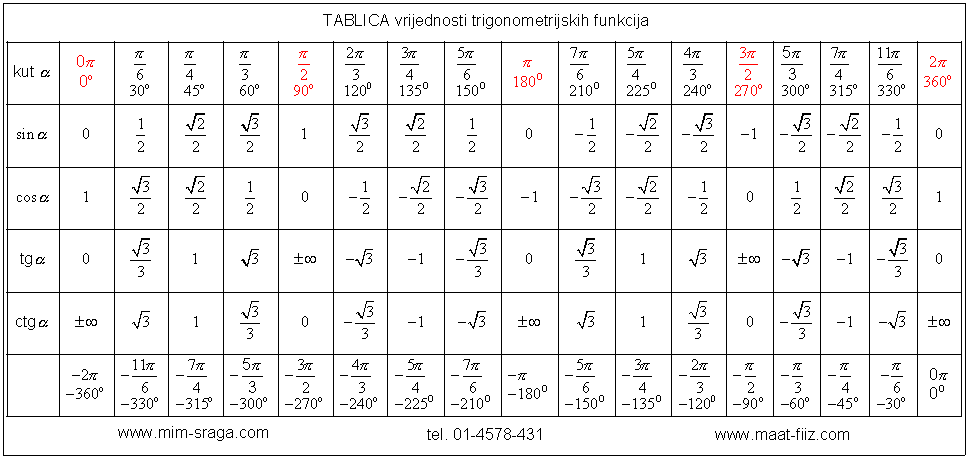
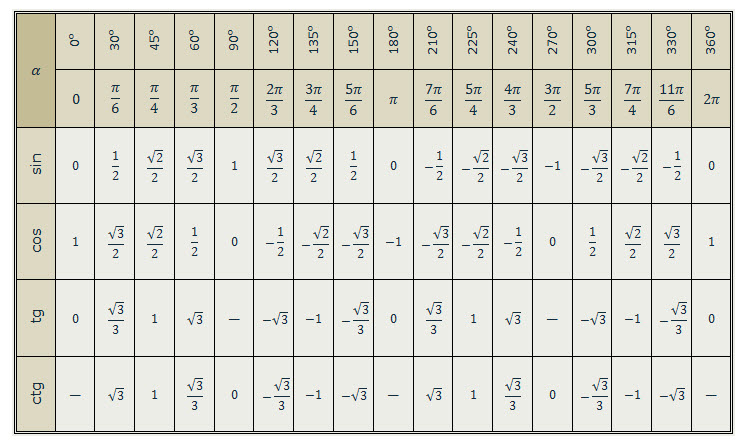 5299
5299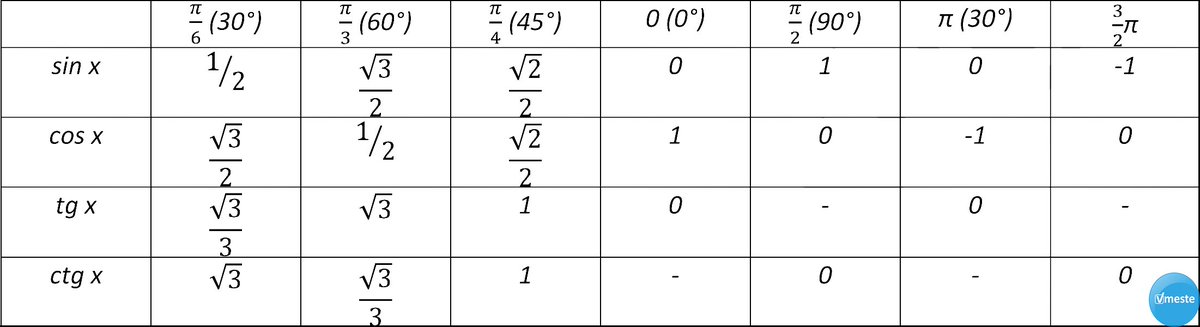 8192
8192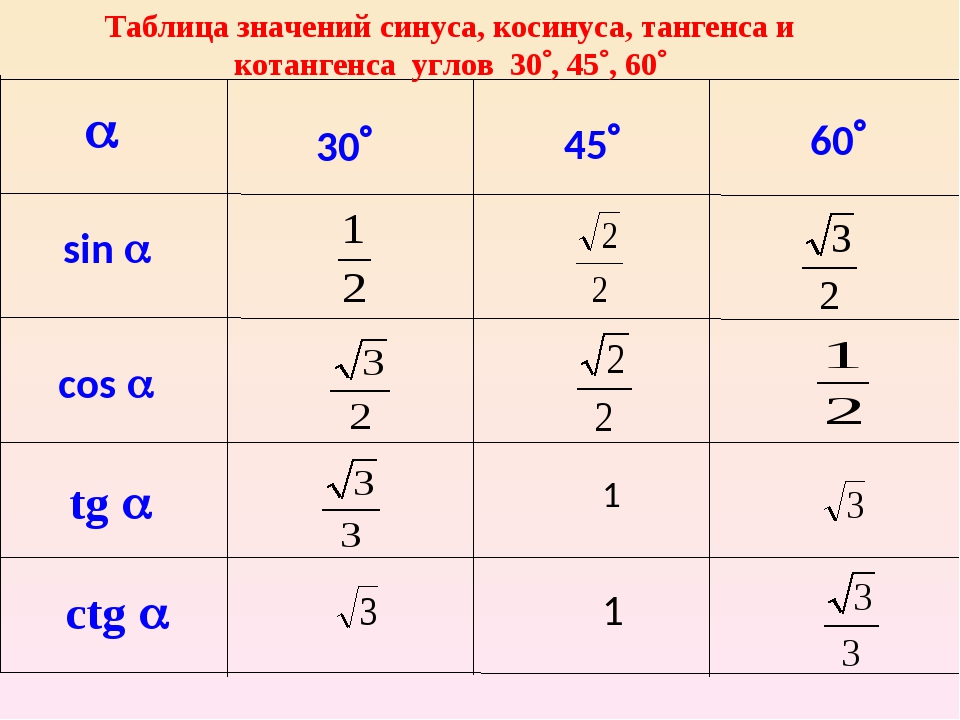 9816
9816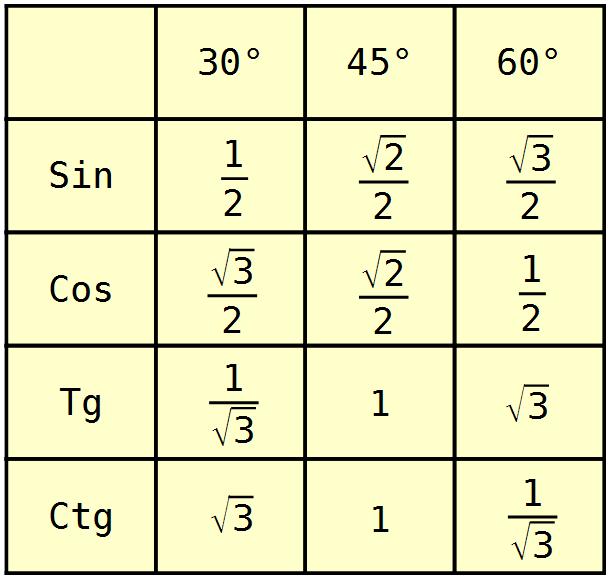 9781
9781 8192
8192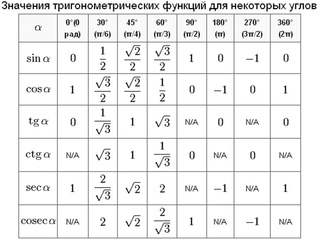 5299
5299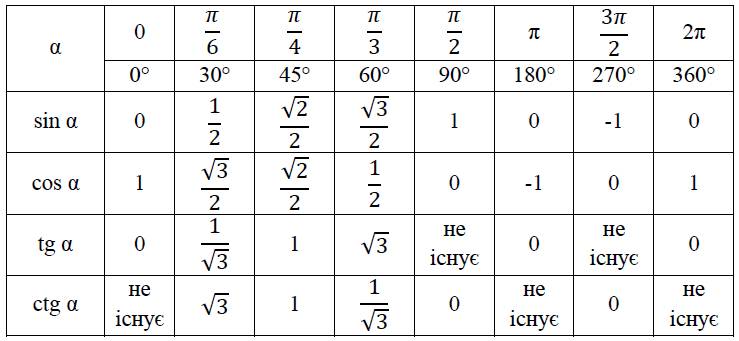 1564
1564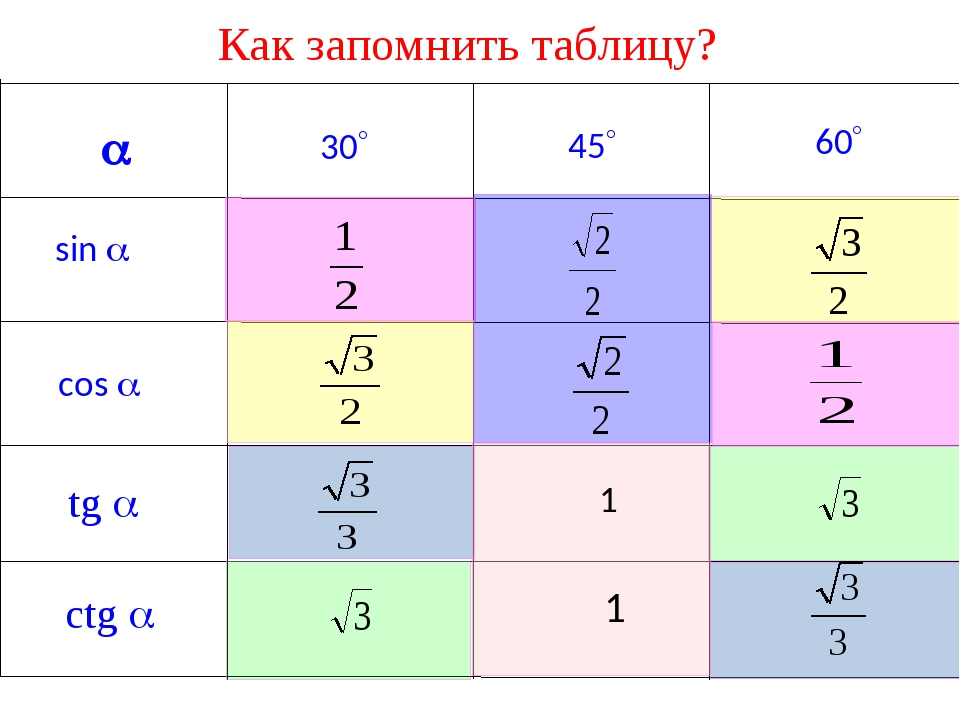 2079
2079
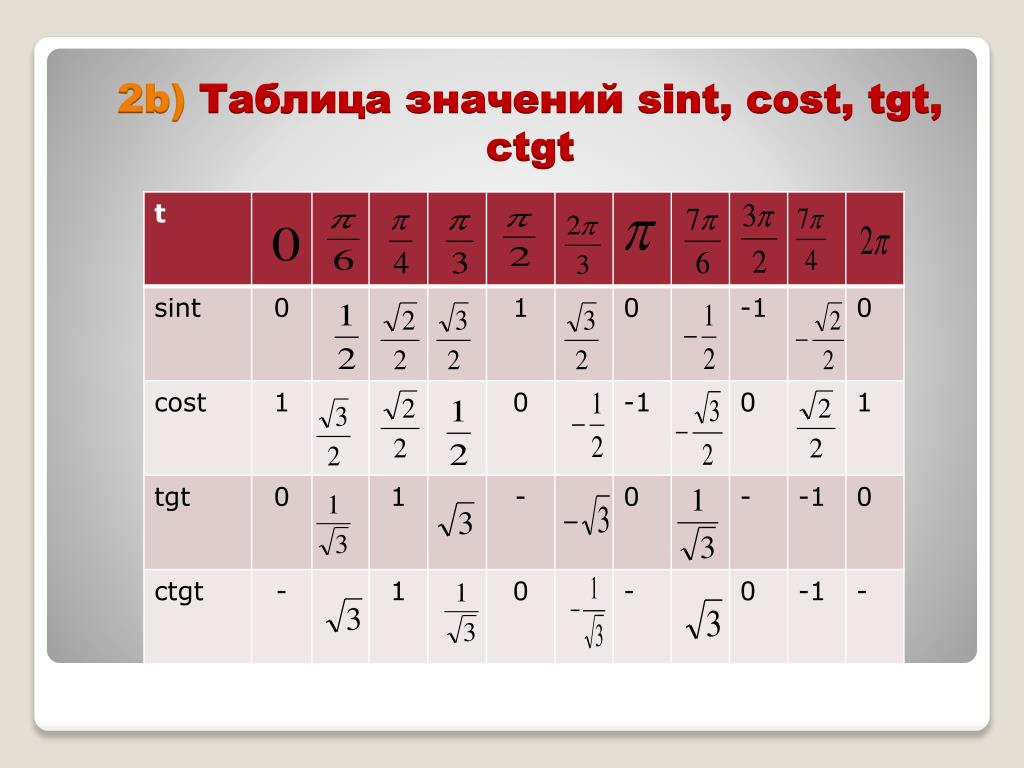 8387
8387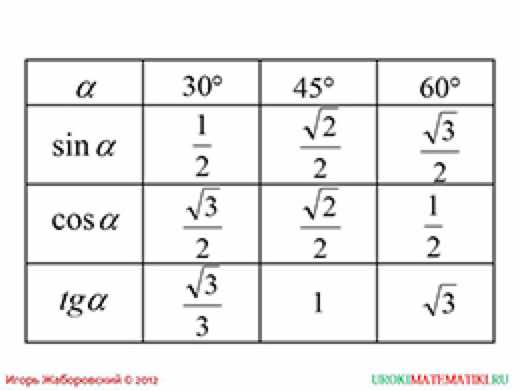 9848
9848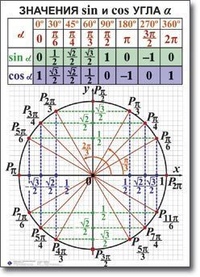 9781
9781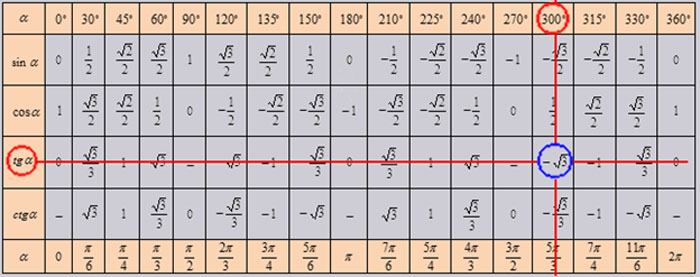 8192
8192 5446
5446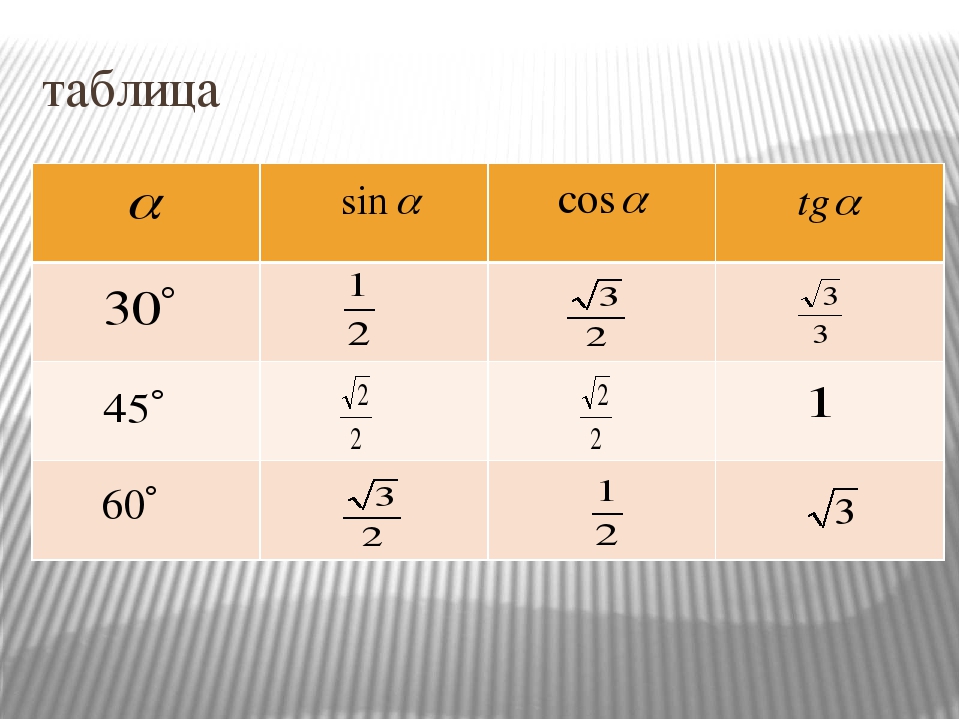 1736
1736 Получим:
Получим: 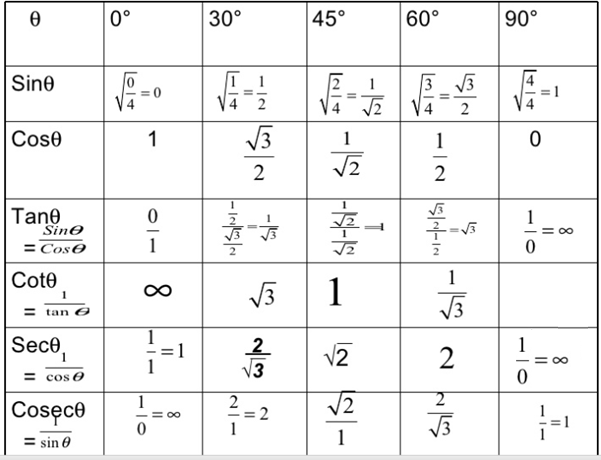 Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.
Но в данной таблице возможно узнать сколько составит тангенс от угла в 1020 градусов, он = -√3 Проверим 1020 0 = 300 0 +360 0 *2. Найдем по таблице.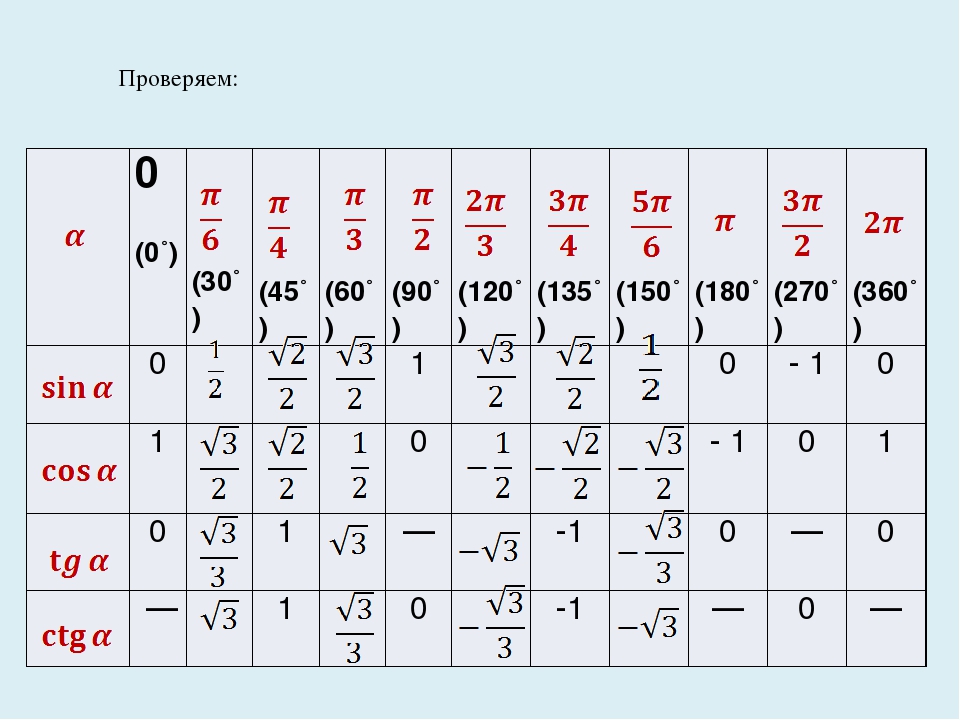 Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046.
Возьмем 44 минуты, а в таблице есть только 42. Берем за основу 42 и воспользуемся добавочными столбцами в правой стороне, берем 2 поправку и добавляем к 0,3040 + 0,0006 получаем 0,3046. Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360
градусов (0, π/6, π/4, π/3, π/2, …, 2π
радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.
Сначала мы приведем таблицу основных значений тригонометрических функций, то есть, таблицу синусов, косинусов, тангенсов и котангенсов углов 0, 30, 45, 60, 90, …, 360
градусов (0, π/6, π/4, π/3, π/2, …, 2π
радиан). После этого мы дадим таблицу синусов и косинусов, а также таблицу тангенсов и котангенсов В. М. Брадиса, и покажем, как использовать эти таблицы при нахождении значений тригонометрических функций.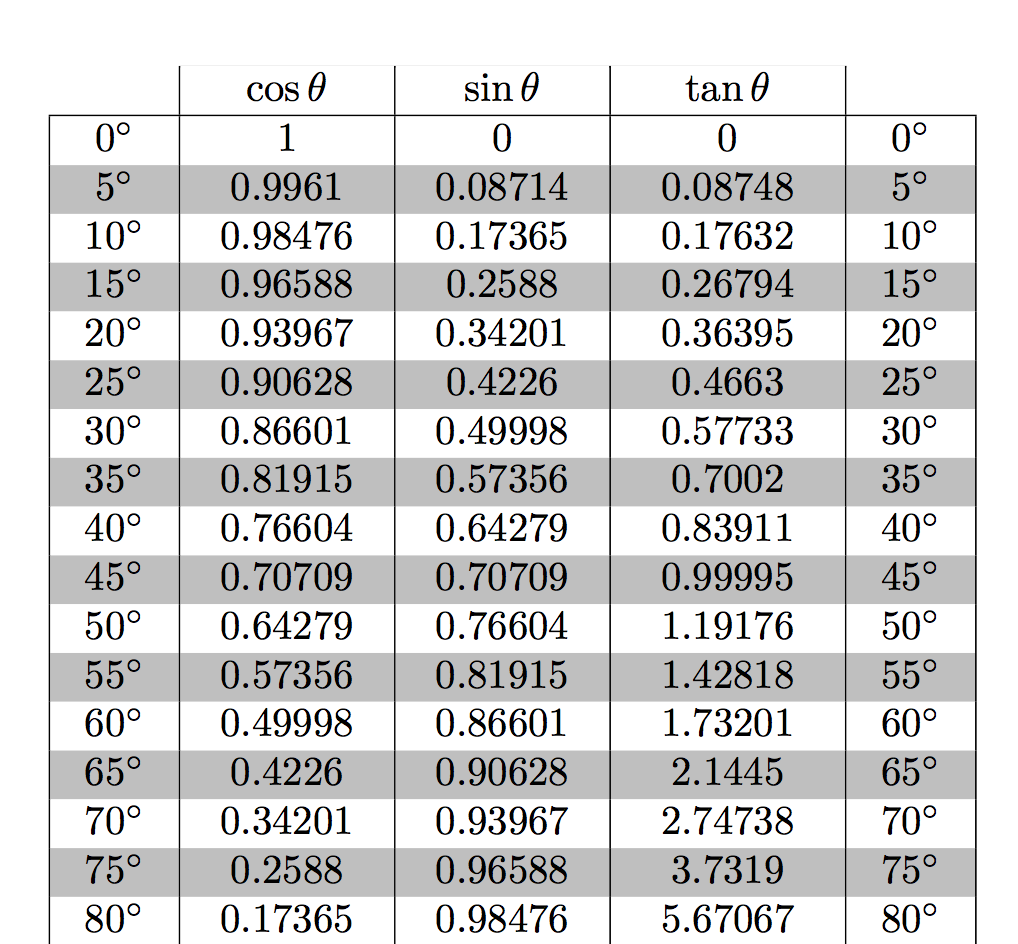 общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3.
общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; Под ред. А. Н. Колмогорова.- 14-е изд.- М.: Просвещение, 2004.- 384 с.: ил.- ISBN 5-09-013651-3. Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.
Для тангенса и котангенса значения некоторых углов не могут быть определены. Для значений тангенса и котангенса таких углов в таблице значений тригонометрических функций стоит прочерк. Принято считать, что тангенс и котангенс таких углов равняется бесконечности. На отдельной странице находятся формулы приведения тригонометрических функций.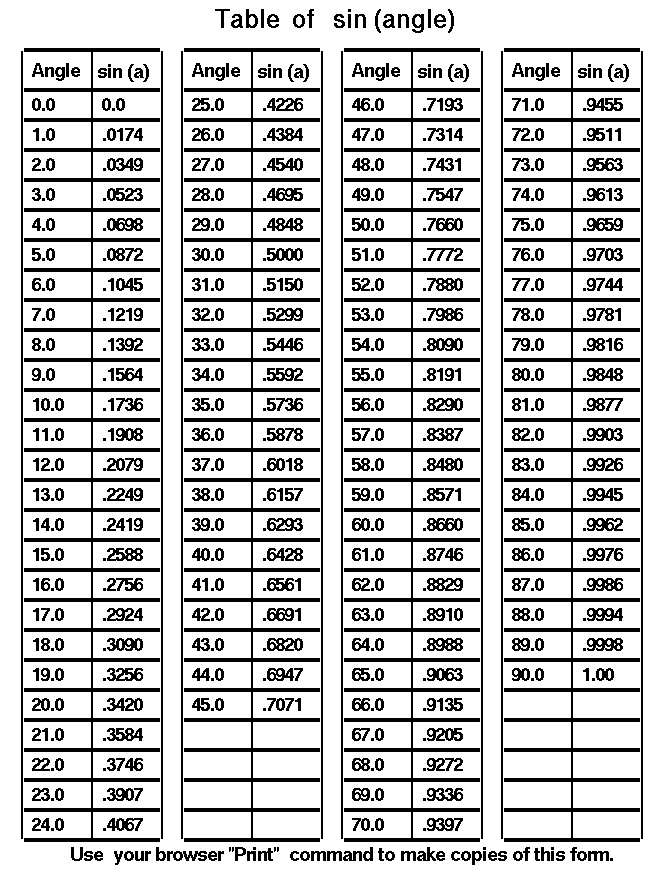
 Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах.
Значения тригонометрических функций выражены через дроби и корни квадратные для упрощения сокращения дробей в школьных примерах.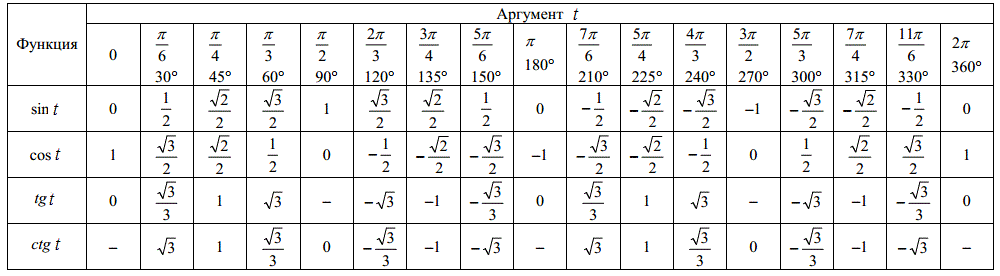
 Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.
Отрицательные значения тангенс и котангенс имеют от 90 до 180 градусов и от 270 до 360 градусов или от 1/2 пи до пи и от 3/2 пи до 2 пи. При определении знаков тригонометрических функций для углов больше 360 градусов или 2 пи следует использовать свойства периодичности этих функций.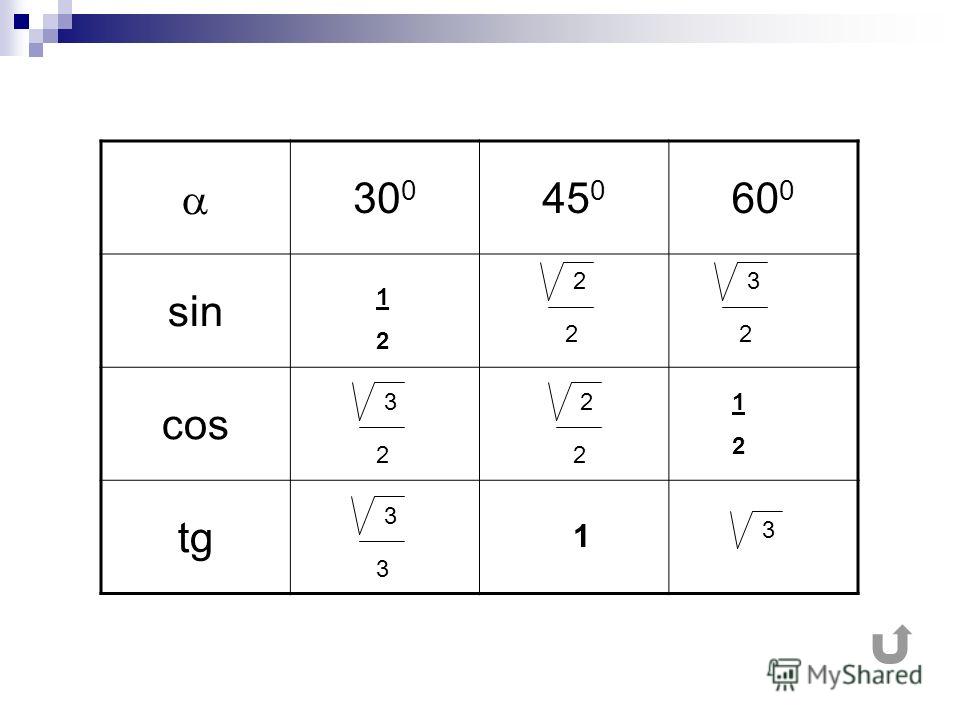 ..
..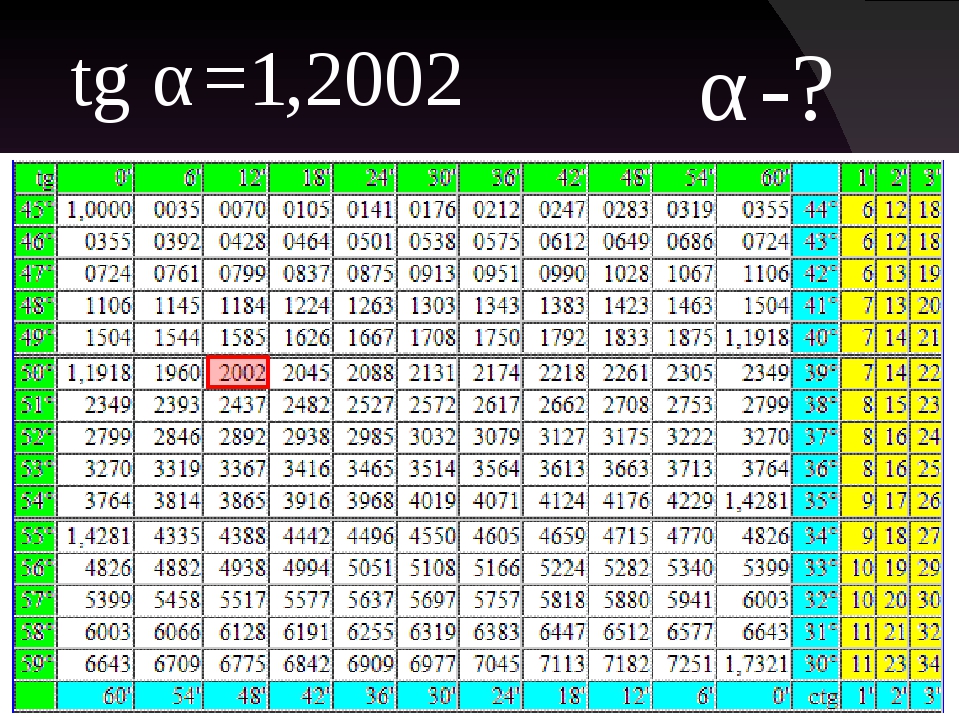 Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху.
Когда Ахиллес пробежит сто шагов, черепаха проползёт ещё десять шагов, и так далее. Процесс будет продолжаться до бесконечности, Ахиллес так никогда и не догонит черепаху. 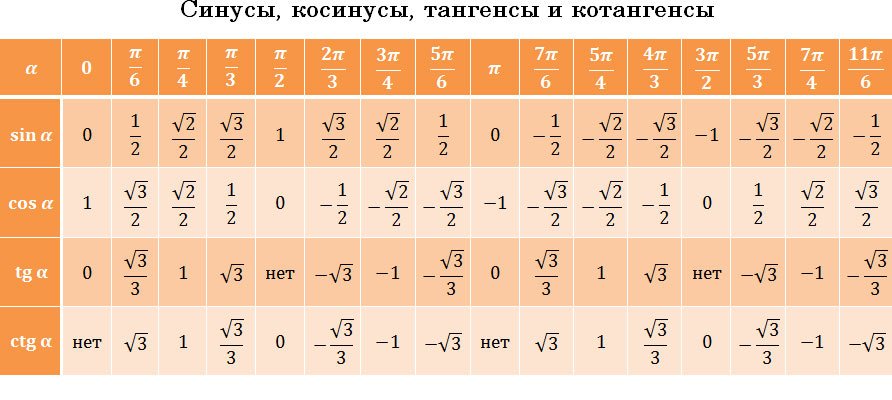 Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.
Применение же нашей обычной логики приводит нас в ловушку. Мы, по инерции мышления, применяем постоянные единицы измерения времени к обратной величине. С физической точки зрения это выглядит, как замедление времени до его полной остановки в момент, когда Ахиллес поравняется с черепахой. Если время останавливается, Ахиллес уже не может перегнать черепаху.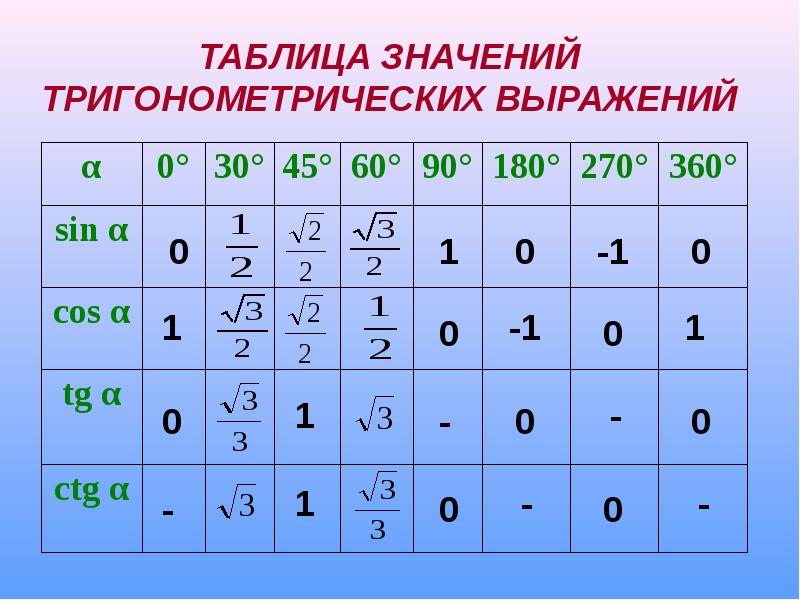 За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху.
За следующий интервал времени, равный первому, Ахиллес пробежит ещё тысячу шагов, а черепаха проползет сто шагов. Теперь Ахиллес на восемьсот шагов опережает черепаху. 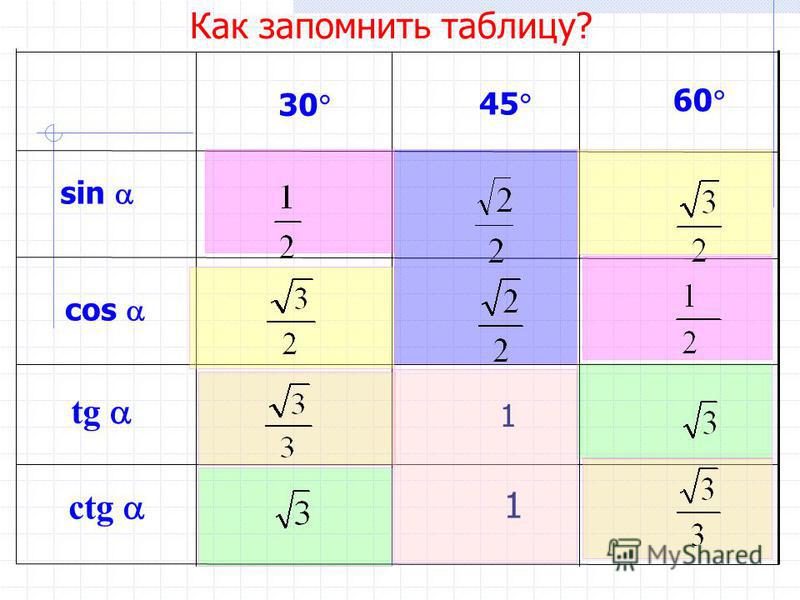 По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования.
По одной фотографии автомобиля на дороге невозможно определить ни факт его движения, ни расстояние до него. Для определения факта движения автомобиля нужны две фотографии, сделанные из одной точки в разные моменты времени, но по ним нельзя определить расстояние. Для определения расстояния до автомобиля нужны две фотографии, сделанные из разных точек пространства в один момент времени, но по ним нельзя определить факт движения (естественно, ещё нужны дополнительные данные для расчетов, тригонометрия вам в помощь). На что я хочу обратить особое внимание, так это на то, что две точки во времени и две точки в пространстве — это разные вещи, которые не стоит путать, ведь они предоставляют разные возможности для исследования. Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи.
Подобную логику абсурда разумным существам не понять никогда. Это уровень говорящих попугаев и дрессированных обезьян, у которых разум отсутствует от слова «совсем». Математики выступают в роли обычных дрессировщиков, проповедуя нам свои абсурдные идеи. Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.
Затем берем с каждой стопки по одной купюре и вручаем математику его «математическое множество зарплаты». Поясняем математику, что остальные купюры он получит только тогда, когда докажет, что множество без одинаковых элементов не равно множеству с одинаковыми элементами. Вот здесь начнется самое интересное.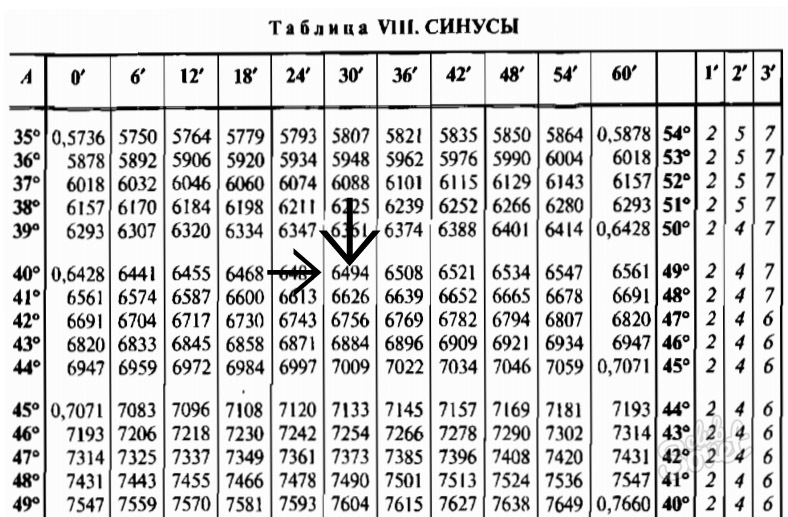
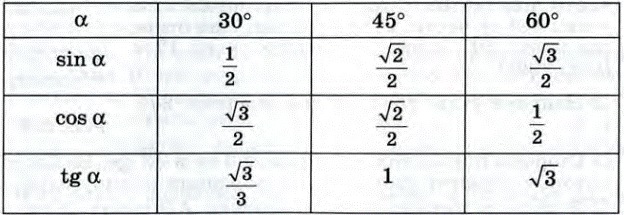
 Это не математическое действие.
Это не математическое действие.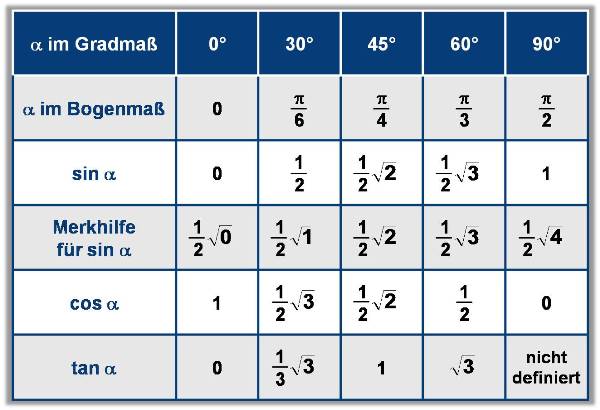 Какой еще туалет?
Какой еще туалет?
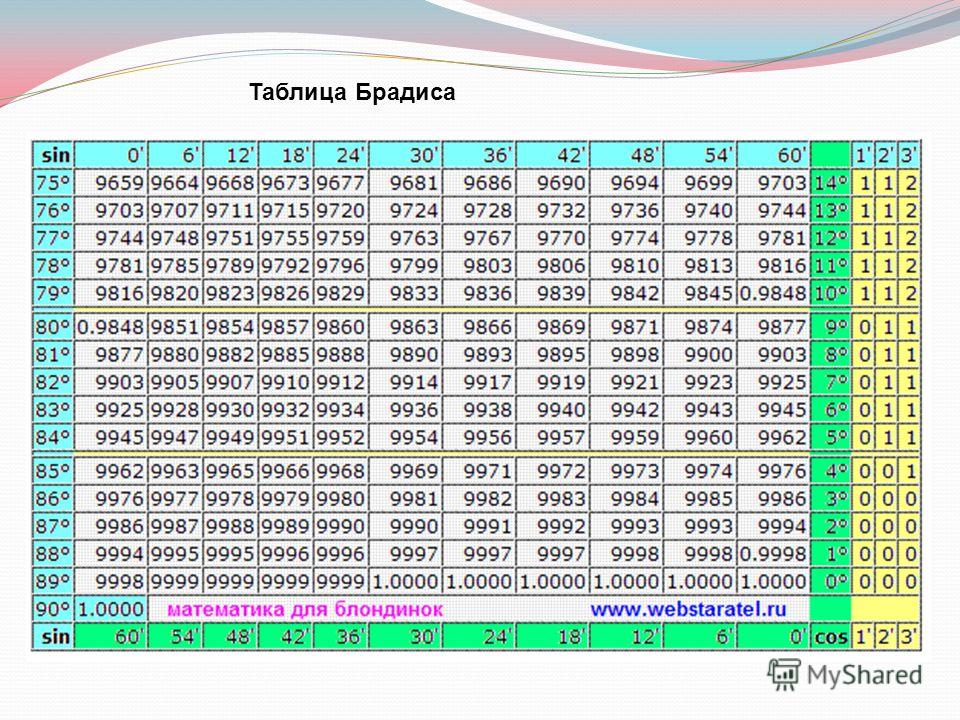
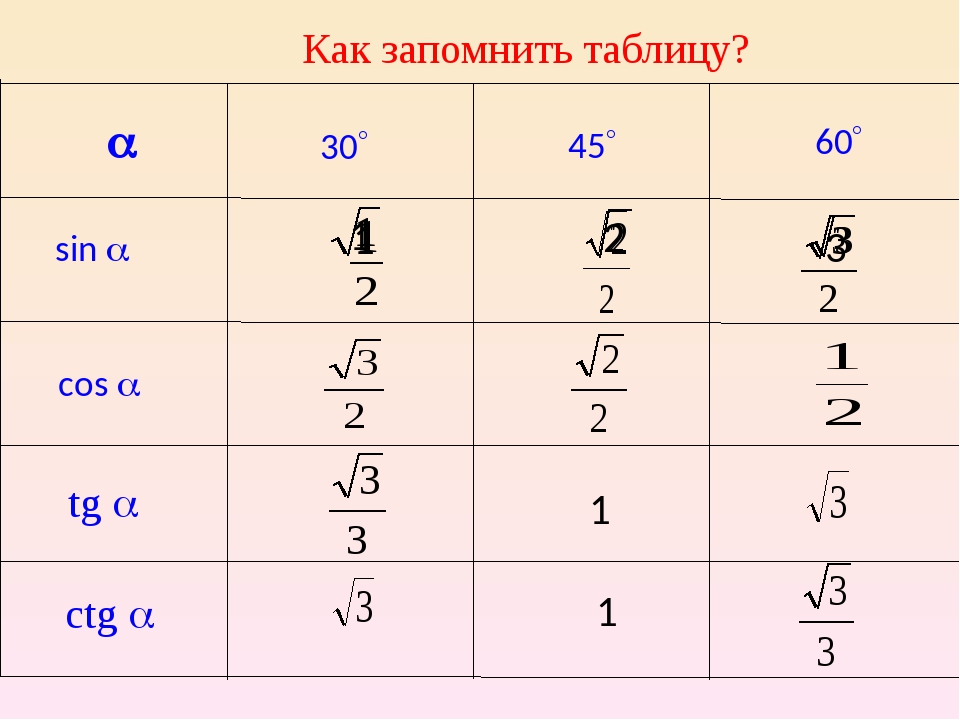
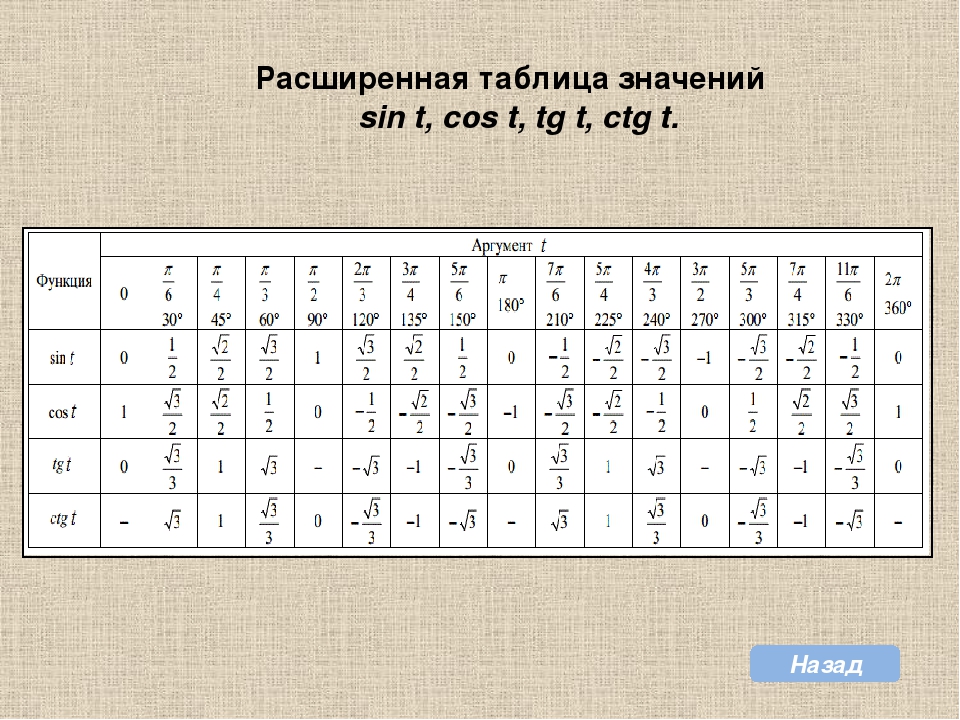 Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики.
Следующий шаг. Выделим таблицу и вызовем
Мастер диаграмм. На первом шаге выберем во
вкладке Нестандартные Гладкие графики. Во вкладке Шкала установим:
цена основного деления: 1. Во вкладке Шрифт
установим размер шрифта 8пт.
Во вкладке Шкала установим:
цена основного деления: 1. Во вкладке Шрифт
установим размер шрифта 8пт.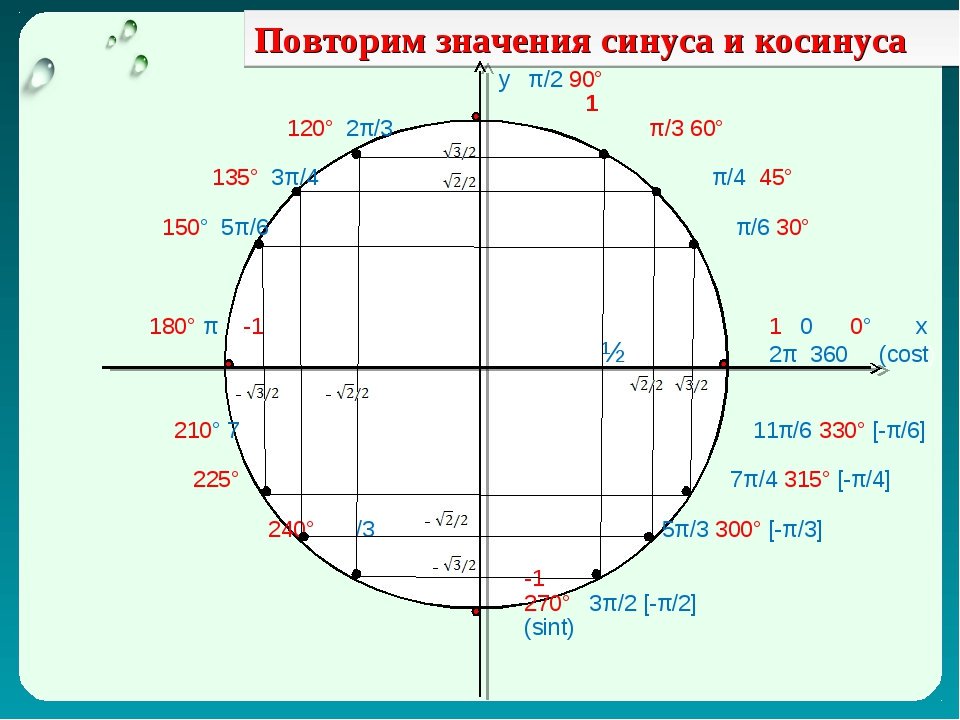 3
3 Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики.
Выделить таблицу и вызвать мастер диаграмм.
На первом шаге выбрать во второй вкладке Гладкие
графики.