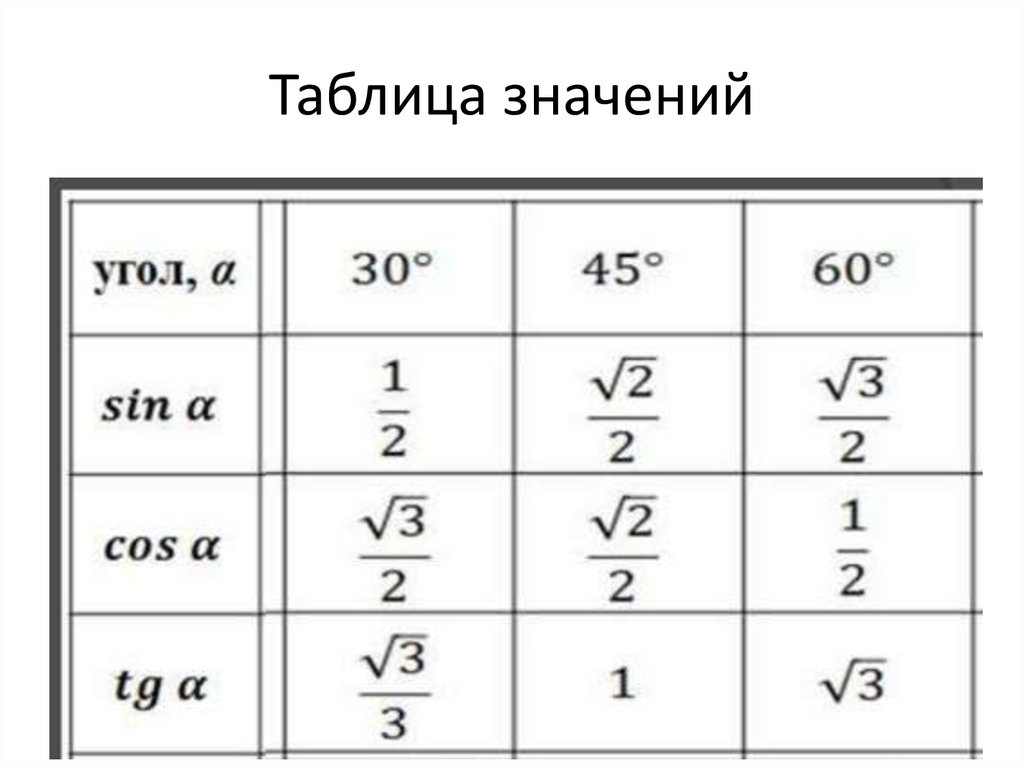
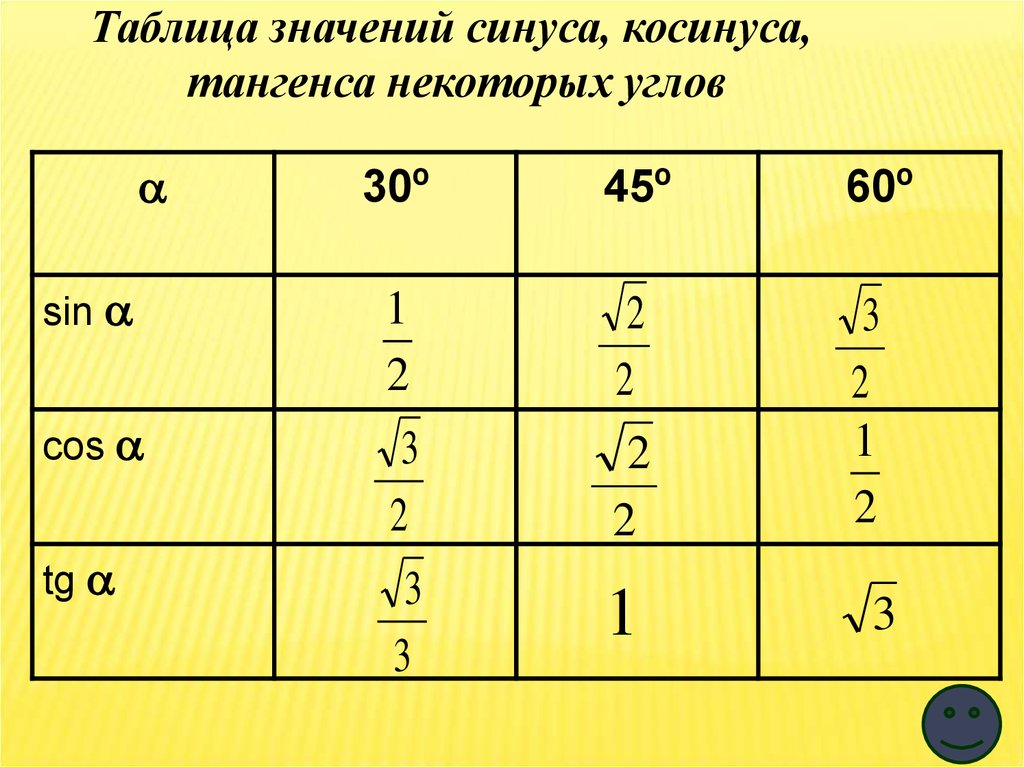
Значения косинуса и синуса таблица: Таблицы значений основных тригонометрических функций: синуса, косинуса, тангенса, котангенса

Содержание

Таблица значений синуса, косинуса и т.д

Функция	Значения
		0⁰	 	30⁰	 	45⁰	 	60⁰	 	90⁰
cosx	1								0
sinx	0								1
tgx	0				1				—
ctgx	—				1				0

Соседние файлы в папке Теория по темам

#
12. 05.201515.87 Кб12Среднее арифметическое.doc
#
12.05.201518.43 Кб13Средняя линия.doc
#
12.05.201522.53 Кб13Степенная функция.doc
#
12.05.201528.16 Кб13Степень.doc
#
12.05.201524.06 Кб12Сумма разность векторов.doc
#
12.05.201530.72 Кб13Таблица значений синуса, косинуса и т.д..doc

#
12.05.201519.46 Кб16Теорема Виета.doc
#
12.05.201520.48 Кб21Теорема косинусов.doc
#
12.05.201520.48 Кб17Трапеция.doc
#
12.05.201522.02 Кб14Углы на плоскости.doc
#
12.05.201518.43 Кб15Уравнение движения.doc

Таблица синусов и косинусов — онлайн справочник для студентов

Таблица синусов и косинусов

Таблица 1

Используя эту таблицу, вы можете найти стандартное значение синуса или косинуса.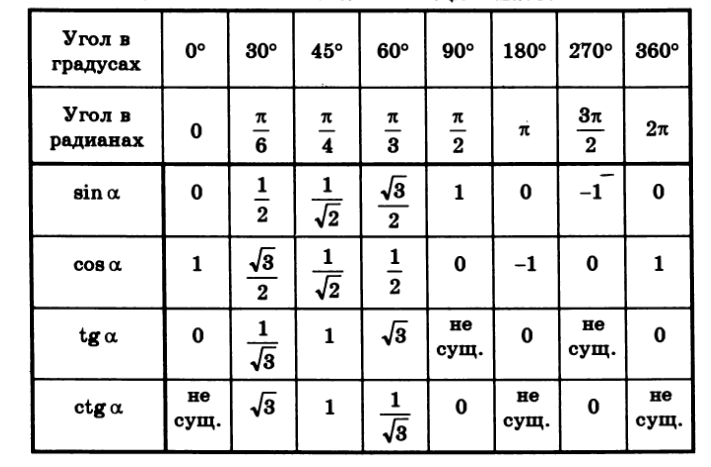 Желаемое значение будет находиться на пересечении столбца, соответствующего данному аргументу (в радианах или градусах), и строке, соответствующей заданной функции.

Примеры решения проблем

ПРИМЕР 1

Задача

Использование таблицы значений синуса и косинуса для поиска: и

Решение

Найдите значение . В таблице значений синуса и косинуса (таблица 1) во второй строке (где углы находятся в градусах) мы находим значение . Тогда на пересечении столбца, соответствующего , и линия соответствующей синусоиды (рис.1) является искомым значением

Рис. 1

Найдем значение . В таблице 1 в первой строке (где углы указаны в радианах) находим значение . Искомое значение лежит на пересечении столбца соответствующего и строки соответствующей функции косинус (рис. 2), таким образом

Рис. 2.

Ответ

ПРИМЕР 2

Задание

Найти значение выражения:

Решение

Используя таблицу значений синусов и косинусов, найдем значения и (рис. 3).

Рис. 3

Подставляя найденные значения в исходное выражение, получим

Ответ

Физика

166

Реклама и PR

Педагогика

Психология

Социология

Астрономия

Биология

Культурология

Экология

Право и юриспруденция

Политология

Экономика

Финансы

История

Философия

Информатика

Право

Информационные технологии

Экономическая теория

Менеджент

719

Математика

338

Химия

Микро- и макроэкономика

Медицина

Государственное и муниципальное управление

География

542

Информационная безопасность

Аудит

Безопасность жизнедеятельности

Архитектура и строительство

Банковское дело

Рынок ценных бумаг

Менеджмент организации

Маркетинг

238

Кредит

Инвестиции

Журналистика

Конфликтология

Этика

Формулы дифференцирования Свойства тригонометрических функций Графики тригонометрических функций Тригонометрические неравенства и их решения Тригонометрические формулы понижения степени

Узнать цену работы

Узнай цену

своей работы

Имя

Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое

Принимаю Политику конфиденциальности

Подпишись на рассылку, чтобы не пропустить информацию об акциях

Тригонометрическая таблица всех углов в радианах

Вы хотите изучать тригонометрию, но чувствуете себя запутанным с тригонометрической таблицей всех углов ? Ну, мы получили вашу спину здесь, так как мы облегчим ваше понимание.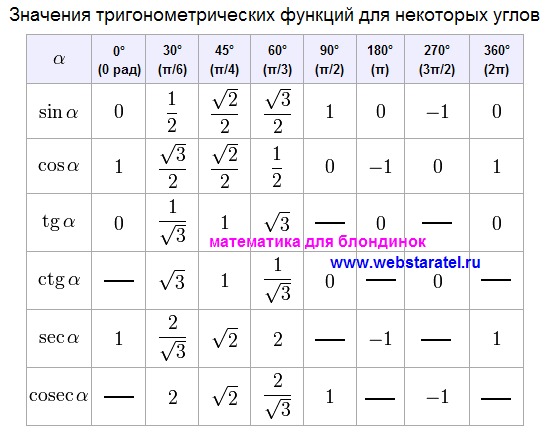 В статье будет объяснено значение таблицы тригонометрии в контексте тригонометрии.

Формула интегрирования
Формула тригонометрии
Тригонометрические соотношения
Тригонометрические функции с формулами
Что такое тригонометрические производные

Высота и расстояние
Тригонометрическая формула, включающая сумму разностей идентичностей продуктов
Триггерные идентификаторы
Теорема Пифагора
Формула дифференциации
Основные идентификаторы триггеров

Таблица тригонометрии является неотъемлемой частью тригонометрии, поскольку она содержит всю структуру тригонометрии. Проще говоря, таблица тригонометрии определяет и указывает значение тригонометрических соотношений. Он включает в себя такие соотношения, как синус, косинус, секанс и т. д. Они также известны как функции тригонометрии. Таким образом, с таблицей тригонометрии можно легко узнать значение этих отношений или функций.

Таблица тригонометрии поэтому очень важна, так как без этой таблицы нельзя решать различные задачи тригонометрии. Вы можете обратиться к таблице тригонометрии, чтобы узнать значения различных тригонометрических функций. Таблица также показывает, как тригонометрические функции или отношения остаются связанными друг с другом.

Однако вариация может быть и в том случае, когда вы берете разные тригонометрические соотношения. Основное использование функций тригонометрии заключается в общем измерении прямоугольного треугольника. С помощью правильных формул тригонометрии вы можете определить общую площадь данного треугольника.

Тригонометрическая таблица в радианах

Ну, как мы все знаем, тригонометрические таблицы очень важны в области математики. Однако есть ряд других мест, где эта таблица имеет значение. До появления компьютерных технологий таблицы тригонометрии были очень полезны в области науки, техники и даже навигации. Именно после внедрения современных технологий таблица тригонометрии потеряла свою актуальность.

В настоящее время основное использование этой таблицы ограничивается только математикой. Ученые обычно запоминают таблицы, чтобы легко вводить различные значения в вопрос. У них также есть возможность понять происхождение основ тригонометрических таблиц для их окончательного понимания.

Часто задаваемые вопросы по тригонометрической таблице всех углов в радианах :

Q : Что такое тригонометрическая таблица?

A: Тригонометрическая таблица — это таблица, в которой перечислены значения тригонометрических функций для определенных углов. Эти таблицы используются в математике, естественных науках и технике для упрощения вычислений с использованием углов и треугольников.

Q : Что такое тригонометрические функции?

A: Тригонометрические функции — это шесть математических функций, которые связывают углы прямоугольного треугольника с длинами его сторон.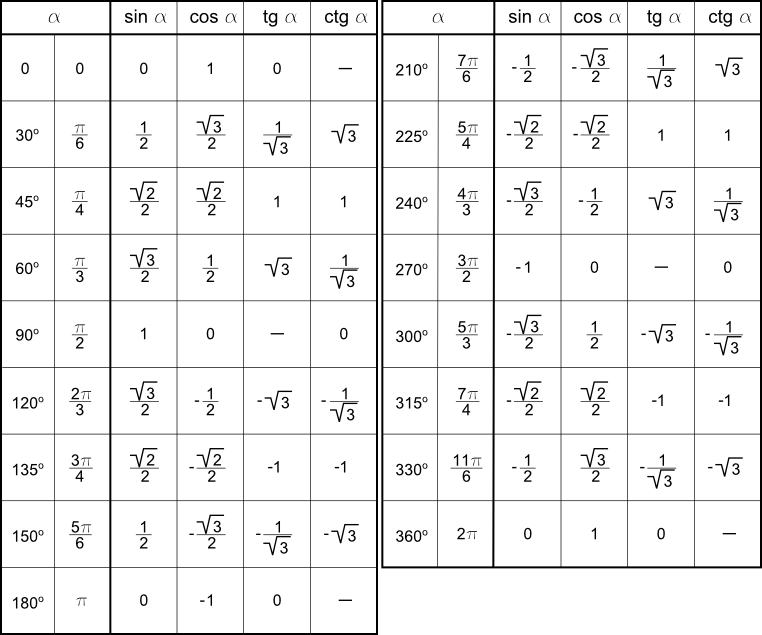 Шесть функций: синус, косинус, тангенс, косеканс, секанс и котангенс.

В: Что такое радианы?

О: Радианы — это единица измерения углов. Один радиан определяется как угол, образуемый в центре окружности дугой, длина которой равна радиусу окружности. Радианы используются в математике и естественных науках, потому что у них есть некоторые свойства, облегчающие работу с ними, чем с другими единицами измерения угла.

Q: Что такое тригонометрическая таблица всех углов в радианах?

A: Тригонометрическая таблица всех углов в радианах — это таблица, в которой перечислены значения шести тригонометрических функций для каждого угла от 0 до 2π радиан (или от 0 до 360 градусов).

В: Зачем мне тригонометрическая таблица?

О: Вы можете использовать тригонометрическую таблицу, если вам нужно выполнить вычисления с использованием углов и тригонометрических функций. Например, если вам нужно найти синус угла, вы можете найти значение синуса для этого угла в таблице, а не вычислять его самостоятельно.

Q: Как читать тригонометрическую таблицу?

О: Чтобы прочитать тригонометрическую таблицу, сначала найдите строку, соответствующую интересующему вас углу. Затем прочитайте строку, чтобы найти значения шести тригонометрических функций для этого угла.

В: Есть ли какие-нибудь хитрости или хитрости для работы с тригонометрической таблицей?

О: Да, есть некоторые хитрости и хитрости, которые можно использовать для облегчения работы с тригонометрической таблицей. Например, вы можете использовать тот факт, что функция синуса является нечетной функцией, а функция косинуса — четной функцией, чтобы быстро найти значения этих функций для определенных углов.

Q: Можно ли использовать калькулятор вместо тригонометрической таблицы?

О: Да, большинство научных калькуляторов имеют встроенные тригонометрические функции, которые можно использовать для быстрого нахождения значений синуса, косинуса, тангенса и других тригонометрических функций для любого угла. Однако в некоторых ситуациях тригонометрическая таблица может быть полезна, например, при работе с историческими или нестандартными единицами измерения углов.

В: Насколько точны тригонометрические таблицы?

О: Тригонометрические таблицы могут быть очень точными, но уровень точности зависит от количества знаков после запятой, используемых в таблице. Большинство таблиц содержат значения, округленные до нескольких знаков после запятой, но если вам нужна большая точность, вам может потребоваться выполнить собственные расчеты, используя более точный метод.

Тригонометрическая таблица — математика GCSE

Введение

Как пользоваться тригонометрической таблицей

Рабочий лист таблицы тригонометрии

Распространенные заблуждения

Практические вопросы по таблице тригонометрии

Таблица тригонометрии GCSE вопросы

Контрольный список обучения

Следующие уроки

После GCSE

Все еще застряли?

Индивидуальные занятия по математике, созданные для успеха KS4

Еженедельные онлайн-уроки повторения математики GCSE теперь доступны

Узнать больше

Введение

Как пользоваться таблицей тригонометрии

Рабочий лист таблицы тригонометрии

Распространенные заблуждения

Практические вопросы по таблице тригонометрии

Таблица тригонометрии GCSE вопросы

Контрольный список обучения

Следующие уроки

После GCSE

Все еще застряли?

Здесь мы узнаем о таблице тригонометрии.

Существуют также тригонометрические таблицы , основанные на экзаменационных вопросах Edexcel, AQA и OCR, а также дополнительные рекомендации о том, что делать дальше, если вы все еще застряли.

Что такое тригонометрическая таблица?

Тригонометрическая таблица представляет собой таблицу точных значений , которые встречаются для конкретного угла для каждой из трех тригонометрических функций – синуса 9{\ круг}.

Используя эти треугольники и тригонометрические отношения синуса, косинуса и тангенса, мы можем заполнить таблицу тригонометрии.

9 0219 \ загар {\ theta}=\frac{O}{A}


\sin{\theta}=\frac{O}{H}	\cos{\theta}=\frac{A}{H}

Синус угла \textbf{θ} есть отношение противоположного и гипотенузы . {\ circ}, мы имеем, 9{2}&=3\\\\ x&=\sqrt{3} \end{выровнено}

Пошаговое руководство: Теорема Пифагора

Это означает, что высота прямоугольного треугольника равна квадратному корню из 3 \ см \ (\sqrt{3} \ см). Разметив это на прямоугольном треугольнике, мы получим

. Если бы мы использовали подобных треугольника , длина каждой стороны увеличилась бы или уменьшилась бы на один и тот же масштабный коэффициент , а углов остались бы теми же . Это означает, что даже если бы мы начали с равностороннего треугольника с длиной стороны x, мы смогли бы получить точно такой же треугольник, как и выше, разделив все длины сторон на коэффициент масштабирования. 9{2}&=2\\\\ x&=\sqrt{2} \end{выровнено}

Итак, длина гипотенузы треугольника B равна \sqrt{2} \ cm.

Длины сторон любого подобного треугольника будут увеличены, но углы останутся прежними, поэтому любой треугольник, содержащий эти углы, будет иметь такое же отношение длин сторон. {\circ}. 9{\circ}, O=\sqrt{3} и A=1, имеем \tan(60)=\frac{\sqrt{3}}{1}=\sqrt{3}.

Это означает, что точное тригонометрическое значение \tan(60) равно \sqrt{3}.

Заполнение тригонометрической таблицы этими значениями дает нам

Прежде чем мы перейдем к треугольнику B, давайте быстро рассмотрим некоторые общие значения в таблице.

Мы видим, что в приведенной выше таблице \sin(30)=\frac{1}{2} и \cos(60)=\frac{1}{2}.

Это означает, что \sin(30)=\cos(60). 9{\circ}, O=1 и A=1, имеем \tan(45)=\frac{1}{1}=1.

Это означает, что точное тригонометрическое значение для \tan(45) равно 1.

Заполнение тригонометрической таблицы этими значениями дает нам

Прежде чем мы перейдем к остальным значениям в таблице, давайте кратко рассмотрим их. новые ценности.

Мы видим, что в приведенной выше таблице \sin(45)=\frac{1}{\sqrt{2}} и \cos(45)=\frac{1}{\sqrt{2}}.

Это означает, что \sin(45)=\cos(45).

9{\circ} угол при вершине становится меньше, длина противоположной стороны должна уменьшаться, а гипотенуза должна уменьшаться, так как она стремится к длине соседней стороны. Это имеет разные результаты для каждой тригонометрической функции.
Поскольку \sin(\theta)=\frac{O}{H} и противоположная сторона становится меньше (стремясь к 0 ), \sin(0) также должна стремиться к 0. Это дает нам значение \ грех(0)=0.
Так как \cos(\theta)=\frac{A}{H} и гипотенуза стремится к длине прилежащей стороны, \cos(0) должно стремиться к 1, так как мы делим примыкающую сторону на прилежащую сторону. Это дает нам значение \cos(0)=1. 9{\circ} угол внизу увеличивается, длина противоположной стороны должна увеличиваться, а гипотенуза должна увеличиваться, поскольку она стремится к длине противоположной стороны. Это имеет разные результаты для каждой тригонометрической функции.
Поскольку \sin(\theta)=\frac{O}{H} и гипотенуза стремится к длине противоположной стороны, \sin(90) также должна стремиться к 1, так как мы разделим противоположную сторону на противоположная сторона. Это дает нам значение \sin(90)=1.
Так как \cos(\theta)=\frac{A}{H} и гипотенуза становится длиннее, \cos(0) должно стремиться к 0, так как мы делим смежную сторону на очень большое значение гипотенузы, что делает результат невероятно мал, как если бы он был равен 0. Это дает нам значение \cos(90)=0.
Поскольку \tan(\theta)=\frac{O}{A}, а противоположная сторона становится длиннее, \tan(90) не определено, например, когда мы делим очень большое число (противоположное) на относительно небольшое число ( соседние), это может мало повлиять на очень большое число. На самом деле значение может быть бесконечно большим. Это означает, что значение \tan(90) мы используем is undefined (мы не можем присвоить этому значение).
Заполнив эти три значения в таблицу, мы получим итоговую таблицу тригонометрии.
Глядя на таблицу, мы теперь можем определить некоторые другие значения, одинаковые для разных тригонометрических функций, в том числе
\sin(0)=\cos(90)=\tan(0)=0
\sin(90)=\cos(0)=\tan(45)=1
Как пользоваться таблицей тригонометрии
Для расчета с использованием точных значений тригонометрии из таблицы тригонометрии:
Вызов точного значения триггера из таблицы.
Подставить значения в уравнение/выражение.
Полностью решить уравнение / упростить выражение.
Объясните, как пользоваться таблицей тригонометрии
Рабочий лист с точными значениями триггера (включает таблицу тригонометрии)
Получите бесплатный рабочий лист с таблицей тригонометрических значений, содержащей более 20 вопросов и ответов по точным значениям триггера. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Икс
Рабочий лист с точными значениями триггера (включает таблицу тригонометрии)
Получите бесплатную рабочую таблицу тригонометрических значений с более чем 20 вопросами и ответами на точные тригонометрические значения. Включает рассуждения и прикладные вопросы.
СКАЧАТЬ БЕСПЛАТНО
Примеры таблиц тригонометрии
Пример 1: умножение точного значения триггера на целое число
Вычислите точное значение 4\cos(30).
Вызов точного значения триггера из таблицы.
Точное значение триггера \cos(30)=\frac{\sqrt{3}}{2}.
2 Подставить значения в уравнение/выражение.
Подставив значение \cos 30 в это выражение, мы получим 4\cos(30)=4\times\frac{\sqrt{3}}{2}.
3 Полностью решить уравнение / упростить выражение.
4 \ times \ frac {\ sqrt {3}} {2} = \ frac {4 \ sqrt {3}} {2} = 2 \ sqrt {3}
Пример 2: упрощение выражений с помощью таблицы тригонометрии
Упростите выражение 2\sin(45)\cos(45)-4\sin(30).
Вызов точного значения триггера из таблицы.
Точное значение триггера \sin(45)=\frac{1}{\sqrt{2}}.

Точное значение триггера \cos(45)=\frac{1}{\sqrt{2}}.

Точное значение триггера \sin(30)=\frac{1}{2}.
Подставить значения в уравнение/выражение.
Подставляя значение \sin{45}, значение \cos{45} и значение \sin{30} в выражение, мы имеем

2\sin(45)\cos(45)-4\sin(30)=2\times\frac{1}{\sqrt{2}}\times\frac{1}{\sqrt{2} }-4\times\frac{1}{2}.
Решить уравнение / полностью упростить выражение.
\begin{выровнено} &2\times\frac{1}{\sqrt{2}}\times\frac{1}{\sqrt{2}}-4\times\frac{1}{2}\\\\ =&2\times\frac{1}{2}-2\\\\ =&1-2\\\\ =&-1 \end{выровнено}

2\sin(45)\cos(45)-4\sin(30)=-1
Пример 3: деление surd на точное значение триггера
Вычислить значение \frac{2\sqrt{ 2}}{\cos(45)}.
Вызов точного значения триггера из таблицы.
Точное значение триггера \cos(45)=\frac{1}{\sqrt{2}}.
Подставить значения в уравнение/выражение.
Подставляя это в выражение, мы имеем

2\sqrt{2}\div\frac{1}{\sqrt{2}}.
Решить уравнение / полностью упростить выражение.
\begin{выровнено} &2\sqrt{2}\div\frac{1}{\sqrt{2}}\\\\ =&2\sqrt{2}\times\sqrt{2}\\\\ =&2\times\sqrt{4}\\\\ =&2\раз{2}\\\\ =&4 \конец{выровнено}

Значение \frac{2\sqrt{2}}{\cos(45)}=4.
Пример 4: расчет с тремя точными значениями триггера
Вычислите точное значение \sin(30)+\cos(60)-\tan(45).
Вызов точного значения триггера из таблицы.
Точное значение триггера \sin(30)=\frac{1}{2}.

Точное значение триггера \cos(60)=\frac{1}{2}.

Точное значение триггера \tan(45)=1.
Подставить значения в уравнение/выражение. 9{2}\\\\ 3y&=3\\\\ y&=1 \end{aligned}
Пример 6: решение уравнений с точными значениями триггера
Учитывая, что x=\sin(45) и y=\cos( 45), определите значение \theta уравнения \tan(\theta)=\frac{x}{y}.
Вызов точного значения триггера из таблицы.
Точное значение триггера \sin(45)=\frac{1}{\sqrt{2}}.

Точное значение триггера \cos(45)=\frac{1}{\sqrt{2}}.
Подставить значения в уравнение/выражение. 9{\circ}).
Распространенные заблуждения
Точные значения
Если вас спросят о точном значении, вы должны оставить свой ответ в грубой форме.
Нет необходимости записывать свой ответ в виде десятичной дроби и округлять. Это уже не будет точным значением.
Использование точных значений
Если вам дали ответ, вы должны четко указать, что вы использовали точное значение триггера в своей работе. 9{\circ}
3+\sqrt{3}
3+\frac{2}{\sqrt{3}}
2\sin(30)=2\times\frac{1}{2}=1.

3\tan(45)=3\times{1}=3.

1+3=4.
\frac{1}{3}
\frac{1}{2}
0,95\text{(2dp)}
\cos(30)=\frac{\sqrt{3}}{2}

9{\ круг}. Его эскиз нарисован ниже.

(a) Укажите ошибку, которую допустил Джеймс в своем наброске.

(b) Вычислите фактическую площадь треугольника, который Джеймс должен был нарисовать.

(3 балла)
Показать ответ
(a)

Любое из следующего.
Он ошибочно назвал гипотенузу перпендикулярной высотой.
Высота перпендикуляра больше гипотенузы (\sqrt{2} и 1). 9{\circ}

Определить длину прямой AE = x \ см.

(5 баллов)
Показать ответ
\tan(60)=\sqrt{3}
(1)
AE = 0,5 \ раз \ sqrt {3} = \ frac {\ sqrt {3}} {2}
(1)
Масштабный коэффициент 1\дел 0,5=2 .
(1)
х = AD = 2 \ раз \ гидроразрыва {\ sqrt {3}} {2}
(1) 9{\circ}
Beyond GCSE
Другие тригонометрические функции, охватываемые на уровне A, включают,
Секанс
Функция секанса (сек) равна 1, деленной на косинус угла.
No related posts.