Внеклассный урок — Тригонометрическая таблица
Тригонометрическая таблицаЗначения синусов, косинусов, тангенсов и катангенсов для углов 0°, 30°, 45°, 60°, 90°, 120°, 135°,
150°, 180°, 210°, 225°, 240°, 270°, 300°, 315°, 330° и 360°, а также значения этих углов в радианах.
Радианы | Градусы | Косинус | Синус | Тангенс | Котангенс |
|
|
|
|
|
|
π |
| √3 | 1 | √3 |
|
π |
| √2 | √2 |
|
|
π |
| 1 | √3 | | √3 |
π |
|
|
|
|
|
2π |
| 1 | √3 | | √3 |
3π |
| √2 | √2 |
|
|
5π |
| √3 | 1 | √3 |
|
|
| | |
|
|
7π |
| √3 | 1 | √3 |
|
5π |
| √2 | √2 |
|
|
4π |
| 1 | √3 | | √3 |
3π |
|
| |
|
|
5π |
| 1 | √3 | | √3 |
7π |
| √2 | √2 |
|
|
11π |
| √3 | 1 | √3 |
|
|
| | |
|
|
Радианы | Градусы | Косинус | Синус | Тангенс | Котангенс |
Примечание 1:
— функция не имеет смысла.
Примечание 2:
В некоторых таблицах значения тангенса и котангенса, равные модулю √3/3, указаны как 1/√3. Ошибки тут нет, так как это равнозначные числа. Если числитель и знаменатель числа 1/√3 умножить на √3, то получим √3/3.
Таблица значений тригонометрических функций | Cubens
Тригонометрическая таблица. Таблица Брадиса. Таблица косинусов. Таблица синусов. Таблица тангенсов. Таблица контангенсів. Таблица тригонометрических функций.
- Таблица Брадиса косинусов, синусов, тангенсов, котангенсів
- Таблица косинусов
- Таблица синусов
- Таблица тангенсов
- Таблица котангенсів
Справочник
- Числа и выражения
- Делимость целых чисел, признаки делимости
- Простые и составные числа простые делители
- Наибольший общий делитель и наименьшее общее кратное
- Проценты, процент от числа
- Действительные числа, числовые множества
- Пропорции и отношения, прямая и обратная пропорциональность
- Модуль числа и свойства модуля
- Среднее арифметическое и среднее геометрическое
- Алгебраические выражения, одночлен и многочлен
- Формулы сокращенного умножения
- Многочлен.

- Формулы Виета и корни многочлена
- Степень, свойства степеней
- Корень n-го степеня, свойства корней n-ой степени
- Логарифм числа, свойства логарифмов
- Последовательности чисел, метод математической индукции
- Арифметическая прогрессия, сумма арифметической прогрессии
- Геометрическая прогрессия, сумма геометрической прогрессии
- Уравнения и неравенства
- Уравнения с одной переменной, область допустимых значений уравнения
- Неравенство с одной переменной ОДЗ неравенства
- Схема решению уравнений, замена переменных
- Решению неравенств, метод интервалов
- Системы уравнений, решению систем линейных уравнений
- Системы неравенств, решению систем линейных неравенств
- Линейные уравнения и неравенства
- Квадратное уравнение, теорема Виета
- Квадратное неравенство
- Дробные уравнения, как розвязати дробное уравнение
- Дробные неравенства, как розвязати дробное неравенство
- Уравнения и неравенства с модулями, геометрический смысл модуля
- Иррациональные уравнения
- Иррациональные неравенства
- Показательные уравнения
- Показательные неравенства
- Показниково-степенные уравнения
- Логарифмические уравнения
- Логарифмические неравенства
- Системы линейных уравнений
- Функции и графики
- Функция, область определения и множество значений функции
- Область определения функции
- График функции
- Четные функции, нечетные функции
- Свойства функций
- Возрастающие функции, убывающие функции
- Непрерывность функции
- Периодичность функции
- Обратная функция
- Асимптоты графика функции
- Элементарные преобразования графика функции
- Линейная функция, график линейной функции
- Дробно-линейная функция
- Квадратичная функция, график квадратичной функции
- Функция корня, график функции корня
- Степенная функция
- Показательная функция, график показательной функции
- Логарифмическая функция, график логарифмической функции
- Алгебра и начала анализа
- Предел функции
- Предел функции в бесконечности
- Вычисление предела функции
- Производная функции, найти производную функции
- Таблица производных
- Применение производной к исследованию функции
- Дифференциал функции, нахождение дифференциала
- Вторая производная, точка перегиба
- Исследование функции, построение графика функции
- Первообразная и интеграл
- Определенный интеграл
- Вычисление площадей и объемов с помощью определенного интеграла
- Тригонометрия
- Тригонометрия.
 Измерение углов
Измерение углов
- Тригонометрия.
- Комбинаторика
- Перестановки
- Дробные числа
- Обыкновенные дроби, виды дробей
- Десятичные дроби
- Деление десятичных дробей, умножения десятичных дробей
- Сокращение дробей, возведение дробей к общему знаменателю
- Умножение дробей
- Сложение и вычитание дробей
- Деление дробей
- Преобразование неправильной дроби в смешанное число
- Преобразование смешанного числа в неправильную дробь
- Преобразование десятичных дробей в обыкновенные дроби
- Среднее арифметическое
- Обучение по скайпу
- Математика по скайпу с репетитором
- 5 советов программистам на успешное собеседование
- Что такое ГДЗ и для чего оно нужно?
- База «Библиофонд» — лучшие рефераты и сочинения для студентов
- Курсы QA\QC, тестирование Львов
- Рабочие тетради для дошкольников Федиенко: учитесь легко и с удовольствием
- Почему стоит выбрать Logos QA Academy?
Таблицы и формулы
- Таблица умножения, таблица квадратов, таблица кубов, таблица степеней
- Таблица умножения
- Таблица квадратов
- Таблица кубов
- Таблица степеней
- Таблица факторіалів
- Таблица чисел
- Таблица деления
- Таблица значений тригонометрических функций
- Таблица Брадиса косинусов, синусов, тангенсов, котангенсів
- Таблица косинусов
- Таблица синусов
- Таблица тангенсов
- Таблица котангенсів
- Таблица производных функций
- Таблица производных элементарных функций, производная функции
- Формулы сокращенного умножения
- Формулы сокращенного умножения
Классы
- 1 Класс
- 2 Класс
- 3 Класс
- 4 Класс
- 5 Класс
- 6 Класс
- 7 Класс
- 8 Класс
- 9 Класс
- 10 Класс
- 11 Класс
Использование Cookies
Если Вы будете продолжать использовать данный веб-сайт, мы предполагаем, что Вы согласны получать все файлы cookie на всех сайтах Cubens. Получить подробную информацию можно здесь.
Получить подробную информацию можно здесь.
в любое время Спасибо, я уже оформил подписку
Синус-косинус-тангенс — Исследовательский центр Гленна
Чтобы лучше понять, что и как сделали братья Райт, необходимо использовать некоторые математические идеи из
В тригонометрии есть много сложных частей, и мы не будем их рассматривать. Мы собираемся ограничиться самыми основами, которые используются при изучении самолетов. Если вы понимаете идею коэффициенты , одна переменная делится на другую переменную, вы должны понять эту страницу. Он не содержит ничего, кроме определений. Слова немного странные, но идеи очень мощные, как вы увидите.
Давайте начнем с некоторых определений и терминологии, которые мы используем на этом слайде. Прямоугольный треугольник – это трехсторонняя фигура, один из углов которой равен 90 градусов. Угол 90 градусов называется прямым углом , отсюда и название прямоугольного треугольника. Мы выбираем один из двух оставшихся углов и обозначаем его 9.0006 c и третий угол мы обозначим d . Сумма углов любого треугольника равна 180 градусам. Если мы знаем значение c , то мы знаем, что значение d :
Прямоугольный треугольник – это трехсторонняя фигура, один из углов которой равен 90 градусов. Угол 90 градусов называется прямым углом , отсюда и название прямоугольного треугольника. Мы выбираем один из двух оставшихся углов и обозначаем его 9.0006 c и третий угол мы обозначим d . Сумма углов любого треугольника равна 180 градусам. Если мы знаем значение c , то мы знаем, что значение d :
90 + c + d = 180
d = 180 – 90 – c
d = 90 – c
Определяем сторона треугольника, противоположная прямому углу, будет гипотенузой . Это самая длинная сторона из трех сторон прямоугольного треугольника. Слово «гипотенуза» происходит от греческих слов «сторона» и «растягиваться», так как это самая длинная сторона. Обозначим гипотенузу символом 9.0006 ч . Существует сторона, противоположная углу c , которую мы обозначаем o для «противоположной». Оставшуюся сторону мы помечаем и как «прилегающая».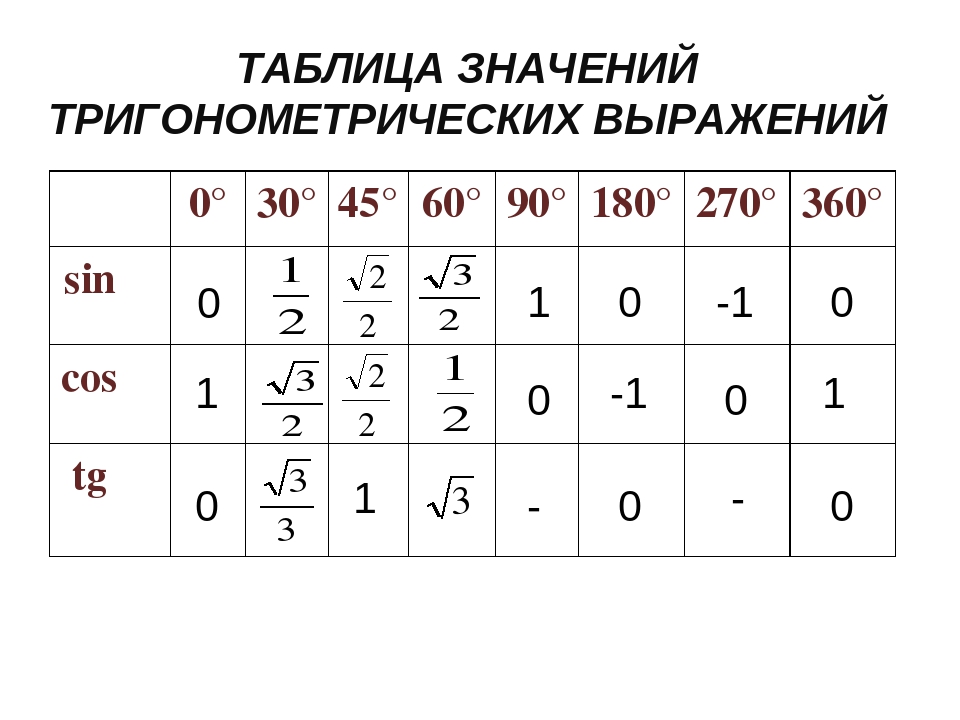 Угол c образован пересечением гипотенузы h и прилежащей стороны a .
Угол c образован пересечением гипотенузы h и прилежащей стороны a .
Нас интересуют отношения между сторонами и углами прямоугольного треугольника. Хотя длина любой стороны прямоугольного треугольника совершенно произвольна, отношение сторон прямоугольного треугольника зависят только от величины угла «с». Мы иллюстрируем этот факт в нижней части этой страницы.
Начнем с некоторых определений. Отношение противоположной стороны прямоугольного треугольника к гипотенузе мы назовем синусом и обозначим его sin .
sin(c) = o / h
Отношение прилежащей стороны прямоугольного треугольника к гипотенузе называется косинусом и обозначается символом cos .
cos(c) = а/ч
Наконец, отношение противолежащей стороны к прилежащей стороне называется тангенсом и обозначается символом tan .
tan(c) = o / a
Мы утверждаем, что значение каждого отношения зависит только от величины угла c , образованного прилежащим и гипотенузой. Чтобы продемонстрировать этот факт, давайте изучим три фигуры в середине страницы. В этом примере у нас есть 8-футовая лестница, которую мы собираемся прислонить к стене. Стена имеет высоту 8 футов, и мы нарисовали белые линии на стене и синие линии вдоль земли с интервалом в один фут. Длина лестницы фиксированная. Если мы наклоним лестницу так, чтобы ее основание находилось в 2 футах от стены, лестница образует с землей угол около 75,5 градусов. Лестница, земля и стена образуют прямоугольный треугольник. Отношение расстояния от стены (а – примыкающей) к длине лестницы (h – гипотенуза) равно 2/8 = 0,25. Это определяется как косинус с = 75,5 градусов. (На другой странице мы покажем, что если бы лестница была в два раза длиннее (16 футов) и наклонена под тем же углом (75,5 градусов), то она располагалась бы в два раза дальше (4 фута) от стены. Соотношение остается одинаковым для любого прямоугольного треугольника с углом 75,5 градусов.) Если мы измерим точку на стене, где лестница соприкасается (o — напротив), расстояние составит 7,745 фута.
Чтобы продемонстрировать этот факт, давайте изучим три фигуры в середине страницы. В этом примере у нас есть 8-футовая лестница, которую мы собираемся прислонить к стене. Стена имеет высоту 8 футов, и мы нарисовали белые линии на стене и синие линии вдоль земли с интервалом в один фут. Длина лестницы фиксированная. Если мы наклоним лестницу так, чтобы ее основание находилось в 2 футах от стены, лестница образует с землей угол около 75,5 градусов. Лестница, земля и стена образуют прямоугольный треугольник. Отношение расстояния от стены (а – примыкающей) к длине лестницы (h – гипотенуза) равно 2/8 = 0,25. Это определяется как косинус с = 75,5 градусов. (На другой странице мы покажем, что если бы лестница была в два раза длиннее (16 футов) и наклонена под тем же углом (75,5 градусов), то она располагалась бы в два раза дальше (4 фута) от стены. Соотношение остается одинаковым для любого прямоугольного треугольника с углом 75,5 градусов.) Если мы измерим точку на стене, где лестница соприкасается (o — напротив), расстояние составит 7,745 фута. Вы можете проверить это расстояние, используя Теорему Пифагора , которая связывает стороны прямоугольного треугольника: 92 = 64 – 4 = 60
Вы можете проверить это расстояние, используя Теорему Пифагора , которая связывает стороны прямоугольного треугольника: 92 = 64 – 4 = 60
o = 7,745
Отношение, противоположное гипотенузе, равно 0,967 и определяется как синус угла c = 75,5 градусов.
Теперь предположим, что мы наклонили 8-футовую лестницу так, чтобы ее основание было в 4 футах от стены. Как показано на рисунке, теперь лестница наклонена под меньшим углом, чем в первом примере. Угол равен 60 градусам, а отношение прилежащего к гипотенузе теперь равно 4/8 = 0,5. Уменьшение угла c увеличивает косинус угла, потому что гипотенуза фиксирована, а прилежащая к ней высота увеличивается по мере уменьшения угла. Если мы наклоним 8-футовую лестницу так, чтобы ее основание находилось на расстоянии 6 футов от стены, угол уменьшится примерно до 41,4 градуса, а отношение увеличится до 6/8, что составляет 0,75. Как видите, для каждого угла существует уникальная точка на земле, которой касается 8-футовая лестница, и это одна и та же точка каждый раз, когда мы устанавливаем лестницу под этим углом. Математики называют эту ситуацию функцией. Отношение прилежащего катета к гипотенузе зависит от угла c , поэтому мы можем записать символ как cos(c) = value .
Математики называют эту ситуацию функцией. Отношение прилежащего катета к гипотенузе зависит от угла c , поэтому мы можем записать символ как cos(c) = value .
Обратите также внимание, что по мере увеличения cos(c) , sin(c) уменьшается. Если мы наклоним лестницу так, чтобы основание было на расстоянии 6,938 фута от стены, угол c станет 30 градусов, а отношение прилежащего к гипотенузе равно 0,866. Сравнивая этот результат со вторым примером, мы находим, что:
cos(c = 60 градусов) = sin (c = 30 градусов)
sin(c = 60 градусов) = cos (c = 30 градусов)
Мы можем обобщить это соотношение:
sin(c) = cos (90 – c)
90 – c является величиной угла d . Вот почему мы называем отношение прилежащего к гипотенузе косинусом угла.
sin(c) = cos (d)
Поскольку синус, косинус и тангенс являются функциями угла «c», мы можем определить (измерить) отношения один раз и составить таблицы значений синуса, косинус и тангенс для различных значений «с».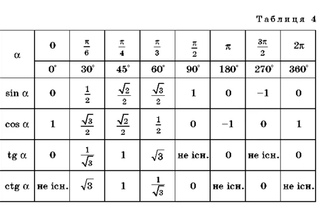 Позже, если мы знаем значение угла в прямоугольном треугольнике, таблицы сообщают нам отношение сторон треугольника. Если мы знаем длину любой стороны, мы можем найти длину других сторон. Или, если мы знаем отношение любых двух сторон прямоугольного треугольника, мы можем найти значение угла между сторонами. Мы можем использовать таблицы для решения задач. Некоторые примеры задач, связанных с треугольниками и углами, включают спуск планера, крутящий момент на шарнире, работу балансиров подъемной силы и лобового сопротивления братьев Райт, а также определение отношения подъемной силы к лобовому сопротивлению для самолета.
Позже, если мы знаем значение угла в прямоугольном треугольнике, таблицы сообщают нам отношение сторон треугольника. Если мы знаем длину любой стороны, мы можем найти длину других сторон. Или, если мы знаем отношение любых двух сторон прямоугольного треугольника, мы можем найти значение угла между сторонами. Мы можем использовать таблицы для решения задач. Некоторые примеры задач, связанных с треугольниками и углами, включают спуск планера, крутящий момент на шарнире, работу балансиров подъемной силы и лобового сопротивления братьев Райт, а также определение отношения подъемной силы к лобовому сопротивлению для самолета.
Вот таблицы синуса, косинуса и тангенса, которые вы можете использовать для решения задач.
Таблица sin(a)
Таблица sin(angle).Таблица cos(a)
Таблица cos(угла).Таблица тан(а)
Таблица тангенса(угла).Эпизод о тригонометрии | Советы и рекомендации MCAT
Последнее обновление 23 июня 2022 г., автор Лора Тернер
Я предполагаю, что к этому моменту подготовки к MCAT вы чувствуете, что припарковали самосвал, полный информации, рядом со своим столом и перелопатили факты.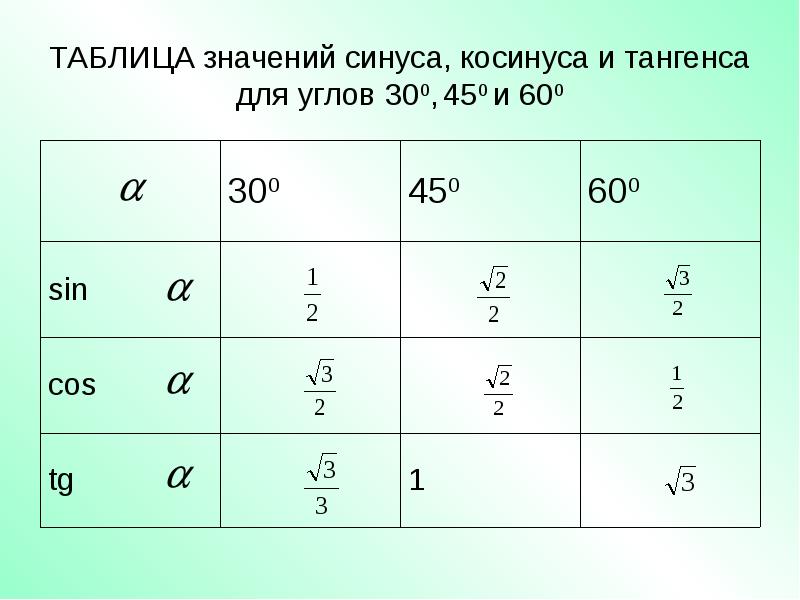 в ваш мозг, пока он не готов взорваться. А потом вы столкнулись с проблемой физики. Тот, который требует от вас знания синуса или косинуса? – 60 градусов.
в ваш мозг, пока он не готов взорваться. А потом вы столкнулись с проблемой физики. Тот, который требует от вас знания синуса или косинуса? – 60 градусов.
Вы просматриваете свой мысленный жесткий диск в поисках ссылок на тригонометрию. Есть что-то в SOH CAH TOA… и 2 и б 2 . О, Боже. Еще кое-что, что можно добавить в список «для запоминания», который разрастается до толщины вашего учебника по органической химии.
Об объявлениях
Существует множество видео и статей о том, как запомнить значения синуса и косинуса, и они являются хорошей отправной точкой, но на самом деле они не так уж полезны для MCAT. (позже мы увидим, почему). Все, что вам действительно нужно запомнить, чтобы выполнять какие-либо тригонометрические вычисления в день экзамена, это «синус — точка 5, точка 7, точка 9».». Вот и все! Давайте посмотрим, как это работает…
В разделе физики MCAT вам нужно будет уметь выполнять вычисления с синусом, косинусом и тангенсом пяти градусных мер — 0°, 30°, 45°, 60° и 90°. Если учащиеся что-нибудь помнят о тригонометрии, то это, вероятно, SOH CAH TOA (см. ниже), что напоминает нам о том, что синус (S) угла равен длине противоположной стороны треугольника (O), деленной на гипотенузу (H ), косинус (C) угла равен прилежащей стороне (A), деленной на гипотенузу (H), а тангенс (T) равен противолежащей стороне (O), деленной на прилежащую сторону (A).
Если учащиеся что-нибудь помнят о тригонометрии, то это, вероятно, SOH CAH TOA (см. ниже), что напоминает нам о том, что синус (S) угла равен длине противоположной стороны треугольника (O), деленной на гипотенузу (H ), косинус (C) угла равен прилежащей стороне (A), деленной на гипотенузу (H), а тангенс (T) равен противолежащей стороне (O), деленной на прилежащую сторону (A).
На рисунке ниже мы видим два прямоугольных треугольника, вписанных в единичную окружность: один с гипотенузой под углом 30° к оси x, а другой с гипотенузой под углом 60° к оси x. Поскольку синус = противоположность/гипотенуза (SOH), синус угла связывает длину стороны треугольника в направлении y с гипотенузой. Чтобы запомнить это, может быть полезно подумать о том, что «sine» и «y» имеют похожие звуки. Вот почему мы пишем «синус» как «син» в рифме.
По мере увеличения степени угла длина треугольника в направлении оси Y увеличивается, как и синус угла. Sin(0°) = 0, потому что «треугольник» не будет иметь длины в направлении y, и sin(90°) = 1, потому что «треугольник» будет иметь всю свою длину в направлении y.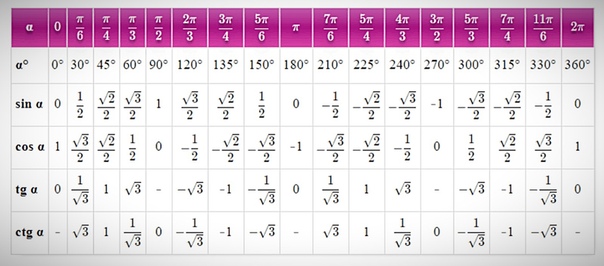
Косинус описывает отношение длины треугольника в направлении x и следует аналогичной схеме, но в обратном направлении. По мере увеличения угла длина треугольника в направлении x уменьшается, как и косинус угла. Косинус 0° = 1 и косинус 90° = 0,
Как насчет значений синуса и косинуса для остальных углов? Здесь вступают в действие точки 5, точки 7, точки 9 рифмы.
Начнем с синуса или «сина» из рифмы. Уловка, которой часто учат запоминать синус обыкновенных углов, состоит в том, чтобы начать с написания пустого знака квадратного корня, деленного на 2.
Теперь под знаком квадратного корня напишите числа 0, 1, 2, 3 и 4. чтобы.
Некоторые из этих дробей легко упрощаются до десятичных, но синус 45° и 60° — нет.
Большинство видео и статей, посвященных этой теме, оставляют вас здесь, но, поскольку вы не можете позволить себе роскошь работать с калькулятором, запоминание величин, например, не очень помогает. Вместо этого лучше запомнить десятичные аппроксимации и , где и появляется рифма.
Если вам нужно вычислить триггер с синусоидой, вы можете быстро записать sin(0°) = 0, sin(90°) = 1 и запомнить рифму: «синус – точка 5, точка 7, точка 9(опять же «синус», потому что синус говорит нам о направлении треугольника по оси Y).
Если вы посмотрите на единичный круг, вы увидите, что значения косинуса для каждого из этих углов являются обратными значениям синуса. Таким образом, косинус 0° = 1, косинус 30° = 0,9 и т. д. Если вам нужен косинус, вы можете просто записать значения синуса, а затем расположить их в обратном порядке, запоминание не требуется.
Наконец, если вам нужен тангенс, разделите синус на косинус. Если у вас возникли проблемы с запоминанием, что на что делить, синус в таблице уже выше косинуса, поэтому вы можете думать о разделительной линии между ними как о дробной черте.
Тангенс 0°, 45° и 90° вычисляется легко. Для тангенса 30° и 60° вы можете получить «достаточно близкий» ответ, аппроксимировав 0,9 с 1.
Фактическое значение тангенса (30°) ≈ 0,57 и тангенса (60°) ≈ 1,7.
Вот это да. Имея все это в памяти, давайте решим примерную задачу:
Ребенок начинает тянуть игрушку за собой с силой 8 Н под углом 45° к земле. Начальное ускорение игрушки 2 м/с 2 . Какова масса игрушки?
a) 1,63 кг
b) 2,84 кг
c) 4,00 кг
d) 6,21 кг
Формула, связывающая силу, массу и ускорение: F = Ma. Поскольку мы хотим использовать силу и ускорение, чтобы найти массу, мы делим обе части на ускорение, чтобы получить формулу M = F/a.
Как и во многих физических задачах, полезно нарисовать схему того, что происходит. Вот ребенок тянет игрушку… гм… что-то такое.
В задаче даны сила и ускорение; однако сила 8 Н, приложенная к игрушке, находится под углом 45 °. Часть этой силы тянет игрушку в направлении y, а часть силы тянет ее в направлении x. Поскольку задача состоит в том, чтобы тянуть игрушку по земле, а не вверх, нас интересует х-компонент силы.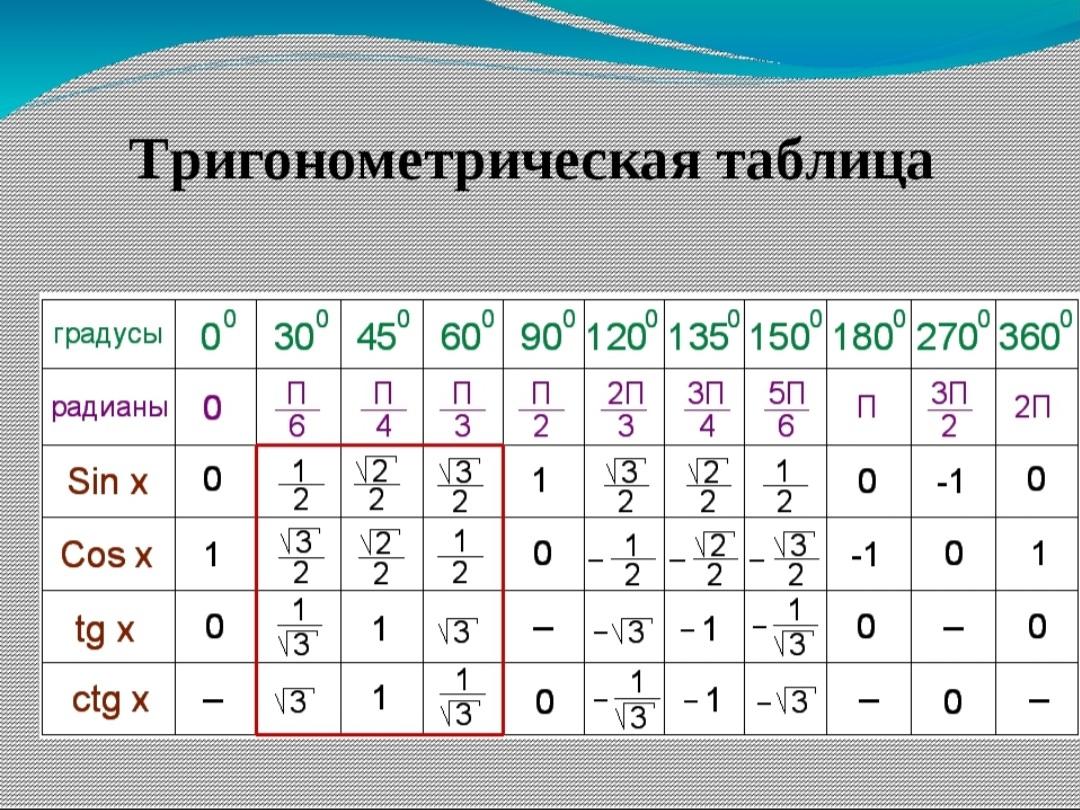
Сначала мы вспоминаем нашу рифму «синус — точка 5, точка 7, точка 9» и знаем, что в этой задаче будем использовать косинус, а не синус. Следовательно, чтобы вычислить x-составляющую силы, мы имеем F x = F * косинус (45°). Беглый взгляд на нашу таблицу значений синуса и косинуса показывает, что cos(45°) = 0,7, поэтому F x = F * косинус (45°) = 8 * 0,7 = 5,6. (Знайте свою таблицу умножения!)
Заполнение формулы M = F/a нашим новым вычисленным F х из задачи, получаем М = 5,6/2 ≈ 6/2 = 3кг, что ближе всего к ответу б) 2,84кг.
Другой пример:
Эвакуатор тянет автомобиль массой 25 000 кг с помощью буксировочного крюка, который встречает автомобиль под углом 30° к земле. Какую силу должен приложить эвакуатор, чтобы тянуть автомобиль с начальным ускорением 3 м/с 2 ?
a) 33,612N
b) 50,319N
c) 75,000N
d) 86,206N
Вот краткое изображение нашего сценария.
Здесь силу, необходимую для тяги автомобиля в направлении x, можно рассчитать по формуле F x = Ма.
В этом сценарии нам даны масса автомобиля и ускорение в задаче. Требуемая сила в направлении x равна F x = 25 000 кг * 3 м/с 90 156 2 90 157 = 75 000 Н. В экспоненциальном выражении это 7,5 x 10 4 Н.
Однако, поскольку грузовик буксирует автомобиль под углом 30°, ему потребуется большее усилие, поскольку автомобиль в обоих направлениях x и y.
В предыдущей задаче мы видели, что F x = F * cos(Θ), где Θ — градус угла, который в данном случае равен 30°. Просмотрев нашу таблицу значений синуса и косинуса, мы видим, что cos(30°) ≈ 0,9. В экспоненциальном представлении это 9 x 10 -1 .
Чтобы найти F, разделите каждую часть уравнения на cos(Θ), что дает формулу .
Мы повторно выражаем F x как 75 x 10 3 N, а не 7,5 x 10 4 N, чтобы немного упростить задачу деления.
Результат тот, который ближе всего к ответу d). Обратите внимание, что это должен быть правильный ответ, потому что это единственный вариант ответа, который превышает 75 000 Н.
Обязательно ознакомьтесь с остальными сериями советов и рекомендаций MCAT:
- Часть I. Преобразование единиц в метрической системе
- Часть II. Вычисление логарифмов без калькулятора
- Часть III. Использование приближений для решения сложных задач расчеты
- Часть IV. Преобразование единиц измерения за восемь простых шагов
Chelsea Myers
Chelsea Myers, M.Stat, является автором серии электронных книг MCAT по математике, доступных на сайте www.mcatmath.com. После десятилетней карьеры исследователя-биостатистика на факультете офтальмологии и визуальных наук Висконсинского университета в Мэдисоне она в настоящее время является профессором математики, статистики и биостатистики в Колледже Роллинза и Колледже Валенсии во Флориде. Она живет с мужем и тремя сыновьями в районе Орландо.


 Измерение углов
Измерение углов