Решение уравнений и задач: Решение задач на составление уравнений — урок. Математика, 6 класс.

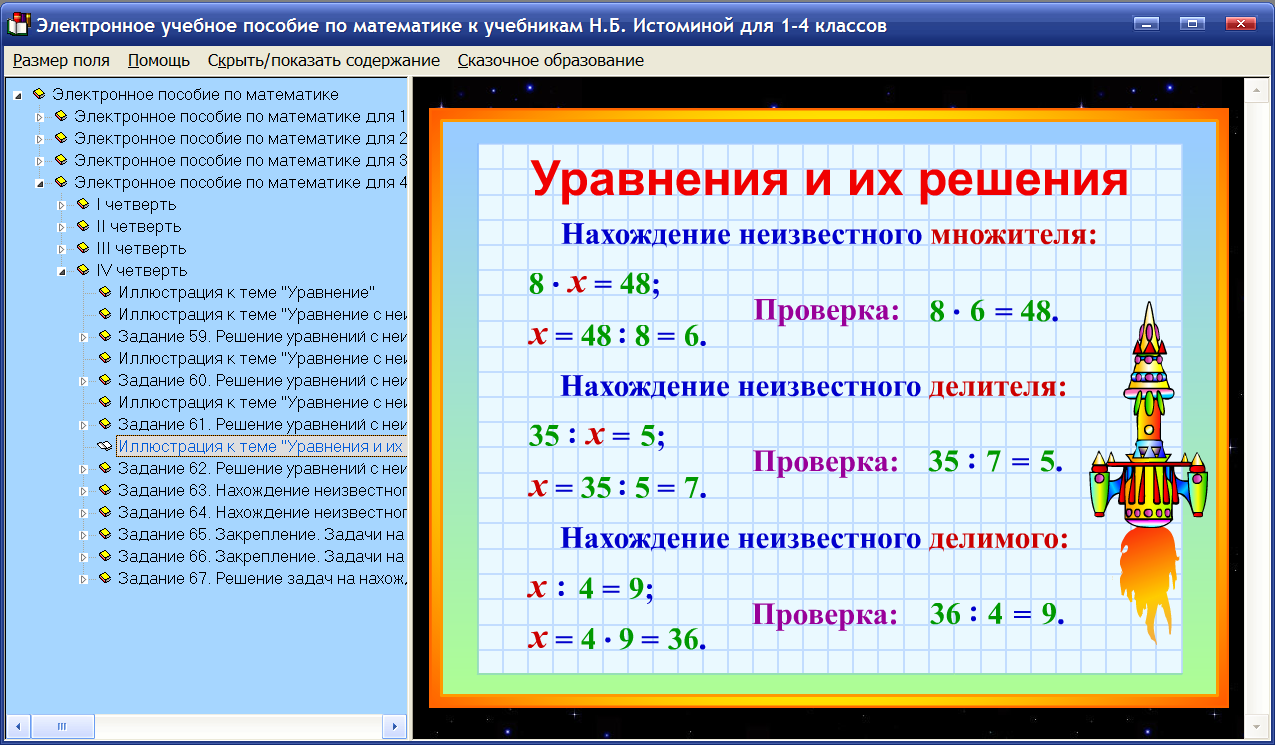
Урок математики во 2 классе. Тема «Решение уравнений и задач»

Урок математики во 2 классе

Тема урока «Решение уравнений и задач»

Цели: закрепить умение решать уравнения на сложение и вычитание с применением правил и с проверкой; формировать умение решать задачи разными способами; развить навыки счёта.

Задачи:

Предметные:

1. Закрепление навыков решения уравнений, основанные на связи между компонентами и результатами действий при сложении и вычитании.

2.Закрепление умений решать задачи разными способами.

3.Знание правила о связи между компонентами и результатами действий сложения и вычитания.

4.Совершенствование навыков счёта.

5.Осознание роли математики в познании окружающего мира.

Метапредметные:

Познавательные

1.Самостоятельное выделение и формулирование познавательной цели.

2.Построение логической цепи рассуждений.

3. Доказательство.

4.Выбор наиболее эффективных способов решения задач.

Коммуникативные

1.Формирование умений слушать и слышать.

2. Задавать вопросы и высказывать своё мнение.

Регулятивные

1.Постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что ещё неизвестно.

2.Развитие умения сличения способа действия и его результата с заданным эталоном с целью обнаружения отклонения от него.

3.Планировать свои действия. Согласовывать.

4.Оценивать свою деятельность.

Личностные

1.Развитие самостоятельности и ответственности.

2.Развитие навыков сотрудничества с одноклассниками и учителем.

Учебное пособие: М.И. Моро, С.И. Волкова. Математика. Учебник для 2-го класса. Часть 1.

Методы  и формы обучения:  частично – поисковый; индивидуальная, фронтальная, работа в парах, групповая..

Оборудование: компьютер, презентация, листы в клеточку, карточки.

Ход урока

I. Организационный момент.

— Здравствуйте, ребята! Сегодня у нас необычный урок математики, потому что к нам пришло много гостей, давайте поздороваемся с ними.
— Возьмитесь за руки и мысленно подарите добрые слова друг другу, улыбнитесь и пожелайте доброго дня.

-С какой целью вы шли на урок математики? ( считать, закрепить знания по решению задач, уравнений, примеров)

— Пригодится ли вам математика в жизни? ( при покупках, в транспорте, подсчёт пирожков, и т.д)

Мы сегодня снова будем наблюдать,

Выводы делать и рассуждать.

А чтобы урок пошёл каждому впрок,

Активно в работу включайся, дружок!

-Вы любите загадки, тогда отгадайте.

Я тепла не потерплю:

Закручу метели,

Все поляны побелю,

Разукрашу ели,

Замету снежком дома.

Потому что я — .. .   (Зима) Слайд №1

Сегодня к нам пришла Зимушка- зима, она подготовила для вас трудные математические задания, с которыми, я надеюсь, вы справитесь, а если не справитесь, она всёх заморозит, нашлёт на нас метели и вьюги, засыпет снегом. Давайте работать дружно и быстро, чтобы Зима стала доброй.

Будем работать под девизом : Слайд №2

«Тот, кто хочет много знать,

Должен сам всё постигать» —

II. Математический диктант. Слайд №3 Белый

— И так первое задание, математический диктант.

(проводится индивидуально на листиках, записывают только ответы).

Т.ж. работают по карточкам №1, у доски работают дети с примерами, по одному ученику от каждого ряда

50+30=80 90-30=60 80-20=60

41-1=40 44+1=45 30+15= 45

84-80 =4 37-20=17 74-20= 54

10+9=19 90+9=99 70+9=79

60-2=58 50-8= 42 40-3=37

Математический диктант

1. найди сумму чисел 6и 8 (14)

2. найди разность чисел 8 и 6 (2)

3. к 15+10 (25)

4. из 25-5 (20)

5. первое слагаемое 9, второе слагаемое 8, найдите значение суммы (17)

6. на сколько число 33 больше числа 30? (на 3)

7. на сколько надо увеличить 10, чтобы получилось 15? (на 5)

8. к какому числу надо прибавить 3, чтобы получилось 23 (20)

9.запиши длину ломаной, если длина первого звена 5 см, второго- 7 см (12 см)

10.запиши число, состоящее из 3 десятков и 2 единиц. (32)

А теперь проверьте. Слайд №4

1. 14

2. 2

3. 25

4. 20

5. 17

6. 3

7. 5

8. 20

9. 12см

10. 32

Проверка самостоятельно по доске (плакат с ответами)

Оценить свой математический диктант. Слайд №5

Оценивание: без ошибок -5,

1,2, ошибки- 4,

3-4 ошибок – 3

Ученики выставляют себе оценку на листах –самооценки. Слайд №6 белый

III. Введение в тему урока. Работа в группах (по рядам)

— Какое сегодня число? Что можно сказать о числе 13? (двузначное, некруглое, непарное, состоит из 1 дес. и 3 ед.) Запишите число, классная работа.

— Чтобы узнать тему нашего урока, я предлагаю вам расшифровать записи, работая в группах по рядам. (Запись темы уже на доске, но закрыта)

Работа в группах по рядам.

Расшифруйте запись

р	е	ш	е	н	и	е
30	3	10	3	6	4	3

           

30+ 0= р 10-7 = е 3+3 = н 5+5= ш 2+2= и

у	р	а	в	н	е	н	и	е
7	6	10	30	12	9	12	14	9

10-4 = р 10-3= у 8+2= а 30+0= в 6+3= е 10+2= н 9+5= и

3 ряд

з	а	д	а	ч	и
8	1	7	1	9	4

6+2= з 3+4= д 10-9= а 2 +2= и 7+2= ч

Какие слова у вас получились?

— Итак, предположите, о чем пойдет речь на уроке? Сформулируйте тему урока. (Решение уравнений и задач) Открываю тему.

Какие задачи урока поставим перед собой? (закрепить умения решать уравнения и задачи, примеры.)

На доске (открыть)

Цели: закрепить умение решать уравнения на сложение и вычитание с применением правил и с проверкой; формировать умение решать задачи разными способами; развить навыки счёта.

— Мы уже встречались с понятием уравнение. Давайте вспомним, что вы знаете об уравнении?

УРАВНЕНИЕ – это равенство, содержащее неизвестное число, которое нужно найти.

Неизвестное число обозначают латинскими буквами.

Решить уравнение – это значит найти такие значения Х, при которых равенство будет верным.

IV. Решение уравнений .

-Следующее задание от Зимы. Слайд №7. Работа в паре

-Рассмотрите записи , найдите уравнения и запишите их в тетрадь.

— Под какими номерами стоят уравнения?

1) 30 + х 40	3) 80 – а	5) 45 – 5 = 40
2) 38 – 8	4) 60 + х = 90	6) х – 8 = 10

– Докажите, что вы правы. (Можно найти значение Х, при котором равенство будет верным)

– Чем являются остальные записи? (Неравенство, буквенное выражение, равенство) Показ номера

–к доске пойдут 2 ученика и решат эти уравнения на отворотах (решают самостоятельно, затем объясняют). (Все ученики записывают уравнения в тетрадь).

1 ученик объясняет решение,

— Назовите компоненты при сложении.

(1 СЛАГАЕМОЕ, 2 , СУММА)

– Что неизвестно? (СЛАГАЕМОЕ)

– Как найти неизвестное слагаемое? (Чтобы найти неизвестное слагаемое, надо из значения суммы вычесть известное слагаемое.)

1 ученик работает у доски, а остальные записывают в тетрадях:

60 + х = 90

х = 90 – 60

х = 30

Чтобы проверить, правильно ли мы нашли корень уравнения, следует сделать проверку, для этого вместо х подставить найденное число:

60 + 30 = 90

90 = 90 Самооценка ученика. (решил самостоятельно, без помощи учителя и класса, поэтому ставлю себе 5)

2) Аналогично разбирается второе уравнение, в котором ученики находят неизвестное уменьшаемое.

(Чтобы найти неизвестное уменьшаемое, нужно к разности прибавить вычитаемое)

Запись в тетрадях и на доске (у доски работает ученик):

х – 8 = 10

х = 10 + 8

х = 18

18 – 8 = 10

10 = 10 Самооценка ученика

Оцените себя в листке самооценки

V. Физминутка. Пяточки-носочки Слайд №9

Что-то стало холодно, Зима старается нас заморозить, давайте согреемся.

Мы отлично потрудились

И немного утомились

Приготовьтесь- ка, ребята,

Танцевальная зарядка

VI. Решение уравнений. Работа в паре

1.Зима злится и предлагает выполнить следующее задание в парах. (Некоторые ученики работают по карточкам) Слайд №10

Задания на каждой парте

—Покажите номера тех уравнения, в которых значение х (икс) является число 10

1) Х+8=18 3) 47-х=40 5) 10=х+7

2) Х-3=10 4) 50-х=40

-Как вы нашли значение х?

1Ученик- Подобрал. В каждое уравнение на место икс подставил число 10, если получалось равенство, то значение икс равно числу 10.

2 ученик – Я решал…..

-Все ли записи для вас понятны?

-Является ли это выражение уравнением? Что здесь не так? (Сумма и значение суммы поменяли местами)

— Как можно по — другому записать это уравнение.

— Давайте решим другие уравнения и узнаем значение Х.

(3 ученика выходят к доске и решают, оценивают своё решение, 2 на отворотах, 1 – на открытой доске) Решают все самостоятельно. Слайд №11

VII. Работа над задачами. Выполнить задание по учебнику на стр. 82 №3 (1)

А. Фронтально разбирается задача 3 (1) (с. 82 учебника, часть 1).

– Прочитайте текст.

– Является ли он задачей? (Да. Есть условие и вопрос)

– Что в задаче известно? (было 15 м. Сшила из 5м костюм, из 4м – платье)

– О чём спрашивается? (Сколько метров ткани осталось)

Какая краткая запись подойдет к этой задаче? (разные виды записи даны на доске) Слайд № 12

– Как можно решить задачу? Ученик у доски

[I. Сначала узнать, сколько ткани портниха потратила на костюм и платье, а затем полученное число вычесть из количества имеющейся у портнихи ткани.

15 – (5 + 4) = 6.(м) осталось

Ответ: осталось 6метров ткани Самооценка

– Как по-другому можно решить задачу?

II. Сначала узнаем, сколько ткани осталось у портнихи, после того как она сшила костюм, а затем из полученного числа вычтем количество ткани, израсходованной на платье.

(15 – 5) – 4 = 6. Самооценка

III. Сначала узнаем, сколько ткани осталось у портнихи, после того как она сшила платье, а затем из полученного числа вычтем количество ткани, израсходованной на костюм.

(15 – 4) – 5 = 6)]

Б. Составьте задачу по второму чертежу

За день в магазине продали 15 м. красной ленты, 4м зелёной и 5 м. жёлтой. Сколько метров ленты продали за день?

-Самостоятельно запишите решение задачи. На отвороте 2 ученика, но записывают по разному.

1)15+4+5= 24м продали.

Ответ : 24 м ленты продали. Самооценивания ученика

2) 15+5+4= 24м

—Как удобнее было посчитать?(удобнее сгруппировать слагаемые 15 и 5, чтобы получилось круглое число, а затем прибавить 4)

Кто решил так же, молодцы оцените себя в листах — самооценки.

В. -Из каких геометрических фигур состоит третий чертёж? (отрезков)

—Посчитайте сколько отрезков на чертеже? Покажите ( 6)

VIII. Рефлексия деятельности на уроке. Слайд №15 (белый)

Выполнили ли мы задачи, которые поставили в начале урока? (На доске)

— Что же такое уравнение? (Уравнение – это равенство, содержащее неизвестное число, которое надо найти.)

— Что значит решить уравнение? (Решить уравнение – значит найти такое значение х, при котором равенство будет верным.)

— Что еще делали на уроке? (Решали уравнения, примеры и задачи.)

Кто научился решать уравнения, поднимите зелёную карточку, кто испытывает еще затруднения — жёлтую.

Молодцы! Вы отлично потрудились. Оцените свою работу на уроке. (дети показывают цветную карточку).

Я согласна с вами. За урок ученики……… получают 5, ……..получают 4.

Продолжите предложения (на доске) Слайд 16

Я доволен…..(получил хорошую отметку, на уроке было интересно)

Я теперь смогу……(решать уравнения, составлять уравнения, составлять условие задачи по чертежу)

Мне было интересно (составлять уравнения , работать в паре, в группе)

Мне было трудно…. .(себя оценить, составлять самому уравнения)

IX. Дом. зад. Составьте уравнения, используя числа 25, 5 и икс Слайд №12

Урок окончен, но я уверена, что на этом не закончилось ваше стремление искать и находить ответы на трудные вопросы

Спасибо за работу на уроке. Молодцы!

Слайд №17. Зима тоже довольна вашей работой, обещает вас не морозить и прийти на новогодний праздник..

1. 2. 3.

50+30=80 90-30=60 80-20=60

41-1=40 44+1=45 30+15= 45

84-80 =4 37-20=17 74-20= 54

10+9=19 90+9=99 70+9=79

60-2=58 50-8= 42 40-3=37

1. 2. 3.

50+30=80 90-30=60 80-20=60

41-1=40 44+1=45 30+15= 45

84-80 =4 37-20=17 74-20= 54

10+9=19 90+9=99 70+9=79

60-2=58 50-8= 42 40-3=37

1. 2. 3.

50+30=80 90-30=60 80-20=60

41-1=40 44+1=45 30+15= 45

84-80 =4 37-20=17 74-20= 54

10+9=19 90+9=99 70+9=79

60-2=58 50-8= 42 40-3=37

1. 2. 3.

50+30=80 90-30=60 80-20=60

41-1=40 44+1=45 30+15= 45

84-80 =4 37-20=17 74-20= 54

10+9=19 90+9=99 70+9=79

60-2=58 50-8= 42 40-3=37

Х-3=10

Х= 10 +3

Х=13

13- 3=10

10=10

47-Х=40

Х=47-40

Х=7

47-7=40

40=40

10=Х+7

Х+7=10

Х=10-7

Х=3

3+7=10

10=10

Я доволен….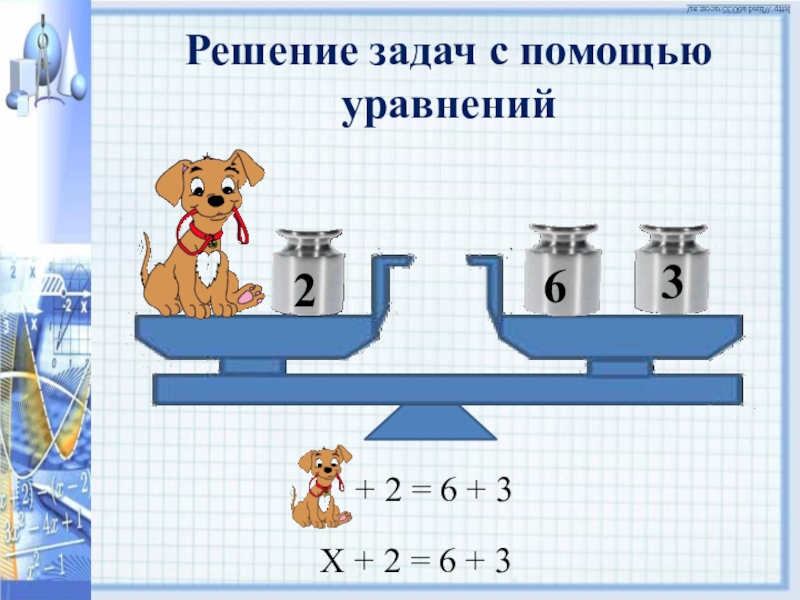 .(получил хорошую отметку,)

Я теперь смогу……(решать уравнения,)

Мне было интересно (НАХОДИТЬ уравнения ,)

Мне было трудно…..(себя оценить,)

Я доволен…..(СВОЕЙ РАБОТОЙ

Я теперь смогу……(решать УРАВНЕНИЯ, РЕШАТЬ ЗАДАЧИ)

Мне было интересно (РЕШАТЬ УРАВНЕНИЯ)

Мне было трудно…..(себя оценить, )

Я доволен…..(получил хорошую отметку, на уроке было интересно)

Я теперь смогу……(решать уравнения , составлять условие задачи )

Мне было интересно ( работать в паре, в группе)

Мне было трудно…..(себя оценить, составлять самому уравнения)

Решение задач с помощью уравнений. | Методическая разработка по алгебре (7 класс):

Урок открытия нового знания.

7 класс, алгебра. (24.11.17)

Тема: Решение задач с помощью уравнений. 

Используемое оборудование:  проектор, компьютер, учебник «Алгебра» 7 класс,  «Просвещение 2016», авторы Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева, под редакцией Г. В. Дорофеева

Цели урока:

Обучающая:

• закрепление понятия дробного рационального уравнения;
• составление математической модели задачи, перевод условия задачи с обычного языка на математический;
• проверка уровня усвоения темы путем проведения проверочной работы.

Развивающая:

• развитие умения правильно оперировать полученными знаниями, логически мыслить;
• развитие интеллектуальных умений;
• развитие умения принимать решения.

Воспитательная:

• воспитание познавательного интереса к предмету;
• воспитание самостоятельности при решении учебных задач;
• воспитание воли и упорства для достижения конечных результатов.

Задачи:

1)  актуализировать знание решения уравнений,  умение решать задачи при помощи уравнений; добиться усвоения алгоритма решения задач;

2) УУД:

1. Познавательные: овладение основами логического и алгоритмического мышления;
2. Регулятивные: развитие умения  читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;
3. Коммуникативные: строить высказывания, аргументировано доказывать  свою точку зрения;
4. Личностные: развитие навыков сотрудничества со сверстниками,

3) воспитывать чувство товарищества.

Оборудование: презентация, конспект урока, компьютер, проектор.

Ход урока:

1. Инициация.

Здравствуйте, ребята. Чем мы занимались на прошлых уроках? (Решали уравнения и задачи с помощью уравнений)

2. Вхождение или погружение в тему

Какая тема нашего урока. (1 слайд)

Какие цели мы себе можем поставить?

3. Формирование ожиданий учеников.

Я раздам вам волшебные конверты, но  чур до конца урока в них не заглядывать.

   Актуализация знаний.

( Фронтальный опрос, устная работа с классом.)

Ответьте, пожалуйста, на следующие вопросы:

— Какие равенства называются уравнениями? (2 слайд)

— Какое число называется корнем уравнения? (3 слайд)

— Что значит решить уравнение? (4 слайд)

— Расскажите алгоритм решения уравнений. (5 слайд)

Работать сегодня мы будем в парах. (  пересадить)

Вспомните правила работы в парах. (6 слайд)

 (Прислушиваться к мнению соседа, работать дружно, помогать друг другу)

Пример. Решите уравнение (на доске)!!!!! Найди ошибку???? (7 слайд)

-7х+5(2х-3)=6 -7х+10х+15=6 -7х+10х=6-15 3х=-9 х=-9:3 х=-3 Ответ. х=-3

-7х+5(2х-3)=6 -7х+10х-3=6 -7х+10х=6+3 3х=9 х=9:3 х=3 Ответ. х=3

-7х+5(2х-3)=6 -7х+10х-3=6 -7х+10х=6-3 -3х=3 х=3:(-3) х=-1 Ответ. х=-1

                                 

(8 слайд)

4. Интерактивная лекция и объяснение информации.

Прежде чем приступить к решению задач на движение, давайте вспомним, какие виды движения (передвижения) могут быть рассмотрены в задачах (ехать, идти, плыть, …), (движения по воде и суше, …).

Раз мы рассматриваем задачи на движение какие величины необходимы для решения данных задач (S, V, t). Как они связаны между собой?

(9 слайд)

(10 слайд) Устная задача про катер

(11 слайд) Если мы будем рассматривать задачи на движение по воде, что необходимо помнить (собственная скорость и скорость течения реки).

Запишите данные формулы в тетради.

(12 слайд) Объясните несостоятельность этой ситуации:

Прежде чем приступать к решению задачи необходимо несколько раз внимательно прочитать условие задачи, понять что дано и какую величину обозначить за неизвестную. Как правило, за неизвестное обозначают наименьшую величину.

(13слайд) Рассмотрим пример.

   Два поезда, встретившись на разъезде, продолжали движение каждый в своём направлении. Скорость одного из них на 20 км/ч больше скорости другого. Через 3 ч расстояние между ними было 480 км. Найдите скорость каждого поезда.

Решение.

Сделаем рисунок, который поможет нам составить уравнение.

        х км/ч        х+20 км/ч

        3 ч        3 ч

        480 км

Составление математической модели:

х км/ч  скорость первого поезда;

(х +20) км/ч – скорость второго поезда;

3х км – расстояние, которое проехал первый поезд;

3(х+20) км — расстояние, которое проехал второй поезд;

По условию задачи известно, что через 3 ч расстояние между поездами было 480 км.

(14 слайд)

Составим табличную модель:

I поезд	х	3	3х
II поезд	х+20	3	3(х+20)

Что нам известно про расстояние?

Составьте уравнение и решите  его. (каждый сам.)

(15 слайд) взаимопроверка по образцу (обмен тетрадями)

Составим уравнение и решим его:

3х+3(х+20)=480

Работа с составленной моделью.

Решив полученное уравнение, находим х=70.

Ответ на вопрос задачи. 70 км/ч скорость первого поезда, 70+20=90 (км/ч) скорость второго поезда.

После решения задачи необходимо ещё раз объяснить ход решения и поинтересоваться у учащихся, понятно ли им данное решение. Так же необходимо заметить, что в некоторых случаях целесообразно создавать геометрические модели для лучшего восприятия условия задачи. Чаще всего такие модели составляются к задачам на движение.

(16 слайд) Физкультминутка

Быстро  встали, улыбнулись.

Выше – выше потянулись

Ну-ка, плечи распрямите,

Поднимите, опустите

Влево, вправо повернитесь,

Рук коленями коснитесь.

Сели, встали. Сели, встали.

И на месте пошагали.

5. Проработка содержания темы

(17 слайд)  Работа в тетрадях. 

Задания из учебника «Алгебра 7», Г.В. Дорофеев

№403(а).

Учитель контролирует выполнение задания, отвечает на возникшие вопросы, оказывает помощь слабоуспевающим ученикам. Учащиеся работают парами  вместе обсуждают решение задачи.

(Дети читают текст задачи, делают выводы)

Раз в задаче используется скорость и время, значит задача на движение, и как следствие мы будем использовать формулу, связывающую все величины.

Учитель проверяет решение задачи, учащиеся комментируют, как решали задачу.

(18 слайд)

(19 слайд) № 410 ( запас времени) (за х обозначить всех учеников)

6. Домашнее задание.

Решить в тетрадях

№ 397 , № 403(б),

по выбору 404 (а)

составить задачу на движение по реке.

7. Рефлексия УД на уроке.

— Итак, над какой темой мы работали? Удалось ли решить поставленную задачу? Каким способом? Какие получили результаты? Что нужно сделать ещё?

— В чём испытывали трудности?

— Где можем применить новые знания? (При решении задач)

— Оцените работу вашего партнёра и себя.

Молодцы. Спасибо за урок.

Эмоциональная разрядка

Откройте конверт и оцените сегодняшний урок

(20 слайд)

Решение проблем | Начальная алгебра

Цели обучения

• Определить процесс решения задач
  • Перевод слов в алгебраические выражения и уравнения
  • Определить процесс решения текстовых задач
• Решить задачи, содержащие ставки
  • Применение шагов решения текстовых задач к задачам на расстояние, скорость и время
  • Применить шаги для решения текстовых задач к задачам с процентными ставками
  • Вычислить формулу, используя замену
  • Переупорядочить формулы, чтобы изолировать определенные переменные
  • Определить неизвестное по формуле
• Решение дополнительных приложений линейных уравнений
  • Применение шагов решения текстовых задач к задачам по геометрии
  • Используйте формулу для перевода градусов Фаренгейта в градусы Цельсия
  • Вычислить формулу с помощью подстановки
  • Переупорядочить формулы, чтобы изолировать определенные переменные
  • Определить неизвестное по формуле

Определите процесс решения проблем

Проблемы с Word могут быть сложными. Часто требуется немного практики, чтобы преобразовать английское предложение в математическое предложение, что является одним из первых шагов к решению текстовых задач. В приведенной ниже таблице слова или фразы, обычно связанные с математическими операторами, распределены по категориям. Текстовые задачи часто содержат эти или похожие слова, поэтому полезно посмотреть, какие математические операторы с ними связаны.

Дополнение [латекс]+[/латекс]	Вычитание [латекс]-[/латекс]	Умножение [латекс]\раз[/латекс]	Переменная ?	равно [латекс]=[/латекс]
Более	Менее	Двойной	Номер	Является
Вместе	В прошлом	Продукт	Часто значение, для которого не предоставляется никакой информации.	То же, что и
Сумма	медленнее, чем	умножить на	Через сколько часов?
Итого	остаток от		Сколько это будет стоить?
В будущем	разница
быстрее, чем

Вот несколько примеров:

• [латекс]х\текст{ равно }5[/латекс] становится [латекс]х=5[/латекс]
• На три больше числа становится [латекс]х+3[/латекс]
• Число на четыре меньше числа становится [латекс]х-4[/латекс]
• Двойная стоимость становится [latex]2\cdot\text{ cost }[/latex]
• Продукты и бензин вместе на неделю стоят 250 долларов, что означает [латекс]\текст{ продукты }+\текст{ газ }=250[/латекс]
• Разница между 9 и числом становится [латекс]9-х[/латекс]. Обратите внимание, что 9 стоит первым в предложении, а выражение

Давайте потренируемся переводить еще несколько английских фраз в алгебраические выражения.

Пример

Переведите таблицу в алгебраические выражения:

некоторое число	сумма числа и 3	удвоенная сумма числа и 3
длина	удвоить длину	удвоить длину, уменьшить на 6
стоимость	разница стоимости и 20	2-кратная разница стоимости и 20
некоторое количество	разность 5 и количество	разность 5 и количества, деленная на 2
количество времени	втрое больше времени	втрое больше времени, увеличено на 5
на расстоянии	сумма [латекс]-4[/латекс] и расстояние	сумма [латекс]-4[/латекс] и удвоенного расстояния

Показать решение

В этом видео-примере мы покажем, как перевести больше слов в математические выражения.

 

Сила алгебры заключается в том, что она может помочь вам смоделировать реальные ситуации, чтобы ответить на вопросы о них.

Вот несколько шагов, чтобы перевести проблемные ситуации в алгебраические уравнения, которые вы можете решить. Задача на каждые слов не идеально вписывается в эти шаги, но они помогут вам начать работу.

1. Прочтите и поймите проблему.
2. Определите константы и переменные в задаче.
3. Перевод слов в алгебраические выражения и уравнения.
4. Напишите уравнение, представляющее проблему.
5. Решите уравнение.
6. Проверьте и интерпретируйте свой ответ. Иногда помогает написание предложения.

Пример

Двадцать восемь меньше, чем в пять раз определенное число равно 232. Что это за число?

Показать решение

В следующем видео мы покажем еще один пример того, как перевести предложение в математическое выражение с помощью метода решения задач.

Другой тип числовой задачи связан с последовательными числами. Последовательные числа — это числа, которые идут одно за другим, например 3, 4, 5. Если мы ищем несколько последовательных чисел, важно сначала определить, как они выглядят с переменными, прежде чем мы начнем уравнение.

Например, предположим, что я хочу узнать следующее целое число после 4. С точки зрения математики, мы должны добавить 1 к 4, чтобы получить 5. Мы можем обобщить эту идею следующим образом: целое число, следующее за любым числом, x , это [латекс]х+1[/латекс]. Если мы продолжим этот шаблон, мы сможем определить любое количество последовательных целых чисел из любой начальной точки. В следующей таблице показано, как описать четыре последовательных целых числа с помощью алгебраической записи.

Первый	[латекс]х[/латекс]
Второй	[латекс]x+1[/латекс]
Третий	[латекс]x+2[/латекс]
Четвертый	[латекс]x+3[/латекс]

Мы применяем идею последовательных целых чисел для решения текстовой задачи в следующем примере.

Пример

Сумма трех последовательных целых чисел равна 93. Что это за числа?

Показать решение

Ставки

Часто существует хорошо известная формула или соотношение, применимое к словесной задаче. Например, если вы планируете поездку на автомобиле, вам нужно знать, сколько времени вам потребуется, чтобы добраться до пункта назначения. [latex]d=rt[/latex] — это хорошо известное соотношение, которое связывает пройденное расстояние, скорость, с которой вы путешествуете, и продолжительность путешествия.

Расстояние, скорость и время

Если известны две величины в соотношении [latex]d=rt[/latex], третью можно легко найти, используя методы решения линейных уравнений. Например, если вы знаете, что будете ехать по дороге с ограничением скорости [латекс]30\frac{\text{миль}}{\текст{час}}[/латекс] в течение 2 часов, вы можете найти расстояние, которое вы проедете, умножив скорость на время или [латекс]\влево(30\frac{\text{миль}}{\text{час}}\вправо)\влево(2\текст{часы}\вправо)= 60\text{ миль }[/latex].

Мы можем обобщить эту идею в зависимости от того, какую информацию нам дают и что мы ищем. Например, если нам нужно найти время, мы можем решить уравнение [latex]d=rt[/latex] для

t , используя деление:

[latex]d=rt\\\frac{d}{r} =t[/latex]

Аналогично, если мы хотим найти скорость, мы можем выделить r с помощью деления:

[latex]d=rt\\\frac{d}{t}=r[/latex]

В следующих примерах вы увидите, как эта формула применяется для ответа на вопросы о сверхмарафонском беге.

Энн Трейсон

Ультрамарафонский бег (определяемый как любой забег длиннее 26,2 миль) становится очень популярным среди женщин, несмотря на то, что он остается нишевым видом спорта, в котором доминируют мужчины. Энн Трейсон за свою карьеру побила двадцать мировых рекордов. Одним из таких рекордов стал забег на выносливость на 50 миль по реке Американ-Ривер, который начинается в Сакраменто, штат Калифорния, и заканчивается в Оберне, штат Калифорния. ^[1] В 1993 году Трэйсон финишировал со временем 6:09:08.

Рекорд среди мужчин на той же трассе был установлен в 1994 Тома Джонсона, завершившего дистанцию ​​со временем 5:33:21. ^[2]

В следующих примерах мы будем использовать формулу [latex]d=rt[/latex], чтобы ответить на следующие вопросы о двух полозьях.

1. Каков был показатель рекордных забегов каждого бегуна?
2. К тому времени, когда Джонсон закончил, сколько еще миль должен был пробежать Трейсон?
3. Насколько дальше мог бы бежать Джонсон, если бы он бежал так же долго, как Трейсон?
4. Сколько времени каждый бегун пробежал одну милю?

Чтобы упростить ответы на вопросы, мы округлим время двух бегунов до 6 часов и 5,5 часов.

Пример

Каков был показатель рекордных забегов каждого бегуна?

Показать решение

Теперь, когда мы знаем скорость каждого бегуна, мы можем ответить на второй вопрос.

Пример

К тому времени, когда Джонсон финишировал, сколько еще миль должен был пробежать Трейсон?

Показать решение

Третий вопрос аналогичен второму. Теперь, когда мы знаем скорость каждого бегуна, мы можем ответить на вопросы об отдельных дистанциях или времени.

Примеры

Насколько дальше мог бы пробежать Джонсон, если бы он бежал так же долго, как Трейсон?

Показать решение

Теперь мы займемся последним вопросом, где нас просят найти время для каждого бегуна.

Пример

За какое время каждый бегун пробежал одну милю?

Показать решение

В следующем видео мы показываем еще один пример ответа на многие вопросы о скорости с учетом расстояния и времени.

Простые проценты

Чтобы побудить клиентов вкладывать свои деньги, многие банки предлагают процентные счета. Счета работают следующим образом: клиент вносит определенную сумму денег (называемую основной суммой, или P ), которая затем медленно растет в соответствии с процентной ставкой ( R , измеряется в процентах) и продолжительностью времени (). T , обычно измеряется в месяцах), что деньги остаются на счете. Сумма, заработанная с течением времени, называется процентами ( I ), которые затем передаются покупателю.

Осторожно! Процентные ставки обычно указываются как годовые, но также могут быть ежемесячными, ежеквартальными, раз в два месяца или даже в течение определенного периода времени. Важно, чтобы единицы времени и единицы процентной ставки совпадали. Вы увидите, почему это важно, в следующем примере.

Самый простой способ рассчитать проценты по счету — использовать формулу [latex]\displaystyle I=P\,\cdot \,R\,\cdot \,T[/latex].

Если мы знаем любую из трех величин, связанных с этим уравнением, мы можем найти четвертую. Например, если мы хотим найти время, необходимое для начисления определенной суммы процентов, мы можем найти T, используя деление:

[латекс]\displaystyle\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,I=P\,\cdot \,R\ ,\cdot \,T\\\\ \frac{I}{{P}\,\cdot \,R}=\frac{P\cdot\,R\,\cdot \,T}{\,P\ ,\cdot \,R}\\\\\,\,\,\,\,\,\,\,\,\,\,{T}=\frac{I}{\,R\,\cdot \,T}\end{array}[/latex]

Ниже приведена таблица, показывающая результат решения для каждой отдельной переменной в формуле.

Решить для	Результат
Я	[латекс]I=P\,\cdot \,R\,\cdot \,T[/латекс]
Р	[латекс]{P}=\frac{I}{{R}\,\cdot \,T}[/латекс]
Р	[латекс]{R}=\frac{I}{{P}\,\cdot \,T}[/латекс]
Т	[латекс]{T}=\frac{I}{{P}\,\cdot \,R}[/латекс]

В следующих примерах мы покажем, как подставить заданные значения в формулу простых процентов и расшифровать, для какой переменной нужно найти.

В следующем видео показан еще один пример определения баланса счета по истечении заданного времени, вложенной основной суммы и ставки.

В следующем примере вы увидите, почему важно убедиться, что единицы процентной ставки соответствуют единицам времени при использовании формулы простых процентов.

Дальнейшие применения линейных уравнений

Формулы встречаются во многих различных сферах жизни. Мы видели формулу, связывающую расстояние, скорость и время, а также формулу простого процента на инвестиции. В этом разделе мы подробнее рассмотрим формулы и увидим примеры формул для размеров геометрических фигур, а также формулу для преобразования температуры между градусами Фаренгейта и градусами Цельсия.

Геометрия

Существует много геометрических фигур, которые хорошо изучены на протяжении многих лет. Мы довольно много знаем о кругах, прямоугольниках и треугольниках. Математики доказали множество формул, описывающих размеры геометрических фигур, включая площадь, периметр, площадь поверхности и объем.

Периметр

Периметр — это расстояние вокруг объекта. Например, рассмотрим прямоугольник с длиной 8 и шириной 3. В прямоугольнике две длины и две ширины (противоположные стороны), поэтому мы добавляем [латекс]8+8+3+3=22[/латекс ]. Поскольку в прямоугольнике две длины и две ширины, периметр прямоугольника можно найти по формуле [латекс]{P}=2\left({L}\right)+2\left({W}\right )[/латекс], где

L = длина

W = ширина

В следующем примере мы будем использовать разработанный нами метод решения задач для нахождения неизвестной ширины с помощью формулы для периметра прямоугольника. Подставив известные нам размеры в формулу, мы сможем выделить неизвестную ширину и найти наше решение.

В этом видео показана аналогичная проблема с садовым ящиком.

Мы могли бы выделить w в формуле для периметра, прежде чем решать уравнение, и если бы мы собирались использовать формулу много раз, это могло бы сэкономить много времени. В следующем примере показано, как изолировать переменную в формуле перед заменой известных размеров или значений в формулу.

Пример

Выделить член, содержащий переменную w, , из формулы периметра прямоугольника :  

[латекс]{P}=2\left({L}\right)+2\ влево({W}\вправо)[/латекс].

Показать решение

Площадь

Площадь треугольника определяется как [латекс] A=\frac{1}{2}bh[/латекс], где

A = площадь
b = длина основания
h = высота треугольника

Помните, что когда две переменные или число и переменная расположены рядом друг с другом без математического оператора между ними, вы можете предположить, что они перемножаются. Это может показаться разочаровывающим, но вы можете думать об этом как о математическом сленге. За прошедшие годы люди, часто использующие математику, просто сделали это сокращение настолько, что оно стало общепринятым.

В следующем примере мы будем использовать формулу площади треугольника, чтобы найти недостающее измерение, а также использовать подстановку, чтобы найти основание треугольника, зная площадь и высоту. {2}[/латекс], через высоту, ч .

В этом примере переменная h довольно глубоко запрятана в формуле площади поверхности цилиндра. Используя порядок операций, его можно выделить. Прежде чем вы посмотрите на решение, используйте поле ниже, чтобы записать то, что вы считаете лучшим первым шагом, чтобы изолировать h .

Показать решение

---

1. «Энн Трейсон». Википедия. По состоянию на 5 мая 2016 г. https://en.wikipedia.org/wiki/Ann_Trason. ↵
2.  «Забег на выносливость на 50 миль по реке Американ-Ривер». Википедия. По состоянию на 5 мая 2016 г. https://en.wikipedia.org/wiki/American_River_50_Mile_Endurance_Run. ↵

Решение линейных уравнений — SAT Mathematics

Все ресурсы по математике SAT

137 Практические тесты Вопрос дня Карточки Learn by Concept

SAT Mathematics Help » Линейная алгебра » Решение линейных уравнений

Если , каково значение ?

Возможные ответы:

19

13

9

23

Правильный ответ:

90 044 19

Объяснение:

Первый шаг в решении этой задачи – взять уравнение, которое вам дано, и решить его. Для этого разделите обе части на  , чтобы получить . Важно понимать, что вопрос касается не значения , а скорее значения выражения . Чтобы найти этот ответ, подключите  и выражение будет выглядеть так . Затем это равно , что дает правильный ответ .

Сообщить об ошибке

Если , то каково значение ?

Возможные ответы:

0,25

36

12

4

Правильный ответ:

0,25

Объяснение:

Всякий раз, когда вы пытаетесь найти переменную в уравнении, содержащем дроби, хорошим первым шагом будет умножение обеих частей на знаменатель, чтобы получить все переменные и значения, не входящие в дроби. Вот что значит. умножив обе части на  , чтобы получить .

Далее у вас есть линейное уравнение, в котором переменная имеет коэффициент, поэтому разделите на коэффициент, чтобы изолировать переменную. Если вы разделите обе части на , вы получите: . Затем вы можете уменьшить дробь до , а поскольку в вариантах ответа используются только целые и десятичные числа, вы можете преобразовать дробь в правильное десятичное число, 

Сообщить об ошибке

Если , каково значение ?

Возможные ответы:

7

11

3

14

Правильный ответ:

11

Объяснение:

Первым шагом в решении этой задачи является использование предоставленного вам уравнения, которое вы можете решить для . Для этого возьмите и разделите обе части на . Это оставляет вас с . Конечно, вопрос касается не значения , а значения . Итак, подключитесь  , и выражение будет выглядеть так:  что есть . Это упрощает , давая вам окончательный ответ.

Сообщить об ошибке

Если , каково значение  ?

Возможные ответы:

Правильный ответ:

Объяснение:

Обратите внимание, что в этой задаче вам нужно решить не конкретную переменную, а конкретную дробь или отношение . По этой причине ваша цель при выполнении алгебры должна состоять в том, чтобы изолировать отношение  и . Это можно сделать, умножив обе части на . Это дает вам:

, что упрощается до .

Затем вы можете просто перевернуть каждую дробь (при этом вы делаете одно и то же для обеих сторон, а именно берете обратное), чтобы получить:

, что упрощает до .

Сообщить об ошибке

Если  и , каково значение ?

Возможные ответы:

6

0

-6

12

Правильный ответ:

900 44 12

Объяснение:

Всякий раз, когда SAT просит вас определить значение переменной, у вас есть два варианта: либо вы можете использовать свои ответы в качестве активов и выполнить обратное решение, либо вы можете найти переменную напрямую. В этом случае оба варианта одинаково хороши, и вы должны использовать тот метод, который наиболее удобен. Однако, как правило, решение напрямую является лучшим вариантом в разделе SAT без калькулятора.

Если вы подставите значение  в приведенное уравнение, оно станет следующим:

Затем вы можете решить, решать ли напрямую или подставлять варианты ответов. Если вы решаете напрямую, то умножьте обе части на  , чтобы исключить знаменатель, что даст:

. Последним шагом будет деление обеих частей на  и у вас есть .

Если бы вы добавили варианты ответов, вы бы обнаружили, что будет работать только  , как .

Сообщить об ошибке

Если , каково значение ?

Возможные ответы:

-3

-1

2

4

Правильный ответ:

9004 4-3

Объяснение:

Первый ключ к решению этой задачи — объединить одинаковые термины; каждая часть уравнения содержит несколько членов, которые нужно суммировать, чтобы упростить уравнение. Ваше упрощенное уравнение должно выглядеть так:

Теперь вы можете получить все термины с одной стороны и все числовые термины с другой, чтобы быть готовыми к решению. Это означает вычитание и  с каждой стороны, что дает:

Затем вы можете разделить обе части на  , чтобы получить окончательный ответ:

Сообщить об ошибке

Если , то каково значение ?

Возможные ответы:

Правильный ответ:

4

Объяснение:

Чтобы решить эту задачу алгебраически, возьмите данное уравнение и вычтите из обеих частей, чтобы выделить член. Это дает вам:

Затем вы можете разделить обе части на  , чтобы получить:

Когда вы подключаетесь к , это дает вам , что есть .

Сообщить об ошибке

Какое значение  в приведенном выше уравнении?

Возможные ответы:

Правильный ответ:

5

Объяснение:

Чтобы решить эту задачу алгебраически, распределите умножение по каждому набору скобок, не забывая умножать каждое слагаемое в скобках на его коэффициент. Это дает вам:

Затем вы можете комбинировать одинаковые термины слева, так как у вас есть два термина и два числовых термина. Это упрощает:

Отсюда вычтите с обеих сторон, и вы получите ответ, .

 

Сообщить об ошибке

Если , каково значение ?

Возможные ответы:

21

29

17

33

Правильный ответ:

29

Объяснение:

Чтобы решить эту задачу, сначала выполните алгебраические действия над данным уравнением, чтобы выделить члены с одной стороны уравнения и числовые члены с другой. Это означает, что нужно вычесть из обеих частей и прибавить к обеим, чтобы получить:

Затем вы можете разделить обе части на , чтобы понять это.

Теперь обратите внимание, что в вопросе вас просили не о значении , а скорее о значении . Итак, теперь вам нужно подключить  для  для завершения работы: 

Сообщить об ошибке

Если , то каково значение ?

Возможные ответы:

171

141

159

129

Правильный ответ: 90 045

159

Объяснение:

Чтобы ответить на эту задачу, вам нужно сначала решить для  в данном уравнении.