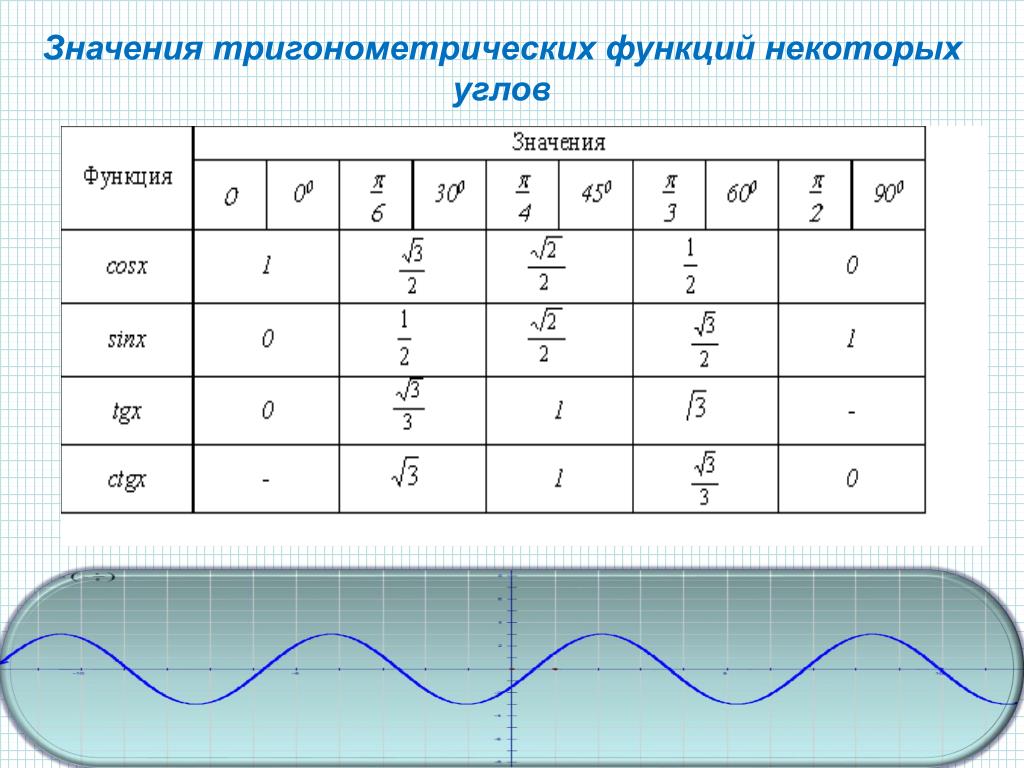
Значения тригонометрических функций
Получи беслпатные курсы подготовки к ЕГЭ и ОГЭ!
ЗАМУЧИЛИ БОЛИ В СПИНЕ?
Александр | 2012-09-23
Значения тригонометрических функций. Друзья, прошлой статье, при рассмотрении тригонометрических уравнений, я пообещал вам привести алгоритм быстрого «восстановления» значений тригонометрических функций от 0 до 90 градусов. Решил далеко не откладывать, будущее уже настало )). Если хотите скачать данную теорию в pdf формате, подпишитесь на рассылку (в МЕНЮ вкладка ПОДАРКИ). Вы получите все прототипы задач базовой части с ответами и теорию систематизированную по группам задач от 1 до 14.
Предлагаю вам алгоритм, благодаря которому вы легко, в течение минуты восстановите в памяти все вышеуказанные значения:
1. Записываем в строчку углы от 0 до 90 градусов. Слева в столбик запишем сначала синус, затем косинус аргумента:
2. Напротив синуса пишем числа от нуля до четырёх (под значениями углов). Напротив косинуса от 4 до 0:
3.
Далее извлекаем корень:
4. Делим на 2:
5. Вычисляем:
Мы получили значения синуса и косинуса углов от 0 до 90 градусов. Далее, зная формулы тангенса и котангенса:
вы сможете найти значения для указанных углов.
Например:
И так для тангенса и котангенса любого угла. Данная шпаргалка представленная выше может выручить.
*Конечно, к пониманию того, каким значениям равны тригонометрические функции различных углов (имею виду углы 0, 30, 45, 60, 90, 120 и так далее), какие ставить знаки при этих значениях лучше прийти через понимание тригонометрической окружности.
Кстати, вы можете расширить диапазон углов и записать углы от 0 до 180 градусов, но тогда напротив синуса и косинуса нужно будет поставить числа в следующем порядке:
Далее выполняем те же действия, учитывая один нюанс: корень в строке с косинусом извлекаем из положительного числа, минус ставим перед корнем:
Описывать подробно, как определять значения функций, которые соответствуют определённому углу здесь не буду, сделаю это в одной из будущих статей, не пропустите!
Объясню лишь принцип: косинус угла – это абсцисса точки на тригонометрической окружности, которая соответствует данному углу; синус угла – это ордината точки на тригонометрической окружности, которая соответствует данному углу.
Например по представленному рисунку видно, что косинус нуля градусов равен 1, косинус 120 градусов равен минус 0,5 и так далее, надеюсь, логику вы уловили.
Спасибо за внимание, учитесь с удовольствием!
С уважением, Александр крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Приёмы | Тригонометрия
Подготовка к ОГЭ по математике. Полный курс!
Полный Видеокурс по РУССКОМУ ЯЗЫКУ!
ПРЕМИУМ-КУРС по математике на 100 баллов!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
Тригонометрические функции
План изучения темы
- Область определения и множество значений тригонометрических функций.
- Чётность, нечётность, периодичность тригонометрических функций.
- Свойства функции y=cosx и её график.
- Свойства функции y=sinx и её график.
- Свойства функции y=tgx и её график.
- Свойства функции y=ctgx и её график.
- Решение задач на применение свойств функций.
Область определения и множество значений тригонометрических функций
Область определения функции — это множество значений, принимаемых независимой переменной (аргументом Х). Для функции, заданной формулой, под область определения часто понимают множество допустимых значений аргумента, то есть всех тех его значений, для которых формула даёт действительное значение для функции.
Разберемся, какая область определения у тригонометрических функций. Каждому действительному числу Х соответствует единственная точка единичной окружности, получаемая поворотом точки (1;0) на угол Х радиан. Таким образом каждому действительному числу Х поставлены в соответствие числа sinx и cosx, т.е. на множестве R всех действительных чисел определены функции y=sinx и y=cosx.
Областью определения функций y=sinx и y=cosx является множество R всех действительных чисел.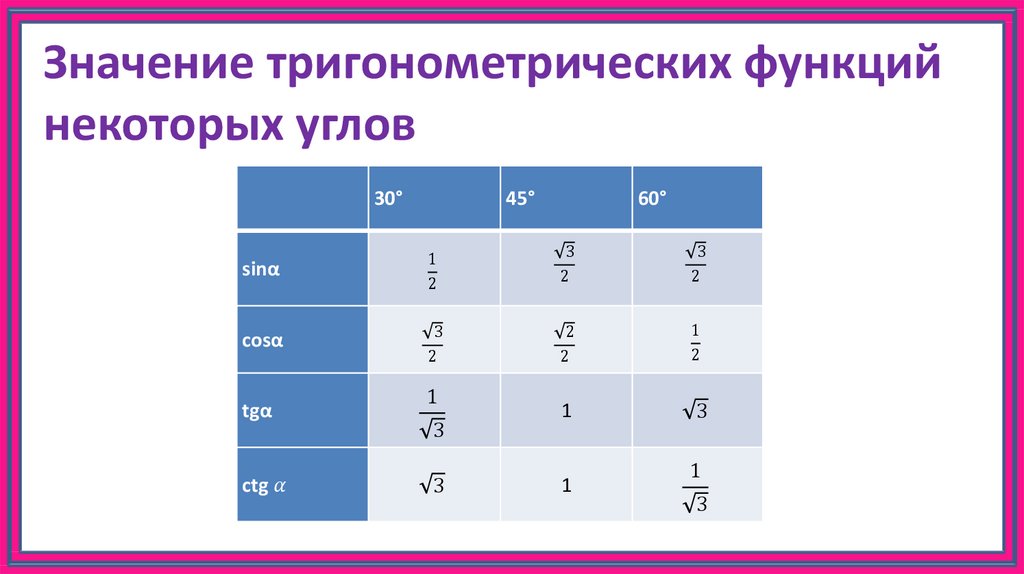
Областью определения функции y=tgx является множество чисел
Множество значений функции — это множество значений, принимаемых зависимой переменной (Y).
Так как функции y=sinx и y=cosx принимают значения в рамках единичной окружности, то множество их значений ею ограничено.
Множеством значений функций y=sinx и y=cosx является отрезок [-1;1].
Функции y=sinx и y=cosx являются ограниченными.
Множеством значений функции y=tgx является множество R всех действительных чисел, так как уравнение tgx=a имеет корни при любом действительном значении a.
Пример 1
Найти область определения функции
Решение: сами функции y=sinx и y=cosx имеют в области определения все действительные числа. Но тут они стоят в сумме, в знаменателе. А мы знаем, что если знаменатель будет равным нулю, то выражение потеряет смысл. Значит, для нахождения области определения необходимо приравнять знаменатель к нулю и решить получившееся уравнение.
Значит, областью определения являются все значения, кроме найденных выше:
Пример 2
Найдите множество значений функции
Решение: видим, что в правой части есть возможность применить тригонометрическую формулу двойного угла для синуса. Сделаем это:
Областью значений функции y=sinx является отрезок [-1;1]. Здесь есть функция синуса, просто она умножена на одну вторую и ещё прибавлено 3. Учтём всё сказанное и получим новое множество значений:
То есть на первом шаге мы умножили концы отрезка на одну вторую, а затем прибавили к ним 3. В итоге мы получили множество значений данной функции. Никакой роли тут не играет двойной угол, так как он влияет на сужение/растяжение графика вдоль оси ОХ.
Ответ: [2,5;3,5]
Чётность, нечётность, периодичность тригонометрических функций
Чётная функция — функция y=f(x), область определения которой симметрична относительно нуля и для каждого Х из области определения имеет место равенство:
График чётной функции симметричен относительно оси ординат.
Нечетная функция — функция y=f(x), область определения которой симметрична относительно нуля и для каждого Х из области определения имеет место равенство:
График нечётной функции симметричен относительно начала координат. Примером может служить кубическая парабола.
Примером может служить парабола.значит, это нечётная функция.
значит, это чётная функция.
значит, это нечётная функция.
значит, это нечётная функция.
Пример 3
Выяснить, является ли функция чётной или нечётной:
Решение:
После применения формулы приведения, мы получаем функцию в виде
Воспользуемся правилом определения чётности/нечётности и проверим, что у нас получится:
То есть, мы видим, что данная функция является чётной, из-за появившегося квадрата в показателе степени.
Ответ: чётная
Период функции — некоторое действительное число Т такое, что для всех Х их области определения функции f числа Х+Т и Х-Т принадлежат области определения функции f и f(X)=f(X+T)=f(X-T).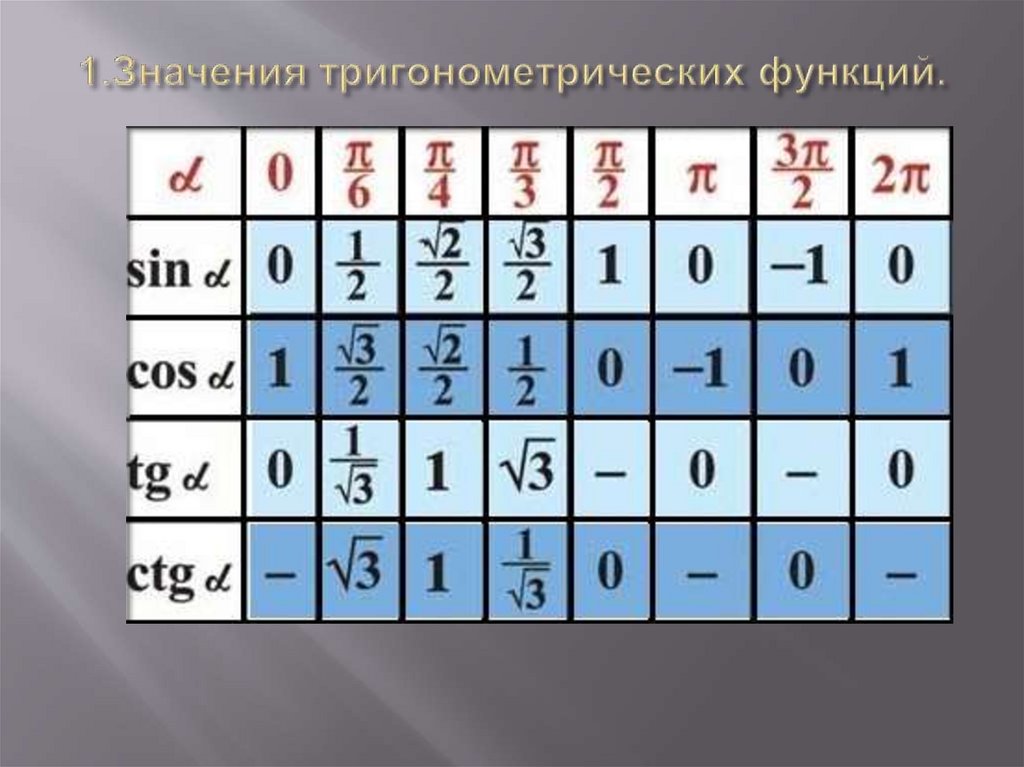
Однако чаще всего лишь наименьшее из всех таких чисел Т положительное, называют наименьшим периодом функции.
Мы с вами знаем, что при полном обороте по единичной окружности мы попадаем в точку с такими же координатами, то есть верны равенства:
Из этих равенств следует, что значения синуса и косинуса периодически повторяются при изменении аргумента на два пи. Такие функции называются периодическими с периодом:
Аналогично, выполняются ещё два равенства:
Значит, тангенс и котангенс — это периодические функции, с периодом:
Пример 4
Найдём несколько периодов функций на конкретных примерах.
Решение:
Задание 1. Смотрим, чем отличается функция от стандартного вида. Видим 3 перед аргументом. Значит, нужно взять основной период для синуса:
и просто поделить его на 3. Значит период для первой функции будет равен:
Задание 2. Перед аргументом у тангенса мы видим дробь 3/2. Значит, основной период тангенса нужно просто разделить на эту дробь.
Получаем:
Задание 3. Перед аргументом стоит дробь 1/2 и прибавлено ещё пи на 6. Это прибавление не играет никакой роли, просто график будет двигаться налево вдоль оси, поэтому ищем период как обычно. Берём основной период косинуса и делим на дробь:
Задание 4. Видим у косинуса аргумент умножен на 4, значит просто на него делим основной период:
Задание 5. Перед аргументом у синуса дробь 1/5, просто делим на неё. Не обращаем на 4 впереди, это просто растяжение графика вдоль оси ОХ.
Задание 6. Перед аргументом синуса стоит 2, делим на неё:
Задание 7. У тангенса перед аргументом стоит 5. Берём основной период и делим на 5:
Задание 8. Аналогично тангенс, просто дробь впереди 1/2:
Задание 9. Тут уже нужно найти период для каждого слагаемого. Для синуса:
Для косинуса:
А общим периодом будет наименьшее общее кратное наших двух, которые мы нашли. То есть тот, который делится на каждый из найденных.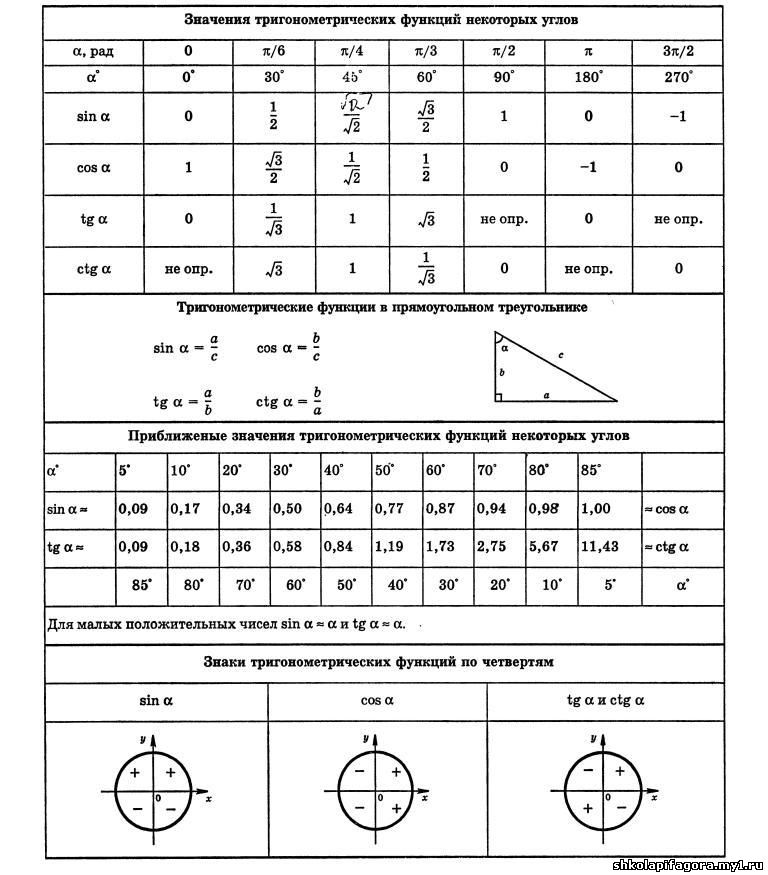
Свойства функции y=cosx и её график
Свойства функции y=sinx и её график
Свойства функции y=tgx и её график
Свойства функции y=ctgx и её график
Решение задач на применение свойств функций
Пояснение к уроку: вычисление значений тригонометрической функции с углами 30, 45 и 60
60-градусные углы.
Начнем с того, что вспомним, что подразумевается под тригонометрическими функциями. В прямоугольном треугольнике мы можем обозначить длины сторон треугольника относительно одного из внутренних углов. Например, мы можем обозначить стороны относительно угла 𝜃 как показано на диаграмме ниже.
Затем мы определяем тригонометрические функции как отношения длин сторон прямоугольного треугольника следующим образом: синоппозитгипотенузакосаджацентгипотэнузатаноппозит смежный𝜃=,𝜃=,𝜃=.
Поскольку мы можем определить значения тригонометрических функций по отношениям длин сторон в прямоугольных треугольниках, построим
несколько прямоугольных треугольников геометрически, чтобы мы могли оценить тригонометрические функции при определенных значениях.
Стоит отметить, что мы можем выбрать любую длину стороны квадрата. Мы выбрали 2, так как это упростит арифметику. Разделим квадрат на два конгруэнтных прямоугольных треугольника вдоль одной из его диагоналей, как показано на рисунке.
Поскольку это равнобедренные прямоугольные треугольники, непрямые углы должны быть равны. В частности, поскольку внутренние углы треугольника в сумме 180∘, мы можем определить, что недостающие углы равны 180−902=45∘∘∘.
Затем мы можем применить теорему Пифагора, чтобы найти длину недостающей стороны. Напомним, что это говорит нам о том, что квадрат гипотенуза равна сумме квадратов двух других сторон. Это дает нам 𝑐=2+2𝑐=4+4𝑐=8.
Мы можем решить это уравнение, взяв квадратный корень из обеих частей уравнения и заметив, что длины должны быть положительными: 𝑐=√8=√4×2=2√2.
Затем мы можем использовать этот прямоугольный треугольник для определения значений тригонометрических функций, вычисляемых под углом 45∘.
Обозначение сторон треугольника по отношению к их положению относительно нижнего левого угла 45∘,
получаем следующее.
Применяя тригонометрию прямоугольного треугольника, мы получаем следующее: синоппозитгипотенузакосадацентгипотенузатаноппозитный смежный45==22√2=1√2=1√2×√2√2=√22,45==22√2=√22,45==22=1.∘∘∘
Мы можем использовать точно такую же технику для вычисления тригонометрических функций под другими углами. Например, мы могли бы использовать равносторонний треугольник со стороной 2, который, как мы помним, имеет внутренние углы, равные 60∘.
Затем мы можем разделить его на два прямоугольных треугольника, используя серединный перпендикуляр, как показано.
Мы рассмотрим только один из этих прямоугольных треугольников. Заметим, что поскольку внутренние углы треугольника в сумме
до 180∘, мы можем определить недостающий угол как
180−60−90=30∘∘∘∘. Мы также можем заметить, что половина основания треугольника имеет длину 1, что дает нам следующее.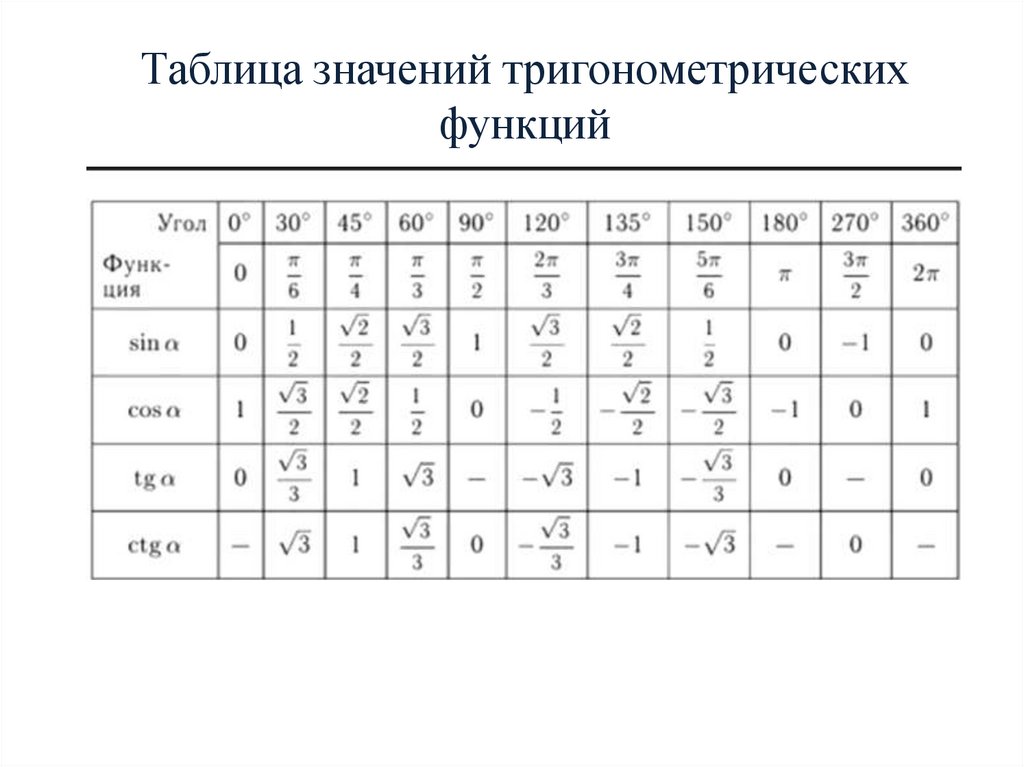
Так как это прямоугольный треугольник, мы можем найти длину недостающей стороны, используя теорему Пифагора. Напомним, что это говорит нам квадрат гипотенузы равен сумме квадратов двух других сторон. Это дает нам 2=1+𝑎4=1+𝑎𝑎=3.
Мы можем найти значение 𝑎, взяв квадратный корень из обеих частей уравнения и заметив, что 𝑎 — это длина, поэтому она должна быть положительной: 𝑎=√3.
Мы можем использовать это для определения значений тригонометрических функций, вычисляемых на 30∘ и 60∘. Сначала обозначим стороны относительно угла 60∘.
Так как синусопротивоположная гипотенуза𝜃=, мы имеем sin60=√32.∘
Точно так же, поскольку косадаприлегающая гипотенуза𝜃= и tanoppositeadjacent𝜃=, имеем costan60=12,60=√31=√3.∘∘
Мы также можем определить значения этих тригонометрических функций на 30∘
обозначив стороны треугольника по отношению к их положению относительно угла 30∘.
У нас есть sinoppositehypotenusecosadjacenthypotenusetanoppositeadjacent30==12,30==√32,30==1√3=1√3×√3√3=√33.∘∘∘
Мы можем обобщить результаты, которые мы показали, в следующей таблице.
Стандартный факт: оценка значений тригонометрической функции с углами 30°, 45° и 60° тригонометрические функции: синус, косинус и тангенс, вычисленные под углами 30∘, 45∘ и 60∘.
| 𝜃∘ | |||
|---|---|---|---|
| 30∘ | 45∘ | 60∘ | |
| sin𝜃 | 12 | √22 | √32 |
| cos𝜃 | √32 | √22 | 12 |
| tan𝜃 | √33 | 1 | √3 |
Эти тригонометрические результаты либо удобны для запоминания, либо полезны
находится геометрически. Давайте теперь рассмотрим несколько примеров использования этих значений для упрощения или вычисления тригонометрических выражений.
Пример 1. Нахождение значений тригонометрических функций специальных углов
Найдите точное значение sin30∘.
Ответ
Мы можем определить точное значение sin30∘, используя Калькулятор; мы бы получили это sin30=12.∘
Однако нам должно быть удобно находить значения трех тригонометрических функций: синуса, косинуса и тангенса. на 30∘, 45∘ и 60∘. Для этого начнем с построения равностороннего треугольника с длина стороны 2,
Затем мы построим следующий прямоугольный треугольник, рассматривая серединный перпендикуляр к основанию.
Поскольку сумма внутренних углов треугольника равна 180∘, мы можем найти недостающее
угол равен 180−90−60=30∘∘∘∘. Мы можем определить длину недостающей стороны, применив теорему Пифагора, которая утверждает, что в прямоугольном треугольнике квадрат
гипотенузы равна сумме квадратов двух других катетов. Это дает
2=1+𝑎,
которое мы можем решить для 𝑎, отметив, что это значение должно быть положительным:
𝑎=4−1𝑎=3𝑎=√3.
Это дает нам следующий прямоугольный треугольник.
Поскольку мы хотим определить значение sin30∘, мы будем обозначать стороны, ссылаясь на их положение относительно угла 30∘.
Напомним, что функция синуса есть отношение длины противолежащего катета к гипотенузе в прямоугольном треугольнике, давая нам синоппозитгипотенуза30==12.∘
Следовательно, sin30=12∘.
В предыдущем примере мы использовали прямоугольные треугольники для определения тригонометрических отношений под определенным углом. На практике это довольно много времени, поэтому проще просто зафиксировать таблицу значений в памяти, а затем применить эти значения для оценки выражений. В остальных примерах мы просто будем ссылаться на таблицу.
Пример 2. Использование тригонометрических значений специальных углов для вычисления тригонометрических выражений
Найдите значение 24530cossin∘∘.
Ответ
Мы можем определить это значение с помощью калькулятора.
Тем не менее, это полезный навык, чтобы уметь оценивать тригонометрические
работает под углами 30∘,
45∘ и 60∘ без
калькулятор, поэтому ответим на этот вопрос без калькулятора.
Можно вспомнить полную таблицу значений тригонометрических функций при углах 30∘, 45° и 60° следующим образом.
| 𝜃∘ | |||
|---|---|---|---|
| 30∘ | 45∘ | 60∘ | |
| sin𝜃 | 12 | √22 | √32 |
| cos𝜃 | √32 | √22 | 12 |
| TAN𝜃 | √33 | 1 | √3 |
или альтернативно, мы можем просто вспомнить, что SIN30 = 12∘ и COS45 = √222∘. Затем мы подставляем эти значения в выражение, чтобы получить 24530=2×√22×12=√22.cossin∘∘
Следовательно, 24530=√22косинус∘∘.
Пример 3: Использование тригонометрических значений специальных углов для вычисления тригонометрических выражений
Найдите значение cossinsintantan6030−6060+30∘∘∘∘∘ без использования калькулятора.
Ответ
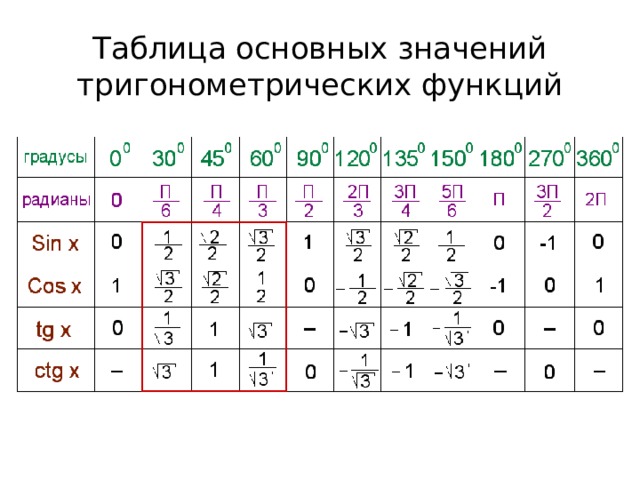
Мы можем точно вычислить это выражение, не используя калькулятор, используя геометрию и тригонометрию прямоугольного треугольника. Однако легче вспомнить следующую таблицу значений.
| 𝜃∘ | |||
|---|---|---|---|
| 30∘ | 45∘ | 60∘ | |
| sin𝜃 | 12 | √22 | √32 |
| cos𝜃 | √32 | √22 | 12 |
| tan𝜃 | √33 | 1 | √3 |
Мы видим, что sin30=12∘, cos60=12∘, tan30=√33∘ и tan60=√3∘. Затем мы можем подставить эти значения в выражение для оценки. У нас есть коссинтантанкоссинстантан6030−6060+30=6030−6060+(30)=1212−√32√3+1√3=14−32+13.∘∘∘∘∘∘∘∘ ∘∘∘
Затем мы убеждаемся, что дроби имеют общий знаменатель, чтобы мы могли их сложить: cossinsintantan6030−6060+30=14−32+13=14×33−32×66+13×44=312−1812+412=−1112.∘∘∘∘∘
Следовательно, точное значение тригонометрического выражения составляет −1112.
Мы видели, как мы можем использовать известные треугольники, чтобы помочь нам вычислить тригонометрические функции под определенными углами. Мы можем использовать это же логика идти в обратном направлении; если отношение длин сторон в прямоугольном треугольнике является величиной, которую мы знаем, то мы можем определить угол.
Например, представьте, что у нас есть следующий треугольник.
А нам говорят, что отношение противолежащей и прилежащей сторон равно 1; другими словами, загар𝜃=1. То есть два способа определить угол 𝜃. Во-первых, мы могли бы сделать это геометрически. Мы знаем противоположный соседний = 1, так противоположный соседний=.
Это означает, что это равнобедренный прямоугольный треугольник. Следовательно, другой неизвестный угол также равен 𝜃.
Затем мы используем тот факт, что сумма внутренних углов треугольника равна 180∘, чтобы найти 𝜃: 𝜃+𝜃+90=1802𝜃=90𝜃=45.∘∘∘∘
Это не единственный метод, который мы можем использовать для определения значения 𝜃.
Мы знаем это
tan45=1∘ и что 45∘
возможный угол прямоугольного треугольника, так как он острый. Итак, мы можем просто заключить, что 𝜃 равно 45∘.
используя наши знания о том, что tan45=1∘.
Мы также можем решить этот пример, используя факт об обратных тригонометрических функциях.
Определение: обратные тригонометрические функции для острых углов.
Для 𝑎>0,
- 𝜃=𝑎tan является единственным решением острого угла уравнения tan𝜃=𝑎.
Следовательно, поскольку tan45=1∘, мы знаем, что 𝜃=45∘ является решением уравнения загар𝜃=1, и мы знаем, что решение единственно для острых углов. Мы знаем, что тан∘1=45. Мы можем сделать то же самое для всех остальных значения, которые мы знаем. Например, поскольку sin60=√32∘, мы знаем, что sin∘√32=60. Все это мы можем записать в следующую таблицу.
Стандартный факт: вычисление обратных тригонометрических функций при определенных значениях
В следующей таблице приведены значения обратных тригонометрических функций, вычисленные при заданных значениях.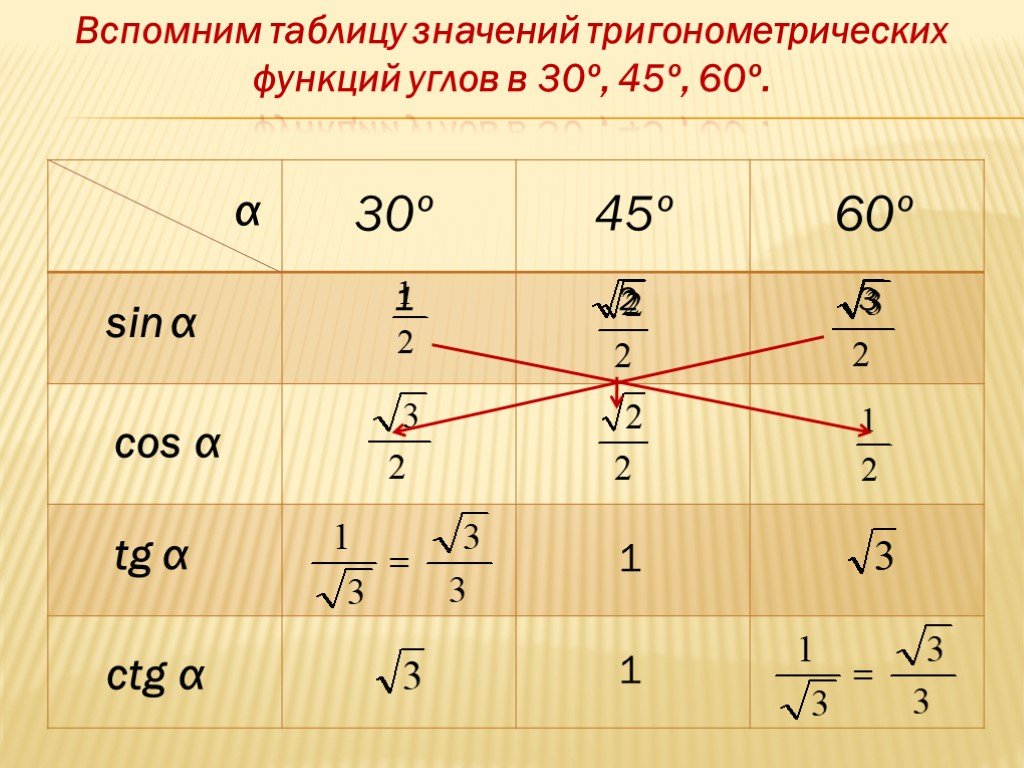
| 𝑎 | |||
|---|---|---|---|
| 12 | √22 | √32 | |
| sin𝑎 | 30∘ | 45∘ | 60∘ |
| cos𝑎 | 60 ∘ | 45∘ | 30∘ |
| 𝑎 | |||
|---|---|---|---|
| √33 | 1 | √3 | |
| tan𝑎 | 30∘ | 45∘ | 60∘ |
Let’s now see an example of solving тригонометрическое уравнение.
Пример 4. Использование обратной тригонометрической функции для нахождения специального угла
Если cos(𝑥)=12, найдите значение 𝑥, где 0𝑥90∘∘.
Ответ
Сначала заметим, что 𝑥 — острый угол, и мы можем решать тригонометрические уравнения, используя обратную
тригонометрические функции. Поскольку cos(𝑥)=12, мы берем арккосинус обеих частей уравнения
увидеть это
𝑥=12.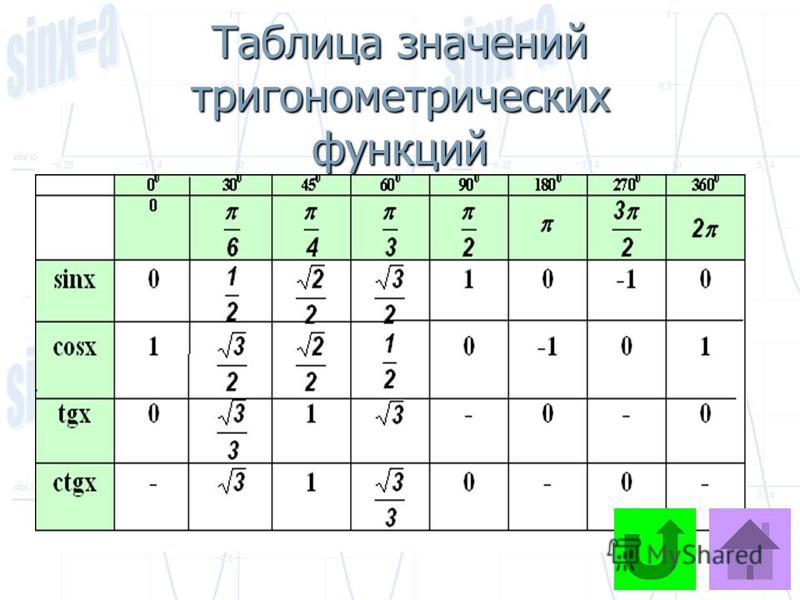
cos
Поскольку 𝑥 острый, мы знаем, что это угол прямоугольного треугольника. Мы помним, что cos60=12∘, поэтому мы можем заключить, что cos∘12=60. Это в указанном интервале, так что 𝑥=60∘.
В нашем последнем примере мы перестроим и решим тригонометрическое уравнение, используя наши знания об обратных тригонометрических функциях.
Пример 5. Использование обратной тригонометрической функции для нахождения специального угла
Учитывая, что √3(𝑥)+2=3tan, найдите значение 𝑥, где 0𝑥90∘∘.
Ответ
Чтобы решить тригонометрическое уравнение, мы должны начать с попытки упростить уравнение; у нас есть √3(𝑥)+2=3√3(𝑥)=1(𝑥)=√33.tantantan
Затем мы вспоминаем, что, поскольку мы ищем острое решение, 𝑥=√33tan является единственным решение этого уравнения.
Однако мы знаем, как вычислять тригонометрические функции при особых значениях. В частности, мы знаем, что
тангенс(30)=√33∘.
Так как острое решение
уникален, мы должны иметь, что 𝑥=30∘.
Давайте закончим повторением некоторых важных моментов этого объяснения.
Ключевые моменты
- Мы можем вычислить тригонометрические функции, построив прямоугольные треугольники и используя отношения длин сторон.
- В частности, мы можем построить следующие два прямоугольных треугольника, используя половину квадрата и половину равностороннего треугольника длины 2.
- Применяя тригонометрию прямоугольного треугольника к этим треугольникам, мы можем вычислить функции синуса, косинуса и тангенса в точках
30∘, 45∘,
и 60∘. Получаем следующую таблицу значений.
𝜃∘ 30∘ 45∘ 60∘ sin𝜃 12 √22 √32 cos𝜃 √32 √22 12 TAN𝜃 √33 1 √3 - для 0𝑎1,
- 𝜃 = 𝑎Sin — уникальный АК -АКТИВА;
- 𝜃=𝑎cos — единственное остроугольное решение уравнения cos𝜃=𝑎.
- Для 𝑎>0,
- 𝜃=𝑎tan является единственным решением острого угла уравнения tan𝜃=𝑎.
- В следующей таблице приведены значения обратных тригонометрических функций, оцененных при заданных значениях.
𝑎 12 √22 √32 sin𝑎 30∘ 45∘ 60∘ cos𝑎 60∘ 45∘ 30∘ 𝑎 √33 1 √3 tan𝑎 30∘ 45∘ 60∘
Нахождение значений тригонометрических функций по одному значению и квадранту
Вопрос 1 :
Найдите значения других пяти тригонометрических функций для следующего:
sin θ = -2/3, θ лежит в IV квадранте.
Решение:
sin θ = противоположная сторона/гипотеновая сторона
sin θ = -2/3
противоположная сторона = 2, гипотеновая сторона = 3
(Гипотеновая сторона) 2 = (противоположная сторона) 2 + (соседняя сторона) 2
соседняя сторона = √ (3 2 — 2 2 )
= √ (9- 4)
= √5
= √ (9- 4)
= √5
.
Примечание. Поскольку θ находится в четвертом квадранте -го -го, все тригонометрические отношения, кроме cos и sec, будут иметь отрицательный знак.
cos θ = Смежная сторона/сторона гипотенузы = √5/3
tan θ = Противоположная сторона/Смежная сторона = -2/√5
cosec θ = Сторона гипотенузы/противоположная сторона 0 0 90 90 = Сторона гипотенузы/Прилегающая сторона = 3/√5
cot θ = Прилегающая сторона/Противоположная сторона = -√5/2
Вопрос 2 :
Найдите значения других пяти тригонометрических функций для следующего:
2 tan θ = -2, θ лежит во II квадранте.
Решение:
TAN θ = противоположная сторона/соседняя сторона
TAN θ = -2/1
противоположная сторона = 2, соседняя сторона = 1
(Сторона гипотенеза) 2 = (противоположная сторона) 2) 2 = (противоположная сторона) 2) + (соседняя сторона) 2
Сторона гипотенузы = √ (2 2 + 1 2 )
= √ (4+ 1)
= √5
Гипотенерация = √ (4+ 1)
= √5
. Примечание. Поскольку θ находится в квадрантах 2 90 515 и 90 516, все тригонометрические отношения, кроме sin и cosec, будут иметь отрицательный знак.
sin θ = Противоположная сторона/сторона гипотенузы = 2/√5
cos θ = Смежная сторона/сторона гипотенузы = -1/√5
cosec θ =
cosec θ =
9000 √5 θ = Сторона гипотенузы/Смежная сторона = -√5/1
cot θ = Смежная сторона/Противоположная сторона = -1/2
Вопрос 3 :
Найдите значения других пяти тригонометрических функций для следующего:
с θ = 13/5, θ лежит в IV квадранте
Решение:
сек θ = сторона гипотенузы/гипотеновая сторона
сек θ = 13/5
соседняя сторона = 5, гипотеновая сторона = 13
(гипотеновая сторона) 2 = (противоположная) (противоположная) (противоположная сторона) (Hypotenus 2 + (соседняя сторона) 2
противоположная сторона = √ (13 2 — 5 2 )
= √ (169 — 25)
= √144
= √ (169 — 25)
= √144
= √ (169 — 25)
= √144
= √ (169 — 25)
=.