Множества: элементы и подмножества. Пересечение и объединение множеств
- Подмножество
- Пересечение и объединение множеств
Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита — от A до Z.
Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:
N — множество натуральных чисел,
Z — множество целых чисел.
Элемент множества — это любой объект, входящий в состав множества. Принадлежность объекта к множеству обозначается с помощью знака ∈
. Запись
5∈Z
читается так: 5 принадлежит множеству Z
или 5 – элемент множества Z
.
Множества делятся на конечные и бесконечные. Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество — множество, содержащее бесконечно много элементов.
Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись
L = {2, 4, 6, 8}
означает, что множество L состоит из четырёх чётных чисел.
Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.
Подмножество
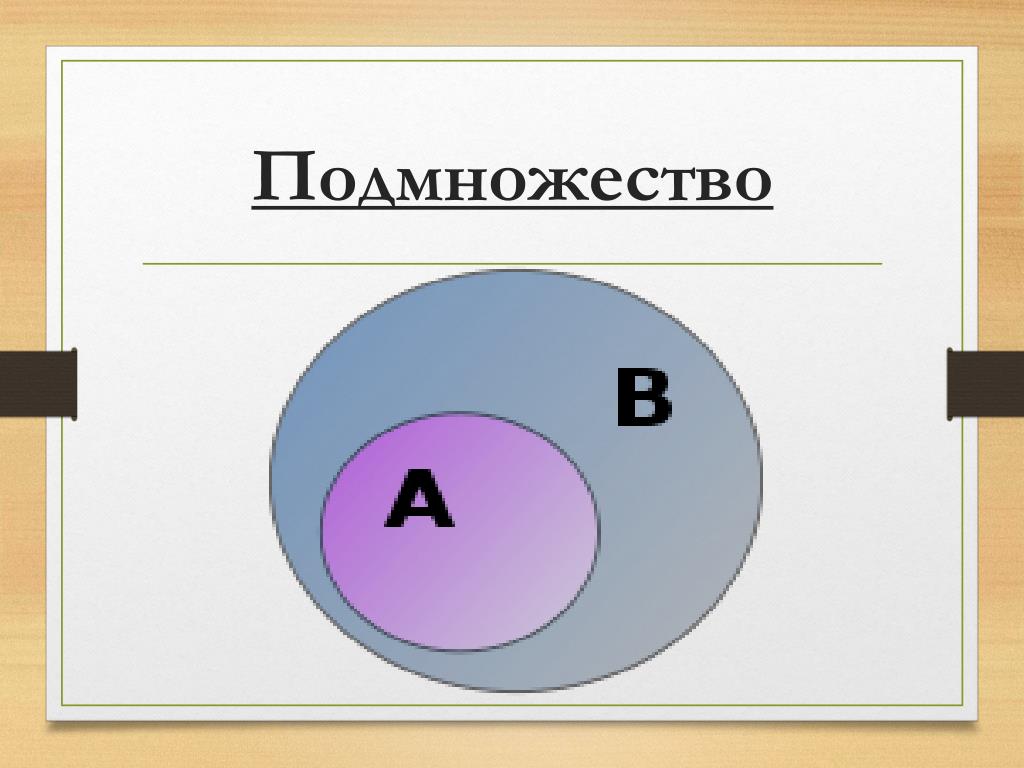
Подмножество — это множество, все элементы которого, являются частью другого множества.
Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.
Рассмотрим два множества:
L = {2, 4, 6, 8} и M = {2, 4, 6, 8, 10, 12}.
Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком
Такое соотношение множеств обозначают знаком ⊂
:
L⊂M.
Запись L⊂M читается так: множество L является подмножеством множества M
.
Множества, состоящие из одних и тех же элементов, независимо от их порядка, называются равными и обозначаются знаком =
.
Рассмотрим два множества:
L = {2, 4, 6} и M = {4, 6, 2}.
Так как оба множества состоят из одних и тех же элементов, то L = M.
Пересечение и объединение множеств
Пересечение двух множеств — это совокупность элементов, принадлежащих каждому из этих множеств, то есть их общая часть. Пересечение обозначается знаком ∩
.
Например, если
L = {1, 3, 7, 11} и M = {3, 11, 17, 19}, то L∩M = {3, 11}.
Запись L∩M читается так: пересечение множеств L и M
.
Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.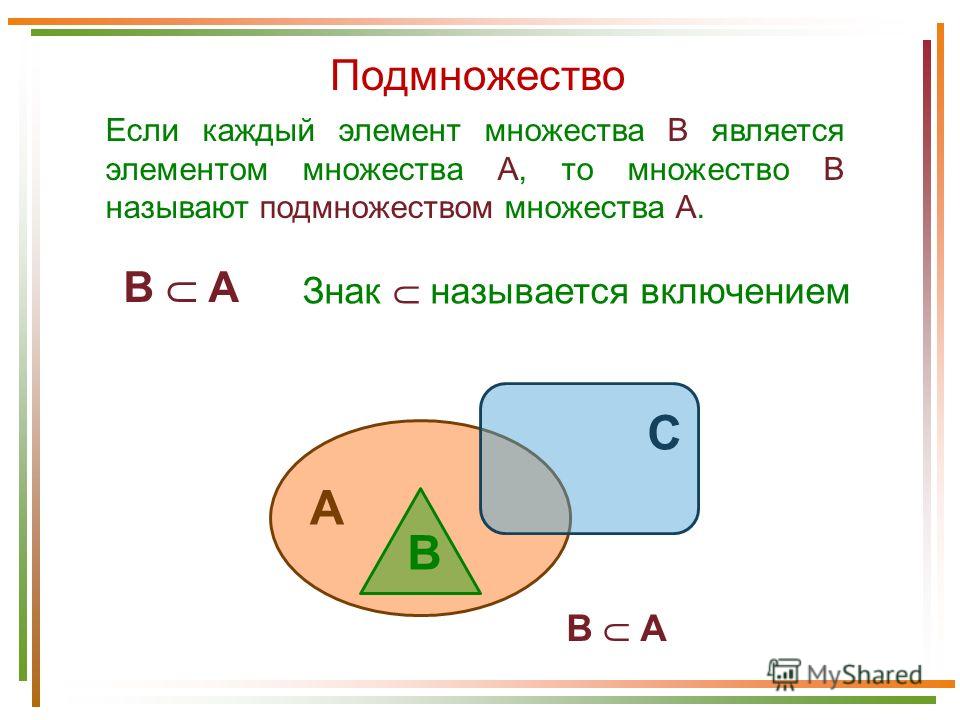
Объединением двух множеств называется множество, содержащее все элементы исходных множеств в единственном экземпляре, то есть если один и тот же элемент встречается в обоих множествах, то в новое множество этот элемент будет включён только один раз. Объединение обозначается знаком ∪
.
Например, если
L = {1, 3, 7, 11} и M = {3, 11, 17, 19},
то L∪M = {1, 3, 7, 11, 17, 19}.
Запись L∪M читается так: объединение множеств L и M
.
При объединении равных множеств объединение будет равно любому из данных множеств:
если L = M, то L∪M = L и L∪M = M.
Перечёркнутый значок подмножества : TeXнические обсуждения
Сообщения без ответов | Активные темы | Избранное
| Mikhail_K |
| |||
26/01/14 |
| |||
| ||||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| Aritaborian |
| ||
11/06/12 |
| ||
| |||
| Mikhail_K |
| |||
26/01/14 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 4 ] |
Модераторы: Karan, Toucan, PAV, maxal, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Outline — это значок подмножества, изолированный черным простым векторным изображением
Outline — это значок подмножества, изолированный черным простым векторным изображениемЛицензияПодробнее
Стандарт Вы можете использовать вектор в личных и коммерческих целях. Расширенный Вы можете использовать вектор на предметах для перепродажи и печати по требованию.Тип лицензии определяет, как вы можете использовать этот образ.
| Станд. | Расшир. | |
|---|---|---|
| Печатный/редакционный | ||
| Графический дизайн | ||
| Веб-дизайн | ||
| Социальные сети | ||
| Редактировать и изменить | ||
| Многопользовательский | ||
| Предметы перепродажи | ||
| Печать по запросу |
Владение Узнать больше
Эксклюзивный Если вы хотите купить исключительно этот вектор, отправьте художнику запрос ниже: Хотите, чтобы это векторное изображение было только у вас? Эксклюзивный выкуп обеспечивает все права этого вектора.
Мы удалим этот вектор из нашей библиотеки, а художник прекратит продажу работ.
Способы покупкиСравнить
Плата за изображение $ 14,99 Кредиты $ 1,00 Подписка 9 долларов0082 0,69Оплатить стандартные лицензии можно тремя способами. Цены составляют $ $.
| Оплата с помощью | Цена изображения |
|---|---|
| Плата за изображение $ 14,99 Одноразовый платеж | |
| Предоплаченные кредиты $ 1 Загружайте изображения по запросу (1 кредит = 1 доллар США). Минимальная покупка 30р. | |
| План подписки От 69 центов Выберите месячный план. Неиспользованные загрузки автоматически переносятся на следующий месяц. | |
Способы покупкиСравнить
Плата за изображение $ 39,99 Кредиты $ 30,00 Существует два способа оплаты расширенных лицензий. Цены составляют
Цены составляют
| Оплата с помощью | Стоимость изображения |
|---|---|
| Плата за изображение $ 39,99 Оплата разовая, регистрация не требуется. | |
| Предоплаченные кредиты $ 30 Загружайте изображения по запросу (1 кредит = 1 доллар США). | |
Оплата
Плата за изображение $ 399Дополнительные услугиПодробнее
Настроить изображение Доступно только с оплатой за изображение 9 долларов0082 85,00Нравится изображение, но нужно всего лишь несколько модификаций? Пусть наши талантливые художники сделают всю работу за вас!
Мы свяжем вас с дизайнером, который сможет внести изменения и отправить вам изображение в выбранном вами формате.
Примеры
- Изменить текст
- Изменить цвета
- Изменить размер до новых размеров
- Включить логотип или символ
- Добавьте название своей компании или компании
Включенные файлы
Подробности загрузки. ..
..
- Идентификатор изображения
- 28253424
- Цветовой режим
- RGB
- Художник
- зауррахимов
Как написать и использовать символ подмножества в LaTeX
латекс7 месяцев назад
от Prateek Jangid
Когда набор содержит те элементы, которые являются членами другого набора, он называется подмножеством. В математике ⊂ показывает «правильное подмножество», а символ ⊆ представляет «подмножество». Это означает, что символ подмножества играет важную роль в математике.
Вот почему обработчики документов, такие как LaTeX, предоставляют простые средства для записи символа подмножества в документе. В этом уроке мы объясним различные способы написания и использования символа подмножества в LaTeX.
Как написать и использовать символ подмножества в LaTeX?
Мы начнем с основного символа подмножества, т. е. правильного подмножества, и вы можете написать его, используя код \subset в LaTeX. Вот простой пример исходного кода:
е. правильного подмножества, и вы можете написать его, используя код \subset в LaTeX. Вот простой пример исходного кода:
\documentclass{article}
\begin{document}
$X \subset Y$
\end{document}
Output
1 Аналогично подмножество с использованием следующего исходного кода:
\documentclass{article}
\begin{document}
$X \subseteq Y$
\end{document}
Вывод
Вы также можете создать символ не подмножества, используя приведенный ниже исходный код, но для этого потребуется amssymb \usepackage:
\documentclass{article}
\usepackage{amssymb}
\begin{document}
$X \nsubseteq Y$
\end{document}
Вывод 011 Вы также можете создайте правильное подмножество с помощью следующего исходного кода: \documentclass{article} Вывод
\usepackage{amssymb}
\begin{document}
$X \not\subset Y$
\end{document}
\documentclass{article}
\usepackage{amssymb}
\begin{document}
$X \subsetneqq Y$ ;
$A \subsetneq B$
\end{document}
Вывод
Теперь давайте рассмотрим пример, включающий символ подмножества в математическое выражение:
\documentclass{article}
\usepackage{amssymb}
\begin{document \{$1,3,5$\}$, поэтому подмножества X равны;\\
$\{$$\}$, $\{$1$\}$, $\{$2$\}$, $ \{$5$\}$, $\{$1,3$\}$, $\{$3,5$\}$, $\{$1,5$\}$ и $\{$1,3,5$ \}$.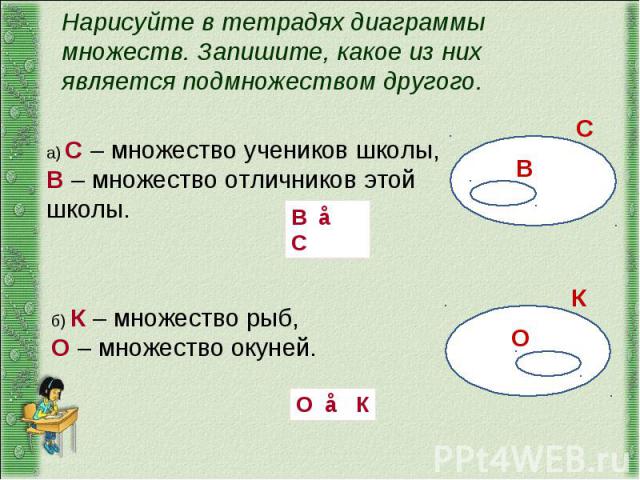

 09.2016, 20:46
09.2016, 20:46  09.2016, 20:51
09.2016, 20:51  09.2016, 20:55
09.2016, 20:55