| СОДЕРЖАНИЕ Введение………..…………………………………………………………………………………3 Нумерология……….………………………………………………………………………………4 Пифагор и его учение о числе……………………………….…………………………………7 Загадочные и таинственные числа…………………………….………………………………10 Числа, окутанные тайной………………………………………………………………………13 Заключение…………………………………………..………………………………………….17 Список литературы…………………………………..…………………………………………18 Приложение 1 «Числа, характеризующие человеческую личность»……………………….19 Приложение 2 «Магическое значение чел от 1 до 49»………………………………………27 ВВЕДЕНИЕ Число есть слово неизреченное; оно есть волна и свет, хотя никто их не видит; оно есть ритм и музыка, хотя их никто не слышит. Оно неизменно, но вибрации его безграничны. Любая форма жизни есть конкретное проявление Числа. М.Дрюон. Воспоминания Зевса Именно поэтому целью данной работы является: изучить роль чисел в жизни человека и, как они взаимосвязаны с его судьбой. Число являлось универсальным символом, носителем мудрости и постижения мира, почти амулетом. Число всегда несло в себе тайну, числа обладали неизмеримой сакральностью, будучи при этом наиболее, понятным и доступным символом общения. Чтобы более подробно раскрыть эти аспекты рассмотрим следующие три главы. В первой главе нашей работы мы используем некоторые нумерологические характеристики человека, чтобы понять, почему люди наделили числа определенным смыслом. Нумерология неотделима от прошлого, настоящего и будущего, отраженных числовым рядом от 1 до 9. Поэтому неудивительно, что всего лишь несколько цифр открывают доступ к источнику всеобъемлющей информации. Современная нумерология — один из самых интересных пережитков магической теории имен. Каждый уважающий себя нумеролог, как и его древние предшественники, верит в то, что имя заключает в себе сущность человека. Во второй главе мы рассматриваем учения Пифагора, как одного из основоположников учения о числах и его знаменитый магический квадрат. Пифагор обратил внимание на то, что рядом последовательных сложений цифр, составляющих любое число, можно прийти к одной из значащих цифр ряда: 1, 2, 3, 4, 5, 6, 7, 8, 9. Также он считал, что нечетные числа более сильны и относятся к мужскому началу, в то время как четные — более слабые и соотносятся с женским началом. А еще мы познакомимся в третьей главе с загадочными и таинственными числами, которые люди наделили магической силой. Особый интерес вызвали такие как « 13 – Чертова дюжина», « 666 – Число Дьявола» и « 137 – Число Смерти». С помощью чисел можно узнать многое и многому научиться. Например, зачем вы пришли в этот мир, иными словами, свое предназначение, а также заложенные природой таланты и способности, можно научиться видеть то, что скрыто, потенциально заложено в человеке. НУМЕРОЛОГИЯ Научные аспекты искусства нумерологии помогают человеку более полно осознать свое место в прошлой, настоящей и будущей жизни. Известно, что жизнь циклична, а любой цикл может быть представлен числовым рядом от 1 до 9. Любое число, сколь велико оно бы не было, можно сократить до одного разряда; таким образом, его всегда можно выразить цифрами от 1 до 9. Современная нумерология имеет вполне научное обоснование. Великий математик и физик сэр Исаак Ньютон (1642-1727) верил в существование некоего «мирового порядка»: коль скоро солнце появилось над горизонтом сегодня, оно непременно взойдет и завтра. Однако, науке известно, что существующий мировой порядок порожден хаосом; соответственно, гармония и стабильность всего сущего подвержена случайным влияниям. Философский аспект нумерологии состоит в обретении жизненной мудрости и предполагает определенный образ мысли и теорию познания. Основоположником нумерологии в современном смысле слова по праву считается греческий философ Пифагор (580 — 500 гг. до н.э.). Он верил, что числа являются «сущностью всей жизни». Нумерологии присуща и психологическая составляющая. Новаторство основоположника современной психологии Зигмунда Фрейда и его ученика Карла Юнга положило начало комплексному исследованию природы человека. На протяжении многих лет эти ученые изучали глубинные процессы, определяющие личностные характеристики и мотивацию поступков людей. Исследования Фрейда были посвящены изучению идеомоторных характеристик, половых инстинктов и интерпретации сновидений. Нумерология рассматривает всю полноту психологических характеристик в диапазоне числового ряда от 1 до 9. Номера, окружающие нас, несут информацию, которую нельзя игнорировать. Понимание значений номеров сделает дорогу по жизни более гладкой и не такой опасной. Среди самых важных в значительных номеров из нашего окружения следует рассмотреть номер дома, в котором мы живем. Этот номер может предсказать некоторые события, как счастливые, так и не очень, которые, скорее всего, произойдут, пока мы живем в этом доме. Все числа имеют дуальную природу, иначе говоря, имеют лицевую и изнаночную, или светлую и темную, стороны. Нельзя сказать, что одно число является лучшим, чем другое. Следует выбирать номер только в соответствии со своими личными надеждами и желаниями. Можно также рассматривать номер дома или квартиры по отдельности, чтобы получить более общие или более частные характеристики. Итак, например, вы живете в доме № 67, корпус 3, квартира 78. Последовательно складываем: 6 + 7 = 13 (1 + 3) = 4 3 7+8= 15(1+ 5) = 6 Итого: 4+3+6= 13 =4 На основе этих данных можно уже делать определенные выводы. Более общая характеристика — характеристика дома — 4. Более частная характеристика — характеристика квартиры — 6. И наконец, наиболее полная характеристика будет отражена в сумме всех чисел, в данном случае это 4. А теперь познакомьтесь с интерпретациями: Дом числа 1 Живя в таком доме, вы будете настойчивы, самоуверенны, склонны к риску. Хорошее место для и раскрытия своего «я», для творчества. Числовая вибрация дома единицы заставляет живущих в нем людей быть немного эгоистичными, самонадеянными и агрессивными. Дом числа 2 Прекрасный дом для влюбленных. Дом числа 3 Место, способствующее общительности, раскрепощению, заставляющее мыслить позитивно. В нем проявляются буйство жизни, активность, решительность. В таком доме хочется творить, так как числовые вибрации тройки дают богатое воображение, бурную фантазию и много энергии. Дом числа 4 Этот дом — символ стабильности, надежности и прочности. В таком доме всегда порядок, а вещи лежат на своих местах. Однако числовая вибрация числа четыре может испытывать человека всяческими ограничениями и создавать ему определенные трудности. В любом случае это дом трудоголиков, людей упорных, настойчивых и ответственных. Дом числа 5 В этом доме всегда много гостей, здесь весело и шумно, кто-то постоянно приходит и уходит. Дом числа 6 Идеальный дом для семьи, для комфорта и благополучия. Как правило, в таком доме не возникает конфликтов и острых материальных проблем. Атмосфера любви, уюта и гармонии царит в этом доме. Живущие здесь люди отличаются практичностью, здравомыслием и склонны придерживаться обычаев и условностей. Дом числа 7 Этот дом хорош для уединения, медитаций, духовных практик. Поэтому если здесь живет слишком много людей, то они могут испытывать отчужденность, разобщенность и дискомфорт. В этом доме каждому необходима своя комната, своя территория для того, чтобы каждый мог побыть наедине со своими мыслями, поразмышлять в одиночестве. Дом числа 8 Дом, символизирующий изобилие, практичность и материальную состоятельность. Дом числа 9 В этом доме, как правило, живут симпатичные и обаятельные люди, с богатым внутренним миром и наполненной событиями жизнью. Они дружелюбны, откровенны, хотя часто подвержены влиянию со стороны. Числовые вибрации дома девятки делают живущих в нем людей идеалистами, мечтателями, мыслящими в широких категориях и не разменивающимися на мелочи. ПИФАГОР И ЕГО УЧЕНИЯ О ЧИСЛЕ Учение Пифагора известно нам лишь в пересказах древних философов. Они не могут дать полного представления об этом человеке и его учении, но из этих малочисленных, отрывочных сведений мы можем судить, насколько умен был этот человек, и его знания математики — лишь частица знаний, которую он не смог оставить будущим поколениям. Не случайно пифагорский вопрос остается одним из самых запутанных и по крайней мере самым дискуссионным в истории науки. Биография работ по пифагоризму насчитывает сотни книг и статей, при этом, однако, трудно найти какой-либо факт, включая само историческое существование Пифагора, с которым согласились бы все высказывающиеся по этому вопросу. Одни считают Пифагора основателем европейской научной традиции, — “шаманом”, предводителем экстатических культов и тайных мистерий, третьи полагают, что он соединял в себе оба этих качества. Огромная слава Пифагора сослужила ему двоякую службу: сделав его имя притягательным для легенд, умножавшаяся от века к веку, оно в тоже время позволила донести до нас память о реальных событиях того времени. Об исключительной популярности Пифагора свидетельствует моменты с его изображениям и с надписью “Пифагор”, выпущенные в 430-420 гг. до н.э. в Абдерах. Для 5 в. до н.э. это случай беспрецедентный и не только потому, что изображения философов на монетах появляются гораздо позже и, как правило, в их родных городах: перед нами первый портрет на греческих монетах, во всяком случае, первый подписанный портрет. Пифагор не записал своего учения. Оно известно лишь в пересказах Аристотеля и Платона. Аристотель писал: “Пифагор признал математические начала за начала всего сущего”. Философская истина переносится им на музыку и числа. Число понимается как термин, приложимый ко всем цифрам и их комбинациям. Пифагор определял число, как энергию и считал, что через науку о числах раскрывается тайна Вселенной, ибо число заключает в себе тайну вещей. Именно наука о числе может обладать ключом жизни и сути бытия. Проникая в свойства чисел, объясняя их различные сочетания, Пифагор пытался создать науку всех наук. Четные числа Пифагор делили на 3 класса: четно-четные, четно-нечетные, нечетно-нечетные. Первый класс составляют числа, которые представляют собой удвоение чисел, начиная с единицы. Таким образом, это 1,2,4,8,16,32,64,128,512 и 1024. Совершенство этих чисел Пифагор видел в том, что они могут делиться пополам и еще раз, и так далее до получения единицы. Четно-четные числа обладают некоторыми уникальными свойствами. Сумма любого числа терминов, кроме последнего, всегда равна последнему за вычетом единицы. К примеру, сумма четырех терминов (1+2+4+8) равна пятому термину — 16 минус один, то есть 15. Ряд четно-четных чисел имеет и такое свойство: первый член, умноженный на последний, дает последний пока в ряду с нечетным числом терминов не останется одно число, которое будучи умножено само на себя даст последнее число в ряду. Четно-нечетные числа — это числа, которые будучи разделены пополам не делятся. Они образуются следующим образом: берется нечетное число, умножается на 2, и так весь ряд нечетных числе. В этом процессе 1,3,5,7,9,11 дают четно-нечетные числа 2,6,10,14,18,22. Таким образом, каждое такое число делится на два один раз и больше делиться не может. Другая особенность этого класса чисел состоит в том, что если делитель — нечетное число, частное — всегда будет четным, и наоборот. Данный класс чисел примечателен еще и тем, что любое число в ряду является половиной суммы терминов по обе стороны его в ряду: 18 есть 1/2 суммы 14 и 22 (чисел стоящих от данного числа по обе стороны). Нечетно-нечетные числа является компромиссными между четно-четными и четно-нечетными числами. В отличие от четно-четных они не могут последовательным делением привести к 1, и в отличие от четно-нечетных они позволяют более чем однократное деление пополам. Нечетно-нечетные числа получаются следующим образом: умножая четно-четное число (больше 2) на нечетное число. Другие нечетно-нечетные числа образуются умножением ряда нечетных чисел на 4 и далее на весь ряд четно-четных чисел. Четные числа разделяются на три других класса: сверхсовершенные, несовершенные и совершенные. Сверхсовершенные числа — это такие числа, сумма дробных частей, которых больше их самих. Несовершенными Пифагор называл числа, сумма дробных частей, которых меньше его самого. Например, число 14 сумма его дробных частей 7+2+1=10, что меньше 14. Совершенное число — это такое число, сумма дробных частей которого равна самому числу. Такие числа чрезвычайно редки. Есть только одно число между 1 и 10, а именно 6; одно между 10 и 100 — число 28, одно между 100 и 1000 — 496, одно между 1000 и 10000 — 8128. Совершенные числа находят следующим образом: первое число ряда четно-четных чисел складывается со вторым числом ряда, и если получается простое число, оно умножается на последнее число ряда четно-четных чисел, участвовавших в образовании суммы. Если сложение четно-четных чисел не приводит к несоставному числу. Например, первые два числа четно-четного ряда (1,2) в сумме 3, которое умножается на 2 и получаем 6, первое совершенное число. Пифагорейцы развивали свою философию из науки о числах. Совершенные числа, считали они, есть прекрасные образы добродетелей. Они представляют собой середину между излишеством и недостатком. Они очень редки и порождаются совершенным порядком. В противоположность этому сверхизобильные и несовершенные числа, которых сколь угодно много, не расположены в порядке и не порождаются с некоторой определенной целью. И поэтому они имеют большое сходство с пороками, которые многочисленны, неупорядочены и неопределены. Нечетные числа не могут быть разделены равным образом, то есть поровну. Пифагор объяснял неспособность таких чисел делится пополам следующим образом: поскольку 1 всегда остается не делимой, нечетное число таким же образом не может быть делимым. Если нечетное число попытаться разделить поровну, то получается два четных числа, а последнее из них единица, которая является неделимой. Нечетные числа имеют и такое свойство — если какое-либо нечетное число разделить на две части, одна всегда будет четной, а другая — всегда нечетной. Пифагорейцы рассматривали нечетное число, прототипом которого была монада, определенным и мужским, хотя по поводу 1 (единицы) среди них существовали определенные разногласия. Некоторые считали его положительным, потому что, если его добавить к нечетному числу, оно станет четным и, таким образом, рассматривается как андрогенное число, совмещающие как мужские, так и женские атрибуты, значит оно и четно и нечетно. Обычаем у пифагорцев было приношение высшим богам нечетного числа предметов, в то время как богиням и подземным духам приносить четное число. Нечетные числа делятся на 3 общих класса: несоставные, составные и несоставные — составные. Несоставные числа — это такие числа, которые не имеют других делителей, кроме себя самого и единицы. Это числа 3,5,7,11,13,17 и т. Составные числа — это числа, делимые не только сами на себя, но и на некоторые другие числа. Такими числами являются те из нечетных чисел, которые не входят в группу несоставных. Это числа 9,15,21,25,27,33,39 и т.д. Несоставные — составные числа — эта числа, не имеющие общего делителя, хотя каждое из них делимо. Если взять два числа и обнаружить, что они не имеют общего делителя, такие числа можно назвать несоставными -составными числами. Например, числа 9 и 25. 9 делимо на 3, а 25 на 5, но ни одно из них не делимо на делитель другого, они не имеют общего делителя. Несоставными — составными они называются потому, что каждое из них имеет индивидуальный делитель, а поскольку эти числа не имеют общего делителя, они называются несоставными. Таким образом, несоставные — составные числа обнаруживаются только попарно друг с другом. ЗАГАДОЧНЫЕ И ТАИНСТВЕННЫЕ ЧИСЛА Оно является «матерью числа» и ассоциируется с самоуверенностью и борьбой. Пары всегда были чем-то неестественным и пугающим. Рождение близнецов становилось большим потрясением в естественном ходе вещей. Обычно близнецы означали опасность, и часто их убивали при рождении. Иногда они приносили и добро. Рим был основан двумя братьями-близнецами Ромулом и Ремом. Иногда они становились богами. Боги-близнецы входили в пантеон, иногда символизируя солнце и луну. Число два также породило пугающую мысль о повторении, о существовании невидимого двойника человека, чье появление, как правило, предвещало неизбежную смерть. Менее сверхъестественное повторение типа отражения в зеркале или в бассейне с водой или просто появление теней также порождало страх. Число три Тройка именовалась «идеальным числом», объединяющим мужское и женское начала и содержащим в себе начало, середину и конец. Она являлась олицетворением христианской Троицы, прошлого, настоящего и будущего, а также трех измерений пространства. Это число означало духовное начало и завершенность, первое по-настоящему мужское число. Число шесть Число шестого года удивительная закономерность, связанная с годами, оканчивающимися на число 6, обнаруженная в 1996 году специалистами Минсельхоза, после того, как они провели прогнозирование величины урожая зерновых в Казахстане и анализ урожайности за все предыдущее время в России и СССР. Оказалось, что в года 1906, 1926, 1936 и т.д., вплоть до 1996 были самыми урожайными по сравнению с предыдущими и последующими. Объяснения этой, как выразились специалисты министерства, «ирреальной мистики» так и не было найдено. Число семь Число семь излучает могущество. Ни одна ведьма не вызывает больше страха, чем та, которая является седьмой дочерью седьмой дочери; ни один врач не лечит так искусно, как седьмой сын седьмого сына. Древние пророки, предсказывавшие конец света, предупреждали о семи печатях, которые должны быть сломаны, о семи эпидемиях чумы, от которых будет страдать человечество, о семи трубных гласах, которые прозвучат перед тем, как наступит конец света. Мудрецы древности, размышлявшие над тайнами времени и пространства, глядя на небо, видели семь планет, насчитывали семь цветов в радуге, изучали изменения Луны и видели, что каждая из ее четырех фаз существует семь дней. Поэты и проповедники рассказывали, как во время космической битвы за души смертных чудовища с отвратительными мордами, олицетворявшие семь смертных грехов, боролись с ангельскими воплощениями семи добродетелей. И жизнь каждого человека делилась на семь возрастов, начиная с детства и заканчивая старостью. Для философов прошлого каждое число было символом высшей правды. Семь было суммой трех, числа, олицетворявшего духовную гармонию, и четырех, представлявших земную надежность. Семь смертных грехов, о которых предупреждали средневековых нечестивцев, были насланы на человечество, чтобы подвергать опасности людские души. Из семи дьяволов, которые искушали людей и толкали их к греху, Люцифер олицетворял чванство, Мамона — алчность, а Вельзевул — обжорство. Семь японских богов, приносивших благосостояние, означали безмятежность, долголетие, мудрость, работоспособность, изобилие, любовь и отвагу в бою. Внешний вид каждого говорил о его качествах. Большой живот бога безмятежности свидетельствовал о его богатых внутренних ресурсах, куполообразные брови бога мудрости — о его умственном превосходстве. Библейская книга Откровения предупреждала о чудовище, которое должно было появиться из моря с семью головами, десятью рогами и десятью коронами на каждом из рогов. Олицетворение дьявола и обмана, это семиликое чудище должно было вступить в борьбу с силами добра, чтобы овладеть человечеством. Древние евреи утверждали, что радуга представляет собой небесное оружие, возложенное на землю в знак договора, заключенного между Богом и смертными. Небесный лук содержал семь цветов спектра: красный, оранжевый, желтый, зеленый, голубой, синий, фиолетовый. В древнем мире насчитывалось семь чудес света: храм Артемиды, древнеегипетские пирамиды, сады Семирамиды, Мавзолей в Галикарнасе, маяк в Александрии, великолепные статуи Зевса в Олимпии и Гелиоса в Родосе. Число семь было, по-видимому, самым мистическим из всех чисел, сплавом духовной тройки и материальной четверки. Существовало семь «планет», известных древним астрологам (Солнце, Луна, Меркурий, Венера, Марс, Юпитер и Сатурн), семь дней недели и семь дней творения. Существовал целый легион связанных с числом семь священных атрибутов. Число восемь Число восемь для пифагорейцев представлялось числом справедливости и полноты. Так как оно дважды содержало число четыре, то рассматривалось как в высшей степени материалистическое число, хотя иногда несло на своих плечах двойную тяжесть связанных с четверкой несчастий. Число девять Число девять отстояло на единицу от восьми и символизировало новую степень совершенства. Как квадрат трех, оно означало троицу троиц, могучую и полную. Девятка обладала также циклическим свойством в том смысле, что, будучи умноженной на любое другое число, вновь давала себя. Ведь 5 х 9 = 45, 4 + 5 = 9. Это число было также самым высоким в основном ряду, так как в науке о числах девять, одиннадцать, двенадцать и все последующие числа сводились к их простейшим формам. Число десять представлялось как единица и нуль и начинало новую последовательность чисел. Число четырнадцать Число 14 играло фатальную роль в жизни и судьбе «короля-солнца», Людовика IV. В самом деле: — он был 14-м по счету королем Франции, взошел на трон 14 мая 1643 года (1+6+4+3=14), был спасен Тюренном в Блину в 1652 г. (1+6+5+2=14), был объявлен совершеннолетним в 14 лет, стал править после Мазарини в 1661 г. Число семнадцать Число 17 — «спокойное, счастливое число «. Для многих исторических деятелей эта цифра была неким талисманом, смысл которого затрудняются определить знатоки. Например, известно, что Наполеон-III считал своим счастливым числом 17. Число 17 имеет глубинные связи с морем и безопасными путешествиями. Оно знаменует день месяца, в который остановился, ковчег Ноя и Великий потоп закончился. Древние греки, строя свои корабли, срубали первое дерево на 17-й день месяца, что должно было наделить корабль удачей. В колоде Таро 17-я карта означает таинственную Звезду, а именно по звездам ориентировались первые мореплаватели. Число двадцать один Число 21 — «странное число «, иногда приносящее удачу, а некоторым — несчастья. Однажды прорицатель предсказал французскому королю Людвику-16, что его несчастливым числом является цифра 21. Каталог: ld Скачать 274. Поделитесь с Вашими друзьями: |
Урок математики. Тема: «Четные и нечетные числа» | План-конспект урока по математике на тему:
ОГКУЗ «Детский противотуберкулёзный санаторий п. Ивня»
Учитель начальных классов Захарова Марина Александровна.
Тема: Чётные и нечётные числа.
Цель: знакомство с чётными и нечётными числами .
Задачи:
- познакомить с чётными и нечётными числами;
- закрепить знания таблицы умножения;
- закрепить знания таблицы умножения и деления с числом 2;
- расширять кругозор учащихся;
- прививать интерес к предмету.
- решать простые задачи на деление, основываясь на знании взаимосвязи умножения и деления.
- развивать интеллектуальные и коммуникативные общеучебные умения.
- развивать организационные общеучебные умения, в том числе самостоятельно оценивать результаты своих действий, самого себя, находить и исправлять собственные ошибки.

Оборудование: учебник «Математика» ( авторы Т. Е. Демидова, С. А. Козлова) , детская энциклопедия «Я познаю мир», рисунки, изречения Пифагора.
Ход урока
I. Организация урока (Мотивация, ведущая к выдвижению гипотез решения проблем):
-Добрый день, дорогие ребята. Поприветствуем друг друга хорошим настроением, добрыми улыбками. А сейчас урок математики.
Вступительное слово учителя:
Изучать науку математику люди начали очень давно. Греки обогнали в математике все другие народы.
— Как вы думаете? Почему? Вы спросите почему?
— Да потому, что они хорошо умели спорить.
В древние времена Греция состояла из многих маленьких государств. Каждый раз, когда приходилось решать какой-нибудь важный государственный вопрос, горожане собирались на площадь, обсуждали, спорили, голосовали
Древние греки считали, что спор помогает найти самое лучшее, самое правильное решение. Они даже придумали следующее изречение:
В споре рождается истина»
И в науке греки стали поступать так же, как на народном собрании. Они не просто заучивали правила, а спорили друг с другом, старались найти в рассуждениях ошибки.
Они не просто заучивали правила, а спорили друг с другом, старались найти в рассуждениях ошибки.
Едва родившись, греческая математика сразу семимильными шагами пошла вперёд. Ей помогали чудесные сапоги- скороходы, которых раньше у других народов не было. Они назывались «Рассуждение», «Доказательство».
- ( Краткий рассказ о Пифагоре.) «Первый греческий учёный, который начал рассуждать о числах явился Пифагор. Затем он пришёл к выводу, что всё на свете можно выразить с помощью чисел.
- «ЧИСЛА ПРАВЯТ МИРОМ» — провозгласил он»
II .Математическая разминка. Рассуждаем и доказываем.
Представьте, что мы юные Пифагоры. Я предлагаю всем надеть на головы вот такие головные уборы. Вот и мы сейчас с вами займёмся рассуждениями и доказательствами.
1) Проверяем таблицу умножения на 2 (работа в парах)
(каждая пара задаёт друг другу выражение на знание таблицы умножения
на 2 и вычисляет значение)
2) Составь выражение и посчитай:
— сколько лапок у 3 гусят? 2*3 = 6
— сколько лапок у 2 котят? 4*2 = 8
— сколько крыльев у 4 утят? 2*4 = 8
3) Определите истинные высказывания и докажите, что они истинные
Квадрат – это четырёхугольник?. .. И
.. И
(это геометрическая фигура, которая имеет четыре угла)
10см=10л Л 1кг=1л Л
(нельзя сравнивать разные величины)
Сложение – это математическое действие?… И (Составьте выражения на сложение)
Периметр квадрата со стороной 3 см равен 12 см И
10- однозначное число Л
(нет, потому что стоит из двух знаков 1 и 0)
Одинаковые слагаемые можно заменить действием умножения И
Пример: 4+4=8 по4 взяли 2 раза 2+2+2+2+2=10 по2 взяли 5раз
4·2=8 2·5=10
От перестановки множителей произведение не изменяется И
2·7=7·2 2·6=6·2
Умножение с нулём и единицей
1·а=а а·1=а 0·а=0 а·0=0
III. Формулирование темы и целей урока
Какие из этих предметов используются только по два?
ТАПОК ПЕРЧАТКА
НОСОК ВАРЕЖКА
ШАПКА ШАРФ
Работа с учебником
- Задание 1 (стр.
 66)
66)
Как разложить варежки по 2 (парами)?
(Проанализировать вместе с детьми задание и рисунок. Сделать вывод, как должны производить деление: варежки разложить парами в соответствии с их цветами, при этом варежка останется без пары.)
Практическая работа
(Варежки разложить в классе не можем, заменим их кругами.)
Возьми 7 кружков и разложи их по 2.
Сколько пар получилось?(получилось 3 пары)
Сколько кружков осталось без пары? (один кружок остался без пары)
(Дети раскладывают на партах 7 кружков по 2. Делают вывод: 7 по 2 не делится, один кружок остается.)
- Задание 2 (стр. 66)
Попробуйте разложить:
а) по два 4 красных кружка, 6 синих кружков, 10 зеленых кружков;
б) 3 красных кружка, 5 синих кружков, 9 зеленых кружков.
Практическая работа
а) дети раскладывают красные, синие, зеленые кружки по 2;
(Дети самостоятельно на партах раскладывают кружки, а два человека работают у доски. После того, как задание выполнено, они объясняют, как делили кружки «по 2».
После того, как задание выполнено, они объясняют, как делили кружки «по 2».
Учитель записывает на доске числа в две строчки:4 6 10
3 5 9
Остальные ребята оценивают выполненное задание, выставляют оценку.
Дети делают вывод сами:
Какие кружки удалось разложить парами?
а) 6, 4, 10- удалось разложить парами ( делятся на 2)
Какие кружки не удалось разложить парами?
б) 3, 9, 5 – нельзя разложить парами ( не делятся на 2)
IV. «Открытие» нового знания
Сравнивают свой вывод с учебником на стр. 66
(дети читают из оранжевой рамочки учебника 1 строчка))
-Как называются числа, которые делятся на 2?
(Числа, которые делятся на 2 называются — чётными)
(Учитель записывает на доске числа:
4, 6, 10- чётные числа
-Как называются числа, которые не делятся на 2)
(Числа, которые не делятся на 2 называются -нечётными)
(Учитель записывает на доске числа:
3, 5, 7, 10-нечётные числа
В тетрадях появляется запись:
4, 6, 10- чётные числа
3, 5, 7, 9- нечётные числа
Что нового мы узнали? (мы узнали, что числа бывают чётные и нечётные)
Чему мы будем учиться? (мы будем учиться определять чётные и нечётные числа)
V. Применяем новые знания
Применяем новые знания
- Задание 3 (стр. 66).
(Дети читают про себя числа:)
1,2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18.
-Назовите сначала чётные числа.
(дети читают по очереди и записывают в тетрадь)
2,4,6,8,10,12,14,16,18.
-Теперь назовите нечётные числа.
(дети читают по очереди и записывают в тетрадь)
1,3,5,7,9,11,13,15,17.
-Какой вывод можем сделать?
(дети из оранжевой рамочки учебника читают вывод)
Вывод: Четные и нечетные числа в числовом ряду чередуются.
ФИЗМИНУТКА
Если я называю чётное число, вы приседаете.
Если называю нечётное число – 1 хлопок
2, 3, 1, 12, 14, 5, 11, 16, 9, 8, 7, 20, 6, 4, 10, 13, 15, 18, 17, 19
VI. Первичное закрепление
(использование нового знания при решении задач)
Задание 5 (а) стр. 67.
(Прочитайте и объясните задание. Как будем его выполнять?)
(Ответы детей, составление плана действий, выполнение задания в тетрадях, на доске)
— Что мы будем делать? (мы будем решать задачу)
(прочитайте задачу про себя)
Восемь ребят разделились в группы по 2 человека. Сколько групп получилось.
Сколько групп получилось.
— Что нам надо сделать? (Сделать рисунок и решить задачу.)
— Что нам известно из условия задачи?
Нам известно, что 8 ребят разделились в группы по 2 человека
Практическая работа (в тетрадях и на доске появляется рисунок)
О О О О О О О О
-Что надо найти в задаче?
Нам надо найти сколько групп получилось.
-Как это показать на рисунке?
Нам надо кружочки разделить по 2(на доске и в тетрадях дети делят
по 2 при помощи вертикальных линий )
О О/ О О/ О О/ О О
-Как записать решение при помощи выражения?
8:2=4(г.)
Ответ: 4 группы получилось.
Оценить работу учащихся. Какую оценку заслужил?
— Ещё во времена Пифагора продавцу на базаре приходилось раскладывать товар попарно и иногда яблок в мешке или баранок оказывалось больше и оставались лишние. И Пифагор стал думать о свойствах чётных и нечётных чисел.
VII. Выполнение задания 4.
Выполни действия:
а) умножь на 2 все четные числа в числовом ряду от 1 до 10. Расскажи, какие получились числа – четные или нечетные?
Расскажи, какие получились числа – четные или нечетные?
б) умножь на 2 все нечетные числа в этом же ряду. Расскажи, какие получились числа – четные или нечетные?
Дети записывают в тетрадь
а) 2 4 6 8 10
4 8 12 16 20
б) 1 3 5 7 9
2 6 10 14 18
Делают вывод: записанные числа четные и нечетные.
Какое число, четное или нечетное получается при умножении любого числа на 2?
Вывод: При умножении любого числа на 2 получается четное число.
.
VIII .Закрепление нового материал
Игра «Найди лишнее»
1) 2 4 7 6 8 10 (все числа чётные, а число 7 нечётное)
-Какие числа называются чётными?
(Числа, которые делятся на 2 называются – чётными
2) 1 3 5 7 9 4 (все числа нечётные, а число 4 чётное )
— Какие числа называются нечётными?
(Числа, которые не делятся на 2 называются – нечётными)
— Где мы можем встретиться с расположениями чётных и нечётных чисел.
(Нумерация домов на улицах нашего посёлка).
— Как располагаются чётные и нечётные числа в числовом ряду?
(Чётные и нечётные числа в числовом ряду чередуются
ХI . Итог урока:
— Чему учились сегодня на уроке?
(Мы учились определять чётные и нечётные числа)
-Какое задание захотелось выполнить еще раз?
-Где мы можем применить полученные знания
Х. Предполагаемая домашняя работа
1) Задание 6, 8, стр. 67.
2) Задание 9 (по желанию), стр. 67.
3) Запомнить вывод в оранжевой рамочке на стр. 66
ХI. Чтобы убедиться, что материал вами усвоен, предлагаю «блиц-опрос»
Он сложил 2 чётных числа и получил снова чётное число. То же самое вышло, когда он сложил 2 нечётных числа. А от сложения чётного числа с нечётным получилось нечётное. Такое много раз случалось и у египтян, и у вавилонян, греков живших до Пифагора.
- какое число получится, если
а) сложить два четных числа;
три четных числа;
два нечетных числа;
три нечетных числа.
б) из четного вычесть четное;
из нечетного вычесть четное;
из нечетного вычесть нечетное.
(Обоснуйте свои ответы)
(после каждого ответа на доске выставляются карточки с буквами
Ч – четное, Н – нечетное)
ч ч ч н ч н ч
А теперь получите оценку за урок.
(карточки переворачиваются, там слово МОЛОДЦЫ)
Рефлексия. Группы оценивают работу каждого участника. Учитель оценивает работу групп в целом.
— Оцените своё участие в уроке, используя условные обозначения:
Мне было очень интересно.
Мне было скучно.
Я затруднялся, работая в группе
Спасибо, ребята, вам за урок. Вы сегодня очень хорошо работали. Мне с вами было интересно.
Фронтальная работа
а) соревнования по группам
«Кто первый решит?»
18 : 9 = 2 4 – 2 = 8 5 – 2 = 10
8 : 2 = 4 12 : 2 = 6 10 : 5 = 2
2 – 3 = 6 2 – 2 = 4 6 – 2 = 12
16 : 2 = 8 14 : 7 = 2 16 : 8 = 2
6 : 2 = 3 18 : 2 = 9 2 – 8 = 16
10 : 2 = 5 14 : 2 = 7 9 – 2 = 18
Что можно сказать об ответах, которые получились в 1, 2, 3 столбиках? Что это за числа?
Физминутка
Мы устали, засиделись
Мы устали, засиделись,
Нам размяться захотелось.
Отложили мы тетрадки,
Приступили мы к зарядке
(Одна рука вверх, другая вниз, рывками менять руки.)
То на стену посмотрели,
То в окошко поглядели.
Вправо, влево поворот.
(Повороты корпусом.)
А потом наоборот.
Приседанья начинаем,
Ноги до конца сгибаем.
Вверх и вниз, вверх и вниз,
Приседать не торопись!
(Приседанья.)
И в последний раз присели,
А теперь за парты сели.
(Дети садятся за парты.)
- Фронтальная работа, на перестановку четырех элементов.
№ 9 (стр. 67)
Сколько различных четных и двузначных чисел можно написать с помощью цифр 1, 3, 2, 0, если:
а) цифры в числе могут повторяться;
б) цифры в числе не повторяются.
Последовательность работы:
а) на доске записаны цифры 1, 3, 2, 0
Детям предлагается назвать все возможные способы получения двухзначных чисел, когда цифры в числе повторяются, отобрать из них только четные. Получается, что возможен только один вариант – 22.
б) устанавливается закономерность, по которой записываются двузначные числа, когда цифры в числе не повторяются (фиксируется первая цифра, а вторые меняются), при этом двузначные числа должны быть четными. Из всех возможных вариантов выбираются следующие числа: 10, 12, 20, 30, 32.
- Познакомиться с понятиями четности-нечетности
(учить видеть, что:
- сумма двух четных чисел – четное число;
- сумма двух нечетных чисел – четное число;
- сумма четного и нечетного чисел – нечетное число).
Тип урока :изучение нового материала с элементами исследовательской деятельности .
Формы обучения: работа под руководством учителя , групповая , самостоятельная работа, фронтальная.
oneВы округляете, потому что десятый разряд имеет число, равное 5 или больше, так что это означает, что вы округляете сотый разряд вверх.
13 500, потому что все, что больше 5 или 5 в разряде 1ps, всегда будет округляться.
Разделение с использованием неполных частных 892÷26
Ответы
Ответ 36 остаток 8
3 400 000 34 00 заполните шаблоны
Ответы
340, 34
я думаю, что это
Классифицируйте каждое число, указав, к какому набору или наборам оно принадлежит 8 и 0,25
Ответы
нам дают два числа: 8 и 0,25. В этом случае в задаче нас просят определить, к какому множеству принадлежат числа. 8 относится к целым числам и целым числам, а также к натуральным числам. 0,25 относится к десятичным числам и целым числам
Пятеро друзей делят между собой три мешка яблок поровну, запишите представленное в данной ситуации деление в виде дроби
Ответы
Нам дано утверждение о том, что пятеро друзей делят поровну три мешка яблок. В этом случае, поскольку 3 не делится на 5, ответом является дробь. В числителе — количество мешков с яблоками, а в знаменателе — количество друзей. Ответ 3/5
В числителе — количество мешков с яблоками, а в знаменателе — количество друзей. Ответ 3/5
Сколько 120 разделить на 8?!?
Ответы
Ответ на этот вопрос 15.
120/8Разделить
Окончательный ответ: 15
Вы можете убедиться, что ответ равен 15, умножив 15 на 8, в результате чего должно получиться 120. Вот как вы знаете, что 15 — правильный ответ.
2-литровая бутылка кока-колы за 1,39 доллара США или упаковка из 12 банок Pepsi по 12 унций за 3,49 доллара США.. Какая сделка лучше?
Ответы
Ответ:
2 литра колы — это выгоднее, чем пепси.
Пошаговое объяснение:
2-литровая бутылка кока-колы за 1,39 доллара.
1 литр колы будет стоить = = $0,695
————————————— ————————————————— ———
12 банок Pepsi по 12 унций за 3,49 доллара.
Означает, что у нас есть 1 упаковка банок по 12 унций за = = $0,291
1 унция = 0,0296 литра
12 унций = = 0,3552 литра
Теперь мы получаем, что 0,3552 литра пепси стоит 0,291 доллара
1 литр пепси будет стоить = = 0,819 доллара
——— ————————————————— —————————————
Сравнивая обе стоимости за литр, мы видим что 2 литра колы лучше, чем пепси.
2-литровая бутылка колы за 1,39 доллара.
Что такое 6 2/3 в виде десятичной дроби
Ответы
Было бы 6.66….. повторяю
Г-н Рамирес делит 12 лягушек поровну на 6 групп, чтобы ученики могли изучить их. Сколько лягушек в каждой группе? Отметьте известную и неизвестную информацию на диаграмме ленты, чтобы помочь вам решить.
Ответы
Ответ будет 2 лягушки в группе ра
Какие коэффициенты используются 4,6,9,14,?49
Ответы
1,2,3,4,7 используются для 4,6,9,14
Спортсмен завершает гонку за 55,72 секунды. Во сколько раз цифра в разряде десятков больше цифры в разряде единиц
Во сколько раз цифра в разряде десятков больше цифры в разряде единиц
Ответы
Поскольку они одинаковые, ответ 1 раз
Объясните, является ли дым, заполняющий комнату, слиянием или нет
Ответы
Нет, это не синтез. Это диффузия…
объяснение :
диффузия — это движение частиц от высокой концентрации к низкой концентрации..
когда дым поднимается в одном углу комнаты, вскоре он распространяется по всей комнате, что является просто диффузией. . Надеюсь, это поможет! 🙂
1 фунт 4 унции рибай за 4,99 доллара или 2 фунта 6 унций филе-миньон за 9,75 доллара. Какая сделка лучше?
Ответы
Ответ:
1 фунт 4 унции рибай за 4,99.
Пошаговое объяснение:
1 унция рибай стоит 0,25 доллара
1 унция филе миньон стоит 0,30 доллара
(16 унций на фунт)
20 унций = 4,99 — > 4,99/20 = 0,2495
38 унций = 9,75 —> 9,75/38 = 0,2565789474
Что это за число в расширенной форме 4408730
Ответы
4 000 000 + 400 000 + 8 000 + 700 + 30
4000000+400000+8000+700+30
Сью и Иона выбрали числа разрядной игры. Сью выбрала число сто пятьдесят две тысячи. Иона выбрал пять миллионов для своего числа кто выбрал число терки объясните
Сью выбрала число сто пятьдесят две тысячи. Иона выбрал пять миллионов для своего числа кто выбрал число терки объясните
Ответы
Ответ:
Иона выбрал большее число .
Пошаговое объяснение:
Примите во внимание предоставленную информацию.
По разрядности:
Миллионы Гунн. Т. Десять Th. Тысячи сотни Десятки единицы
1000 000 100 000 10 000 1000 100 10 1
Сью выбрала число сто пятьдесят две тысячи.
Это число можно записать так: 152 000
Иона выбрал пять миллионов.
Теперь мы можем записать 5 миллионов как 5000000.
Число Миллион в 10 раз больше сотни тысяч.
Таким образом, 5 миллионов больше, чем 152 000, поэтому Иона выбрал большее число.
Что лучше всего описывает число 5?
Ответы
Ответ будет простым числом
Ответ: это нечетное число
Напишите число, состоящее из 5 десятков и 13 единиц
Ответы
Ответ будет 50 + 13 = 63.
Равно будет 6 десяткам и 3 единицам
Скорость юнита 25 метров за 2сек??
Ответы
Перемножить, чтобы найти x:Найдите сумму 6 и 4 и затем вычтите 2
Ответы
ответ 8 я думаю
Ответ 8!!!!!!!!
У вас есть 43 карандаша. Кроме 1 группы из 43 карандашей, можно ли разделить карандаши на группы с таким же количеством карандашей, чтобы не осталось карандашей?
Ответы
Ответ:
Нет, это не так.
Пошаговое объяснение:
43 — простое число. это означает, что он делится только на 1 и 43; других факторов нет.
13 458 округлено до сотых
Компания, производящая рубашки для универмага, решает создать новый стиль хлопчатобумажных рубашек. Компания, скорее всего, будет производить рубашки, которые будут
Как окружающая среда влияет на образ жизни в обществе?
Что такое Нах3????????
Каким образом судебный приказ о хабеас корпус защищает личную свободу?
В приведенном выше отрывке присутствуют все эти типы образного языка, кроме __________.
Может ли жидкость или газ воздействовать на объект?
Разделение с использованием неполных частных 892÷26
3 400 000 34 00 завершить шаблоны
Почему медведь учится охотиться и плавать
Какие детали вы бы предложили, чтобы поддержать идею прихода в новый мир?
В соответствии с доктриной Трумэна Соединенные Штаты взяли на себя обязательство помогать странам,
Классифицируйте каждое число, указав, к какому набору или наборам оно принадлежит 8 и 0,25.
Компания, скорее всего, будет производить рубашки, которые будут
Как окружающая среда влияет на образ жизни в обществе?
Что такое Нах3????????
Каким образом судебный приказ о хабеас корпус защищает личную свободу?
В приведенном выше отрывке присутствуют все эти типы образного языка, кроме __________.
Может ли жидкость или газ воздействовать на объект?
Разделение с использованием неполных частных 892÷26
3 400 000 34 00 завершить шаблоны
Почему медведь учится охотиться и плавать
Какие детали вы бы предложили, чтобы поддержать идею прихода в новый мир?
В соответствии с доктриной Трумэна Соединенные Штаты взяли на себя обязательство помогать странам,
Классифицируйте каждое число, указав, к какому набору или наборам оно принадлежит 8 и 0,25. Пятеро друзей делят три мешка яблок поровну между собой и записывают деление, представленное в данной ситуации, в виде дроби.
Сколько будет 120 разделить на 8?!?
2-литровая бутылка колы за 1,39 доллара.или 12 упаковок банок Pepsi по 12 унций за 3,49 доллара. Какая сделка лучше?
Зачем белому медведю учиться охотиться и плавать?
Что такое 6 2/3 в виде десятичной дроби?
24 балла! Какое утверждение о Конституции США верно? а.
Пятеро друзей делят три мешка яблок поровну между собой и записывают деление, представленное в данной ситуации, в виде дроби.
Сколько будет 120 разделить на 8?!?
2-литровая бутылка колы за 1,39 доллара.или 12 упаковок банок Pepsi по 12 унций за 3,49 доллара. Какая сделка лучше?
Зачем белому медведю учиться охотиться и плавать?
Что такое 6 2/3 в виде десятичной дроби?
24 балла! Какое утверждение о Конституции США верно? а.




 Узнав о том, как числа влияют на судьбу, человек извлечет положительный опыт даже из неблагоприятных жизненных обстоятельств и, вооружившись полученным знанием, сможет противостоять грядущим потрясениям. Нумерология — это практическая дисциплина, развивающая человека как личность.
Узнав о том, как числа влияют на судьбу, человек извлечет положительный опыт даже из неблагоприятных жизненных обстоятельств и, вооружившись полученным знанием, сможет противостоять грядущим потрясениям. Нумерология — это практическая дисциплина, развивающая человека как личность. Иными словами, его научный подход лежал в области разума. Труды Юнга посвящены скорее исследованию духовных аспектов и паранормальных явлений. В то же время, он посвятил немало времени исследованию личностных категорий человека.
Иными словами, его научный подход лежал в области разума. Труды Юнга посвящены скорее исследованию духовных аспектов и паранормальных явлений. В то же время, он посвятил немало времени исследованию личностных категорий человека.
 Живущие в таком доме люди легко находят общий язык. В этом доме могут сполна проявиться ваши артистические, психологические и дипломатические способности Числовая вибрация дома двойки заставляет живущих в нем людей быть мягкими, спокойными, дружелюбными, но непостоянными.
Живущие в таком доме люди легко находят общий язык. В этом доме могут сполна проявиться ваши артистические, психологические и дипломатические способности Числовая вибрация дома двойки заставляет живущих в нем людей быть мягкими, спокойными, дружелюбными, но непостоянными. Это, можно сказать, дом свиданий. Здесь царят чувственная любовь, атмосфера жизнелюбия и оптимизма. Числовая вибрация дома пятерки склоняет живущих в нем людей жить на широкую ногу, избегать всяческой ответственности и предаваться излишествам.
Это, можно сказать, дом свиданий. Здесь царят чувственная любовь, атмосфера жизнелюбия и оптимизма. Числовая вибрация дома пятерки склоняет живущих в нем людей жить на широкую ногу, избегать всяческой ответственности и предаваться излишествам. Люди, живущие в таком доме, часто удачливые бизнесмены или предприниматели, однако их отличает безжалостность и упрямство. Числовая вибрация дома восьмерки провоцирует вспыльчивость и нервозность. В таком доме часто живут люди, склонные к тирании и эксцентричным выходкам.
Люди, живущие в таком доме, часто удачливые бизнесмены или предприниматели, однако их отличает безжалостность и упрямство. Числовая вибрация дома восьмерки провоцирует вспыльчивость и нервозность. В таком доме часто живут люди, склонные к тирании и эксцентричным выходкам.

 Все числа он разделил на два вида: четные и нечетные, и с удивительной чуткостью выявил свойства чисел каждой группы. Четные числа обладают следующими свойствами: любое число может быть разделено на две равные части, обе из которых либо четны, либо нечетны. Например, 14 делится на две равные части 7 + 7, где обе части нечетные; 16 = 8 + 8, где обе части четные. Пифагорейцы рассматривали четное число, прототипом которого была дуада, неопределенным и женским. “Четные числа, допускавшие раздвоение, казались более разумными, олицетворяли некоторое положительное явление”, — писал Аристотель. Так число получало характер, теряло вечное, абстрактное начало.
Все числа он разделил на два вида: четные и нечетные, и с удивительной чуткостью выявил свойства чисел каждой группы. Четные числа обладают следующими свойствами: любое число может быть разделено на две равные части, обе из которых либо четны, либо нечетны. Например, 14 делится на две равные части 7 + 7, где обе части нечетные; 16 = 8 + 8, где обе части четные. Пифагорейцы рассматривали четное число, прототипом которого была дуада, неопределенным и женским. “Четные числа, допускавшие раздвоение, казались более разумными, олицетворяли некоторое положительное явление”, — писал Аристотель. Так число получало характер, теряло вечное, абстрактное начало.
 Например, если 22 разделить на 2, четный делитель, частное 11 будет нечетно.
Например, если 22 разделить на 2, четный делитель, частное 11 будет нечетно. Например, 24 имеет суммой своих дробных частей 12+6+4+8+3+2+1 число 33, что превышает 24, исходное число.
Например, 24 имеет суммой своих дробных частей 12+6+4+8+3+2+1 число 33, что превышает 24, исходное число. Совершенные числа, будучи умноженными на 2, дают сверхсовершенные числа, а будучи разделенными пополам, — несовершенные.
Совершенные числа, будучи умноженными на 2, дают сверхсовершенные числа, а будучи разделенными пополам, — несовершенные. Например, 9 есть 4+4+1.
Например, 9 есть 4+4+1. д.
д. Христианские ученые, занимавшиеся наукой о числах, связывали это число с дьяволом, отмечая, что в Библии говорится, «И увидел Бог, что это хорошо» после каждого дня творения, кроме второго. Но за предложенными Пифагором основаниями гармонии лежала темная магия, которая уходила своими корнями в глубины истории человечества.
Христианские ученые, занимавшиеся наукой о числах, связывали это число с дьяволом, отмечая, что в Библии говорится, «И увидел Бог, что это хорошо» после каждого дня творения, кроме второго. Но за предложенными Пифагором основаниями гармонии лежала темная магия, которая уходила своими корнями в глубины истории человечества.
 В предсказаниях число семь появляется с жуткой периодичностью.
В предсказаниях число семь появляется с жуткой периодичностью. И нельзя было найти никаких чисел, при перемножении дававших семь. Оно было одиноким, чистым и девственным, и в этом заключалась его магическая сила.
И нельзя было найти никаких чисел, при перемножении дававших семь. Оно было одиноким, чистым и девственным, и в этом заключалась его магическая сила.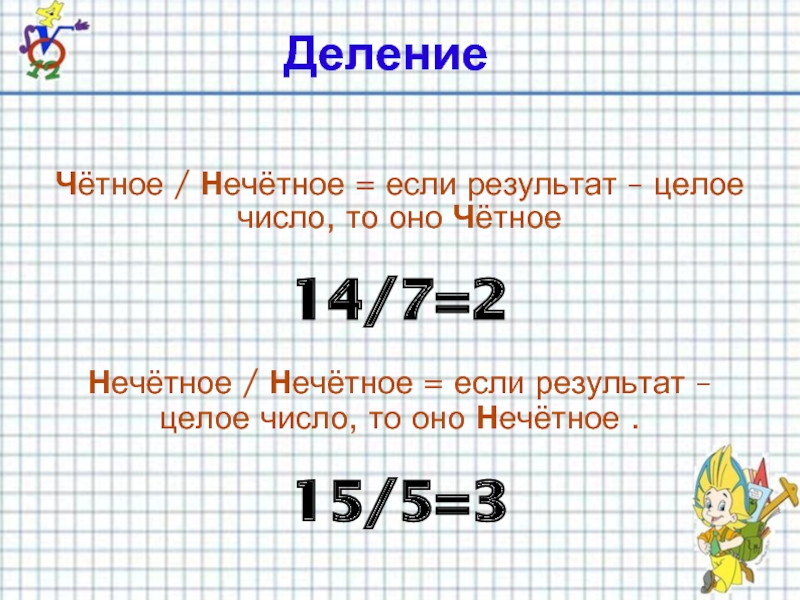
 Кроме того, в полный аккорд входило восемь нот, что служило мерой Пифагора для человека.
Кроме того, в полный аккорд входило восемь нот, что служило мерой Пифагора для человека. (1+6+6+1=14), подписал договор в Дувре в 1670 г. (1+6+7+0=14), и, наконец, умер в возрасте 77 лет (7+7=14), то есть именно в 1715 г. (1+7+1+5=14)!
(1+6+6+1=14), подписал договор в Дувре в 1670 г. (1+6+7+0=14), и, наконец, умер в возрасте 77 лет (7+7=14), то есть именно в 1715 г. (1+7+1+5=14)! И действительно, 21 июня 1791 года, самодержца схватили революционеры, когда тот пытался бежать из мятежного Парижа; 21 сентября 1792 года король вынужден был отказаться от трона; А 21 января 1793 года Людвигу отрубили голову…
И действительно, 21 июня 1791 года, самодержца схватили революционеры, когда тот пытался бежать из мятежного Парижа; 21 сентября 1792 года король вынужден был отказаться от трона; А 21 января 1793 года Людвигу отрубили голову… 5 Kb.
5 Kb.
 66)
66)