Знак подобности треугольников: Знак подобия в геометрии

Признаки подобия треугольников

При изучении геометрии вы непременно обращали внимание, что часть фигур очень похожа на другие. Отличаются только размеры. Но геометрия — наука точная и слово «похожие» не всегда определяет реальное положение вещей. Например, прямоугольный треугольник похож на равносторонний, но при ближайшем рассмотрении легко обнаружить различия, — отличаются углы, длины сторон, конфигурация.

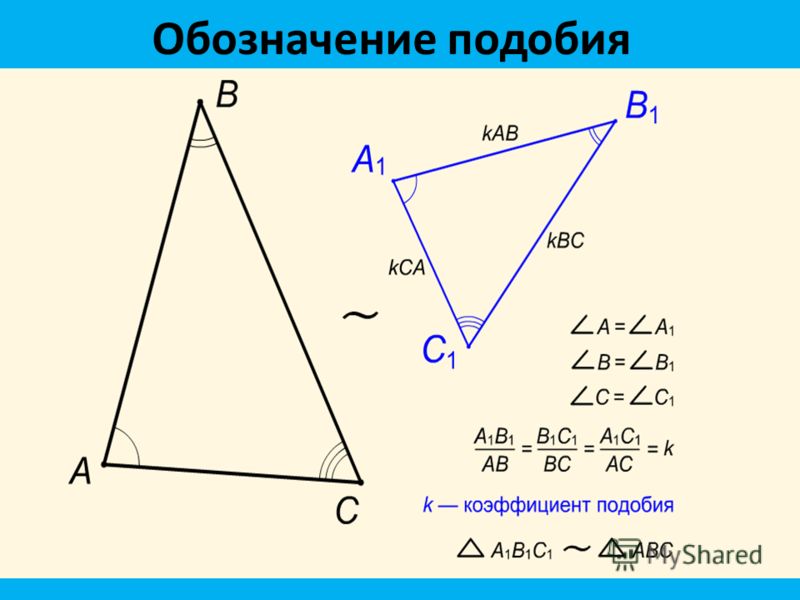
В геометрии применяется другое понятие — «подобие». Это более узкий термин, который определяет фигуры, которые идентичны по всем параметрам, кроме размера. Если увеличить, или уменьшить одну из фигур, то получится другая, с полным соответствием. Знак подобия в геометрии  «~» имеет очень большой смысл. Это не просто обозначение «похожести», а специальный термин. Он говорит о том, что из одной фигуры можно получить другую, если преобразовать ее особым образом.

Самый простой способ — увеличение размеров. Но не простое увеличение, а пропорциональное. То есть, каждая сторона фигуры увеличивается на строго определенную величину. Соотношение новой длины и исходной называется коэффициентом подобия. Согласно правилам математики К≠ 0. Смысл ясен, на ноль делить нельзя. В остальном значение К может принимать любое значение, в том числе, и дробное. Если в десятичном исчислении коэффициент находится в диапазоне от ноля до единицы, то фигура уменьшается при проецировании, если К ≥ 1, то фигура получится больше, или идентичной исходной.

Содержание

1. Подобие треугольников
2. Первый признак подобия
3. Второй признак подобия
4. Третий признак подобия треугольников
5. Примеры прикладного применения признаков подобия треугольников

Каждая из геометрических фигур имеет ряд признаков, по которым ее можно сравнить с другой и определить, подобные фигуры, или просто похожие. У треугольников таких признаков три. Рассмотрим их более подробно. В идеале, треугольники называются подобными, если у них три угла одинаковые, а три стороны пропорциональны, согласно коэффициенту К. Но не всегда есть возможность измерить углы и стороны.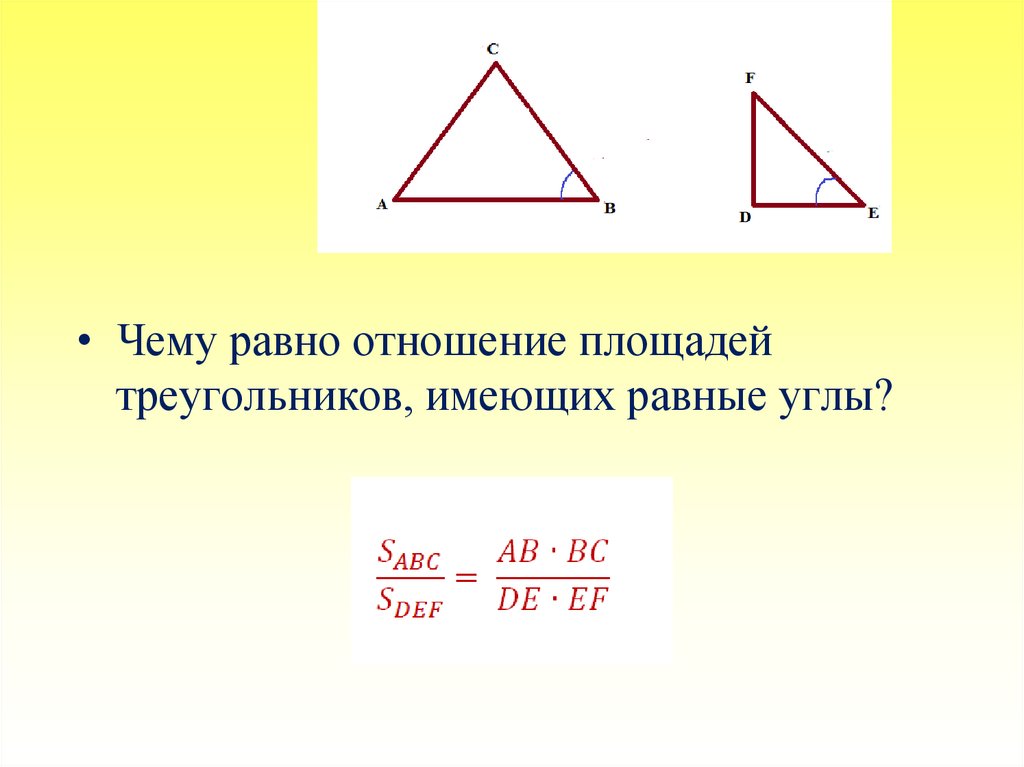 Есть ряд признаков, требующих меньшего числа измерений, по которым легко определить, подобные треугольники, или нет.

Если два угла произвольного треугольника равны двум углам другого, значит, фигуры подобные.  В геометрической графике это записывается так:

ΔАВС ~ΔА1В1С1  А=∠А1, ∠В=∠В1, ∠С=∠С1.

Доказательство первого признака подобия приводить не будем, ввиду того, что признак проверен и доказан, информация об этом есть в любом учебнике. Намного важнее, что из этого признака вытекает следствие, которое не менее важно, чем сам признак. Во многих задачах на ЕГЭ и в учебниках упор делается именно на знание этого правила. «Если три стороны одного треугольника попарно параллельны трем сторонам другого, то эти фигуры подобны».

Утверждение не менее очевидно, чем первый признак подобия. Формулируется оно так:

Если две соответствующие стороны треугольников пропорциональны, а углы между ними равные, то фигуры подобные.

Это правило называется признаком подобия по двум сторонам и углу между ними.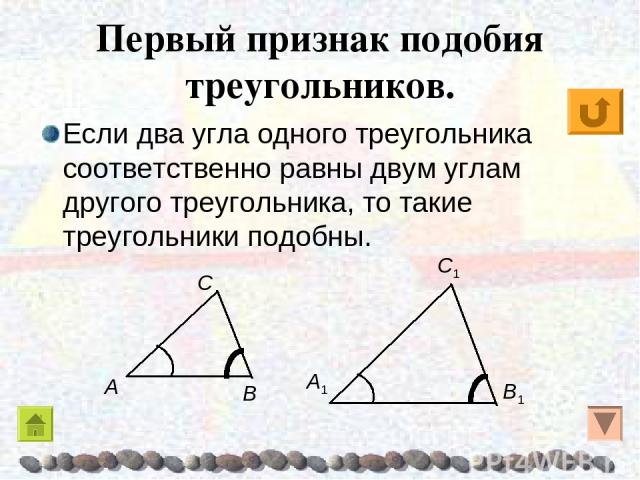 Геометрическая запись выглядит так:

ΔАВС ~ΔА1В1С1 ↔ ∠ А=∠А1, АВ/А1В1 = АС/А1С1.

Самый простой и наиболее понятный признак подобия: если три стороны одной фигуры пропорциональны трем сторонам другой с одинаковым коэффициентом К, то треугольники подобные. Записывается такое утверждение таким образом:

ΔАВС ~ΔА₁В₁С₁↔АВ/А₁В₁ = АС/А₁С₁= ВС/В₁С_1..

Доказательство этого утверждения опять же приводить не будем вследствие дефицита размера статьи. Лучше остановимся на следствиях, которые вытекают из этих утверждений. Многие из параметров геометрических фигур можно определить, пользуясь названными правилами.

Один из способов применения признаков подобия демонстрирует теорема об отношении периметров подобных треугольников. В формулировке говорится о том, что отношение периметров подобных треугольников равно коэффициенту пропорциональности сторон. На практике это выглядит так — вам нужно найти периметр треугольника со сторонами в несколько километров, что часто требуется в строительстве, агротехнике и геодезии.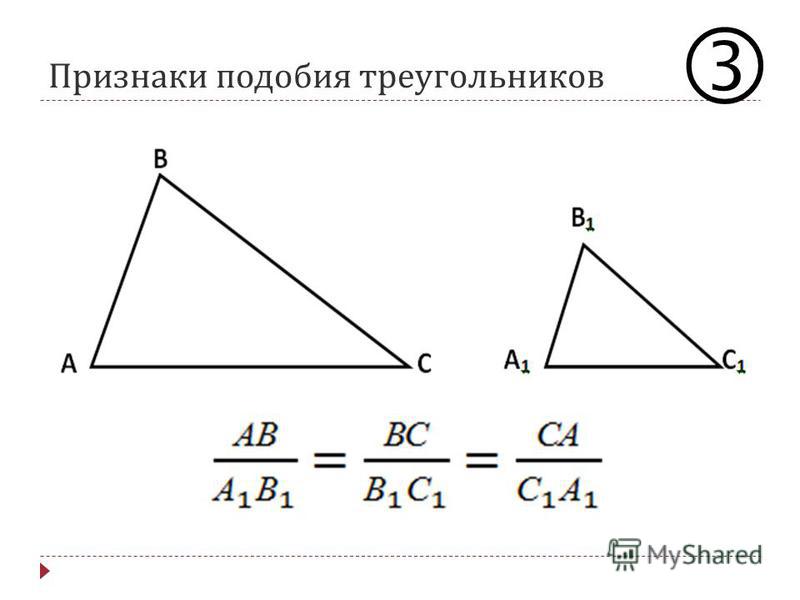 Если нарисовать подобный треугольник на бумаге, со сторонами в несколько сантиметров и вычислить периметр, то он будет ровно настолько же меньше, как и стороны треугольников. То есть, коэффициент К работает и в случае с периметром.

Вторая задача — найти соотношение площадей подобных треугольников. Здесь тоже существует определенная пропорция, но уже квадратичная. То есть, соотношение площадей фигур равно квадрату К.

S1/S = k2.

При решении задач поможет также лемма о подобных треугольниках, говорящая о том, что любая прямая, пересекающая треугольник параллельно одной из сторон, отсекает от него подобную фигуру.

Пользуясь полученной информацией, несложно решить любую задачу по определению параметров подобных треугольников.

 

 

 

Подобные треугольники | Математика

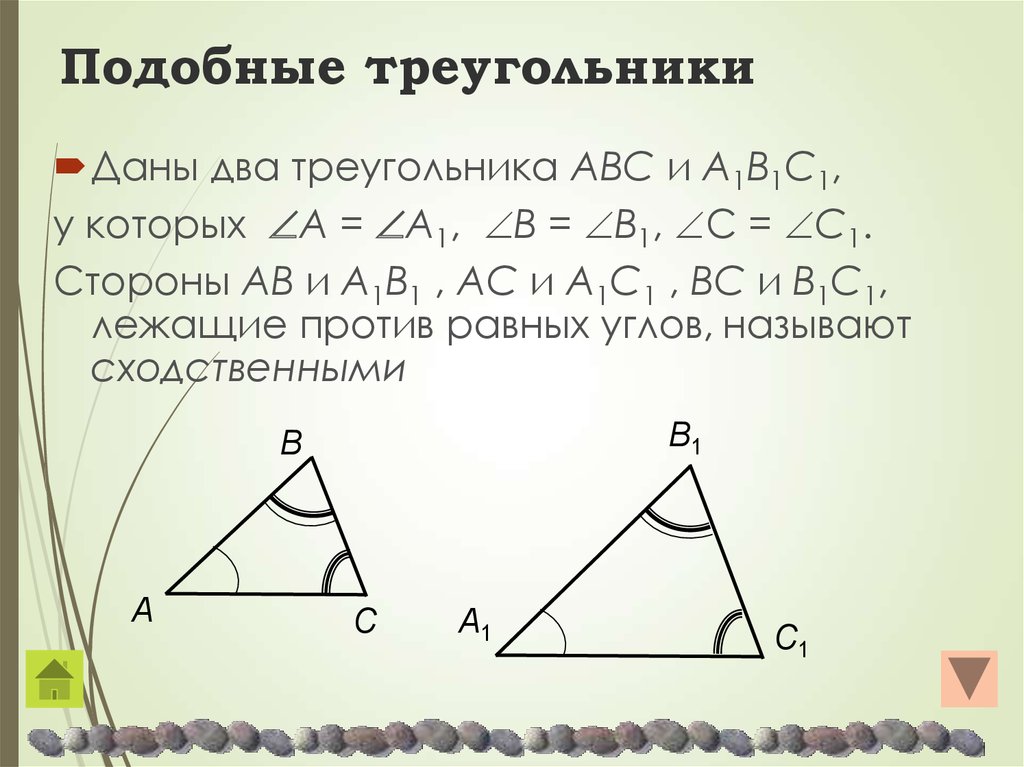
В двух треугольниках, имеющих равные углы, стороны, лежащие против одинаковых углов, называются сходственными (соответственными).

В треугольниках ABC и DEF (черт. 152), в которых

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

стороны AB и DE, BC и EF, AC и DF, лежащие против равных углов C и F, A и D, B и E будут соответственными сторонами.

Определение подобных треугольников. Подобными называются такие два треугольника, у которых углы равны и сходственные стороны пропорциональны.

Если в двух треугольниках (черт. 152) ABC и DEF углы равны

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

и соответственные стороны пропорциональны

AB/DE = AC/DF = BC/EF

то треугольники называются подобными.

Подобие обычно выражают знаком ∼.

Подобие двух треугольников изображают письменно:

ABC ∼ DEF.

Случаи подобия треугольников

Теорема 89. (Первый случай подобия.) Два треугольника подобны, если три угла одного равны трем углам другого треугольника.

Дано. В треугольниках ABC и DEF углы равны (черт. 153).

∠A = ∠D, ∠B = ∠E, ∠C = ∠F

Требуется доказать, что они подобны. Для этого нужно доказать, что их стороны пропорциональны, т. е. удовлетворяют отношениям:

AB/DE = AC/DF = BC/EF

Доказательство. Наложим треугольник DEF на ABC так, чтобы вершина E совпала с вершиной B, сторона ED со стороной AB. По равенству углов B и E сторона EF пойдет по стороне BC. Положим, точка D упадет в D’, а точка F в E’. Треугольник D’BE’ равен треугольнику DEF, следовательно,

∠D’ = ∠D, ∠D = ∠A

откуда

∠D’ = ∠A.

Если соответственные углы равны, то D’E || AC.

По теореме 86 имеют место равенства

AC/D’E’ = AB/BD’ = BC/BE’

Так как BD’ = ED, BE’ = EF, D’E’ = DF, то

AC/DF = AB/ED = BC/EF (ЧТД).

Теорема 90 (второй случай подобия). Два треугольника подобны, если они имеют по два равных угла.

Доказательство. Если в двух треугольниках ABC и DEF два угла равны (черт. 153).

A = D, B = E

то и третьи углы тоже равны, а в таком случае треугольники подобны (теорема 89).

Теорема 91 (третий случай подобия). Два треугольника подобны, если они имеют по равному углу, заключающемуся между пропорциональными сторонами.

Дано. В треугольниках ABC и DEF (черт. 153) углы B и E равны, и стороны, их содержащие, пропорциональны, т. е.

∠B = ∠E и AB/DE = BC/EF.

Требуется доказать, что треугольники подобны.

Доказательство. Совместим угол E с углом B, и отложим BD’ = ED, BE’ = EF, тогда ∆BD’E’ = ∆DEF, следовательно,

∠D’ = ∠D, ∠E’ = ∠F.

Так как имеет место пропорция

AB/BD’ = BC/BE’

то сторона D’E’ || AC (теорема 87).

Поэтому ∠D’ = ∠A, ∠C = ∠E’.

Следовательно,

∠A = ∠D, ∠C = ∠F, ∠B = ∠E

т. е. три угла одного равны трем углам другого треугольника.

В этом же случае треугольники ABC и DEF подобны (ЧТД).

Теорема 92 (четвертый случай подобия). Два треугольника подобны, если стороны одного пропорциональны сторонам другого.

Дано. В треугольниках ABC и abc (черт. 154) стороны пропорциональны:

AB/ab = BC/bc = AC/ac (1)

Требуется доказать, что у них углы равны, т. е.

A = a, B = b, C = c.

Доказательство. Отложим на стороне BA отрезок Ba’, равный ba, и проведем отрезок a’c’, параллельный AC, тогда будут иметь место отношения:

AB/Ba’ = BC/Bc’ = AC/a’c’

Так как Ba’ = ba, то рядом с этими имеют место отношения:

AB/ab = BC/Bc’ = AC/a’c’ (2)

Сопоставляя отношения (1) и (2), заключаем, что

Bc’ = bc, a’c’ = ac,

следовательно, два треугольника a’Bc’ и abc равны, откуда

∠B = ∠b, ∠Ba’c’ = ∠a, ∠Bc’a’ = ∠c

а так как

∠A = ∠a’, ∠C = ∠c’, то
B = b, A = a, C = c,

следовательно, углы двух треугольников ABC и abc равны (ЧТД).

Теорема 93 (пятый случай подобия). Два треугольника подобны, если стороны одного параллельны сторонам другого.

Доказательство. Здесь могут быть два случая:

1-й случай. Если углы двух треугольников с параллельными сторонами обращены в одну сторону. В таком случае в двух таких треугольниках ABC и abc (черт. 155) все углы одного соответственно равны углам другого, и, следовательно, треугольники подобны.

2-й случай. Когда углы с параллельными сторонами обращены в разные стороны. Так в треугольниках ABC и a’b’c’ стороны параллельны.

AB || a’b’, AC || a’c’, BC || b’c’.

Углы же между параллельными сторонами обращены в разные стороны.

В таком случае, продолжив стороны a’c’ и a’b’, откладываем на продолжении их части a’b» = a’b’ и a’c» = a’c’.

Треугольники a’b»c» и a’b’c’ равны. Треугольник a’b»c» подобен треугольнику ABC, ибо у него стороны параллельны и углы, направленные в одну сторону, равны, следовательно,

∆ABC ~ a’b»c», следовательно, ∆ABC ~ a’b’c’ и
AB/a’b’ = AC/a’c’ = BC/b’c’

Теорема 94 (шестой случай подобия). Два треугольника подобны, если стороны одного перпендикулярны к сторонам другого.

Даны два треугольника ABC и abc (черт. 156), стороны которых перпендикулярны:

ab ⊥ AB, ac ⊥ AC, bc ⊥ BC

Требуется доказать, что треугольники подобны.

Доказательство. Продолжим стороны ac и bc до пересечения их со сторонами AC и BC в точках n и p. Тогда в двух треугольниках mcn и mCp все углы равны, ибо

n = p как прямые

Углы при точке m равны как вертикальные,

а следовательно, и третьи углы равны ∠pCm = ∠mcn.

Так как

∠pCm = ∠ACB, ∠mcn = ∠acb

следовательно,

∠ACB = ∠acb

Подобным же образом можно доказать, что A = a, B = b, следовательно, треугольники ABC и abc подобны и имеет место пропорция

AB/ab = AC/ac = BC/bc

Подобие прямоугольных треугольников

Теорема 95. Два прямоугольных треугольника подобны, если они имеют по равному острому углу.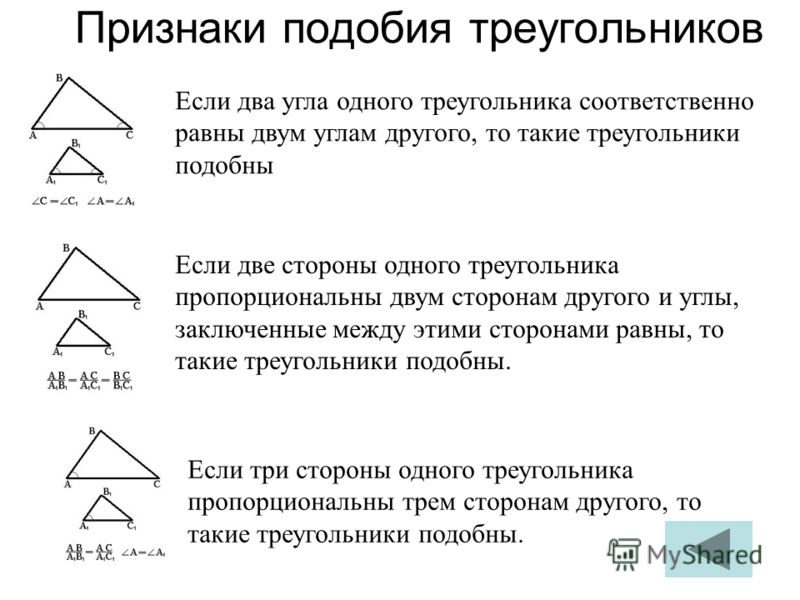

Дано. У прямоугольных треугольников ABC и abc (черт. 157) острые углы C и c равны.

Требуется доказать, что треугольники ABC и abc подобны.

Доказательство. Углы B и b равны как прямые, углы C и c равны по условию, следовательно, они подобны (теорема 90).

Теорема 96. Два прямоугольных треугольника подобны, если катет и гипотенуза одного пропорциональна катету и гипотенузе другого.

Дано. В прямоугольных треугольниках ABC и abc (черт. 157)

AC/ac = AB/ab (a)

Требуется доказать, что ∠A = ∠a, ∠C = ∠c.

Доказательство. Отложим на отрезке BA отрезок Bm, равный ba и из точки m проведем отрезок mn, параллельный ac, тогда имеет место пропорция:

AC/mn = AB/Bm (b)

Так как Bm = ab по построению, то, сравнивая две пропорции (a) и (b), заключаем, что ac = mn, следовательно, два прямоугольных треугольника Bmn и abc, имея по равному катету и равной гипотенузе, равны.

Действительно, у них Bm = ab, mn = ac.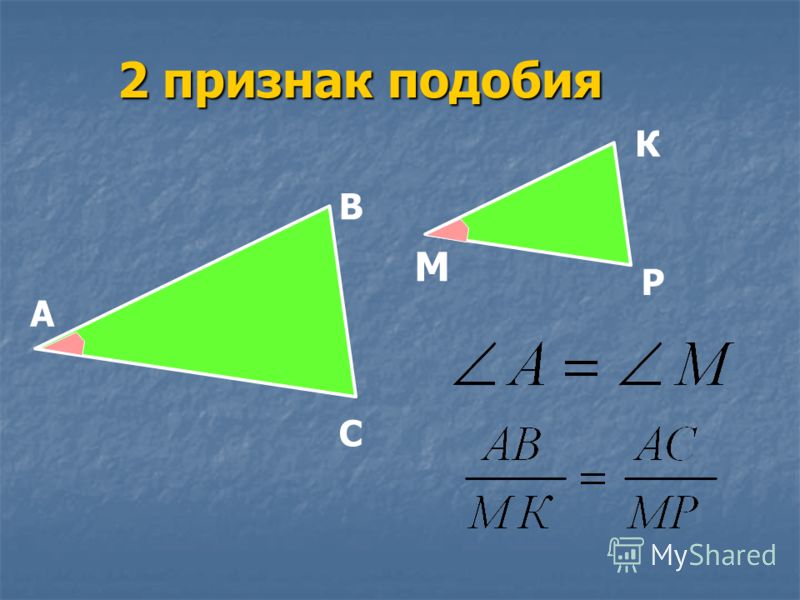 У равных треугольников и углы равны:

∠m = ∠a = ∠A и ∠n = ∠c = ∠C

следовательно, два треугольника ABC и abc подобны.

Теорема 97. В подобных треугольниках высоты пропорциональны сторонам.

Даны два подобных треугольника ABC и FED (черт. 158), следовательно,

∠A = ∠F, ∠B = ∠E, ∠C = ∠D и
AB/FE = BC/ED = AC/DF

и проведены высоты BH и Eh.

Требуется доказать, что AB/FE = BH/Eh.

Доказательство. Прямоугольные треугольники ABH и FEh подобны, ибо ∠A = ∠F по условию, ∠AHB = ∠FhE как прямые, следовательно,

AB/FE = BH/Eh (ЧТД).

Теорема 98. Прямая, разделяющая угол треугольника пополам, делит его противоположную сторону на части пропорциональные двум другим сторонам.

Дано. Отрезок BD делит угол B треугольника ABC пополам (черт. 159).

∠ABD = ∠DBC или ∠α = ∠β

Требуется доказать, что AB/BC = AD/DC.

Доказательство.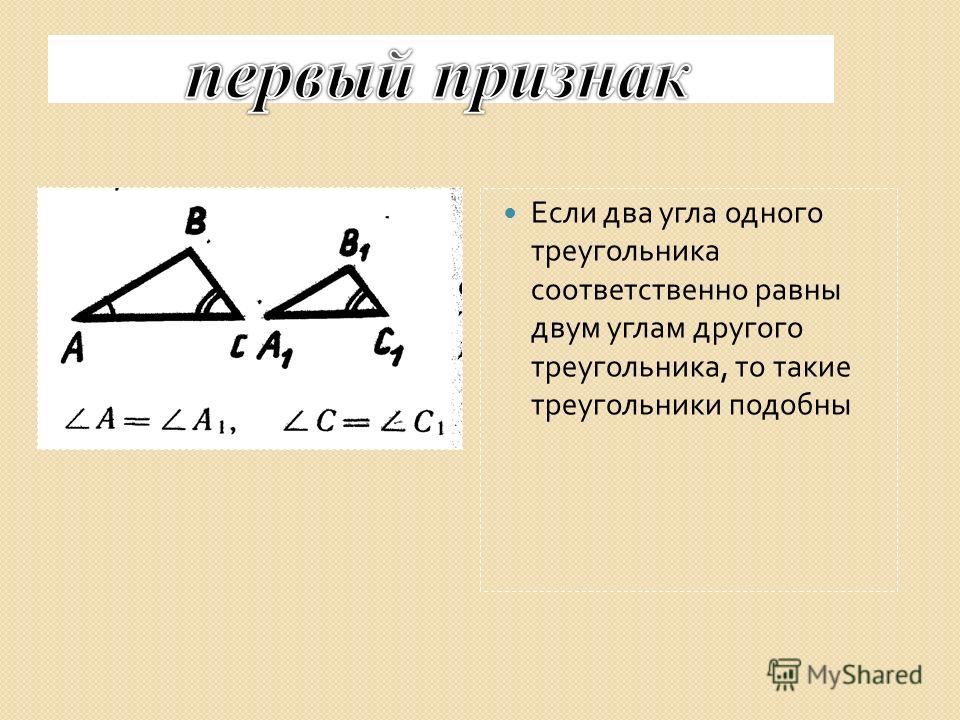 Проведем из точки A отрезок AF параллельный BD до пересечения его с прямой BC в точке F. В треугольнике FBA

∠AFB = ∠β как соответственные углы,
∠FAB = ∠α как внутренние накрест-лежащие углы от пересечения параллельных AF и BD третьей прямой AB.

Так как ∠α = ∠β по условию, то

∠AFB = ∠FAB, т. е. треугольник FAB равнобедренный, поэтому FB = AB.

Из того, что AF || BD вытекает пропорция:

FB/BC = AD/DC

Заменяя FB равным отрезком AB, получим пропорцию:

AB/BC = AD/DC (ЧТД).

Теорема 99 (обратная 98). Прямая, проведенная из вершины треугольника и делящая противоположную сторону на части, пропорциональные двум другим сторонам, делит угол при вершине пополам.

Дано. В треугольнике ABC (черт. 159) прямая BD рассекает противоположную сторону так, что имеет место пропорция:

AB/BC = AD/DC (a)

Требуется доказать, что ∠α = ∠β.

Доказательство. Проведем отрезок AF параллельно BD, тогда из треугольника AFC вытекает пропорция:

FB/BC = AD/DC (b)

Сравнивая две пропорции (a) и (b), заключаем, что FB = AB, следовательно,

∠AFB = ∠FAB.

Так как ∠α = ∠FAB, ∠β = ∠AFB, то и

∠α = ∠β (ЧТД).

Отношения в прямоугольном треугольнике

Теорема 100. Перпендикуляр, опущенный из вершины прямого угла на гипотенузу, среднепропорционален между частями гипотенузы.

Дано. В треугольнике ABC угол ABC прямой (черт. 160) и BD ⊥ AC.

Требуется доказать, что AD/BD = BD/DC.

Доказательство. Треугольники ABD и BDC подобны, ибо углы при точке D равны как прямые; кроме того из равенств ∠A + ∠α = d, ∠α +∠β = d вытекает

A + α = α + β, или A = β, следовательно и C = α.

Из подобия треугольников ABD и BDC вытекает пропорция

AD/BD = BD/DC (ЧТД).

Примечание. Если составляют одно отношение из сторон одного треугольника, то другое отношение составляется из соответственных сторон другого треугольника. При этом рассуждают следующим образом: против стороны AD лежит угол α, которому в подобном треугольнике BCD равен угол C, а против него лежит сходственная сторона BD треугольника BCD и т. д.

Теорема 101. Каждый катет среднепропорционален между целой гипотенузой и отрезком, прилежащим катету.

Доказательство. a) Треугольники ABC и ABD (черт. 160) подобны, ибо ∠ABC = ∠ADB как прямые, ∠A общий, следовательно,

∠C = ∠α

Из подобия треугольников вытекает пропорция:

AD/AB = AB/AC (a)

b) Треугольники ABC и BCD подобны, ибо ∠ABC = ∠BDC как прямые, ∠C общий, следовательно,

∠A = ∠β, откуда
DC/BC = BC/AC (b)

Теорема 102. Квадрат гипотенузы равен сумме квадратов катетов.

Из предыдущих пропорций (a) и (b) вытекают равенства:

AB² = AD · AC
BC² = DC · AC

Складывая их, получим:

AB² + BC² = AD · AC + DC · AC или
AB² + BC² = AC (AD + DC) = AC · AC = AC², т. е.
AC² = AB² + BC²

откуда

a) Гипотенуза равна корню квадратному из суммы квадратов катетов.

b) Катет равен корню квадратному из квадрата гипотенузы без квадрата другого катета.

Теорема 103. Диагональ квадрата несоизмерима с его стороной, или гипотенуза равнобедренного прямоугольного треугольника несоизмерима с катетом.

Дано. В квадрате ABCD проведена диагональ AC (черт. 161).

Требуется доказать, что отношение AC/AD есть величина несоизмеримая.

Доказательство. Станем сравнивать больший отрезок AC с меньшим BC по обыкновенным приемам нахождения общей меры, т. е. наложим меньший отрезок на больший, первый остаток на меньший и т. д.

a) Наложим отрезок BC на отрезок AC. Отложив отрезок AE, равный AB или BC, мы видим, что отрезок BC уложился один раз, ибо

AB + BC > AC.

Так как AB = BC, то 2BC > AC и BC > ½AC, следовательно, первый остаток EC < BC.

b) Наложим первый остаток EC на отрезок BC. Для этого из точки E восставим перпендикуляр EF и соединим точку F с A.

c) Треугольник FEC равнобедренный, ибо ∠EFC = ∠BAC как углы с перпендикулярными сторонами

∠BAC = ∠ECF, следовательно,
∠EFC = ∠ECF

На этом основании стороны EF и EC равны:

EF = EC (1)

Треугольники ABF и AEF равны, ибо они прямоугольны и у них

AF сторона общая
AB = AE по построению, следовательно,
BF = EF (2)

Таким образом из равенств (1) и (2) выходит, что

EC = EF = BF

Не трудно видеть, что первый остаток укладывается в отрезке BC не более двух раз.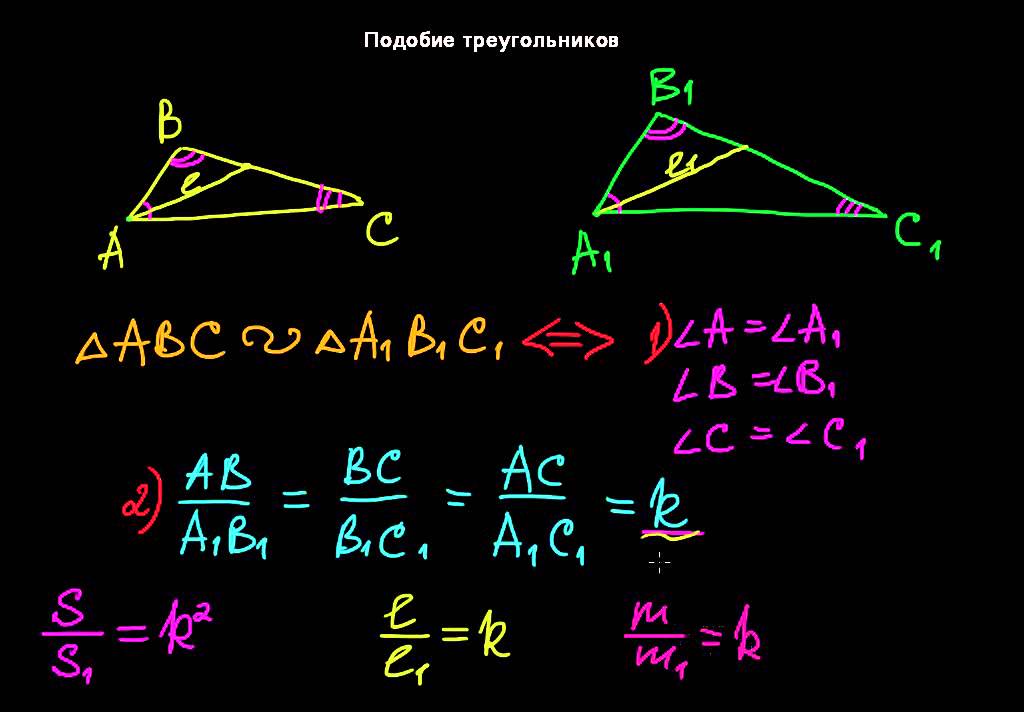 Отложив EC два раза на отрезке BC, найдем точку G и второй остаток GC. Таким образом, остаток после наложения сторон квадрата на диагональ укладывается в стороне квадрата не более двух раз.

d) Наложим второй остаток GC на первый EC.

В прямоугольном и равнобедренном треугольнике FEC соотношение между отрезками GC, FC и EC то же самое как и соотношение между данными отрезками EC, AC и BC в треугольнике ABC, ибо треугольник FEC прямоугольный и равнобедренный, следовательно, при дальнейшем наложении мы будем снова получать остаток. Продолжая так поступать, мы всегда будем получать остатки, поэтому общей меры мы никогда не получим, следовательно, отрезки AC и BC несоизмеримы.

Обозначив длину диагонали черед l, длину стороны квадрата через a, последовательные величины остатков через d₁, d₂ и т. д., т. е. положив

AC = l, BC = a, CE = d₁, GC = d₂ и т. д.

имеем равенства:

l = a + d₁, a = 2d₁ + d₂, d₁ = 2d₂ + d₃ и т.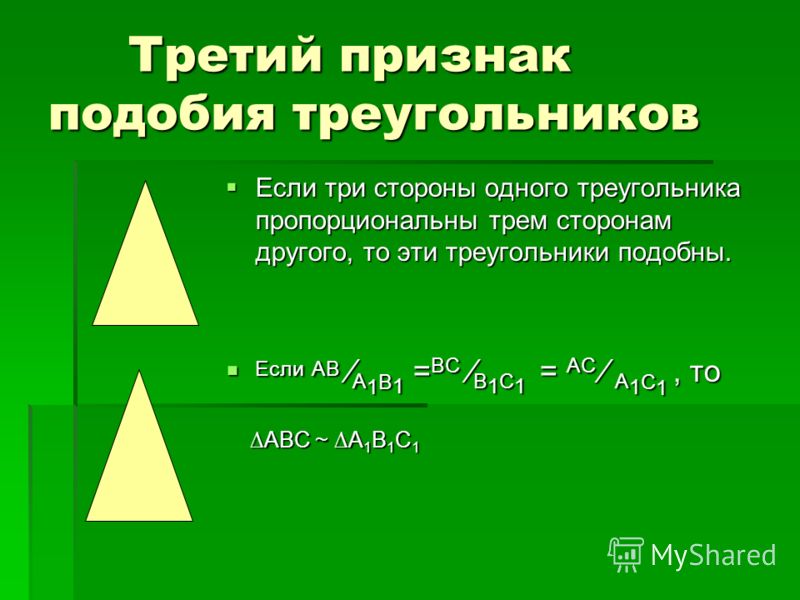 д.

откуда

l/a = 1 + d₁/a
a/d₁ = 2 + d₂/d₁ или d₁/a = ½ + d₂/d₁
d₁/d₂ = 2 + d₃/d₂ или d₂/d₁ = ½ + d₃/d₂

следовательно,

l/a = 1 + ½ + ½ + …

Отношение между длинами l и a выражается бесконечной непрерывной дробью. Несоизмеримость впрочем прямо вытекает из выражения диагонали квадрата по катетам.

Действительно,

AC² = AB² + BC².

Так как AB = BC, то AC² = 2AB², откуда AC = AB√2 и AC/AB = √2 величина несоизмеримая.

Соотношение между сторонами остроугольного и тупоугольного треугольника

Теорема 104. Квадрат стороны, лежащей против острого угла, равен сумме квадратов прочих двух сторон треугольника без удвоенного произведения основания на отрезок, заключающийся между вершиной острого угла и высотой.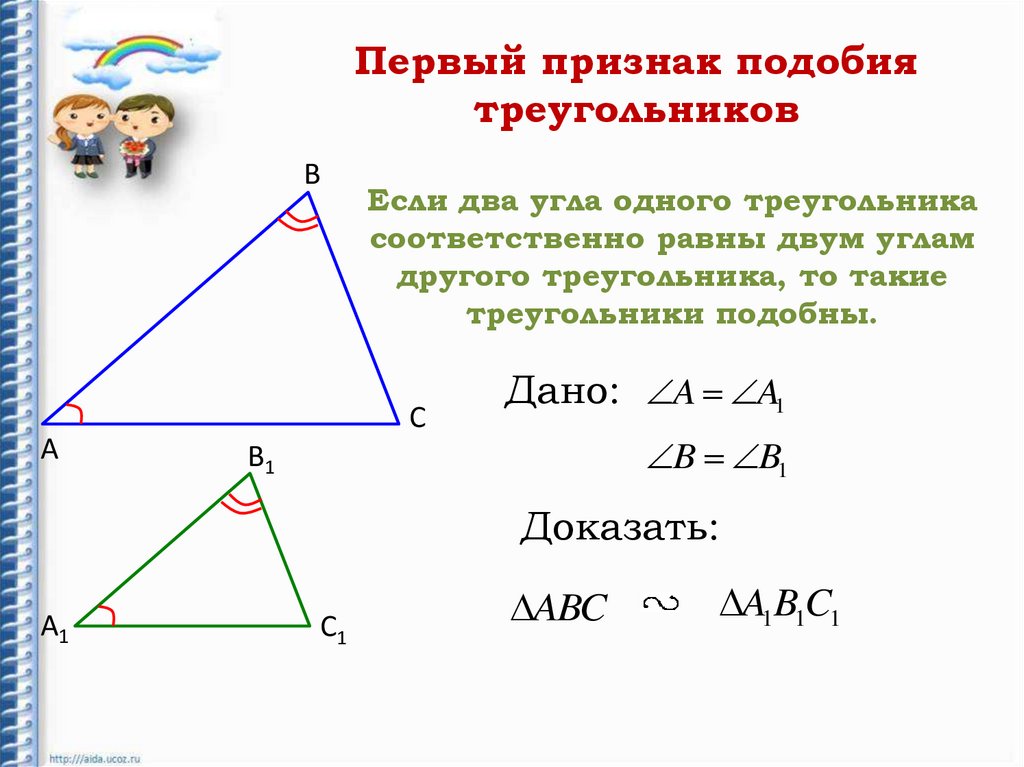

Здесь могут быть два случая: 1) когда перпендикуляр, выражающий высоту, пойдет внутри и 2) когда он пойдет вне треугольника.

Первый случай. Перпендикуляр BD (черт. 162), опущенный из вершины B на основание AC треугольника ABC, пойдет внутри треугольника.

Требуется доказать, что AB² = BC² + AC² — 2AC · DC.

Доказательство. Для прямоугольного треугольника ABD имеем равенство:

AB² = BD² + AD² (a)
AD = AC — DC, AD² = (AC — DC)² = AC² + DC² — 2AC · DC

Из прямоугольного треугольника BDC имеем:

BD² = BC² — DC²

Вставляя величины BD² и AD² в равенство (a), получим:

AB² = BC² — DC² + AC² + DC² — 2AC · DC, откуда
AB² = BC² + AC² — 2AC · DC (ЧТД).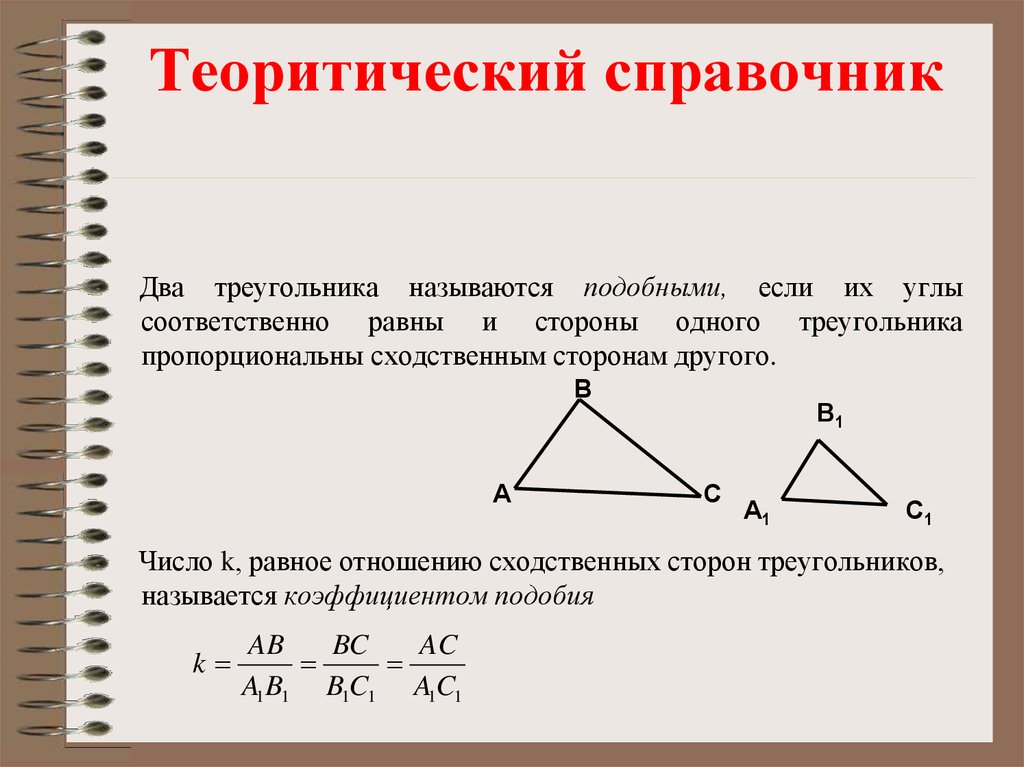

2-й случай. Перпендикуляр BD (черт. 163) лежит вне треугольника ABC.

Доказательство. Из прямоугольного треугольника ABD имеем:

AB² = BD² + DA²

Из прямоугольного треугольника BCD имеем:

BD² = BC² — CD²

следовательно,

AB² = BC² — CD² + DA².

Так как

DA = CD — AC
DA² = (CD — AC)² = CD² + AC² — 2CD · AC, то
AB² = BC² — CD² + CD² + AC² — 2CD · AC, откуда
AB² = BC² + AC² — 2CD · AC (ЧТД).

Теорема 105. Квадрат стороны, лежащей против тупого угла, равен сумме квадратов прочих двух сторон треугольника с удвоенным произведением основания на отрезок его от вершины тупого угла до высоты.

Дано. В тупоугольном треугольнике ABC отрезок CD (черт. 164) есть отрезок, лежащий между вершиной тупого угла и высотой.

Требуется доказать, что

AB² = AC² + BC² + 2AC · CD

Доказательство. Из тупоугольного треугольника ABC имеем:

AB² = BD² + AD² (a)
AD = AC + CD, AD² = AC² + CD² + 2AC · CD

Из прямоугольного треугольника BCD вытекает, что

BD² = BC² — CD²

Заменяя AD² и BD² в равенстве (a), получим:

AB² = BC² — CD² + AC² + CD² + 2AC · CD

откуда

AB² = BC² + AC² + 2AC · CD (ЧТД).

Теорема 106. Сумма квадратов диагоналей равна сумме квадратов всех четырех сторон параллелограмма.

Дан параллелограмм ABCD (черт.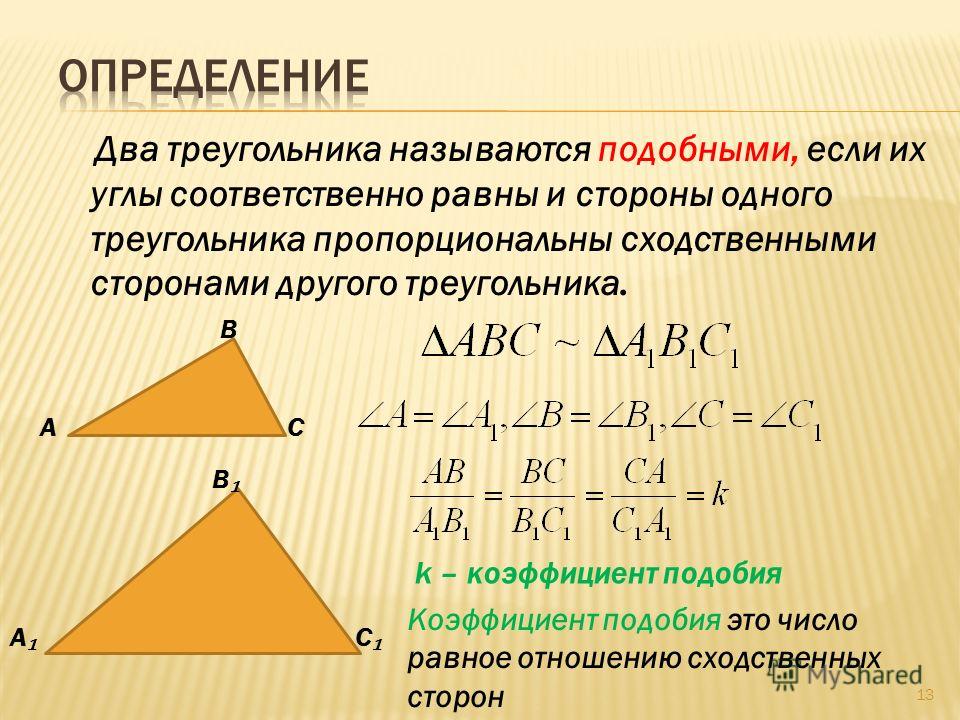 165) и проведены его диагонали AC и BD.

Требуется доказать, что

AC² + BD² = AB² + BC² + CD² + AD²

Доказательство. Опустив перпендикуляры BE и CF, имеем из косоугольного треугольника ABD равенство:

BD² = AB² + AD² — 2AD · AE (1)

Из тупоугольного треугольника ACD равенство:

AC² = CD² + AD² + 2AD · DF (2)

Отрезки AE и DF равны, ибо прямоугольные треугольники ABE и DCF равны, так как они имеют по равному катету и равной гипотенузе.

Сложив равенства (1) и (2), имеем:

BD² + AC² = AB² + AD² + CD² + AD²

Так как AD = BC, то

BD² + AC² = AB² + BC² + CD² + AD² (ЧТД).

Теорема 107.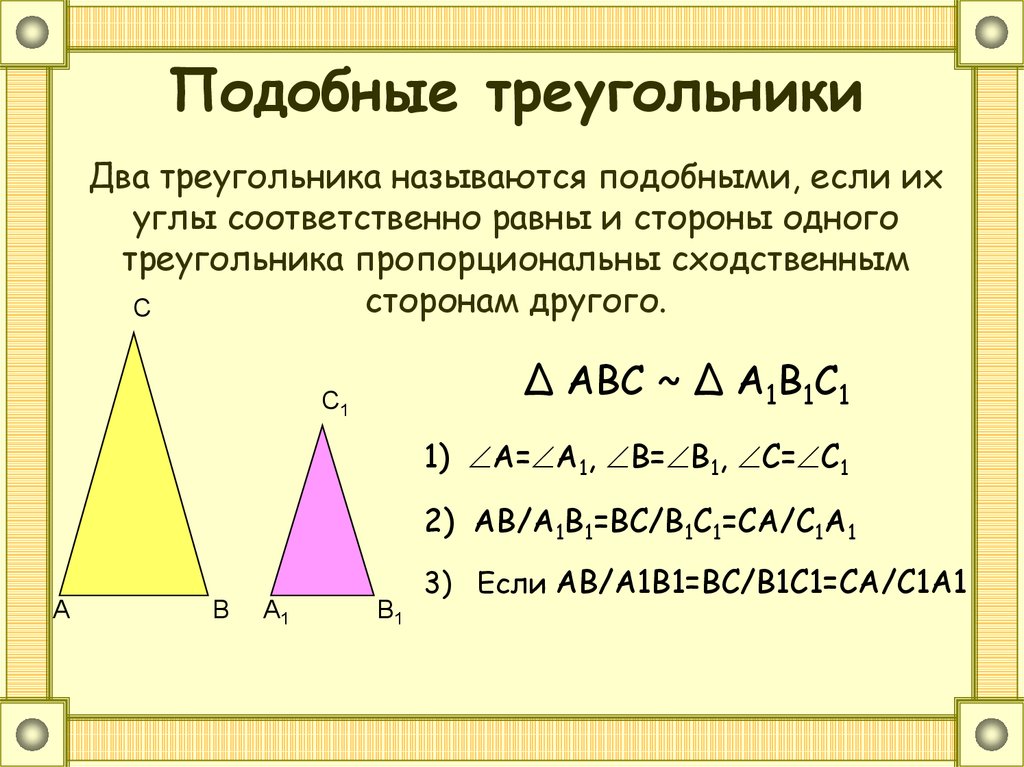 Сумма квадратов двух сторон треугольника равна сумме удвоенного квадрата отрезка, соединяющей вершину с серединой основания, с удвоенным квадратом половины основания.

Дано. Соединим вершину B с серединой основания D треугольника ABC так, что AD = DC (черт. 166).

Требуется доказать, что

AB² + BC² = 2AD² + 2BD²

Доказательство. Проведем высоту BE.

Из прямоугольных треугольников ABE и BCE вытекают равенства:

AB² = BE² + AE²
BC² = BE² + CE²

Сложив их, находим:

AB² + BC² = 2BE² + AE² + CE² (a)

Так как AE = AD + DE = CD + DE, CE = CD — DE, то

AE² = (CD + DE)² = CD² + DE² + 2CD · DE
CE² = (CD — DE)² = CD² + DE² — 2CD · DE

откуда

AE² + CE² = 2CD² + 2DE² (b)

Заменяя в равенстве (a) сумму AE² + CE² из равенства (b), имеем:

AB² + BC² = 2BE² + 2CD² + 2DE².

Из прямоугольного треугольника BDE видно, что

BE² = BD² — DE²

следовательно

AB² + BC² = 2BD² — 2DE² + 2CD² + 2DE²

откуда

AB² + BC² = 2BD² + 2CD² (ЧТД).

 

Подобные треугольники – формулы, свойства, теоремы, доказательства

Подобные треугольники – это треугольники, у которых соответствующие стороны пропорциональны друг другу, а соответствующие углы равны друг другу. Подобные треугольники выглядят одинаково, но размеры могут быть разными. В общем, подобные треугольники отличаются от конгруэнтных треугольников. Существуют различные методы, с помощью которых мы можем определить, подобны два треугольника или нет. Давайте узнаем больше о подобных треугольниках и их свойствах вместе с несколькими решенными примерами.

1.	Что такое подобные треугольники?
2.	Формулы подобных треугольников
3.	Теоремы о подобных треугольниках
4.	Свойства подобных треугольников
5.	Как найти подобные треугольники?
6.	Разница между подобными треугольниками и конгруэнтными треугольниками
7.	Часто задаваемые вопросы о подобных треугольниках

Что такое подобные треугольники?

Подобные треугольники — это треугольники, которые выглядят похожими друг на друга, но их размеры могут не совпадать. Два объекта можно назвать похожими, если они имеют одинаковую форму, но могут различаться по размеру. Это означает, что похожие формы при увеличении или уменьшении накладываются друг на друга. Это свойство подобных фигур называется «сходством».

Определение подобных треугольников

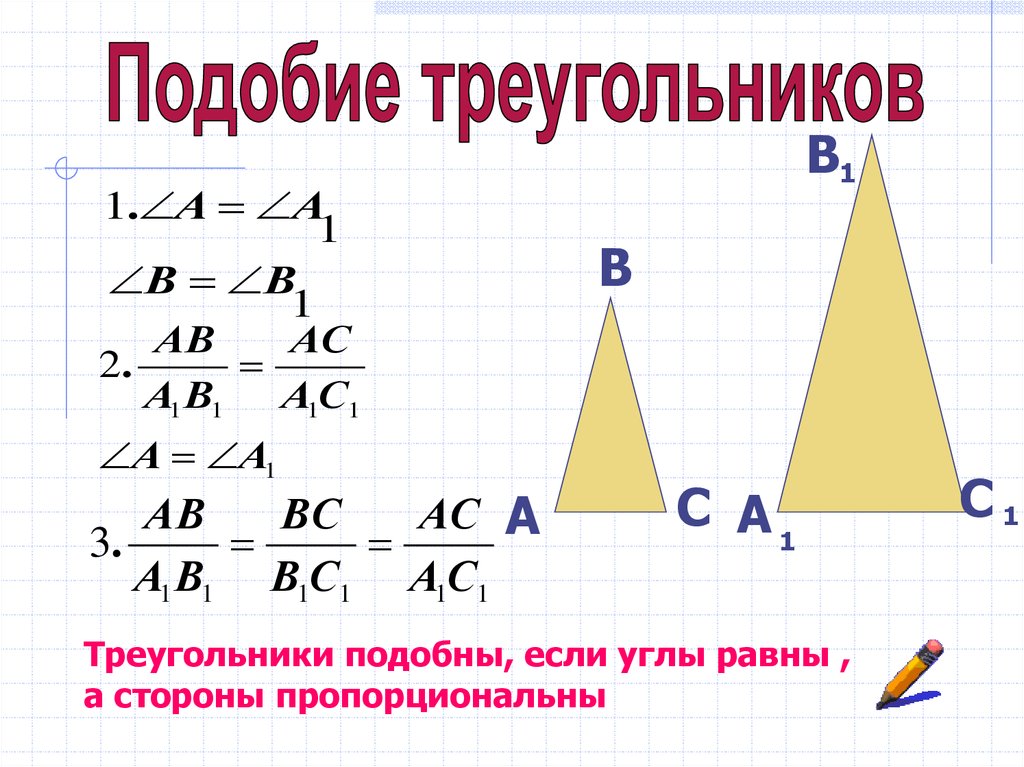
Два треугольника будут подобны, если углы равны (соответствующие углы) и стороны находятся в одинаковом отношении или пропорции (соответствующие стороны).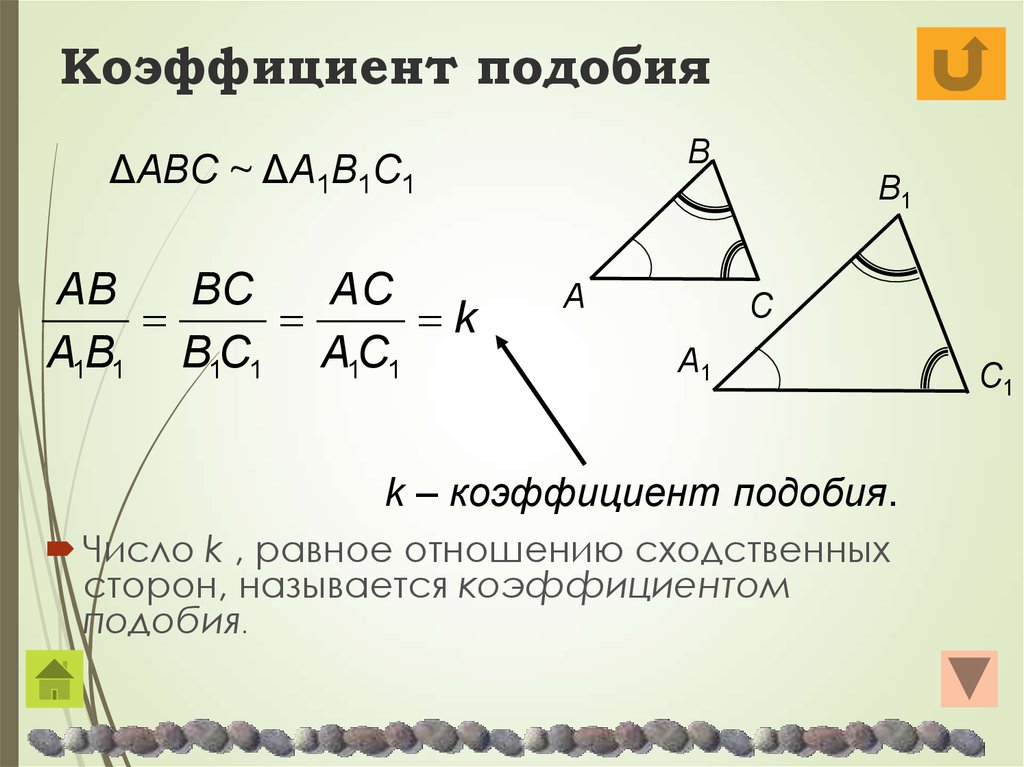 Подобные треугольники могут иметь разные индивидуальные длины сторон треугольников, но их углы должны быть равны, и их соответствующее отношение длин сторон должно быть одинаковым. Если два треугольника подобны, это означает, что

• Все соответствующие пары углов треугольников равны.
• Все соответствующие стороны треугольников пропорциональны.

Мы используем символ «∼» для обозначения сходства. Итак, если два треугольника подобны, мы показываем это как △QPR ∼ △XYZ

Примеры подобных треугольников

Подобные треугольники — это треугольники, у которых соответствующие пары углов равны. Это означает, что равноугольные треугольники подобны. Следовательно, все равносторонние треугольники являются примерами подобных треугольников. На следующем изображении показаны похожие треугольники, но мы должны заметить, что их размеры различаются.

Формулы подобных треугольников

В предыдущем разделе мы видели, что есть два условия, с помощью которых мы можем проверить, подобны ли данный набор треугольников или нет.

Эти условия гласят, что два треугольника можно назвать подобными, если их соответствующие углы равны или конгруэнтны, или если их соответствующие стороны пропорциональны. Следовательно, два треугольника △ABC и △EFG могут быть доказаны подобными (△ABC ∼ △EFG), используя любое условие из следующего набора формул подобных треугольников,

Формула для подобных треугольников в геометрии:

• ∠A = ∠E, ∠B = ∠F и ∠C = ∠G
• AB/EF = BC/FG = AC/EG

Теоремы о подобных треугольниках

Мы можем узнать или доказать, подобны ли два треугольника, используя теоремы подобия. Мы используем эти критерии подобия, когда у нас нет меры всех сторон треугольника или меры всех углов треугольника. Эти теоремы о подобных треугольниках помогают нам быстро выяснить, подобны два треугольника или нет. Существует три основных типа правил подобия, как указано ниже:

• AA (или AAA) или Теорема подобия углов
• SAS или теорема о сходстве стороны-угла-стороны
• SSS или теорема о сходстве сторон

Давайте разберемся в этих теоремах о подобных треугольниках и их доказательствах.

AA (или AAA) или Критерий подобия углов

Критерий подобия AA утверждает, что если любые два угла в треугольнике соответственно равны любым двум углам другого треугольника, то они должны быть подобными треугольниками. Правило подобия AA легко применить, когда мы знаем только меру углов и не имеем никакого представления о длине сторон треугольника. На изображении, приведенном ниже, если известно, что ∠B = ∠G и ∠C = ∠F.

И мы можем сказать, что по критерию сходства АА △ABC и △EGF подобны или △ABC ∼ △EGF.
⇒AB/EG = BC/GF = AC/EF и ∠A = ∠E.
Нажмите здесь, чтобы подробно ознакомиться с критерием сходства AA — критерий сходства AA

SAS или критерий сходства стороны-угла-стороны

Согласно теореме подобия SAS, если любые две стороны первого треугольника находятся в точной пропорции к двум стороны второго треугольника вместе с углом, образованным этими двумя сторонами отдельных треугольников, равны, то они должны быть подобными треугольниками.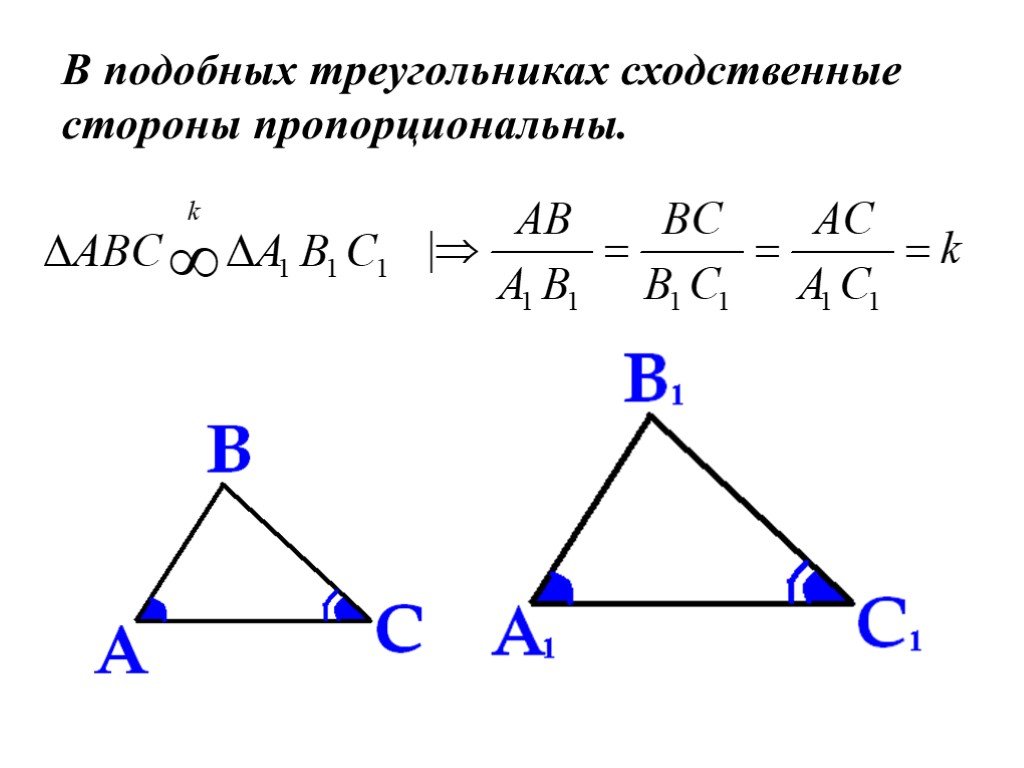 Это правило обычно применяется, когда мы знаем только меру двух сторон и угол, образованный между этими двумя сторонами в обоих треугольниках соответственно.

На изображении ниже, если известно, что AB/DE = AC/DF и ∠A = ∠D

И мы можем сказать, что по критерию подобия SAS △ABC и △DEF подобны или △ABC ∼ △DEF.

SSS или Критерий подобия сторона-сторона-сторона

Согласно теореме подобия SSS два треугольника будут подобны друг другу, если соответствующие отношения всех сторон двух треугольников равны. Этот критерий обычно используется, когда у нас есть только мера сторон треугольника и меньше информации об углах треугольника.

На приведенном ниже изображении, если известно, что PQ/ED = PR/EF = QR/DF

И мы можем сказать, что по критерию подобия SSS △PQR и △EDF подобны или △PQR ∼ △EDF .

Свойства подобных треугольников

Если два треугольника подобны или доказаны подобными по любому из вышеприведенных критериев, то они обладают немногими свойствами подобных треугольников. Ниже приведены свойства подобных треугольников.

• Подобные треугольники имеют одинаковую форму, но разные размеры.
• В подобных треугольниках соответствующие углы равны.
• Соответствующие стороны подобных треугольников находятся в одинаковом отношении.
• Отношение площадей подобных треугольников равно отношению квадратов любой пары их соответствующих сторон.

Как найти подобные треугольники?

Два заданных треугольника можно доказать как подобные треугольники, используя вышеприведенные теоремы. Мы можем выполнить шаги, указанные ниже, чтобы проверить, подобны ли данные треугольники,

• Шаг 1: Запишите заданные размеры треугольников (соответствующие стороны или соответствующие углы).
• Шаг 2: Проверьте, соответствуют ли эти размеры условиям теорем о подобных треугольниках (AA, SSS, SAS).
• Шаг 3: Данные треугольники, если они удовлетворяют любой из теорем подобия, могут быть представлены с использованием «∼» для обозначения подобия.

Давайте лучше разберем эти шаги на примере.

Пример: Проверить, являются ли △ABC и △PQR подобными треугольниками или нет, используя данные: ∠A = 65°, ∠B = 70º и ∠P = 70°, ∠R = 45°.

Решение:

Используя данное измерение углов, мы не можем сделать вывод, соответствуют ли данные треугольники критерию подобия AA или нет. Найдем меру третьего угла и оценим.
Мы знаем, используя свойство суммы углов треугольника, ∠C в △ABC = 180° — (∠A + ∠B) = 180° — 135° = 45°
Точно так же ∠Q в △PQR = 180° — (∠P + ∠R) = 180° — 115° = 65°
Следовательно, мы можем заключить, что в △ABC и △PQR ∠A = ∠Q, ∠B = ∠P и ∠C = R
⇒ △ABC ∼ △QPR

Разница между подобными треугольниками и конгруэнтными треугольниками

Подобие и конгруэнтность — два разных свойства треугольников. Следующая таблица помогает отличить подобные треугольники от конгруэнтных треугольников:

.

Подобные треугольники	Конгруэнтные треугольники
Подобные треугольники имеют одинаковую форму, но могут быть разными по размеру. Они накладываются друг на друга при увеличении или уменьшении.	Конгруэнтные треугольники одинаковы по форме и размеру. Они накладываются друг на друга в своей первоначальной форме.
Они представлены с помощью символа «~». Например, подобные треугольники ABC и XYZ будут представлены как △ABC ∼ △XYZ	Они представлены с помощью символа «9».0196 ≅’. Например, конгруэнтные треугольники ABC и XYZ будут представлены как △ABC ≅ △QPR
В подобных треугольниках отношение всех соответствующих сторон равно. Это общее отношение также называется «масштабным коэффициентом» в подобных треугольниках.	Отношение соответствующих сторон равно 1 для конгруэнтных треугольников.

☛ Темы, относящиеся к подобным треугольникам:

• Что такое сходство
• ССС
• САС
• Треугольники

Важные замечания о подобных треугольниках:

• Отношение площадей подобных треугольников равно квадрату отношения их соответствующих сторон.
• Все конгруэнтные треугольники подобны, но не все подобные треугольники обязательно могут быть конгруэнтными.
• Подобные треугольники обозначаются символом «~».

 

Примеры подобных треугольников

1. Пример 1:

   Рассмотрим два подобных треугольника, ΔABC и ΔDEF:

   AP и DQ являются медианами в двух треугольниках соответственно. Покажите, что

   AP/BC = DQ/EF

   Решение:

   Поскольку эти два треугольника подобны, они равноугольны.

   Это означает, что

   ∠B=∠E

   Также

   AB/DE = BC/EF→ (1)

   ⇒AB/DE = [(BC/2)/(EF/2)] = BP/EQ

   Следовательно, по критерию подобия SAS ,

   ΔABP∼ΔDEQ

   Таким образом, стороны этих двух треугольников будут соответственно пропорциональны, и поэтому:

   AB/DE = AP/DQ

   ⇒AP/DQ = BC/EF . . . [Из (1)]

   ⇒AP/BC = DQ/EF

   Отсюда доказано.

2. Пример 2: Джеймс ростом 140. Он стоит в 320 дюймах от фонарного столба. Его тень от света имеет длину 80 дюймов. Какая высота фонарного столба?

   Решение:

   Взяв △ABD и △ECD, мы можем видеть, что

   ∠B = ∠C = 90 ^o , а ∠Dcom угол = ∠mon угол △ABD похож на △ECD.

   Следовательно,

   AB/EC = BD/CD = AD/ED

   Подставляя данные значения

   AB/140 = (320+80)/80

   AB/140 = 5

   AB = 0700 Ответ: Высота столба 700 дюймов.

перейти к слайдуперейти к слайду

Разложите сложные концепции с помощью простых визуальных средств.

Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.

Записаться на бесплатный пробный урок

Практические вопросы по подобным треугольникам

 

перейти к слайдуперейти к слайду

Часто задаваемые вопросы о подобных треугольниках

Что понимают под подобными треугольниками в геометрии?

Подобные треугольники в геометрии — это треугольники, имеющие одинаковую форму, но не равные по размеру.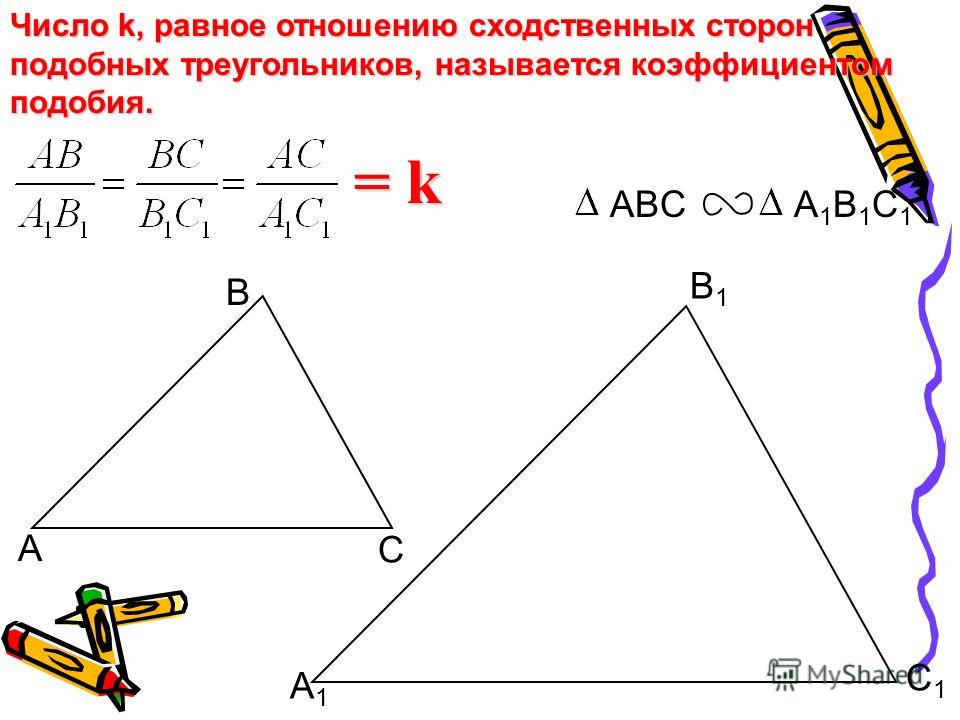 Все равносторонние треугольники являются примерами подобных треугольников.

Какой символ используется для подобных треугольников?

Подобные треугольники можно выразить с помощью символа «~». Этот символ означает, что данные две фигуры имеют одинаковую форму, но не обязательно одинаковый размер.

Что такое формула подобных треугольников?

Формула, используемая для проверки того, подобны ли два треугольника или нет, зависит от условия подобия. Для двух треугольников △PQR и △XYZ подобие можно доказать с помощью любого из следующих условий:

• ∠P = ∠X, ∠Q = ∠Y и ∠R = ∠Z
• PQ/XY = QR/YZ = PR/XZ

Каковы 3 теоремы о подобных треугольниках?

Три теоремы подобия, используемые для проверки подобия в треугольниках, приведены ниже:

• AA (или AAA) или теорема о сходстве углов
• SAS или теорема о сходстве стороны-угла-стороны
• SSS или теорема о сходстве сторон

Каковы свойства подобных треугольников?

Важные свойства двух подобных треугольников можно представить как.

• Форма двух подобных треугольников одинакова, но их размеры могут быть разными.
• В подобных треугольниках соответствующие углы равны.
• В подобных треугольниках соответствующие стороны находятся в одинаковом отношении.

Каковы правила для подобных треугольников?

Правила или условия, используемые для проверки того, подобны ли данный набор треугольников или нет, как указано,

• Все соответствующие пары углов треугольников должны быть одинаковыми.
• Все соответствующие стороны треугольников находятся в одной пропорции.

Как узнать, подобны ли два треугольника?

Два треугольника подобны, если их соответствующие углы равны и их соответствующие стороны находятся в одном и том же отношении. Подобные треугольники — это треугольники, которые выглядят одинаково, но могут быть разными по размеру.

Как найти долю подобных треугольников?

В подобных треугольниках пары соответствующих сторон пропорциональны. Это отношение / пропорциональность соответствующих сторон можно использовать для нахождения длины недостающей стороны фигуры, учитывая аналогичную фигуру, для которой известны соответствующие измерения.

Как найти недостающие стороны подобных треугольников?

Недостающие стороны подобного треугольника можно узнать, сравнив отношения последовательных соответствующих сторон треугольника. Сравниваем отношения и находим длину неизвестной стороны треугольника.

Могут ли два треугольника быть подобными и конгруэнтными?

Все конгруэнтные треугольники также являются подобными треугольниками, но не все подобные треугольники являются конгруэнтными треугольниками. Таким образом, два подобных треугольника могут быть равны, но не всегда. Чтобы два подобных треугольника были равны, они должны иметь одинаковый размер, одинаковую форму и одинаковую меру соответствующих углов.

Какой тип треугольников всегда похож?

Равносторонние треугольники всегда подобны.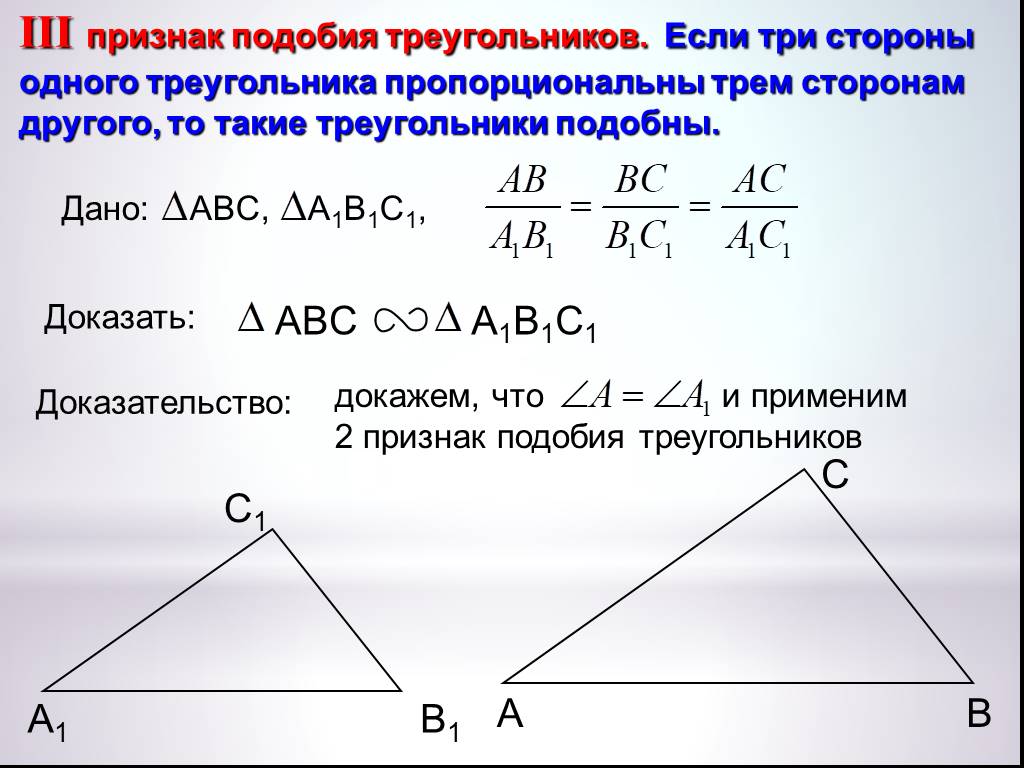 Любые два равносторонних треугольника всегда подобны независимо от длины сторон равностороннего треугольника. Два равнобедренных прямоугольных треугольника также всегда подобны.

Могут ли быть подобны два равнобедренных треугольника?

Два равнобедренных треугольника могут быть подобны тогда и только тогда, когда их соответствующие углы равны и их соответствующие стороны находятся в одном и том же отношении. Следовательно, не всегда верно, что равнобедренные треугольники подобны.

Как вводить подобные треугольники?

Подобные треугольники могут быть представлены как треугольники одинаковой формы, но не обязательно одинакового размера. Подобные треугольники — это треугольники, которые выглядят одинаково, но могут быть разными по размеру.

Как найти отношение площадей двух подобных треугольников?

Если два треугольника подобны, то отношение площадей обоих треугольников пропорционально квадрату отношения их соответствующих сторон. Если два подобных треугольника имеют две соответствующие длины сторон, равные a и b, то отношение их площадей это а2:b2.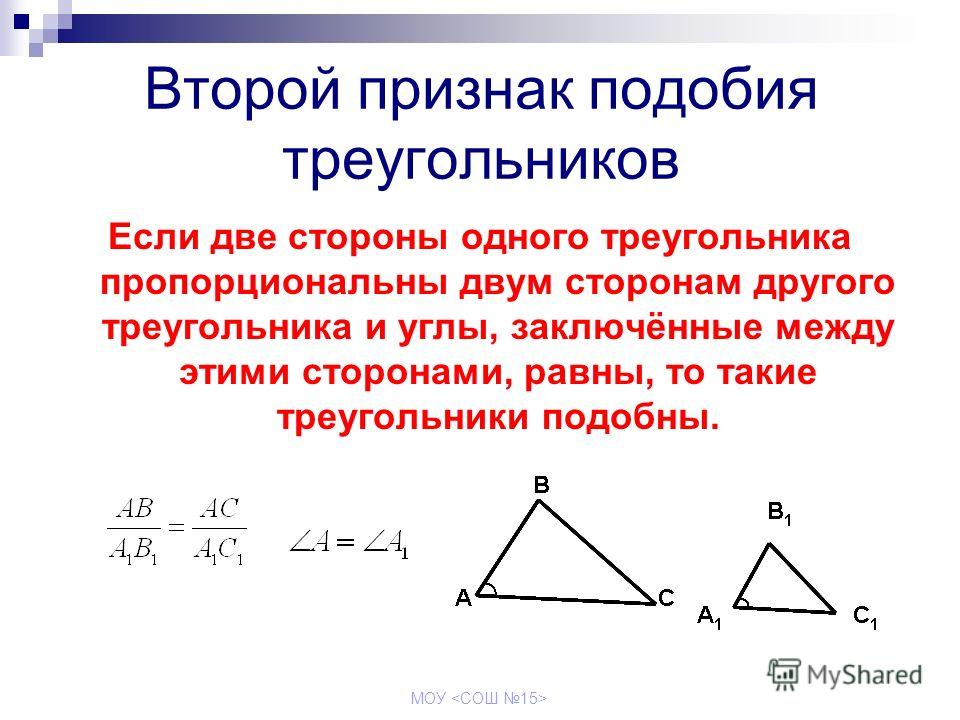

Как определить, подобны ли треугольники

Два треугольника подобны, если они имеют:

• все их углы равны
• соответствующие стороны находятся в одинаковом соотношении

Но нам не нужно знать все три стороны и все три угла… двух-трех из шести обычно достаточно.

Есть три способа определить, подобны ли два треугольника: AA , SAS и SSS :

АА

AA означает «угол, угол» и означает, что у треугольников два угла равны.

Если у двух треугольников два угла равны, то треугольники подобны.

Пример: эти два треугольника подобны:

Если два их угла равны, то и третий угол тоже должен быть равен, потому что сумма углов треугольника всегда составляет 180°.

В этом случае недостающий угол равен 180° − (72° + 35°) = 73°

Таким образом, АА можно также назвать ААА (потому что, когда два угла равны, все три угла должны быть равны).

САС

SAS означает «сторона, угол, сторона» и означает, что у нас есть два треугольника, где:

• соотношение между двумя сторонами такое же, как соотношение между двумя другими сторонами
• и мы также знаем, что прилежащие углы равны.

Если у двух треугольников по две пары сторон в одинаковом отношении и прилежащие к ним углы также равны, то такие треугольники подобны.

Пример:

В этом примере мы видим, что:

• одна пара сторон находится в соотношении 21 : 14 = 3 : 2
• другая пара сторон находится в соотношении 15 : 10 = 3 : 2
• между ними имеется соответствующий угол 75°

Итак, информации достаточно, чтобы сказать нам, что два треугольника подобны .

Использование тригонометрии

Мы могли бы также использовать тригонометрию для вычисления двух других сторон, используя закон косинусов:

Продолжение примера

В треугольнике ABC:

• a ² = b ² + c ² — 2bc cos A
• a ² = 21 ² + 15 ² — 2 × 21 × 15 × Cos75°
• a ² = 441 + 225 — 630 × 0,2588. ..
• a ² = 666 — 163,055…
• a ² = 502,944…
• Итак, а = √502,94 = 22,426…

В треугольнике XYZ:

• x ² = y ² + z ² — 2yz cos X
• x ² = 14 ² + 10 ² — 2 × 14 × 10 × Cos75°
• х ² = 196 + 100 — 280 × 0,2588…
• х ² = 296 — 72,469…
• х ² = 223,530…
• Итак, х = √223,530… = 14,950…

Теперь давайте проверим отношение этих двух сторон:

a : x = 22,426… : 14,950… = 3 : 2

то же соотношение, что и раньше!

Примечание: мы также можем использовать закон синусов, чтобы показать, что два других угла равны.

ССС

SSS расшифровывается как «сторона, сторона, сторона» и означает, что у нас есть два треугольника со всеми тремя парами соответствующих сторон в одинаковом соотношении.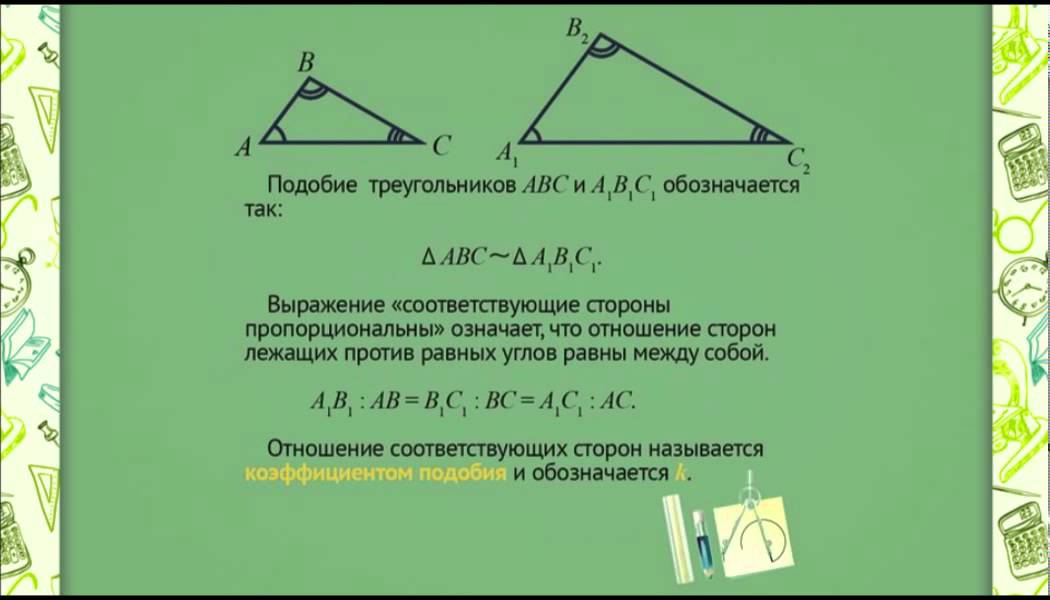