Множества: элементы и подмножества. Пересечение и объединение множеств
- Подмножество
- Пересечение и объединение множеств
Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита — от A до Z.
Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:
N — множество натуральных чисел,
Z — множество целых чисел.
Элемент множества — это любой объект, входящий в состав множества. Принадлежность объекта к множеству обозначается с помощью знака ∈
. Запись
5∈Z
читается так: 5 принадлежит множеству Z
или 5 – элемент множества Z
.
Множества делятся на конечные и бесконечные. Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество — множество, содержащее бесконечно много элементов.
Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись
L = {2, 4, 6, 8}
означает, что множество L состоит из четырёх чётных чисел.
Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.
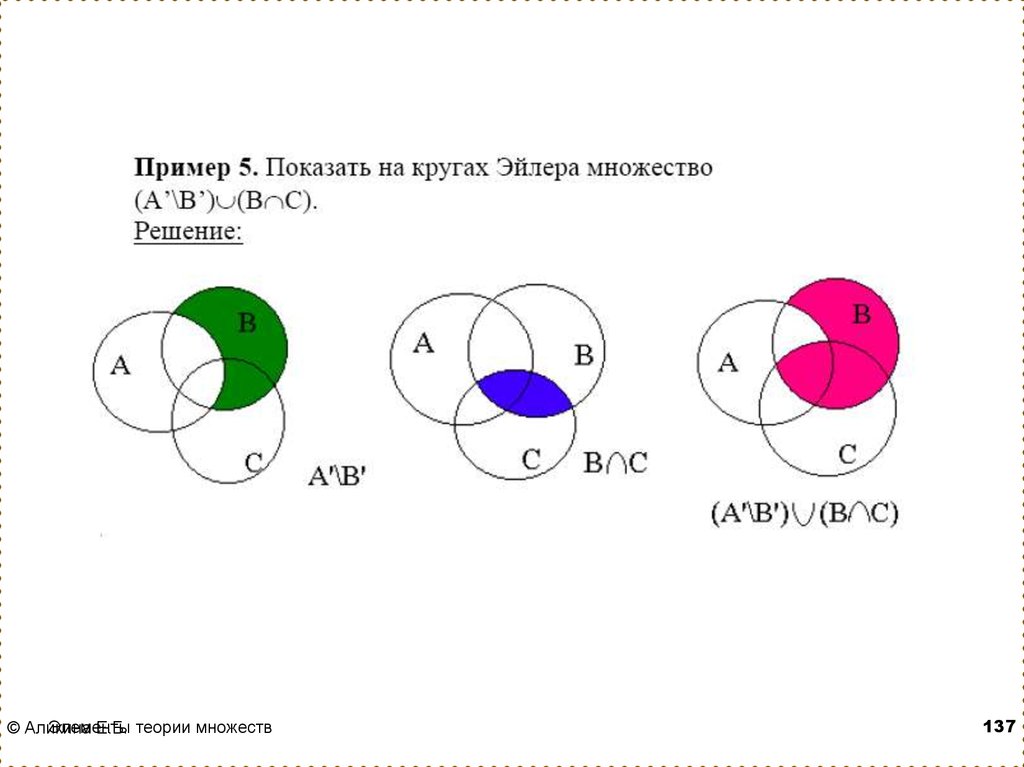
Подмножество
Подмножество — это множество, все элементы которого, являются частью другого множества.
Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.
Рассмотрим два множества:
L = {2, 4, 6, 8} и M = {2, 4, 6, 8, 10, 12}.
Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком
Такое соотношение множеств обозначают знаком ⊂
:
L⊂M.
Запись L⊂M читается так: множество L является подмножеством множества M
.
Множества, состоящие из одних и тех же элементов, независимо от их порядка, называются равными и обозначаются знаком =
.
Рассмотрим два множества:
L = {2, 4, 6} и M = {4, 6, 2}.
Так как оба множества состоят из одних и тех же элементов, то L = M.
Пересечение и объединение множеств
Пересечение двух множеств — это совокупность элементов, принадлежащих каждому из этих множеств, то есть их общая часть. Пересечение обозначается знаком ∩
.
Например, если
L = {1, 3, 7, 11} и M = {3, 11, 17, 19}, то L∩M = {3, 11}.
Запись L∩M читается так: пересечение множеств L и M
.
Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.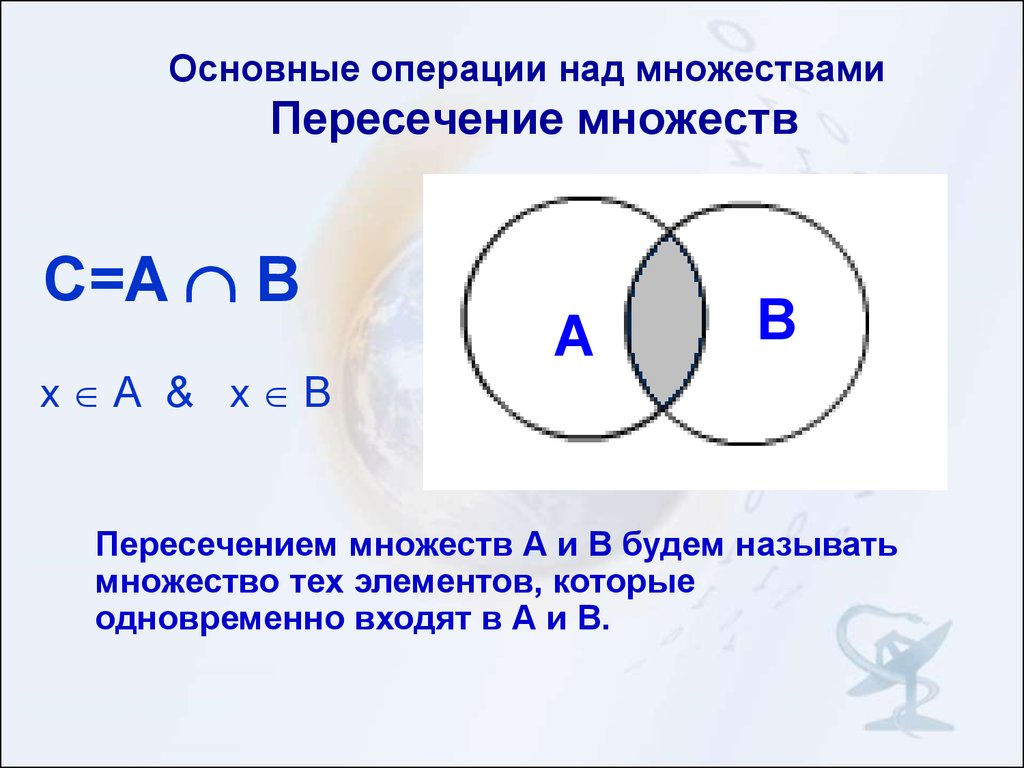
Объединением двух множеств называется множество, содержащее все элементы исходных множеств в единственном экземпляре, то есть если один и тот же элемент встречается в обоих множествах, то в новое множество этот элемент будет включён только один раз. Объединение обозначается знаком ∪
.
Например, если
L = {1, 3, 7, 11} и M = {3, 11, 17, 19},
то L∪M = {1, 3, 7, 11, 17, 19}.
Запись L∪M читается так: объединение множеств L и M
.
При объединении равных множеств объединение будет равно любому из данных множеств:
если L = M, то L∪M = L и L∪M = M.
1.3.2 Объединение множеств
Вновь
возьмём множества Х
=
{0, 1, 3, 5} и
Y
= {1, 2, 3, 4} и наряду с ними рассмотрим
множество {0, 1, 2, 3, 4, 5}. Это множество
содержит все элементы множества Х
и
все элементы множества Y
и
не содержит никаких других элементов.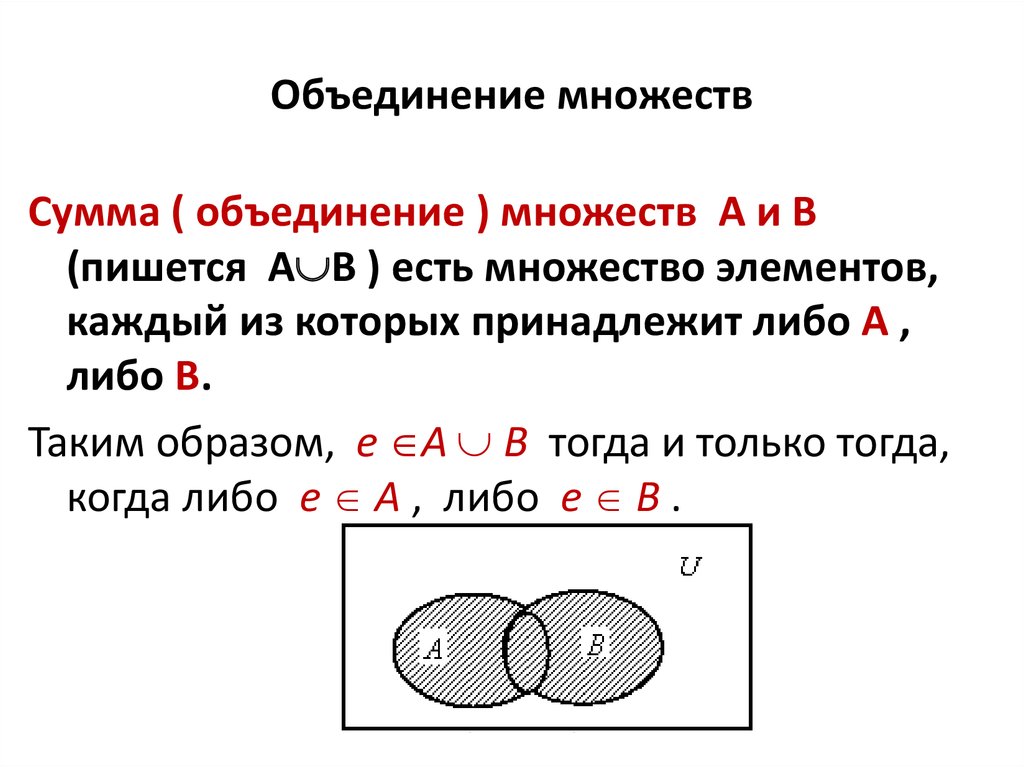
Множество, состоящее из всех элементов, принадлежащих или множеству
А или множеству В, называется объединением множеств А и В, обозначается А U В. А U В = { х А или х В }Итак, {0, 1, 3, 5} {1, 2, 3, 4} = {0, 1, 2, 3, 4, 5}.
Если изобразить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью.
А U В
Если множества не имеют общих элементов, то их объединение выглядит так:
А U В
Если одно из множеств является подмножеством другого, то их объединение будет выглядеть так:
А U В
Часто
приходится рассматривать объединение
и пересечение трёх и более множеств.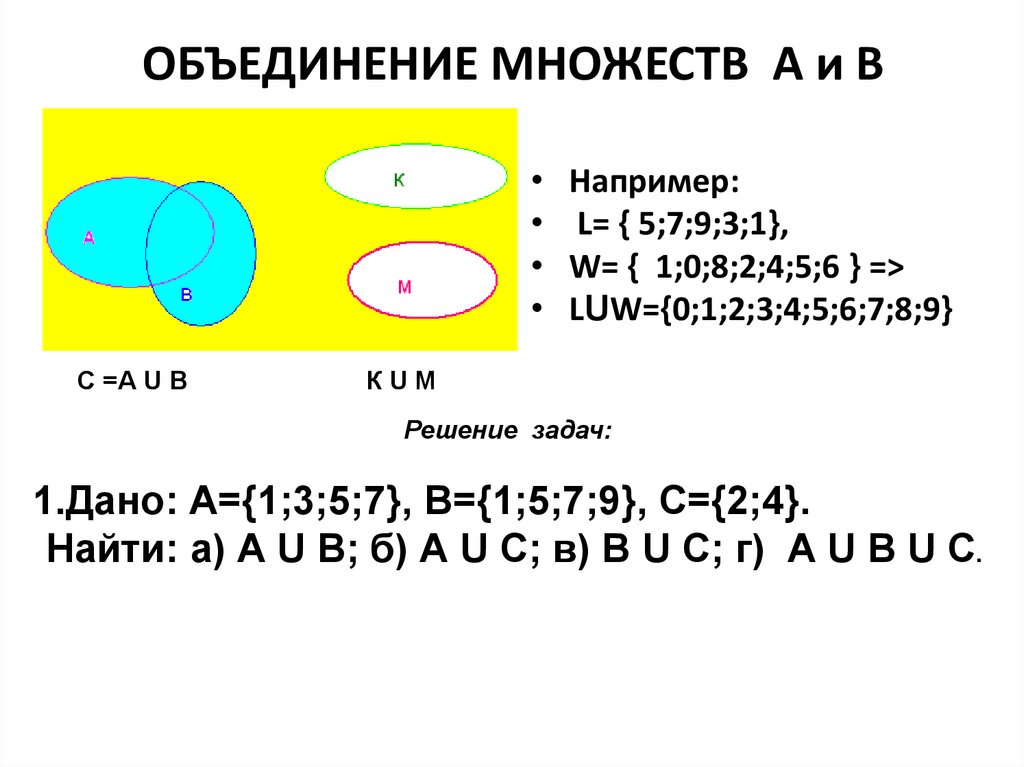
А U В U С А ∩ В ∩ С
Например, объединение множеств остроугольных, тупоугольных и прямоугольных треугольников есть множество всех треугольников.
Еще операции над множествами можно показать с помощью детского анекдота: Однажды лев, царь зверей, собрал зверей на поляне и повелел им разделиться на умных и красивых. После того, как пыль улеглась, лев увидел на поляне две большие группы зверей и мартышку, прыгающую между ними. На вопрос: почему она прыгает туда, сюда, мартышка ответила: «Что мне, разорваться, что ли?». Так вот, мартышка из анекдота – это пример пересечения умных зверей и красивых. А объединением умных и красивых зверей является все множество зверей.
Объединение и пересечение множеств обладают многими свойствами, аналогичными свойствам суммы и произведения чисел:
№ п/п | Свойство операций над множествами | Свойство арифметических операций | Название свойства |
1 | a + b = b + a | Коммутативность | |
2 | |||
3 | (а+b)+c = a+(b+c) | Ассоциативность | |
5 | Дистрибутивность |
Однако эта аналогия
не всегда имеет место.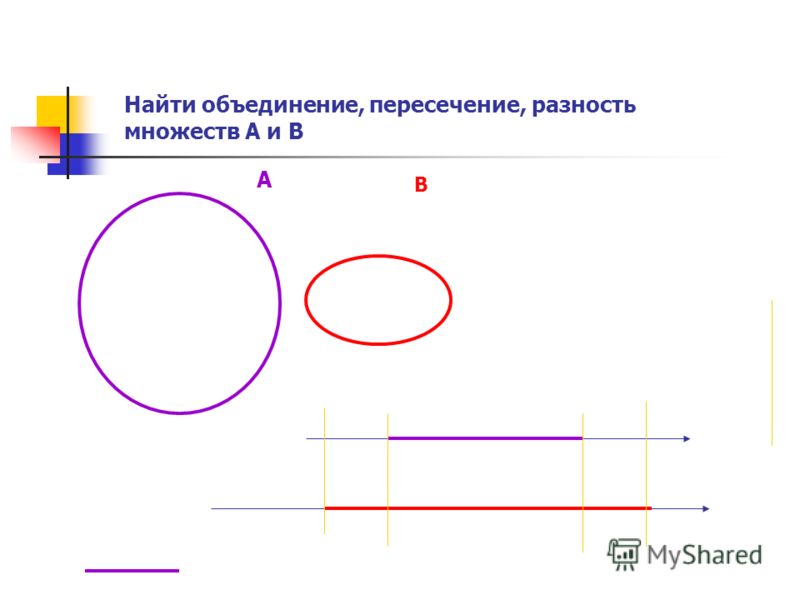 Например, для
множеств справедливы равенства:
Например, для
множеств справедливы равенства:
6. (А U С) ∩ (В U С) = (A ∩ B) U С.
7. А U А = А.
8. А ∩ А = А.
Соответствующие равенства для чисел верны не всегда.
Заметим, что, если в выражении есть знаки пересечения и объединения множеств, и нет скобок, то сначала выполняют пересечение, так как считают, что пересечение более «сильная» операция, чем объединение.
Если заданы два множества, то можно не только найти их пересечение и объединение, но и вычесть из одного множества другое. Результат вычитания называют разностью и определяют следующим образом.
Разностью множеств А и В называется
множество, содержащее все элементы,
которые принадлежат множеству А и не
принадлежат множеству В,
обозначается А \ В.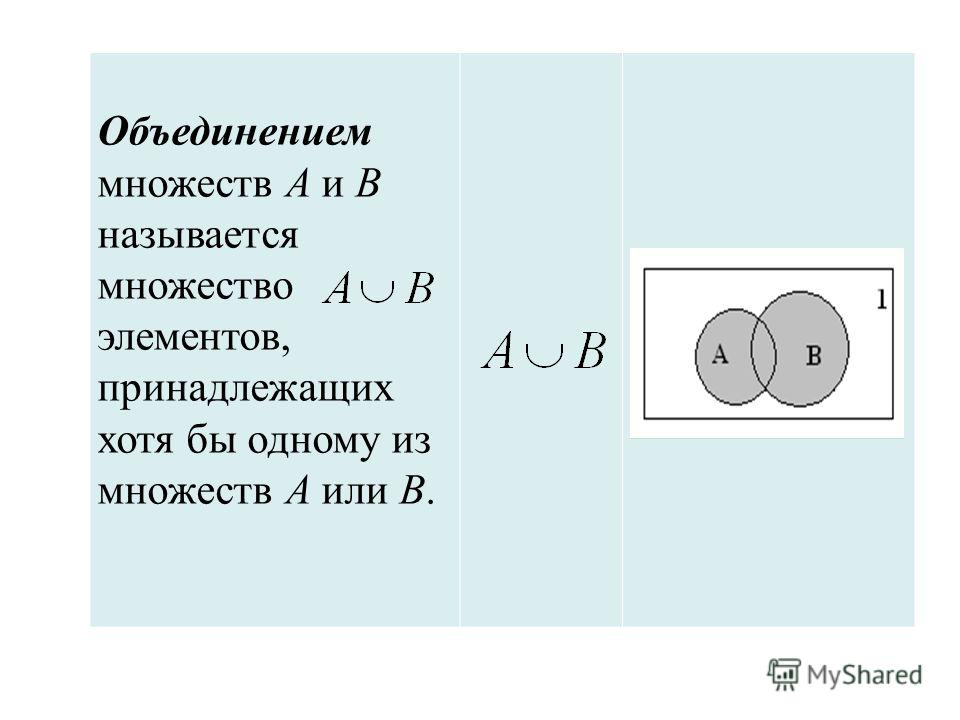 А \ В = {х А и х
В}.
А \ В = {х А и х
В}.
Х \ Y = {0, 1, 3, 5} \ {1, 2, 3, 4} = {0, 5}. Если мы найдем разность множеств Y и Х, то результат будет выглядеть так: Y \ X = {2; 4}. Таким образом, разность множеств не обладает переместительным (коммутативным) свойством.
Если изобразить множестваА и В при помощи кругов Эйлера, то разность данных множеств изобразится заштрихованной областью.
А \ В
Если множества не имеют общих элементов, то их разность будет изображаться так:
В
А
А \ В
Если одно из множеств является подмножеством другого, то их разность будет изображаться так:
А
В
\ В
Пересечение
– более «сильная» операция, чем вычитание. Поэтому порядок выполнения действий в
выражении А \ В ∩ С такой: сначала
находят пересечение множеств В и С,
а затем полученное множество вычитают
из множества А. Что касается
объединения и вычитания множеств, то
их считают равноправными. Например, в
выражении А \ В U С надо сначала выполнить
вычитание (из А вычесть В), а затем
полученное множество объединить с
множеством С.
Поэтому порядок выполнения действий в
выражении А \ В ∩ С такой: сначала
находят пересечение множеств В и С,
а затем полученное множество вычитают
из множества А. Что касается
объединения и вычитания множеств, то
их считают равноправными. Например, в
выражении А \ В U С надо сначала выполнить
вычитание (из А вычесть В), а затем
полученное множество объединить с
множеством С.
Вычитание множеств обладает рядом свойств:
(А \ В) \ С = (А \ С) \ В.
(А U В) \ С = (А \ С) U (В \ С).
(А \ В) ∩ С = (А ∩ С) \ (В ∩С).
А \ (В U С) = (А \ В) ∩ (А \ С).
А \ (В ∩ С) = (А \ В) U (А \ С).
Символы диаграммы Венна и обозначения
Время чтения: около 6 мин. Полная диаграмма Венна представляет объединение двух множеств.
∩: Пересечение двух множеств. Пересечение показывает, какие элементы являются общими для категорий.
A c : Дополнение к набору. Дополнением является то, что не представлено в наборе.
Пришло время серьезно поговорить о диаграммах Венна, и мы говорим не о диаграммах Венна из вашей начальной школы. Мы говорим о хардкорных визуальных эффектах, созданных серьезными профессионалами для представления сложных математических идей.
Диаграммы Венна — это визуальное представление математических множеств или коллекций объектов, которые изучаются с помощью раздела логики, называемого теорией множеств. Теория множеств — одна из основополагающих систем математики, и она помогла развить наше современное понимание бесконечности и действительных чисел.
Исследователи и математики разработали язык и систему обозначений на основе теории множеств. Если вы хотите узнать их секреты, вам следует ознакомиться с этими символами диаграммы Венна.
Это руководство проведет вас через процесс создания диаграммы Венна, объясняя используемые символы. Мы будем использовать Lucidchart для создания наших примеров, потому что он прост в использовании и совершенно бесплатен. Если вы хотите следовать инструкциям или создать собственную диаграмму Венна, все, что вам нужно сделать, это нажать ниже и создать бесплатную учетную запись. Теперь приступим!
Диаграммы Венна и теория множеств
В теории множеств используется более 30 символов, но для понимания основ необходимо знать только три. Как только вы освоите их, не стесняйтесь переходить к более сложным вещам.
Объединение двух наборов: ∪
Каждый круг или эллипс представляет категорию. Объединение двух множеств представлено ∪. (Не путайте этот символ с буквой «u».)
Это диаграмма Венна с двумя кругами. Зеленый кружок — это A, а синий — B. Полная диаграмма Венна представляет собой объединение A и B, или A ∪ B. Не стесняйтесь щелкать изображение, чтобы попробовать эту диаграмму в качестве шаблона.
Не стесняйтесь щелкать изображение, чтобы попробовать эту диаграмму в качестве шаблона.
Как будет выглядеть объединение двух множеств в реальном мире? Набор А может представлять группу людей, играющих на фортепиано. Набор B может представлять гитаристов. A ∪ B представляет тех, кто играет на фортепиано, гитаре или и на том, и на другом.
Пересечение двух множеств: ∩
При построении диаграммы Венна нас часто интересует пересечение двух множеств, то есть какие элементы являются общими для категорий. На этой диаграмме бирюзовая область (где синий и зеленый перекрываются) представляет собой пересечение A и B, или A ∩ B.
Пересечение двух наборов Диаграмма Венна (Щелкните изображение, чтобы изменить его онлайн)В продолжение примера, пересечение пианистов и гитаристов включает тех, кто владеет обоими инструментами.
Дополнение к набору: A
c При построении диаграммы Венна вы также можете учитывать то, что не представлено в наборе. Это дополнение множества, или A c для множества A.
Это дополнение множества, или A c для множества A.
Абсолютное дополнение множества — это все, что не входит в множество. Это означает, что для данной вселенной (U, на этот раз буква), все, что есть во вселенной, за исключением A, является абсолютным дополнением A в U. Это может быть представлено уравнением A c = U \ A.
Ниже приведена диаграмма Lucidchart для абсолютного дополнения A в U. Серая секция показывает все за пределами A. В случае с музыкальными инструментами это будут все, кто не играет на фортепиано.
Дополнение к диаграмме Венна множества (Щелкните изображение, чтобы изменить его онлайн)Диаграмма Венна быстрого питания, иллюстрирующая теорию множеств
Чтобы помочь вам закрепить практическое применение теории множеств, давайте рассмотрим пример. Начнем с опроса о предпочтениях трех человек в отношении фаст-фуда. Эти три человека, которых мы назначим A, B и C, указывают, какие рестораны им нравятся.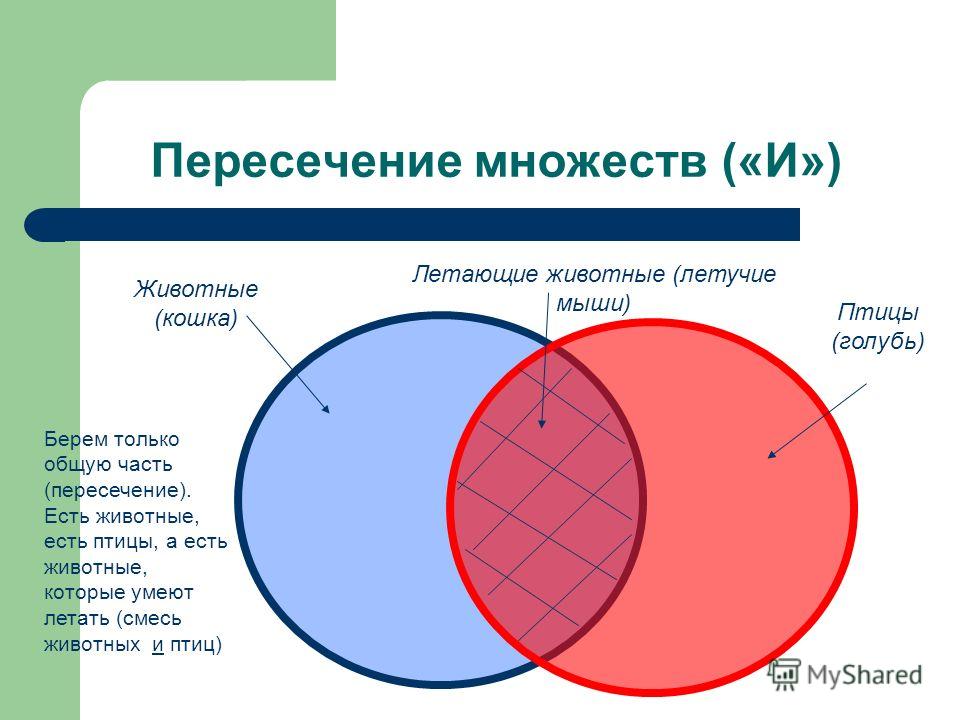 Диаграмма с тремя кругами охватывает все возможности: ресторан не выберет ни один респондент, один, два или все три.
Диаграмма с тремя кругами охватывает все возможности: ресторан не выберет ни один респондент, один, два или все три.
Here were the results:
| Restaurant | A | B | C |
|---|---|---|---|
| McDonald’s | X | X | |
| Wendy’s | X | X | |
| Burger King | |||
| In-N-Out | X | X | |
| Taco Bell | X | X | |
| KFC | |||
| A&W | |||
| Chick-fil-A | X | X | X |
Теперь пришло время создать диаграмму Венна, представляющую результаты. Мы начали с этого шаблона ниже.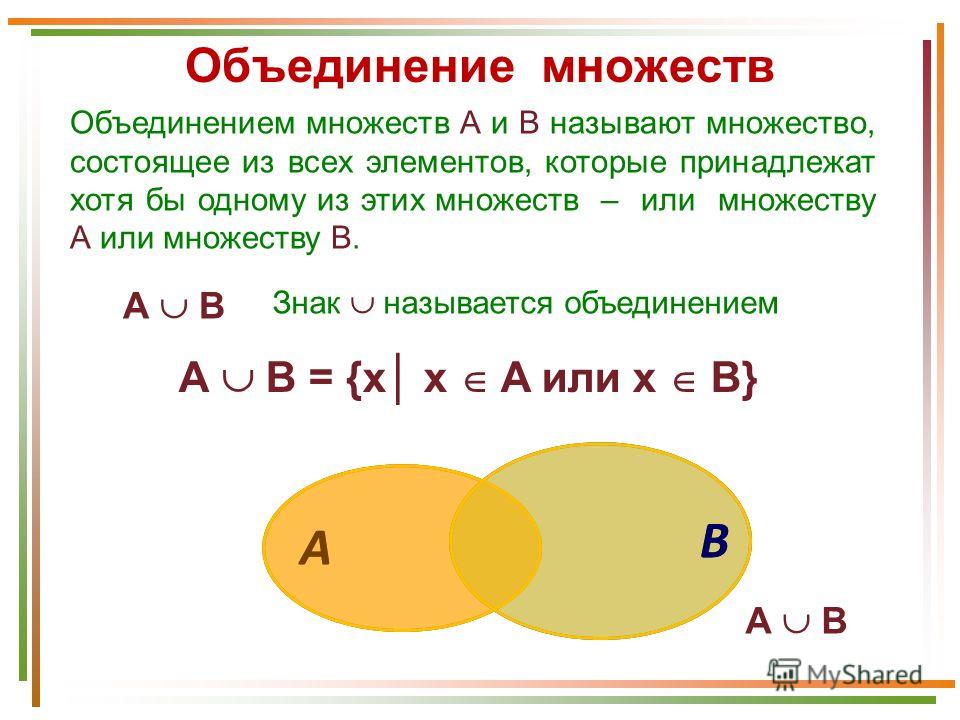 Он использует объясняемый нами символ ∩, чтобы показать пересечение между двумя и тремя множествами. Есть восемь регионов, которые могли бы занять наши рестораны.
Он использует объясняемый нами символ ∩, чтобы показать пересечение между двумя и тремя множествами. Есть восемь регионов, которые могли бы занять наши рестораны.
Теперь мы заполним нашу диаграмму Венна в соответствии с результатами. В A ∩ B у нас есть Wendy’s, потому что ее выбрали и респондент A, и респондент B. Burger King никто не выбирал, но он существует во вселенной доступных ресторанов быстрого питания, поэтому он находится в белом пространстве за пределами диаграммы. Пересечение всех трех, A ∩ B ∩ C, имеет Chick-fil-A, поскольку его выбрали все три респондента.
Вот как выглядит окончательная диаграмма:
Диаграмма Венна о ресторанных предпочтениях (Нажмите на изображение, чтобы изменить его онлайн)Теперь у нас есть наглядное пособие, если мы выбираем, куда эти три человека должны пойти на обед!
Теперь, когда вы увидели диаграмму Венна в действии, вот пример, который вы можете легко изменить, чтобы создать свой собственный!
Пример диаграммы Венна (Нажмите на изображение, чтобы изменить его онлайн)Теперь, когда вы знаете символы диаграммы Венна, прочитайте, как их составить!
Узнайте, какДополнительная литература по символам диаграммы Венна
Если вы хотите узнать больше о теории множеств и создать высококачественные диаграммы Венна, есть несколько доступных ресурсов. Например, в Стэнфордской энциклопедии есть введение в теорию основных множеств.
Например, в Стэнфордской энциклопедии есть введение в теорию основных множеств.
Чтобы узнать больше об истории диаграмм Венна, прочитайте нашу страницу с ответом «Что такое диаграмма Венна?» Хотя Джон Венн популяризировал представление теории множеств с помощью перекрывающихся кругов, идеи и символы на диаграммах Венна фактически предшествовали ему.
Быстрое слово
Если вы следили за Lucidchart, вы поняли, что это идеальное решение для диаграмм Венна. Поскольку вы редактируете в облаке, вы можете легко сотрудничать с коллегами, импортировать изображения и делиться своими диаграммами в цифровом или печатном виде.
Посмотрите, как работает наш конструктор диаграмм Венна.
Узнать большеНачните строить диаграммы с Lucidchart сегодня — попробуйте бесплатно!
Зарегистрируйтесь бесплатноСейчас популярно
4 фазы жизненного цикла управления проектамиНабор инструментов для удобного документированияПередача технической информации нетехническому персоналуЗарегистрируйтесь, чтобы получать последние обновления и советы Lucidchart по электронной почте один раз в месяц.
 Подпишитесь на нашу рассылку
Подпишитесь на нашу рассылкуО Lucidchart
Lucidchart — это интеллектуальное приложение для построения диаграмм, которое позволяет командам прояснять сложность, согласовывать свои идеи и строить будущее быстрее. С помощью этого интуитивно понятного облачного решения каждый может работать визуально и сотрудничать в режиме реального времени, создавая блок-схемы, макеты, диаграммы UML и многое другое.
Самая популярная онлайн-альтернатива Visio, Lucidchart, используется в более чем 180 странах миллионами пользователей, от менеджеров по продажам, планирующих целевые организации, до ИТ-директоров, визуализирующих свою сетевую инфраструктуру.
Объединение, пересечение и дополнение | Математика для гуманитарных наук Необходимый предмет
Результаты обучения
- Выполнение операций объединения, пересечения, дополнения и разности над множествами, используя соответствующие обозначения.

- Уметь рисовать и интерпретировать диаграммы Венна отношений множеств и операций.
Обычно наборы взаимодействуют. Например, вы с новым соседом по комнате решаете устроить домашнюю вечеринку и приглашаете друзей. На этой вечеринке объединяются два набора, хотя может оказаться, что есть друзья, которые были в обоих наборах.
Математические слова и обозначения
Чтобы получить новый словарь на новом для вас языке, требуется повторение и практика. Математика во многих отношениях ничем не отличается от изучения нового языка со всем его словарным запасом, синтаксисом и орфографическими соглашениями. Символы в этом разделе могут быть вам совершенно незнакомы. Если это так, вам нужно будет проводить с ними время, используя карточки и записывая их от руки в контексте.
Дайте себе время выучить и оценить язык математики!
Объединение, пересечение и дополнение
Объединение двух наборов содержит все элементы, содержащиеся в любом наборе (или в обоих наборах). 6 ∈ A или x 6 ∈ A или x 6 ∈ A или x 6 ∈ A или x 6 ∈ a или x 6 ∈ A или x 6 ∈ A (или x 6. пересечение двух множеств содержит только те элементы, которые есть в обоих множествах. Перекресток обозначен цифрой 9.0225 A The complement of a set A содержит все, что , а не в наборе A . Дополнение обозначается как A’ , или A c , или иногда ~ A . Универсальный набор — это набор, содержащий все интересующие нас элементы. Это должно определяться контекстом. Предположим, что универсальный набор равен U = все целые числа от 1 до 9. Если A = {1, 2, 4}, то A c = {3, 5 6, 7, 8, 9}. Символы пересечения [латекс]\чашка[/латекс] и объединения [латекс]\шапка[/латекс] немного напоминают буквы в алфавите. На самом деле, это уловка для их запоминания. Символ объединения выглядит как заглавная буква U, что означает союз . Символ пересечения немного похож на большую строчную букву n для на пересечении Рассмотрим наборы: A = {красный, зеленый, синий} B 5 = {красный, желтый, оранжевый} Найдите следующее: Показать решение Обратите внимание, что в приведенном выше примере было бы сложно просто попросить A c , поскольку все, от цвета фуксии до щенков и арахисового масла, входит в комплект набора. По этой причине дополнения обычно используются только с пересечениями или когда у нас есть универсальный набор. Как мы видели ранее с выражением A c ⋂ C операции над множествами можно группировать вместе. Символы группировки можно использовать так же, как и с арифметикой — для принудительного порядка операций. Предположим, H = {кошка, собака, кролик, мышь}, F = {собака, корова, утка, свинья, кролик}, и W = {утка, кролик, олень, лягушка, мышь} Показать решение Чтобы визуализировать взаимодействие множеств, Джон Венн в 1880 году решил использовать перекрывающиеся круги, опираясь на аналогичную идею, использованную Леонардом Эйлером в 18 веке. Эти иллюстрации теперь называются Диаграммы Венна .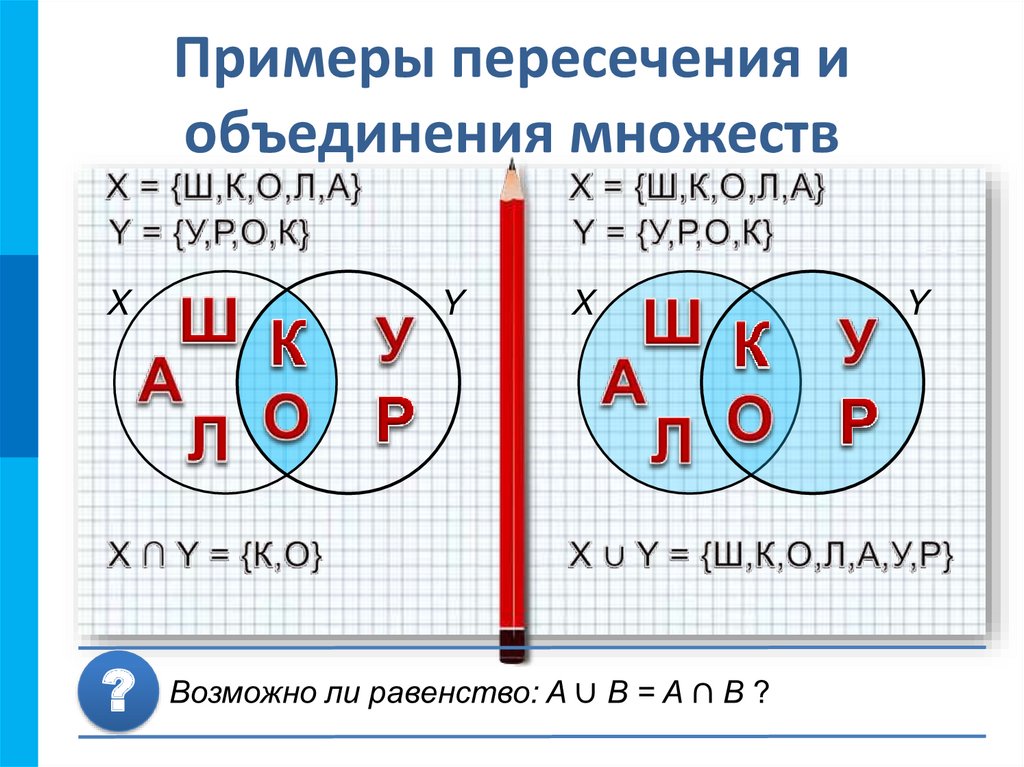 Союз отмечен A ⋃ B. Более формально, x ∊ A ⋃ B , если x
Союз отмечен A ⋃ B. Более формально, x ∊ A ⋃ B , если x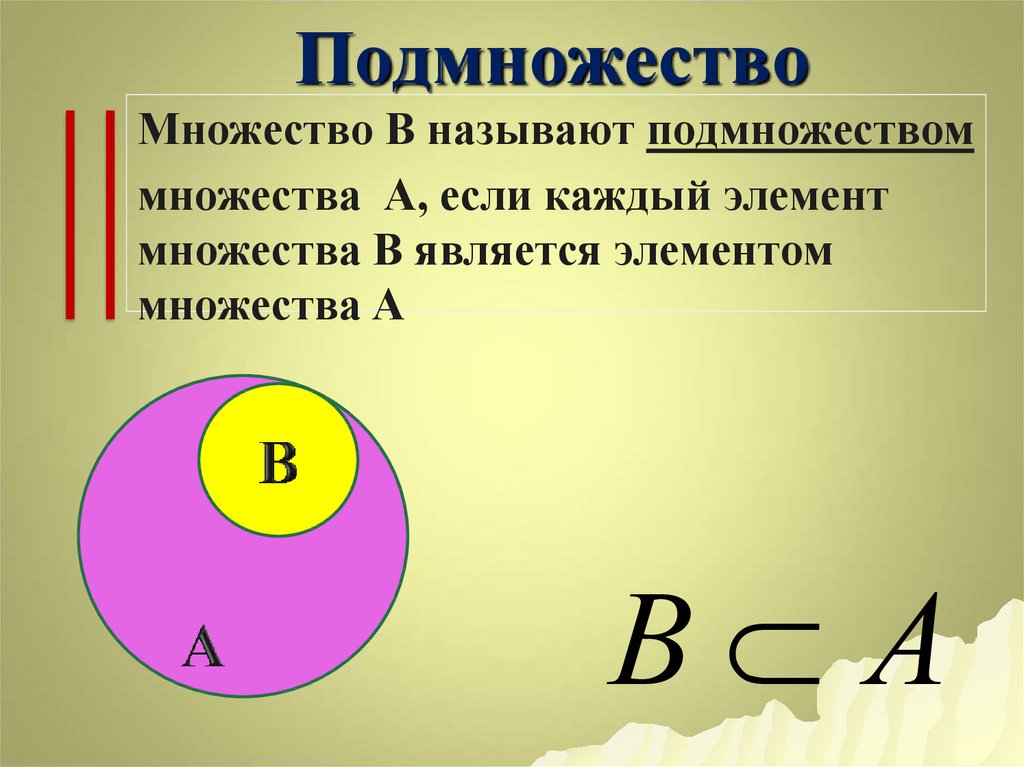 9{c}[/латекс]. Этот верхний индекс не является показателем степени. Это украшение, которое обозначает дополнение к набору .
9{c}[/латекс]. Этот верхний индекс не является показателем степени. Это украшение, которое обозначает дополнение к набору . Пример
Пример
Попробуйте
Символы пересечения и объединения
Пример
C = {красный, оранжевый, желтый, зеленый, синий, фиолетовый} Попробуйте

Пример