Зная периметр окружности найти диаметр окружности: Онлайн калькулятор диаметра круга. Как узнать диаметр круга, окружности.

Как найти периметр окружности зная диаметр. Как определить радиус окружности, зная ее длину

Интернет

Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.

Что такое окружность и где она встречается?

Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром. Это расстояние называется радиусом.

В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.

В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.

Обозначения величин и формулы

Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:

Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:

l = π * d.

Как быть, если нужно вычислить периметр круга?

Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.

Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.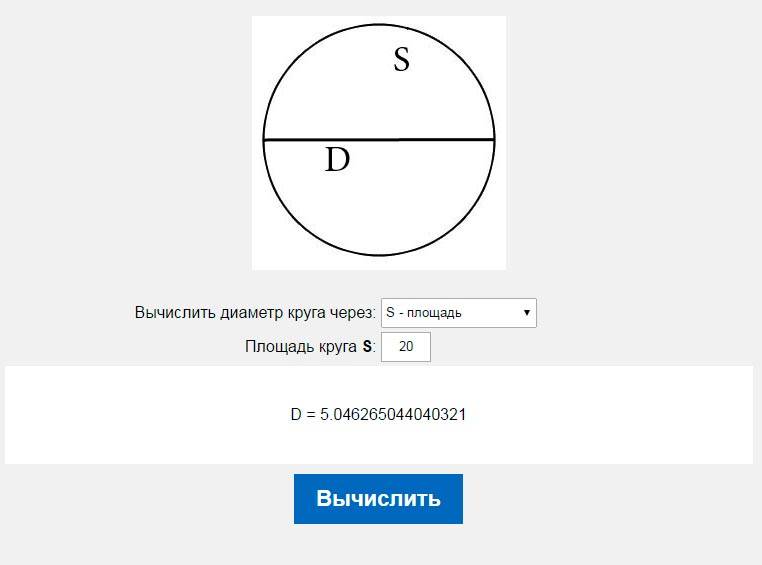

Примеры заданий

Задача первая

Условие. Узнать длину окружности, радиус которой равен 5 см.

Решение. Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).

Ответ: l = 31,4 см.

Задача вторая

Условие. Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.

Решение. В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.

Ответ: r = 200 мм.

Задача третья

Условие. Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.

Решение. Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.

Ответ: d = 18 см.

Задача четвертая

Условие. Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.

Решение. Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.

Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.

Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.

Ответ: l 1 = 18,84 см, l 2 = 31,4 см.

Задача пятая

Условие. Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?

Решение. Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.

Ответ: Белка пробегает 6,28 м.

Часто звучит, как часть плоскости, которая ограничена окружностью. Окружность круга является плоской замкнутой кривой. Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние. В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415 .

Определение периметра круга

Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(~3.1415)

Формула периметра круга

Периметр круга радиуса \(r\) :

\[ \LARGE{P} = 2 \cdot \pi \cdot r \]

\[ \LARGE{P} = \pi \cdot d \]

\(P \) – периметр (длина окружности).

\(r \) – радиус.

\(d \) – диаметр.

Окружностью будем называть такую геометрическую фигуру, которая будет состоять из всех таких точек, которые находятся на одинаковом расстоянии от какой-либо заданной точки. 0}{n}}=\frac{2τ}{2τ»} \)

Получаем, что отношение \(\frac{ρ}{ρ»}=\frac{2τ}{2τ»} \) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть

\(\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»} \)

С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \) ), будем получать равенство:

\(lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»} \)

Из последних двух равенств получим, что

\(\frac{C}{C»}=\frac{2τ}{2τ»} \)

\(\frac{C}{2τ}=\frac{C»}{2τ»} \)

Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть

\(\frac{C}{2τ}=const \)

Эту постоянную принять называть числом «пи» и обозначать \(π \) . Приближенно, это число будет равняться \(3,14 \) (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом

\(\frac{C}{2τ}=π \)

Окончательно, получим, что длина окружности (периметр круга) определяется формулой

\(C=2πτ \)

В вашем браузере отключен Javascript.

Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.

Вычислить радиус

Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.

Рассчитать диаметр

Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.

Узнать длину окружности

Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.

Вычислить площадь круга

Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.

Рассчитать площадь шара

Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.

Вычислить объем шара

Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.

И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг.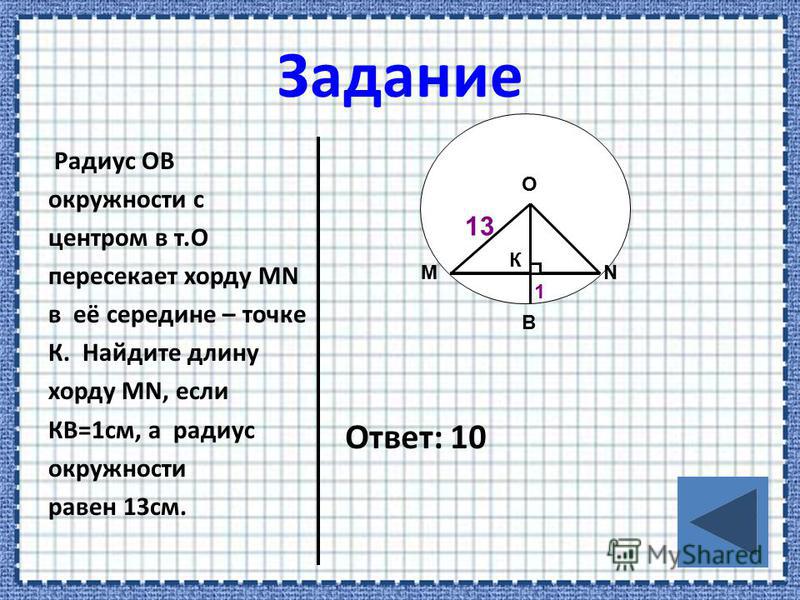 Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность. А вот синее содержимое внутри нее — и есть круг.

Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.

Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.

Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.

Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:

К примеру, радиус — 7 см. Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.

Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом

Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:

Ответ: диаметр равен 21,98 метрам.

Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:

D = 2 * (S / Пи) * (1 / 2)

S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:

D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414

При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.

Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:

R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).

Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.

Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки. Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности. А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.

1. Сложнее найти длину окружности через диаметр

, по этому сначала разберём этот вариант.

Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.

После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.

2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см

Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.

5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!

Онлайн калькулятор длины окружности

Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.

Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.

Как вычислить диаметр окружности: 8 шагов

‘).insertAfter(«#intro»),$(‘

‘).insertBefore( «.youmightalsolike»),$(‘

‘).insertBefore(«#quiz_container»),$(‘

‘).insertBefore(«#newsletter_block_main»),ja(!0),c=document.getElementsByClassName(«scrolltomarker»),a=0;a

В этой статье:

Вычисление диаметра окружности с использованием радиуса, длины окружности или площади круга

Вычисление диаметра окружности из чертежа окружности

Дополнительные статьи

Вычислить диаметр окружности не составит труда, если вы знаете какие-либо другие ее размеры: радиус, длину окружности или площадь ограничиваемого ею круга. Диаметр можно вычислить, даже не зная этих размеров — при наличии начерченной окружности. Если вы хотите узнать, как вычислить диаметр окружности, следуйте указанным ниже шагам.

Шаги

1. 1

   Если вам известен радиус окружности, то, для того чтобы узнать диаметр, удвойте его. Радиус — это расстояние от центра окружности до любой точки, лежащей на ней. Например, если радиус окружности равен 4 см, то диаметр окружности составляет 4 см x 2, или 8 см.

2. 2

   Если вам известна длина окружности, то, для того чтобы вычислить диаметр, разделите ее на π. Число π равно примерно 3,14; но чтобы получить наиболее точное значение, вам следует воспользоваться калькулятором. Например, если длина окружности равна 10 см, то диаметр окружности составляет 10 cm/π, или 3,18 см.

3. 3

   Если вам известна площадь круга, то для нахождения диаметра разделите ее на π и извлеките из результата квадратный корень, чтобы получить радиус; затем умножьте на 2 для получения диаметра. Данное вычисление вытекает из формулы площади круга, A = πr², преобразованной для нахождения диаметра. Например, если площадь круга равна 25 см², разделите ее на число π и извлеките квадратный корень: √(25/3,14) = √7,96 = 2,82 см. Это радиус окружности. Умножьте его на 2, и вы получите диаметр: 2,82 х 2 = 5,64 см.

   Реклама

1. 1

   Внутри окружности начертите горизонтальную прямую, проходящую от одной точки окружности к другой. Для этого воспользуйтесь линейкой или угольником. Прямая может проходить в верхней части круга, в нижней, или где-нибудь посередине.

2. 2

   Пометьте точки, в которых прямая пересекает окружность, буквами «A» и «B.»

3. 3

   Начертите две пересекающиеся окружности, одну — с центром в точке A, а другую — с центром в точке B. Убедитесь, что две окружности пересекаются так, будто образуют диаграмму Венна.

4. 4

   Через две точки, в которых окружности пересеклись, проведите прямую. Отрезок этой прямой между двумя точками и будет равен диаметру окружности.

5. 5

   Измерьте диаметр. Измерьте его с помощью линейки, а если нужна большая точность — штангенциркулем с цифровой индикацией. Готово!

   Реклама

Советы

• Научитесь пользоваться циркулем. Это очень полезный инструмент, который предназначен для многих целей, включая определение диаметра окружности описанным выше графическим способом. Для этого можно также использовать измерительный циркуль.
• Работа с геометрическими формулами и уравнениями станет легче при условии постоянной практики. Попросите кого-то, кто работал с окружностями или другими геометрическими фигурами, помочь вам. Когда вы наберетесь немного опыта, вы скорее всего почувствуете, что задачи по геометрии будут казаться легче.

Реклама

Что вам понадобится

• Калькулятор
• Карандаш
• Циркуль
• Линейка
• Штангенциркуль с цифровой индикацией (при необходимости)

Об этой статье

На других языках

Как вычислить диаметр окружности — Wiki How Русский

Вычислить диаметр окружности не составит труда, если вы знаете какие-либо другие ее размеры: радиус, длину окружности или площадь ограничиваемого ею круга. Диаметр можно вычислить, даже не зная этих размеров — при наличии начерченной окружности. Если вы хотите узнать, как вычислить диаметр окружности, следуйте указанным ниже шагам.

Эту страницу просматривали 1 245 957 раз.

Реклама

Diameter — SAT Math

Все математические ресурсы SAT

16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 Следующая →

SAT Math Help » Геометрия » Плоская геометрия » Круги » Диаметр

Если площадь круга в четыре раза больше длины окружности того же круга, то каков диаметр круга?

Возможные ответы:

2

32

4

8

16

Правильный ответ:

16

Объяснение:

Установите площадь круга, равную четырехкратной длине окружности πr ² = 4(2 πr ).

Вычеркните оба символа π  и по одному r с каждой стороны, и у вас останется r = 4(2), поэтому r = 8 и, следовательно, d  = 16.

Сообщить об ошибке

Периметр круга равен 36 π. Каков диаметр круга?

Возможные ответы:

3

72

18

36

6

Правильный ответ:

36

Объяснение:

Периметр круга = 2 πr = πd

Следовательно, d = 36

Сообщить об ошибке

Если площадь круга, касающегося квадрата на рисунке выше, равна , каково ближайшее значение к площадь квадрата?

Возможные ответы:

Правильный ответ:

Объяснение:

Получите радиус круга из площади.

Разделите квадрат на 4 треугольника, соединив противоположные углы. Эти треугольники будут иметь прямой угол в центре квадрата, образованный двумя радиусами круга, и двумя углами по 45 градусов в углах квадрата. Потому что у тебя 45-45-90 треугольник, вы можете вычислить стороны треугольников как , , и . Радиусы круга (от центра до углов квадрата) будут 9. Гипотенуза (сторона квадрата) должна быть .

Тогда площадь квадрата равна .

Сообщить об ошибке

Две стороны прямоугольного треугольника имеют соответственно 3 и 4 длины. Чему равна площадь окружности, описанной около треугольника?

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы окружность содержала все 3 вершины, гипотенуза должна быть равна диаметру окружности. Гипотенуза и, следовательно, диаметр равны 5, так как это должен быть прямоугольный треугольник 3-4-5.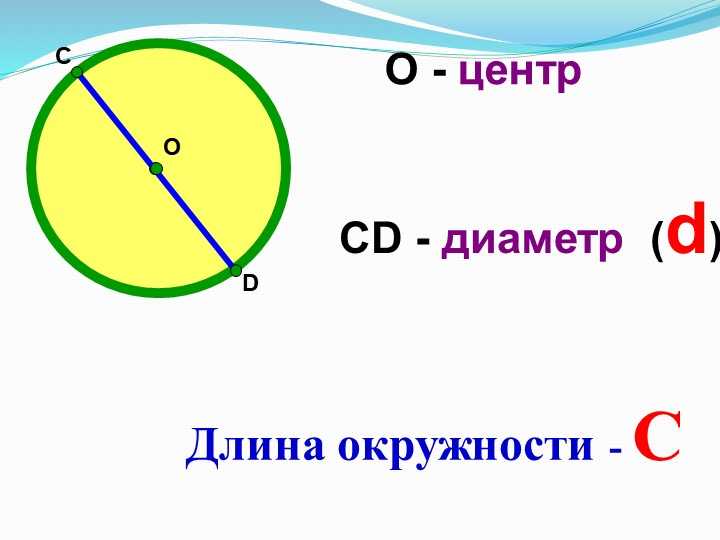

Уравнение площади круга: A = πr ² .

Сообщить об ошибке

Длина окружности . Какой диаметр?

Возможные ответы:

Правильный ответ:

Пояснение:

Напишите формулу длины окружности.

Подставить окружность.

Сообщить об ошибке

Найдите диаметр круга, площадь которого равна .

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить, просто используйте формулу площади круга, чтобы найти радиус, а затем умножьте ее на 2, чтобы найти диаметр. Таким образом,

Отчет о ошибке

Найдите длину диаметра, данный радиус 1.

Возможные ответы:

Правильный ответ:

. Объяснение:

Чтобы решить, просто используйте формулу диаметра круга. Таким образом,

Сообщить об ошибке

Найдите длину диаметра, если радиус равен 5.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить, просто используйте формулу диаметра круга

, где r равно 5. Таким образом,

Помните, что диаметр — это самое длинное расстояние по окружности, а поскольку радиус равен 5 , вы можете просто удвоить это. Таким образом, ответ равен 10.

Сообщить об ошибке

Найдите диаметр круга, если радиус равен 6.

Возможные ответы:

Правильный ответ:

Объяснение:

Чтобы решить, просто используйте формулу диаметра круга.

Помните, поскольку диаметр — это расстояние между двумя точками на противоположных сторонах круга, вы просто удваиваете радиус. Пи не участвует в диаметре, только в окружности, площади и т. д.

Сообщить об ошибке

Длина окружности данного круга составляет половину его площади. Каков диаметр круга?

Возможные ответы:

Правильный ответ:

Объяснение:

Помните, что длина окружности определяется как  , а площадь – как .

Если длина окружности этого круга составляет половину его площади, то можно сказать . Или, .

Мы можем решить это уравнение для r следующим образом:

Поскольку диаметр круга в два раза больше его радиуса, то диаметр этого круга равен 8. 

Чтобы проверить ответ, подставьте r=4 в формулы длины окружности и площади. Вы увидите, что площадь этого круга  и его длина окружности , что составляет ровно половину его площади.

Сообщить об ошибке

← Предыдущая 1 2 Следующая →

Уведомление об авторских правах

Все математические ресурсы SAT

16 Диагностические тесты 660 практических тестов Вопрос дня Карточки Учитесь по концепции

Окружность и площадь кругов — Easy Peasy All-in-One Homeschool

На этом уроке вы расширите свои знания о периметре и площади, включив в них круги. Вы также научитесь писать и решать задачи на сравнение длины окружности и площади круга с использованием как радиуса, так и диаметра.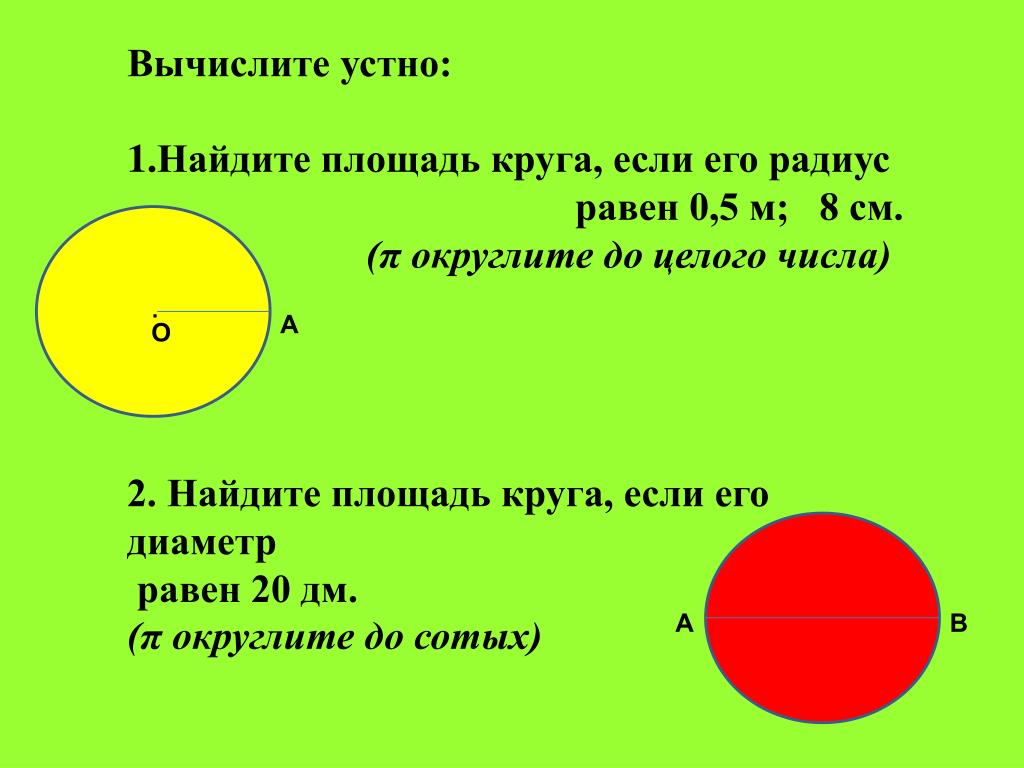

Для многоугольника расстояние вокруг фигуры называется периметром. Для круга расстояние вокруг фигуры называется окружностью  круга. Диаметр  – это расстояние поперек круга через его центр. Радиус    – это расстояние от центра до любой точки окружности и размер диаметра.

Отношение длины окружности к диаметру одинаково для каждого круга и обозначается греческой буквой  , известной как пи. Мы аппроксимируем десятичную дробь числа пи как 3,14 и используем дробь .

Формула для нахождения длины окружности:

Помните, что диаметр в два раза больше радиуса, поэтому, если вам известен радиус, вы можете использовать следующую формулу: 

Пример

Джефф строит тележку. Колеса, которые он использует на картинге, имеют радиус 8 дюймов. Какова окружность каждого колеса?

1. Какова формула длины окружности, если известен радиус?
   С = 2πr
2. Используйте 3. 14 для π и подставьте длину радиуса в формулу.
   С = 2(π)(8)
3. Умножить.
   C = 2 x 3,14 x 8 = 50,24
   Окружность каждого колеса составляет около 50,24 дюйма.

Пример

Давайте применим эти знания к следующей задаче:

Круглый бассейн имеет радиус 15 футов. Семья, которой принадлежит бассейн, ставит круглый забор, который находится на расстоянии 5 футов от бассейна во всех точках. Приблизительно, сколько футов ограждения им потребуется для этого проекта?

Прежде чем приступить к математике, посмотрите на размеры, которые будут использоваться для строительства забора. Мы знаем, что бассейн имеет радиус 15 футов, но нам нужно добавить к этому 5 футов, потому что забор будет в 5 футах от бассейна. Поэтому мы изменим радиус на 20 футов. Разберись с этим сам.

1. Какова формула длины окружности, если известен радиус?
2. Используйте 3.14 для  и подставьте длину радиуса в формулу.
3. Умножить.
   Им нужно будет купить около 126 футов забора.

Пример

Еще одна проблема с диаметром!

В пиццерии Джеки пицца продается по диаметру. Райан заказывает 14-дюймовую пиццу. Какова окружность ее пиццы?

1. Какова формула длины окружности, если известен диаметр?
2. Используйте 3.14 для и подставьте длину радиуса в формулу.
3. Умножить.
   Ее пицца будет 43,96 дюйма в диаметре!

 

Посмотрите видео, чтобы узнать, как найти длину окружности.

Теперь мы научимся находить площадь круга. Вы можете использовать то, что вы уже знаете о кругах, и π, чтобы найти площадь круга. Формула нахождения площади прямоугольника: A=bh. Замените b и r на высоту.

Следовательно, формула площади круга:

Помните, что диаметр в два раза больше радиуса, поэтому, если вам известен диаметр, вы должны запомнить .

Осторожно! Распространенной ошибкой является умножение радиуса на 2.
Это не то же самое, что квадрат радиуса.

Пример

Циферблат часов имеет диаметр 12 дюймов. Какова площадь циферблата часов?

1. Как найти площадь круга, зная диаметр?
2. Используйте 3.14 и подставьте радиус в формулу.
3. Умножить.
   Площадь циферблата часов составляет около 113 квадратных дюймов.

Пример

Давайте попробуем с заданным радиусом — просто подставьте числа! У Сары есть круглый розарий. Радиус сада 7 футов. Какова площадь сада?

1. Как найти площадь круга, зная радиус?
2. Используйте 3.14 и подставьте радиус в формулу.
3. Умножить.
   Площадь розария Сары составляет около 153,9 квадратных футов.

 

Посмотрите видео Хана ниже, чтобы увидеть больше примеров нахождения площади круга.

ЕЩЕ ОДНО… Иногда вас могут попросить ответить на эти вопросы в терминах

.

Круглый сад площадью 64

квадратных ярдов. Какова окружность сада? Дайте свой ответ в терминах .

Во-первых, вспомним формулу площади круга: . Теперь замените это на  . Вы можете видеть, что 64 заменили  , поэтому найдите квадратный корень из 64.  , или  равно 64. Теперь, когда мы знаем радиус, мы можем найти диаметр (2 x радиус). Итак, диаметр равен 16. Если мы ответим через

, значит оставляем греческую букву и не используем 3.14. Окружность .

Формулы великолепны! …Если вы знаете формулу, вы просто подставляете известные значения, чтобы найти неизвестные значения. Я могу использовать площадь, чтобы найти радиус, длину окружности и диаметр!

Пример: площадь круга равна 50,24 квадратных единиц

Чтобы найти радиус:

*Используйте калькулятор, чтобы найти квадратный корень.