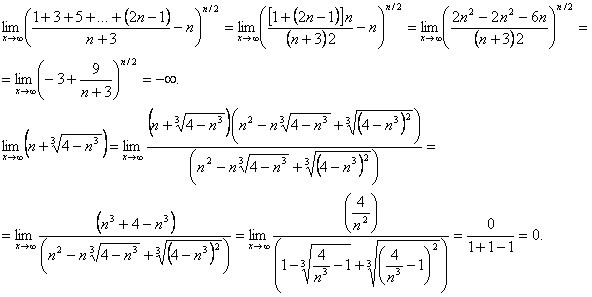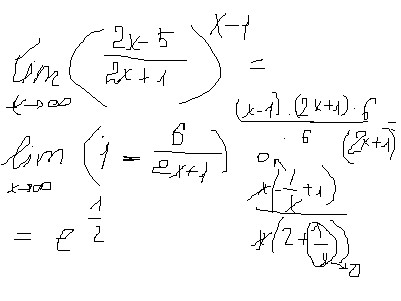1.пределы, производная
Математический анализ.
§1. Функция. Предел функции
Определение 1. Функция, заданная уравнением , называется явной.
Пример: у=2х, у=sinx — явные функции,
У явно выражен через Х
Определение 2. Функция, заданная уравнением , называется неявной
Например, — неявная функция от х.
У явно не выражен через Х
Определение 3 (по Гейне). Число b называется пределом функции при , если для любой последовательности значений аргумента х, сходящейся к а, соответствующая последовательность значений функций сходится к числу
Обозначение:
b = lim f(x)
x a
Если , то х может оставаться меньше а или больше а.
В связи с этим существуют так называемые односторонние пределы:
Пример.
Если функция в данной точке непрерывна, то односторонние пределы равны.
§2. Теоремы о пределах
Предел постоянной:
- Предел алгебраической суммы функций.
Предел произведения функций:
Следствие: постоянный множитель можно выносить за знак предела:
Предел частного функций: где
Предел степени :
§3.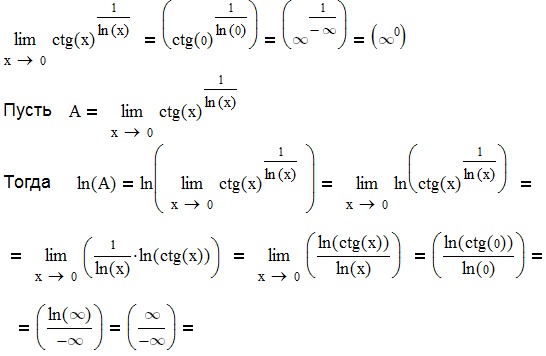
Бесконечно малые и бесконечно большие
функции
Определение 1. Функция — бесконечно большая при значении , если .
Определение 2. Функция — бесконечно малая при значении , если .
1. Сумма, разность, произведение б.м.ф., а также произведение б.м.ф. на постоянную величину – б.м.ф.
— является неопределенностью вида
2. , , — б.б.ф.
, — являются неопределенностями.
3. Если — б. б. ф. при значении , то — б. м. ф. при значении , где , .
4. Если — б. м. ф. при значении , то — б. б. ф. при значении , где , .
5. Соотношения
вида
,
,
,
,
, тоже являются неопределённостями.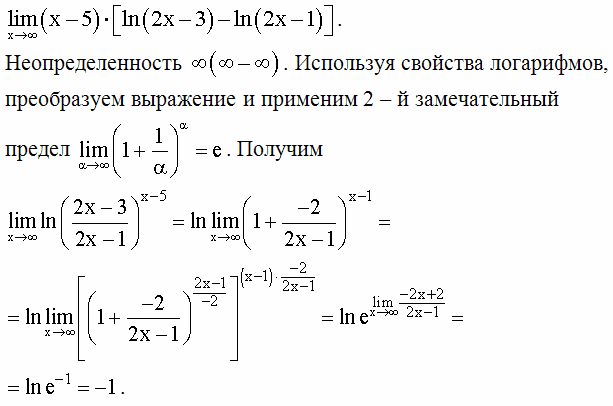
§4. Раскрытие неопределенности вида при вычислении пределов.
Непосредственное вычисление пределов.
Вместо аргумента х подставляют его предельное значение в функцию.
Пример:
Правило раскрытия неопределенности вида
Если дробь содержит многочлены, то их следует разложить на линейные множители и выполнить сокращение.
Пример:
Если под знаком предела есть иррациональные выражения, то нужно умножить числитель и знаменатель на сопряженные множители к этим выражениям.
§5. Раскрытие неопределенности вида при вычислении пределов.
Состоит
в почленном делении числителя и
знаменателя на переменную в наивысшей
степени.
Пример:
Замечание:
Если старшие степени числителя и знаменателя равны, то предел равен отношению коэффициентов при старших степенях переменной.
Если степень числителя меньше степени знаменателя, то предел равен нулю.
Если степень числителя больше степени знаменателя, то предел равен бесконечности.
§6. Два замечательных предела
Первый замечательный предел.
или
Он раскрывает неопределенность вида .
Пример: .
Второй замечательный предел.
или
Он раскрывает
неопределенность вида (е ≈ 2, 718281828459045….
.).— неперово число.
(е ≈ 2, 72).
Пример:
§7. Непрерывность функции. Точки разрыва.
Определение 1. Функция называется непрерывной в некоторой точке , если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции, т.е.
Определение 2. Функция , непрерывная в каждой точке некоторого интервала , называется непрерывной на всем интервале
Определение 3. Точка, в которой нарушается непрерывность функции, называется точкой разрыва.
Существуют точки разрыва 1-го и 2-го рода.
Если односторонние пределы функции в данной точке не равны и конечные, то такая точка называется точкой разрыва 1-го рода.
Скачок функции в этой точке равен модулю разности односторонних пределов:
Пример:
– точка разрыва 1-го рода. Можно указать скачок функции:
Если в данной точке хотя бы один из односторонних пределов бесконечен или не существует, то такая точка называется точкой разрыва 2-го рода.
§8. Свойства функций, непрерывных на отрезке
1)
Функция , непрерывная на отрезке , достигает на этом отрезке своего наибольшего и наименьшего значения.
Если
функция непрерывна на отрезке и принимает на концах этого отрезка
значения разных знаков, то на этом
отрезке существует, по крайней мере,
одно такое значение
,
что
.
3) Если две функции и непрерывны на отрезке , то непрерывны , , на этом отрезке.
§9. Производная функции. Дифференцируемость функций
Определение 1.
Обозначения:
Определение 2. Функция , имеющая в точке производную, называется дифференцируемой в этой точке.
Определение 3. Функция , дифференцируемая в каждой точке интервала , дифференцируема на этом интервале.
Связь непрерывности и дифференцируемости функции.
Теорема.
Если
функция дифференцируема в некоторой точке
,
то в этой точке она и непрерывна. Обратное
утверждение неверно, т.к. есть функции
непрерывные в точке, но не имеющие
производной в этой точке.
Пример:
Функция в точке непрерывна, но не имеет производной.
Таблица основных производных
15.
16.
17.
18.
19.
20.
21.
22.
23.
§10.
1. производная сложной функции Если и , то — сложная функция от х, где
u — промежуточный аргумент,
х — конечный аргумент.
Теорема. Производная сложной функции равна производной функции по промежуточному аргументу u умноженной на производную промежуточного аргумента по конечному аргументу х, т.е.
или
Пример.
(sinU)′ = cosU U′
(sin3х)′ = cos3х (3х)′
2.
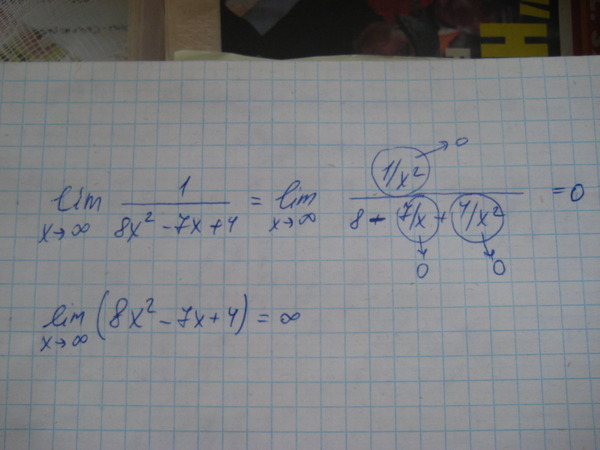производная обратной функции
Пусть дифференцируемая и строго монотонная функция на некотором промежутке х. Тогда функция — ей обратная функция.
Теорема. Производная обратной функции равна:
.
§11. Производные высших порядков
Пусть задана некоторая дифференцируемая функция . Тогда:
— производная 1-го порядка.
Если — это опять функция от х, то от нее можно найти производную:
— производная 2-го порядка.
— производная 3-го порядка.
… …………. …………………………… .
n) — производная n-го
порядка.
Пример:
§12. Дифференцирование неявных функций
— функция, заданная неявно, т.е. функция не разрешена относительно у.
Чтобы найти производную неявной функции, следует все члены выражения продифференцировать по х, а затем выразить у´ через х; у и const, помня, что , а .
Пример:
Аналогично можно находить производную 2-го порядка . Для этого выражение (1) нужно еще раз продифференцировать по х и выразить у´´ через х; у; у´ и const. Затем в полученное выражение подставить значение у´.
§12А. Геометрический смысл производной
Значение производной функции в точке равно тангенсу угла наклона касательной, проведенной к графику функции в этой точке:
Уравнение касательной:
Уравнение нормали:
,
где (
— точка
касания.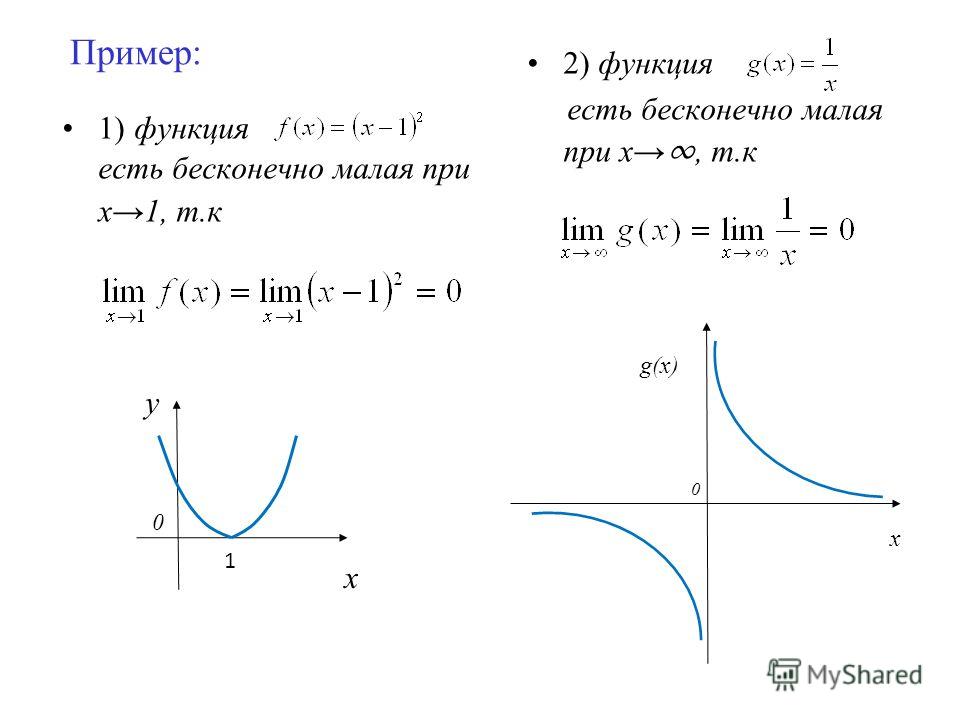
12б Производная – это мгновенная скорость изменения функции
§13. Понятие дифференциала
Пусть дана функция . По определению: . По теореме о пределах имеем: если , то — значит , получим: .
Определение 1. Главная часть приращения , линейная относительно , называется дифференциалом функции и обозначается dy:
.
.
Рассмотрим функцию . . Следовательно, формула дифференциала функции в конечном результате имеет вид:
.
Пример:
С геометрической точки зрения дифференциал функции равен
приращению ординаты касательной.
§14.
Применение
дифференциала функции к приближенным
вычислениям
Пусть задана функция . Воспользуемся приближенным равенством:
.
Сравнивая (1) и (2) выражения, получим:
— формула для приближенного вычисления значений функции.
Можно доказать, что абсолютная погрешность этой формулы не превышает величины .
Пример: Вычислить .
Пусть
§15. Правило Лопиталя при вычислении пределов
Пусть заданы некоторые функции и , дифференцируемые на некотором интервале , а в точке обращающиеся в ноль. Тогда имеет место равенство:
-для
раскрытия неопределенностей и — правило Лопиталя
Пример1: Найти предел.
;
Пример2: Найти предел .
; ;
— опять получилась неопределенность. Применим правило Лопиталя еще раз.
; ;
— применяем правило Лопиталя еще раз.
; ;
Исчисление— Как оценить предел, когда что-то возведено в степень $x$?
спросил
Изменено 3 года, 10 месяцев назад
Просмотрено 2к раз
$\begingroup$
Я пытаюсь оценить следующий предел: 9x=\exp x\ln \left(\dfrac{x+3}{x+8}\right)$$
$\endgroup$
возведение в степень — предел функции, возведенной в степень
спросил
Изменено 7 лет, 4 месяца назад
Просмотрено 23 тысячи раз
$\begingroup$ 9x $$
Может кто-нибудь объяснить, как получить этот предел.