§ 2. Решение задач с помощью уравнений лагранжа 2 -го рода ( ул
Литература: [1] § 178 ; [2] § 128; [4] § 155.
Существенным достоинством метода УЛ-2 является стандартность действий, необходимых для решения задач.
Решение задач рекомендуется проводить последующему плану.
План решения задач с помощью УЛ-2 1. Определить число степеней свободы механической системы и выбрать обобщенные координаты. 2. Изобразить механическую систему в произвольном положении, указать все действующие активные силы и выяснить, являются ли они потенциальными. | |
Вариант — А В случае потенциальных сил: 3. Выразить потенциальную энергию системы в обобщенных координатах. | Вариант – Б В случае непотенциальных сил: 3. Найти обобщенные силы Qj |
4.Найти выражение кинетической энергии системы в обобщённых координатах и скоростях. | |
5. Составить функцию Лагранжа и найти частные производные | 5. Найти частные производные 6.
Подставить выражения |
7. Решать уравнения, полученные на предыдущем этапе. 8. Исследовать решение. | |
 с
горизонтом (рис. 2.1).
с
горизонтом (рис. 2.1).Определить ускорения призм, пренебрегая трением между призмой А и горизонтальной плоскостью.
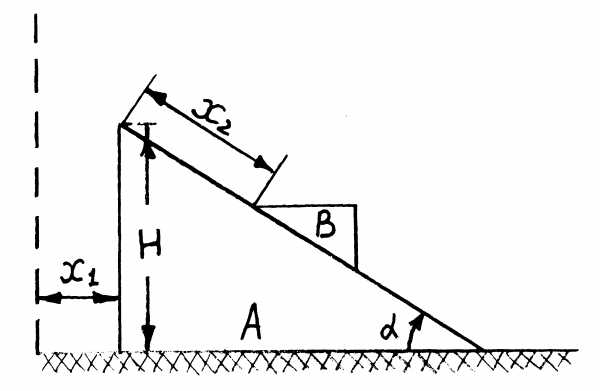

Рис. 2.1 Рис.2.2
За
обобщенные координаты примем декартовы
координаты 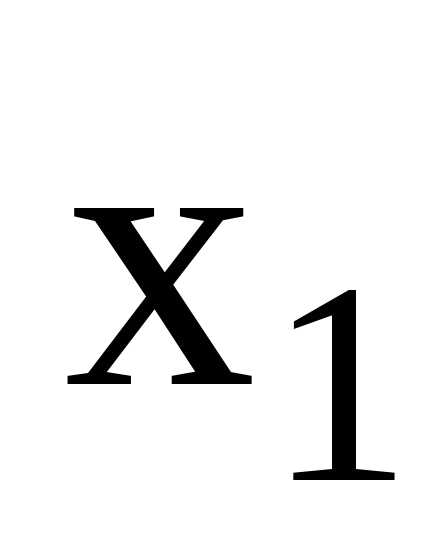 и
и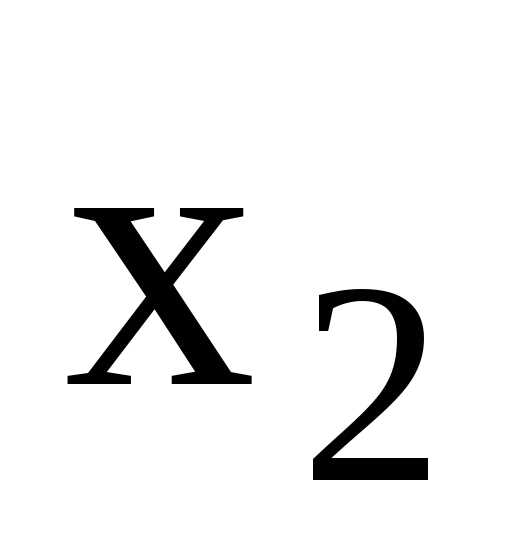 (рис.
2.1). Система имеет две степени свободы.
(рис.
2.1). Система имеет две степени свободы.
Единственными активными силами, действующими на систему, являются силы тяжести. Так как эти силы — потенциальные, то при составлении УЛ-2 используем вариант А общего плана.
Потенциальная энергия системы, отсчитывается от уровня Н (рис. 2.1),
. (2.1)
Кинетическая энергия системы складывается из кинетической энергии призм А и В, движущихся поступательно,
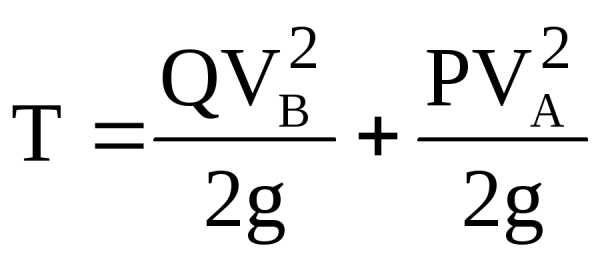 .
.
Призма А совершает сложное движение: она движется вместе с призмой В (переносное движение) и, кроме того, скользит вдоль грани призмы В (относительное движение). В силу теоремы о сложении скоростей
,
где  ,
,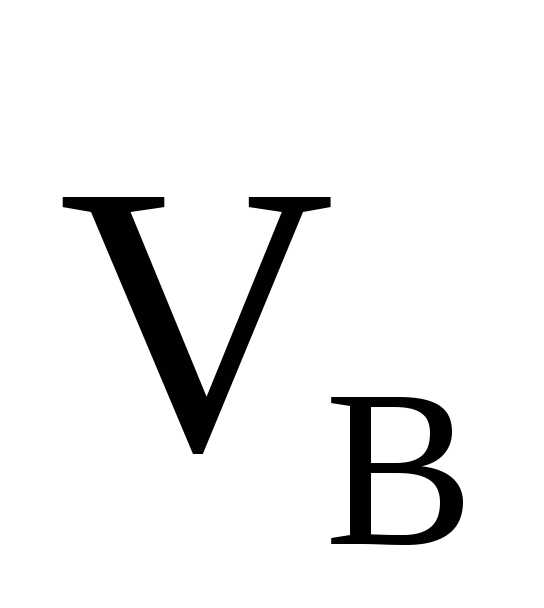 — абсолютные скорости призм А и В;
— абсолютные скорости призм А и В; — скорость призмы А относительно призмы
В. Из треугольника СДЕ (рис. 2.2) с помощью
теоремы косинусов получим
— скорость призмы А относительно призмы
В. Из треугольника СДЕ (рис. 2.2) с помощью
теоремы косинусов получим
.
Так как
то
.
Таким образом,
. (2.2)
Составим функцию Лагранжа, используя (2.1) и (2.2)
.
Найдем частные производные
Уравнения Лагранжа
(2.3)
Из
(2.3)
. (2.4)
Подставляя (2.4) в (2.3)1, получим
Отсюда
. (2.5)
Из (2.4) с помощью (2.5) находим
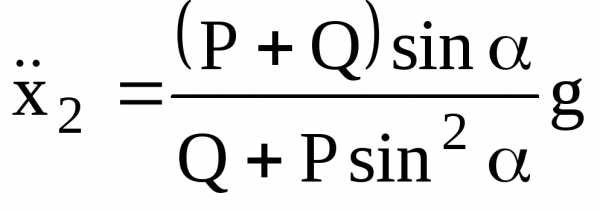 .
(2.6)
.
(2.6)
Формула (2.5) доставляет абсолютное ускорение призмы А, а формула (2.6) — относительное ускорение призмы В (относительно призмы А). Абсолютное ускорение призмы В можно найти с помощью теоремы о сложении ускорений
.
Здесь 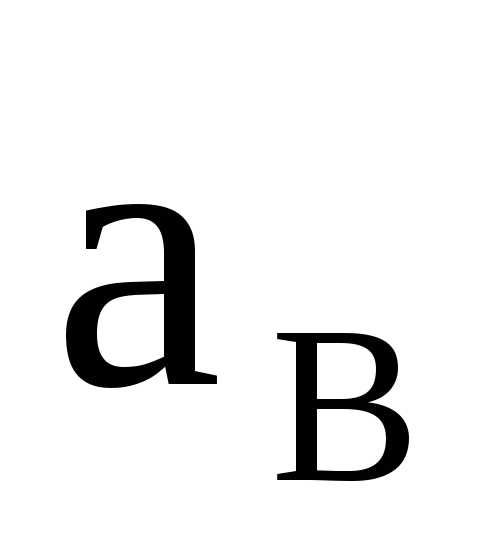
 — абсолютное ускорение
призмы В (относительно призмы А).
— абсолютное ускорение
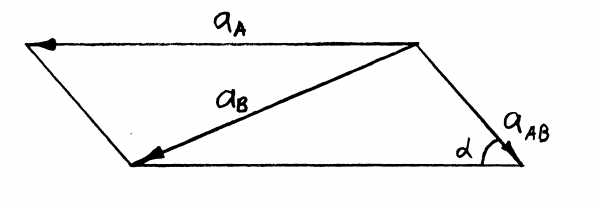
призмы В (относительно призмы А).С помощью теоремы косинусов получим (рис. 2.3)
 .
(2.7)
.
(2.7)
Подставляя  и
и из (2.5) и (2.6) в (2.7), найдем искомое абсолютное
ускорение призмы В.
из (2.5) и (2.6) в (2.7), найдем искомое абсолютное
ускорение призмы В.
2.
Исследуйте поведение решений (2.5) и (2.6) предыдущей
задачи при  ,
предполагая, что
масса тел А и В
,
предполагая, что
масса тел А и В
Рис. 2.3 остается постоянной. Объясните полученные результаты.
3. Докажите, что уравнение (2.3)1 задачи 1 выражает следующий факт: проекция ускорения центра масс системы па горизонтальную плоскость равна нулю. Объясните этот результат с помощью теоремы о движении центра масс системы.
4. Предполагая, что в задаче призмы А и В в начальный момент находились в покое, найдите: а)движение центра масс системы, б) движение каждой призмы относительно центра масс.
5. Решите задачу 47.23 из [5].
6. Решите задачу 1, учитывая трение между призмой и горизонтальной плоскостью. Коэффициент трения равен f.

7.
Эллиптический маятник (рис.2.4) состоит
из ползуна массой m1,
расположенного на гладкой горизонтальной
плоскости и груза массой m2,
шарнирно соединенного c
ползуном стержнем длиной 
Рис 2.4
а) 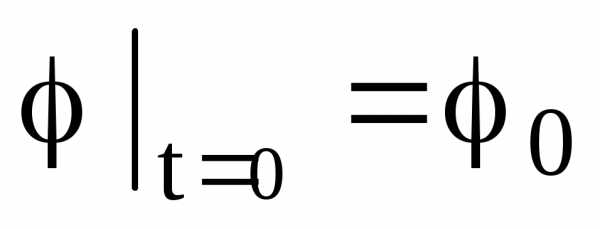 ;
;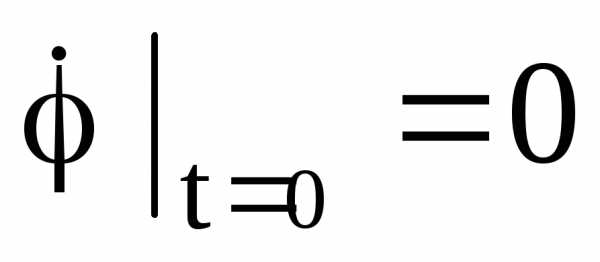 ;
;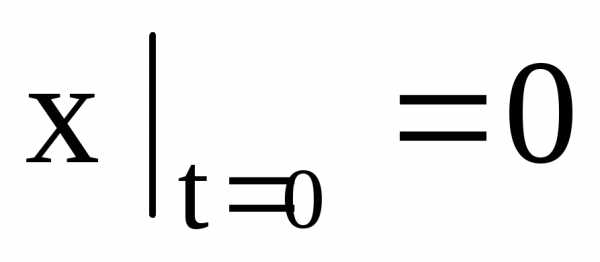 ;
;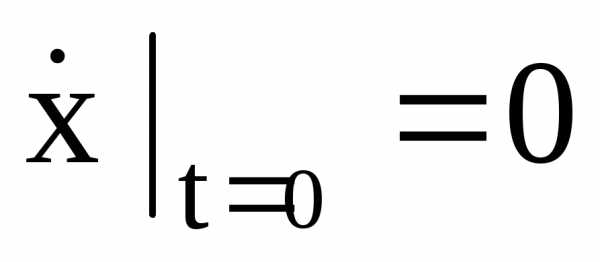 ;
;
б) 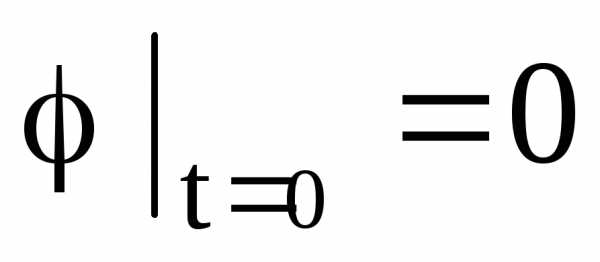 ;
; ;
;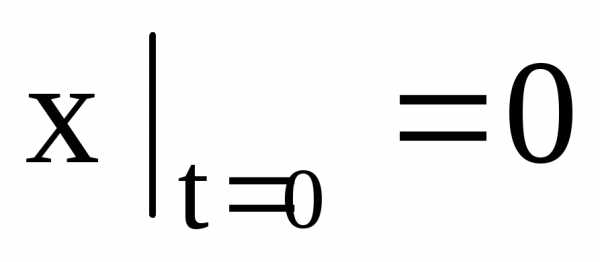 ;
;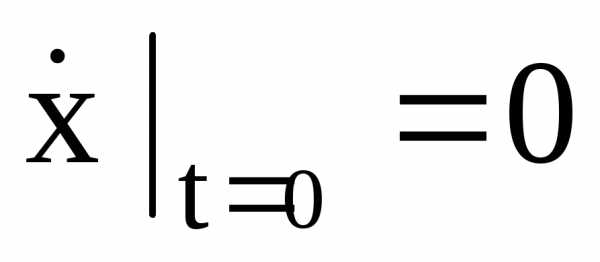 .
.
Указание: принять за обобщенные координаты  и
и (рис.2.4).
(рис.2.4).
Решение этой задачи дано в [2], § 128, пример 89 и в [4] , § 155,пример 155.
8.
Решите предыдущую задачу, учитывая
массу m
9. Решите задачу 7, учитывая трение между ползуном и горизонтальной плоскостью. Коэффициент трения равен f.
Указания: о влиянии сил трения на колебания см. [4], § 98. Воспользуйтесь УЛ-2 в форме (1.1).
10. Связанные
маятники.
Два однородных стержня длиной 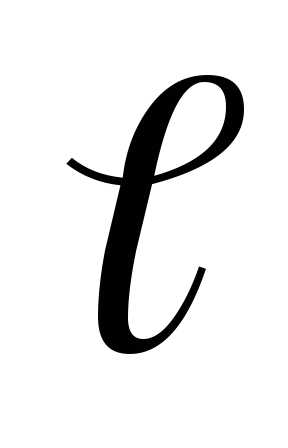 и весом Р каждый соединены на уровнеh
(рис.2.5) пружиной жесткости «С»,
прикрепленной концами к стержням.
и весом Р каждый соединены на уровнеh
(рис.2.5) пружиной жесткости «С»,
прикрепленной концами к стержням.
Найти малые колебания маятников в плоскости их равновесного положения.
В начальный момент (2.8)

Выберем
в качестве обобщенных координат углы 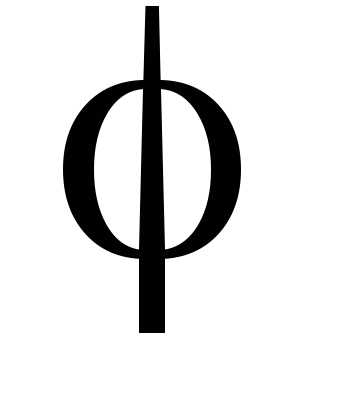 и
и отклонения стержней от вертикала
(рис.2.5). Механическая система имеет две
степени свободы.
отклонения стержней от вертикала
(рис.2.5). Механическая система имеет две
степени свободы.
Рис. 2.5
Будем пренебрегать силами трения в шарнирах. Так как силы тяжести и сила упругости пружины являются потенциальными, то применяем вариант Б общего плана решения задач методом УЛ-2.
Потенциальная энергия системы
,
где  и
и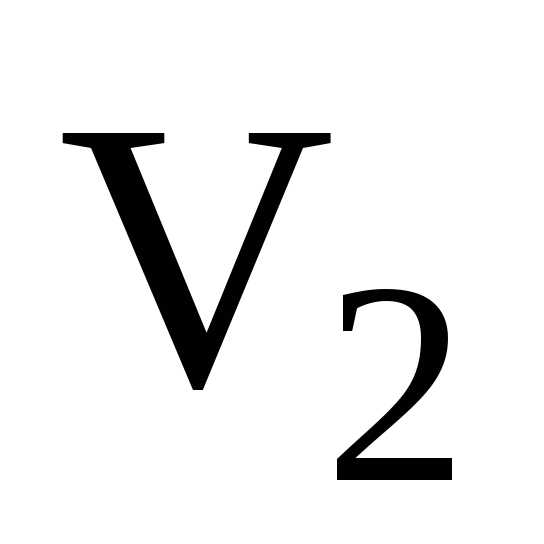 —
потенциальная энергия сил тяжести
первого и второго стержня;
—
потенциальная энергия сил тяжести
первого и второго стержня; —
потенциальная энергия пружины.
—
потенциальная энергия пружины.
Имеем (рис.4.2)
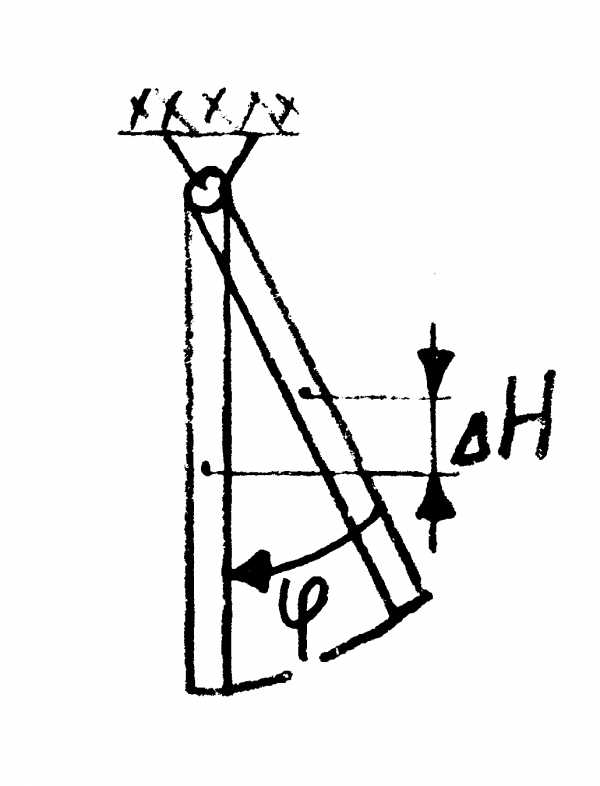 .
.
Аналогично находим
.
Потенциальная энергия растянутой пружины при малых ее деформациях (см. (2), Прилож. 1 ).
Рис.
2.6 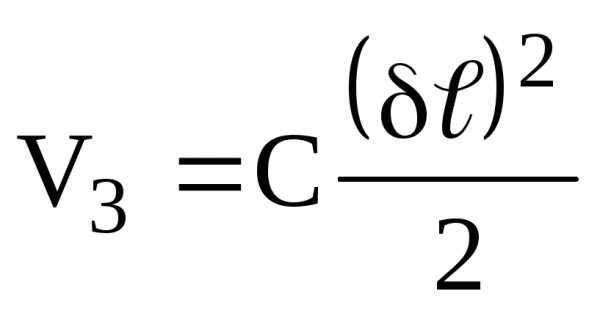
где  —
деформация пружины. При малых углах
отклонения стержней можно пренебречь
вертикальными составляющими перемещений
концов пружины, учитывая только
горизонтальные составляющие и отождествляя
их с длинами дуг, описываемых точкамиB
и D,
в которых пружина прикреплена к стержням.
Отсюда следует, что
—
деформация пружины. При малых углах
отклонения стержней можно пренебречь
вертикальными составляющими перемещений
концов пружины, учитывая только
горизонтальные составляющие и отождествляя
их с длинами дуг, описываемых точкамиB
и D,
в которых пружина прикреплена к стержням.
Отсюда следует, что
.
Поэтому
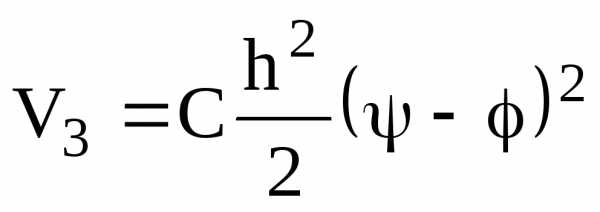 .
.
Таким образом,
. (2.8)а
Найдем теперь кинетическую энергию системы. Так как каждый из стержней вращается около неподвижной оси, то согласно (2), (приложение 3)
,
где
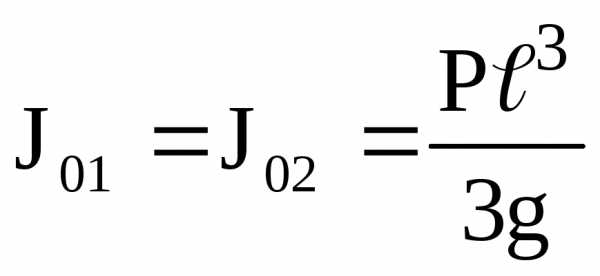 .
.
Следовательно,
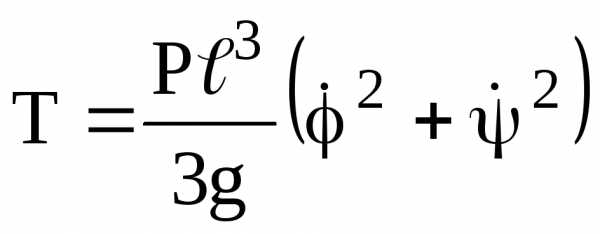 .
(2.9)
.
(2.9)
Образуем функцию Лагранжа, используя (2.8)а и (2.9)
.
Найдем частные производные
(2.10)
.
Составим уравнения Лагранжа. Используя (1.2) и (2.10), получим
;
(2.11)
.
Вводя для краткости обозначения
запишем (2.11) в виде
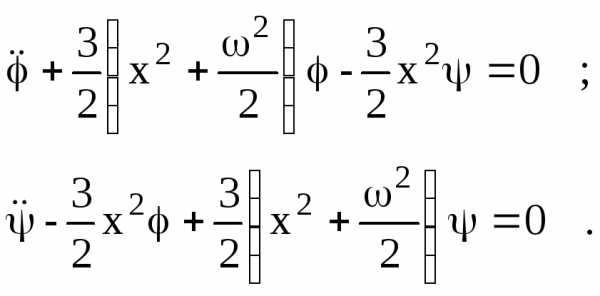 (2.12)
(2.12)
Для интегрирования системы (2.12) применим следующий прием.
Положим
. (2.13)
Складывая и вычитая уравнения (2.12), получим
(2.14)
(2.15)
Уравнения (2.14) и (2.15) описывают свободные гармонические колебания с частотами
.
Общие решения равнений (2.14) и (2.15) имеют вид
. (2.16)
Из (2.13) с помощью (2.16) получаем
(2.17)
Постоянные
А1,
А2,  определяем из
начальных условий (2.8).
определяем из
начальных условий (2.8).
Из (2.17) следует
(2.18)
Дифференцируя
(2.17) и используя начальные условия для 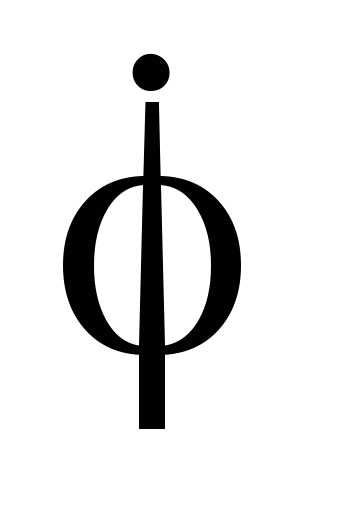 и
и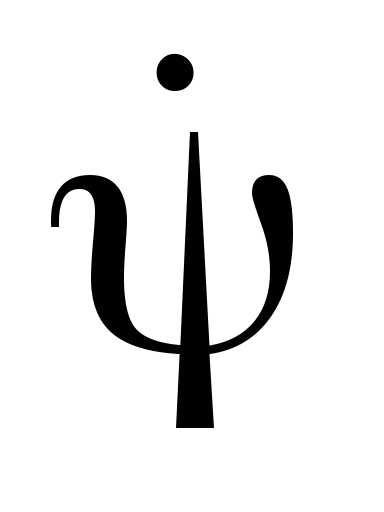 ,
получим
,
получим
(2.19)
Складывая и вычитая уравнения (2.19), получим
Отсюда 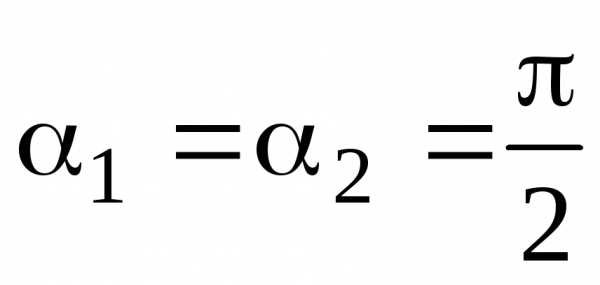 .
Из (2.18) следует.
.
Из (2.18) следует.
Окончательно имеем
(2.20)
Положим
(2.21)
(2.22)
Тогда из (2.20) следует
(2.23)
Колебания, представленные уравнениями (2.21) и (2.22) называются главными. Уравнения (2.21) представляют первое, а уравнения (2.22) второе главные колебания.
Каждому главному колебанию отвечает определенная частота и форма колебаний.
На
рис.2.7 изображена форма колебаний,
соответствующая главному колебанию
(2.21). Здесь маятники колеблются в
одинаковой фазе с одной и той же частотой 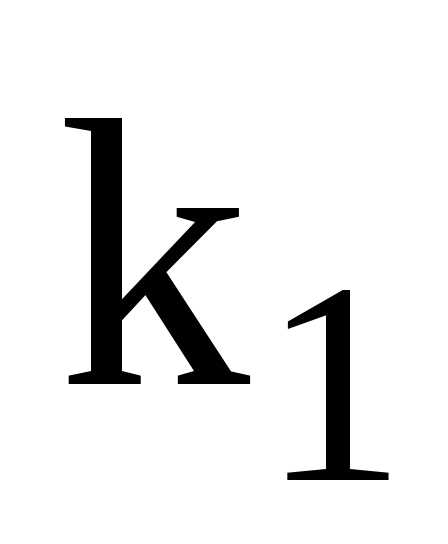 и
амплитудой
и
амплитудой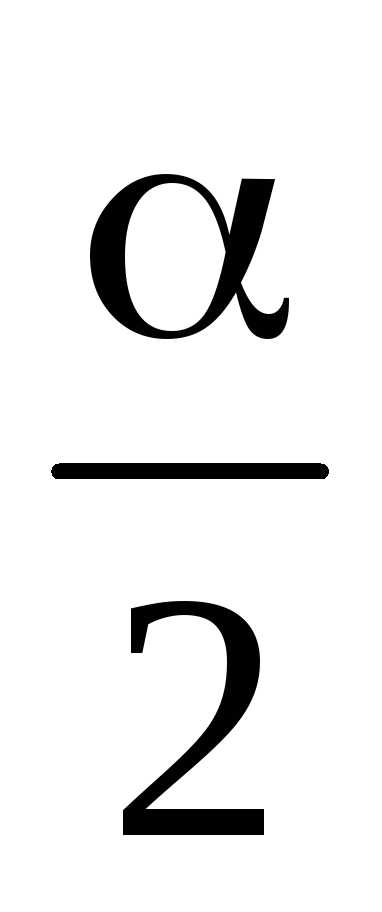 .
.
Пружина
не деформирована. На рис.2.8 показана
форма колебаний, отвечающая главному
колебанию (2.22). Маятники колеблются с одной
и той же частотой 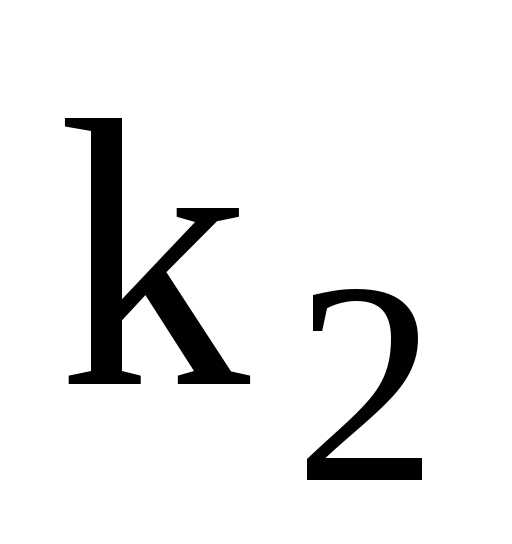 и амплитудой
и амплитудой .
Пружина деформирована.
.
Пружина деформирована.
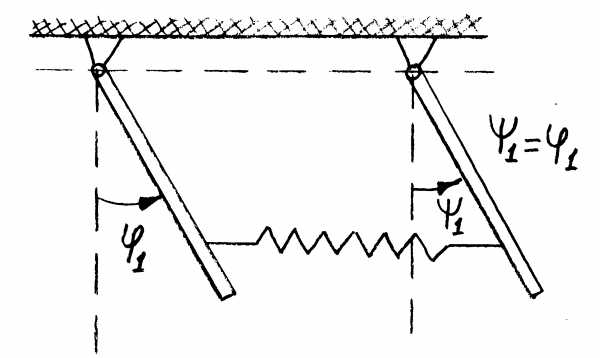

Рис. 2.7 Рис. 2.8
Из
(2.33) следует, что колебания каждого из
маятников О1А1 и O1A1 являются результатом наложения главных
колебаний с частотами  и
и .
.
Примечание. После введения нормальных координат  и
и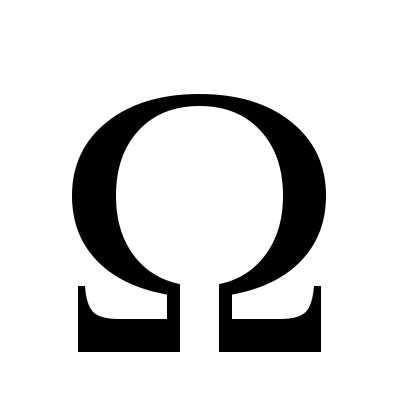 система уравнений (2.12) распалась на два
независимых уравнения свободных
гармонических колебаний (2.14) и (2.15). Успех
этого приема связан с тем, что в
нормальных координатах потенциальная
и кинетическая энергии приводятся
к сумма квадратов.
система уравнений (2.12) распалась на два
независимых уравнения свободных
гармонических колебаний (2.14) и (2.15). Успех
этого приема связан с тем, что в
нормальных координатах потенциальная
и кинетическая энергии приводятся
к сумма квадратов.
Описанный прием можно, обобщить на малые колебания любой механической системы и выделить главные колебания ([4], § 175; [10], § 30). При этом общее решение задачи о малых свободных колебаниях системы является результатом наложения главных (гармонических) колебаний.
11.
В предыдущей задаче исследуйте поведение
частот колебаний при изменении «с»
в (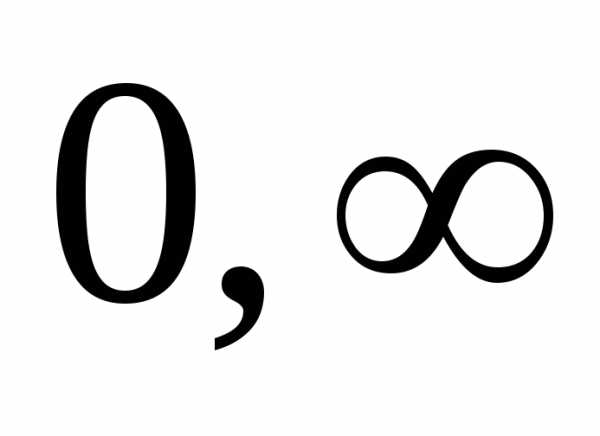 ).
Постройте графики.
).
Постройте графики.
12. Найдите решение задачи 10 при следующих начальных условиях:
Предполагая,
что пружина слабая  показать, что через некоторый
промежуток времени
показать, что через некоторый
промежуток времени первый маятник почти остановится, а вся
энергия перейдет ко второму (перекачка
энергии, биения). Постройте графики
колебаний маятников.
первый маятник почти остановится, а вся
энергия перейдет ко второму (перекачка
энергии, биения). Постройте графики
колебаний маятников.
13. Двойной физический маятник состоит из двух однородных стержней длиной весом Р каждый (рис.1.2). Найдите малые колебания маятника.
За
обобщенные координаты примем углы
и (рис.1.2). Воспользуемся выражениями
потенциальной энергии (1.15) и кинетической
энергии (1.22) двойного маятника, полученными
при решении примеров 12 и 15 в §1. Функция
Лагранжа
(рис.1.2). Воспользуемся выражениями
потенциальной энергии (1.15) и кинетической
энергии (1.22) двойного маятника, полученными
при решении примеров 12 и 15 в §1. Функция
Лагранжа
(2.24)
Дифференцируя (2.24), находим
Уравнения Лагранжа имеют вид
или
 (2.25)
(2.25)
Используя примечание к задаче 10, ищем решение системы (2.25) в виде
(2.26)
Подставляя (2.26) в (2.25), подучим
 (2.27)
(2.27)
Так как по физическому смыслу задачи А и В не равны одновременно нулю, то система (2.27) должна допускать нетривиальное решение. Это возможно тогда и только тогда, когда определитель системы равен нулю:
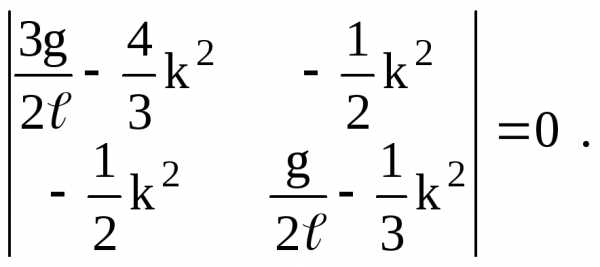 (2.28)
(2.28)
Уравнение (2.28) называют уравнением частот (вековым уравнением). В развернутом виде оно имеет вид
или
(2.29)
Из (2.29) находим
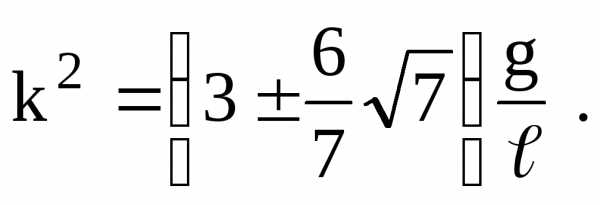
Отсюда
Общее решение системы (2.25) имеет вид
(2.30)
Из (2.27) следует
 .
.
Заменяя  их числовыми значениями, получим
их числовыми значениями, получим
Уравнения (2.30) принимают вид
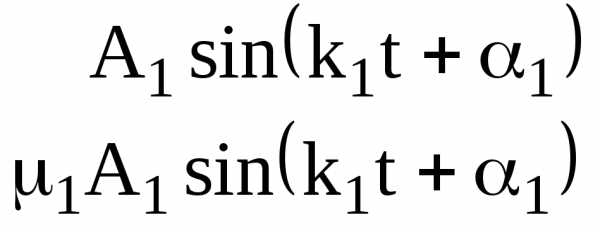

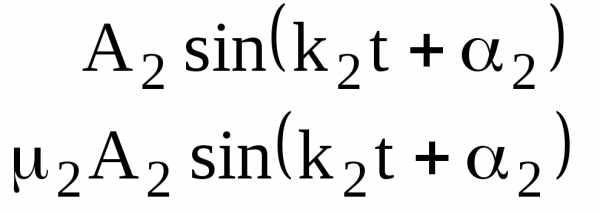 (2.31)
(2.31)
В (2.31) слагаемые в рамках соответствуют
первому и второму главным колебаниям.
Первое главное колебание происходит с
частотой
(2.31) слагаемые в рамках соответствуют
первому и второму главным колебаниям.
Первое главное колебание происходит с
частотой .
Его форма показана на рис.2.9. Второе
главное колебание совершается с частотой
.
Его форма показана на рис.2.9. Второе
главное колебание совершается с частотой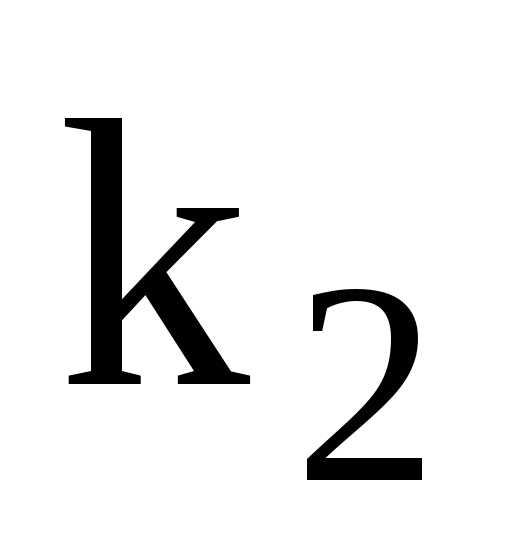 .
Его форма показана на рис.2.10.
.
Его форма показана на рис.2.10.

Рис. 2.9 Рис. 2.10
4. В предыдущем примере найти амплитуды и начальные фазы колебаний маятников при следующих начальных условиях:
а) 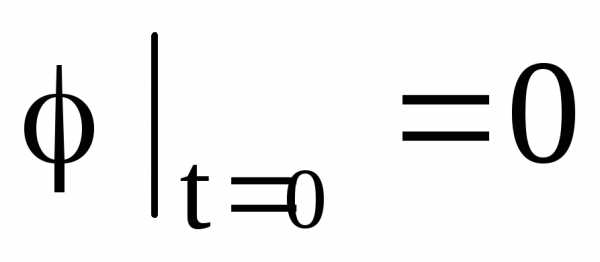 ;
;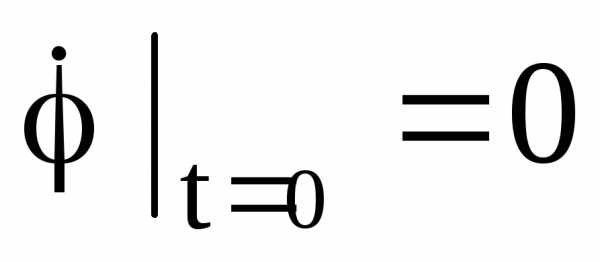 ;
;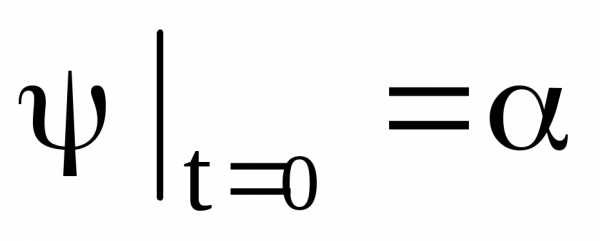 ;
; ;
;
б) 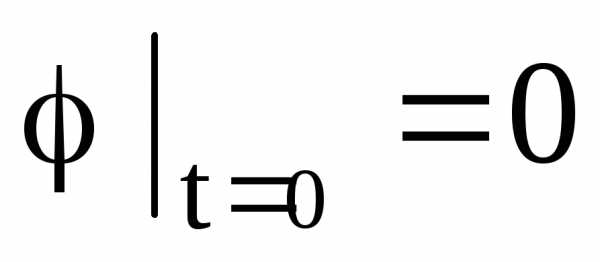 ;
;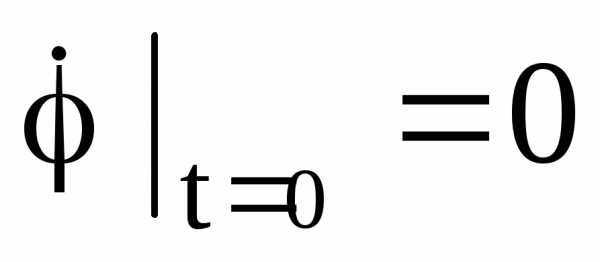 ;
; ;
; .
.
Указание: Подставьте начальные условия в (2.31) и в уравнения, полученные дифференцированием уравнении (2.31) по времени.
studfiles.net
2.2.Решение с помощью ms Excel
Для решения транспортной задачи для фирмы «Х» использовались электронные таблицы MS Excel. Порядок выполнения действий приведен ниже:
1. Создаем таблицу с условиями задачи.
2. Рядом создаем еще одну таблицу, в которую будут занесены данные, после выполнения команды «Поиск решения». Во второй таблице с помощью формулы «СУММ( …) » выполняем подсчет запасов и потребностей.
3. С помощью функции «Поиск решения» выполняем подсчет транспортных расходов с указанием некоторых ограничений. Ряд ограничений приведен в самой функции «Поиск решения» в поле «Ограничения».
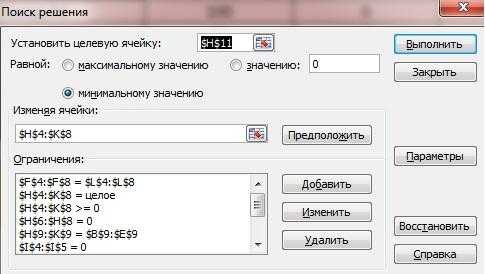
4. В функцию «Поиск решения» заносятся данные целевой ячейки (в работе ячейка имеет адрес h21), устанавливается стремление функции к минимальному значению, вводятся ограничения и нажимается кнопка «Выполнить», после чего пустая таблица заполняется данными.
5. В ячейке h21 указана формула « СУММПРОИЗВ(B4:E8; h5:K8) » которая позволяет сложить и перемножить массивы данных ячеек «В4-Е8» и «Н4-К8».15
6. В итоге при правильной последовательности всех действий был получен итог:
Минимальными транспортными затратами на перевозку продуктов в школы 1, 2, 3, 4 со складов А1, А2, А3, А4 для фирмы «Х» является 1740 у.е.
Заключение
Склады играют значительную роль в производстве. Ведь каждой организации необходимо иметь складское помещение для достижения эффективности работы организации. Кроме этого, необходимо наличие автоматизированных систем складского учета товара, чтобы увеличить производительность и минимизировать затраты.
Стоит отметить, что склад – это здания (сооружения) и разнообразные устройства, которые предназначены для приемки, размещения и хранения товаров. В складах выполняются операции по приемке, сортировке, хранению, фасовке и отпуску товаров. Существует множество классификаций складов, различных по характеристикам.
Кроме этого склад обладает большим количеством функций, которые позволяют производителям и потребителям эффективно взаимодействовать друг с другом, зачастую использование складских помещений существенно облегчает весь логистический процесс.
Безусловно, для любых складов характерно существование множества операций. Они реализуются в процессе его работы (погрузка, перемещение внутри склада, разгрузка, упаковка, отбор и комплектации груза). И, конечно же, все эти операции должны быть контролируемы, и отвечали единым стандартам и требованиям.
Одной из важнейших логистический операций является внутрискладская транспортировка. Она оказывает большое влияние на материальные средства. От того, как проводятся складские операции, зависит как сохранность груза, так и его целостность, и, конечно же, минимальные затраты на его перемещение.
Грузовая единица – это такой элемент логистики, который своими параметрами связывает технологические процессы участников логистического процесса в единое целое. Она обладает рядом особых характеристик и обеспечивает свое существование за счет операций пакетирования.
Складирование и хранение – одни из основных составляющих логистических процессов. Рациональное использование складских помещений позволяет максимизировать прибыль и минимизировать расходы, и, следовательно, оказывает огромное влияние на рентабельность работы склада.
Стоит также отметить, что использование новых технологий и программного обеспечения, автоматизирующие складской учет, позволяет предлагать заказчикам качественные логистические услуги. Складские комплексы становятся высокотехнологичны, позволяют решать задачи обеспечения экономической эффективности путем уменьшения дополнительных издержек.
Для того чтобы эффективно использовать все ресурсы и минимизировать затраты на транспортировку необходимо ссылаться на транспортную задачу. Она, позволяет оптимизировать транспортные расходы и тем самым свести к минимуму все затраты в целом.
В ходе решения транспортной задачи для фирмы «Х» найден оптимальный план перевозок и сведены к минимуму затраты на транспортировку продуктов питания в школы 1, 2, 3, 4. Результатом проделанной работы является снижение транспортных затрат на 50 у.е., что является показателем правильного решения задачи оптимизации.
Решение задачи проводилось двумя способами: вручную и с помощью Microsoft Excel. При решении задачи обоими способами выявлено, что при решении задачи с помощью электронных таблиц, решение занимает меньше времени и при этом исключает ошибки в подсчетах, а так же при изменении данных позволяет автоматически менять данные в формулах.
studfiles.net
2.2. Решение систем трех линейных уравнений с тремя неизвестными
Для системы  составляем
главный определитель
составляем
главный определитель
 и вычисляем его.
и вычисляем его.
Затем составляем дополнительные определители
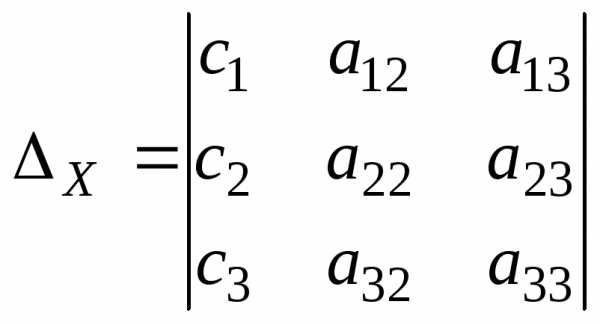


и вычисляем их.
По правилу Крамера решение системы находят по формулам
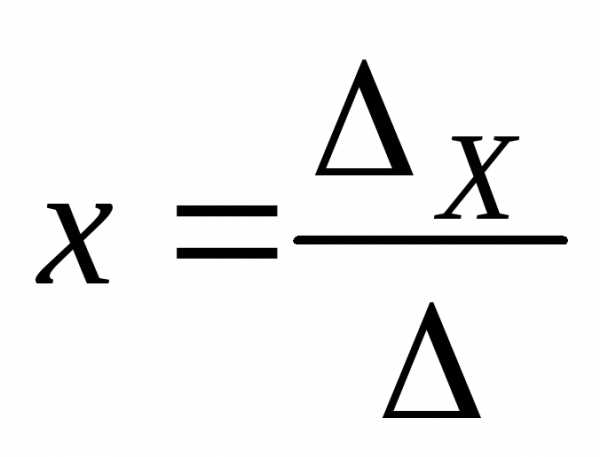 ;
; 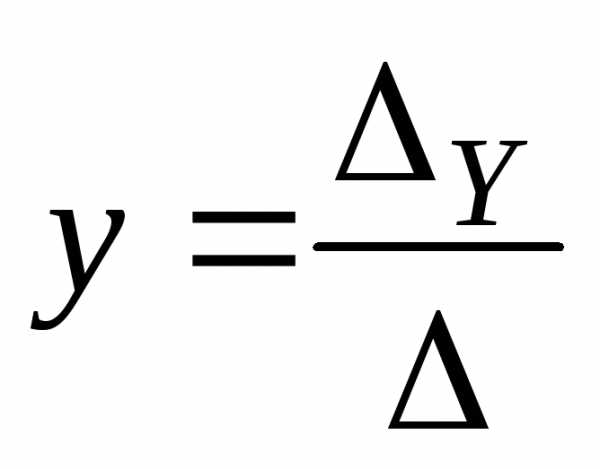 ;
; 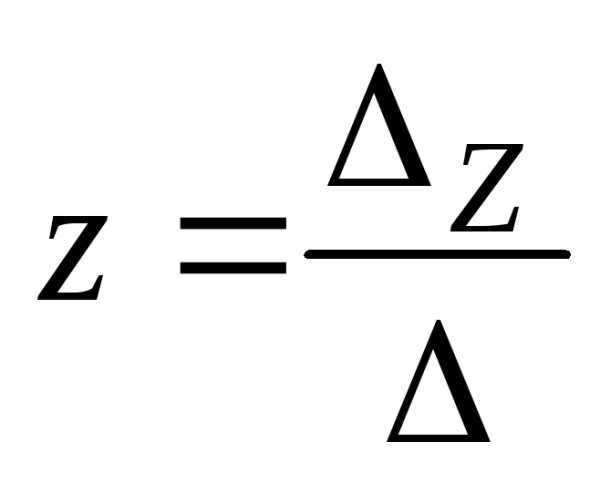 ,если
,если 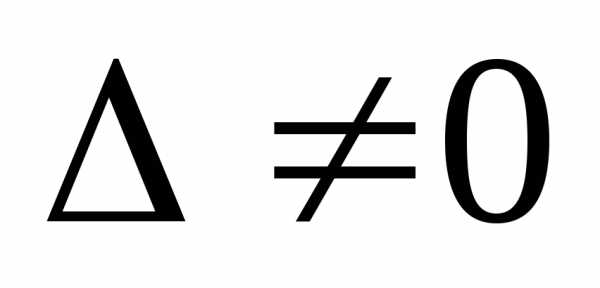
Примеры:
1) 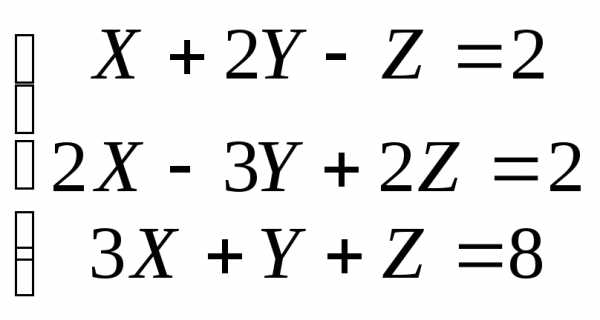
Вычислим:
По формулам Крамера находим:
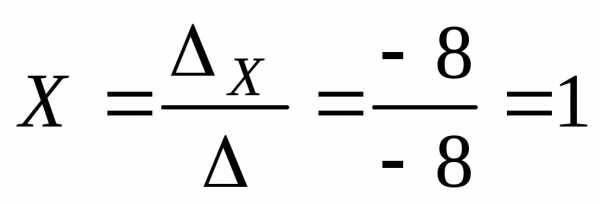
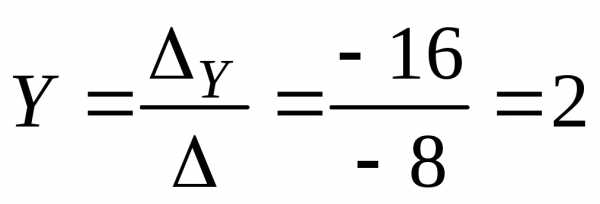
Ответ: (1; 2; 3)
2) 
Вычислим:
Так как главный
определитель  ,
а хотя бы один дополнительный не равен
нулю (в нашем случае
,
а хотя бы один дополнительный не равен
нулю (в нашем случае  ),
то решения у системы нет.
),
то решения у системы нет.
3) 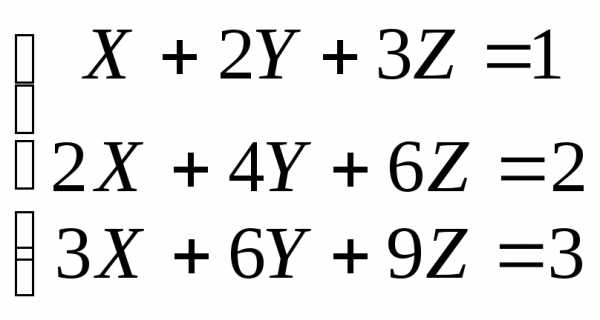
Вычислим:
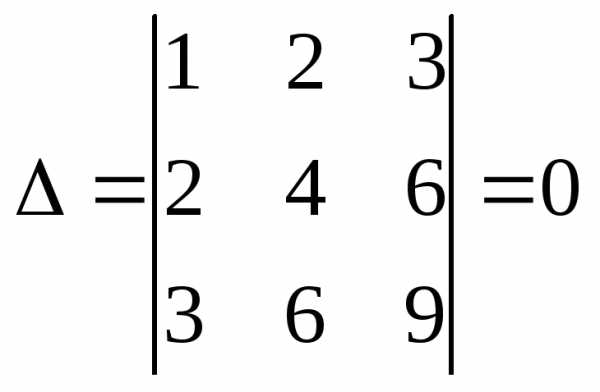
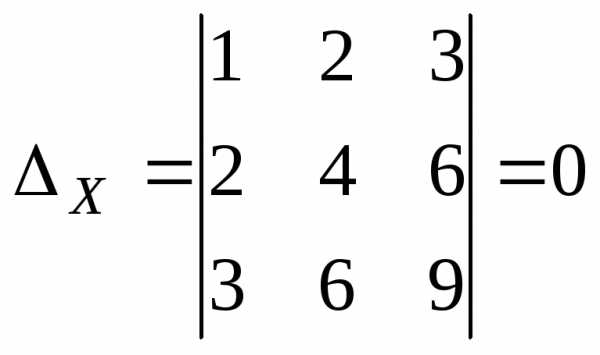
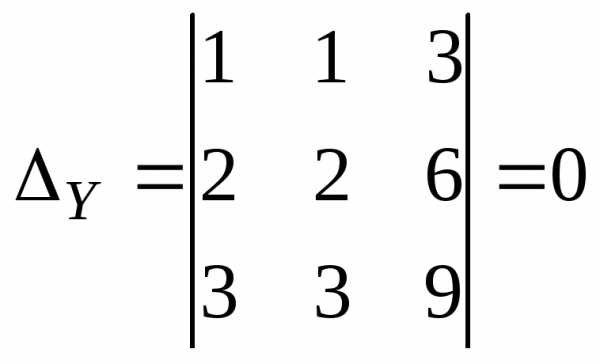
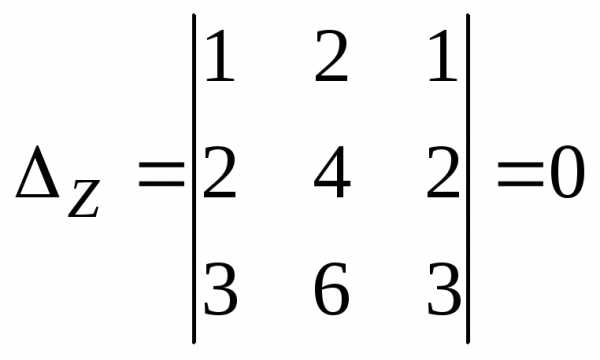
Так как все
определители равны нулю, то система
имеет бесконечное множество решений,
которое можно найти так 
Решите самостоятельно системы:
а)  б)
б) 
Ответ: а) ( 1; 2; 5 )
б) 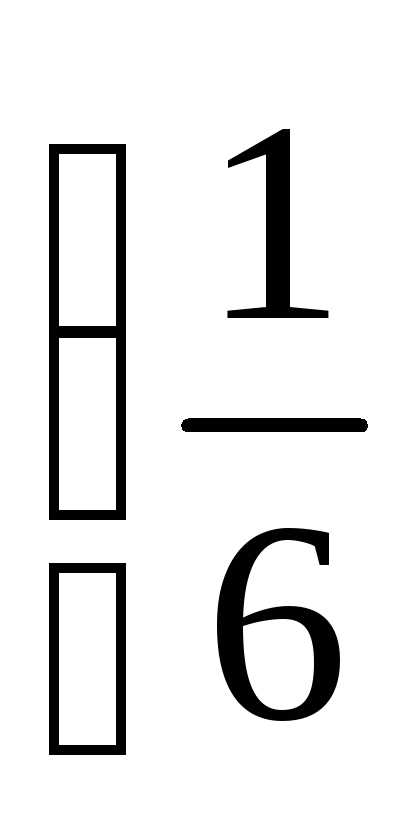 ;
; ;
;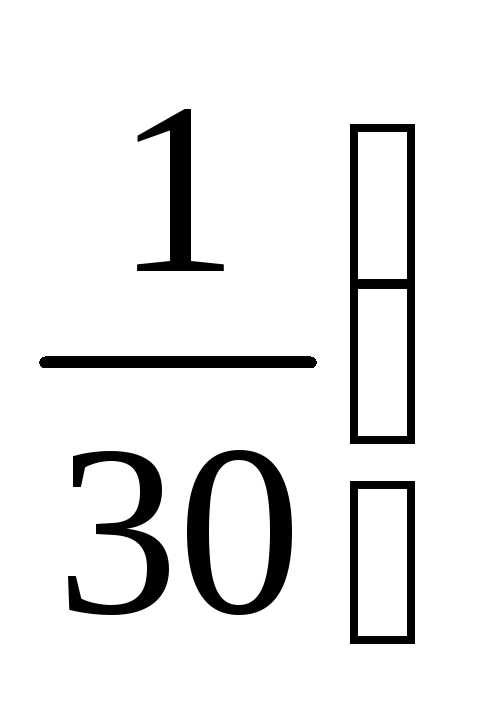
Практическое занятие № 3 на тему:
Скалярное произведение двух векторов и его приложение
1. Если дан  и
и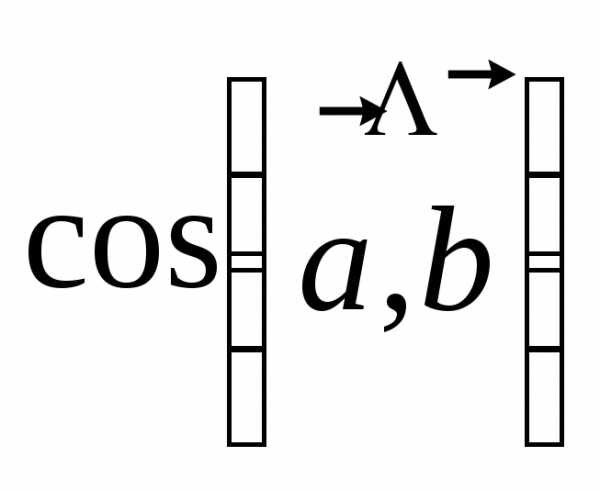 ,
то скалярное произведение находим по
формуле:
,
то скалярное произведение находим по
формуле: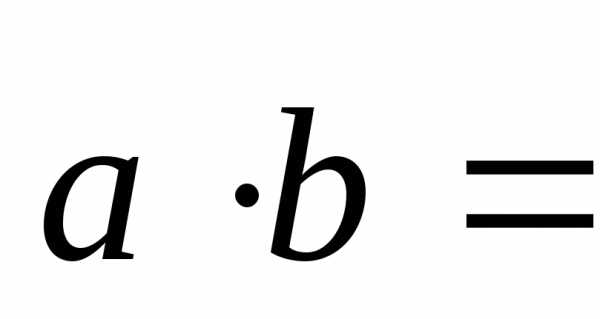
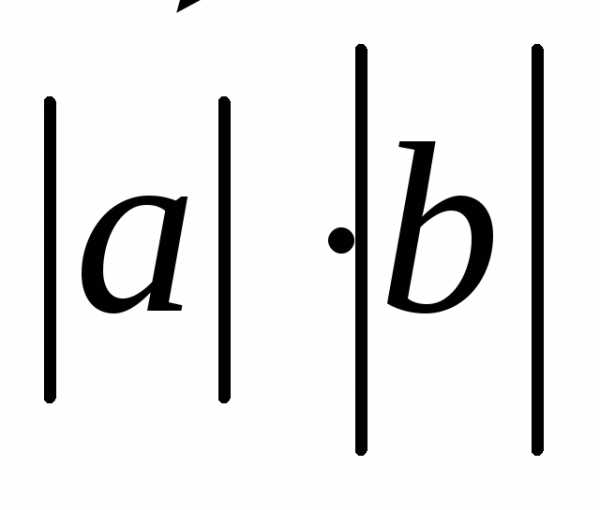 ∙
∙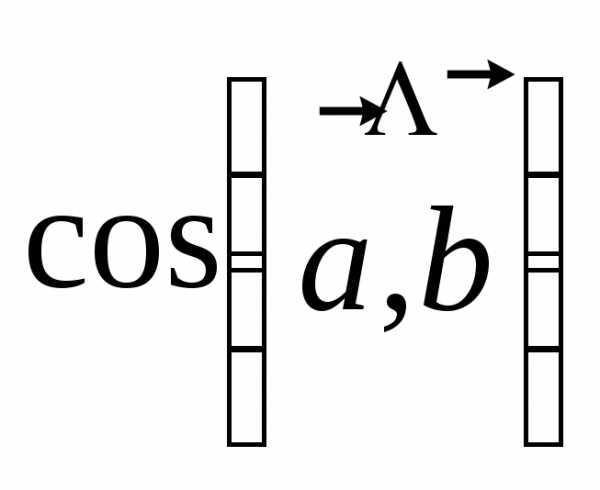
2.Если, то скалярное произведение этих двух векторов находим по формуле
Примеры:
1. Даны два вектора и
Их скалярное произведение находим так:
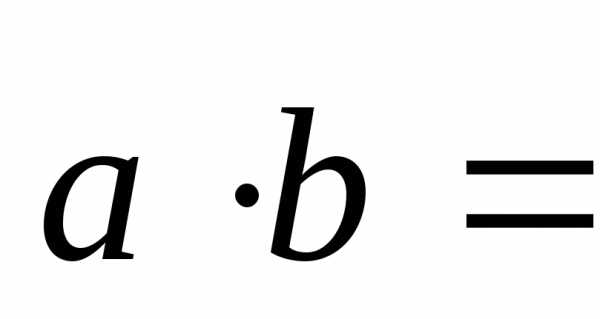 .
.
2. Даны два вектора:
={2;3;–4} ={1; –5; 6}
скалярное произведение находят так:
3., 
3.1 Нахождение работы постоянной силы на прямолинейном участке пути
Примеры:
1) Под действием силы в 15Н тело переместилось по прямой на 2 метра. Угол между силой и направлением перемещения =600. Вычислить работу силы по перемещению тела.
Дано: 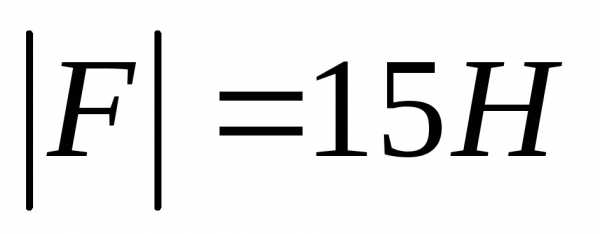
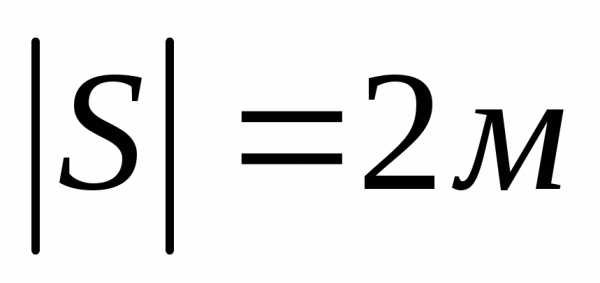
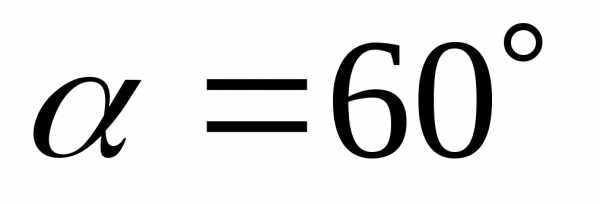
Решение:
2) Дано:
Найти А.
Решение:
3) Из точки М(1; 2; 3) в точку N(5; 4; 6) переместилось тело под действием силы 60Н. Угол между направлением силы и вектором перемещения =450. Вычислить работу, совершаемую этой силой.
Решение: находим
вектор перемещения 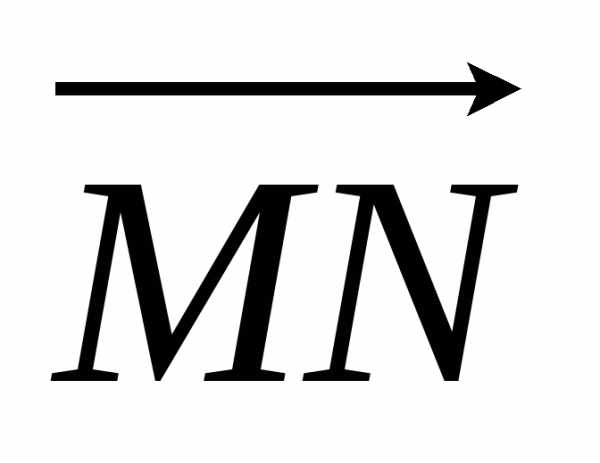
Находим модуль вектора перемещения:
По формуле находим работу:
3.2 Определение ортогональности двух векторов
.
Два вектора
ортогональны, если 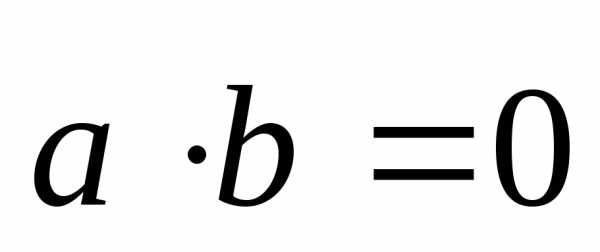 ,
то есть
,
то есть
так как 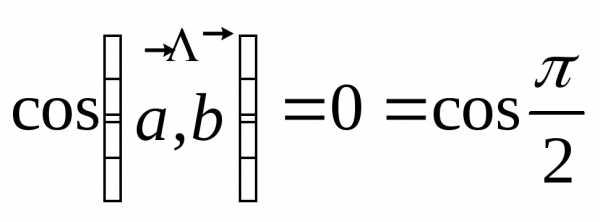
Примеры:
1)

 –не ортогональны
–не ортогональны
2)

 –ортогональны
–ортогональны
3) Определить, при каком векторы и взаимно-ортогональны.
Так как  ,
то
,
то 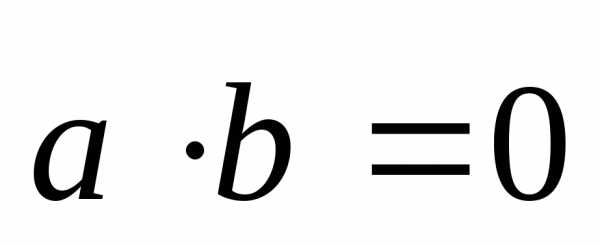 ,
значит
,
значит
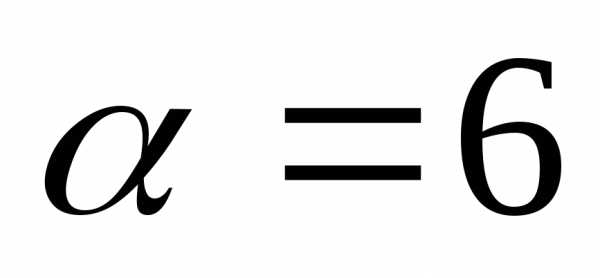
Решите самостоятельно:
а)
. Найти их скалярное произведение.
б) Вычислить, какую работу производит сила , если точка ее приложения, двигаясь прямолинейно, переместилась из точки M (5; -6; 1) в точку N (1; -2; 3)
в) Определить, ортогональны ли вектора и
Ответы: а) 1 б) 16 в) да
3.3.Нахождение угла между векторами
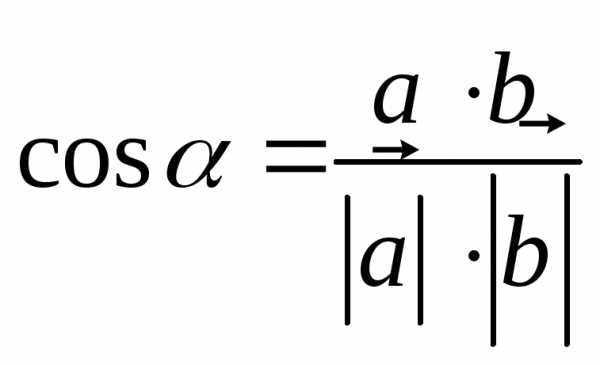
Примеры:
1)
.
Найти  .
.
Решение:
Находим
подставляем в формулу:
.
1). Даны вершины треугольника А(3; 2; –3), В(5; 1; –1), С(1; –2; 1). Найти угол при вершине А.
Решение:
Находим
Подставим в формулу:
Решите самостоятельно:
Даны вершины треугольника А(3; 5; -2), В(5; 7; -1), С(4; 3; 0). Определить внутренний угол при вершине А.
Ответ: 90о
Практическое занятие № 4 на тему:
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ДВУХ ВЕКТОРОВ И ЕГО ПРИЛОЖЕНИЕ.
Формула для нахождения векторного произведения двух векторов:
Примеры:
1) Найти модуль векторного произведения:
Решение:
Составим определитель и вычислим его (по правилу Саррюса или по теореме о разложении определителя по элементам первой строки).
1-ый способ: по правилу Саррюса
2-й способ: разложим определитель по элементам первой строки.
2) Найти модуль векторного произведения:
4.1. ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПАРАЛЛЕЛОГРАММА, ПОСТРОЕННОГО НА ДВУХ ВЕКТОРАХ.
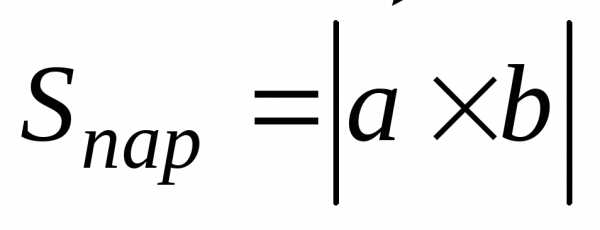
Примеры:
1) Вычислить площадь параллелограмма, построенного на векторах
Решение.
2). Найти векторное произведение и его модуль
Ответ:
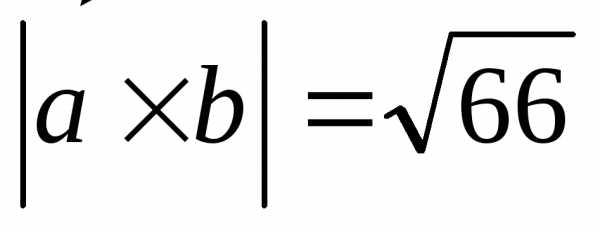
4.2. ВЫЧИСЛЕНИЕ ПЛОЩАДИ ТРЕУГОЛЬНИКА
Пример: даны вершины треугольника А(1; 0; -1), В(1; 2; 0), С(3; -1; 1). Вычислить площадь треугольника.
Решение:
Сначала найдем координаты двух векторов, выходящих из одной вершины.
Найдем их векторное произведение
найдем
4.3. ОПРЕДЕЛЕНИЕ КОЛЛИНЕАРНОСТИ ДВУХ ВЕКТОРОВ
Если вектора
и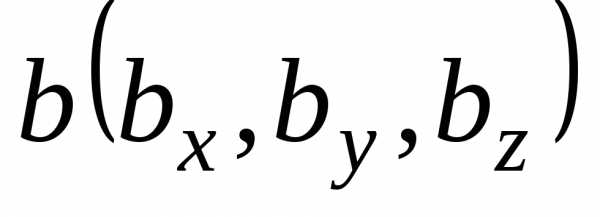 коллинеарны, то
коллинеарны, то
 , т. е. координаты
векторов должны быть пропорциональны.
, т. е. координаты
векторов должны быть пропорциональны.
Примеры:
а) Даны вектора:: , .
Они коллинеарны
потому, что  и
и
после сокращения
каждой дроби получается соотношение 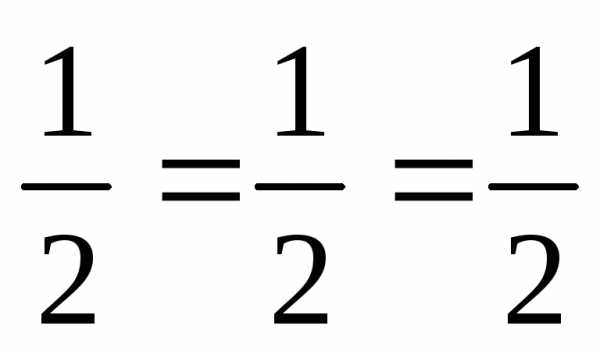
б) Даны вектора: .
Они не коллинеарны,
потому, что 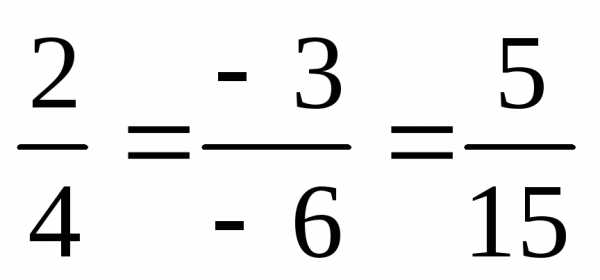 или
или 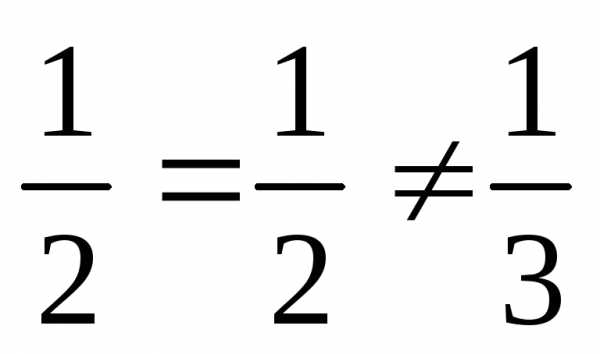
Решите самостоятельно:
а) При каких значениях m и n вектора коллинеарны?
Ответ: 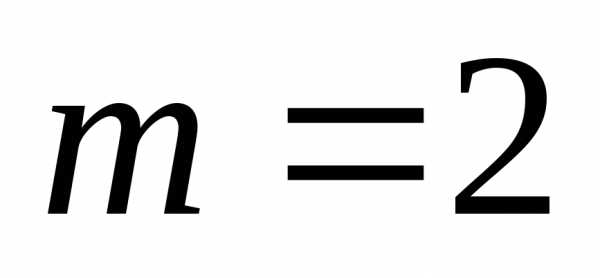 ;
; 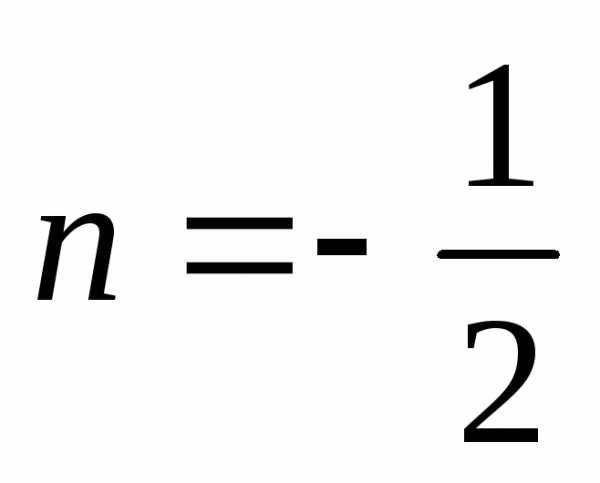
б) Найти векторное произведение и его модуль , .
Ответ:
,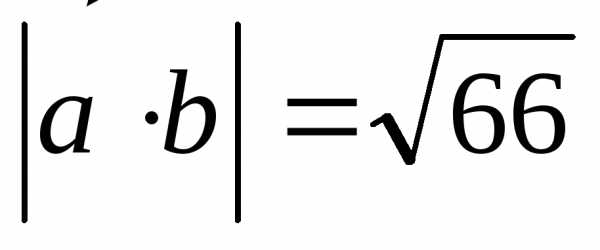 .
.
Практическое занятие № 5 на тему:
ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ
Примеры:
Задача № 1. Найти уравнение прямой, проходящей через точку А(-2; 3) параллельно прямой
Решение:
1. Найдем угловой коэффициент прямой .
— это уравнение
прямой с угловым коэффициентом и
начальной ординатой ().
Поэтому 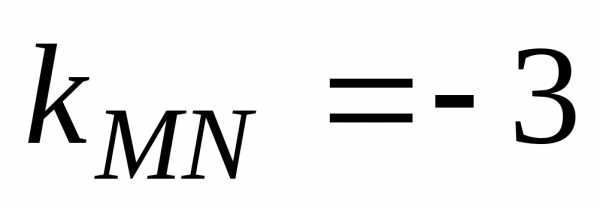 .
.
2. Так как прямые MN и АС параллельны, то их угловые коэффициенты равны, т.е. .
3. Для нахождения уравнения прямой АС воспользуемся уравнением прямой, проходящей через точку с данным угловым коэффициентом:
.
В эту формулу вместо 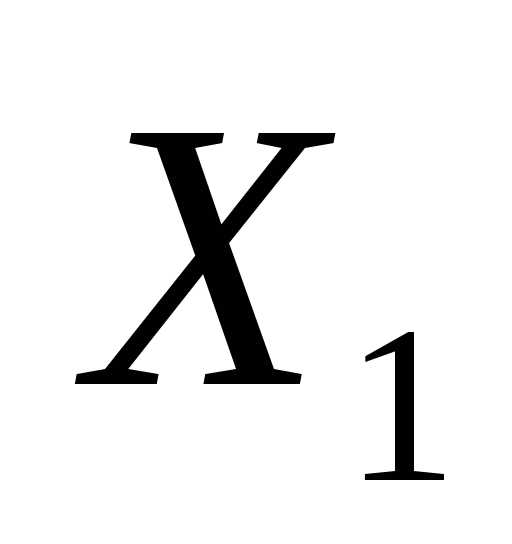 и
и  подставим координаты точки А(-2; 3), вместо
подставим координаты точки А(-2; 3), вместо 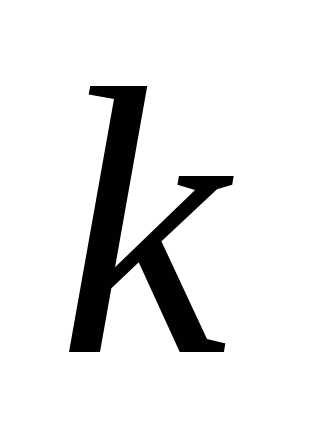 подставим
– 3. В результате подстановки получим:
подставим
– 3. В результате подстановки получим:
Ответ:
Задача №2. Найти уравнение прямой, проходящей через точку К(1; –2) параллельно прямой .
Решение:
1. Найдем угловой коэффициент прямой .
—
это общее уравнение прямой, которое в
общем виде задается формулой
.
Сравнивая уравнения и находим, что А
= 2, В = –3. Угловой
коэффициент прямой, заданной уравнением ,
находится по формуле  .
Подставив в эту формулу А = 2 и В = –3,
получим угловой коэффициент прямой MN.
Итак,
.
Подставив в эту формулу А = 2 и В = –3,
получим угловой коэффициент прямой MN.
Итак, 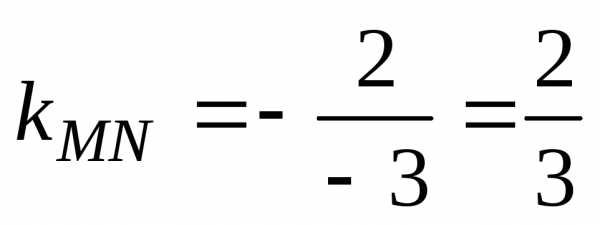 .
.
2. Так как прямые
MN
и КС параллельны, то их угловые коэффициенты
равны:  .
.
3. Для нахождения
уравнения прямой КС воспользуемся
формулой уравнения прямой, проходящей
через точку с данным угловым коэффициентом .
В эту формулу вместо 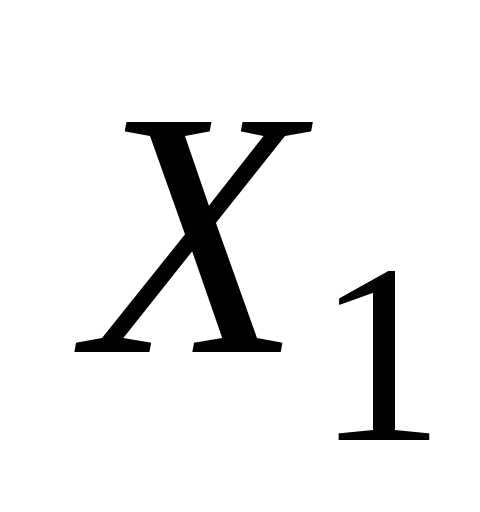 и
и  подставим координаты точки К(–2; 3),
вместо
подставим координаты точки К(–2; 3),
вместо  подставим
подставим 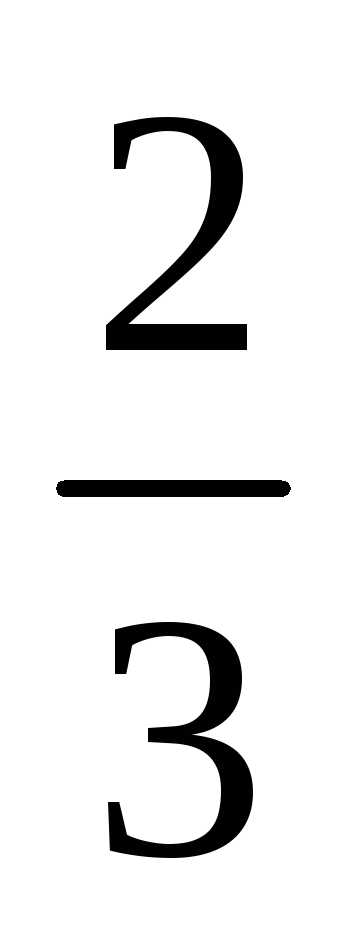 .
В результате подстановки получим:
.
В результате подстановки получим:
Ответ:
Задача № 3. Найти уравнение прямой, проходящей через точку К(–1; –3) перпендикулярно прямой .
Решение:
1. – это общее уравнение прямой, которое в общем виде задается формулой .
и находим, что А = 3, В = 4.
Угловой коэффициент
прямой, заданной уравнением
,
находится по формуле: 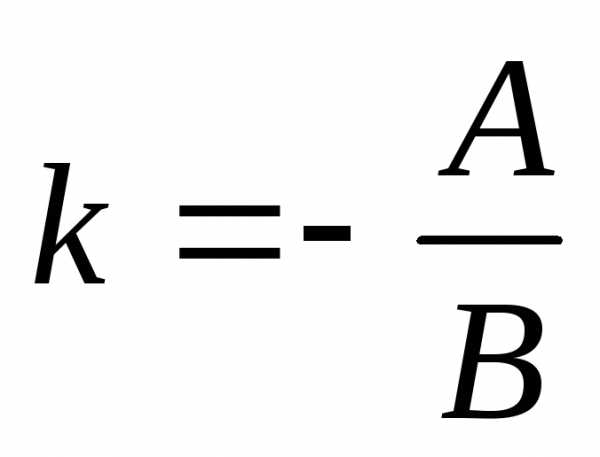 .
Подставив в эту формулу А
= 3 и В = 4, получим
угловой коэффициент прямой MN:
.
Подставив в эту формулу А
= 3 и В = 4, получим
угловой коэффициент прямой MN: 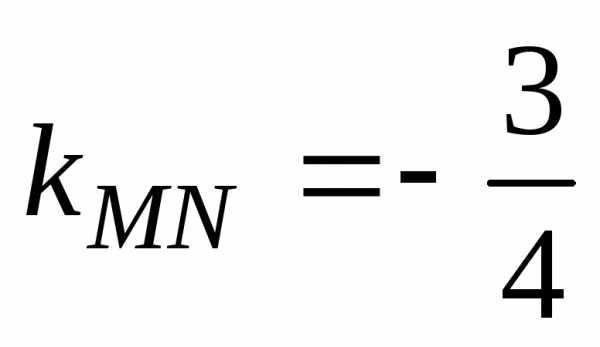 .
.
2. Так как прямые MN и КD перпендикулярны, то их угловые коэффициенты обратно пропорциональны и противоположны по знаку:
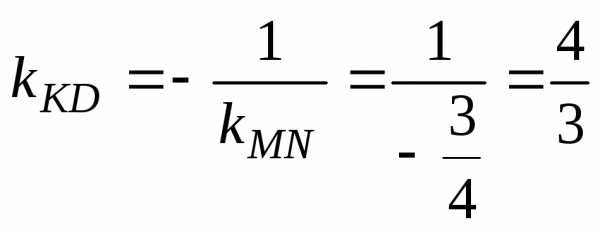 .
.
3. Для нахождения уравнения прямой КD воспользуемся формулой уравнения прямой, проходящей через точку с данным угловым коэффициентом
.
В эту формулу вместо 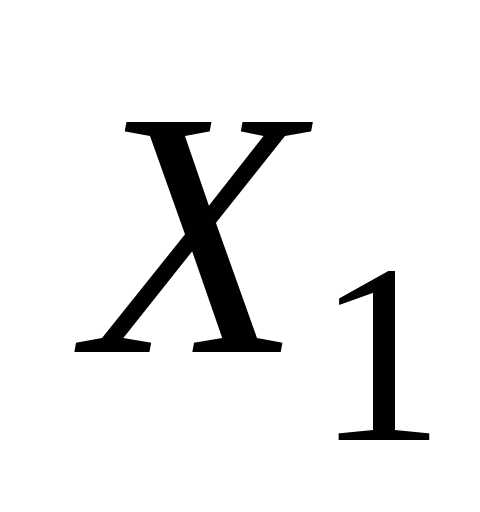 и
и  подставим координаты точки К(–1;
–3), вместо
подставим координаты точки К(–1;
–3), вместо 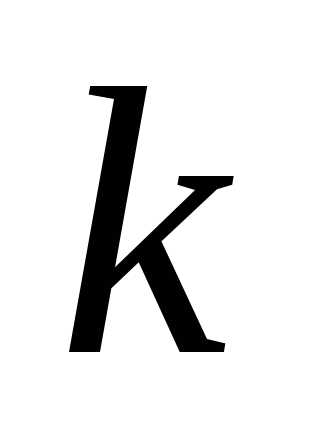 подставим
подставим  .
В результате подстановки получим:
.
В результате подстановки получим:
Ответ:
Решите самостоятельно:
1. Найти уравнение прямой, проходящей через точку К(–4; 1) параллельно прямой .
Ответ: .
2. Найти уравнение прямой, проходящей через точку К(5; –2) параллельно прямой .
Ответ: .
3. Найти уравнение прямой, проходящей через точку К(–2; –6) перпендикулярно прямой .
Ответ: .
4. Найти уравнение прямой, проходящей через точку К(7; –2) перпендикулярно прямой .
Ответ: .
5. Найти уравнение перпендикуляра, опущенного из точки К(–6; 7) на прямую .
Ответ: .
Практическое занятие № 6 на тему:
studfiles.net

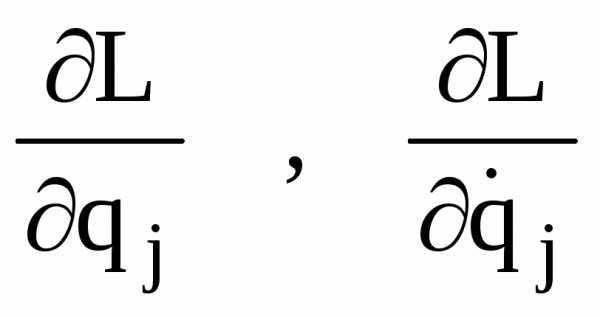 .
6. Подставить выражения производных
.
6. Подставить выражения производных в
(1.2)
в
(1.2)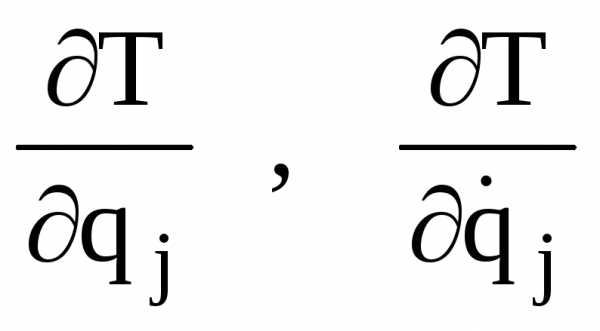
 ,
, в
(1.1).
в
(1.1).