решение задач с помощью алгебры логики.
Одним из мощных методов решения логических задач является решение с помощью законов алгебры логики.
Алгоритм решения логических задач с помощью алгебры логики: 1) внимательно изучить условие; 2) выделить простые высказывания и обозначить их латинскими буквами; 3) записать условие задачи на языке алгебры логики; 4) составить конечную формулу, для этого объединить логическим умножением формулы каждого утверждения, приравнять произведение единице; 5) упростить формулу, проанализировать полученный результат или составить таблицу истинности, найти по таблице значения переменных, для которых F = 1, проанализировать результаты.

Задача1 » Кто преступник»
Определить участника преступления, исходя из двух
посылок:
1) «Если Иванов не участвовал или Петров участвовал,
то Сидоров участвовал»;
2) «Если Иванов не участвовал, то Сидоров не
участвовал».
Рассмотрим решение этой несложной задачи двумя способами: с помощью таблиц истинности и с помощью алгебраических преобразований.
1 способ
Составим выражения:
I — «Иванов участвовал в преступлении»;
P — «Петров участвовал в преступлении»;
S — «Сидоров участвовал в преступлении»
.
Запишем посылки в виде формул:
¬I˅P→S и ¬I→¬S
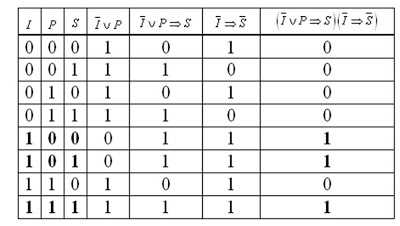
Из таблицы видно, что совершил преступление Иванов
Способ 2
Применим для решения этой же задачи преобразования с
помощью законов алгебры логики:
( ¬I˅P→S) &( ¬I→¬S)=(¬(¬I˅P)˅S) & (I˅¬S) =
= (I & ¬P ˅S) &(I ˅¬S) = I&¬P˅ I & S˅ I &¬P &¬S ˅0=
= I&¬P ˅ I & S =I & (¬P˅S)
Из последнего выражения видно, что выражение верно, если I=1, значит преступник — Иванов.
Задача 2 «Прогноз погоды»
Решим эту задачу средствами алгебры логики.
1. Выделим простые высказывания и запишем их через переменные
A – «Ветра нет»
B – «Пасмурно»
С – «Дождь» 2. Запишем логические функции (сложные высказывания) через введенные переменные:
Если не будет ветра, то будет пасмурная погода без дождя:
A → B & C
Если будет дождь, то будет пасмурно и без ветра:
С → B & A
Если будет пасмурная погода, то будет дождь и не будет ветра
B → C &
в) Запишем произведение указанных функций:
F=(A→ B & C) & (C→B & A) & (B→ C & A)
Упростим формулу (используются законы де Моргана, переместительный закон, закон противоречия):
= (¬A v B & ¬C) & (¬C v B&A) & (¬B v C&A) =
= (¬A v B & ¬C) & (¬B v C&A) & (¬C v B&A) =
= (¬A &¬ B v B&¬C&¬B v ¬A&C&A v B&¬C&C&A) &
= ¬A & ¬B &(C v B&¬A) =A&¬B&C v¬ A&¬B&B&¬A = 3. Приравняем результат единице, т.е. наше выражение должно быть истинным:F = ¬A &¬ B & ¬C = 1 и проанализируем результат: Логическое произведение равно 1, если каждый множитель равен 1. ¬A = 1; ¬B = 1; ¬C = 1.значит: A = 0; B = 0; C = 0;
Ответ: погода будет ясная, без дождя, но ветреная.
Задача 3 «История с амфорой».
Алеша, Боря и Гриша нашли в земле сосуд.
Рассматривая удивительную находку, каждый высказал по два предположения.
Введем следующие обозначения:
«Это сосуд греческий» — G;«Это сосуд финикийский» — F;
«Сосуд изготовлен в III веке» — V3;
«Сосуд изготовлен в IV веке» — V4;
«Сосуд изготовлен в V веке» — V5. Формализуем задачу, записав в данных обозначениях условия задачи. Со слов учителя следует, что Алеша прав только в чем-то одном: или G = 1, или V5 = 1. Таким образом, тождественно истинным будет высказывание: G¬V5 v ¬GV5.=1 Аналогично, из слов Бори и учителя следует: F¬V3 v ¬FV3 = 1, а из слов Гриши и учителя: ¬G¬V4 v GV 4 = 1. Кроме того, ясно, что сосуд может быть изготовлен только в одном из веков и только в одной из стран. Эти условия можно записать так: V3¬V4¬V5 ˅ ¬V3V4¬V5 ˅ ¬V3¬V4V5 = 1, Итак, мы получили пять тождественно истинных высказываний. Их нужно логически перемножить. Результат должен быть также тождественно истинным высказыванием: 1 = (G¬V5 v ¬GV5) & (F¬V3 v ¬FV3) & (¬G¬V4 v GV4) & (F¬G v ¬FG) & (V3¬V4¬V5 ˅ ¬V3V
Задача 4 «Поход в кино».
Андрей, Аня и Маша решили пойти в кино. Каждый из них высказал свои пожелания по поводу выбора фильма. Андрей сказал: «Я хочу посмотреть французский боевик». Маша сказала: «Я не хочу смотреть французскую комедию».
в) «Нефранцузская комедия» ¬¬A&C˅¬A&¬C
3. Запишем произведение :(¬A&B˅A&¬B) & (¬¬A&¬B˅¬ А&¬¬В)&( ¬¬A&C˅¬A&¬C)=1. Упростим формулу: (¬A&B˅A&¬B) & (¬¬A&¬B˅¬ А&¬¬В)&( ¬¬A&C˅¬A&¬C)= (¬A&B˅A&¬B) & (A&¬B˅¬ А&В)&( A&C˅¬A&¬C)= =(¬A&B& A&¬B˅ A&¬B& A&¬B˅¬A&B &¬А&В˅ A&¬B&¬A&B)&( A&C˅¬A&¬C)= =(A&¬B ˅¬A&B)&( A&C˅¬A&¬C)= A&¬B& A&C˅¬A&B& A&C˅ A&¬B&¬A&¬C˅¬A&B&¬A&¬C= = ¬A&B&¬C˅ A&¬B&C =1 6. Составим таблицу истинности для выражения:
¬A&B&¬C˅ A&¬B&C:
Ответ: ребята выбрали американский боевик.
А
inf61.blogspot.com
Применение инструмента алгебры логики при решении логических задач
История с амфорой
Антон, Борис и Григорий нашли в земле сосуд, о котором каждый высказал по два предположения:
Антон: «Сосуд греческий и изготовлен в V столетии»;
Борис: «Сосуд финикийский и изготовлен в III столетии»;
Григорий: «Сосуд не греческий и изготовлен в IV столетии».
Специалист сказал ученикам, что каждый из них не ошибся только в одном из двух предположений. Определить место и столетие изготовления сосуда.
Решение:
Введем следующие обозначения:
$G$ — «Сосуд греческий»;
$F$ — «Сосуд финикийский»;
$S_3$ — «Сосуд изготовлен в $III$ столетии»;
$S_4$ — «Сосуд изготовлен в $IV$ столетии»;
$S_5$ — «Сосуд изготовлен в $V$ столетии».
Запишем условие задачи с помощью обозначений:
Антон прав только в одном предположении: $G = 1$ или $S_5 = 1$. Тогда $G\overline{S_5}\vee \overline{G}S_5=1$.
Аналогично для слов Бориса: $F\overline{S_3}\vee \overline{F}S_3=1$.
Для слов Григория: $\overline{G}\overline{S_4}\vee GS_4=1$.
Т.к. сосуд может быть изготовлен только в одном из столетий и только в одной из стран, запишем условия:
\[S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5=1,\] \[F\overline{G}\vee \overline{F}G=1.\]Применим операцию логического умножения к полученным тождественно истинным высказываниям, результат которого также должен быть тождественно истинным:
\[\left(G\overline{S_5}\vee \overline{G}S_5\right)\wedge \left(F\overline{S_3}\vee \overline{F}S_3\right)\wedge \left(\overline{G}\overline{S_4}\vee GS_4\right)\wedge \left(F\overline{G}\vee \overline{F}G\right)\wedge \] \[\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\]Перемножим первую на третью скобку и вторую на четвертую:
\[=\left(G\overline{S_5}\overline{G}\overline{S_4}\vee \overline{G}S_5\overline{G}\overline{S_4}\vee G\overline{S_5}GS_4\vee \overline{G}S_5GS_4\right)\wedge \] \[\wedge \left(F\overline{S_3}F\overline{G}\vee \overline{F}S_3F\overline{G}\vee F\overline{S_3}\overline{F}G\vee \overline{F}S_3\overline{F}G\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\]Т.к. $G\overline{G}=0$, $GG=G$, $\overline{G}\overline{G}=\overline{G}$, упростим выражения:
\[=\left(\overline{G}S_5\overline{S_4}\vee G\overline{S_5}S_4\right)\wedge \left(F\overline{S_3}\overline{G}\vee \overline{F}S_3G\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\]Перемножим первые две скобки и упростим выражение:
\[=\left(\overline{G}S_5\overline{S_4}\overline{F}S_3G\vee G\overline{S_5}S_4\overline{F}S_3G\vee \overline{G}S_5\overline{S_4}F\overline{S_3}\overline{G}\vee G\overline{S_5}S_4F\overline{S_3}\overline{G}\right)\wedge \] \[\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\] \[=\left(G\overline{S_5}S_4\overline{F}S_3\vee \overline{G}S_5\overline{S_4}F\overline{S_3}\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\] \[=\left(G\overline{S_5}S_4\overline{F}S_3\vee \overline{G}S_5\overline{S_4}F\overline{S_3}\right)\wedge \left(S_3\overline{S_4}\overline{S_5}\vee \overline{S_3}S_4\overline{S_5}\vee \overline{S_3}\overline{S_4}S_5\right)=\overline{G}S_5\overline{S_4}F\overline{S_3};\]$\overline{G}S_5\overline{S_4}F\overline{S_3}=1$, что возможно только в случае:
\[\overline{G}=1, S_5=1, \overline{S_4}=1, F=1, \overline{S_3}=1.\]Ответ: сосуд финикийский и изготовлен в $V$ столетии.
spravochnick.ru
Решение логических задач средствами алгебры логики
Обычно используется следующая схема решения:- изучается условие задачи;
- вводится система обозначений для логических высказываний;
- конструируется логическая формула, описывающая логические связи между всеми высказываниями условия задачи;
- определяются значения истинности этой логической формулы;
- из полученных значений истинности формулы определяются значения истинности введённых логических высказываний, на основании которых делается заключение о решении.
Три свидетеля дорожного происшествия сообщили сведения о скрывшемся нарушителе. Боб утверждает, что тот был на красном «Рено», Джон сказал, что нарушитель уехал на синей «Тойоте», а Сэм показал, что машина была точно не красная, и по всей видимости, это был «Форд».
Когда удалось отыскать машину, выяснилось, что каждый из свидетелей точно определил только один из параметров автомобиля. А в другом ошибся, какая и какого цвета была машина у нарушителя?
Ответ записать в виде двух слов, разделенных пробелом: МАРКА, ЦВЕТ.
Решение.
Обозначим высказывания:
A = «машина красного цвета»;Согласно условию:
B = «машина была «Рено»;
C = «машина синего цвета»;
D = «машина была «Тойота»;
E = «машина была «Форд».
из показаний Боба следует, что A \/ B истинно;Следовательно, истинна конъюнкция (A \/ B) /\ (C \/ D) /\ (¬A \/ E) = 1
из показаний Джона следует, что C \/ D истинно;
из показаний Сэма следует, что ¬A \/ E истинно.
Раскрывая скобки, получаем:
(A \/ B) /\ (C \/ D) /\ (¬A \/ E) = (A /\ C \/ A /\ D \/ B /\ C \/ B /\ D) /\ ( ¬A \/ E) =
A /\ C /\ ¬A \/ A /\ D /\ ¬A \/ B /\ C /\ ¬A \/ B /\ D /\ ¬A \/ A /\ C /\ E \/ A /\ D /\ E \/ B /\ C /\ E \/ B /\ D /\ E = 1.
Из полученных восьми слагаемых семь (согласно условию) являются ложными. Остается единственное истинное слагаемое:
B /\ C /\ ¬A = 1.
Значит, нарушитель скрылся на автомобиле «Рено» синего цвета.
Ответ: РЕНО, СИНИЙ.
Пример.
Трое друзей, болельщиков автогонок
«Формула-1», спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об
Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих
друзей подтвердилось, а оба предположения третьего из друзей оказались неверны.
Кто выиграл этап гонки?
Решение.
Введем обозначения для логических высказываний:Ш — победит Шумахер;
Х — победит Хилл;
А — победит Алези.
Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
Учитывая то, что предположения двух друзей подтвердились, а предположения третьего неверны, запишем и упростим истинное высказывание
Высказывание истинно только при Ш=1, А=0, Х=0.
Ответ.
Победителем этапа гонок стал Шумахер.
Задача для самопроверки:
На перемене в кабинете биологии 8 ребят баловались и разбили дорогой микроскоп. Их всех вызвали к директору и выслушали:
Ира: Это Антон разбил.
Наташа: Нет, Антон не бил!
Сергей: А я тоже знаю, что это Наташа разбила!
Антон: Нет, ни Наташа, ни Сергей этого не делали!
Оля: А я видела, что разбил Сергей!
Максим: Это кто-то чужой!
Костя: Это либо Наташа, либо Сергей – больше некому!
Кто разбил микроскоп, если известно, что из этих восьми высказываний истинны только два?
Ответ записать в виде первой буквы имени.
logikinformatik.blogspot.com
Презентация и конспект урока на тему «Решение задач по информатике с использованием элементов алгебры логики»
План- конспект урока
на тему: решение задач по информатике с использованием элементов алгебры логики
Цели урока:
Формирование умения применять полученные знания на практике;
Развитие умения построения таблиц истинности по заданным формулам;
Развитие умения решать текстовые задачи с использованием законов логики.
Задачи урока:
Воспитательная – развитие познавательного интереса, логического мышления.
Образовательная – повторение основ математической логики, выполнение практических заданий.
Развивающая – развитие логического мышления, внимательности.
Ход урока
Организационный момент (2 мин)
Актуализация знаний. Повторение логических операций и законов. (5 мин)
Решение задач. Применение логических операций и законов на практике + задача модуль ЭОР(15 мин)
Практическая работа (модуль 31 ЭОР «Решение логических задач») (12 мин)
Физкультминутка (2 мин)
Работа с тренажером Логика (5 мин)
Итоги урока (2 мин)
Домашнее задание (1 мин)
Выставление оценок (1 мин)
Организационный момент
Сегодня мы с вами завершаем тему “Основы логики” и применим основные логические операции, законы преобразования для решения задач по информатике.
Урок идет параллельно с презентацией. <Приложение1>
Актуализация знаний. Повторение логических операций и законов.
Алгебра логики – раздел математической логики, изучающий строение сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Вопросы:
1. Основоположник формальной логики? (Аристотель.)
2. Основоположник алгебры логики? (Джордж Буль. (сообщение))
3. Перечислите логические операции:
¬ отрицание (инверсия)
&, /\ конъюнкция (“И”)
V дизъюнкция (“ИЛИ”)
логическое следование (импликация)
4. В чем смысл закона двойного отрицания?
Двойное отрицание исключает отрицание.
5. Законы де Моргана (законы общей инверсии).
Отрицание дизъюнкции является конъюнкцией отрицаний:
¬(A V B) = ¬A /\ ¬B
Отрицание конъюнкции является дизъюнкцией отрицаний:
¬(A /\B) = ¬A V ¬B
6. Как выразить импликацию через дизъюнкцию?
А В = ¬A V В
Решение задач. Применение логических операций и законов на практике
Пример 1.
Для какого имени истинно высказывание:
¬ (Первая буква имени гласная -> Четвертая буква имени согласная)?
1) ЕЛЕНА
2) ВАДИМ
3) АНТОН
4) ФЕДОР
Решение. Сложное высказывание состоит из двух простых высказываний:
А – первая буква имени гласная,
В – четвертая буква имени согласная.
¬ (А В) = ¬ (¬A V В) = (¬ (¬А) /\ ¬B) = A /\ ¬B
Применяемые формулы:
1. Импликация через дизъюнкцию А В = ¬A V В
2. Закон де Моргана ¬(A V B) = ¬A /\ ¬B
3. Закон двойного отрицания.
(Первая буква имени гласная /\ Четвертая буква имени гласная)
Ответ: 3
Пример 2.
Какое логическое выражение равносильно выражению ¬ (А \/ ¬B)?
1) A \/ B
2) A /\ B
3) ¬A \/ ¬B
4) ¬A /\ B
Решение. ¬ (А \/ ¬B)= ¬ А /\ ¬ (¬B)= ¬ А /\ B
Ответ: 4
Пример 3.
Составить таблицу истинности для формулы
¬ (B /\ C) V (A/\C B)
Порядок выполнения логических операций:
¬ (B /\ C) V (A/\C B)
2 1 5 3 4
Составить таблицу истинности.
Сколько строк будет в вашей таблице? 3 переменных: А, В, С; 23=8
Сколько столбцов? 5 операций + 3 переменных = 8
Решение:
A
B
C
(B /\ C)
¬ (B /\ C)
A/\C
(A/\C B)
¬ (B /\ C) V (A/\C B)
0
0
0
0
1
0
1
1
0
0
1
0
1
0
1
1
0
1
0
0
1
0
1
1
0
1
1
1
0
0
1
1
1
0
0
0
1
0
0
1
1
0
1
0
1
1
1
1
1
1
0
0
1
0
0
1
1
1
1
1
0
1
1
1
Какие ответы получились в последнем столбце?
Ответ: 1
Логическое выражение называется тождественно-истинным, если оно принимает значения 1 на всех наборах входящих в него простых высказываний. Тождественно-истинные формулы называют тавтологиями.
Пример 4.
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдёт поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” в запросе используется символ I, а для логической операции “И” – символ &.
А
Законы & Физика
Б
Законы I (Физика & Биология)
В
Законы & Физика & Биология & Химия
Г
Законы I Физика I Биология
Решение:
Первый способ основан на рассуждении. Рассуждая логически, мы видим, что больше всего будет найдено страниц по запросу Г, так как при его исполнении будут найдены и страницы со словом “законы”, и страницы, со словом “физика”, и страницы со словом “биология”. Меньше всего будет найдено страниц по запросу В, так как в нем присутствие всех четырех слов на искомой странице. Осталось сравнить запросы А и Б. По запросу Б будут найдены все страницы, соответствующие запросу А, (так как в последних обязательно присутствует слово “законы”), а также страницы, содержащие одновременно слова “физика” и “биология”. Следовательно по запросу Б будет найдено больше страниц, чем по запросу А. Итак, упорядочив запросы по возрастанию страниц, получаем ВАБГ.
Ответ: ВАБГ.
Второй способ предполагает использование графического представления операций над множествами. (Смотри презентацию)
Пример 5.
Практическая работа (модуль 31 ЭОР «Решение логических задач»)
Загрузить модуль ЭОР- задание 31
Физкультминутка
Работа с тренажером Логика
Итоги урока
Для чего мы изучаем логику?
Домашнее задание (задачи)
Задание 1.
В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции “ИЛИ” в запросе используется символ |, а для логической операции “И” – &.
А
волейбол | баскетбол | подача
Б
волейбол | баскетбол | подача | блок
В
волейбол | баскетбол
Г
волейбол & баскетбол & подача
Задание 2
Перед началом Турнира Четырех болельщики высказали следующие предположения по поводу своих кумиров:
A) Макс победит, Билл – второй;
B) Билл – третий. Ник – первый;
C) Макс – последний, а первый – Джон.
Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.
Какое место на турнире заняли Джон, Ник, Билл, Макс?
(В ответе перечислите подряд без пробелов места участников в указанном порядке имен.)
Выставление оценок
infourok.ru
Алгебра логики. Решение упражнений — информатика, уроки
Вариант 1
1. Выбрать пример, не являющийся высказыванием:
А) «Приезжайте в Белгород»
Б) «Белгород – областной центр»
В) «Экономика Белгорода развивается»
Г) «Некоторые области больше Белгородской»
2. Высказывание «Все растения съедобны»:
А) простое и истинное
Б) сложное и истинное
В) простое и ложное
Г) сложное и ложное
3. Отрицанием высказывания «Для каждого из нас учить второй иностранный язык легче, чем первый» является высказывание:
А) «Не для каждого из нас учить второй иностранный язык легче, чем первый»
Б) «Для каждого из нас не учить второй иностранный язык легче, чем первый»
В) «Неверно, что для каждого из нас учить второй иностранный язык легче, чем первый»
Г) «Неверно, что для каждого из нас учить второй иностранный язык не легче, чем первый»
4. Формулой логического высказывания «Если у меня будет свободное время и не будет дождя, то я не буду писать сочинение, а пойду на дискотеку» является:
А) (АΛ)→()
Б)
В)
Г)
5. С = «Меркурий – спутник Марса». Установить истинность высказывания .
А) 1
Б) 0
В) не определено, т.к. недостаточно данных
Г) предложение С высказыванием не является
6. А = «Сегодня воскресенье», В = «Воробей – перелетная птица». Предложение
А) истинно
Б) ложно
В) не определено, т.к. недостаточно данных
Г) высказыванием не является
7. А = «Сегодня воскресенье», В = «Воробей – перелетная птица». Предложение
А) истинно
Б) ложно
В) не определено, т.к. недостаточно данных
Г) высказыванием не является
Вариант 2
1. Выбрать пример, не являющийся высказыванием:
А) «Герб является важнейшим государственным символом»
Б) «В Белгород приезжать приятно»
В) «Где ты живешь?»
Г) «Все птицы зимой улетают на юг»
2. Высказывание «Прозвенел звонок и закончился урок»:
А) простое и истинное
Б) сложное и истинное
В) простое и ложное
Г) сложное и ложное
3. Отрицанием высказывания «Некоторые школьники предпочитают изучать испанский язык» является высказывание:
А) «Некоторые школьники не предпочитают изучать испанский язык»
Б) «Некоторые школьники предпочитают изучать не испанский язык»
В) «Неверно, что некоторые школьники предпочитают изучать испанский язык»
Г) «Неверно, что школьники предпочитают не изучать испанский язык»
4. Формулой логического высказывания «Если не будет дождя и будет светить солнце, то мы не останемся дома, а пойдем за грибами» является:
А) ()→()
Б)
В)
Г)
5. С = «Луна – спутник Земли». Установить истинность высказывания .
А) 1
Б) 0
В) не определено, т.к. недостаточно данных
Г) предложение С высказыванием не является
6. А = «Идет урок информатики», В = «Все грибы съедобны». Предложение
А) истинно
Б) ложно
В) не определено, т.к. недостаточно данных
Г) высказыванием не является
7. А = «Идет урок информатики», В = «Все грибы съедобны». Предложение
А) истинно
Б) ложно
В) не определено, т.к. недостаточно данных
Г) высказыванием не является
kopilkaurokov.ru
ОГЭ — вопрос 02 (Алгебра логики) — 9 класс — Каталог статей
Темы для которых создаются проверочные задания №2 основного государственного экзамена (ОГЭ) по информатике |
|---|
Обработка информации:
|
ОГЭ — 2 (А) Часть 1, базовый уровень, задание подразумевает выбор и запись ответа в виде одной цифры, время выполнения – 3 мин, максимальный балл за выполнение задания — 1. Требования к уровню подготовки, освоение которых проверяется в ходе экзамена при ответе на данное задание: выполнять базовые операции над объектами: цепочками символов, числами, списками, деревьями; проверять свойства этих объектов; выполнять и строить простые алгоритмы;
Что нужно знать
Теоретическая справка
Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Высказывания делятся на три типа: общие, частные или единичные. Общее высказывание начинается со слов: все, всякий, каждый, ни один. Частное высказывание начинается со слов: некоторые, большинство и т.п. во всех других случаях высказывание является единичным.
Логическое высказывание – это повествовательное предложение, про которое однозначно можно сказать: истинно (1) оно или ложно (0).
Составные (сложные) высказывания строятся из простых с помощью базовых логических связок (операций) «и», «или», «не».
| Операция И (логическое умножение, конъюнкция) А ^ В | Операция ИЛИ (логическое сложение, дизъюнкция) А v В | Операция НЕ (инверсия, отрицание) ¬А | Импликация (следование («если …, то …»)) A → B = ¬А v В | Эквивалентность (тождество, равносильность («тогда и только тогда, …»)) A = B = А ^В v ¬А ^ ¬В | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Высказывание «A и B» истинно тогда и только тогда, когда А и B одновременно истинны. | Высказывание «A и B» истинно тогда и только тогда, когда А и B одновременно истинны. | Если высказывание A истинно, то «не А» ложно, и наоборот. | Высказывание «A → B» истинно, если не исключено, что из А следует B | Высказывание «A = B» истинно тогда и только тогда, когда А и B равны | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Приоритет выполнения операций:
- Выражение в скобках
- Инверсия
- Конъюнкция
- Дизъюнкция
- Импликация
- Эквивалентность
Ссылки на ресурсы Интернета:
Для дополнительного изучения темы можно воспользоваться материалом Шабалдиной Натальи Владимировны: основы логики.pptx
Пример задания
Для какого из названий животных ложно высказывание:
В слове 4 гласных буквы и не (пятая буква гласная) или в слове 5 согласных букв?
1) Шиншилла 2) Кенгуру 3) Антилопа 4) Крокодил
Решение:
Введем обозначения:
А = «В слове 4 гласных буквы»;
В = «пятая буква гласная»;
С = «в слове 5 согласных букв».
Составим логическое выражение: А и не В или С.
Определим порядок действий и заполним таблицу:
| А | В | С | не В | А и (не В) | (А и (не В)) или С | |
| Шиншилла | 0 | 1 | 1 | 0 | 0 | 1 |
| Кенгуру | 0 | 1 | 0 | 0 | 0 | 0 |
| Антилопа | 1 | 0 | 0 | 1 | 1 | 1 |
| Крокодил | 0 | 1 | 1 | 0 | 0 | 1 |
Из таблицы истинности видно, что высказывание ложно только для слова «Кенгуру».
Ответ: 2
Задачи для тренировки
- Для какого из указанных значений числа X ложно выражение
(X > 2) ИЛИ НЕ (X > 1)?
- Для какого числа X истинно высказывание (X > 2)v(X > 5)→(X < 3)
1) 5 2) 2 3) 3 4) 4
- Для какого из указанных значений числа X истинно выражение
(X > 2) И НЕ (X > 3)?
1) 1 | 2) 2 | 3) 3 | 4) 4 |
- Для какого из указанных значений числа X истинно выражение
(X < 3) И ((X < 2) ИЛИ (Х > 2))?
1) 1 | 2) 2 | 3) 3 | 4) 4 |
- Для какого из указанных значений числа X истинно выражение
(X < 4) И (X > 1) И (Х ≠ 2)?
1) 1 | 2) 2 | 3) 3 | 4) 4 |
- Для какого из указанных значений числа X истинно выражение
(X > 4) ИЛИ (X < 7) И (Х < 6)?
1) 1 | 2) 2 | 3) 3 | 4) 4 |
- Для какого из указанных значений числа X истинно выражение
(X > 1) И (X > 2) И (Х ≠ 3)?
1) 1 | 2) 2 | 3) 3 | 4) 4 |
8. Для какого из приведенных чисел истинно высказывание:
НЕ(Первая цифра четная) И НЕ(Вторая цифра нечетная)?
1) 4562 | 2) 6843 | 3) 3561 | 4) 1234 |
9) Для какого из приведенных слов истинно логическое выражение
НЕ(первая буква гласная) И НЕ (третья буква согласная)?
1) модем | 2) адрес | 3) связь | 4) канал |
- Для какого имени истинно высказывание:
¬ (Первая буква имени гласная → Четвертая буква имени согласная)?
1) ЕЛЕНА 2) ВАДИМ 3) АНТОН 4) ФЕДОР
- Для какого символьного выражения неверно высказывание:
Первая буква гласная → ¬ (Третья буква согласная)?
1) abedc 2) becde 3) babas 4) abcab
- Для какого символьного набора истинно высказывание:
Вторая буква согласная ^ (В слове 3 гласных буквы v Первая буква согласная)?
1) УББОШТ 2) ТУИОШШ 3) ШУБВОИ 4) ИТТРАО
- Для какого имени ложно высказывание:
(Первая буква гласная ^ Последняя буква согласная) → ¬(Третья буква согласная)?
1) ДМИТРИЙ 2) АНТОН 3) ЕКАТЕРИНА 4) АНАТОЛИЙ
- Для какого имени истинно высказывание:
Первая буква гласная ^ Четвертая буква согласная v В слове четыре буквы?
1) Сергей 2) Вадим 3) Антон 4) Илья
- Для какого имени истинно высказывание:
(Первая буква согласная → Вторая буква гласная) ^ Последняя буква согласная?
1) АЛИСА 2) МАКСИМ 3) СТЕПАН 4) ЕЛЕНА
- Для какого имени истинно высказывание:
(Вторая буква гласная → Первая буква гласная) ^ Последняя буква согласная?
1) АЛИСА 2) МАКСИМ 3) СТЕПАН 4) ЕЛЕНА
- Для какого названия реки ложно высказывание:
(Вторая буква гласная → Предпоследняя буква согласная) ^ Первая буква стоит в алфавите раньше третьей?
1) ДУНАЙ 2) МОСКВА 3) ДВИНА 4) ВОЛГА
18) Для какого из указанных значений числа Х истинно выражение (X<3) & ((X<2) V (X>2))?
19) Для какого из указанных значений X истинно высказывание ((X<5) & ((X>5)) → (X>15))?
20) Для какого из указанных значений числа Х истинно выражение (X>1) & (X>2) & (X≠3)?
21) Для какого числа истинно высказывание ((X > 3)v(X < 3)) →(X < 1)
1) 1 2) 2 3) 3 4) 4
22) Для какого числа истинно высказывание (X > 1) ^ ((X < 5)→(X < 3))
1) 1 2) 2 3) 3 4) 4
Литература:
- кодификатор элементов содержания и требований к уровню подготовки обучающихся для проведения основного государственного экзамена по ИНФОРМАТИКЕ, 2015 — 2019 г.одов;
- спецификация контрольных измерительных материалов для проведения в 2015 — 2019 году основного государственного экзамена по ИНФОРМАТИКЕ и ИКТ;
- открытый банк заданий по информатике и ИКТ: http://oge.fipi.ru/os/xmodules/qprint/index.php?proj=74676951F093A0754D74F2D6E7955F06.
latnatbron.ucoz.net
Урок по информатике «Основы логики»
Разделы: Информатика
Цели:
- Введение в предмет “Алгебра логики”.
- Сформировать у учащихся понятия: формы мышления, алгебра высказываний, логическое высказывание, логические величины, логические операции.
- Способствовать формированию логического мышления, интереса к разделу информатики - алгебре логики.
- Закрепить полученные ЗУН.
Формы организации урока: объяснительно-иллюстративный, диалогический.
Ход урока.
I. Изложение нового материала.
1. Этапы развития логики.
Логика очень древняя наука.
1-й этап связан с работами ученого и философа Аристотеля (384-322 г.г. до н.э.). Он пытался найти ответ на вопрос “Как мы рассуждаем”, изучал правила мышления. Аристотель впервые дал систематическое изложение логики. Он подверг анализу человеческое мышление, его формы – понятие, суждение, умозаключение. Так возникла формальная логика.
2-й этап – появление математической, или символической, логики. Основы ее заложил немецкий ученый и философ Г.В. Лейбниц (1646-1716). Он сделал попытку построить первые логические исчисления, считал, что можно заменит простые рассуждения действиями со знаками, и привел соответствующие правила. Но он выдвинул только идею, а развил её окончательно англичанин Д. Буль (1815-1864). Буль считается основоположником математической логики как самостоятельной дисциплины. В его работах логика обрела свой алфавит, свою орфографию и грамматику.
2. Формы мышления.
Опр.1 Логика – эта наука, изучающая законы и формы мышления; учение о способах рассуждений и доказательств.
Основными формами мышления являются понятие, суждение, умозаключение.
Опр.2 Понятие – это форма мышления, выделяющая существенные признаки предмета или класса предметов, позволяющих отличить их от других.
Например: компьютер, трапеция, портфель, ураганный ветер.
Упражнение 1 (устно). Приведите свои примеры.
Понятие имеет две стороны: содержание и объем.
Содержание понятия – совокупность существенных признаков, отраженных в этом понятии. Например, содержание понятия персональный компьютер-это универсальное электронное устройство для автоматической обработки информации, предназначенное для одного пользователя.
Объем понятия – множество предметов, каждому из которых принадлежат признаки, составляющие содержание понятий.
Например:
1. Объем понятия город – это множество,
состоящее из городов, носящих имя Москва, Одесса,
Казань, Уфа, Нижнекамск и др.
2. Объем понятия персональный компьютер –
совокупность существующих в мире персональных
компьютеров.
Упражнение 2 (устно)
1. Перечислите существенные признаки,
составляющие содержание понятий: добродетель,
истинна, ложь.
2. Определите объем понятий: столица России,
столица, река.
Опр.3 Суждение (высказывание, утверждение) – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо истинным, либо ложным, и может быть либо простым, либо составным (сложным).
Например:
1. Истинное и простое высказывание: Буква “т” -
согласная.
2. Ложное и сложное высказывание: Осень наступила,
и грачи прилетели.
Вопросительные и восклицательные предложения не являются высказываниями, так как в них ни чего не утверждается и не отрицается.
Например:
1. Уходя, гасите свет!
2. Кто хочет быть счастливым?
Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Например: 5>3, H2O+SO2=H2SO4.
Упражнение 3 (устно). Объясните, почему следующие высказывания не являются высказываниями:
1. Какого цвета твой велосипед?
2. Число Х больше пяти?
3. 5Х-2
4. Посмотрите в окно.
5. Пейте томатный сок!
6. Вы были в музее?
7. Разность чисел 12 и Х равна 6.
Упражнение 4 (устно). Какие из следующих высказываний являются истинными, а какие ложными?
1. Город Москва – столица России.
2. Число 12 – простое.
3. 7*3=1.
4. 12<15.
5. Сканер – устройство, которое может напечатать
на бумаге то, что изображено на экране
компьютера.
6. Клавиатура – устройство ввода информации.
Упражнение 5 (устно). Приведите свои примеры истинных и ложных высказываний.
Опр.4 Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение.
Посылками умозаключения по правилам формальной логики могут быть только истинные суждения. Тогда, если умозаключение проводится в соответствии с правилами формальной логики, то оно будет истинным. В противном случае можно прийти к ложному умозаключению.
Например:
| 1. Все металлы – простые вещества. Литий – металл. Литий – простое вещество. |
2. Все школьники – отличники. Вовочка – школьник. Вовочка – отличник. |
Упражнение 6.
1. Дано высказывание “Все углы равнобедренного
треугольника равны”. Путем умозаключений
получить высказывание “Этот треугольник
равносторонний”.
2. Оцените правильность следующего рассуждения:
сидящий встал; кто встал, тот стоит; значит,
сидящий стоит.
3. Алгебра высказываний.
Алгебра высказываний была разработана для того, чтобы можно было определять истинность или ложность составного высказывания, не вникая в их содержание.
Опр.5 Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Под высказыванием (суждением) будем понимать повествовательное предложение, относительно которого можно сказать, истинно или ложно.
В алгебре высказываний простым высказываниям ставятся в соответствии логические переменные, обозначаемые прописными буквами латинского алфавита.
Например:
А= “Листва на деревьях опадает осенью”.
В= “Земля прямоугольная”.
Высказывания, как говорилось уже ранее, могут быть истинными или ложными. Истинному высказыванию соответствует значение логической переменной 1, а ложному – значение 0 .
Например:
А=1
В=0
Опр.6 В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения: “истинна” (1) и “ложь” (0).
В алгебре высказываний над высказываниями можно производить логические операции, в результате которых получаются новые, составные (сложные) высказывания.
Опр.7 Логическая операция – способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
Рассмотрим три базовых логических операций – инверсию, конъюнкцию, дизъюнкцию и дополнительные – импликацию и эквивалентность.
| Логическая операция | Название | Соответствует союзу | Обозначение знаками | Таблица истинности | Логическая операция | |||||||||||||||
| Инверсия (от лат. inversion – переворачиваю) |
отрицание | не А |
|
Опр. 8 Инверсия логической переменной истина, если переменная ложна, и, наоборот, инверсия ложна, если переменная истинна. | ||||||||||||||||
| Конъюнкция (от лат. conjunction – связываю) |
Логическое умножение | А и В |
|
Опр.9Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания, истинны. | ||||||||||||||||
| Дизъюнкция (от лат. disjunction – различаю) |
Логическое сложение | А или В |
|
Опр. 10 Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны. | ||||||||||||||||
| Импликация (от лат. implication – тесно связывать) |
Логическое следование | Если А, то В; Когда А, тогда В |
А–условие В-следствие |
|
Опр. 11 Импликация двух логических переменных ложна тогда и только тогда, когда из истинного основания следует ложное следствие. | |||||||||||||||
| Эквивалентность (от лат. equivalents — равноценность) | Логическое равенство | А тогда и только тогда, когда В |
|
Опр. 12 Эквивалентность двух логических переменных истинна тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны |
Упражнение 7. Даны два простых высказывания:
А= “Щука – рыба”;
В=“Ворона – певчая птица”.
Составьте из них все возможные составные (сложные) высказывания и определите их истинность.
При вычислении значения логического выражения (формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:
- инверсия,
- конъюнкция,
- дизъюнкция,
- импликация и эквивалентность.
Операции одного приоритета выполняются слева направо. Для изменения порядка действий используются скобки.
Например: дана формула
Порядок вычисления:
— инверсия
— конъюнкция
— дизъюнкция
— импликация
-
эквивалентность.
Упражнение 8.
Дана формула . Определите порядок вычисления.
II. Закрепление изученного материала.
1. Среди следующих высказываний укажите составные, выделите в них простые, обозначьте их каждое из них буквой. Запишите с помощью логических операций каждое составное высказывание.
- Число 456 трехзначное и четное.
- Неверно, что Солнце движется вокруг Земли.
- Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
- Луна – спутник Земли.
- На уроке химии ученики выполняли лабораторную работу, и результаты исследований записывали в тетрадь.
- Если число оканчивается на 0, то оно делится на 10.
- Чтобы погода была солнечной, достаточно, чтобы не было ни ветра, ни дождя.
- Если у меня будет свободное время и не будет дождя, тоя не буду писать сочинения, а пойду на дискотеку.
- Без Вас хочу сказать Вам много
При Вас я слушать Вас хочу. - Если человек с детства и юности своей не давал нервам властвовать над собой, то они не привыкнут раздражаться и будут ему послушны.
2. Постройте отрицания следующих высказываний.
- На улице сухо.
- Сегодня выходной день.
- Ваня не был готов сегодня к урокам.
- Неверно, что число 3 не является делителем числа 198.
- Некоторые млекопитающие не живут на суше.
- Неверно, что число 17 – простое.
3. Из каждых трех выберите пару высказываний, являющихся отрицаниями друг друга.
- “Луна – спутник Земли”, “Неверно, что Луна спутник Земли”, “Неверно, что Луна не является спутником Земли”;
- “2007 < 2008”, “2007 > 2008”, “2007 ? 2008”;
- “Прямая а перпендикулярна прямой с”; “Прямая а не параллельна прямой с”; “Прямая а не пересекается с прямой с”.
4. По данным формам сложных высказываний запишите высказывания на русском языке.
1.
2.
3.
4.
5.
5. Найдите значения логических выражений:
6. Даны два высказывания: А = “2 х 2 = 4”, В = “2 х 2 = 5”. Очевидно, что А=1, В=0. Какие из высказываний истинны?
а)
б)
в) А
г)
д)
е)
7. Даны простые высказывания: А= {15>13}, В={4=5}, C= {7<4}. Определите истинность составных высказываний:
8. При каких значениях числа Х логическое выражение не ((Х>15) или (Х<-5)) примет значение:
- ложь,
- истинна.
9. Какие из высказываний А, В должны быть истинны и какие ложны, чтобы было ложное высказывание ?
III. Итог урока.
Обобщить пройденный материал, оценить работу активных учеников.
IV. Домашнее задание.
1. Выучить определения, знать обозначения.
2. Даны высказывания:
А = {На улице светит солнце},
В = {На улице дождь},
С = {На улице пасмурная погода},
В = {На улице идет снег}.
Составьте два сложных высказывания, одно из которых в любой ситуации всегда будет ложным, а другое истинным.
3. Переведите сложное высказывание на русский язык.
4. Какое логическое выражение описывает условие:
“Точка Х не принадлежит отрезку [А; В]”?
- не (Х А) или Х < B,
- X < A и X > B,
- не (X B и X A),
- X A или X В.
Литература:
- Информатика и информационные технологии. Учебник для учащихся 10-11 классов. / Угринович Н.Д., — М. Лаборатория Базовых Знаний, 2004.
- Практикум по информатике и информационным технологиям. Учебное пособие для общеобразовательных учреждений. / Угринович Н.Д., Босова Л.Л., Михайлова Н.И. — М. Лаборатория Базовых Знаний, 2001.
- Логика в информатике. / Лыскова В.Ю., Ракитина Е.А. — М. Лаборатория Базовых Знаний, 2001.
- Информатика. Элементы Алгебры логики. Еженедельное приложение к газете “Первое сентября”. №27, 1998.
- Информатика. Логика. Еженедельное приложение к газете “Первое сентября”. №26, 1997.
25.03.2008
xn--i1abbnckbmcl9fb.xn--p1ai
