Алгебра модули как решать – Как решать уравнения с модулем

Неравенства с модулями. Видеоурок. Алгебра 11 Класс

Тема: Уравнения и неравенства. Системы уравнений и неравенств

Урок: Неравенства с модулями

Существует несколько определений модуля. Эти определения должны быть равноценны, эквивалентны, т. е. из первого определения следует второе, а из второго первое.

Определение:

Модулем числа t называется само число t, если оно больше нуля, модулем нуля является ноль, и если под модулем отрицательное число, то модуль t равен минус t.

 

Обычно в задачах под модулем стоит целое выражение, зависящее от х, тогда:

Из вешесказанного следует простое правило: если под модулем стоит положительное число, то модуль можно отбросить. Если же под модулем стоит отрицательное число, то модуль следует отбросить, но поставить знак минус перед всем подмодульным выражением.

Определение:

Модуль числа t – это расстояние от точки t до точки 0.

В частности, 

Например:

Рис. 1. Модули чисел 3 и -3

 

Из определения модуля следует основной прием решения задач с модулем, а именно, освободиться от модуля на основе его определения. Поясним на конкретном примере.

Пример 1 – построить график функции:

Согласно определению модуля, рассматриваем два случая:

Рис. 2. График функции

Пример 2 – решить неравенства:

a)

Решим, опираясь на второе определение:

Проиллюстрируем:

Рис. 3. Решение примера 2.a

Любая точка, не принадлежащая выбранному отрезку, не будет являться решением, так как расстояние от нее до точки 3 будет больше заданного расстояния.

Ответ:

б)

Проиллюстрируем:

Рис. 4. Решение примера 2.б

Любая точка, не принадлежащая выбранным промежуткам, не будет являться решением, так как расстояние от нее до точки 3 будет меньше заданного расстояния.

Ответ:

Рассмотрим неравенства вида:

Данное неравенство можно решать двумя способами.

Способ 1 (по определению):

Способ 2:

Строгое доказательство данного способа опустим, приведем и прокомментируем его.

Поясним на графике (рисунок 5)

Рис. 5. Пояснительный график

Итак, на рисунке 12.5 изображен график функции . Решения неравенства  заштрихованы зеленым цветом. Если функция g(x) задана как константа, то нас удовлетворит промежуток значений (-g; g) – показано красным.

Рассмотрим следующий тип неравенств с уединенным модулем:

Аналогично предыдущему неравенству, покажем два способа решения.

Способ 1:

Способ 2:

Доказательство данного способа можно получить, продолжив преобразовывать совокупность, полученную в первом способе. Мы проиллюстрируем данный способ решения:

Рис. 6. Пояснительный график

Итак, на рисунке 6 изображен график функции . Решения неравенства  заштрихованы зеленым цветом. Если функция g(x) задана как константа, то нас удовлетворят промежутки значений  – показано красным.

 

Пример 3 – решить неравенство:

Решаем неравенство вторым способом:

Проиллюстрируем решение системы:

Рис. 7 Решение системы в примере 3

Ответ:

Пример 4 – решить неравенство:

Решаем вторым способом:

Проиллюстрируем решение совокупности:

Рис. 8. Решение совокупности в примере 4

Ответ:

Неравенства с модулем можно решать методом интервалов.

Пример 5 – решить неравенства:

а)

б)

Согласно стандартному алгоритму, рассматриваем функцию, стоящую в левой части, если справа ноль:

Исследуем функцию. ОДЗ:

Чтобы найти корни, решим уравнение:

Выделяем интервалы знакопостоянства и определяем знаки функции:

Рис. 9. Интервалы знакопостоянства функции

Ответ: а); б) ;

Рассмотрим неравенство, в котором сравниваются два модуля.

Пример 6 – решить неравенство:

Напомним, что если обе части неравенства положительны, мы имеем право возвести их в квадрат, при этом равносильность не теряется. В данном случае каждый модуль неотрицателен, имеем право возвести в квадрат, при этом модули уничтожатся, согласно свойству ():

Перенесем все в одну сторону и разложим на множители:

Вынесем из скобок константные множители:

Разделим обе части неравенства на минус три, при этом знак неравенства меняется на противоположный:

Получено простейшее квадратное неравенство. Парабола, ветви направлены вверх, интересующие нас значения находятся в интервале между корнями.

Ответ:

            Итак, мы рассмотрели различные типовые неравенства с модулем, привели некоторые схемы решения и решили примеры. Далее перейдем к системам уравнений.

 

Список литературы

1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.

2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа. 

3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.

  

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Портал естественных наук (Источник).

2. ЕГЭ по математике (Источник).

3. Математика, которая мне нравится (Источник).

 

Домашнее задание

1. Решить неравенство:

а) ;

б) ;

в) ;

г) ;

2. Решить неравенство:

а) ;

б);  

в);  

г) ;

3. Решить неравенство:

а) ;

б) ;

в) ;

г) ;

 

interneturok.ru

Уравнение с модулем. наглядное пособие по алгебре ( 7 класс)

Уравнение, содержащие переменную под знаком модуля.

Модулем неотрицательного действительного числа a называют само это число:

|а| = а

Модулем отрицательного действительного числа х называют противоположное число:

|а| = — а

Короче это записывают так:

Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули:

|-а| = |а|

Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета 0, т.е. удалена от нее на 0 единичных отрезков:

|0| = 0

На доске записали решение линейного уравнения, но часть уравнения вытерли. Восстановите их.

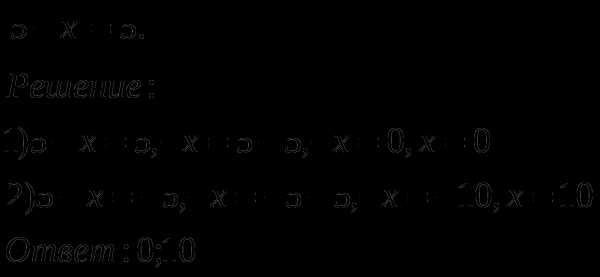
infourok.ru

Модуль Алгебра — ЁП

Модуль алгебра первой части содержит четырнадцать (1 — 14) заданий, каждое из которых оценивается в один балл.

Действия с дробями

Понятие обыкновенной и десятичной дроби. Сложение, вычитание, умножение, деление дробей. Сравнение дробей. Перевод обыкновенной дроби в десятичную и обратно.

Действия со степенями

Понятие степени. Свойства степеней. Возведение отрицательного числа в степень. 

Задание №2

Анализ диаграмм, таблиц, графиков.
Разные таблицы. Таблицы нормативов. Диаграммы.

Задание №3

Координатная прямая

Понятие координатной прямой. Расположение чисел на координатной прямой. Сравнение чисел, расположенных на координатной прямой. Сопоставление чисел, изображенных на прямой с некоторым числом. 

Модуль числа

Понятие модуля числа. 

Квадратный корень из числа

Понятие квадратного корня. Расположение квадратного корня из числа на координатной прямой. 

Задание №4

Преобразования и вычисления

Свойства квадратного корня, свойства степеней. Вынесение множителя за знак квадратного корня.  

ФСУ

Формулы сокращенного умножения.

Стандартный вид числа

Понятие стандартного вида числа. Перевод приставок в множитель.

Задание №5

Анализ диаграмм, таблиц, графиков.
Анализ таблиц. Вычисление величин по графику или диаграмме. Определение величины по графику.

Задание №6

Уравнения
Линейные уравнения. Квадратные уравнения. Рациональные уравнения. ОДЗ. 

Системы уравнений
Понятие системы уравнений. Отбор решений. 

Задание №7

Простейшие текстовые задачи.
Пропорции. Проценты. Разные задачи.

Задание №8

Анализ диаграмм.
Столбчатые диаграммы. Круговые диаграммы.

Задание №9

Статистика, вероятности.
Статистика. Теоремы о вероятностных событиях. Классические вероятности.

Задание №10

Неравенства

Линейные неравенства. Квадратные неравенства. Рациональные неравенства. ОДЗ. 

Системы неравенств

Понятие системы неравенств. Отбор решений. 

Задание №11

Виды графиков

Прямая. Парабола. Гипербола. Квадратный корень.

Действия с графиками

Растяжение графиков. Сдвиги графиков. 

Задание №12

Числовые последовательности

Понятие числовой последовательности. Нахождение n-ных членов последовательности. Принцип работы с числовыми последовательностями. 

Арифметическая прогрессия.

Понятие арифметической прогрессии. Разность арифметической прогрессии. Рекуррентная формула. Сумма первых n членов арифметической прогрессии.

Геометрическая прогрессия

Понятие геометрической прогрессии. Знаменатель прогрессии. Рекуррентная формула. Сумма первых n членов геометрической прогрессии. Полезные формулы. 

Задание №13

Расчеты по формулам.
Вычисление по формуле. Линейные уравнения. Разные задачи.

Задание №14

Формулы сокращенного умножения

ФСУ. Применение ФСУ в различных выражениях. 

Упрощение выражений

Разложение на множители: вынесение общего множителя, группировка, применение ФСУ. Приведение выражений к общему знаменателю. 

В модуле алгебра второй части содержится три задания (21 — 23), каждое из которых оценивается в два балла.

Задание №21

Алгебраические выражения, уравнения, системы уравнений, неравенства, системы неравенств.

Задание №22

Текстовые задачи
Задачи на движение по воде. Задачи на проценты, сплавы и смеси. Задачи на совместную работу. Движение по прямой. Разные задачи.

Задание №23

Функции и их свойства. Графики функций.
Гиперболы. Параболы. Кусочно-непрерывные функции. Разные задачи.

epmat.ru

Урок «Решение заданий Модуля «Алгебра»

Решение заданий Модуля «Алгебра»

(подготовка к ОГЭ математика)

Тема: Решение заданий модуля «Алгебра». Подготовка к ОГЭ

Учебный предмет: Практикум по математике

Класс: 9 класс

Тип урока: урок коррекции, закрепления и совершенствования умений и навыков

Формы организации деятельности учащихся: фронтальная, групповая, индивидуальная

Цели урока

образовательные:

• знать свойства, определения, алгоритм по данным содержательным линиям: «Алгебраические выражения. Функции. Уравнения и неравенства», вырабатывать умение применять накопленные знания для решения заданий ГИА по математике;

• находить значение выражений, применяя свойства степени, аналитическую формулу функции, решение неравенств и систем неравенств;

• анализировать учебный материал, сравнивать личное решение с эталоном;

• выделять главное в учебном материале, личные ошибки при выполнении заданий

развивающие: развитие умения пользоваться приемами сравнения, обобщения, делать выводы, применять полученные знания при решении алгебраических выражений, неравенств и систем неравенств, моделировать решение с помощью логических цепочек рассуждений, правильно использовать в речи математические термины

воспитательные: работать самостоятельно, в малых группах, в парах, выполнять самооценку учебной деятельности, оказывать помощь, вести диалог, навык работы в группе, вести дискуссию.

Технологическая карта урока

Предмет: Практикум по математике (урок в рамках подготовки к ГИА по математике)

Класс: 9

Тема урока: Решение заданий модуля «Алгебра».

Тип урока: урок коррекции, закрепления и совершенствования умений и навыков

Форма урока: урок-практикум

I этап

1.Организация начала урока

(1 мин)

Полная готовность класса и оборудования, быстрое включение учащихся в деловой ритм.

Приветствие учащихся.

Озвучивание темы урока.

Создание мотивации успеха

Приветствует обучающихся, проверяет их готовность к уроку.

Активизирует внимание учащихся.

Создает эмоциональный настрой на урок.

Приветствуют учителя, проверяют свою готовность к уроку.

Приветствуют друг друга, настраиваются на совместное сотрудничество.

Настраиваются на работу на уроке, готовятся к получению новых знаний.

2. Анализ ошибок модуля «Алгебра»

(1 мин)

Установление рейтинга наиболее сложных заданий выполнения теста ГИА Модуля «Алгебра» всеми учащимися.

Общий вывод: (содержательные линии наиболее сложных заданий модуля «Алгебра»)

• Алгебраические выражения

• Функции и графики

• Уравнения и неравенства

Уточняет рейтинг сложных заданий по таблице мониторинга.

Выдвигает проблему.

Побуждает учащихся к анализу.

Устанавливают вместе с учителем наиболее сложный учебный материал.

Формулируют собственное мнение по презентации.

Принимают информацию, акцентируя внимание на результатах тестирования.

3. Подготовка к основному этапу урока

(2 мин)

Обеспечение мотивации и принятия учащимися цели учебно-познавательной деятельности на уроке.

Подведение детей к постановке целей урока.

Формулирование целей урока.

Предложение самооценки учащимися по таблице:

3 балла — знаю и могу

2 балла – знаю, но допускаю ошибки

1 балл — надо повторить

Организация погружения в проблему.

Проводит диалог с учащимися.

Предлагает учащимся обозначить цели урока.

Озвучивают и фиксируют цели урока.

Настраиваются на самооценку учебной деятельности.

Слушают учителя.

Строят понятные для собеседника высказывания.

Используют диалогическую форму речи.

Принимают и формулируют учебную цель.

II этап

Усвоение знаний и способов действий по содержательным линиям Модуля «Алгебра»

(30 мин)

Организация восприятия, повторения, закрепления учебного материала по теме «Степени»

«Алгебраические выражения»

Задание №3 по теме «Степени»

1. Актуализация знаний (демонстрация презентации по теме «Свойства степени»)

2. Контролирующий элемент (4 задания по презентации)

3. Самооценка по эталону

Предлагает к просмотру презентацию, повторить свойства и решить задания фронтально и индивидуально с фронтальной проверкой.

Сопоставляют свойства степени с предложенным действием.

Отбирают нужное свойство для решения.

Формулируют актуализацию знаний для себя.

Выбор и использование свойства в соответствии с заданием.

Принимают и сохраняют учебную информацию.

Самостоятельно организуют учебную деятельность.

Анализируют и сравнивают личный результат с правильным решением.

Самооценка данного этапа урока.

Организация восприятия, повторения, закрепления учебного материала по теме «Функции и их графики»

«Функции и графики»

Задание №5 по теме «Функции»

1. Актуализация знаний (демонстрация видеолекции по теме «Функции»)

2. Контролирующий элемент (задание «Выполни соответствие»)- работа в парах

3. Самооценка по таблице

Демонстрирует видеофрагмент.

Предлагает решить задание в парах и выполнить проверку.

Актуализируют знания по теме «Функции»

Применяют знания для решения учебной задачи в парах.

Формулируют актуализацию знаний для себя.

Договариваясь с партнером, приходят к общему решению.

Принимают и сохраняют учебную информацию.

Организуют учебную деятельность.

Анализируют и сравнивают результат с результатом партнера, с правильным решением.

Формулируют собственную позицию.

Корректируют ошибки.

Самооценка этапа урока.

Электронная физминутка для глаз

Здоровьесбережение

Предлагает просмотр презентации для снятия напряжения глаз и релаксации.

По презентации выполняют зрительную гимнастику.

Используют внешний источник для снятия напряжения.

Релаксация.

Организация восприятия, повторения, закрепления учебного материала

«Уравнения и неравенства»

Задание №8 по теме «Неравенства»

1. Актуализация знаний (демонстрация презентации по теме «Неравенства. Системы неравенств»)

2. Контролирующий элемент (задания, тест интерактивный)

3. Самооценка по таблице

Демонстрирует презентацию.

Задания по теме «Неравенства».

Актуализируют знания по теме «Неравенства»

Применяют знания для решения учебной задачи.

Формулируют актуализацию знаний для себя.

Использование знаний для решения заданий.

Принимают и сохраняют учебную информацию.

Самостоятельно организуют учебную деятельность.

Анализируют и сравнивают результат с результатом у доски.

Формулируют собственную позицию.

Корректируют ошибки.

Самооценка этапа.

III.этап

1. Информация о домашнем задании

(1 мин)

Обеспечение понимания цели, содержания и способов выполнения домашнего задания.

Домашнее задание

решить 5 заданий на различные действия с алгебраическими дробями и решить.

Реализует необходимые и достаточные условия для успешного выполнения домашнего задания всеми учащимися.

Проводят сверку соответствующих записей в тетрадях и дневниках.

Настраиваются на верное выполнение домашнего задания.

Оценивают свои возможности для выполнения домашнего задания.

2. Подведение итогов урока

(2 мин)

Подведение итогов усвоения знаний.

Достижение целей урока.

Выставление оценок.

Информация для учащихся

Организует диалог с учащимися о достижении целей.

Комментирует и выставляет оценки за урок.

Оценивают достижение целей урока.

Подают учителю дневники на выставление оценок.

Сдают тетради и таблицу самоанализа.

Проводят оценку своих возможностей на успешное усвоение материала урока.

Анализируют и сравнивают результаты своей деятельности за урок с результатами одноклассников.

3. Рефлексия

(3 мин)

Мобилизация учащихся на рефлексию своего поведения (мотивации, способов деятельности, общения)

Диалог с учащимися.

Акцентирование внимания на конечных результатах учебной деятельности обучающихся на уроке.

Предлагает учащимся проанализировать их деятельность на уроке.

Оценка усвоения материала за урок

на основе результатов таблицы.

Мотивируют свои успехи и неудачи в процессе учебной деятельности.

Формулируют выводы.

Усваивают и прогнозируют принципы саморегуляции и сотрудничества.

Используют диалогическую форму речи.

Осмысливают свои действия и дают самооценку.

infourok.ru