cosx меньше a
Рассмотрим решение тригонометрических неравенств вида cosx меньше a (cosx<a) на единичной окружности.
Снова применяем ассоциацию косинус-колобок. Оба кругленькие, оба начинаются с ко-. Колобку, в силу особенности его фигуры, удобнее двигаться влево-вправо, а не вверх-вниз. Влево-вправо на координатной плоскости — движение по оси ox. Значит, косинус — это x. То есть абсцисса, координата x точки на окружности. Геометрически cosx=a в точках пересечения единичной окружности и прямой x=a (прямая, параллельная оси ox). Соответственно, точки окружности, находящиеся правее этой прямой, соответствуют значениям косинуса, большим a, а cosx меньше a — левее этой прямой. Прямая и окружность могут пересекаться, не пересекаться и касаться. От их взаимного расположения зависит решение тригонометрического неравенства cosx меньше a.
1) cosx<a, при 0<a<1.
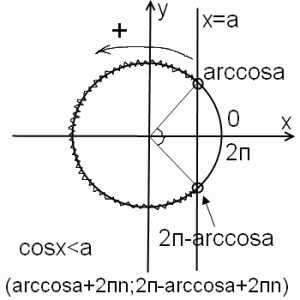
Первая точка пересечения прямой и окружности находится, как обычно, — это arccos a. Поскольку нам нужны значения, в которых cos x меньше a, из первой точки ко второй мы идем по верхнему пути, против часовой стрелки. При таком направлении обхода угол увеличивается. Вторую точку получили, немного не дойдя до 2п. На сколько не дошли? На тот же угол, который соответствует arccos a. Раз не дошли, то это число вычитаем из 2п. Поэтому вторая точка пересечения прямой с окружностью есть 2п-arccos a. Итак, решением неравенства cos x меньше a является промежуток (arccos a; 2п-arccos a). Поскольку период косинуса равен 2п, к каждому из концов промежутка прибавляем 2пn, где n -целое число (то есть n принадлежит Z). Получаем окончательный вариант ответа: (arccos a+2пn; 2п-arccos a+2пn). Для нестрогого неравенства точки закрашиваем и ставим квадратные скобки.
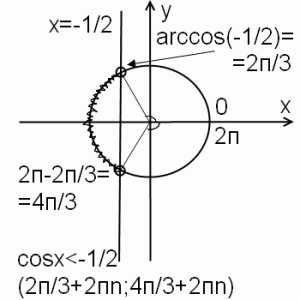
2) cos x меньше -a, при 0<a<1.
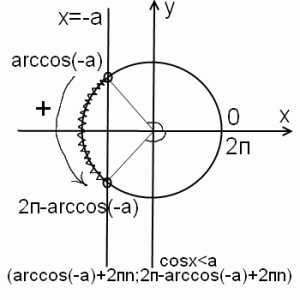
Решение неравенства аналогично первому случаю. Отличие — нужно вычислить арккосинус отрицательного числа (чуть позже я расскажу, как легко запомнить значения arccos (-a) с помощью ассоциации). А пока что arccos (-a)= п-arccos a. Ко второй точке здесь тоже идем против часовой стрелки, то есть значение угла увеличивается. Не доходим до 2п на величину arccos(-a), отсюда вторая точка есть 2п-arccos(-a). Чтобы учесть все решения неравенства, к концам промежутка прибавляем 2пn. Если неравенство нестрогое, точки закрашиваем и включаем в ответ (с квадратной скобкой).
3) cosx<0
То есть ищем, где косинус отрицательный. 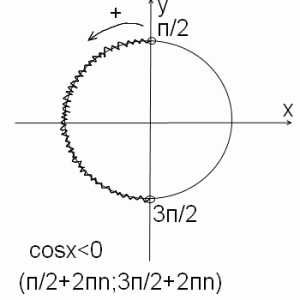
В качестве первой точки промежутка, на котором косинус принимает отрицательные значения, берем п/2, вторая точка — 3п/2. Чтобы учесть все промежутки, на которых косинус отрицательный, прибавляем к концам промежутка 2пn. Таким образом, решение тригонометрического неравенства cosx<0 есть промежуток (п/2+2пn; 3п/2+2пn), где n — целое число. Если неравенство нестрогое, то есть ищем неотрицательные значения косинуса, точки закрашиваем, скобки берем квадратные.
4) cosx<1
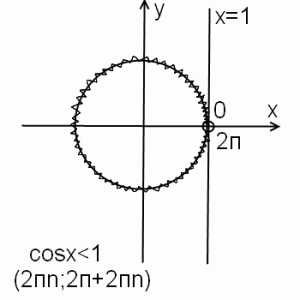
В этом случае окружность и прямая x=a касаются в одной точке — в нуле. Таким образом, за исключением этой точки, окружность расположена левее прямой. Значит, cosx меньше 1 в любой точке, кроме точек вида 0+2пn. Чтобы записать решение тригонометрического неравенства cosx<1 в виде интервала, в качестве второго конца промежутка берем 2п и к обоим концам прибавляем 2пn. Получаем (2пn; 2п+2пn).
5) cosx<a, при a>1.
В этом случае окружность целиком лежит левее прямой x=a и любое значение x удовлетворяет условию неравенства. Таким образом, в этом случае косинус меньше a на промежутке (-∞;+∞).
6) cosx<-a, при a>1.
При таких a окружность целиком расположена правее прямой x=-a и нет ни одного x, удовлетворяющего требованию cosx меньше -a. Поэтому решений нет.
В этом случае точку пересечения окружности и прямой исключать из решения не нужно, значит, x — любое число и решением является вся числовая прямая: (-∞;+∞).
Единственным решением этого тригонометрического неравенства является точка п. С учетом периодичности косинуса, решением является множество точек вида п+2пn, где n — целое число.
И в заключении — пример решения тригонометрического неравенства вида cosx меньше a: cosx<-1/2:
www.uznateshe.ru
Решите неравенство cos(x)*cos(x)>0 (косинус от (х) умножить на косинус от (х) больше 0)
Дано неравенство:$$\cos{\left (x \right )} \cos{\left (x \right )} > 0$$
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$\cos{\left (x \right )} \cos{\left (x \right )} = 0$$
Дано уравнение
$$\cos{\left (x \right )} \cos{\left (x \right )} = 0$$
преобразуем
$$\cos^{2}{\left (x \right )} = 0$$
$$\cos{\left (x \right )} \cos{\left (x \right )} = 0$$
Сделаем замену
$$w = \cos{\left (x \right )}$$
Это уравнение вида
a*w^2 + b*w + c = 0
Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$w_{1} = \frac{\sqrt{D} — b}{2 a}$$
$$w_{2} = \frac{- \sqrt{D} — b}{2 a}$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = 0$$
$$c = 0$$
, то
D = b^2 - 4 * a * c =
(0)^2 - 4 * (1) * (0) = 0
Т.к. D = 0, то корень всего один.
w = -b/2a = -0/2/(1)
$$w_{1} = 0$$
делаем обратную замену
$$\cos{\left (x \right )} = w$$
Дано уравнение
$$\cos{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
Или
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = \pi n + \operatorname{acos}{\left (w_{1} \right )}$$
$$x_{1} = \pi n + \operatorname{acos}{\left (0 \right )}$$
$$x_{1} = \pi n + \frac{\pi}{2}$$
$$x_{2} = \pi n + \operatorname{acos}{\left (w_{1} \right )} — \pi$$
$$x_{2} = \pi n — \pi + \operatorname{acos}{\left (0 \right )}$$
$$x_{2} = \pi n — \frac{\pi}{2}$$
$$x_{1} = \frac{\pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
$$x_{1} = \frac{\pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
Данные корни
$$x_{1} = \frac{\pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_{0} Возьмём например точку
$$x_{0} = x_{1} — \frac{1}{10}$$
=
$$- \frac{1}{10} + \frac{\pi}{2}$$
=
$$- \frac{1}{10} + \frac{\pi}{2}$$
подставляем в выражение
$$\cos{\left (x \right )} \cos{\left (x \right )} > 0$$
$$\cos{\left (- \frac{1}{10} + \frac{\pi}{2} \right )} \cos{\left (- \frac{1}{10} + \frac{\pi}{2} \right )} > 0$$
2
sin (1/10) > 0
значит одно из решений нашего неравенства будет при:
$$x
_____ _____
\ /
-------ο-------ο-------
x1 x2Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ:
$$x $$x > \frac{3 \pi}{2}$$
www.kontrolnaya-rabota.ru
Решите неравенство cos(x)^3>=0 (косинус от (х) в кубе больше или равно 0)
Дано неравенство:$$\cos^{3}{\left (x \right )} \geq 0$$
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$\cos^{3}{\left (x \right )} = 0$$
Решаем:
Дано уравнение
$$\cos^{3}{\left (x \right )} = 0$$
преобразуем
$$\cos^{3}{\left (x \right )} = 0$$
$$\cos^{3}{\left (x \right )} = 0$$
Сделаем замену
$$w = \cos{\left (x \right )}$$
Дано уравнение
$$w^{3} = 0$$
значит
$$w = 0$$
Получим ответ: w = 0
делаем обратную замену
$$\cos{\left (x \right )} = w$$
Дано уравнение
$$\cos{\left (x \right )} = w$$
— это простейшее тригонометрическое ур-ние
Это ур-ние преобразуется в
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
Или
$$x = \pi n + \operatorname{acos}{\left (w \right )}$$
$$x = \pi n + \operatorname{acos}{\left (w \right )} — \pi$$
, где n — любое целое число
подставляем w:
$$x_{1} = \pi n + \operatorname{acos}{\left (w_{1} \right )}$$
$$x_{1} = \pi n + \operatorname{acos}{\left (0 \right )}$$
$$x_{1} = \pi n + \frac{\pi}{2}$$
$$x_{2} = \pi n + \operatorname{acos}{\left (w_{1} \right )} — \pi$$
$$x_{2} = \pi n — \pi + \operatorname{acos}{\left (0 \right )}$$
$$x_{2} = \pi n — \frac{\pi}{2}$$
$$x_{1} = \frac{\pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
$$x_{1} = \frac{\pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
Данные корни
$$x_{1} = \frac{\pi}{2}$$
$$x_{2} = \frac{3 \pi}{2}$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_{0} \leq x_{1}$$
Возьмём например точку
$$x_{0} = x_{1} — \frac{1}{10}$$
=
$$- \frac{1}{10} + \frac{\pi}{2}$$
=
$$- \frac{1}{10} + \frac{\pi}{2}$$
подставляем в выражение
$$\cos^{3}{\left (x \right )} \geq 0$$
$$\cos^{3}{\left (- \frac{1}{10} + \frac{\pi}{2} \right )} \geq 0$$
3
sin (1/10) >= 0
значит одно из решений нашего неравенства будет при:
$$x \leq \frac{\pi}{2}$$
_____ _____
\ /
-------•-------•-------
x1 x2Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ:
$$x \leq \frac{\pi}{2}$$
$$x \geq \frac{3 \pi}{2}$$
www.kontrolnaya-rabota.ru
Решите неравенство -cos(2*x)>0 (минус косинус от (2 умножить на х) больше 0)
Дано неравенство:$$- \cos{\left (2 x \right )} > 0$$
Чтобы решить это нер-во — надо сначала решить соотвествующее ур-ние:
$$- \cos{\left (2 x \right )} = 0$$
Решаем:
Дано уравнение
$$- \cos{\left (2 x \right )} = 0$$
— это простейшее тригонометрическое ур-ние
с изменением знака при 0
Получим:
$$- \cos{\left (2 x \right )} = 0$$
Разделим обе части ур-ния на -1
Ур-ние превратится в
$$\cos{\left (2 x \right )} = 0$$
Это ур-ние преобразуется в
$$2 x = \pi n + \operatorname{acos}{\left (0 \right )}$$
$$2 x = \pi n — \pi + \operatorname{acos}{\left (0 \right )}$$
Или
$$2 x = \pi n + \frac{\pi}{2}$$
$$2 x = \pi n — \frac{\pi}{2}$$
, где n — любое целое число
Разделим обе части полученного ур-ния на
$$2$$
$$x_{1} = \frac{\pi n}{2} + \frac{\pi}{4}$$
$$x_{2} = \frac{\pi n}{2} — \frac{\pi}{4}$$
$$x_{1} = \frac{\pi n}{2} + \frac{\pi}{4}$$
$$x_{2} = \frac{\pi n}{2} — \frac{\pi}{4}$$
Данные корни
$$x_{1} = \frac{\pi n}{2} + \frac{\pi}{4}$$
$$x_{2} = \frac{\pi n}{2} — \frac{\pi}{4}$$
являются точками смены знака неравенства в решениях.
Сначала определимся со знаком до крайней левой точки:
$$x_{0} Возьмём например точку
$$x_{0} = x_{1} — \frac{1}{10}$$
=
$$\frac{\pi n}{2} + \frac{\pi}{4} + — \frac{1}{10}$$
=
$$\frac{\pi n}{2} — \frac{1}{10} + \frac{\pi}{4}$$
подставляем в выражение
$$- \cos{\left (2 x \right )} > 0$$
/ /pi pi*n 1 \\
-cos|2*|-- + ---- - --|| > 0
\ \4 2 10// sin(-1/5 + pi*n) > 0
значит одно из решений нашего неравенства будет при:
$$x
_____ _____
\ /
-------ο-------ο-------
x1 x2Другие решения неравенства будем получать переходом на следующий полюс
и т.д.
Ответ:
$$x $$x > \frac{\pi n}{2} — \frac{\pi}{4}$$
www.kontrolnaya-rabota.ru
решение неравенство COSX = -0,5 помогите решить плиз
Такое простейшее уравнение решается классически: x 1 = — arccos(A) + 2 pi n, где n — целое число x 2 = arccos(A) + 2 pi n, где n — целое число
Тяжело отвечать на некорректные вопросы, но умные, образованные люди здесь вопросов не задают.. . Предупреждаю сразу, я не напишу ответов, поэтому не читай, если не хочешь разобраться и понять как решать. Для тупого списывания используй другие ответы или решебники. cosx = -0.5 — вообще-то, это равенство, а точнее, уравнение. В тригонометрии основой всех вычислений является окружность единичного радиуса. Каждая точка на окружности задает значения косинуса и синуса определенного угла, где косинус — абсцисса этой точки (проекция на ось Х) , а синус — ордината (проекция на ось У) . Угол в 0 радиан соответствует точке (1;0), т. е. для угла в 0 радиан косинус равен 1, а синус — 0. Отсчет остальных углов идет против часовой стрелки, либо по часовой стрелке, но угол тогда учитывается со знаком минус. Все это показано на этом рисунке: <img src=»//otvet.imgsmail.ru/download/9b0e06f9f60ee05ffd4294e3565cb7f5_i-1.gif» > Если косинус угла равен -0.5, то нужно отложить эту точку на оси Х и посмотреть, какой угол соответствует этому значению. Для этого можно условно провести вертикальную линию до пересечения с окружностью (как будто была из точек на окружности сделана проекция на ось Х) . Очевидно, что таких угла будет два. Один дает точку над осью Х, другой под. Рекомендую так же запомнить базовые значения косинусов и синусов для часто используемых углов в 30, 45 и 60 градусов (Пи / 6, Пи / 4, Пи / 3 — соответственно в радианах) . Полный круг соответствует углу 2*Пи (360 градусов) . Четверть круга соответственно Пи / 2 (90 градусов) . Теперь просто смотрим, какой угол у нас получается для обеих точек. Но надо не забыть, что все это повторяется каждый круг (+2Пи*n). Еще в случае с косинусом обычно точку под осью Х описывают отрицательным углом, он получается равным первому, но с отрицательным знаком, т. к. движение по окружности меняется в противоположную сторону. По идее этого должно хватить для решения, если что — задавай вопросы.
touch.otvet.mail.ru
