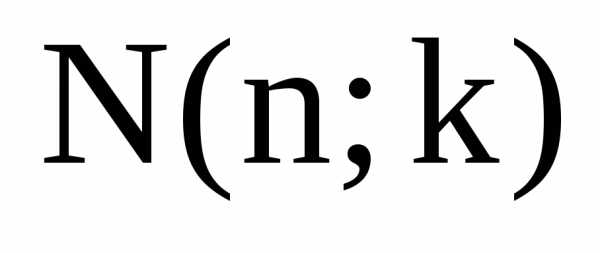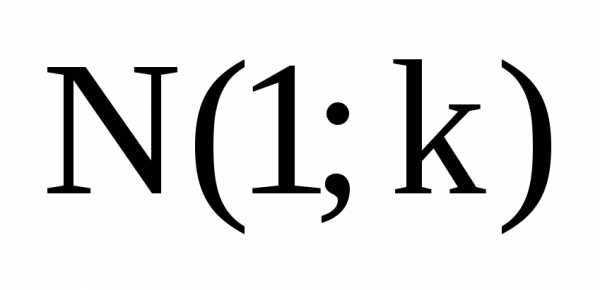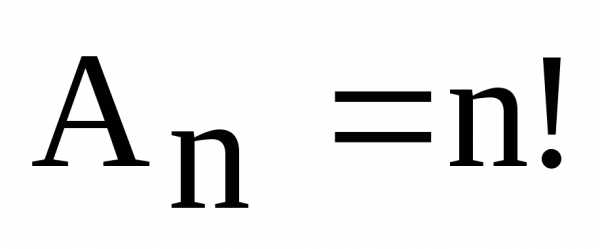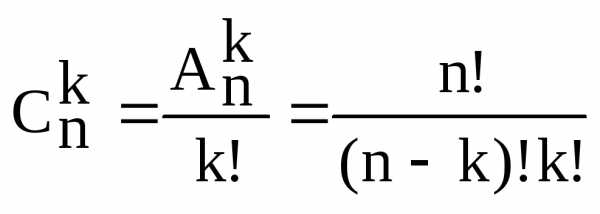Выбор без возвращения и без учёта порядка
Теорема 3. Общее количество различных наборов при выборе элементов из без возвращения и без учёта порядка равняется
и называется числом сочетаний из элементов по элементов.
Доказательство. Согласно следствию 1, различных номеров шаров можно упорядочить способами. Поэтому из каждого набора, выбранного без возвращения и без учёта порядка, можно образовать наборов, отличающихся друг от друга порядком следования номеров. Т.е. при выборе без возвращения и с учётом порядка возможно в раз больше наборов, чем при выборе без учёта порядка. Поэтому число наборов при выборе без учёта порядка равно
QED
Упражнение 4. Найти, сколько всего возможно различных результатов в следующих экспериментах:
а)
из колоды в 36 карт без возвращения, без учёта порядка вынимают три карты;
б)
из русского алфавита выбрасывают четыре буквы.
Выбор с возвращением и с учётом порядка
Теорема 4. Общее количество различных наборов при выборе элементов из с возвращением и с учётом порядка равняется .
Доказательство. Первый шар можно выбрать способами. При каждом из этих способов второй шар можно выбрать также способами, и так раз. Общее число наборов равно.
QED
Упражнение 5. Найти, сколько всего возможно различных результатов в следующих экспериментах:
а)
из колоды в 36 карт тянут три раза карту с учётом порядка и с возвращением;
б)
пятизначное число составляется из одних нечётных цифр;
в)
обезьяна напечатала на машинке слово из десяти букв.
Выбор с возвращением и без учёта порядка
Рассмотрим урну с двумя пронумерованными шарами и перечислим результаты выбора двух шариков из этой урны при выборе с возвращением.
с учётом порядка | без учёта порядка |
(1,1) | (1,1) |
(2,2) | (2,2) |
(1,2) (2,1) | } (1,2) |
Видим, что в схеме «без учёта порядка» получилось три различных результата, в отличие от четырёх результатов в схеме «с учётом порядка». Заметим также, что никаким делением на «число каких-нибудь перестановок», которое помогло избавиться от учёта порядка при выборе без возвращения, число 3 из числа 4 получить не удастся.
Теорема 5. Общее количество различных наборов при выборе элементов из с возвращением и без учёта порядка равняется
Упражнение 6. Проверить, что при и получается ровно 3.
Доказательство. Рассмотрим подробно, чем отличаются друг от друга два разных результата такой схемы выбора. Нам не важен порядок номеров, т.е. мы учитываем только, сколько раз в нашем наборе из номеров шаров появился каждый номер. Поэтому результат выбора можно представить набором чисел , в котором — число появлений шара номер в наборе, и . Числа принимают значения из . Два результата выбора в схеме выбора с возвращением и без учёта порядка различаются, если соответствующие им наборы не совпадают (порядок следования элементов учитывается).
Представим себе другой эксперимент, имеющий точно такие же результаты, и посчитаем их количество. Есть ящиков, в которых размещаются шаров. Нас интересует только число шаров в каждом ящике. Результатом эксперимента снова является набор чисел , где равно числу шаров в ящике с номером , и . Числа принимают натуральные значения или равны нулю.
А теперь изобразим результат такого размещения в виде схемы, в которой вертикальные линии обозначают перегородки между ящиками, а точки — находящиеся в ящиках шары:
Мы видим результат размещения девяти шаров по семи ящикам. Первый ящик содержит три шара, второй и шестой ящики пусты, третий ящик содержит один шар, в четвёртом и пятом ящиках лежит по два шара. Переложим один шар из первого ящика во второй и изобразим таким же образом ещё два результата размещения:
Видим, что все размещения можно получить, меняя между собой шары и перегородки, или расставляя шаров на местах. Число получается так: у ящиков есть ровно перегородка, считая крайние, но из них перемещать можно лишь внутреннюю перегородку. Таким образом, имеется мест, которые можно занять шарами либо внутренними перегородками. Перебрав все возможные способы расставить шаров на этих местах (заполняя оставшиеся места перегородками), переберем все нужные размещения.
Осталось заметить, что способов расставить шаров на местах существует
Именно столько есть способов выбрать из номеров мест номеров мест для шаров.
Упражнение 7.
а)
Найти количество способов разложить натуральное число в сумму целых неотрицательных слагаемых, если важен порядок следования этих слагаемых.
б)
Найти число различных производных порядка функции переменных.
в)
Найти число возможных результатов подбрасывания двух игральных костей, если кости считаются неразличимыми. То же самое для трёх игральных костей.
studfiles.net
Выбор с возвращением.
Выборка с возвращением, упорядоченная. | Выборка с возвращением, неупорядоченная. |
Имеется хранилище с n различными предметами. Имеется k занумерованных ящиков. Из хранилища берем один случайный предмет. Информацию о нем фиксируем в первой ячейке. Сам предмет возвращаем в хранилище. Затем берем следующий предмет и информацию фиксируем во второй ячейке. И т.д. В данной схеме различными считаются варианты, которые отличаются хотя бы одной позицией. Общее
число |
Имеется хранилище с n различными предметами.
Имеется ящик объемом k. Из хранилища берем один случайный предмет. Информацию о нем фиксируем в ящике. Сам предмет возвращаем в хранилище. Затем берем следующий предмет и информацию фиксируем в ящике. И т.д. В данной схеме различными считаются варианты, которые отличаются набором элементов. Доказательство. Используем математическую индукцию.
K=1; 2.
Предположим, что для некоторого k
N(p
, k
) = Докажем,
что для k+1
формула справедлива а – наименьший номер элемента попавшего во второе хранилище. Если а = 1, то оставшиеся k позиций могут быть заполнены . a=1
→ a=2 → a=3 → ….. a=n-1
→ a=n
→
|
Выборка без возвращения.
Выборка без возвращения, упорядоченная. | Выборка без возвращения, неупорядоченная. |
Имеется хранилище с n различными предметами. Имеется k занумерованных ящиков. Из хранилища берем один случайный предмет и кладем в первую ячейку. Затем берем следующий предмет и кладется во вторую ячейку. И т.д. Любой вариант заполнения упорядоченной выборки без возвращения, называется размещением. Два размещения считаются различными, если они отличаются хотя бы одной позицией. Есть особый случай размещения предметов n=k. Размещение n различных предметов по n ячейкам, называется перестановками.
|
Имеется хранилище с n различными предметами. Имеется ящик объемом k. Из хранилища берем один случайный предмет и кладем в ящик. Затем берем следующий предмет и кладем в ящик. И т.д. Неупорядоченная выборка в процедуре выбора без возвращения, называется сочетанием. Два сочетания считаются различными, если они отличаются набором элементов.
|
Размещения с повторениями.
Имеется хранилище с n предметами, но среди них, n1 – предметов одного типа (неотличимых друг от друга) n2 – предметов второго типа и n3 – предметов третьего типа… nm– предметов m-ого типа. n1+ n2+…+ nm= n.
Размещением такой совокупности предметов по n занумерованным ячейкам, называется размещением с повторениями.
Два размещения с повторениями считаются различными, если они отличаются хотя бы одной позицией.
Общее количество размещений с повторениями.
studfiles.net
Схема выбора без возвращений — МегаЛекции
Элементы комбинаторики
Согласно классическому определению подсчет вероятности события А сводится к подсчету числа благоприятствующих ему исходов. Делают это обычно комбинаторными методами.
Комбинаторика — раздел математики, в котором изучаются задачи выбора элементов из заданного множества и расположения их в группы по заданным правилам, в частности задачи о подсчете числа комбинаций (выборок), получаемых из элементов заданного конечного множества. В каждой из них требуется подсчитать число возможных вариантов осуществления некоторого действия, ответить на вопрос «сколькими способами?».
Многие комбинаторные задачи могут быть решены с помощью следующих двух важных правил, называемых соответственно правилами умножения и сложения.
Правило умножения. Если из некоторого конечного множества первый объект (элемент х) можно выбрать n1 способами и после каждого такого выбора второй объект (элемент у) можно выбрать n2 способами, то оба объекта (х и у) в указанном порядке можно выбрать n1∙n2 способами.
Этот правило распространяется на случай трех и более объектов.
Пример 2.1.Сколько трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, если а) цифры не повторяются? б) цифры могут повторяться?
Решение:
а) Имеется 5 различных способов выбора первой цифры в числе. После того как первую цифру выбрали, осталось четыре цифры для выбора второй цифры числа. Для выбора третьей цифры числа остается три цифры. Следовательно, согласно правила умножения имеем способов расстановки цифр, т.е искомое число трехзначных чисел — 60.
б) если цифры могут повторятся, то трехзначных чисел .
Правило суммы. Если некоторый объект х можно выбрать n1 способами, а объект у можно выбрать n2 способами, причем первые и вторые способы не пересекаются, то любой из указанных объектов (х или у), можно выбрать n1 + n2 способами.
Это правило распространяется на любое конечное число объектов.
Пример 2.2. В студенческой группе 14 девушек и 6 юношей. Сколькими способами можно выбрать для выполнения различных заданий двух студентов одного пола?
Решение:
По правилу умножения двух девушек можно выбрать 14∙13=182 способами, а двух юношей — 6∙5=30. Следует выбрать 2 студентов одного пола: 2 студенток или 2 юношей. Согласно правилу сложения таких способов будет 182+30 = 212.
Решение вероятностных задач часто облегчается, если использовать комбинаторные формулы. Каждая из них определяет число всевозможных исходов в некотором опыте, состоящем в выборе наудачу r элементов из n различных элементов рассматриваемого множества.
Существуют две схемы выбора r элементов (0< r ≤ n) из исходного множества: без возвращения (без повторений) и с возвращением (с повторениями). В первом случае выбранные элементы не возвращаются обратно; можно отобрать сразу все r элементов или отбирать их по одному. Во второй схеме выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге.
Схема выбора без возвращений
Пусть дано множество, состоящее из n различных элементов.
Размещением из n элементов по r элементов (0< r ≤ n) называется любое упорядоченное подмножество данного множества, содержащее r элементов.
Из определения вытекает, что размещения – это выборки, состоящие из r элементов, которые отличаются друг от друга либо составом элементов, либо порядком их расположения. Число размещений из n элементов по r элементов обозначается символом и вычисляется по формуле:
| , | (2.1) |
или
| , | (2.2) |
где , ,
Для составления размещения надо выбрать r элементов из множества с n элементами и упорядочить их, т.е. заполнить r мест элементами множества. Первый элемент можно выбрать n способами, т.е. на первое место можно поместить любой из n элементов. После этого второй элемент можно выбрать из оставшихся n-1 элементов n-1 способами. Для выбора третьего элемента имеется n-2 способа, четвертого — n-3 способа, и наконец, для последнего r-го элемента — (n-(r-1)) способов. Таким образом, по правилу умножения, существует n(n-1)( n-2) … (n-(r-1)) способов выбора r элементов из данных n элементов, т.е. .
Пример 2.3. Составить различные размещения по 2 элемента из множества и подсчитать их число.
Решение:
Из трех элементов можно образовать следующие размещения по два элемента:
(a, b), (a, c), (b, a), (c, a), (b, c), (c, b).
Согласно формуле (2.2) их число
.
Перестановкой из n элементов называется размещение из n элементов по n элементов.
Из определения вытекает, что перестановки – это выборки, состоящие из n элементов и отличающиеся друг от друга только порядком следования элементов. Число перестановок из n элементов обозначается символом Рn и вычисляется по формуле:
Формула следует из определения перестановки:
| (2.4) |
Пример 2.4. Сколько различных перестановок можно составить из элементов множества ?
Решение:
Из элементов данного множества можно составить следующие перестановки:
(2, 7, 8), (2, 8, 7), (7, 2, 8), (7, 8, 2), (8, 2, 7), (8, 7, 2).
По формуле (2.3) имеем
.
Сочетанием из n элементов по r (0 ≤ r ≤ n) элементов называется любое подмножество, которое содержит r элементов данного множества.
Из определения вытекает, что сочетания – это выборки, каждая из которых состоит из r элементов, взятых из данных n элементов, которые отличаются друг от друга хотя бы одним элементом.
Число сочетаний из n элементов по r элементов обозначается символом и вычисляется по формуле:
| . | (2.5) |
или
| . | (2.6) |
Число размещений из n элементов по r элементов можно найти следующим образом: выбрать r элементов из множества, содержащего n элементов, затем в каждом из полученных сочетаний сделать все перестановки для упорядочивания подмножеств. Следовательно, согласно правилу умножения можно записать: , Отсюда или .
Можно показать, что имеют место формулы:
Пример 2.5.Сколькими способами можно выбрать 3 цветка из вазы, в которой стоят 10 красных и 4 розовых гвоздики? Если выбрать 1 красную и 2 розовых гвоздики?
Решение:
Так как порядок выбора цветов не имеет значения, то выбрать 3 цветка из вазы, в которой стоят 14 гвоздик, можно способами. По формуле (2.6) находим, что
.
Красную гвоздику можно выбрать способами. Выбрать две розовые из четырех имеющихся можно способами. По правилу произведения букет из одной красной и двух розовых гвоздик можно составить способами.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
0/ /Выбор с возвращением и с учётом порядка.
Теорема 4. Общее количество различных наборов при выборе k элементов из n с возвращением и с учётом порядка равняется nk.
Доказательство. Первый шар можно выбрать n способами. При каждом из этих способов второй шар можно выбрать также n способами, и так k раз. Общее число наборов равно n . n .… . n=n!
Выбор с возвращением и без учёта порядка.
Рассмотрим урну с двумя пронумерованными шарами и перечислим результаты выбора двух шариков из этой урны при выборе с возвращением.
С учётом порядка | Без учёта порядка |
(1,1) | (1,1) |
(2,2) | (2,2) |
(1,2) (2,1) | } (1,2) |
Видим, что в схеме «без учёта порядка» получилось три различных результата, в отличие от четырёх результатов в схеме «с учётом порядка». Заметим также, что никаким делением на «число каких-нибудь перестановок», которое помогло избавиться от учёта порядка при выборе без возвращения, число 3 из числа 4 получить не удастся.
Теорема 5. Общее количество различных наборов при выборе k элементов из n с возвращением и без учёта порядка равняется
Доказательство. Рассмотрим подробно, чем отличаются друг от друга два разных результата такой схемы выбора. Нам не важен порядок номеров, т.е. мы учитываем только, сколько раз в нашем наборе из k номеров шаров появился каждый номер. Поэтому результат выбора можно представить набором чисел k1, k2,…, kn, в котором ki — число появлений шара номер i в наборе, и k1+ k1+…+ kn=k. Числа ki принимают значения из . Два результата выбора в схеме выбора с возвращением и без учёта порядка различаются, если соответствующие им наборы k1, k2,…, kn не совпадают (порядок следования элементов ki учитывается).
Представим себе другой эксперимент, имеющий точно такие же результаты, и посчитаем их количество. Есть n ящиков, в которых размещаются k шаров. Нас интересует только число шаров в каждом ящике. Результатом эксперимента снова является набор чисел k1, k2,…, kn, где ki равно числу шаров в ящике с номером i, и k1+ k1+…+ kn=k. Числа ki принимают натуральные значения или равны нулю.
А теперь изобразим результат такого размещения в виде схемы, в которой вертикальные линии обозначают перегородки между ящиками, а точки — находящиеся в ящиках шары:
| . . . | | . | . . | . . | | . |
Мы видим результат размещения девяти шаров по семи ящикам. Первый ящик содержит три шара, второй и шестой ящики пусты, третий ящик содержит один шар, в четвёртом и пятом ящиках лежит по два шара. Переложим один шар из первого ящика во второй и изобразим таким же образом ещё два результата размещения:
| . . | . | . | . . | . . | | . | | | | | | | | . . . . . . . . . |
Видим, что все размещения можно получить, меняя между собой шары и перегородки, или расставляя k шаров на n-1+k местах. Число n-1+k получается так: у n ящиков есть ровно n+1 перегородка, считая крайние, но из них перемещать можно лишь n-1 внутреннюю перегородку. Таким образом, имеется n-1+k мест, которые можно занять шарами либо внутренними перегородками. Перебрав все возможные способы расставить k шаров на этих n-1+k местах (заполняя оставшиеся места перегородками), переберем все нужные размещения.
Осталось заметить, что способов расставить k шаров на n-1+k местах существует
Именно столько есть способов выбрать из n-1+k номеров мест k номеров мест для шаров.
studfiles.net
выбор с возвращением и без учета порядка
Теорема 5.
Общее количество выборок в схеме выбора элементов из с возвращением и без учета порядка определяется формулой
Теорема сложения вероятностей.
Рассмотрим теоремы, позволяющие вычислить вероятность появления события А или В в результате одного испытания, т.е. вероятность суммы этих событий А+В. Возможны два случая: события совместны и несовместны.
Теорема1: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).
Доказательство:
Число всех исходов N, число исходов благоприятствующих событию А- К, событию В- L. Так как А и В несовместны, то ни один из этих исходов не может благоприятствовать А и В одновременно, т.е. А и В взаимно исключающие, следовательно число благоприятствующих исходов для события А+В равно К+L. Тогда вероятность равна
Теорема2: Вероятность суммы двух совместных событий А и В равна сумме их вероятностей без вероятности их совместного появления, т.е. Р(А+В)=Р(А)+Р(В)-Р(АВ).
Доказательство:
Всего исходов N, благоприятствующих событию А- К, событию В- L, совместному появлению А и В- М. Следовательно, благоприятных исходов для события А+В : K+L—M. Откуда вероятность события А+В:
Сумма и произведение совместных событий и их геометрическая интерпретация.
Суммой двух событий А и В называется событие С, состоящее в появлении или события А или события В или их вместе.
хотя бы одно из событий А или В. С=А+В Геометрическая интерпретация
u– множество исходов некоторого опыта.
Произведением двух событий А и В называется событие С, состоящее в одновременном появлении события А и В. С=А*В
Разностью событий А и В называется событие С, состоящее в появлении события А и не появлении события В С=А\В.
Два случайных события называются противоположными, если одно из них происходит в том и только в том случае, когда не происходит другое. . А+=U A*=V–невозможно.
Зависимые и независимые события. Теорема умножения вероятностей.
Теорема умножения вероятностей.
Теорема 2.3 (теорема умножения). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло:
р (АВ) =р (А) ·р (В/А). (2.6)
Доказательство.
Воспользуемся обозначениями теоремы 2.1. Тогда для вычисления р(В/А) множеством возможных исходов нужно считатьтА (так какАпроизошло), а множеством благоприятных исходов – те, при которых произошли иА, иВ(тАВ ). Следовательно,
откуда следует утверждение теоремы.
Следствие. Если подобным образом вычислить вероятность событияВА, совпадающего с событиемАВ, то получим, чтор (ВА) =р (В) ·р (А/В). Следовательно,
р (А) ·р (В/А) =р (В) ·р (А/В). (2.7)
Событие Вназываетсянезависимым от событияА, если появление событияАне изменяет вероятностиВ, то естьр (В/А) =р(В).
Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий, в противном случае события называют зависимыми.
Если событие Вне зависит отА, то иАне зависит отВ. Действительно, из (2.7) следует при этом, чтор (А) ·р (В) =р (В) ·р (А/В), откудар (А/В) =р (А). Значит,свойство независимости событий взаимно.
Теорема умножения для независимых событий имеет вид:
р (АВ) =р (А) ·р (В) , (2.8)
то есть вероятность произведения независимых событий равна произведению их вероят-ностей.
При решении задач теоремы сложения и умножения обычно применяются вместе.
studfiles.net
Схема выбора с возвращением.
Если при выборке элементов из элементы возвращаются обратно и упорядочиваются, то говорят, что это размещения с повторениями.
Вычисляются по формуле
.
Пример 10. Сколько пятизначных чисел можно составить, используя цифры 2, 5, 7, 8?
Решение. Все пятизначные числа, составленные из заданных цифр, могут отличаться либо порядком их следования, либо самими цифрами, следовательно, они являются размещениями из 4-х элементов по 5 с повторениями.
= 45= 1024 (этот результат можно получить, используя правило умножения).
Если при выборке элементов из элементов множества элементы возвращаются, но не упорядочиваются, то говорят, что это сочетания с повторениями.
.
Пример 11. Сколькими способами можно составить букет из 5 цветов, если в наличии есть цветы трех сортов?
Решение. Рассматриваемое множество состоит из трех различных элементов, а выборки имеют объем, равный 5. Поскольку порядок расположения цветов в букете не играет роли, то искомое число букетов равно числу сочетаний с повторениями из трех элементов по 5 в каждом. По формуле имеем
Пусть во множестве из элементов есть различных элементов, при этом 1-ый элемент повторяется раз, второй элемент – раз,…, -тый элемент – раз, причем . Перестановки из элементов данного множества называют перестановками с повторениями из элементов
Пример 12. Сколько различных пятизначных чисел можно составить из цифр 3,3,5,5,8?
Решение. Всего элементов 5 ( ).
Первый элемент 3 повторяется 2 раза, следовательно,
.
Второй элемент 5 повторяется 2 раза,
Третий элемент 8 повторяется 1 раз,
Похожие статьи:
poznayka.org
Элементы комбинаторики. Модели случайного выбора
Вопросы, которые рассматриваются в этом параграфе, не имеют особого значения с точки зрения общей теории, так как здесь изучается некоторая частная модель, связанная с классическим определением вероятности. Но модели случайного выбора широко используются в экономике, социологии, демографии и других науках. В силу этого они очень важны с практической точки зрения.
Как мы видели выше, при классическом определении вероятности нам нужно решить две задачи: вычислить число всех элементарных исходов и число благоприятных исходов для события А. Обычно это сводится к подсчету того, сколькими способами может быть выполнено некоторое действие, т. е. сколько существует вариантов. Задачами такого типа занимается специальный раздел математики, называемыйкомбинаторикой. Мы начнем изучение основ комбинаторики с одной элементарной, но очень полезной леммы.
Лемма 1 (умножения). Пусть некоторое действие осуществляется в два этапа. На первом этапе мы имеем вариантов его осуществления, а на втором, независимо от того, что произошло на первом этапе,- вариантов. Тогда общее число вариантов осуществления такого действия равно
Доказательство этой леммы сводится к установлению взаимно однозначного соответствия между двухэтапными вариантами и клетками таблицы размера
Нас в основном будут интересовать задачи комбинаторики, которые можно сформулировать в терминах выбора некоторого количества предметов из заданной совокупности При этом необходимо учитывать два обстоятельства: как производился выбор и как фиксировался результат выбора. В первом случае мы имеем два варианта: выбор с повторением, когда на каждом этапе выбранный предмет возвращается назад и выбор производится из одной и той же совокупности; выбор без повторения, когда выбранный на некотором шаге предмет уже не используется в дальнейшем. При фиксации результата мы также имеем два варианта: с учетом порядка (в этом случае мы знаем, какие выбраны предметы и в каком порядке) и без учета порядка (здесь мы знаем только, какие были выбраны предметы, но не имеем информации о порядке их появления). Имея в виду вероятностные и статистические применения рассматриваемых задач, мы будем называть результат выбора элементарным исходом или выборкой. Число элементов в выборке называется ееобъемом. Рассмотрим несколько стандартных примеров.
Определение 1. Размещением с повторением изэлементов по называется произвольная упорядоченная выборка с возвращением, объемаиз совокупности
В этом случае , где. Используя лемму
умножения, легко подсчитать, что число различных элементарных исходов будет равно
Определение 2. Размещением (без повторения) из элементов по называется произвольная упорядоченная выборка без возвращения объема из совокупности
Здесь . Вновь по лемме
умножения получаем ,что число различных размещений равно
Если , то такое размещение называется перестановкой. Число различных перестановок элементов равно
Определение 3. Сочетанием (без повторений) из элементов по называется произвольная неупорядоченная выборка без возвращения объема из совокупности
В этом случае мы отмечаем только, какие именно элементы вошли в эту выборку, и не учитываем порядок их появления. Поэтому для каждого элемента достаточно указать, входит он в выборку или нет. Таким образом, , где , если входит в выборку , и равно 0 в противном случае. Из каждого сочетания, переставляя его элементы, мы получаем различных размещений. В силу этого число сочетаний в раз меньше числа размещений, т. е.
Определение 4. Сочетанием с повторением из элементов по называется произвольная неупорядоченная выборка с возвращением объема из совокупности
Так как теперь один элемент может входить в выборку несколько раз, то элементарный исход имеет вид , где означает, что элемент входит в выборку раз. Для подсчета числа таких выборок применим следующий вспомогательный прием. Выпишем сначала все элементы , затем и так далее. Между элементами разных типов поставим перегородки. Таким образом, мы имеем элементов и перегородку. Если каких-то элементов нет, то перегородки стоят рядом. Для задания сочетания с повторением достаточно расставить перегородку на возможных мест без учета порядка. Это можно сделать способами.
Рассмотрим два важных с практической точки зрения примера.
Пример 1. Пусть мы имеем некоторую совокупность, содержащую предметов, из которых — одного типа и — другого типа. С возвращением выбираем предметов из этой совокупности. Найти вероятность события того, что среди них будет предметов первого типа.
Так как выбор осуществляется с возвращением, то мы имеем всего различных элементарных исходов в этой задаче. Благоприятные исходы легче пересчитать, используя следующее замечание. Сначала мы должны выбрать, на каких шагах мы будем отбирать предметы первого типа. Это можно сделать способами. Затем на каждом из этих шагов мы имеем вариантов, а на остальных- вариантов. По лемме умножения число благоприятных исходов будет равно . Если обозначить через долю предметов первого типа во всей совокупности, то получим
Пример 2. Пусть мы имеем ту же задачу, что и в примере 1, но выбор осуществляется без возвращения.
В этом примере удобнее фиксировать результат без учета порядка следования элементов. Тогда общее число элементарных исходов . Для получения благоприятного исхода нужно в два этапа набрать элементов первого типа (из ) и элементов второго типа (из ), т. е. по лемме умножения . Тогда по классическому определению вероятности получаем
Задача 1. Пусть в примере так что (0,1), а и — фиксированы. Тогда
Таким образом, в этом случае выбор с возвращением и выбор без возвращения эквивалентны. Легко понять, почему так получилось. Дело в том, что для больших совокупностей удаление небольшого числа элементов не меняет практически пропорций, т. е. мы имеем на каждом шаге выбор из той же совокупности.
Пример 3. В некотором городе живет 100 ООО человек, среди которых 60 ООО женщин. Для проведения социологического обследования производят выборку объема 500. Найти вероятность того, что среди них будет 300женщин.
Так как отбор 500 человек не изменит существенно пропорций, то можно считать, что мы имеем выбор с возвращением. Здесь
. Тогда
Примеры 1 и 2 можно обобщить на случай выбора из совокупностей, где есть предметы типов
itteach.ru

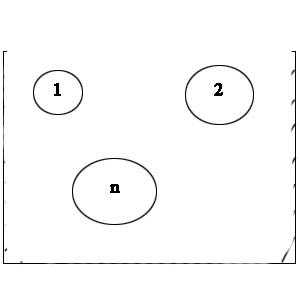
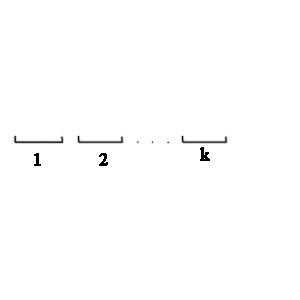
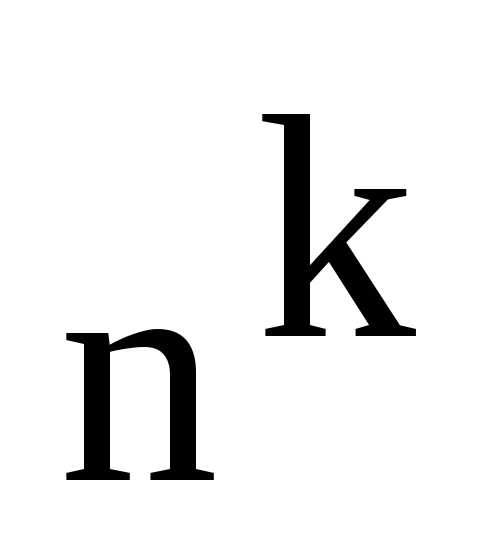 ;
; 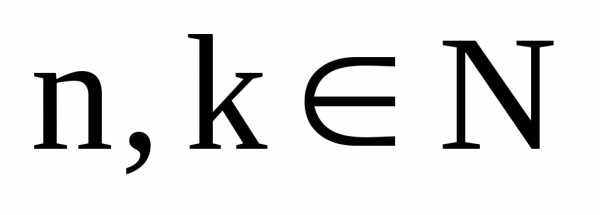
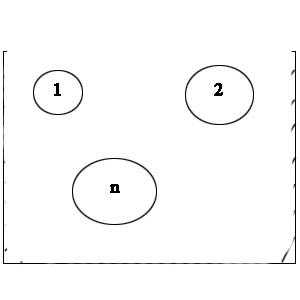

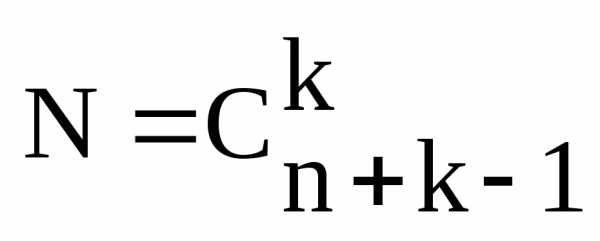

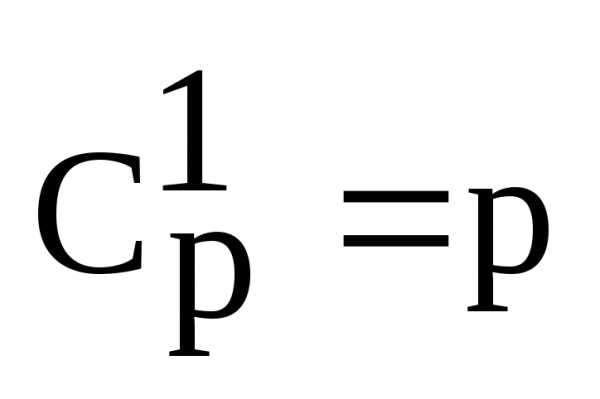
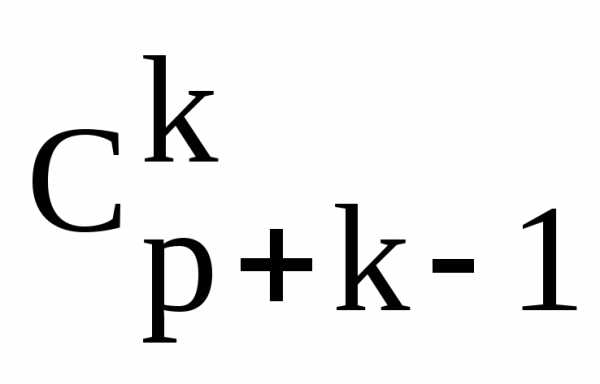
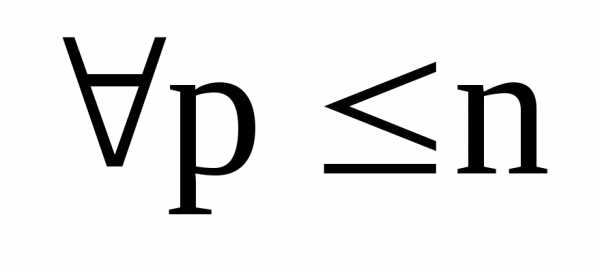
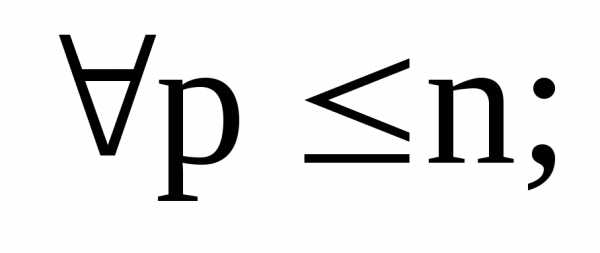 .
.