Рассчитать график смен онлайн
Вы можете рассчитать любой график сменности за несколько секунд!
Укажите дату Вашего первого рабочего дня:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 Январь Февраль Март Апрель Май Июнь Июль Август Сентябрь Октябрь Ноябрь Декабрь 2017 2018 2019 2020 2021 2022 2023 2024 2025 2026 2027 2028 2029 2030
Укажите ваш тип сменности:
1 2 3 4 5 6 7 × 1 2 3 4 5 6 7
Сколько часов длится ваша смена:
Доп. настройкиОтметьте, если первая смена — ночь ()
На какое количество месяцев рассчитать график: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
Рассчитать график смен онлайн!
| Июнь 2019 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| Смен в этом месяце: 12 Всего часов: 132 | ||||||
| Июль 2019 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 24 | 25 | 26 | 27 | 28 | |
| 29 | 30 | 31 | ||||
| Смен в этом месяце: 16 Всего часов: 176 | ||||||
| Август 2019 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | |
| Смен в этом месяце: 16 Всего часов: 176 | ||||||
| Сентябрь 2019 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | ||||||
| Смен в этом месяце: 14 Всего часов: 154 | ||||||
| Октябрь 2019 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 | |||
| Смен в этом месяце: 16 Всего часов: 176 | ||||||
| Ноябрь 2019 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | |
| Смен в этом месяце: 15 Всего часов: 165 | ||||||
| Декабрь 2019 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | |||||
| Смен в этом месяце: 15 Всего часов: 165 | ||||||
| Январь 2020 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 | ||
| Смен в этом месяце: 16 Всего часов: 176 | ||||||
| Февраль 2020 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | ЧТ | ПТ | СБ | ВС | |
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | |
| Смен в этом месяце: 14 Всего часов: 154 | ||||||
| Март 2020 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 | 31 | |||||
| Смен в этом месяце: 16 Всего часов: 176 | ||||||
| Апрель 2020 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | |||
| Смен в этом месяце: 15 Всего часов: 165 | ||||||
| Май 2020 | ||||||
|---|---|---|---|---|---|---|
| ПН | ВТ | СР | ЧТ | ПТ | СБ | ВС |
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
| Смен в этом месяце: 15 Всего часов: 165 | ||||||
Смен за рассчитанный Вами период: 180
Всего рабочих часов: 1980
Ваш график всегда под рукой! Просто сохраните ссылку на него в закладки:
http://grafik-smen.ru/
Скопировать ссылку:
http://grafik-smen.ru/»
Последние расчёты
Сменный график работы для многих очень удобен, так как позволяет иметь больше выходных дней в неделю в отличии от пятидневневки. Но несмотря на привлекательность такого формата, не легко высчитать на продолжительный период времени, какие дни будут являться выходными, а какие рабочими. А ведь хочется знать, как выпадет ваш график смен на день рождения, Новый Год, или субботу и воскресенье.
Наш сервис решает эту проблему! Благодаря Grafik-Smen.Ru у Вас есть возможность составить свой график смен на любой период. Также Вы можете сохранить постоянную ссылку в закладки браузера, и открывать свой график смен в один клик даже со смартфона! Для того чтобы составить свой график смен, вам нужно выполнить всего лишь три действия: указать первый рабочий день, выбрать формат графика работы, нажать на кнопку. Поздравляем! Ваш график смен уже доступен для Вас в любое время и в любом месте.
grafik-smen.ru
| Название функции | Формула функции | График функции | Название графика | Комментарий |
|---|---|---|---|---|
| Линейная, прямая пропорциональность | y = kx | 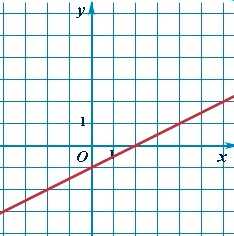 |
Прямая | Cамый простой частный случай линейной зависимости — прямая пропорциональность у = kx, где k ≠ 0 — коэффициент пропорциональности. На рисунке пример для k = 1, т.е. фактически приведенный график иллюстрирует функциональную зависимость, которая задаёт равенство значения функции значению аргумента. |
| Линейная, прямая пропорциональность со сдвигом | y = kx + b | Прямая | Общий случай линейной зависимости: коэффициенты k и b — любые действительные числа. Здесь k = 0.5, b = -1. | |
| Квадратичная функция | y = x2 | 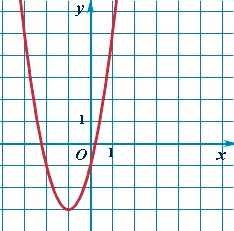 |
Парабола | Простейший случай квадратичной зависимости — симметричная парабола с вершиной в начале координат. |
| Квадратичная функция | y = ax2 + bx + c | 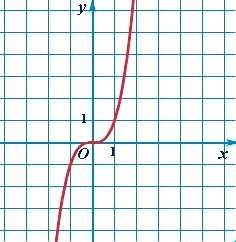 |
Парабола | Общий случай квадратичной зависимости: коэффициент a — произвольное действительное число не равное нулю (a принадлежит R, a ≠ 0), b, c — любые действительные числа |
| Степенная функция | y = x3 | 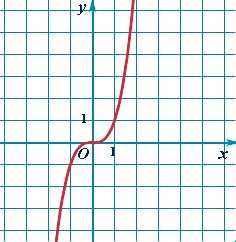 |
Кубическая парабола | Самый простой случай для целой нечетной степени. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
| Степенная — корень квадратный | y = x1/2 |  |
График функции y = √x |
Самый простой случай для дробной степени (x1/2 = √x). Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
| Степенная — обратная пропорциональность | y = k/x | 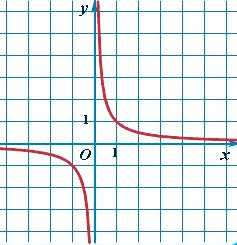 |
Гипербола | Самый простой случай для целой отрицательной степени (1/x = x-1) — обратно-пропорциональная зависимость. Здесь k = 1. |
| Показательная функция | y = ex | Экспонента | Экспоненциальной зависимостью называют показательную функцию для основания e — иррационального числа примерно равного 2,7182818284590… | |
| Показательная функция | y = ax | График показательной функции а>1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 2x (a = 2 > 1). | |
| Показательная функция | y = ax | График показательной функции 0<a<1 | Показательная функция определена для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = 0,5x (a = 1/2 < 1). | |
| Логарифмическая функция | y = ln(x) | График логарифмической функции — натуральный логарифм | График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой. | |
| Логарифмическая функция | y = logax | График логарифмической функции — логарифм по основанию а>1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log2x (a = 2 > 1). | |
| Логарифмическая функция | y = logax | График логарифмической функции 0<a<1 | Логарифмы определены для a > 0 и a ≠ 1. Графики функции существенно зависят от значения параметра a. Здесь пример для y = log0,5x (a = 1/2 < 1). | |
| Синус | y = sinx | Синусоида | Тригонометрическая функция синус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Косинус | y = cosx | Косинусоида | Тригонометрическая функция косинус. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Тангенс | y = tgx | Тангенсоида | Тригонометрическая функция тангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». | |
| Котангенс | y = сtgx | Котангенсоида | Тригонометрическая функция котангенс. Случаи с коэффициентами изучаются в разделе «Преобразование графиков функций». |
tehtab.ru
Свойства функции y = cosx и её график — урок. Алгебра, 10 класс.
Функция y=cosx определена на всей числовой прямой, и множеством её значений является отрезок −1;1.
Следовательно, график этой функции расположен в полосе между прямыми y=−1 и y=1.
Так как функция y=cosx периодическая с периодом 2π, то достаточно построить её график на каком-нибудь промежутке длиной 2π, например, на отрезке −π≤x≤π, тогда на промежутках, получаемых сдвигами выбранного отрезка на 2πn,n∈ℤ, график будет таким же.
Функция y=cosx является чётной. Поэтому её график симметричен относительно оси \(Oy\).
Для построения графика на отрезке −π≤x≤π достаточно построить его для 0≤x≤π, а затем симметрично отразить его относительно оси \(Oy\).
Найдём несколько точек, принадлежащих графику на этом отрезке 0≤x≤π: cos0=1;cosπ6=32;cosπ4=22;cosπ3=12;cosπ2=0;cosπ=−1.
Итак, график функции y=cosx построен на всей числовой прямой.
Свойства функции y=cosx
1. Область определения — множество ℝ всех действительных чисел.
2. Множество значений — отрезок −1;1.
3. Функция y=cosx периодическая с периодом 2π.
4. Функция y=cosx — чётная.
5. Функция y=cosx принимает:
— значение, равное \(0\), при x=π2+πn,n∈ℤ;
— наибольшее значение, равное \(1\), при x=2πn,n∈ℤ;
— наименьшее значение, равное \(-1\), при x=π+2πn,n∈ℤ;
— положительные значения на интервале −π2;π2 и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈ℤ;
— отрицательные значения на интервале π2;3π2 и на интервалах, получаемых сдвигами этого интервала на 2πn,n∈ℤ.
6. Функция y=cosx:
— возрастает на отрезке π;2π и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈ℤ;
— убывает на отрезке 0;π и на отрезках, получаемых сдвигами этого отрезка на 2πn,n∈ℤ.
www.yaklass.ru
