Что такое синус угла

Содержание

Что такое синус?

Эта тема доставляет массу проблем ученикам. Считается одной из самых суровых. Что такое синус и косинус? Что такое тангенс и котангенс? Что такое числовая окружность? Стоит задать эти безобидные вопросы, как человек бледнеет и пытается увести разговор в сторону… А зря. Это простые понятия. И ничем эта тема не сложнее других. Просто нужно с самого начала чётко уяснить ответы на эти самые вопросы. Это очень важно. Если уяснили – тригонометрия вам понравится. Итак,

Что такое синус и косинус? Что такое тангенс и котангенс?

Синус:

* Синус — одна из тригонометрических функций.

* Гиперболический синус — одна из гиперболических функций.
* Интегральный синус — одна из специальных функций.

* Синус (лат. sinus — пазуха, залив) — пазуха, углубление, полость, выпячивание, длинный замкнутый канал; пазуха (канал) твёрдой мозговой оболочки у позвоночных животных и человека, наполненный венозной кровью (венозная пазуха), полость некоторых черепных костей (придаточные пазухи носа).

* Каротидный синус — место расширения общей сонной артерии перед разветвлением её на наружную и внутреннюю.
* Синус аорты (пазуха аорты) — у млекопитающих животных — начальная, расширенная часть восходящей аорты, то же, что аортальная луковица; у человека — часть полости аортальной луковицы, расположенная между полулунным клапаном и стенкой аорты.
* Синусы твёрдой мозговой оболочки (синусы головного мозга, венозные синусы, венозные пазухи) — венозные коллекторы, расположенные между листками твёрдой мозговой оболочки.
* Венозный синус (ланцетник) — у ланцетника, не имеющего сердца — непарный сосуд, собирающий венозную кровь из печёночной вены и кювьеровых протоков и переходящий в брюшную аорту.
* Венозный синус (низшие позвоночные) — у низших позвоночных (круглоротых, рыб и земноводных) — отдел сердца.
* Венозные лакуны — венозный синус у ряда беспозвоночных.

Начнём с глубокой древности. Не волнуйтесь, все 20 веков тригонометрии мы пройдём минут за 15. И, незаметно для себя, повторим кусочек геометрии из 8 класса.

Напомню, что стороны, которые образуют прямой угол, называются катетами. а и в – катеты. Их два. Оставшаяся сторона называется гипотенузой. с – гипотенуза.

Треугольник и треугольник, подумаешь! Что с ним делать? А вот древние люди знали, что делать! Повторим их действия. Измерим сторону в. На рисунке специально клеточки нарисованы, как в заданиях ЕГЭ бывает. Сторона в равна четырём клеточкам. Ладно. Измерим сторону а. Три клеточки.

А теперь поделим длину стороны а на длину стороны в. Или, как ещё говорят, возьмём отношение а к в. а/в = 3/4.

Можно наоборот, поделить в на а. Получим 4/3. Можно в поделить на с. Гипотенузу с по клеточкам не посчитать, но она равна 5. Получим в/с = 4/5. Короче, можно делить длины сторон друг на друга и получать какие-то числа.

Ну и что? Какой смысл в этом интересном занятии? Пока никакого. Бестолковое занятие, прямо скажем.

А теперь сделаем вот что. Увеличим треугольник. Продлим стороны в и с, но так, чтобы треугольник остался прямоугольным. Угол х, естественно, не меняется. Чтобы это увидеть, наведите курсор мышки на картинку. Кликать не надо, ничего интересного не будет. Просто наведите. а, в и с превратятся в m, n, k, и, понятное дело, длины сторон изменятся.

А вот их отношения – нет!

Отношение а/в было: а/в = 3/4, стало m/n = 6/8 = 3/4. Отношения других соответствующих сторон также не изменятся. Можно как угодно менять длины сторон в прямоугольном треугольнике, увеличивать, уменьшать, не меняя угла х – отношения соответствующих сторон не изменятся. Можно проверить, а можно поверить древним людям на слово.

А вот это уже очень важно. Отношения сторон в прямоугольном треугольнике не зависят от длин сторон (при одном и том же угле), но резко зависят от этого самого угла! В математике этот факт заслуживает внимания. А отношения – специальных названий. Своих имён, так сказать. Знакомьтесь.

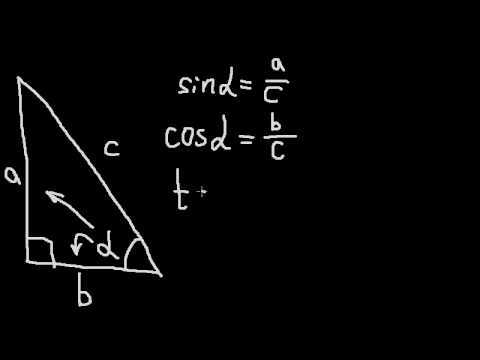
Что такое синус угла х? Это отношение противолежащего катета к гипотенузе:

sinx = а/с

Что такое косинус угла х? Это отношение прилежащего катета к гипотенузе:

сosx= в/с

Что такое тангенс угла х? Это отношение противолежащего катета к прилежащему:

tgx = а/в

Что такое котангенс угла х? Это отношение прилежащего катета к противолежащему:

ctgx = в/а

Всё очень просто. Синус, косинус, тангенс и котангенс – это некоторые числа. Безразмерные. Просто числа. Для каждого угла – свои.

Зачем я так занудно всё повторяю? Затем, что это надо запомнить. Железно запомнить. Запоминание можно облегчить. Фраза «Начнём издалека…» знакома? Вот и начинайте издалека.

Синус угла – это отношение дальнего от угла катета к гипотенузе. Косинус – отношение ближнего к гипотенузе.

Тангенс угла – это отношение дальнего от угла катета к ближнему. Котангенс – наоборот.

Уже проще, правда?

Ну а если запомнить, что в тангенсе и котангенсе сидят отношения только катетов, а в синусе и косинусе гипотенуза появляется, то всё станет совсем просто.

А теперь вопрос на внимательность.

Здесь мы определили синус, косинус, тангенс и котангенс как разнообразные отношения сторон в прямоугольном треугольнике. Все ли возможные отношения мы рассмотрели? Может, забыли что?

Да. Забыли отношение гипотенузы к катетам. Эти отношения тоже существуют в математике, называются секанс и косеканс. Но эти отношения в школьном курсе не рассматриваются. И мы не будем. На радость ученикам.

Всю эту славную семейку – синус, косинус, тангенс и котангенс называют ещётригонометрическими функциями.

Что главное во всём сказанном? Ну, само собой, определения синуса, косинуса, тангенса, котангенса. Их нужно запомнить, вызубрить, как хотите. Эти определения постоянно нужны для решения разнообразных задач.

И ещё надо железно уяснить, что угол неразрывно связан со своими тригонометрическими функциями. У каждого угла есть свой синус и косинус. И почти у каждого — свой тангенс и котангенс. Это важно. Считается, что если нам дан угол, то его синус, косинус, тангенс и котангенс нам известны! И наоборот. Дан синус, или любая другая тригонометрическая функция – значит, мы знаем угол. Существуют специальные таблицы, где для каждого угла расписаны его тригонометрические функции. Таблицы Брадиса называются. Они очень давно составлены. Когда ещё не было ни калькуляторов, ни компьютеров…

Конечно, тригонометрические функции всех углов запомнить нельзя. Вы обязаны знать их только для нескольких углов, об этом дальше будет. Но заклинание «знаю угол – значит, знаю его тригонометрические функции» — работает всегда!

Всё. Больше никаких данных нет. Надо найти длину катета ВС.

Клеточки слабо помогают, треугольник как-то неправильно расположен…. Специально, поди… Из информации есть длина гипотенузы. 8 клеток. Ещё зачем-то дан угол. Вот здесь надо сразу вспоминать про тригонометрию. Есть угол, значит, мы знаем его тригонометрические функции. Какую функцию из четырёх в дело пустить? А посмотрим-ка, что нам известно? Нам известен угол, гипотенуза, а найти надо прилежащий катет! Ясно дело, косинус нужно в дело запускать! Вот и запускаем. Просто пишем, по определению косинуса (отношениеприлежащего катета к гипотенузе):

cosC = ВС/8

Угол С у нас 60 градусов, его косинус равен 1/2. Это знать надо, безо всяких таблиц! Стало быть:

1/2 = ВС/8

Элементарное линейное уравнение. Неизвестное – ВС. Кто подзабыл, как решать уравнения, прогуляйтесь по ссылке, остальные решают:

ВС = 4

Эту задачку можно и иначе решить, но нам здесь тригонометрию осваивать надо.

Считаем, что освоение началось.

Практические советы:

1. Запомните определения синуса, косинуса, тангенса и котангенса. Очень пригодится.

2. Чётко усваиваем: синус, косинус, тангенс и котангенс накрепко связаны с углами. Знаем одно — значит, знаем и другое.

В этом уроке дано очень ограниченное понятие тригонометрических функций. В пределах 8-го класса. Восьмиклассники могут уже пройти за своими пятёрками. А у старших остаются вопросы…

Например, если угол х (смотрите вторую картинку на этой странице) — сделать тупым!? Треугольник-то вообще развалится! И как быть? Ни катета не будет, ни гипотенузы… Пропал синус…

Если бы древние люди не нашли выход из этого положения, не было бы у нас сейчас ни мобильников, ни TV, ни электричества. Да-да! Теоретическая основа всех этих вещей без тригонометрических функций — ноль без палочки. Но древние люди не подвели. Как они выкрутились — в следующем уроке.

Синус — одна из тригонометрических функций, обозначается sin.

В прямоугольном треугольнике синус острого угла равен отношению катета, лежащего напротив этого угла (противолежащего катета), к гипотенузе.

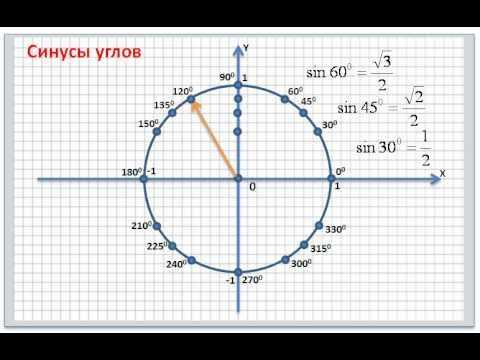
Значения синусов для часто встречающихся углов (π — число пи, √ — корень квадратный):

sin (0°) = 0
sin (30°) = sin (π/6) = 1/2
sin (45°) = sin (π/4) = (√2)/2 = 1/√2
sin (60°) = sin (π/3) = (√3)/2
sin (90°) = sin (π/2) = 1
sin (180°) = sin (π) = 0
sin (270°) = sin (3π/2) = –1

wikibig.imagetube.xyz

Разберем что такое синус угла, начиная с его определения.
Наверное, многие со школы помнят, что:
Синус острого угла в прямоугольном треугольнике называют отношение противолежащего катета к его гипотенузе:

Пример 1.
В прямоугольном треугольнике гипотенуза равна 17 см, а один катет 13 см. Найдем синус угла, который является противолежащим к этому катету.

Решение.
По определению синуса угла известно, что он равен отношению противолежащего катета к гипотенузе. Запишем:

Ответ. .

Обратим внимание, что выше мы рассмотрели понятие синуса ОСТРОГО угла. Что делать, если нужно найти синус любого угла или нам неизвестно — тупой угол или острый?

Синус произвольного угла, который образован осью Ох и произвольным радиус-вектором , — это отношение проекции данного вектора на ось Оу к длине вектора :

Пример 2.
Найдем синус угла, который образован вектором с осью Ox.

Решение.
Воспользуемся определением синуса угла и запишем:

Можно найти приближенное значение:

Ответ. .

ru.solverbook.com

СИНУС — это… Что такое СИНУС?

СИНУС — (лат.). Тригонометрическая величина означающая половину хорды двойной дуги или угла а также перпендикуляр, опущенный из конца дуги на радиус. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. СИНУС в тригонометрии… … Словарь иностранных слов русского языка

СИНУС — • СИНУС, в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (например, венозный синус, каротидный синус). • СИНУС, в ТРИГОНОМЕТРИИ отношение длины противолежащего (для данного острого угла) катета к длине… … Научно-технический энциклопедический словарь

СИНУС — в анатомии пазуха, углубление, впадина, выпячивание, расширение, длинный замкнутый канал (напр., венозный синус, каротидный синус) … Большой Энциклопедический словарь

СИНУС — 1. СИНУС1, синуса, муж. (лат. sinus изгиб, кривизна) (мат.). Тригонометрическая функция угла, в прямоугольном треугольнике равная отношения катета, противолежащего углу, к гипотенузе. 2. СИНУС2, синуса, муж. (лат. sinus изгиб, кривизна) (анат.).… … Толковый словарь Ушакова

СИНУС — мат. отвес с конца дуги на луч (радиус). Обращенный синус, косинус, часть луча, меж дуги и синуса. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

синус — канал, пазуха, функция, углубление Словарь русских синонимов. синус сущ., кол во синонимов: 4 • канал (68) • пазуха … Словарь синонимов

СИНУС — (лат. sinus) одна из тригонометрических функций … Большой Энциклопедический словарь

Синус — верзус см. Тригонометрия … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

dic.academic.ru

Как найти синус?

Изучение геометрии помогает развивать мышление. Этот предмет обязательно входит в школьную подготовку. В жизнедеятельности знание этого предмета может пригодиться — например, при планировке квартиры.

Из истории

В рамках курса геометрии изучается также тригонометрия, которая исследует тригонометрические функции. В тригонометрии мы изучаем синусы, косинусы, тангенсы и котангенсы угла.

Но на данный момент начнем с самого простого – синуса. Давайте рассмотрим более детально самое первое понятие — синус угла в геометрии. Что такое синус и как его найти?

Понятие «синус угла» и синусоиды

Синус угла – это соотношение значений противоположного катета и гипотенузы прямоугольного треугольника. Это прямая тригонометрическая функция, которая на письме обозначается как «sin (x)», где (х) – угол треугольника.

На графике синус угла обозначается синусоидой со своими особенностями. Синусоида выглядит как непрерывная волнообразная линия, которая лежит в определенных рамках на плоскости координат. Функция нечетная, поэтому симметрична относительно 0 на плоскости координат (выходит из начала отсчета координат).

Область определения этой функции лежит в диапазоне от -1 до +1 на декартовой системе координат. Период функции синус угла составляет 2 Пи. Это означает, что каждые 2 Пи рисунок повторяется, и синусоида проходит полный цикл.

Уравнение синусоиды

sin х = a / c
где а – противолежащий к углу треугольника катет

с – гипотенуза прямоугольного треугольника

Свойства

elhow.ru