Транспортная задача линейного программирования — matematiku5.ru
ИСПОЛЬЗОВАНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ И ЭЛЕКТРОННЫХ ВЫЧИСЛИТЕЛЬНЫХ МАШИН ДЛЯ ПЛАНИРОВАНИЯ ПЕРЕВОЗОК
§ I. ВЫБОР ОПТИМАЛЬНОГО ВАРИАНТА
Транспортная задача линейного программирования
Целью использования математических методов при планировании перевозок является разработка оптимального плана. Оптимальным называют наилучший вариант плана при данных заданных условиях перевозок, обеспечивающий наиболее эффективное выполнение перевозочного процесса.
Выбор оптимального варианта является весьма сложной за дачей, так как количество возможных вариантов решения различных транспортных задач может быть чрезвычайно велико. Например, при двух поставщиках и двух потребителях может быть шесть различных вариантов перевозок, при трех поставщиках и трех потребителях — 90 вариантов, при четырех поставщиках и четырех потребителях — 6256 вариантов, а при пяти поставщиках и восьми потребителях количество вариантов будет около миллиарда. Поэтому при практической работе «нельзя, сравнивая результаты расчета каждого варианта между собой, выбрать лучший, так как это займет много времени.
В последние годы разработаны математические методы планирования, позволяющие найти решение не путем перебора и сравнения всех возможных вариантов, а путем применения определенного математического расчета, который рядом последовательных приближений приводит к оптимальному решению. В настоящее время среди математических методов планирования наиболее разработанными являются методы линейного программирования. Слово «программирование» показывает, что эти математические методы применяют для планирования, т. е. для составления программы (плана). Слово «линейное» определяет математическую природу этих методов, которая заключается в том, что этими методами решают задачи с линейными связями и ограничениями, т. е. если выразить задачу в математической форме, то в ней все неизвестные будут в первой степени.
Это видно на примере так называемой транспортной задачи линейного программирования, которая получила наибольшее применение при оптимальном планировании автомобильных перевозок.
Условия примера транспортной задачи приведены в табл. 10 где в верхних правых углах клеток дано расстояние между пунктами. Каждый пункт производства условно обозначен буквой А с порядковым номером, а пункт потребления — буквой Б с порядковым номером. В табл. 10 также указаны объемы производства и потребления. Необходимо так организовать пере возки, чтобы общий объем транспортной работы в тонно-километрах был минимальный.
Если обозначить количество груза буквой х с двумя индексами, первый из которых показывает, куда везут груз, а второй— откуда везут груз (например, х23 — это количество груза, доставляемого во второй пункт потребления Б2 из третьего пункта производства А3), то в математическом виде эту задачу можно записать в следующем виде:
1) количество доставляемого груза в каждый пункт потребления равно:
x11+x12+x13 = 60;
x21+x22 + x23 = 40;
x31+x32+x33 = 90;
x41 + x42 + x43=10;
x51+x52 + x53 = 40;
2) количество отправляемого груза из каждого пункта производства равно:
x11+x21+x31 + x41 + x51 = 100;
x12 + x22 + x32 + x42 + x52 = 90;
x13 + x23+x33 + x43 + x53 = 50;
3) необходимо определить такие неотрицательные значения неизвестных х (т. е. x=>0), при которых будет обеспечен минимальный объем транспортной работы в тонно-километрах
Сmin =6x11 + 3x12 + 2x13 + 3x2,+7x22 + 6x23 + 2x31 + 8x32+4x33+4x41 + 6x42+5x43 + 2x51+2x52 + 6x53
Таким образом, пример получил математическую формулировку и в ней все неизвестные находятся в первой степени.
В данном примере имеется 15 неизвестных и 8 уравнений. Кроме того, решение необходимо получить при минимальной функции Cmin. Из этого видно, что решение этих уравнении обычными алгебраическими методами невозможно и его можно получить только с помощью методов линейного программирования.
Несмотря на то, что методы линейного программирования основаны на одном из разделов высшей математики — линейной алгебре, техника расчетов по этим методам несложна. Как только становится известен порядок вычислений, для вычисления достаточно знания основных арифметических действий.
В настоящее время известно несколько различных алгоритмов решения транспортной задачи линейного программирования. Одним из них является так называемый модифицированный распределительный метод.
Порядок вычислений с помощью этого метода покажем на примере решения транспортной задачи, условия которой приведены в табл.10.
Таблица 10 Пример транспортной задачи
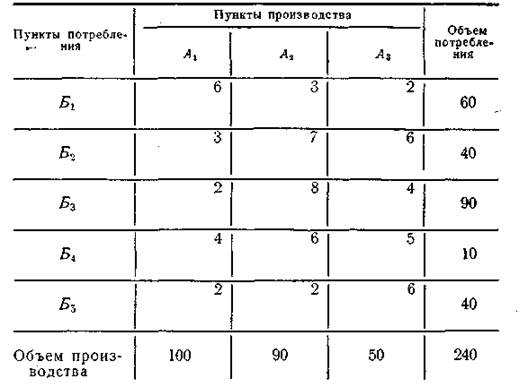
Для этого все исходные данные перенесены в новую таблицу, называемую матрицей (табл. 11). В ней, кроме строк и столбцов, которые были в табл. 10, даны вспомогательные строка и столбец, которые потребуются в дальнейшем.
Порядок вычисления.
1. Первоначально груз распределяют путем последовательной записи по каждому столбцу количества груза в клетки с наименьшим расстоянием. В столбце А1 наименьшее расстояние 2 км имеется в клетках А1Б3 и А1Б5. В первую клетку записываем 90, так как потребность пункта Б3 равна этой величине, а остаток груза по пункту А1 записываем в клетку А1Б5. Так как весь груз поставщика А1 распределен, переходим к следующему столбцу A2. Наименьшее расстояние здесь находится в клетке
Таблица 11 Первоначальное распределение
А2Б5. Записываем в эту клетку цифру 30, так как потребность пункта Б5 составляет 40 единиц груза, а 10 ему уже доставляется из пункта А1 Следующее наименьшее расстояние в этом столбце находится в клетке A2Б1. Записываем туда цифру 60. В последнем столбце A3 цифры записываются в клетки, принадлежащие строкам тех потребителей, которые еще не обеспечены грузом. В табл. 11 это клетки Б2А3 и Б4А3.
Клетки, где проставлено количество груза, называют загруженными.
2. Для проверки оптимальности полученного распределения определяют специальные индексы, проставляемые в клетках вспомогательного столбца и строки. Это делается по следующему правилу: в клетке вспомогательного столбца, соответствующей первой строке (строке Б1), записывают 0. Остальные индексы рас считывают, исходя из того, что величина расстояния, записанная в верхнем правом углу каждой загруженной клетки, должна быть равна сумме индексов в соответствующих клетках вспомогательной строки и столбца.
Так, в табл. 11 записываем 0 в клетке вспомогательного столбца строки Б1. Загруженной клеткой в этой строке является клетка А2Б1 с расстоянием 3 км. Если обозначить индекс, который должен находиться в клетке вспомогательной строки, соответствующей столбцу А2, буквой α2, то расстояние в клетке A2Б1 должно быть равно 0+α2 = 3. Отсюда α2 = 3—0 = 3. Запишем эту цифру в клетку вспомогательной строки соответствующей столбцу А2. Будем называть это индексом столбца А2.
Так как определен индекс столбца А2, а в этом столбце имеется загруженная клетка A2Б5 с расстоянием 2 км, то индекс строки Б5 будет равен β5 =2 — 3 = — 1.
Индекс для столбца А1 можно определить по загруженной клетке А1Б5,
он будет равен α1 = 2—(—1) =3.Теперь можно определить по клетке A1Б3 индекс βз = 2— 3 = —1.
Для остальных строк Б2 и Б4 и столбца А3 индексы определить нельзя, так как в табл. 11 количество загруженных клеток меньше числа т + п—1, где т — количество строк;
п — количество столбцов, т. е. должно быть загружено 5 + 3—1 = 7, а в табл. 11 только 6 загруженных клеток. Такого положения не должно быть.
Если количество загруженных клеток меньше числа т + п—1, то необходимо искусственно загрузить недостающее количество клеток матрицы, для чего в них записывают 0. В последующих расчетах с этой клеткой оперируют как с загруженной.
Постановка нулевой загрузки не повлияет на сумму наличия и потребности груза. Нуль следует ставить в ту клетку, которая лежит на пересечении строки или столбца, не имеющих коэффициента, со строкой или столбцом, для которых индексы уже определены. Наиболее целесообразно при этом выбрать из этих клеток такую, в которой имеется наименьшее расстояние.
Сделаем это в табл. 11. Клеткой с наименьшим расстоянием, которая лежит на пересечении столбца, не имеющего индекса, со строкой, коэффициент которой уже определен, будет клетка А3Б1. Туда записываем 0 и считаем эту клетку загруженной. Это дает возможность определить индексы и для строк Б2 и Б4 и для столбца А3. Теперь все индексы определены.
3. После определения всех значений индексов выполняется следующее:
находят такие незагруженные клетки, в которых расстояния, указанные в верхнем правом углу, будут меньше суммы цифровых значений индексов строки и столбца, соответствующих рассматриваемой клетке.
В табл. 11 для клетки А1Б1, сумма индексов будет меньше указанного в ней расстояния (0 + 3<6). Значит, эта клетка не отвечает вышеуказанному условию.
Проверив таким же путем все остальные клетки матрицы, находим клетку А1Б2, где сумма индексов будет больше указанного в ней расстояния. Разность между этой суммой и расстоянием показывает величину экономии, которую можно получить на каждую единицу загрузки, перемещенную в эту клетку.
В табл. 11 в клетке А1Б2 указано расстояние 3. Разность между суммой соответствующих индексов и этим расстоянием составляет (3+4) — 3 = 4.
Это показывает, что на каждую тонну груза, перемещенного в клетку A1Б2, можно получить экономию в расстоянии пере возок 4 км. Другой такой же клеткой будет клетка А1Б4 с разностью между суммой индексов и расстоянием (3 + 3)—4 = 2.
Цифру разности записывают в верхнем левом углу соответствующих клеток и берут в рамку. В табл. И это сделано в клетках А1Б2 и А1Б4. Других таких клеток в матрице нет.
4. Для дальнейших расчетов выбирают клетку с наибольшим числом в левом углу клетки. В табл. 11 этой клеткой является клетка А1Б2.
5. Для определения величины загрузки, которую следует проставить в выбранную клетку, для нее строят «контур» — замкнутую линию, состоящую из прямых горизонтальных и вертикальных отрезков, все вершины которой лежат в загруженных клетках (кроме клетки, с которой начинают строить контур). Каждой выбранной клетке может соответствовать только один «контур».
«Контур» строят следующим образом. От выбранной незагруженной клетки ведут прямую линию по строке или столбцу до такой загруженной клетки, которой под прямым углом соответствует еще одна загруженная клетка, и так до тех пор, пока линия не замкнется в исходной незагруженной клетке. Движение при определении «контура» совершается строго под прямым углом, причем в каждой строке и столбце, которые находятся в замкнутой линии, в состав «контура» должны входить две клетки.
В табл. 11 построен контур для клетки A1Б2.
Всем вершинам «контура» попеременно присваивают знаки «—» и «+», начиная с выбранной для начала построения «контура» клетки, которой всегда дается знак «—».
Затем из всех величин загрузок клеток, обозначенных знаком « + », выбирается наименьшая цифра загрузки. Такая загрузка находится в клетке А1Б5 и составляет 10 единиц. Это количество груза отнимают из загрузки, указанной в клетках со знаком «+» и прибавляют к загрузке, указанной в клетке со знаком«—». Полученные цифры записывают в новую матрицу, куда также без изменений переносят загрузку тех клеток, которые не являлись вершинами «контура».
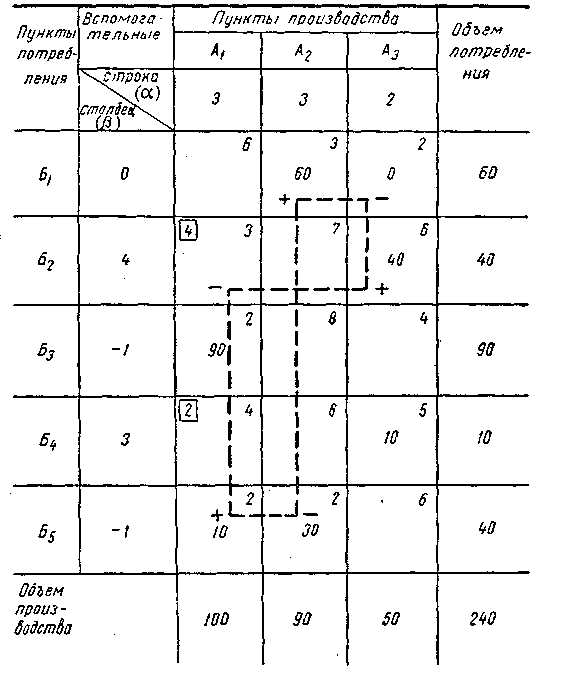
Это сделано в табл. 12, которая является новым вариантом распределения. Теперь с этой новой матрицей производят все операции, которые были описаны выше.
Таблица 12 Улучшенное распределение
Определим индексы во вспомогательных строке и столбце в табл. 12. Затем отыскиваем клетку, где сумма индексов больше расстояния. Такой клеткой в табл. 12 является клетка А3Б3-Записываем в ней в рамке соответствующую разность и строим «контур», вершины которого обозначаем знаками «—» и « + ».
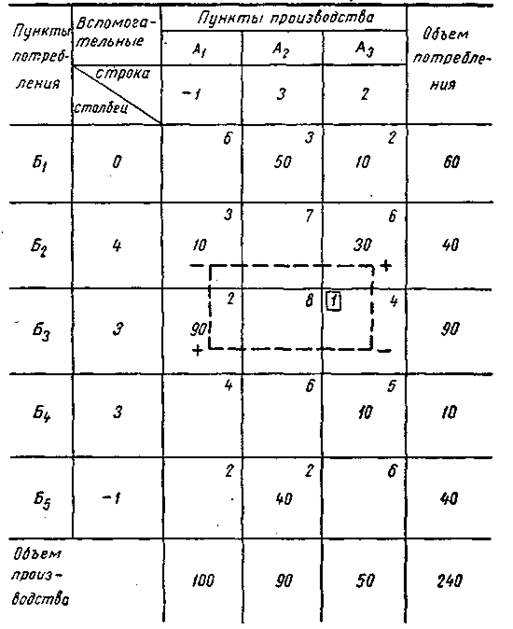
Наименьшая загрузка в клетке со знаком « + » составляет 30. Прибавляем ее к загрузке в клетках со знаком «—» и отнимаем ее от загрузки в клетках со знаком « + ». Вновь полученное распределение записываем в следующую таблицу (табл. 13). В табл. 13 снова находим вспомогательные индексы, а затем просматриваем все незагруженные клетки, чтобы среди них найти ту, для которой сумма двух соответствующих индексов будет больше указанного в ней расстояния. Но в табл. 13 таких клеток нет. Их отсутствие говорит о том, что дальнейшее улучшение плана невозможно и получен оптимальный вариант решения.
Таблица 13 Оптимальное распределение
Если в рассматриваемом примере сравнить объем транс портной работы в тонно-километрах, который был получен в первоначальном распределении (см. табл. 11), где он равнялся 730 ткм, с оптимальным решением (см. табл. 13), где он составляет 660 ткм, то видно, что он снизился почти на 10%.
Не всегда такое оптимальное распределение является единственно возможным. Если в матрице, где записано оптимальное распределение, имеются незагруженные клетки, для которых разность между суммой индексов и расстоянием оказывается равной 0, то можно получить и другие оптимальные варианты распределения. Это делается путем построения «контура»»для клетки с нулевой разностью и соответствующих перемещений всей наименьшей загрузки или части этой загрузки по «контуру»-Эти варианты будут тоже оптимальными, т. е. сумма тонно-километров останется минимальной, но закрепление потребителей за поставщиками будет иное.
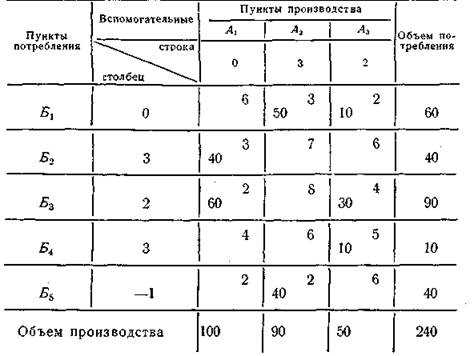
В табл. 13 для клетки А2Б4 соответствующая разность равна 0. Значит, можно дать другие оптимальные закрепления потребителей за поставщиками при всех тех же исходных данных, например, так, как это сделано в табл. 14. Легко подсчитать, что здесь количество тонно-километров тоже составляет 660.
Таблица 14 Второе оптимальное распределение
Возможность получить в некоторых случаях одинаковые по сумме тонно-километров, но различные по закреплению оптимальные решения может быть использована в практической работе.
В основу решения может быть положено не только получение минимума тонно-километров. Критерием оптимальности можно, в зависимости от конкретных условий, избрать достижение минимума стоимости перевозок. Тогда в верхних правых углах клеток матрицы проставляют стоимость перевозок между пунктами. Если нужно найти минимум затрачиваемого времени на перевозки, тогда, соответственно, указывают время перевозки между пунктами и т. д.
С целью уменьшения трудоемкости решения рекомендуется:
1) писать матрицу на плотной бумаге;
2) все исходные данные (наименование поставщиков, потребителей, расстояния между ними, потребность в грузе и наличие груза) писать чернилами;
3) все остальные операции (предварительное распределение, передвижение загрузки по строкам и столбцам, индексы во вспомогательных клетках, цифры, разностей, ломаные линии — «контуры») писать карандашом;
4) после обработки каждого варианта распределения не переписывать таблицу заново, а стирать резинкой старые, изменяющиеся цифры и на их место заносить карандашом новые;
5) окончательное решение, т. е. оптимальное распределение, записать в таблицу чернилами.
Необходимо отметить, что наряду с модифицированным распределительным методом, транспортная задача может быть решена и другими методами, например, методом разрешающих слагаемых А. Лурье — Ю. Олейника, дифференциальных рент А. Брудно и рядом других.
Имеются также различные способы первоначального распределения, которые могут значительно снизить трудоемкость решения.
Практика решения задач показала, что без помощи электронных цифровых вычислительных машин (ЭЦВМ) задачи размером тxп<= 500, вручную решаются при наличии определенного навыка за 2—3 часа, а задачи, размером тхп <=2000— за несколько дней.
§ 2. ОПТИМАЛЬНОЕ ЗАКРЕПЛЕНИЕ ПОТРЕБИТЕЛЕЙ ЗА ПОСТАВЩИКАМИ И КЛИЕНТУРЫ ЗА АВТОХОЗЯЙСТВАМИ
Одним из основных вопросов планирования перевозок является закрепление потребителей за поставщиками. Постановка этой задачи состоит в следующем.
Имеется ряд поставщиков и потребителей однородной продукции. Заданы расстояния между всеми поставщиками и потребителями, объем поставок и потребления каждым из них. Необходимо найти такой план закрепления потребителей за поставщиками, который обеспечивает минимальный объем транс портной работы в тонно-километрах или наименьшее среднее расстояние перевозки груза.
Аналогичны постановка и задачи по закреплению клиентуры за автохозяйствами: имеются автохозяйства, начальные пункты погрузки и конечные пункты разгрузки. Заданы расстояния между автохозяйствами и всеми указанными пунктами, известно количество подвижного состава, которое необходимо подавать на каждый маршрут или клиенту. Строится план за крепления маршрутов и клиентуры за автохозяйствами, при котором общий нулевой пробег всех автомобилей будет минимальным.
К этому же типу задач относится оптимальное закрепление автобусных маршрутов за несколькими автобусными парками.
Оптимальный вариант решения всех указанных задач можно получить, используя методы решения транспортной задачи линейного программирования, один из которых дан в § 1 главы XIII.
Однако в практике работы автотранспортных организаций при решении этих задач могут возникать различные дополнительные требования, которые необходимо учитывать в процессе планирования. Ограничения, вытекающие из этих требований, следует внести в матрицу для того, чтобы они были учтены.
Одним из таких условий может стать невозможность поставок некоторым потребителям продукции определенных поставщиков (или закрепления той или иной клиентуры за некоторыми автохозяйствами) по дорожным условиям из-за договорных отношений ввиду специальных требований к продукции или к подвижному составу.
Такое ограничение можно учесть при решении, если в матрице в клетку, которая лежит на пересечении строки соответствующего потребителя (клиента) и столбца соответствующего поставщика (автохозяйства), вместо фактического расстояния между этими пунктами записать расстояние, значительно боль шее любого другого расстояния в матрице. Если при этом потребность данного потребителя (клиента) не превышает наличия груза (подвижного состава) у остальных поставщиков (автохозяйств), то указанная клетка в оптимальном решении останется незагруженной, и тем самым будет выдержано заданное ограничение.
В некоторых случаях необходимо решать задачи, когда наличие груза (автомобилей) и спрос не являются сбалансированными.
Если общий объем наличия превышает спрос всех потребителей, то в матрицу дополнительно вводится так называемый фиктивный потребитель, для которого отводится отдельная строка. Его спрос принимается равным превышению общего объема наличия груза (автомобилей) над суммарным объемом спроса всех реальных потребителей. Вместо расстояний в клетках этой строки матрицы записывают любое произвольно вы бранное число, но одинаковое по всем столбцам.
Если общий объем наличия меньше суммарного спроса всех потребителей, то в матрицу вводят столбец фиктивного поставщика (автохозяйства), размер поставок которого принимают равным превышению суммарного спроса над общим объемом поставок и в этом столбце также вместо расстояния по всем клеткам записывают любое одинаковое число.
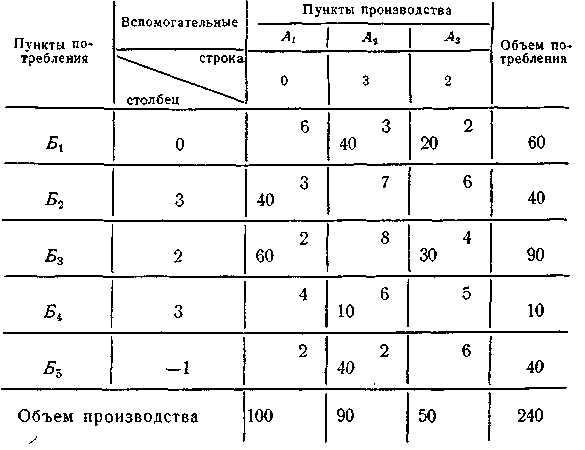
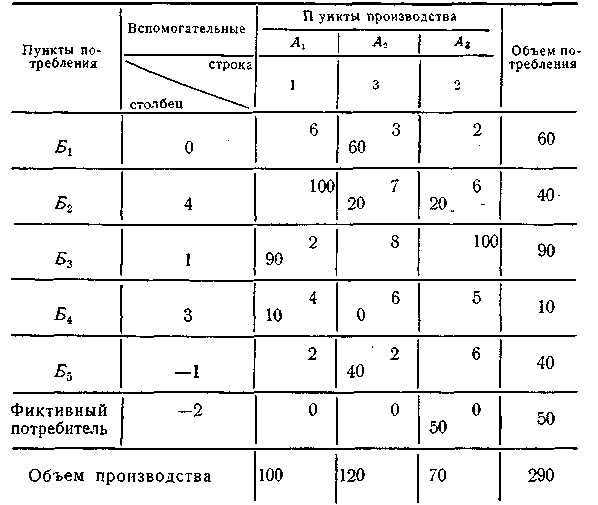
Введем некоторые указанные выше факторы в решение задачи, данной в § 1 главы XIII (см. табл. 13).
Так, устанавливаем, что потребителю Б2 нельзя доставлять груз от поставщика А1, а потребителю Б3 — от поставщика А3. В связи с этим в матрице (табл. 15) в соответствующих клетках вместо фактических расстояний поставим большое число—100.
Кроме того, объем производства в пункте А1 примем за 100, А2—120 и А3—70, т. е. общий объем производства превышает спрос на 50. В связи с этим в матрицу вводим строку «фиктивный потребитель» с объемом потребления 50, а во всех клетках этой строки вместо расстояния записываем любое одинаковое число, в данном случае 0.
Решают эту матрицу распределительным методом. Полученный оптимальный вариант представлен в табл. 15.
Таблица 15 Матрица с учетом заданных условий перевозок
Известны способы учета при решении транспортных задач и некоторых других факторов: ограниченных пропускных способностей дорог, верхних и нижних границ объемов производства, взаимозаменяемости грузов и т. д.
С помощью указанных выше методов могут быть найдены оптимальные решения задачи размещения автохозяйств на территории города, области, а также распределения различного подвижного состава по автохозяйствам.
§ 3. МАРШРУТИЗАЦИЯ ПЕРЕВОЗОК МАССОВЫХ ГРУЗОВ
В основе оптимальной маршрутизации перевозок также лежат методы решения транспортной задачи линейного программирования.
Постановка этой задачи состоит в следующем: имеется ряд поставщиков, от каждого из которых необходимо доставить различные грузы потребителям в заданном количестве и однотипном подвижном составе. Известны расстояния между всеми поставщиками и потребителями. Необходимо составить маршруты перевозок, обеспечивающие минимальный пробег подвижного состава без груза.
Рис. 164. Схема перевозок
В качестве примера решения указанной задачи примем данные заявок на перевозку груза автомобилями-самосвалами, представленные в табл. 16. Схема перевозок дана на рис. 164.
Каждому отправителю присвоено условное обозначение — буква А с со ответствующим порядковым цифровым индексом, каждому потребителю — буква Б также с соответствующим цифровым индексом. Это сделано для того, чтобы упростить запись при после дующих расчетах.
Следует отметить, что один и тот же пункт иногда имеет два условных обозначения. Например, железнодорожная станция как отправитель обозначена А1, а как получатель — Б5. Целлюлозный завод является только получателем, но он имеет то же два условных обозначения—Б1 и Б5. Это связано с тем, что этот потребитель имеет двух различных поставщиков — железнодорожную станцию и мебельную фабрику.
Таблица 16 Заявка на перевозку грузов
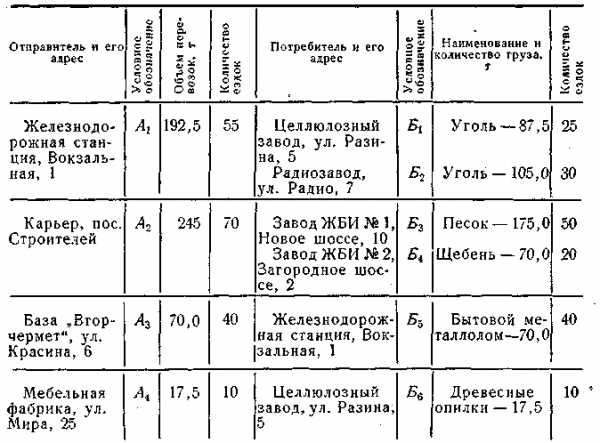
В табл. 16, кроме количества груза, показано количество ездок, которое необходимо сделать, чтобы выполнить заявленные перевозки с учетом коэффициента использования грузоподъемности на автомобиле ЗИЛ-585.
На основании заявок на перевозки составляют матрицу (табл. 17). В ней указано количество ездок из каждого пункта А в каждый пункт Б и расстояния между этими пунктами, которые проставлены в верхних правых углах соответствующих клеток.
Таблица 17 Решение на минимум пробега автомобилей без груза
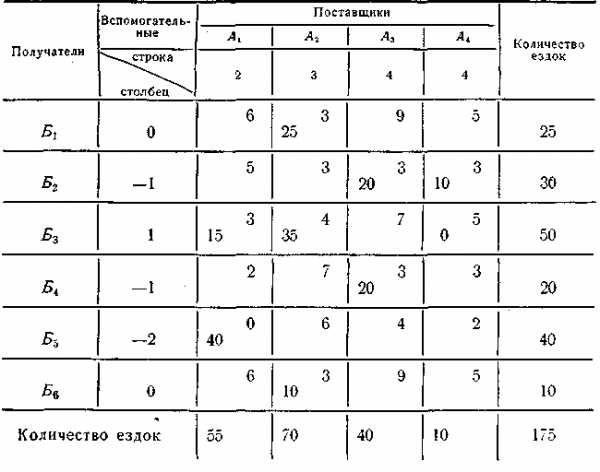
Решают эту матрицу на минимум пробега либо методом, описанным в § 1 главы XIII, либо другим любым методом решения транспортной задачи линейного программирования. Результат решения (см. табл. 17) показывает, какое количество ездок без груза надо сделать из каждого пункта Б после разгрузки автомобиля в каждый пункт А для последующей погрузки, чтобы общий пробег без груза всех автомобилей был минимальным.
Из табл. 17 видно, что из пункта Б1 в пункт А2 необходимо сделать 25 ездок без груза, из Б2 в А3 — 20 ездок и в А4 — 10 ездок и т. д.
В табл. 17 в клетке А4Б3 стоит 0. Его не следует принимать во внимание, так как этот нуль появился в таблице при определении вспомогательных индексов и служит только для этих целей (см. § 1 настоящей главы).
После получения оптимального распределения ездок без груза в эту же таблицу (табл. 18 повторяет табл. 17) вносят план ездок с грузом (полужирные цифры в скобках), который указан в табл. 16.
Таблица 18 Совмещенный план порожних и груженых ездок
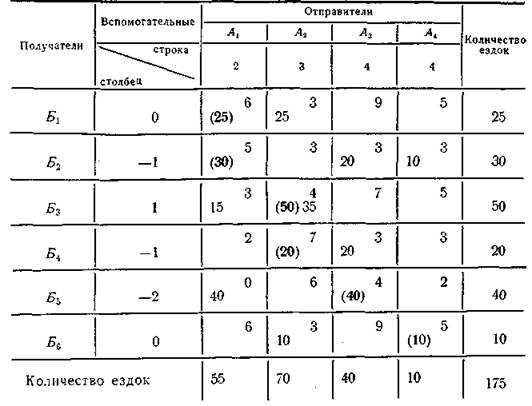
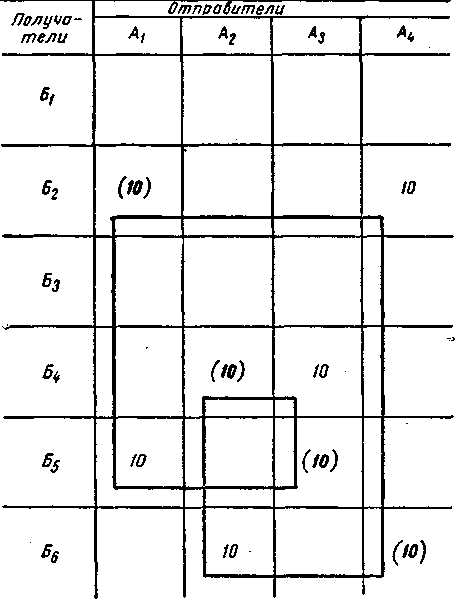
В тех клетках, где две цифры, получаются маятниковые марш руты, количество ездок по которым равно наименьшей цифре. Так, в клетке А2Б3 получен маятниковый маршрут № 1 А2Б3Б2А2 с 35 ездками. Это количество исключается из обеих рас смотренных цифр.
Когда все маятниковые маршруты найдены, в матрице строят четырехугольные «контуры», все вершины которых лежат в загруженных клетках, причем вершины с гружеными ездками должны чередоваться с вершинами с порожними ездками. В табл. 19 показаны два таких контура. Каждый из них дает маршрут. «Контур», показанный сплошной линией — маршрут №2 А1Б1Б1А2А2Б3Б3А1Х15, а штриховой «контур» — маршрут № 3 А1Б2Б2А3А3Б5БА1Х20.
Таблица 19 Составление маршрутов по четырехугольному контуру
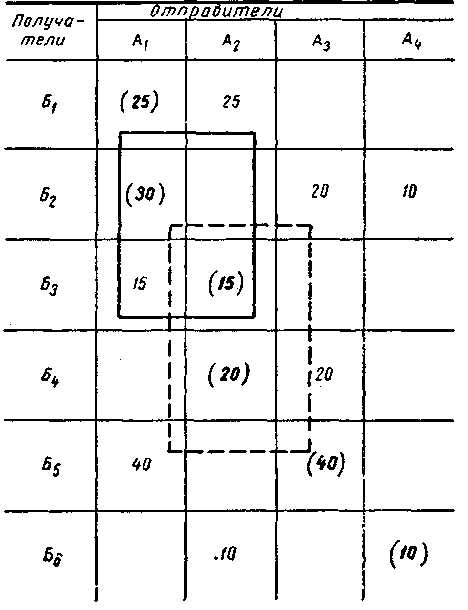
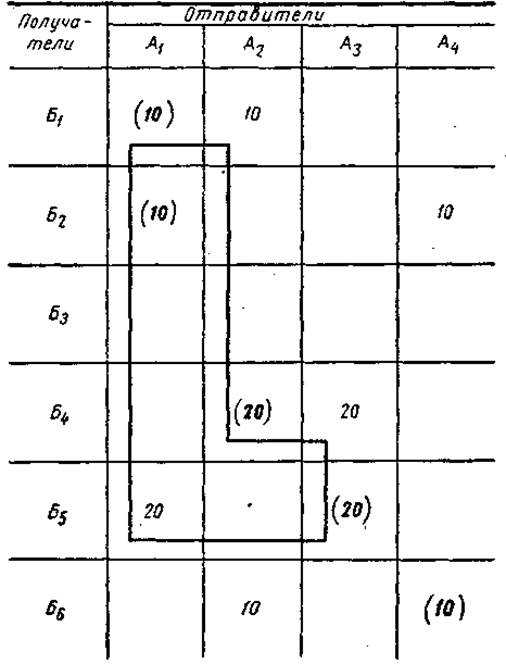
Количество ездок определяется наименьшим числом в вер шинах контура. Выбранное количество ездок из клеток таблицы исключается. Затем строят контур с шестью вершинами (табл. 20), который дает маршрут № 4 А1Б1Б1А2А2Б4Б4А3А3Б5Б5А1*10, с восемью вершинами (табл. 21), маршрут № 5 А1Б2Б2А4А4Б6Б6А2А2Б4Б4А3А3Б5Б5А1х10.
Решение ведется до полного исключения всего количества ездок из матрицы. На рис. 165 представлены схемы полученных маршрутов.
Все действия обычно производятся в одной и той же таблице, где количество ездок с грузом записывают цветным карандашом, а ездки без груза и контуры — простым карандашом. По ходу решения из таблицы стирают резинкой те цифры и контуры, которые ликвидируются на каждом новом шаге решения.
Таблица 20 Составление маршрута по шестиугольному контуру
По получении маршрутов необходимо их расшифровать и определить, какое количество автомобилей необходимо направить на каждый маршрут, чтобы обеспечить выполнение перевозок. Это делается с помощью табл. 16, где указаны обозначения каждого пункта отправления и получения груза, и табл. 17, где даны все расстояния между этими пунктами. Расшифровку производят в специальной таблице (табл. 22), которая построена так же, как та часть путевого листа, где записывается задание шоферу. Зная, из какого автохозяйства следует подавать автомобиль на каждый маршрут, легко определить и нулевые пробеги.
Таблица 21 Составление маршрута по восьмиугольному контуру
В табл. 22, где в качестве примера дана расшифровка, марш рута № 2, условные обозначения А и Б введены для лучшего усвоения методики расшифровки маршрутов. В практической работе запись условных обозначений при расшифровке маршрутов производить не нужно.
Количество оборотов одного автомобиля по каждому маршруту определяют следующим образом: записав маршрут в табл. 22 и определив расстояние между пунктами, подсчитывают общую длину маршрута без учета нулевого пробега из авто хозяйства в первый пункт погрузки и от последнего пункта раз грузки до автохозяйства. Например, по маршруту № 2 это расстояние составит (см. таблицы 18 и 19) 6 + 3+4 + 3 = 16 км.
Время движения определяют делением пробега по маршруту на норму технической скорости, например 20 км/час. На марш руте № 2 оно составит 16 км : 20 км/час = 0,8 часа.
Затем определяют время на погрузку и выгрузку груза. На маршруте № 2 необходимо сделать две погрузки и выгрузки. Их общее время при механизированном способе выполнения этих работ составит 0,4 часа.
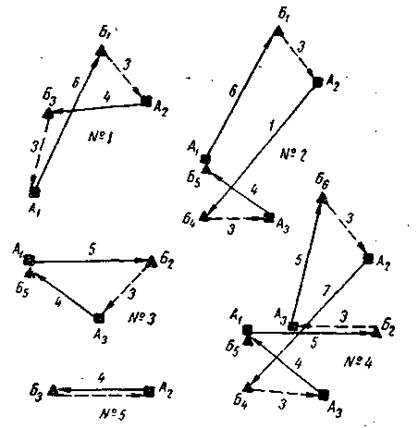
Рис. 165. Схема маршрутов
Общее время оборота автомобиля на маршруте № 2 будет равно 0,8+0,4 = 1,2 часа.
Зная время оборота и продолжительность смены, например, 7 час., с учетом возможного отклонения ±0,5 часа, получаем возможное количество оборотов одного автомобиля на маршруте № 2 — (7±0,5) : 1,2 = 5 оборотов.
Округление количества оборотов на маршруте до целых чисел целесообразно производить в сторону уменьшения. Это дает возможность в определенной мере учитывать время, необходимое для нулевых пробегов автомобиля.
Полученное количество оборотов записывают в табл. 22. При этом дополнительно осуществляется пробег автомобиля из авто хозяйства на первый пункт погрузки и с последнего пункта вы грузки в автохозяйство, что также записывают в таблицу.
Пробег одного автомобиля подсчитывают умножением количества ездок (оборотов) на соответствующие пробеги, указанные в табл. 22.
Таблица 22 Расшифровка маршрута № 2
№ маршрута | Откуда | Куда | Наименование груза | Пробег одного автомобиля, км | Количество оборотов | Количество автомобилей | ||||
Условное обозначение | Наименование | Условное обозначение | Наименование | |||||||
с грузом | без груза |
| ||||||||
2 | Автохозяйство № 2 | А1 | Железнодорожная станция | — | — | 5 | 1 | — |
| |
А1 | Железнодорожная станция | Б1 | Целлюлозный завод | Уголь | 6 | — | 5 | — |
| |
Б1 | Целлюлозный завод | А2 | Карьер | — | — | 3 | 5 | — |
| |
А2 | Карьер | Б3 | Завод ЖБИ № 1 | Песок | 4 | — | 5 | — |
| |
Б3 | Завод ЖБИ,№ 1 | А1 | Железнодорожная станция | — | — | 3 | 4 | — |
| |
Б3 | Завод ЖБИ № 1 | Автохозяйство | — | — | 2 | 1 | — |
| ||
Итого | — | 50 | 34 | — | 3 |
|
Количество автомобилей, направляемых на каждый маршрут, определяют делением всего количества оборотов по каждому маршруту на количество оборотов, которое может быть сделано одним автомобилем. Для маршрута № 2 это 15: 5 = 3 автомобиля.
Если при выполнении перевозок на каком-либо маршруте автомобиль неполностью загружен работой на всю смену, то целесообразно предусматривать его переключение на перевозку по другим маршрутам. Если такое переключение сделать нельзя, то предусматривается возврат автомобиля в автохозяйство до окончания смены, хотя это и нежелательно.
На этом расчеты и составления табл. 22 заканчивают и можно приступить к выписке путевых листов.
Каждый маршрут, имеющий два и более пунктов отправления, можно начинать с любого из них, при этом пробег автомобилей без груза останется минимальным. Например, маршрут № 2 можно начинать с пункта А1, тогда окончание работы на маршруте будет в пункте Б3. Но перевозки по маршруту можно начинать и с пункта А2, тогда автомобиль будет возвращаться в автохозяйство из пункта Б1. И в том, и в другом случае про бег по маршруту останется одинаковым, хотя может измениться нулевой пробег. Но так как нулевой пробег относительно невелик, то им приходится пренебречь для того, чтобы избежать одновременной подачи на один и тот же пункт большого количества автомобилей.
Чтобы избежать одновременную подачу на один и тот же пункт погрузки большого количества автомобилей, можно начинать маршрут с другого пункта отправления, который в нем имеется.
Если в перевозках могут быть заняты автомобили разной грузоподъемности, то метод расчета рациональных маршрутов остается таким же, как это описано выше.
Распределить автомобили различной грузоподъемности по маршрутам, можно следующим способом.
Количество ездок, рассчитанное в табл. 22 для одной основ ной марки автомобилей (например, автомобилей ЗИЛ-585), уменьшают или увеличивают соответственно увеличению или уменьшению грузоподъемности другой марки автомобилей, которые будут направлены на данный маршрут.
Например, если на маршрут № 2 вместо автомобилей ЗИЛ-585 грузоподъемностью 3,5 т, будут направлены автомобили МАЗ-205 грузоподъемностью 5 т, то количество ездок по маршруту № 2, полученное в табл. 22, необходимо уменьшить на 30% (3,5 : 5 = 0,7), тогда будет не 15, а 11 ездок. Но теперь рас считывая количество оборотов и другие данные в табл. 22, не обходимо учитывать увеличение времени на погрузку и выгрузку при работе автомобилей МАЗ-205.
matematiku5.ru
Транспортная задача линейного программирования
СОДЕРЖАНИЕ
Введение 5
1 Объект исследования 6
2 Математическое обеспечение 8
2.1 Математическая модель 82.2 Выбор метод составления опорного плана 92.3 Нахождение оптимального решения 11
3 Практическая реализация 13
4 Руководство пользователя 17
Заключение 19
Библиографический список 20
Приложение А. Блок-схема 21
Приложение Б. Листинг программы 22
ВВЕДЕНИЕ
В любой сфере своей деятельности человек неизбежно сталкивается с задачами оптимизации. Экономическое планирование, управление, распределение ограниченных ресурсов, анализ производственных процессов, проектирование сложных объектов всегда должно быть направлено на поиск наилучшего варианта с точки зрения намеченной цели.
Одной из распространенных задач оптимизации является задача о минимизации затрат при транспортировке грузов. Данная задача является одной из центральных в экономическом планировании наряду с задачей максимизации доходов при ограниченных ресурсах.
Задача минимизации затрат сводится к отысканию наименьшего значения функции, которую принято называть целевой. Целевая функция является линейной функцией своих аргументов, а условия, определяющие их допустимые значения, имеют вид линейных уравнений и неравенств.
В рамках реальных экономических задач число аргументов целевой функции обычно бывает очень большим. Поэтому практическая реализация алгоритмов решения таких задач принципиально невозможна без использования современной вычислительной техники.
Целью данной курсовой работы является поиск оптимального распределения транспортных средств по маршрутам. За счет правильного составления плана можно минимизировать затраты на перевозку.
1 ОБЪЕКТ ИССЛЕДОВАНИЯ И ПОСТАНОВКА ЗАДАЧИ
Однородная транспортная задача есть прикладная задача линейного программирования, в которой требуется найти оптимальный план транспортировки некоторого однородного продукта из конечного числа пунктов поставки с заданными объемами производства в конечное число пунктов потребления с известными объемами потребностей:
· минимизирующий суммарную стоимость транспортировки,
· не превышающий объем производства в каждом пункте поставки,
· полностью покрывающий потребности в каждом пункте потребления,
при заданной стоимости перевозки единицы транспортируемого продукта между каждой парой пунктов поставки и потребления.
Транспортная задача была впервые сформулирована Хитчкоком и с тех пор применяется для решения практических задач доставки и распределения однородных продуктов.
Для решения транспортной задачи разработано несколько методов, каждый из которых отличается от другого методом заполнения матрицы перевозок. Существуют два типа транспортной задачи: открытая и закрытая. Транспортная задача называется открытой если сумма запасов товара на складах отличается от суммы потребностей товаров у магазинов. Транспортная задача называется закрытой, если сумма запасов товара на складах равняется сумме потребностей магазинов. Решение существует только для закрытой транспортной задачи, поэтому если транспортная задача открытая, то ее надо привести к закрытому типу. Для этого в случае, если запас товара на складах превышает потребность магазинов, то вводят фиктивного потребителя, который выбирает весь избыток товара. В случае же, если существует дефицит товара, т.е. потребность магазинов больше, чем запас товаров на складах, то вводят фиктивного поставщика, с фиктивным запасом товара на складе. В обоих случаях в матрице тарифов перевозок данному складу или магазину проставляется нулевая цена перевозки.
В качестве задания транспортная задача имеет следующий вид:
Таблица 1
В таблице 1 приведены расходы на транспортировку партий товаров с трех фабрик (А, Б и В) к четырем складам (Г, Д, Е и Ж). в ней также приведены количество товара на каждой из фабрик и вместимость складов. Требуется определить маршруты, по которым следует направлять товары, чтобы минимизировать общие расходы.
2 МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ 2.1 Математическая модель
Имеется m пунктов поставки (поставщиков) и n пунктов потребления некого однородного продукта. Для каждого поставщика i = 1,…,m задан объем производства Ai , а для каждого потребителя j = 1,…,n задан объем потребления Bj и известна стоимость доставки единицы продукта Ci,j из пункта производства i в пункт потребления j. Управляемые параметры Xi,j характеризуют объем перевозки между каждым поставщиком i = 1,…,m и потребителем j = 1,…,n. В случае сбалансированного производства и потребления:
A1 + … + Am = B1 + … + Bn (1)
оптимальный план транспортировки соответствует минимизации линейной целевой функции:
(2)
при m линейных ограничениях по поставке:
Xi,1 + … + Xi,j + … + Xi,n = Ai , i = 1,…,m (3)
и n линейных ограничениях пo потреблению:
X1,j + … + Xi,j + … + Xm,j = Bj , j = 1,…,n, (4)
а также при очевидном условии неотрицательности управляемых переменных:
, i = 1,…,m и j = 1,…,n.
(5)2.2 Выбор метод составления опорного планаРешение транспортной задачи, после того, когда было установлено, что она открытая либо устранен путем коррекции несбалансированность ее, начинается с составления опорного плана, то есть отыскания начального базисного решения.Существует большой выбор методов составления опорного плана, рассмотрим некоторые из них. Метод минимального элемента. Алгоритм метода минимального элемента состоит в следующем.
Как решить транспортную задачу?
Просматривается вся матрица тарифов перевозок, и из нее выбирается позиция с наименьшим значением тарифа C, затем просматриваются значения наличия запасов на складе A и потребности у потребителя B, затем в данную клетку записывается величина D=MIN(A,B). Из запасов соответствующего склада и потребностей магазина вычитается величина D. Если запас товара на складе исчерпан, то эта строка исключается из дальнейшего рассмотрения. Если потребность магазина в товаре удовлетворена полностью, то этот столбец исключается из дальнейшего рассмотрения. Может быть случай, когда одновременно исключаются и строка и столбец, этот случай называется вырожденным. В дальнейшем весь процесс повторяется до тех пор, пока не будет исчерпан весь запас товаров на складах и не будет удовлетворена потребность всех магазиновМетод Фогеля. Просматриваются все строки и столбцы матрицы тарифов, вычисляется разность между двумя наименьшими элементами в строке или в столбце. Затем из всех этих разностей выбирается строка или столбец с максимальной разность. В выбранной строке или столбце, как и в методе минимального элемента, заполняется клетка с наименьшим значением тарифа. Затем обнулявшаяся строка или столбец исключаются из рассмотрения и весь процесс повторяется до полного исчерпания запаса товаров на складах. Метод двойного предпочтения. В начальной своей стадии этот метод похож на метод минимального элемента, но для столбцов. Просматривается первый столбец матрицы тарифов, в нем находится наименьший элемент. Затем проверяется, минимален ли этот элемент в своей строке. Если элемент минимален в своей строке, то по методу минимального элемента в эту клетку заносится значение D=MIN(A,B), соответствующие запас и потребность уменьшаются на эту величину.Обнулившаяся строка или столбец исключаются из рассмотрения и процесс повторяется, начиная с первого не исключенного столбца. Если найденный минимальный элемент не минимален в своей строке, то происходит переход к следующему столбцу и так до тех пор, пока не будет найден такой элемент. Метод северо-западного угла. Просматривается матрица тарифов перевозок C, начиная с левого верхнего угла (клетки). В эту клетку записывается величина D=MIN(A,B). Она вычитается из запасов и потребностей соответствующего склада и магазина. Обнулившаяся строка или столбец исключаются из рассмотрения, затем процесс опять повторяется для левой верхней клетки оставшейся матрицы и так до тех пор пока весь запас товаров не будет исчерпан.
Метод Фогеля приводит к лучшему начальному решению, чем два других метода. Однако он сложен для реализации на ЭВМ, так включает в себя множественные проверки, а также метод наименьшего расстояния. Несмотря на то, что метод наименьших расстояний дает лучшее начальное решение, чем метод «северо-западного» угла, он также сложен из-за большего числа различных проверок и постоянного определения минимума. Метод северо-западного угла наиболее прост, так базисное решение получается путем последовательного перехода по столбцам и строкам. Кроме этого стоит учитывать, что алгоритм выбора начального базисного решения не влияет на алгоритм поиска оптимального решения, то есть в любом случае дальнейшее решение задачи происходит по одной и той же схеме. Исходя из этого, при программной реализации задачи для поиска начального решения был выбран метод «северо-западного» угла. Даже если при этом потребуется большее количество итераций для поиска оптимального решения, более выгодно использовать этот метод, так как в этом случае возрастает точность решения, при этом структура программы будет заметно проще.
2.3 Нахождение оптимального решения задачиТак как не известно: оптимален ли полученный опорный план или нет, то стоит провести оценки базисных и небазисных переменных. Для этого воспользуемся методом потенциалов.
В этом методе строке i и столбцу j ставятся в соответствие числа Ui и Vj. Для каждой базисной переменной Хij текущего решения потенциалы Ui и Vj должны удовлетворять условию:
laservirta.ru
Методы решения транспортных задач линейного программирования Транспортная
Методы решения транспортных задач линейного программирования
Транспортная задача является одной из наиболее распространенных задач линейного программирования и находит широкое практическое применение.
Постановка задачи. Некоторый однородный продукт, сосредоточенный у m поставщиков в количестве Аi(i=1. . m) единиц соответственно, необходимо доставить n потребителям в количестве Вj (j=1. . n) единиц. Известна стоимость Сij перевозки единицы груза от iго поставщика к j-му потребителю. Определить оптимальный(имеющий минимальную стоимость) план поставок продукции, позволяющий вывести все грузы и полностью удовлетворить потребности потребителей.
Предварительный анализ задачи. Пусть Хij –количество единиц груза, запланированных к перевозке от i-го поставщика к j-му потребителю. Тогда Z=Σi Σj Cij Xij –стоимость всего плана. Ограничения: 1. Xij>=0 2. ΣXij=Аi, где j=1. . n -размер поставок. -объем поставок равен количеству ΣXij=Вj, где i=1. . m -объем поставок равен спросу, т. е. Z=Σi Σj Cij Xij → min -план должен быть минимальным. продаж, т. е. все грузы должны быть перевезены. 3. все потребности должны быть удовлетворены. 4. В данной модели предполагается, что Σ Аi= Σ Вj.
Решение задачи. Решение транспортной задачи осуществляется в три этапа: Ø Составление матрицы поставок Ø Составление первоначального опорного плана. Ø Оптимизация плана.
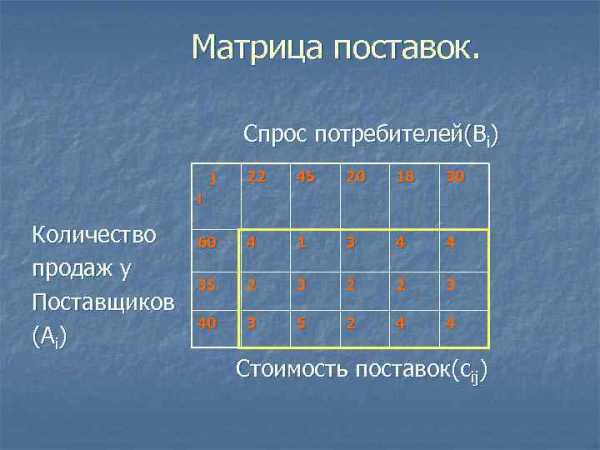Матрица поставок. Спрос потребителей(Bi) j 22 45 20 18 30 60 4 1 3 4 4 35 2 3 2 2 3 40 3 5 2 4 4 i Количество продаж у Поставщиков (Ai) Стоимость поставок(сij)
Построение первоначального опорного плана. В любой транспортной задаче можно найти бесчисленное множество вариантов плана перевозок. Допустимый — это такой план (такое распределение поставок), в котором все мощности используются, а спрос всех потребителей удовлетворен. Наиболее распространенные методы построения данной матрицы: ü Юго — восточного угла. ü Северо-западного угла ü Минимального элемента в ü Минимум в столбце матрице. ü Минимум в строке ü Фогеля. ü Двойного предпочтения ü Лебедева — Тихомирова. ü Лебедева Следующий этап.
Метод северо-западного угла. Данный метод легко алгоритмизировать, однако в подавляющем большинстве случаев он приводит к плану поставок, весьма далекому от оптимального. При этом способе «поставки» располагаются, начиная от левого верхнего и кончая нижним правым углом матрицы. На географических картах левый верхний угол соответствует северо-западу, эта аналогия и дала название способу. j 22 45 20 18 30 i 60 4 22 35 1 3 4 4 3 2 2 3 4 4 38 2 План: Z=4*22+1*38+. . +4*30=363 7 40 3 20 5 8 2 10 все методы. 30
Ход решения. 0 j 7 0 0 10 0 0 22 45 20 18 30 i 0 38 60 4 22 0 8 28 35 1 3 4 4 3 2 2 3 4 4 38 2 7 0 30 40 3 20 5 8 2 10 30
Метод юго-восточного угла. Данный метод легко алгоритмизировать, однако в подавляющем большинстве случаев он приводит к плану поставок, весьма далекому от оптимального. При этом способе «поставки» располагаются, начиная от правого нижнего и кончая верхним левым углом матрицы. На географических картах правый нижний угол соответствует юговостоку, эта аналогия и дала название способу. j 22 45 20 18 30 i 60 4 22 35 План: Z=4*22+1*38+. . +4*30=363 1 3 4 4 3 2 2 3 4 4 38 2 7 40 3 20 5 8 2 10 все методы. 30
Ход решения. 0 j 38 22 0 0 45 8 0 0 20 18 30 i 0 22 60 4 22 0 7 27 35 1 3 4 4 3 2 2 3 4 4 38 2 7 0 10 40 3 20 5 8 2 10 30
Метод минимального элемента в столбце. Метод заключается в том, что поочередно в столбцах матрицы отмечаются минимальные показатели и в соответствующие клетки заносятся поставки в зависимости от спроса и предложения. Если при записи поставок спрос по столбцу удовлетворен не полностью, ищется следующий по величине элемент в данном столбце, отмечается новый элемент и так до полного удовлетворения спроса. Только после этого переходят на следующий столбец. Если в столбце два или несколько одинаковых по величине минимальных показателя, то может быть отмечен любой из них. j 22 45 20 18 30 i 60 План: Z=1*45+4*15+. . +4*30=321 4 4 2 2 3 2 4 4 45 35 2 15 3 22 все методы. 3 40 13 3 5 7 3 30
Ход решения. 0 j 0 7 0 3 22 45 20 0 0 18 30 i 0 15 60 4 1 3 4 4 2 2 3 2 4 4 45 0 13 35 0 30 33 40 2 15 3 22 13 3 5 7 3 30
Метод минимального элемента в строке. Метод заключается в том, что поочередно в строках матрицы отмечаются минимальные показатели и в соответствующие клетки заносятся поставки в зависимости от спроса и предложения. Если при записи поставок спрос по строке удовлетворен не полностью, ищется следующий по величине элемент в данной строке, отмечается новый элемент и так до полного удовлетворения спроса. Только после этого переходят на следующую строку. Если в строке два или несколько одинаковых по величине минимальных показателя, то может быть отмечен любой из них. j 22 45 20 18 30 i 60 План: Z=1*45+3*15+. . +4*30=320 4 1 45 35 2 все методы. 4 4 2 2 3 4 4 15 3 22 40 3 5 8 2 10 30
Ход решения. 0 j 0 7 22 45 0 3 0 20 0 18 30 i 0 15 60 4 1 45 0 13 35 2 4 4 2 2 3 4 4 15 3 22 0 30 40 3 5 8 2 10 30
Метод минимального элемента в матрице. Данный метод дает лучший результат, особенно в более крупных матрицах, но его использование требует большого внимания. При использовании этого способа удобно после записи очередной поставки отмечать (хотя бы крестиками) все клетки соответствующего столбца или соответствующей строки (в зависимости от того, удовлетворен ли спрос или исчерпана мощность). Тогда количество элементов матрицы, которые нужно просматривать после записи каждого нового кружка, все время уменьшается. j 22 45 20 18 30 i 60 4 1 3 4 4 2 2 3 2 4 4 45 План: Z=1*45+4*15+. . +4*30=321 все методы. 35 2 15 3 22 40 13 3 5 7 3 30
Ход решения. 0 j ν 0 22 ν 7 0 45 ν 3 0 20 ν 18 0 ν 30 i ν 0 15 ν 0 13 ν 0 33 60 4 1 3 4 4 2 2 3 2 4 4 45 35 2 15 3 22 40 13 3 5 7 3 30
Метод двойного предпочтения. Ищется минимальный элемент в первом столбце и проверяется является ли он минимальным в строке, если ответ положительный, то данная клетка запоминается, то есть в зависимости от спроса и предложения в данную графу-клетку ставится поставка, затем, при превращении в нуль, вычеркивается строка либо столбец. Пройдя таким образом всю матрицу переходят к первому столбцу из оставшихся(не вычеркнутых) и тек до тех пор пока распределение не будет закончено. j 22 45 20 18 30 i 60 4 1 3 4 4 2 2 3 2 4 4 45 План: Z=2*22+1*45+. . 4*30=321 35 2 15 3 22 все методы. 40 13 3 5 7 3 30
Ход решения. 0 j 0 7 0 3 22 45 20 0 0 18 30 i 0 15 60 4 1 3 4 4 2 2 3 2 4 4 45 0 13 35 0 30 33 40 2 15 3 22 13 3 5 7 3 30
Метод Лебедева. При данном методе подсчитывается Сij по строкам и столбцам и каждая сумма делится на число элементов в строке или строке, в результате чего получаются средние величины. Каждый элемент вычитается из суммы двух соответствующих средних. При этом разности называются коэффициентами очередности. Распределение поставок производится сначала в клетку таблицы с наибольшими коэффициентами, далее в следующую за ним по величине и т. д. Коэффициенты вписаны в правых верхних углах каждой клетки. Этот способ, предложенный А. В. Лебедевым, несложен и дает в общем неплохие результаты. Так же как и в способе наименьшего элемента, здесь можно для каждой данной матрицы определить последовательность записи поставок (в порядке убывания величин коэффициентов) и руководствоваться этой последовательностью при базисном распределении в зависимости от конкретных величин показателей мощностей и спроса. План: Z=1*45+4*15. . 2*20=326 все методы. j 22 45 20 18 30 i 60 4 1 3 4 45 35 2 15 3 2 2 40 20 2 18 3 4 5 2 20 3 15 4 4
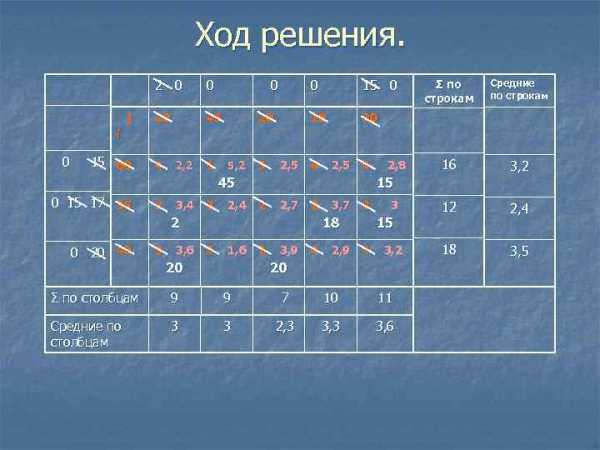Ход решения. 2 0 j 0 0 22 45 0 18 20 15 0 30 Σ по строкам Средние по строкам 16 3, 2 12 2, 4 18 3, 5 i 0 15 60 4 2, 2 1 5, 2 3 2, 5 4 45 0 15 17 35 2 3, 4 3 2, 4 15 2 2, 7 2 2 0 20 40 3 3, 6 3, 7 3 18 5 1, 6 20 2, 8 2 3, 9 4 2, 9 3 15 4 3, 2 20 Σ по столбцам 9 9 7 10 11 Средние по столбцам 3 3 2, 3 3, 6
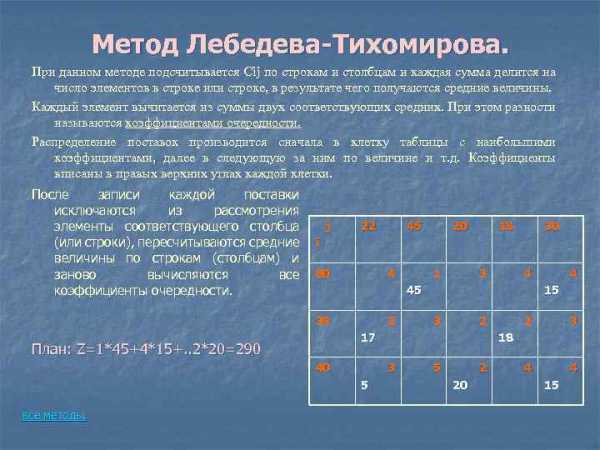Метод Лебедева-Тихомирова. При данном методе подсчитывается Сij по строкам и столбцам и каждая сумма делится на число элементов в строке или строке, в результате чего получаются средние величины. Каждый элемент вычитается из суммы двух соответствующих средних. При этом разности называются коэффициентами очередности. Распределение поставок производится сначала в клетку таблицы с наибольшими коэффициентами, далее в следующую за ним по величине и т. д. Коэффициенты вписаны в правых верхних углах каждой клетки. После записи каждой поставки исключаются из рассмотрения элементы соответствующего столбца (или строки), пересчитываются средние величины по строкам (столбцам) и заново вычисляются все коэффициенты очередности. j 22 20 18 30 i 60 4 1 3 4 45 35 2 40 3 2 2 3 4 4 18 3 5 4 15 17 План: Z=1*45+4*15+. . 2*20=290 все методы. 45 5 2 20 15
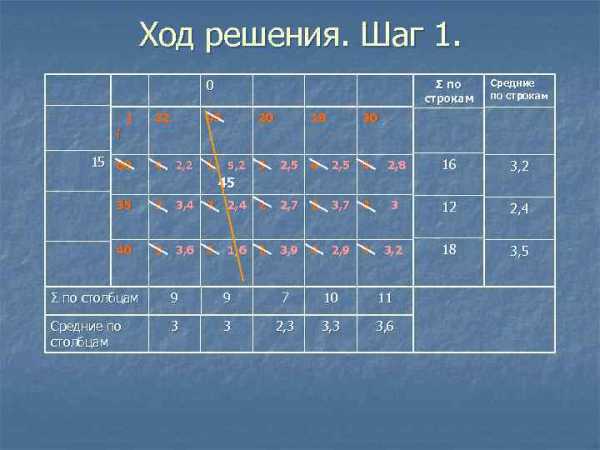Ход решения. Шаг 1. 0 j 22 Σ по строкам 45 20 18 Средние по строкам 30 i 15 60 4 2, 2 1 5, 2 3 2, 5 4 2, 8 16 3, 2 45 35 2 3, 4 3 2, 4 2 2, 7 2 3, 7 3 3 12 2, 4 40 3 3, 6 5 1, 6 2 3, 9 4 2, 9 4 3, 2 18 3, 5 Σ по столбцам 9 9 7 10 11 Средние по столбцам 3 3 2, 3 3, 6
Ход решения. Итог. 5 0 j 0 22 0 45 0 15 20 18 30 2. 5 3. 05 2, 9 3, 1 2. 5 3. 05 2. 8 3. 35 3, 2 3, 6 i 0 15 60 2. 2 2, 75 2, 4 3, 5 5. 2 45 15 0 17 35 3. 4 3, 25 3, 3 2. 4 2. 7 2, 55 2, 6 17 0 15 35 40 3. 6 3, 25 3 3, 5 3. 7 3, 55 3 2, 85 2, 9 18 1. 6 3. 9 3, 5 3, 3 3, 5 3 3 20 2. 9 2, 55 3. 2 2, 85 2, 6 3 3 3 15
Метод Фогеля. Процесс начинается с определения разности между двумя наименьшими Сij каждого столбца и строки. Минимальный элемент в соответствующей строке(столбце) запоминается и на его место записывается поставка, после чего данная строка(столбец) исключается. Если наибольшая разность оказывается сразу в двух столбцах(строках), тогда проверяют является ли какой-либо элемент минимальным в строке и столбце одновременно. Если ответ положительный, тогда записывают поставку, если нет, тогда произвольно выбираем либо столбец, либо строку. Смысл способа Фогеля легко понять. Найденные разности показывают, насколько больше будут расстояния, если в соответствующем столбце j 22 45 20 18 30 (или строке) поставка будет записана не в клетку, i где находится минимальный в этом столбце (строке) элемент, а в клетку, где находится 60 4 1 3 4 4 элемент, следующий за ним по величине. Там, где 45 15 разность оказывается наивысшей и, 35 2 3 2 2 3 следовательно, там, где будут наибольшие потери 18 17 в расчете на единицу продукции, если поставка попадет не на наименьший элемент, там, 40 3 5 2 4 4 очевидно, и нужно в первую очередь записать 22 5 13 поставку. План: Z=1*45+3*15+. . 4*13=305 все методы.
Ход решения. 0 j 0 5 22 45 0 0 20 17 0 18 Разности по строкам 30 i 0 15 60 4 1 45 0 17 35 2 3 4 4 211 2 2 3 00000 4 1111 15 3 18 0 13 35 40 3 5 2 17 4 22 Разности по столбцам 5 13 11112 2 00002 22 11113
Построение оптимального распределения. Данный этап решения задачи может быть осуществлен с помощью различных методов, среди которых: ü Потенциалов. ü Квадратов. ü Распределительный. ü Венгерский. ü Форда- Фулкерсона. ü Разрешающих слагаемых. ü Дифференциальных рент. Предыдущий этап
Метод квадратов. Пусть предварительный план поставок будет иметь следующий вид: j 22 45 20 18 30 i 60 4 22 35 1 3 4 4 3 2 2 3 4 4 38 2 7 40 3 20 5 План: Z=4*22+1*38+. . +4*30=363 8 2 10 30 Назовём квадратом 4 клетки, стоящие в углах такого прямоугольника, который хотя бы по одной диагонали стоят 2 положительные поставки. В клетках, стоящих на других диагоналях могут быть либо нулевыми, либо нуль и поставка, либо обе поставки. Например: B 1 A 1 B 2 4 22 A 2 1 38 2 3 7 (4+3)>(1+2) Квадрат будет «неправильный» , если сумма двух Сij , стоящих в клетке с положительными(полными) поставками, на одной диагонали будет больше суммы Сij на другой.
Теорема. В оптимальном распределении нет неправильных квадратов. Известно, что любой неправильный квадрат можно превратить в правильный, используя следующий алгоритм: вычтем из чисел по одной диагонали соответствующей левой части неравенства наименьшую поставку и прибавим к другой. (в нашем примере: из 22 и 7 выберем 7, после чего из 22 вычитаем 7, а к 38 прибавим 7, тогда получим: ) B 1 A 1 B 2 4 15 A 2 45 2 7 1 3
j 22 45 20 18 30 i 60 4 15 35 1 3 4 4 3 2 2 3 4 4 45 2 7 40 10 3 5 18 2 10 30 План: Z=4*15+1*45+. . +4*30=315 Преобразовав таким образом базовую матрицу мы получим оптимальное распределение, что и требовалось найти. Задача решена.
present5.com
Математическое программирование. Транспортная задача. Примеры решения задач
Транспортная задача
Схема решения
| Потребители (Bj) |
| ||
Поставщики (Ai) | B1 | … | Bn | Запасы |
A1 | C11 | … | C1n | A1 |
… | … | … | … | … |
Am | Cm1 | … | Cmn | Am |
Потребности | B1 | … | Bn |
|
Cij – цена перевозки от i-поставщика к j-потребителю
1) Проверить, является задача открытой или закрытой
нужно добавить недостающего поставщика или потребителя в таблицу с ценой перевозок С=0
2) Составить начальный план перевозок
а) методом наименьшей цены – распределение груза начинается с клетки, где Cij наименьшая;
или
б) методом северо-западного угла.
3) Проверить невырожденность плана перевозок: количество занятых клеток = m+n-1
4) Проверить оптимальность плана методом потенциалов
ui – потенциалы поставщиков (вписываются в таблицу на месте Ai)
vj – потенциалы потребителей (вписываются в таблицу на месте Bj)
Потенциалы считаются по занятым клеткам: ui + vj = Cij (Занятая клетка – где есть перевозки)
Далее для свободных клеток вычисляется Δij = (ui + vj ) — Cij (вписывается в углах свободных клеток)
Если все Δij ≤ 0, то план оптимальный
Если есть хоть одно Δij > 0, то план не оптимальный, требуется перераспределение перевозок по циклу, и проверка нового плана, начиная с пункта 3.
5) Построить цикл перевозок
За начало цикла берется клетка с наибольшим положительным Δij
В начале цикла всегда добавляется перевозка (+).
Значением добавляемой перевозки берется наименьшая перевозка в отрицательных (-) вершинах цикла.
Цикл строится по одной из схем:
Видео-урок: Решить транспортную задачу методом потенциалов:
Задача. Имеются три пункта поставки однородного груза А1, А2, А3 и пять пунктов В1, В2, В3, В4, В5 потребления этого груза. На пунктах А1, А2, А3 находится груз в количествах 90, 70, 110 тонн. В пункты В1, В2, В3, В4, В5 требуется доставить соответственно 50, 60, 50, 40, 70 тонн груза. Расстояния в сотнях километрах между пунктами поставки и потребления приведены в матрице-таблице D:
Найти такой план перевозок, при котором общие затраты будут минимальными.
УКАЗАНИЕ. 1) Считать стоимость перевозок пропорциональной количеству груза и расстоянию, на которое этот груз перевозится, т.е. для решения задачи достаточно минимизировать общий объем плана, выраженный в тонно-километрах.
2) для решения задачи использовать методы северо-западного угла и потенциалов.
Решение.
Составим математическую модель задачи:
Обозначим — количество груза, перевезенного от поставщика i к потребителю j.
Становятся очевидными следующие ограничения (т.к. весь груз должен быть вывезен, и все потребности удовлетворены полностью):
При этом должна быть минимизирована целевая функция
Построим опорный план методом северо-западного угла:
Принцип заполнения таблицы состоит в том, что, начиная с крайней левой верхней ячейки (принцип северо-западного угла), количество грузов вписывается в таблицу так, чтобы потребности полностью удовлетворялись или груз полностью вывозился.
Построим систему потенциалов. — потенциалы, соответствующие поставщикам, — потенциалы, соответствующие потребителям.
Полагаем U1=0, а далее Ui + Vj = dij для занятых клеток таблицы.
U1 + V1 = 9 V1 = 9
U1 + V2 = 1 V2 = 1
U2 + V2 = 4 U2 = 3
U2 + V3 = 6 V3 = 3
U3 + V4 = 5 U3 = 0 V4 = 5
U3 + V5 = 3 V5 = 3
Проверим критерий оптимальности : Ui + Vj dij для свободных клеток.
U1 + V3 = 3>1 на 2
U1 + V4 = 5=5
U1 + V5 = 3<6
U2 + V1 = 12>6 на 6
U2 + V4 = 8=8
U2 + V5 = 6>5 на 1
U3 + V1 = 9>2 на 7
U3 + V2 = 1<9
U3 + V3 = 3=3
Из тех условий, где критерий не выполняется, выбираем то условие, где разница максимальна. Это – ячейка (3 , 1)
Перебросим в ячейку (3 , 1) 50 единиц груза из ячейки (1 , 1).
Чтобы компенсировать недостаток в первой строке, перебросим те же 50 единиц груза из ячейки (2 , 3) в ячейку (1 , 3).
Теперь чтобы компенсировать недостаток в строке 2, перебросим из ячейки
(3 , 5) 50 единиц в ячейку (2 , 5).
Таким образом, образовался цикл, показанный в таблице пунктиром.
Получаем новую таблицу, для которой повторяем расчет потенциалов:
Полагаем U1=0, а далее Ui + Vj = dij для занятых клеток таблицы.
U1 + V2 = 1 V2 = 1
U1 + V3 = 1 V3 = 1
U2 + V2 = 4 U2 = 3
U2 + V5 = 5 V5 = 2
U3 + V5 = 3 U3 = 1
U3 + V1 = 2 V1 = 5
U3 + V4 = 5 V4 = 4
Проверим критерий оптимальности : Ui + Vj dij для свободных клеток.
U1 + V1 = 1<9
U1 + V4 = 4<5
U1 + V5 = 2<6
U2 + V1 = 4<6
U2 + V3 =4<6
U2 + V4 =7<8
U3 + V2 =2<9
U3 + V3 =2<3
Критерий выполнен, значит, полученное решение оптимально.
Найдем минимальную стоимость перевозок.
www.matem96.ru
| Обратная связь ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса — ваш вокал Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими Целительная привычка Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Тренинг уверенности в себе Вкуснейший «Салат из свеклы с чесноком» Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Как слышать голос Бога Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д. Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. |
Таблица1.10. Исходные данные для решения транспортной задачи.
Вопросы к зачёту по дисциплине «Методы оптимальных решений»
Список литературы Основная литература
1. Алесинская Т.В.Экономико-математические методы и модели. Учебное пособие по решению задач. Таганрог: изд-во ТРТУ, 2002, 153 с. 2. Вагнер Г. Основы исследования операций. Тома I-III. –М.: Мир, 1972-73гг. 3. Гнеденко Б.В., Коваленко И.Н.. Введение в теорию массового обслуживания. М., 1987. 4. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: ДИС, 1997 5. Ивченко Г.И., Каштанов В.А., Коваленко И.Н.. Теория массового обслуживания. М., 1982. 6. Карлин С. Математические методы в теории игр, программирование и экономика. – М.: Мир, 1964 7. Сидин Э.Ф. Экономико-математическое моделирование. Учебное пособие/ Чернигов. Изд-во Черниговского гос. ин-та экономики и управления, 1999г 8. Солопахо А.В. Математика в экономике. Учебно-практическое пособие/Тамбов. Изд-во Тамб.гос.техн. ун-та,2001. ч. 1. 71с. 9. Тарасов В.Л. Экономико-математические методы и модели. Учебное пособие/ Нижний Новгород. Изд-во Нижегородского гос. ун-та,2003. 64с. 10. Аллен Р. Математическая экономика- – М. Ил, 1963 11. Ашманов С.А. Введение в математическую экономику. – М.: Наука, 1984 12. Громенко В.В.Математическая экономика. Учебно-практическое пособие. М.:МЭСИ, 2004-100с. 13. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М.: ДИС, 1997 14. Колесников А. Н. Краткий курс математики для экономистов. – М.: ИНФРА-М, 1997 15. Сидин Э.Ф. Экономико-математическое моделирование. Учебное пособие/ Чернигов. Изд-во Черниговского гос. ин-та экономики и управления, 1999г 16. Солопахо А.В. Математика в экономике. Учебно-практическое пособие/Тамбов. Изд-во Тамб.гос.техн. ун-та,2001. ч. 1. 71с. 17. Тарасов В.Л. Экономико-математические методы и модели. Учебное пособие/Нижний Новгород. Изд-во Нижегородского гос. ун-та,2003. 64с.
Дополнительная литература
Экланд И. Элементы математической экономики. – М.: |
megapredmet.ru