cos (pi / 4)
Расскажу, как найти значение функции cos (pi / 4) тремя способами.
Первый.
Этим способом чаще всего пользуются при решении тригонометрических уравнений в школе. Он заключается в использовании таблицы, в которой содержатся значения четырех тригонометрических функций от самых распространенных аргументов.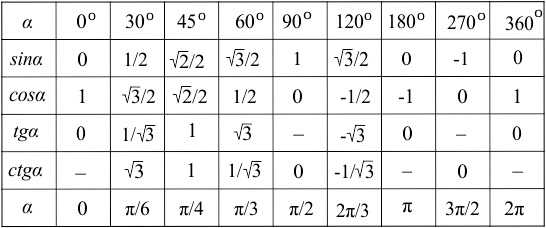
Такие таблицы существуют в нескольких вариантах. Различаются они тем, что значения углов представлены в градусах, в радианах или и в градусах и радианах (что наиболее удобно).
В таблице находим угол (в данном случае pi / 4) и нужную функцию (нам нужна функция косинус) и на пересечении этих значений получаем число корень из 2 / 2.
Математически это записывают так:
Второй.
Также распространенный способ, который всегда можно использовать, если таблицы нет. Заключается в использовании тригонометрического круга (или тригонометрической окружности).
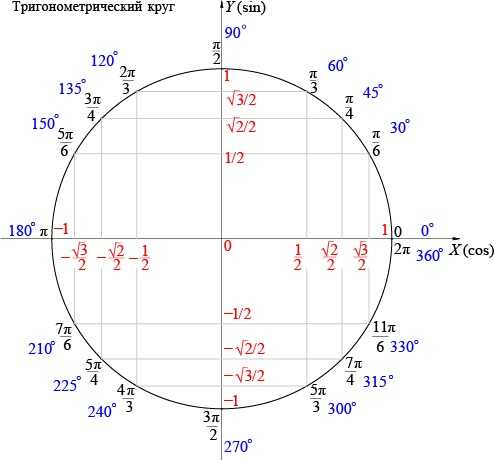
На таком тригонометрическом круге значения косинуса расположены на горизонтальной оси — оси абсцисс, а аргументы — на кривой самой окружности.
В нашем случае аргумент косинуса равен pi / 4. Определим, где находится это значение на окружности. Далее опустим перпендикуляр на ось Ох. Значение, в котором окажется конец этого перпендикуляра, и будет значением заданного косинуса. Следовательно, косинус от pi / 4 равен корень из 2 / 2.
Третий.
Удобно использовать также график соответствующей функции — график косинуса. Несложно запомнить, как он выглядит.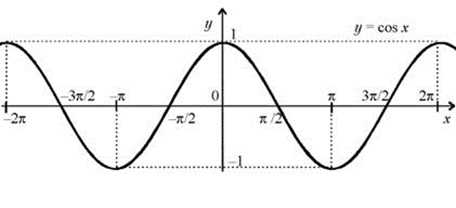
При использовании графика необходимы некоторые знания для определения значения косинуса pi / 4, который равен . В этом случае нужно понимать, что значение дроби больше 0,5 и меньше 1.
Есть, конечно, еще несколько способов. Например, вычисление значения косинуса с помощью калькулятора. Но для этого нужно предварительно угол pi / 4 перевести в градусы. Также могут быть полезными и таблицы Брадиса.
ru.solverbook.com
cos (п / 4)
Для вычисления значения функции cos (п / 4) можно использовать как минимум три способа.
1-ый способ.
Наиболее распространенный среди школьников и студентов. Значение четырех основных тригонометрических функций от основных аргументов можно найти с помощью таблицы значений тригонометрических функций.
Удобнее всего использовать таблицу, где есть значения углов и в радианах, и в градусах. В таком случае не придется переводит значения углов из радиан в градусы и наоборот.
По таблице определяем, что косинус от Пи / 4 равен корень из 2 / 2.
Математическая запись:
2-ой способ.
Если такой таблицы нет, а значения наизусть не помните (раньше в школах требовали заучивать их наизусть), то можно воспользоваться тригонометрическим кругом (или окружностью).

На тригонометрическом круге все значения косинуса лежат на оси абсцисс, а аргументы — на самой окружности.
В нашем случае аргумент косинуса равен Пи / 4. Определим, где находится это значение на окружности. Далее опустим перпендикуляр на ось Ох. Значение, в котором окажется конец этого перпендикуляра, и будет значением заданного косинуса. Следовательно, косинус от Пи / 4 равен корень из 2 / 2.
3-ий способ.
Если таблицы нет, на память ее не выучили, тригонометрическим кругом пользоваться не умеем, то можно использовать график функции косинус. Думаю, все должны помнить как он выглядит.
Но в этом случае все же понадобятся некоторые знания, чтобы определить с помощью графика, что косинус Пи / 4 будет равен . Для этого нужно помнить основные значения косинуса и понимать, что больше 0,5 и меньше 1.
ru.solverbook.com
Ответы@Mail.Ru: помогите чему равен cos(31пи/4)
Сos -периодическая функция, период=2Пи, поэтому это равно cos (31пи/4-7пи) =cos(3пи/4)=cos (пи-пи/4)=cosпи/4=корень из2/2
cos(7(3/4)p)=cos(1)3/4)p)=cos(2p-(p/4))=cosp/4=(sqrt2)/2
cos(31пи/4)= cos( 8пи- 1/4пи) = cos /4 пи== корень из двух деленное на 2touch.otvet.mail.ru
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(60) | |
| 4 | Найти точное значение | sin(30 град. ) | |
| 5 | sin(60 град. ) | ||
| 6 | Найти точное значение | tan(30 град. ) | |
| 7 | Найти точное значение | arcsin(-1) | |
| 8 | Найти точное значение | sin(pi/6) | |
| 9 | Найти точное значение | cos(pi/4) | |
| 10 | Найти точное значение | sin(45 град. ) | |
| 11 | Найти точное значение | sin(pi/3) | |
| 12 | Найти точное значение | arctan(-1) | |
| 13 | Найти точное значение | cos(45 град. ) | |
| 14 | Найти точное значение | cos(30 град. ) | |
| 15 | Найти точное значение | tan(60) | |
| 16 | Найти точное значение | csc(45 град. ) | |
| 17 | Найти точное значение | tan(60 град. ) | |
| 18 | Найти точное значение | sec(30 град. ) | |
| 19 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 20 | График | y=sin(x) | |
| 21 | Преобразовать из радианов в градусы | pi/6 | |
| 22 | Найти точное значение | cos(60 град. ) | |
| 23 | Найти точное значение | cos(150) | |
| 24 | Найти точное значение | tan(45) | |
| 25 | Найти точное значение | sin(30) | |
| 26 | Найти точное значение | sin(60) | |
| 27 | Найти точное значение | cos(pi/2) | |
| 28 | Найти точное значение | tan(45 град. ) | |
| 29 | График | y=sin(x) | |
| 30 | Найти точное значение | arctan(- квадратный корень 3) | |
| 31 | Найти точное значение | csc(60 град. ) | |
| 32 | Найти точное значение | sec(45 град. ) | |
| 33 | Найти точное значение | csc(30 град. ) | |
| 34 | Найти точное значение | sin(0) | |
| 35 | Найти точное значение | sin(120) | |
| 36 | Найти точное значение | cos(90) | |
| 37 | Преобразовать из радианов в градусы | pi/3 | |
| 38 | Найти точное значение | sin(45) | |
| 39 | Найти точное значение | tan(30) | |
| 40 | Преобразовать из градусов в радианы | 45 | |
| 41 | Найти точное значение | tan(60) | |
| 42 | Упростить | квадратный корень x^2 | |
| 43 | Найти точное значение | cos(45) | |
| 44 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 45 | Преобразовать из радианов в градусы | pi/6 | |
| 46 | Найти точное значение | cot(30 град. ) | |
| 47 | Найти точное значение | arccos(-1) | |
| 48 | Найти точное значение | arctan(0) | |
| 49 | График | y=cos(x) | |
| 50 | Найти точное значение | cot(60 град. ) | |
| 51 | Преобразовать из градусов в радианы | 30 | |
| 52 | Упростить | ( квадратный корень x+ квадратный корень 2)^2 | |
| 53 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 54 | Найти точное значение | sin((5pi)/3) | |
| 55 | Упростить | 1/( кубический корень от x^4) | |
| 56 | Найти точное значение | sin((3pi)/4) | |
| 57 | Найти точное значение | tan(pi/2) | |
| 58 | Найти угол А | tri{}{90}{}{}{}{} | |
| 59 | Найти точное значение | sin(300) | |
| 60 | Найти точное значение | cos(30) | |
| 61 | Найти точное значение | cos(60) | |
| 62 | Найти точное значение | cos(0) | |
| 63 | Найти точное значение | arctan( квадратный корень 3) | |
| 64 | Найти точное значение | cos(135) | |
| 65 | Найти точное значение | cos((5pi)/3) | |
| 66 | Найти точное значение | cos(210) | |
| 67 | Найти точное значение | sec(60 град. ) | |
| 68 | Найти точное значение | sin(300 град. ) | |
| 69 | Преобразовать из градусов в радианы | 135 | |
| 70 | Преобразовать из градусов в радианы | 150 | |
| 71 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 72 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 73 | Преобразовать из градусов в радианы | 89 град. | |
| 74 | Преобразовать из градусов в радианы | 60 | |
| 75 | Найти точное значение | sin(135 град. ) | |
| 76 | Найти точное значение | sin(150) | |
| 77 | Найти точное значение | sin(240 град. ) | |
| 78 | Найти точное значение | cot(45 град. ) | |
| 79 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 80 | Упростить | 1/( кубический корень от x^8) | |
| 81 | Найти точное значение | sin(225) | |
| 82 | Найти точное значение | sin(240) | |
| 83 | Найти точное значение | cos(150 град. ) | |
| 84 | Найти точное значение | tan(45) | |
| 85 | Вычислить | sin(30 град. ) | |
| 86 | Найти точное значение | sec(0) | |
| 87 | Упростить | arcsin(-( квадратный корень 2)/2) | |
| 88 | Найти точное значение | cos((5pi)/6) | |
| 89 | Найти точное значение | csc(30) | |
| 90 | Найти точное значение | arcsin(( квадратный корень 2)/2) | |
| 91 | Найти точное значение | tan((5pi)/3) | |
| 92 | Найти точное значение | tan(0) | |
| 93 | Вычислить | sin(60 град. ) | |
| 94 | Найти точное значение | arctan(-( квадратный корень 3)/3) | |
| 95 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 96 | Вычислить | arcsin(-1) | |
| 97 | Найти точное значение | sin((7pi)/4) | |
| 98 | Найти точное значение | arcsin(-1/2) | |
| 99 | Найти точное значение | sin((4pi)/3) | |
| 100 | Найти точное значение | csc(45) |
www.mathway.com
Ответы@Mail.Ru: cos(Пи/4-2X) — cos(Пи/4+2X)=1 Как Это решить? помогите плиз.
Решам так: cos(pi/4-2*x)-cos(pi/4+2*x)=1 2*sin((pi/4-2*x+pi/4+2*x)/2)*sin((-pi/4+2*x+pi/4+2*x)/2)=1 2*sin(pi/4)*sin(2*x)=1 sin(2*x)=sqrt(2)/2 2*x=pi/4 и 3*pi/4+2*pi*z x=pi/8+pi*z и x=3*pi/8+pi*z, где z- любое целое
cos(Пи/4-2X) — cos(Пи/4+2X)=1 -(cos(Пи/4+2X) — cos(Пи/4-2X))=1 2sin(Пи/4)sin(2X)=1 sin(2X)=koren(2)/2 2X=Пи/4 X=Пи/8
<img src=»//otvet.imgsmail.ru/download/0d3738f9642e17573c859d38f52835f3_i-41.jpg» >
Андрей Байбаков решил абсолютно верно!
touch.otvet.mail.ru
