Дисперсия и ее свойства. Среднее квадратическое отклонение
Дисперсией называется математическое ожидание квадрата отклонения случайной величины от :
Стандартное (среднее квадратичное) отклонение случайной величины определяется как корень из дисперсии и обозначается
Для вычисления дисперсии на практике удобно пользоваться следующей формулой:
Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.
Изучение переменных факторов по их дисперсиям называется методом дисперсионного анализа.
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение или онлайн-помощь на зачете/экзамене 〉〉
Свойство 1.
Свойство 2.
Дисперсия константы равна нулю:
Свойство 3.
Постоянный множитель выносится из-под знака дисперсии в квадрате:
Свойство 4.
Дисперсия суммы случайных величин:
где – ковариация случайных величин и
В частности, если и независимы, то
Прибавление константы в случайной величине не меняет ее дисперсии:
Дисперсия разности равна сумме дисперсий:
100task.ru
18. Дисперсия дискретной случайной величины
Зная лишь математическое ожидание случайной величины, еще нельзя судить ни о том, какие возможные значения она принимает, ни о том, как они рассеяны вокруг математического ожидания.
Рассмотрим, например, дискретные случайные величины X и Y , заданные следующими законами распределения:
Математические ожидания этих величин
Другими словами, математическое ожидание полностью случайную величину не характеризует. По этой причине наряду с математическим ожиданием вводят и другие числовые характеристики.
Определение7.1: Отклонением называют разность между случайной величиной и ее математическим ожиданием: X – M(X).
Свойство отклонения: Математическое ожидание отклонения равно нулю:
M[X – M(X)] = 0.
Доказательство: Пользуясь свойствами математического ожидания и тем, что M(X)- Постоянная величина, имеем
M[X – M(X)] = M(X) – M[M(X)] = M(X) –M(
Замечание: Наряду с термином “отклонение” используют термин “центрированная величина”. Центрированной случайной величиной Называют разность между случайной величиной и ее математическим ожиданием: = X – M(X).
Определение7.2:Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D(X) = M[X – M(X)]2.
Пусть дискретная случайная величина задана рядом распределения
X | x1 | X2 | X3 | ….. | Xn | |
P | p1 | P2 | P3 | ….. | Pn |
Тогда
D(X) = M[X – M(X)]2 = [x1-M(X)]2p1+ [x2-M(X)]2p2+…+ [Xn-M(X)]2Pn.
Таким образом, Чтобы найти дисперсию, достаточно вычислить сумму произведений возможных значений квадрата отклонения на их вероятности.
Пример. Найти дисперсию случайной величины X , которая задана следующим рядом распределения:
Решение: Математическое ожидание M(X) = 1∙0,3+2∙0,5+5∙0,2 = 2,3.
Тогда D(X) = (1 — 2,3)2∙0,3 + (2 — 2,3)2∙0,5 + (5 — 2,3)2∙0,2 = 1,69 ∙ 0,3 + 0,09 ∙ 0,5 + 7,29 ∙ 0,2 = 2,01.
Для вычисления дисперсии часто удобно пользоваться другой формулой:
D(X) = M(X2) – [M(X)]2.
Доказательство:
D(X) = M[X – M(X)]2=M[X2 — 2X∙M(X) + M2(X)]= M(X2) – 2M(X)∙M(X) + M2(X) =
= M(X2) – 2M2(X)+ M2(X) = M(X2)- M2(X).
Таким образом, Дисперсия равна разности между математическим ожиданием квадрата случайной величины и квадратом ее математического ожидания.
Пример. Найти дисперсию случайной величины X , которая задана следующим рядом распределения:
Решение: Математическое ожидание M(X) = 2∙0,1+3∙0,6+5∙0,3 = 3,5. Тогда M(X2) = 22∙0,1+32∙0,6+52∙0,3 = 13,3. Дисперсия D(X) = M(X2) – [M(X)]2=13,3 – (3,5)2=1,05.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Дисперсия и среднее квадратичное отклонение. Примеры вычисления
Математическое ожидание не дает достаточно полной информации о случайной величине, поскольку одному и тому же значению математического ожидания может соответствовать множество случайных величин, будут различаться не только возможными значениями, но и характером распределения и самой природой возможных значений.
Например. Законы распределения двух случайных величин и заданные таблицами:
Вычислить математическое ожидание и
Решение. Находим математическое ожидание по класической формуле
Получили, что для двух различных законов распределения математическое ожидание принимает одинаковое значения (0), при этом возможные значения случайных величин и различаются. Из приведенного примера видно, что в случае равенства математических ожиданий случайные величин и имеют тенденцию к колебаниям относительно и причем имеет больший размах рассеяния относительно сравнительно случайной величине относительно . Поэтому математическое ожидание еще называют центром рассеяния. Для определения рассеяния вводится числовая характеристика, называемая дисперсией.
Для определения дисперсии рассматривается отклонение случайной величины от своего математического ожидания
Математическое ожидание такого отклонения случайной величины всегда равна нулю. В этом легко убедиться из следующего соотношения
Таки образом, отклонение не может быть мерой рассеивания случайной величины.
Дисперсией случайной величины называют математическое ожидание квадрата отклонения случайной величины от своего математического ожидания
Для дискретной случайной величины дисперсия вычисляется по формуле
для непрерывной находят интегрированием
Если непрерывная величина заданная на интервале то дисперсия равна интегралу с постоянными пределами интегрирования
Дисперсия обладает следующими свойствами
1. Если случайная величина состоит из одной тотчки — постоянная величина, то дисперсия равна нулю
2. Дисперсия от произведения постоянной на случайную величину равна квадрату постоянной умноженной на дисперсию случайной величины
3. Если и — постоянные величины, то для дисперсии справедлива зависимость
Это следует из двух предыдущих свойств.
Дисперсию можно вычислить по упрощенной формуле:
которая в случае дискретной случайной величины имеет вид
для непрерывной определяется зависимостью
и для непрерывной на промежутке соотношением
Приведенные формулы очень удобны в вычислениях, и их, в отличие от предыдущих, используют в обучении
Также следует помнить, что дисперсия всегда принимает неотрицательные значения . Она характеризует рассеяние случайной величины относительно своего математического ожидания. Если случайная величина измерена в некоторых единицах, то дисперсия будет измеряться в этих же единицах, но в квадрате.
Для сравнения удобно пользоваться числовыми характеристиками одинаковой размерности случайной величиной. Для этого вводят в рассмотрение среднее квадратичное отклонение – корень квадратный из дисперсии. Ее обозначают греческой буквой «сигма»
—————————————-
Рассмотрим примеры для ознакомления с практической стороной определения этих величин.
Пример 1. Закон распределения дискретной случайной величины заданы таблицей:
Вычислить дисперсию и среднее квадратическое отклонение .
Решение. Согласно свойствами дисперсии получим:
—————————————-
Пример2. Есть четыре электрические лампочки, каждая из которых имеет дефект с вероятностью ( — вероятность того, что лампочка без дефекта). Последовательно берут по одной лампочке, вкручивают в патрон и включают электрический ток. При включении тока лампочка может перегореть, и ее заменяют на другую. Построить закон распределения дискретной случайной величины — число лампочек, которые будут опробованы. Вычислить среднее квадратическое отклонение
Решение. Дискретная случайная величина — число лампочек, которые будут опробованы — приобретает такие возможных значений:
Вычислим соответствующие вероятности:
Последнюю вероятность можно трактовать следующим образом: четвертая лампочка будет испытана, когда третья перегорит, а четвертая — нет, или если и четвертая перегорит.
В табличной форме закон распределения иметь следующий вид:
Для нахождения среднего квадратического отклонения найдем сначала значение дисперсии. Для дискретной случайной величины она примет значение:
Среднее квадратичное отклонение находим добычей корня квадратного из дисперсии.
—————————————-
Пример 3. Закон распределения вероятностей дискретной случайной величины заданы в виде функции
Вычислить среднее квадратическое отклонение и дисперсию
Решение. С помощью функции распределения вероятностей формируем закон распределения в виде таблицы
На основе таблицы распределения вычисляем дисперсию
————————
Подобных примеров можно привести множество, основная их суть в правильном применении приведенных в начале статьи формул для вычисления дисперсии и математического ожидания. Применяйте их там где это необходимо и не допускайте ошибок при определении дисперсии.
yukhym.com
Примеры решения задач
Пример 1. Пусть  – количество очков при бросании игральной
кости. Найти математическое ожидание,
дисперсию и среднее квадратическое
отклонение случайной величины
– количество очков при бросании игральной
кости. Найти математическое ожидание,
дисперсию и среднее квадратическое
отклонение случайной величины .
.
Решение. Закон распределения имеет вид:
.
Дисперсию вычислим по формуле:
.
Закон распределения случайной величины 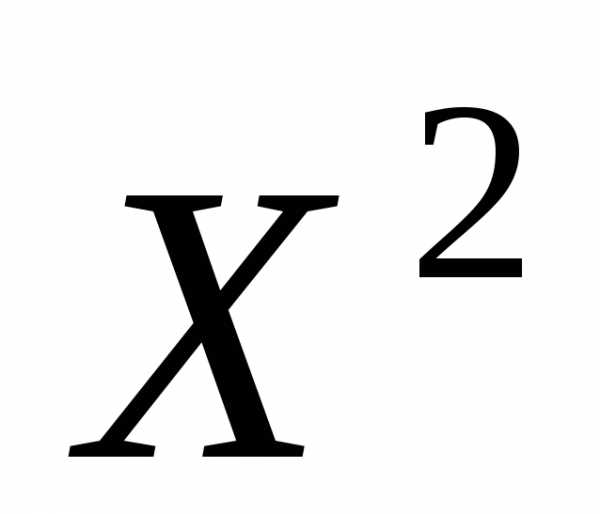 имеет вид:
имеет вид:
,
,
.
Пример 2.
Случайная величина 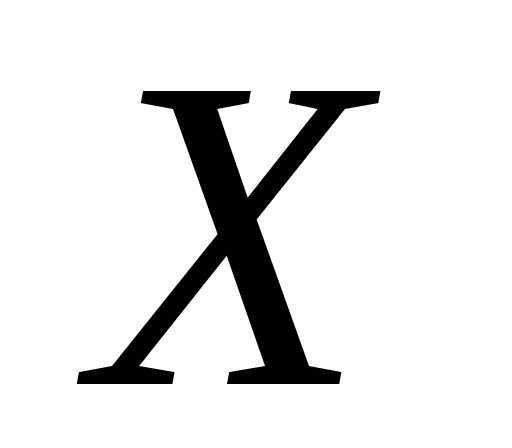
 .
Вне этого интервала
.
Вне этого интервала .
Найти математическое ожидание величины
.
Найти математическое ожидание величины .
.Решение.
Для 
 . Если.
. Если.
Для 
.
Пример 3.
Найти дисперсию случайной величины  ,
заданной интегральной функцией
,
заданной интегральной функцией
Решение.Найдем дифференциальную
функцию распределения случайной величины :
:

.
.
Пример 4.
Дана функция
Определить, при каком значении  функция
функция может быть принята за плотность
вероятности случайной величины
может быть принята за плотность
вероятности случайной величины
 ,
найти
,
найти и
и .
.Решение.
– плотность некоторой случайной величины .
.
.
 .
.
.
 .
.
,.
§ 3. Примеры распределения случайных величин
3.1 Биномиальное распределение
Определение. Распределение случайной
величины ,
равной количеству появлений события
,
равной количеству появлений события в схеме Бернулли из
в схеме Бернулли из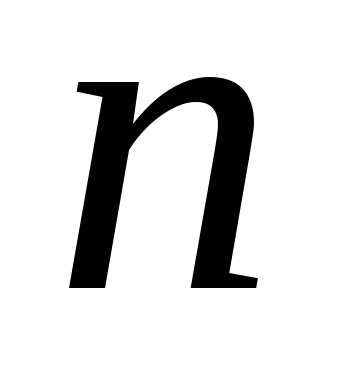 испытаний, называетсябиномиальным
распределением.
испытаний, называетсябиномиальным
распределением.
В этом распределении значению 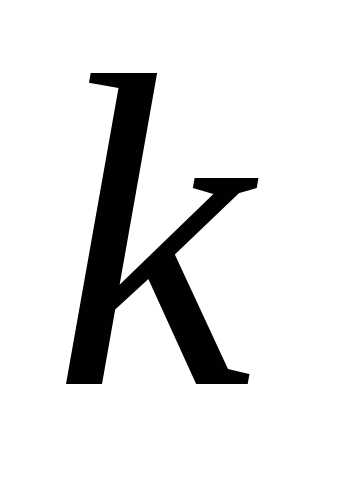 случайной величины
случайной величины соответствует вероятность,
где
соответствует вероятность,
где – вероятность наступления события
– вероятность наступления события
Теорема. Пусть – случайная величина с биномиальным
распределением. Тогда
– случайная величина с биномиальным
распределением. Тогда
,,.
Доказательство.
Т.к. биномиальное распределение дискретно, имеем:
Очевидно, что  ,
где
,
где – случайная величина, равная количеству
наступлений события
– случайная величина, равная количеству
наступлений события в
в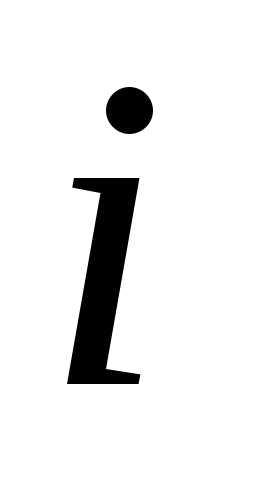 -ом
испытании. Все
-ом
испытании. Все независимы и имеют закон распределения:
независимы и имеют закон распределения:
О
0 | 1 |
|
|
.
Согласно свойствам математического ожидания и дисперсии имеем:
,
,
.
3.2 Распределение Пуассона
Определение. Распределение случайной
величины ,
принимающей значенияс вероятностями
,
принимающей значенияс вероятностями ,
где
,
где – некоторый параметр, называетсяпуассоновским распределениемилираспределением Пуассона.
– некоторый параметр, называетсяпуассоновским распределениемилираспределением Пуассона.
Теорема. Пусть – случайная величина, подчиненная
пуассоновскому закону распределения.
Тогда
– случайная величина, подчиненная
пуассоновскому закону распределения.
Тогда
,,.
Доказательство.
Т.к. пуассоновское распределение дискретно, имеем:
.
.
.
3.3 Нормальное распределение
Определение. Распределение
непрерывной случайной величины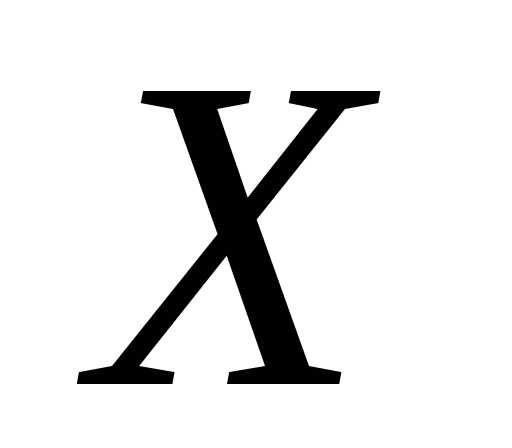 ,
заданное дифференциальной функцией
распределения
,
заданное дифференциальной функцией
распределения
, (1)
где  и
и – некоторые параметры, называетсянормальным распределением.
– некоторые параметры, называетсянормальным распределением.
Теорема.Если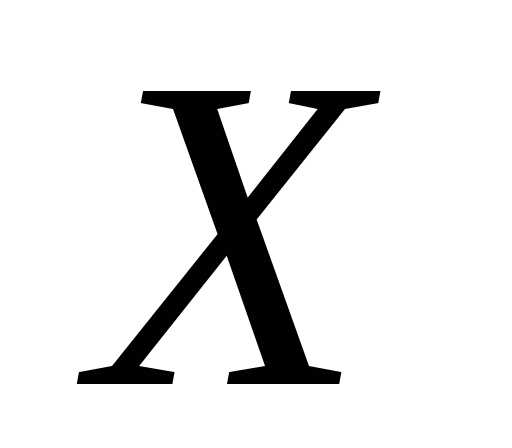 – нормально распределенная случайная
величина с дифференциальной функцией
распределения (1), то
– нормально распределенная случайная
величина с дифференциальной функцией
распределения (1), то
,,.
Теорема устанавливает, таким образом, вероятностный смысл параметров нормального распределения.
Нормальное распределение (нормальная случайная величина) играет исключительно важную роль в теории вероятностей и в приложениях теории вероятности к практическим задачам.
Эта роль объясняется установленным
фактом. Если известно, что изучаемая
случайная величина  складывается из большого количества
случайных величин, каждое из которых
оказывает лишь небольшое влияние на
всю сумму, то можно считать, что
складывается из большого количества
случайных величин, каждое из которых
оказывает лишь небольшое влияние на
всю сумму, то можно считать, что распределена нормально.
распределена нормально.
Например, ошибка, допускаемая при измерении какой-либо физической величины, складывается, по-видимому, из большого числа ошибок, вызванных многочисленными причинами. Поэтому, как правило, случайная ошибка измерения имеет нормальное распределение.
Рассмотрим нормальное распределение более подробно.
График функции (1) изображен на рис.
14.1. Его можно получить из “стандартного
графика” нормального распределения 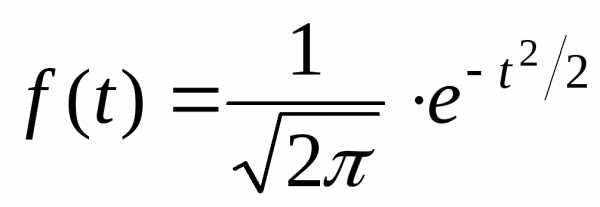 (
( ,
, )
сдвигом на
)
сдвигом на единиц вправо, с последующим растяжением
по горизонтали относительно оси симметрии
в
единиц вправо, с последующим растяжением
по горизонтали относительно оси симметрии
в раз. Функция
раз. Функция табулирована. Она упоминается в
формулировке локальной теоремы
Муавра-Лапласа. Криваясимметрична относительно прямой
табулирована. Она упоминается в
формулировке локальной теоремы
Муавра-Лапласа. Криваясимметрична относительно прямой .
Точка
.
Точка является точкой максимума функции, а
точки
является точкой максимума функции, а
точки – точками перегиба. Чем больше
– точками перегиба. Чем больше ,
тем кривая положе.
,
тем кривая положе.
Интегральный закон распределения, соответствующий дифференциальному закону (1), имеет вид:
. (2)
Интеграл (2) нельзя вычислить по формуле
Ньютона-Лейбница. Однако удобно выразить  через табулированную функцию Лапласа:
через табулированную функцию Лапласа:
 . (3)
. (3)
Именно,
. (4)
По интегральной теореме Муавра-Лапласа имеем:
(5)
или
 , где
, где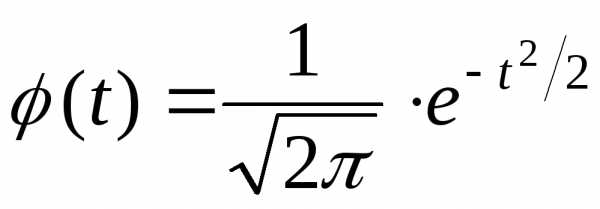 .
.
Пример.
Величина  распределена нормально с параметрами
распределена нормально с параметрами ,
,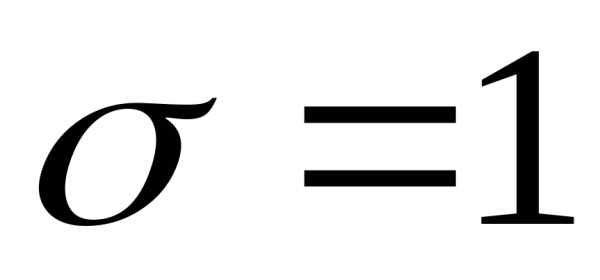 .
Найти вероятность того, что
.
Найти вероятность того, что примет значение в интервале
примет значение в интервале .
.
Решение.
.
Функция  быстро убывает при.
Площадь под всей кривой равна 1. Площади
криволинейных трапеций над интервалами,иравны соответственно
быстро убывает при.
Площадь под всей кривой равна 1. Площади
криволинейных трапеций над интервалами,иравны соответственно ,
, ,
, .
Таким образом, почти вся площадь под
кривой сосредоточена над интервалом.
Поскольку площадь криволинейной трапеции
численно равна вероятности того, что
случайная величина примет значение в
соответствующем интервале, имеем
.
Таким образом, почти вся площадь под
кривой сосредоточена над интервалом.
Поскольку площадь криволинейной трапеции
численно равна вероятности того, что
случайная величина примет значение в
соответствующем интервале, имеем
.
Это утверждение составляет содержание
правила “трех сигм” для нормального
распределения: практически достоверно,
что нормальная случайная величина с
параметрами  и
и принимает значения в интервале.
Слова “практически достоверно” означают
– с вероятностью
принимает значения в интервале.
Слова “практически достоверно” означают
– с вероятностью .
.
studfiles.net
§13. Дисперсия случайной величины
Дисперсиейслучайной величиныXназывается математическое ожидание квадрата отклонения этой величины от ее математического ожидания:
DX=E[X−EX]2
Интуитивно, дисперсия показывает «кучность» распределения X, т.е. близость конкретных значений случайной величины к ее математическому ожиданию10. Чем меньшеDX, тем более определено значениеX.
Свойства
DC = 0, при C = const (т.к. EC = C)
.
Доказательство. Действительно, изE[−EX+X]2= 0 с вероятностью 1 следует, чтоX – EX = 0 с вероятностью 1.
D[X + C] = D[X], при C = const. («инвариантность к сдвигу»)
Доказательство.D[X+C] =E[X+C–E[X+C]]2=E[X+C–EX–EC]2=
= E[X + C – EX – C]2 = E[X – EX]2 = DX.
D[CX] = C2DX, при C = const
Доказательство.D[CX] =E[CX–E[CX]]2=E[C2(X–EX)2] =
= C2 E[X − EX]2 = C2 DX.
Если XиYнезависимы, тоD[X+Y] =DX+DY.
Доказательство. Будем рассматривать вместоX — (X–EX), вместоY — (Y –EY), при этом дисперсия, очевидно, не изменится (математическое ожидание есть константа). Тогда, не умаляя общности, будем считатьEX= =EY= 0, и
D[X+Y] =E[X+Y]2=E[X2] +E[Y 2] + 2E[XY] =E[X2] +E[Y 2] +
+ 2E[X] E[Y] = E[X 2] + E[Y 2] = DX + DY,
где E[XY] =E[X] E[Y] справедливо лишь в предположении о независимости величинXиY.
Заметим, что при тех же условияхD[X–Y] =D[X+Y] =DX+DY, поскольку константа (−1) в (X–Y) = (X+ (−1)Y) выносится в квадрате по свойству 4).
Часто оказывается полезной следующая формула вычисления дисперсии:
DX=E[X 2] – (EX)2.
Доказательство.DX = E[X – EX]2 = E[X 2] – 2E[X EX] + E[(EX)2] =
= E[X 2] − 2(EX)2 + (EX)2= E[X 2] – (EX)2.
Вводят также стандартное отклонение(параметр масштаба) .
Откуда идет название «параметр масштаба»?
А из свойства,
гдеC=const— масштабный множитель (например, для
перевода измеренной величины из одних
единиц в другие).
.
Откуда идет название «параметр масштаба»?
А из свойства,
гдеC=const— масштабный множитель (например, для
перевода измеренной величины из одних
единиц в другие).
§14. Примеры вычисления математического ожидания и дисперсии
14.1 Вырожденное распределение
X=const=C
EX=EC=C
DX=DC= 0
14.2 Распределение Бернулли
P(X= 0) =q,P(X= 1) =p,p+q= 1
EX=p· 1 +q· 0 =p
E[X 2] =p· 12+q· 02=p
DX=E[X 2] – (EX)2=p–p2=p(1 –p) =pq
14.3 Биномиальное распределение
Для отыскания математического ожидания
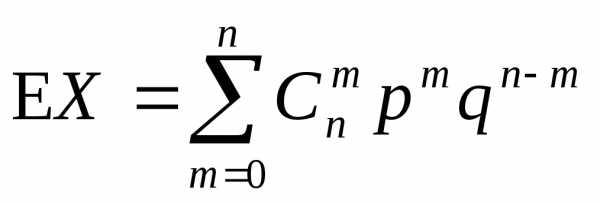
введем случайную величину
.
Заметим, что X= ∑Xi, аEXi=pпо п. 14.2. Тогда
.
Так как производятся nнезависимыхиспытаний,Xiнезависимы между собой и дисперсия равна по п. 14.2
.
14.4 Распределение Пуассона
.
.
.
Вывод: параметрλв распределении Пуассона играет роль как дисперсии, так и математического ожидания.
14.5 Геометрическое распределение
Заготовки по суммированию рядов
Геометрическая прогрессия:
.
При рядAможно дифференцировать
сколько угодно раз:
рядAможно дифференцировать
сколько угодно раз:
,.
Отсюда
.
При геометрическом распределении

Тогда
 .
.
Аналогично,
.
Отсюда
DX=E[X 2] – (EX)2= 2λ2+λ–λ2=λ2+λ.
14.6 Равномерное распределение на интервале [a,b]
 .
.
.
.
При a= 0,b= 1 (стандартное равномерное распределение)EX= 1/2,DX= 1/12.
14.7 Показательное распределение
 .
.
.
.
.
14.8 Симметричное показательное распределение
 .
.
(т.к.p(x) четная).
.
14.9 Нормальное распределение
.

14.10 Другие задачи
Имеется дискретная случайная величина Xс распределением
x | 0 | π/6 | π/2 | 5π/6 | π |
p | 1/10 | 3/10 | 1/10 | 2/10 | 3/10 |
а случайная величина Y=sin X. НайтиEY,DY.
Решение. РаспределениеY имеет вид
Тогда
EY = 1/2 · 1/2 + 1 · 1/10 = 1/4 + 1/10 = 7/20,
E[Y 2] = 1/4 · 1/2 + 1 · 1/10 = 1/8 + 1/10 = 9/40,
DY = E[Y 2] – (EY)2 = 9/40 – 49/400 = 41/400.
На гранях тетраэдра написаны числа 1, 2, 3, 4. Тетраэдр бросают на стол. Если он падает i-й гранью, то выигрыш составляет
 .
Найти ожидаемое значение выигрыша и
дисперсию, если совершено 10 бросков.
.
Найти ожидаемое значение выигрыша и
дисперсию, если совершено 10 бросков.
Решение. Введем случайную величинуX1(выигрыш при одном броске). Тогда ее математическое ожидание равно
.
Матожидание квадрата X1
.
Дисперсия
.
Тогда для 10 бросков выигрыш будет равен ожидаемый сумме матожиданий выигрышей при отдельных бросках:
EX= 10EX1= 150/2 = 75.
Дисперсия при этом также увеличится в 10 раз:
DX = 10DX1 = 1290/4 = 645/2.
Пусть X,Y ~U(0,1) и независимы,Z=max(X,Y). НайтиEZ, DZ.
Решение. Функция распределения
F(z) =P(Z<z) =P(X<z,Y<z) =P2(X<z) =z2,
плотность распределения p(z) = 2z(приz[0,1]). Тогда

Распределение случайной величины задано графиком:
 .
.
Найти математическое ожидание и дисперсию.
Решение.
Пусть X,Y ~N(0,1) и независимы,U=max(X,Y),V=min(X,Y). НайтиE[U−V].
Решение.
P(U < x) = P(max(X, Y) < x) = P(X < x, Y < x) = P2(X < x) = Φ2(x).
Обозначим плотность распределения Uзаq, тогда
q(x) = (Φ2(x))′ = 2Φ(x) φ(x).
Математическое ожидание Uравно
Проводя аналогичные рассуждения для V, получим. Тогда.
Пусть X,Y ~N(0,1) и независимы, аY1=exp{2X+ 3Y}. НайтиE[Y1].
Решение. Можно было бы воспользоваться известным фактом, что линейное преобразование нормально распределенной случайной величины снова дает случайную величину с нормальным распределением. Однако в этой задаче проще поступить иначе. Т.к.XиYнезависимы, то
E[exp{2X + 3Y}] = E[exp 2X exp 3Y] = E[exp 2X] E[exp 3Y].
Теперь найдем
Последнее равенство верно в силу того, что под интегралом стоит плотность распределения N(a, 1). С учетом полученной нами формулы имеем
.
studfiles.net
18. Дисперсия дискретной случайной величины (определение, формула для вычисления). Основные свойства дисперсии.
ДисперсиейДСВназывается математическое ожидание квадрата отклонения СВ от ее математического ожидания
Дисперсия служит для характеристики рассеяния СВ относительно ее математического ожидания
Свойства дисперсии:
а) , где;
б) ;
в),
где – ковариация двух случайных величини;
г) если инекоррелированы, то, тогда.
19. Биномиальное распределение и его числовые характеристики. Привести пример. Биномиальный закон распределения.Случайная величина, распределенная по биномиальному закону, принимает значения:
0, 1, 2, …, nс вероятностями, определяемыми по формулам Бернулли:
Числовые хар-ки: Математическое ожидание: . Дисперсия:.
Пример.В рекламных целях торговая фирма вкладывает в каждую пятую единицу товара денежный приз размером 100 тенге. Найти закон распределения числа сотен тенге, полученных при четырёх сделанных покупках.
20. Распределение Пуассона и его числовые характеристики. Привести пример.Закон распределения Пуассона. Случайная величина, распределенная по закону Пуассона, принимает бесконечное счетное число значений: 0, 1, 2, …,m, …, с соответствующими вероятностями, определяемыми по формуле Пуассона
При ибиномиальный закон распределения приближается к закону распределения Пуассона, гдеa=np
Математическое ожидание M(ξ) = ДисперсияD(ξ) =a.
Пример: число родившихся за определённый период близнецов, число опечаток в большом тексте.
21. Непрерывные случайные величины. Способы задания закона распределения (функция распределения, плотность вероятности). Привести пример. Функция распределения представляет собой универсальный способ задания СВ в том смысле, что она существует только для дискретной СВ, а плотность распределения – только для непрерывной.
Для непрерывной СВ функция распределения F(x)=P(ξ<x) непрерывна в любой точке числовой прямой. Более того, P(ξ=x0)=0, т.е. вероятность того, что непрерывная СВ примет заранее указанное значение, равна нулю.
F(x) можно представить в виде интеграла
Функция называется функциейплотности распределения вероятностей.
22. Плотность вероятности Основные свойства. Функцияназывается функциейплотности распределения вероятностей.
Из определения вытекают свойства функции плотности распределения :
1.Плотность распределения неотрицательна: .
2. Интеграл по всей числовой прямой от плотности распределения вероятностей равен единице:
3. В точках непрерывности плотность распределения равна производной функции распределения: .
4. Плотность распределения определяет закон распределения случайной величины, т.к. определяет вероятность попадания случайной величины на интервал :
.
5. Вероятность того, что непрерывная случайная величина примет конкретное значение равна нулю:. Поэтому справедливы следующие равенства:
23. Числовые характеристики непрерывной СВ. Математическое ожидание для непрерывно распределенных случайных величин определяется по формуле При этом интеграл, стоящий справа, должен абсолютно сходиться. Пусть имеет плотность р(х) и (х) — некоторая функция. Математическое ожидание величины () можно вычислить по формуле
, если интеграл, стоящий справа, абсолютно сходится.
Дисперсия может быть вычислена по формуле , а также, как и в дискр-ом случае, по ф-ле, где24. Равномерный закон распределения и его числовые характеристики. Пример. Равномерное распределение. Непрерывная случайная величинаимеет равномерное распределение на отрезке [a,b], если плотность распределения р(x) сохраняет постоянное значение на этом промежутке:
Функция распределения F(x) равномерно распределенной случайной величины равна F(x)=
Математическое ожидание и дисперсия ;.
studfiles.net
Пример 13. Вероятность попадания в цель у стрелка р = 0,8. Производится три выстрела. Построить ряд распределения случайной величины X — числа попаданий в цель. Найти математическое ожидание М [X] и дисперсию D [X].  Пример 14. Производится испытание n=3 приборов на надежность. Вероятность выдержать испытание для каждого прибора равна р=0.7 . Случайная величина X — число приборов, не выдержавших испытание. Построить ряд распределения случайной величины X. Найти математическое ожидание М[Х] и дисперсию D [X].  Контрольная работа ЗАДАНИЕ №1
Варианты 1-6.
Из партии, состоящей из N изделий, среди которых имеются М бракованных, выбраны случайным образом к
изделий для проверки их качества. Построить ряд распределения случайного числа X бракованных изделий, содержащихся в выборке, график функции распределения. Найти математическое ожидание и дисперсию величины X .
Варианты 7 — 12.
Телефон — автомат обеспечивает нужное соединение с вероятностью р. Вы пытаетесь дозвониться по определенному номеру, имея к началу опыта N двадцати пяти копеечных монет. Случайная величина X — число истраченных монет. Построить ряд распределения, график функции распределения, найти математическое ожидание и дисперсию.
Варианты 13 — 19.
Вероятность попадания стрелком в цель при одном выстреле равна р. Случайная величина X — число удач стрелка, сделавшего М выстрелов. Построить ряд распределения, график функции распределения величины X. Найти математическое ожидание и дисперсию величины X.
Варианты 20-25.
С подводной лодки выпускают торпеды последовательно по одной до первого попадания в цель или полного израсходования всего боекомплекта, состоящего из М торпед. Все выстрелы независимы, а вероятность попадания в цель каждой торпеды равна р. Случайная величина X — число израсходованных торпед. Построить ряд и график функции распределения случайной величины X. Найти математическое ожидание и дисперсию величины X .
Варианты 26 — 30.
Проводятся испытания N изделий на надежность, причем вероятность выдержать испытания для каждого
изделия равна р. Случайная величина X — число изделий, выдержавших испытания. Построить ряд распределения, график функции распределения, найти математическое ожидание и дисперсию случайной величины X . Контрольная работа ЗАДАНИЕ №1
Варианты 1-6.
Из партии, состоящей из N изделий, среди которых имеются М бракованных, выбраны случайным образом к
изделий для проверки их качества. Построить ряд распределения случайного числа X бракованных изделий, содержащихся в выборке, график функции распределения. Найти математическое ожидание и дисперсию величины X .
Варианты 7 — 12.
Телефон — автомат обеспечивает нужное соединение с вероятностью р. Вы пытаетесь дозвониться по определенному номеру, имея к началу опыта N двадцати пяти копеечных монет. Случайная величина X — число истраченных монет. Построить ряд распределения, график функции распределения, найти математическое ожидание и дисперсию.
Варианты 13 — 19.
Вероятность попадания стрелком в цель при одном выстреле равна р. Случайная величина X — число удач стрелка, сделавшего М выстрелов. Построить ряд распределения, график функции распределения величины X. Найти математическое ожидание и дисперсию величины X.
Варианты 20-25.
С подводной лодки выпускают торпеды последовательно по одной до первого попадания в цель или полного израсходования всего боекомплекта, состоящего из М торпед. Все выстрелы независимы, а вероятность попадания в цель каждой торпеды равна р. Случайная величина X — число израсходованных торпед. Построить ряд и график функции распределения случайной величины X. Найти математическое ожидание и дисперсию величины X .
Варианты 26 — 30.
Проводятся испытания N изделий на надежность, причем вероятность выдержать испытания для каждого
изделия равна р. Случайная величина X — число изделий, выдержавших испытания. Построить ряд распределения, график функции распределения, найти математическое ожидание и дисперсию случайной величины X . |
www.reshim.su


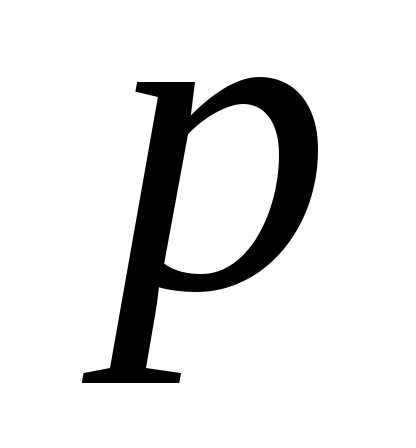
 .
Найти ожидаемое значение выигрыша и
дисперсию, если совершено 10 бросков.
.
Найти ожидаемое значение выигрыша и
дисперсию, если совершено 10 бросков.