Докажите тождество онлайн решение – Калькулятор онлайн — Решение тригонометрических уравнений

• Тождеством называют равенство, которое выполняется при всех значениях переменных, которые в него входят.

Некоторые тождества мы уже знаем. Например, все формулы сокращенного умножения являются тождествами.

Доказать тождество – это значит установить, что для любого допустимого значение переменные его левая часть равна правой части.

В алгебре существует несколько различных способов доказательства тождеств.

Способы доказательства тождеств

• Выполнить равносильные преобразования левой части тождества. Если в итоге получим правую часть, тогда тождество считается доказанным.
• Выполнить равносильные преобразования правой части тождества. Если в итоге получим левую часть, тогда тождество считается доказанным.
• Выполнить равносильные преобразования левой и правой части тождества. Если в результате получим одинаковый результат, тогда тождество считается доказанным.
• Из правой части тождества вычитаем левую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.
• Из левой части тождества вычитают правую часть. Производим над разностью равносильные преобразования. И если в итоге получаем нуль, то тождество считается доказанным.

Следует так же помнить, что тождество справедливо лишь для допустимых значений переменных.

Как видите способов достаточно много. Какой способ выбрать в данном конкретном случае, зависит от тождества, которое вам необходимо доказать. По мере того, как вы будете доказывать различные тождества, придет и опыт в выборе способа доказательства.

Рассмотрим несколько простых примеров

Пример 1.

Докажите тождество x*(a+b) + a*(b-x) = b*(a+x).

Решение.

Так как в правой части небольшое выражение, попытаемся преобразовать левую часть равенства.

Имеем,

• x*(a+b) + a*(b-x) = x*a+x*b+a*b – a*x.

Приведем подобные слагаемые и вынесем общий множитель за скобку.

• x*a+x*b+a*b – a*x = x*b+a*b = b*(a+x).

Получили что левая часть после преобразований, стала такой же как и правая часть. Следовательно, данное равенство является тождеством.

Пример 2.

Докажите тождество a^2 + 7*a + 10 = (a+5)*(a+2).

Решение.

В данном примере можно поступить следующим способом. Раскроем скобки в правой части равенства.

Получим,

• (a+5)*(a+2) = (a^2) +5*a +2*a +10= a^2+7*a+10.

Видим, что после преобразований, правая часть равенства стала такой же как и левая часть равенства. Следовательно, данное равенство является тождеством.

Нужна помощь в учебе?

Предыдущая тема: Разложение многочлена на множители способом группировки
Следующая тема:&nbsp&nbsp&nbspВозведение в квадрат суммы и разности двух выражений: формулы и примеры

Все неприличные комментарии будут удаляться.

www.nado5.ru

Основное тригонометрическое тождество

Основное тригонометрическое тождество связывает синус и косинус одного и того же угла. Сформулируем его: для любого угла справедливо:

   

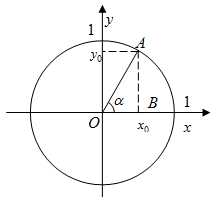
Рис. 1

Доказательство тождества

Рассмотрим тригонометрическую окружность (рис. 1). Выберем произвольный угол , тогда , а . В , как радиус единичной окружности. Так как треугольник прямоугольный, то для него можно записать теорему Пифагора:

   

Учитывая, что и , получаем

   

Что и требовалось доказать.

Следствие 1. Основное тригонометрическое тождество позволяет находить синус угла по известному косинусу или, наоборот, косинус угла по известному синусу. Справедливы формулы

   

Но для определения знака искомой тригонометрической функции требуется дополнительная информация о величине угла (например, в какой четверти расположен угол ).

Следствие 2. Из основного тригонометрического тождества можно вывести две формулы, связывающие соответственно косинус с тангенсом и синус с котангенсом.

1. Пусть тогда . Разделим обе части основного тригонометрического тождества на :

   

после преобразования получим

   

2. Пусть тогда . Разделим обе части основного тригонометрического тождества на :

   

после преобразования получим

   

Примеры решения задач

Основное тригонометрическое тождество, так же используется при тождественных преобразованиях.

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

No related posts.