Как найти стационарные точки функции 🚩 Математика
Автор КакПросто!
Процесс исследования функции на наличие стационарных точек а также их нахождения является одним из важных элементов при построении графика функции. Найти стационарные точки функции можно, обладая определенным набором математических знаний.

Статьи по теме:
Вам понадобится
- — функция, которую необходимо исследовать на наличие стационарных точек;
- — определение стационарных точек: стационарные точки функции — это точки (значения аргумента), в которых производная функции первого порядка обращается в нуль.
Инструкция
Используя таблицу производных и формулы дифференцирования функций, необходимо найти производную функции. Этот шаг является наиболее сложным и ответственным в ходе выполнения задачи. Если допустить ошибку на данном этапе, дальнейшие вычисления не будут иметь смысла.

Проверьте, зависит ли производная функции от аргумента. Если найденная производная не зависит от аргумента, то есть является числом (к примеру, f'(x) = 5), то в таком случае функция не имеет стационарных точек. Такое решение возможно, только если исследуемая функция является линейной функцией первого порядка (к примеру, f(x) = 5x+1). Если производная функции зависит от аргумента, то приступите к последнему этапу.
Составьте уравнение f'(x)= 0 и решите его. Уравнение может не иметь решений — в таком случае у функции стационарных точек не имеется. Если решения у уравнения есть, то именно эти найденные значения аргумента и будут являться стационарными точками функции. На данном этапе следует провести проверку решения уравнения методом подстановки аргумента.
Обратите внимание
При нахождении производной функции могут возникнуть трудности, если функция является сложной. В таком случае нужно использовать прием замены части функции промежуточным аргументом.
Полезный совет
Для выполнения данной задачи необходимо уделить особое внимание правилам дифференцирования.Внимание и концентрация на задаче также помогут с ней справиться — перед выполнением задачи убедитесь в том, что вас ничто не будет отвлекать в процессе ее решения.
Знание стационарных точек функции значительно облегчает построение ее графика, так как именно в этих точках находится максимальное и минимальное значения функции.
Источники:
- Производная функции — Википедия
- Критическая точка (математика) — Википедия
Критической точкой функции называется точка, в которой производная функции обращается ноль. Значение функции в критической точке называется критическим значением.

Вам понадобится
- Знания по математическому анализу.
Инструкция
Производной функции в точке называется отношение приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю. Но для стандартных функций существуют так называемые табличные производные, а также при дифференцировании функций применяют различные формулы, существенно упрощающих это действие.Пусть дана функция f(x) = x^2. Для поиска критических точек необходимо найти ее производная функции f(x) равна: f'(x) = 2x.
Далее приравниваем производную к нулю и решаем полученное уравнение. В результате корни этого уравнения и будут критическими точками исходной функции f(x). Приравниваем производную к нулю: f'(x) = 0 или 2x = 0. Решая полученное уравнение получим, что x=0. Эта точка и будет являться критической для исходной функции.
Обратите внимание
У некоторых функций не существует критических точек или значение в этих точках равны бесконечности, в этом случае через эти точки проходят асимптоты функции.
Полезный совет
Уравнение прямой не имеет критических точек, так как ее производная никогда не обращается в ноль, но прямые типа: f(x) = C, где С — некоторая константа, имеют бесконечно много критических точек.
www.kakprosto.ru
Как найти экстремум?
Прежде, чем научиться находить экстремумы функции, необходимо понять, что же такое экстремум. Самое общее определение экстремума гласит, что это употребляемое в математике наименьшее или наибольшее значение функции на определенном множестве числовой линии или графике. В том месте, где находится минимум, появляется экстремум минимума, а там, где максимум – экстремум максимума. Также в такой дисциплине, как математический анализ, выделяют локальные экстремумы функции. Теперь давайте рассмотрим, как найти экстремумы.
Экстремумы в математике относятся к важнейшим характеристикам функции, они показывают её самое большое и самое маленькое значение. Находятся экстремумы преимущественно в критических точках находимых функций. Стоит отметить, что именно в точке экстремума функция кардинально меняет своё направление. Если просчитать производную от точки экстремума, то она, согласно определению, должна быть равна нулю или же вовсе будет отсутствовать. Таким образом, чтобы узнать, как найти экстремум функции, необходимо выполнить две последовательные задачи:
- найти производную для той функции, которую необходимо определить заданием;
- найти корни уравнения.
Последовательность нахождения экстремума
- Оформите в письменном виде функцию f(x), которая задана. Найдите её производную первого порядка f ‘(x). То выражение, которое получится, приравняйте к нулю.
- Теперь вам предстоит решить то уравнение, которое получилось. Результирующие решения и будут корнями уравнения, а также критическими точками определяемой функции.
- Теперь определяем, какими именно критическими точками (максимума или минимума) являются найденные корни. Следующим этапом, после того, как мы узнали, как находить точки экстремума функции, является нахождение второй производной от искомой функции f ‘ (x). Необходимо будет подставить в конкретное неравенство значения найденных критических точек и затем посчитать, что получится. Если произойдет так, что вторая производная окажется больше нуля в критической
elhow.ru
Экстремумы функции
Введение
Во многих областях науки и в практической деятельности часто приходится сталкиваться с задачами поиска экстремума функции. Дело в том, что многие технические, экономические и т.д. процессы моделируются функцией или несколькими функциями, зависящими от переменных – факторов, влияющих на состояние моделируемого явления. Требуется найти экстремумы таких функций для того, чтобы определить оптимальное (рациональное) состояние, управление процессом. Так в экономике, часто решаются задачи минимизации издержек или максимизации прибыли – микроэкономическая задача фирмы. В этой работе мы не рассматриваем вопросы моделирования, а рассматриваем только алгоритмы поиска экстремумов функций в простейшем варианте, когда на переменные не накладываются ограничения (безусловная оптимизация), и экстремум ищется только для одной целевой функции.
ЭКСТРЕМУМЫ ФУНКЦИИ

Рассмотрим график непрерывной функции y=f(x) , изображенной на рисунке. Значение функции в точке x 1 будет больше значений функции во всех соседних точках как слева, так и справа от x 1 . В этом случае говорят, что функция имеет в точке x 1 максимум. В точке x 3 функция, очевидно, также имеет максимум. Если рассмотреть точку x 2 , то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x 2 минимум. Аналогично для точки x 4 .
Функция y=f(x) в точке x 0 имеет максимум , если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x 0 , т.е. если существует такая окрестность точки x 0 , что для всех x ≠x 0, принадлежащих этой окрестности, имеет место неравенство f(x) <f(x 0) .
Функция y=f(x) имеет минимум в точке x 0, если существует такая окрестность точки x 0, что для всех x ≠x 0 , принадлежащих этой окрестности, имеет место неравенство f(x) >f(x0 .
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.
Отмети, что если функция имеет в точке максимум, то это не означает, что в этой точке функция имеет наибольшее значение во всей области определения. На рисунке, рассмотренном выше, функция в точке
Теорема 1. (Необходимое условие существования экстремума.) Если дифференцируемая функция y=f(x) имеет в точке x= x 0 экстремум, то ее производная в этой точке обращается в нуль.
Доказательство . Пусть для определенности в точке x 0 функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x 0 + Δx)<f(x 0) , т.е.
Но тогдаПереходя в этих неравенствах к пределу при Δx → 0 и учитывая, что производная f ‘(x 0 ) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f’ (x 0 ) ≥ 0 а при Δx → 0 + 0 f’ (x 0 ) ≤ 0. Так как f ‘ (x 0 ) определяет число, то эти два неравенства совместны только в том случае, когда f ‘ (x 0 ) = 0.
Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль.
Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры.
Примеры.
y =|x |.
Функция не имеет производной в точке x =0 (в этой точке график функции не имеет определенной касательной), но в этой точке функция имеет минимум, так как
Функция
не имеет производной при x =0, так как обращается в бесконечность приx =0. Но в этой точке функция имеет максимум.Функция
не имеет производной при x =0, так как при x →0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x) =0 и при xf(x)x >0f(x) >0.Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует.
Однако, если в некоторой точке x 0 мы знаем, что f ‘(x 0) =0, то отсюда нельзя делать вывод, что в точке x 0 функция имеет экстремум.
Например.
.Но точка x =0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox , а справа выше.
Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками .
Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.
Теорема 2. (Достаточное условие существования экстремума.) Пусть функция непрерывна на некотором интервале, содержащем критическую точку x 0 , и дифференцируема во всех точках этого интервала (кроме, быть может, самой точки x 0 ). Если при переходе слева направо через эту точку производная меняет знак с плюса на минус, то в точке x = x 0 функция имеет максимум. Если же при переходе через
Таким образом, если
f ‘(x) >0 при x <x 0 и f ‘(x)< 0 при x> x 0 , то x 0 – точка максимума;
при xx 0 и f ‘(x)> 0 при x> x 0 , то x 0 – точка минимума.Доказательство . Предположим сначала, что при переходе через x 0 производная меняет знак с плюса на минус, т.е. при всех x , близких к точке x 0f ‘(x)> 0 для x< x 0 , f ‘(x)< 0 для x> x 0 . Применим теорему Лагранжа к разности f(x) — f(x 0) = f ‘(c)(x- x 0 ), где c лежит между x и x 0 .
Пусть x < x
0 . Тогда c< x 0 и f ‘(c)> 0. Поэтомуf ‘(c)(x- x 0 )< 0и, следовательно,f(x) — f(x 0)< 0,т.е. f(x)< f(x 0).
Пусть x > x 0 . Тогда c> x 0 и f ‘(c)< 0. Значитf ‘(c)(x- x 0 )< 0. Поэтому f(x) — f(x 0) <0,т.е.f(x) < f(x 0) .
Таким образом, для всех значений x достаточно близких к x 0f(x) < f(x 0) . А это значит, что в точке x 0 функция имеет максимум.
Аналогично доказывается вторая часть теоремы о минимуме.
Проиллюстрируем смысл этой теоремы на рисунке. Пусть f ‘(x 1) =0 и для любых x, достаточно близких к x 1 , выполняются неравенства
f ‘(x)<
mirznanii.com
Локальный экстремум функции. Примеры
Отыскание локальных максимумов и минимумов не обходится без дифференцирования и является необходимым при исследовании функции и построении ее графика.
Точка называется точкой локального максимума (или минимума) функции , сли существует такой окрестность этой точки, принадлежащий области определения функции, и для всех из этого окрестности выполняется неравенство (или ).
Точки максимума и минимума называются точками экстремума функции, а значения функции в экстремальных точках — ее экстремальными значениями.
НЕОБХОДИМОЕ УСЛОВИЕ ЛОКАЛЬНОГО ЭКСТРЕМУМА:
Если функция имеет в точке локальный экстремум, то либо производная равна нулю , либо не существует.
Точки которые удовлетворяют выписанным выше требованиям называют критическими точками.
Однако в каждой критической точке функция имеет экстремум. Ответ на вопрос: будет критическая точка точкой экстремума дает следующая теорема.
ДОСТАТОЧНОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА ФУНКЦИИ
Теорема І. Пусть функция непрерывна в некотором интервале, содержащем критическую точку и дифференцированная во всех точках этого интервала (за исключением, возможно, самой точки ).
Тогда для точки функция имеет максимум, если для аргументов выполняется условие, что производная больше нуля , а для условие — производная меньше нуля .
Если же для производная меньше нуля , а для больше нуля , то для точки функция имеет минимум.
Теорема ІІ. Пусть функция дважды дифференцируема в окрестности точки и производная равна нулю . Тогда в точке функция имеет локальный максимум, если вторая производная меньше нуля и локальный минимум, если наоборот .
Если же вторая производная равна нулю , то точка может и не быть точкой экстремума.
При исследовании функций на экстремумы используют обе теоремы. Первая на практике проще, поскольку не требует нахождения второй производной.
ПРАВИЛА НАХОЖДЕНИЯ ЕКСТРЕМУМОВ (МАКСИМУМОВ И МИНИМУМОВ) С ПОМОЩЬЮ ПЕРВОЙ ПРОИЗВОДНОЙ
1) найти область определения ;
2) найти первую производную ;
3) найти критические точки;
4) исследовать знак производной на интервалах, которые получили от разбиения критическими точками области определения .
При этом критическая точка является точкой минимума, если при переходе через нее слева направо производная меняет знак с отрицательного на положительный , в противном случаэ является точкой максимума.
Вместо данного правила можно определять вторую производную и исследовать согласно второй теоремы.
5) вычислить значения функции в точках экстремума.
Рассмотрим теперь исследование функции на экстремумы на конкретных примерах.
————————————
Примеры.
Сборник В.Ю. Клепко, В.Л. Голец «Высшая математика в примерах и задачах»
1. (4.53.7)
1) Областью определения будет множество действительных чисел
;
2) Находим производную
3) Вычисляем критические точки
Они разбивают область определения на следующие интервалы
4) Исследуем знак производной на найденных интервалах методом подстановки значений
Таким образом первая точка является точкой минимума, а вторая — точкой максимума.
5) Вычисляем значение функции
——————————
2. (4.53.9)
1) Областью определения будет множество действительных чисел , так корень всегда больше единицы
и функция арктангенс определена на всей действительной оси.
2) Находим производную
3) С условия равенства производной нулю находим критическую точку
Она разбивает область определения на два интервала
4) Определим знак производной в каждой из областей
Таким образом находим, что в критической точке функция принимает минимальное значение.
5) Вычислим экстремум функции
——————————
3. (4.53.13)
1) Функция определена когда знаменатель не превращается в ноль
Из этого следует, что область определения состоит из трех интервалов
2) Вычисляем производную
3) Приравниваем производную к нулю и находим критические точки.
4) Устанавливаем знак производной в каждой из областей, подстановкой соответствующих значений.
Таким образом точка является точкой локального максимума, а локального минимума. В имеем перегиб функции, но о нем будет больше материала в следующих статьях.
5) Находим значение в критических точках
Несмотря на то, что значение функции , первая точка является точкой локального максимума, а дуга — минимума. Не бойтесь, если у Вас выйдут подобные результаты, при определении локальных экстремумов такие ситуации допустимы.
———————————————-
Посмотреть материалы:
yukhym.com
Второй признак экстремума функции.
Пусть ,
если , то — точка минимума;
если , то — точка максимума.
Как видите, этот признак экстремума функции требует существования производной как минимум до второго порядка в точке .
Пример.
Найти экстремумы функции .
Решение.
Начнем с области определения:
Продифференцируем исходную функцию:
Производная
обращается в ноль при x=1,
то есть, это точка возможного экстремума.
Находим вторую производную функции
и вычисляем ее значение при x
= 1: 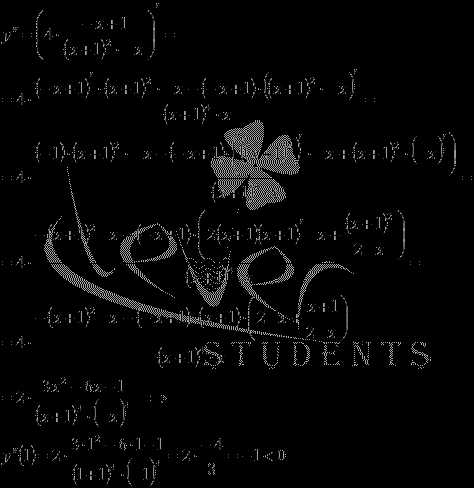
Следовательно, по второму достаточному условию экстремума, x=1 — точка максимума. Тогда — максимум функции.
Графическая иллюстрация.
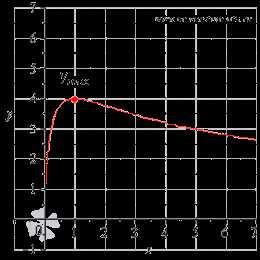
Ответ:
Третье достаточное условие экстремума функции.
Пусть функция y=f(x) имеет производные до n-ого порядка в -окрестности точки и производные до n+1-ого порядка в самой точке . Пусть и .
Тогда,
Пример.
Найти точки экстремума функции .
Решение.
Исходная функция является целой рациональной, ее областью определения является все множество действительных чисел.
Продифференцируем функцию:
Производная обращается в ноль при , следовательно, это точки возможного экстремума. Воспользуемся третьим достаточным условием экстремума.
Находим вторую производную и вычисляем ее значение в точках возможного экстремума (промежуточные вычисления опустим):
Следовательно, — точка максимума (для третьего достаточного признака экстремума имеем n=1 и ).
Для выяснения характера точек находим третью производную и вычисляем ее значение в этих точках:
Следовательно, — точка перегиба функции (n=2 и ).
Осталось разобраться с точкой . Находим четвертую производную и вычисляем ее значение в этой точке:
Следовательно, — точка минимума функции.
Графическая иллюстрация.
Ответ:
— точка максимума, — точка минимума функции.
10. Экстремумы функции Определение экстремума
Функция y = f(x) называется возрастающей (убывающей) в некотором интервале, если при x1< x2 выполняется неравенство (f(x1) < f (x2) (f(x1) > f(x2)).
Если дифференцируемая функция y = f(x) на отрезке [a, b] возрастает (убывает), то ее производная на этом отрезке f ‘(x) 0
(f ‘ (x) 0).
Точка xо называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки xо, для всех точек которой верно неравенство f(x) ≤ f(xо) (f(x) ≥ f(xо)).
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках — ее экстремумами.
Точки экстремума
Необходимые условия экстремума. Если точка xо является точкой экстремума функции f(x), то либо f ‘(xо) = 0, либо f (xо) не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек.
Первое достаточное условие. Пусть xо — критическая точка. Если f ‘ (x) при переходе через точку xо меняет знак плюс на минус, то в точке xо функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
Второе достаточное условие. Пусть функция f(x) имеет производную f ‘ (x) в окрестности точки xо и вторую производную в самой точке xо. Если f ‘ (xо) = 0, >0 (<0), то точка xо является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Пример 3.22. Найти экстремумы функции f(x) = 2x3 — 15x2+ 36x — 14.
Решение. Так как f ‘(x) = 6x2 — 30x +36 = 6(x -2)(x — 3), то критические точки функции x1 = 2 и x2 = 3. Экстремумы могут быть только в этих точках. Так как при переходе через точку x1 = 2 производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку x2 = 3 производная меняет знак минус на плюс, поэтому в точке x2 = 3 у функции минимум. Вычислив значения функции в точках x1 = 2 и x2 = 3, найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) = 13.
studfiles.net
Как найти точки экстремума функции и экстремум функции? Объясните не научным языком, понятно Заранее благодарю :3
1. Взять производную функции. 2. Приравнять эту производную к нулю. Решив это уравнение, получаете одно или несколько значений Х. Это — критические точки. 3. Рисуете числовую прямую (прямую линию со стрелочкой на правом конце) , последовательно наносите на нее эти точки. У вас получилось несколько интервалов — на 1 больше, чем точек. 4. Из каждого интервала выбираете число (например, из промежутка «от минус бесконечности до нуля» берете значение «-5») и подставляете его вместо Х в выражение производной функции. Вычисляете. Если получаете положительное значение производной — значит, функция на этом участке ВОЗРАСТАЕТ; если отрицательное — УБЫВАЕТ. 5. Точками экстремума являются те критические точки, которые разделяют интервалы возрастания-убывания. Например: на первом участке функция убывает, на втором возрастает, на третьем возрастает, на четвертом убывает. Значит, точек экстремума будет две: та, которая разделяет 1й и 2й участки; и та, которая разделяет 3й и 4й участки. Та точка, в которой функция перестает убывать и начинает возрастать, называется точкой МИНИМУМА; в которой функция перестает возрастать и начинает убывать — точкой МАКСИМУМА.
Науку не излагают не научным языком.. . Это тебе к гадалкам…
пожалуйста. Что такое экстремум — это максимум или минимум чего-то. В жизни экстремум роста дерева — это его наибольшая высота, или наибольшая толщина, в общем что-то наибольшее или наименьшее. Как найти экстремум этого дерева — нужно мереть каждый год, затем найти наибольшее или наименьшее значение, это и будет экстремум. В математике меряют не деревья, а функции и там нашли очень хитрый способ нахождения экстремума этих функций. Процедура такова: 1) нужно найти производную от функции 2) затем эту производную приравнять к нулю и найти X 3) найденные X будут экстремумы, но не все 4) нужно подставить X из 3) в самую первую функцию (то, что было дано) и посмотреть результаты. Самые большие и малые значения будут экстремумы
О каких функциях идет речь: сколько переменных?
touch.otvet.mail.ru
Экстремумы, наибольшие и наименьшие значения функций
19. Локальный экстремум функции. Необходимое условие существования экстремума
Говорят, что функция
имеет вовнутреннейточкеобластиD локальный максимум(минимум),
если существует такая окрестностьточки ,
для каждой точки
,
для каждой точки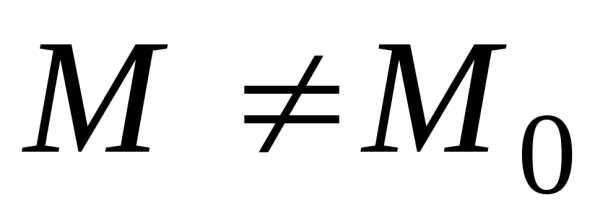 которой выполняется неравенство
которой выполняется неравенство
Если функция имеет в
точке  локальный максимум или локальный
минимум, то говорят, что она имеет в этой
точкелокальный экстремум (или просто экстремум).
локальный максимум или локальный
минимум, то говорят, что она имеет в этой
точкелокальный экстремум (или просто экстремум).
Теорема (необходимое
условие существования экстремума).
Если дифференцируемая функциядостигает экстремума в точке,
то каждая частная производная первого
порядка от функции в этой точке обращается в нуль.
в этой точке обращается в нуль.
Точки, в которых все
частные производные первого порядка
обращаются в нуль, называются стационарными
точками функции.
Координаты этих точек можно найти,
решив систему из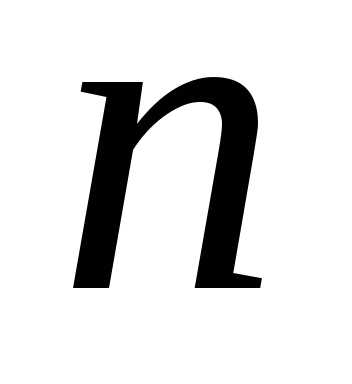 уравнений
уравнений
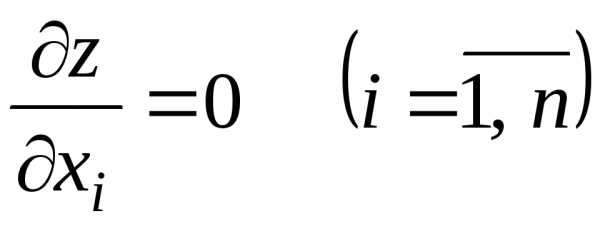 .
.
Необходимое условие существования экстремума в случае дифференцируемой функции коротко можно сформулировать и так:
.
Встречаются случаи, когда в отдельных точках некоторые частные производные имеют бесконечные значения или не существуют (в то время как остальные равны нулю). Такие точки называются критическими точками функции.Эти точки тоже нужно рассматривать в качестве «подозрительных» на экстремум, как и стационарные.
В случае функции двух
переменных необходимое условие
экстремума, а именно равенство нулю
частных производных (дифференциала) в
точке экстремума, имеет геометрическую
интерпретацию: касательная плоскость
к поверхности
в точке экстремума должна быть параллельна
плоскости .
.
20. Достаточные условия существования экстремума
Выполнение в некоторой
точке необходимого условия существования
экстремума вовсе не гарантирует наличия
там экстремума. В качестве примера можно
взять дифференцируемую всюду функцию 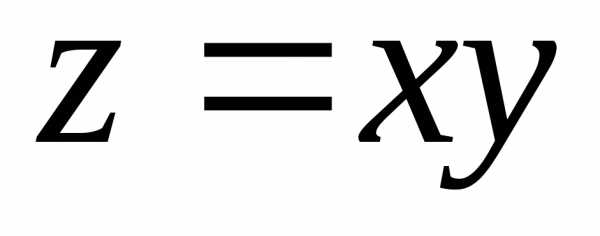 .
Обе ее частные производные и сама
функция обращаются в нуль в точке
.
Обе ее частные производные и сама
функция обращаются в нуль в точке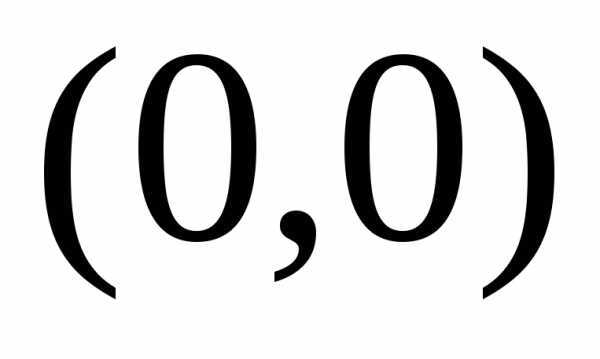 .
Однако в любой окрестности этой точки
есть как положительные (большие
.
Однако в любой окрестности этой точки
есть как положительные (большие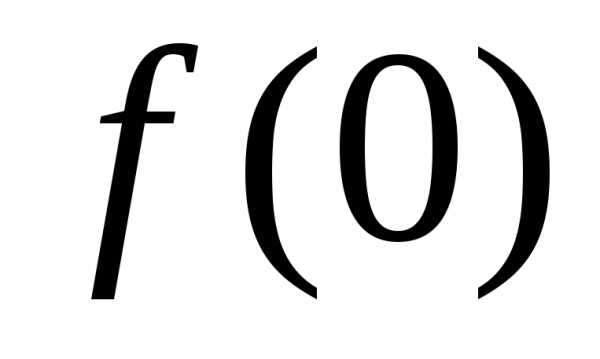 ),
так и отрицательные (меньшие
),
так и отрицательные (меньшие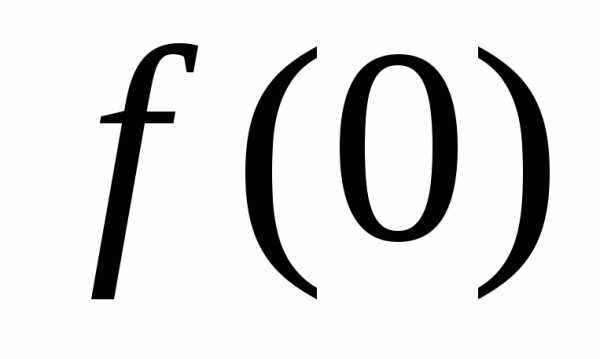 )
значения этой функции. Следовательно,
в этой точке, по определению, экстремума
не наблюдается. Поэтому необходимо
знать достаточные условия, при которых
точка, подозрительная на экстремум,
является точкой экстремума исследуемой
функции.
)
значения этой функции. Следовательно,
в этой точке, по определению, экстремума
не наблюдается. Поэтому необходимо
знать достаточные условия, при которых
точка, подозрительная на экстремум,
является точкой экстремума исследуемой
функции.
Рассмотрим случай функции двух переменных. Предположим, что функция определена, непрерывна и имеет непрерывные частные производные до второго порядка включительно в окрестности некоторой точки, которая является стационарной точкой функции, то есть удовлетворяет условиям
,.
Введем обозначения:
Теорема(достаточные условия существования
экстремума). Пусть функцияудовлетворяет вышеприведенным условиям,
а именно: дифференцируема в некоторой
окрестности стационарной точкии дважды дифференцируема в самой точке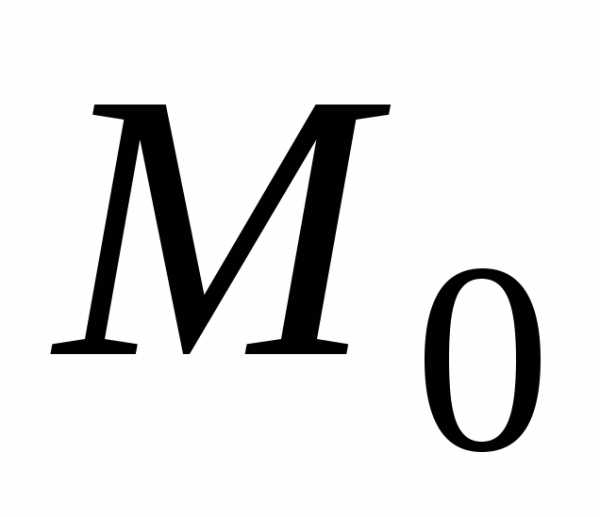 .
Тогда, если
.
Тогда, если
 ,
то в исследуемой точке функция имеет
локальный экстремум,
,
то в исследуемой точке функция имеет
локальный экстремум, то экстремума нет,
то экстремума нет, то требуется дополнительное исследование.
то требуется дополнительное исследование.
В
случае если 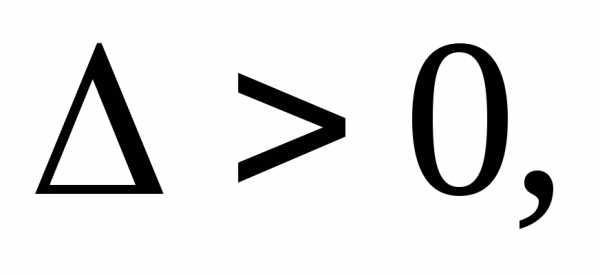 то функцияв точкедостигает
то функцияв точкедостигает
локального максимумапри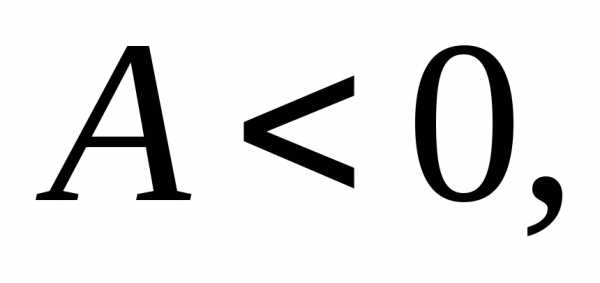 и
и
локального минимумапри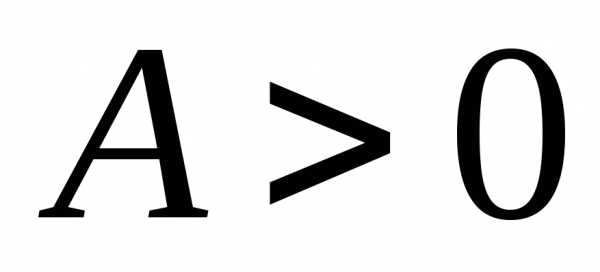 .
.
В общем случае, для функции достаточным условием существования в точкелокальногоминимума(максимума) являетсяположительная (отрицательная) определённость второго дифференциала.
Иными словами, справедливо следующее утверждение.
Теорема. Если в точкедля функции
для любых
не равных одновременно нулю 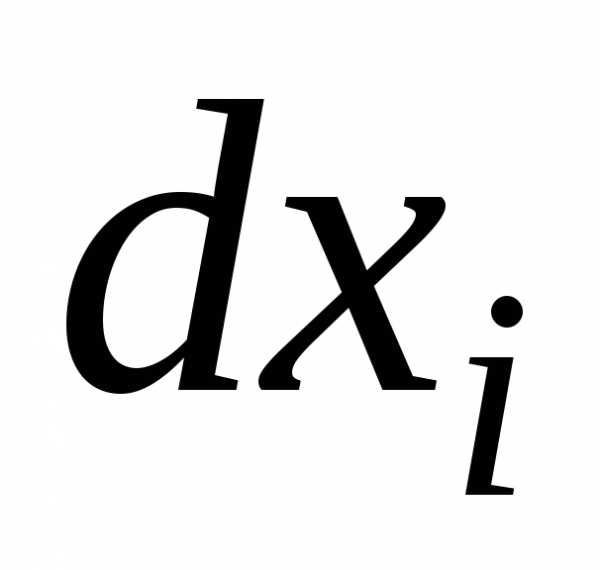 ,
то в этой точке функция имеетминимум (аналогичномаксимум, если).
,
то в этой точке функция имеетминимум (аналогичномаксимум, если).
Пример 18.Найти точки локального экстремума функции
Решение. Найдем частные производные функции и приравниваем их к нулю:
Решая эту систему, находим две точки возможного экстремума:
Найдем частные производные второго порядка для данной функции:
В первой стационарной точке , следовательно, иПоэтому для этой точки требуется дополнительное исследование. Значение функциив этой точке равно нулю:Далее,
при а
при
Следовательно, в любой
окрестности точки 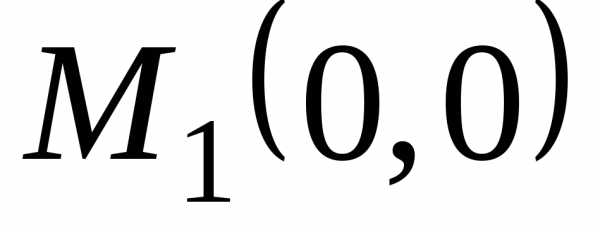 функцияпринимает значения как большие
функцияпринимает значения как большие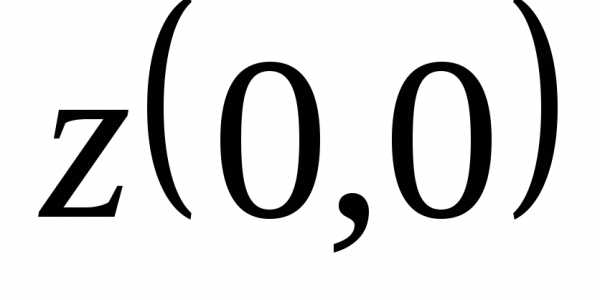 ,
так и меньшие
,
так и меньшие ,
и, значит, в точке
,
и, значит, в точке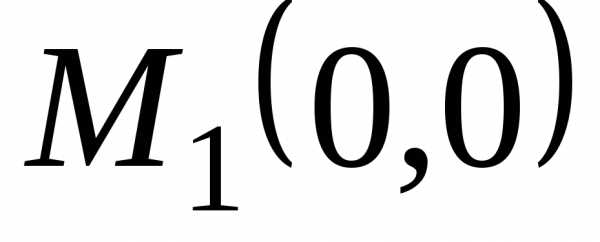 функция,
по определению, не имеет локального
экстремума.
функция,
по определению, не имеет локального
экстремума.
Во второй стационарной
точке 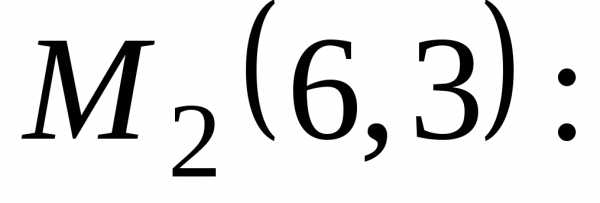
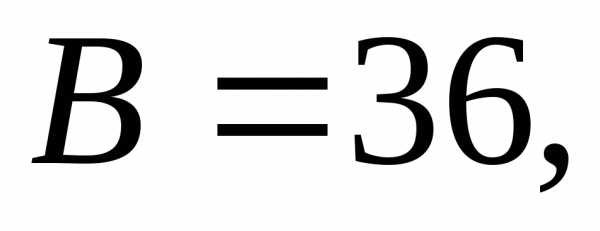 следовательно,Поэтому, так как
следовательно,Поэтому, так как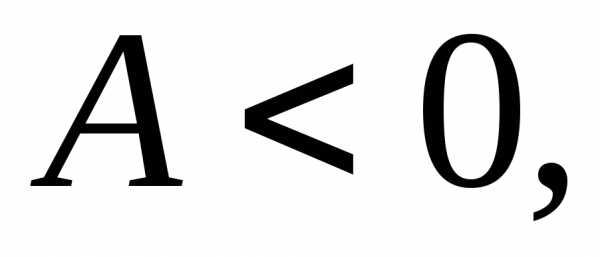 то в точке
то в точке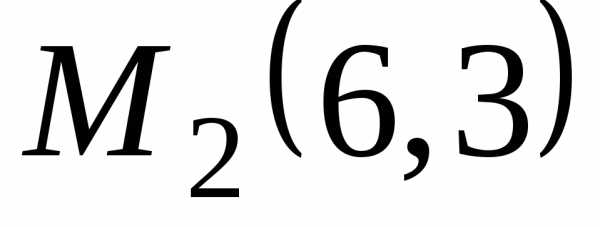 функция имеет локальный максимум:
функция имеет локальный максимум:
.
studfiles.net

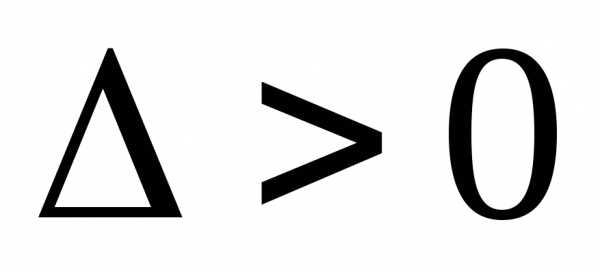 ,
то в исследуемой точке функция имеет
локальный экстремум,
,
то в исследуемой точке функция имеет
локальный экстремум,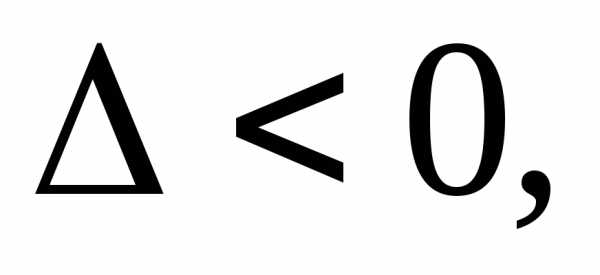 то экстремума нет,
то экстремума нет,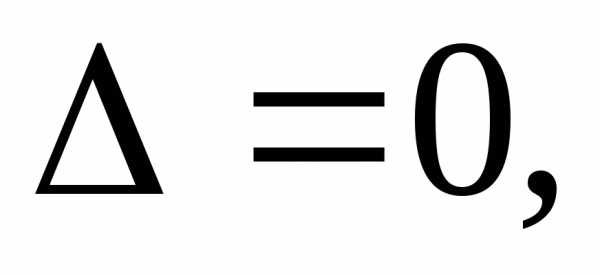 то требуется дополнительное исследование.
то требуется дополнительное исследование.