Элементарный исход — это… Что такое Элементарный исход?
- Элементарный исход
Пространство элементарных событий — множество Ω всех различных исходов случайного эксперимента.
Элемент этого множества называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его элементов конечно или счётно. Любое пространство элементарных событий не являющееся дискретным, называется недискретным, и при этом, если наблюдаемыми результатами (нельзя произносить случайными событиями) являются точки того или иного числового арифметического или координатного пространства, то пространство называется непрерывным (континуум). Пространство элементарных событий Ω вместе с алгеброй событий и вероятностью образует тройку , которая называется вероятностным пространством.
См.также
- Элементарная функция
- Элемент состава преступления
Смотреть что такое «Элементарный исход» в других словарях:
Вероятностное пространство — У этого термина существуют и другие значения, см. Пространство. Вероятностное пространство понятие, введённое А. Н. Колмогоровым в 30 х годах XX века для формализации понятия вероятности, которое дало начало бурному развитию теории вероятностей… … Википедия
Случайный процесс — (случайная функция) в теории вероятностей семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или координаты. Другое определение: Случайным называется процесс u(t), мгновенные значения… … Википедия
Пространство элементарных событий — Пространство элементарных событий множество всех различных исходов случайного эксперимента. Элемент этого множества называется элементарным событием или исходом. Пространство элементарных событий называется дискретным, если число его… … Википедия
Элементарное событие — В теории вероятностей элементарные события или события атомы это исходы случайного эксперимента, из которых в эксперименте происходит ровно один. Множество всех элементарных событий обычно обозначается Ω. Всякое подмножество множества Ω… … Википедия
Выборочная функция распределения — Выборочная (эмпирическая) функция распределения в математической статистике это приближение теоретической функции распределения, построенное с помощью выборки из него. Определение Пусть выборка из распределения случайной величины , задаваемого… … Википедия
Реализация случайной функции — Случайный процесс (случайная функция) в теории вероятностей семейство случайных величин, индексированных некоторым параметром, чаще всего играющим роль времени или пространства. Содержание 1 Определение 2 Терминология 3 Классификация … Википедия
Эмпирическая функция распределения — Выборочная (эмпирическая) функция распределения в математической статистике это приближение теоретической функции распределения, построенное с помощью выборки из него. Определение Пусть выборка из распределения, задаваемого функцией распределения … Википедия
Эмпирическое распределение — Выборочная (эмпирическая) функция распределения в математической статистике это приближение теоретической функции распределения, построенное с помощью выборки из него. Определение Пусть выборка из распределения, задаваемого функцией распределения … Википедия
Россия. История: История России — I Приднепровская Россия IX XII вв. земель , занятых племенами, определились частью естественными пределами линиями водораздельных волоков, частью перекрестным столкновением отдельных волн колонизационного потока. Быть может, взаимная борьба… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
ТУБЕРКУЛЕЗ — ТУБЕРКУЛЕЗ. Содержание: I. Исторический очерк…………… 9 II. Возбудитель туберкулеза………… 18 III. Патологическая анатомия………… 34 IV. Статистика……………….. 55 V. Социальное значение туберкулеза……. 63 VІ.… … Большая медицинская энциклопедия
dic.academic.ru
Теория вероятностей и математическая статистика — SAVANT.PRO
Определение
Элементарным исходом (или элементарным событием) называют любой простейший (т.е. неделимый в рамках данного опыта) исход опыта. Множество всех элементарных исходов будем называть пространтсвом элементарных исходов.
Другими словами, множество исходов опыта образует пространство элементарных исходов, если выполнены следующие требования:
- в результате опыта один из исходов обязательно происходит;
- появление одного из исходов опыта исключает появление остальных;
- в рамках данного опыта нельзя разделить элементарный исход на более мелкие составляющие.
В дальнейшем пространство элементарных исходов будем обозначать прописной буквой %%\Omega%%, а сами элементарные исходы — строчной буквой %%\omega%%, снабженной, при необходимости, индексами. То, что элемент %%\omega%% принадлежит %%\Omega%%, записывают в виде %%\omega \in \Omega%%, а тот факт, что множество %%\Omega%% состоит из элементов %%\omega_1, \omega_2, \ldots, \omega_n, \ldots,%% и только из них, записывают в виде $$ \Omega = \{\omega_1, \omega_2, \ldots, \omega_n, \ldots\} $$ или в виде $$ \Omega = \{\omega_i, i=1, 2, \ldots, n,\ldots\}. $$
В частности, %%\Omega%% может содержать конечное число элементарных исходов.
Примеры
Пример 1
Пусть опыт состоит в однократном подбрасывании монеты. При математическом описании этого опыта естественно отвлечься от несущественных возможностей (например, монета встанет на ребро) и ограничиться только двумя элементарными исходами: выпадением «герба» (можно обозначить этот исход как %%w_1%%) и выпаденим «цифры» (%%w_2%%). Таким образом, %%\Omega = \{w_1, w_2\}%%.
При двукратном подбрасывании монеты (или однократном подбрасывании двух монет) пространство элементарных исходов будет содержать четыре элемента, т.е. $$ \Omega = \{w_{11}, w_{12}, w_{21}, w_{22}\}, $$ где, например, %%w_{12}%% — появление «герба» при первом броске и появление «цифры» при втором.
Пример 2
При двукратном бросании игральной кости, каждый из шести возможных исходов, при первом бросании может сочетаться с каждым из шести исходов второго бросания, т.е. $$ \Omega = \{w_{ij}, i, j=\overline{1,6}\}, $$ где, %%w_{ij}%% — исход опыта, при котором сначала выпало %%i%%,а затем %%j%% очков.
Нетрудно посчитать, что пространство элементарных исходов %%\Omega%% содержит %%36%% элементарных исходов.
v1.savant.pro
2. Полная группа событий. Пространство элементарных исходов. Примеры.
Полная группа событий. Полной группой событий называется совокупность всех возможных результатов опыта. Теорема. Сумма вероятностей событий А1 , А2 , …, Аn , образующих полную группу, равна единице:
Р (A1) + Р (А2) + … + Р (Аn) = 1.
Пространство элементарных исходов
Теория вероятностей изучает случайные явления не непосредственно, а с помощью идеализированных математических моделей случайных опытов.
Всякий случайный опыт (испытание, эксперимент) состоит в осуществлении некоторого комплекса условий и наблюдении результата. Любой наблюдаемый результат опыта интерпретируется как случайный исход (случайное событие). Случайное событие в результате опыта может произойти, а может и не произойти.
Каждому опыту ставится в соответствие пространство элементарных исходов
Пример 1.1.1.
Опыт состоит в бросании одной правильной шестигранной игральной кости и наблюдении числа выпавших очков.
Элементарные исходы: {выпалоочков},.
Неэлементарные исходы (события): ={выпало чётное число очков},={выпало число очков, большее, чем 2} и т.п. Исходне является элементарным, т.к. он разлагается на более простые исходы.
Пространство элементарных исходов данного случайного опыта состоит из шести элементов.
3. Классическое определение вероятности события. Свойства вероятности события. Примеры.
Вероятностью события называется отношение числа элементарных исходов, благоприятствующих данному событию, к числу всех равновозможных исходов опыта, в котором может появиться это событие. Вероятность события А обозначают через Р (А). В соответствии с определением P(A)=m/n , где m — число элементарных исходов, благоприятствующих событию А; n — число всех равновозможных элементарных исходов опыта, образующих полную группу событий. Это определение вероятности называют классическим.
Основные свойства вероятности. Пусть задано пространство элементарных событий Е , а вероятности Р определены на событиях из Е . Тогда:
Пример 1.
В урне 10 одинаковых по размерам и весу шаров, из которых 4 красных и 6 голубых. из урны извлекается один шар. Какова вероятность того, что извлеченный шар окажется голубым?
Решение. Событие «извлеченный шар оказался голубым» обозначим буквой А. Данное испытание имеет 10 равновозможных элементарных исходов, из которых 6 благоприятствуют событию А. В соответствии с формулой P(A)=m/n , получаем P(A)=6/10=0,6
4. Статистическое определение вероятности события. Примеры. Теорема Бернулли (с доказательством).
Статистической вероятностью события А называется относительная частота (частость) появления этого события в n произведенных испытаниях, т.е.
w(A) – относительная частота (частость) события А;
m – число испытаний, в которых появилось событие А;
n – общее число испытаний.
Статистическое определение вероятности, как и понятия и методы теории вероятности, применимы только к тем событиям, которые обладают свойствами:
Рассматриваемые события должны быть исходами только тех испытаний, которые могут быть воспроизведены неограниченное число раз при одном и том же комплексе условий.
События должны обладать статистической устойчивостью, или устойчивостью относительных частот. Это означает, что в серии испытаний относительная частота события меняется незначительно.
Число испытаний, в результате которых появляется событие А, должно быть достаточно велико, ибо только в этом случае можно считать вероятность события Р(А) приближенно равной ее относительной частоте.
Пример. Английский учёный Пирсон произвел 23000 бросаний монеты, герб появился 11512 раз.
W(A) = = 0.5005
Теорема Бернулли.
Частость события в n повторных независимых испытаниях в каждом из которых оно может произойти с одной и той же вероятностью p, при неограниченном увеличении числа n сходится по вероятности к вероятности р этого события в отдельном испытании:
Cмысл теоремы состоит в том, что при большом числе n повторных независимых испытаний практически достоверно, что частость события m/n – величина случайная, как угодно мало отличается от неслучайной величины p – вероятности события, т.е. практически перестает быть случайной.
Доказательство:
0 | 1 | |
q | p |
г
E(=p ; D(=pq
Таким образом, выполняются все условия теоремы Чебышева, т.е.
.
studfiles.net
Элементарное событие — это… Что такое Элементарное событие?
В теории вероятностей элементарные события или события-атомы — это исходы случайного эксперимента, из которых в эксперименте происходит ровно один. Множество всех элементарных событий обычно обозначается Ω.
Всякое подмножество множества Ω элементарных событий называется случайным событием. Говорят, что в результате эксперимента произошло случайное событие , если (элементарный) исход эксперимента является элементом A.
В определении вероятностного пространства на множестве случайных событий вводится сигма-аддитивная конечная мера, называемая вероятностью.
Примеры
Примеры пространств исходов эксперимента, Ω, и элементарных событий:
- Если объекты счётны, а пространство исходов Ω = {0,1,2,3,…} (натуральные числа), то элементарные события — это любые множества {k}, где .
- Если монета бросается дважды, Ω = {OO,OP,PO,PP}, O для орла, а P для решки, то элементарные события: {OO}, {OP}, {PO} и {PP}.
- Если X — это нормально распределенные случайные величины, , реальные числа, то элементарные события — любые множества {x}, где . Этот пример показывает, что непрерывное вероятностное распределение не определяется вероятностями событий-атомов, поскольку здесь вероятности всех элементарных событий равны нулю.
Замечания
Элементарные события могут иметь вероятности, которые строго положительны, нули, неопределенны, или любая комбинация из этих вариантов. Например, любое дискретное вероятностное распределение определяется вероятностями того, что может быть названо элементарными событиями. Напротив, все элементарные события имеют вероятность нуль для непрерывного распределения. Смешанные распределения, не будучи ни непрерывными, ни дискретными, могут содержать атомы, которые могут мыслиться как элементарные (то есть события-атомы) события с ненулевой вероятностью. В теории меры в определении вероятностного пространства вероятность произвольного элементарного события не могла быть определена до тех пор, пока математики не увидели различие между пространством исходов S и событиями, которые представляют интерес, и которые определяются как элементы σ-алгебры событий из S.
Формально говоря, элементарное событие — это подмножество пространства исходов случайного эксперимента, которое состоит только из одного элемента; то есть элементарное событие — это всё ещё множество, но не сам элемент. Однако элементарные события обычно записываются как элементы, а не как множества с целью упрощения, когда это не может вызвать недоразумения.
См. также
dic.academic.ru
Советы по построению пространства элементарных исходов.
Имейте в виду задачу, которую вы хотите решить — то случайное событие, вероятность которого вам необходимо найти, должно описываться с помощью указания элементарных исходов, приводящих к этому событию.
На первых порах старайтесь вводить наиболее детальное описание опыта, – потом начнете понимать, в каких случаях можно, без ущерба для конечного результата, упростить модель.
Между разными подходящими моделями предпочтительнее выглядит модель, в которой элементарные исходы симметричны и равновероятны.
Очень удобно выбирать элементарные исходы в виде векторов, размерность которых равна количеству различных случайных факторов (источников) в случайном явлении, а координаты которых соответствуют различным вариантам значений этих факторов. Например, при бросании двух костей элементарный исход имеет размерность 2 и каждая координата 6 значений. При одновременном бросании монеты и кости вектор имеет размерность 2, первая координата 2 значения, вторая – 6 (или наоборот). Если бросаем 10 монет, то в качестве пространства элементарных исходов можно взять множество различных двоичных векторов размерности 10 из нулей и единиц.
Определения Подмножества
Если пространство элементарных исходов определено, то появляется возможность описать любое событие, происшедшее в опыте, просто указав, какие элементарные исходы ему соответствуют.
Пример.3.5 Элементарные исходы, 5 вариант: числа очков на костях с различением игральных костей [(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…] –36 исходов.
Элементарный исход можно представить в виде
 ,
,где i – число очков на первой кости, j – второй кости.
Тогда событие «на двух костях выпало в сумме 7 очков» можно представить в виде следующего подмножества элементарных исходов:
Заметим, что порядок перечисления элементарных исходов может быть произвольным. В дальнейшем подмножества пространства элементарных исходов будем обозначать большими латинскими буквами A, B, C…
A =
Пустое подмножество обозначим

Так как пустое подмножество не содержит никаких элементарных исходов, в теории вероятностей оно обозначает невозможное событие.
Множество всех элементарных событий называется, естественно, достоверное событие.
Элементарный исход как случайное событие представляет собой простейшее одноточечное подмножество.
Операции над подмножествами
Стандартные операции над подмножествами, естественно, применяются в теории вероятностей и имеют вероятностную интерпретацию.
Дополнение
Дополнение до подмножества A — это подмножество
т. е. дополнением к Aявляется подмножество, включающее в себя все элементарные исходы, не содержащиеся вA. С точки зрения теории вероятностей подмножествоAпредставляет событие, которое естественно назвать отрицаниеAили не-A. Т.е.A в опыте не произошло («не наступило»).
Объединение
Объединением двух подмножеств AиBявляется подмножество
Соответственно и интерпретация : произошло или A илиB.
Пересечение
Пересечением двух подмножеств : AиBявляется подмножество
Соответственно и интерпретация : и A иB произошли одновременно.
Разность
Разностью двух подмножеств AиBявляется подмножество
Соответственно и интерпретация : A произошло,B — нет.
Симметричная разность
Симметричной разностью двух подмножеств AиBявляется подмножество
Соответственно и интерпретация : произошло только одно из этих двух событий.
Количество элементов в подмножестве
Если количество элементов в подмножестве A конечно, то будем обозначать его так

Отношения между подмножествами
Вложение
Подмножество В вложено в подмножествоA, если любой элементарный исход, содержащийся вBтакже содержится и вA.

Интерпретация:
Стрелкой | из BследуетA |
Т.е, если произошло B, то произошло и A.
Несовместность
Подмножества A и B называются несовместными (непересекающимися), если они не содержат общих элементарных исходов.
В теории вероятностей это означает, что A и B одновременно произойти не могут.
Противоположность
Подмножества A и B называются противоположными или дополнительными друг к другу, если они несовместны и их объединение достоверно.
В теории вероятностей это означает, что в опыте обязательно произойдет одно и только одно из этих событий.
Убывающая последовательность событий
Пусть
последовательность событий.
Она называется убываюшей, если каждое следующее событие этой последовательности вложено в предыдущее.
Аналогично можно определить возрастающую последовательность событий.
Формулы
Для доказательства равенства двух подмножеств AиBдостаточно показать, чтоAвложено вB,и чтоBвложено вA | Следующие формулы позволяют выразить одни операции с подмножествами через другие. Доказательства проведите сами. |
Полная группа подмножеств
Полной группой подмножеств называется конечный набор или счетная последовательность попарно несовместных подмножеств объединение которых достоверно:

В опыте обязательно произойдет одно и только одно из этих событий.
Любые два противоположных подмножества образуют полную группу подмножеств.
Если пространство элементарных исходов конечно или счетно, то сами элементарные исходы являются полной группой подмножеств.
Алгебра и сигма-алгебра
При построении математической модели случайного объекта необходимо не только указать все возможные элементарные исходы опыта, но и определить (перечислить) все возможные события, которые могут произойти в этом опыте. Принято следующее определение:
Алгебра
событий A это набор подмножеств
пространства элементарных исходов для которого выполняются следующие
условия:
для которого выполняются следующие
условия:
Сигма —
алгебра событий F это набор подмножеств
пространства элементарных исходов для которого выполняются следующие
условия:
для которого выполняются следующие
условия:
и для любой счетной последовательности
Очевидно, что любая сигма-алгебра является алгеброй, но не наоборот.
Колмогоров показал, что естественной математической моделью для множества событий является сигма-алгебра.
Очевидным примером сигма-алгебры является набор всех подмножеств пространства элементарных исходов – это наибольшая сигма-алгебра, возможная на данном пространстве элементарных исходов.
Наименьшая (тривиальная) сигма-алгебра это следующий набор подмножеств
Если алгебра или сигма-алгебра содержит событие A , то она обязана содержать и отрицаниеA. Поэтому минимальное число подмножеств в нетривиальной сигма-алгебре равно 4.
Алгебры и сигма-алгебры обозначаем жирными наклонными латинскими буквами.
studfiles.net
Советы по построению пространства элементарных исходов.
Имейте в виду задачу, которую вы хотите решить — то случайное событие, вероятность которого вам необходимо найти, должно описываться с помощью указания элементарных исходов, приводящих к этому событию.
На первых порах старайтесь вводить наиболее детальное описание опыта, – потом начнете понимать, в каких случаях можно, без ущерба для конечного результата, упростить модель.
Между разными подходящими моделями предпочтительнее выглядит модель, в которой элементарные исходы симметричны и равновероятны.
Очень удобно выбирать элементарные исходы в виде векторов, размерность которых равна количеству различных случайных факторов (источников) в случайном явлении, а координаты которых соответствуют различным вариантам значений этих факторов. Например, при бросании двух костей элементарный исход имеет размерность 2 и каждая координата 6 значений. При одновременном бросании монеты и кости вектор имеет размерность 2, первая координата 2 значения, вторая – 6 (или наоборот). Если бросаем 10 монет, то в качестве пространства элементарных исходов можно взять множество различных двоичных векторов размерности 10 из нулей и единиц.
Определения Подмножества
Если пространство элементарных исходов определено, то появляется возможность описать любое событие, происшедшее в опыте, просто указав, какие элементарные исходы ему соответствуют.
Пример.3.5 Элементарные исходы, 5 вариант: числа очков на костях с различением игральных костей [(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…] –36 исходов.
Элементарный исход можно представить в виде
 ,
,где i – число очков на первой кости, j – второй кости.
Тогда событие «на двух костях выпало в сумме 7 очков» можно представить в виде следующего подмножества элементарных исходов:
Заметим, что порядок перечисления элементарных исходов может быть произвольным. В дальнейшем подмножества пространства элементарных исходов будем обозначать большими латинскими буквами A, B, C…
A =
Пустое подмножество обозначим

Так как пустое подмножество не содержит никаких элементарных исходов, в теории вероятностей оно обозначает невозможное событие.
Множество всех элементарных событий называется, естественно, достоверное событие.
Элементарный исход как случайное событие представляет собой простейшее одноточечное подмножество.
Операции над подмножествами
Стандартные операции над подмножествами, естественно, применяются в теории вероятностей и имеют вероятностную интерпретацию.
Дополнение
Дополнение до подмножества A — это подмножество
т. е. дополнением к Aявляется подмножество, включающее в себя все элементарные исходы, не содержащиеся вA. С точки зрения теории вероятностей подмножествоAпредставляет событие, которое естественно назвать отрицаниеAили не-A. Т.е.A в опыте не произошло («не наступило»).
Объединение
Объединением двух подмножеств AиBявляется подмножество
Соответственно и интерпретация : произошло или A илиB.
Пересечение
Пересечением двух подмножеств : AиBявляется подмножество
Соответственно и интерпретация : и A иB произошли одновременно.
Разность
Разностью двух подмножеств AиBявляется подмножество
Соответственно и интерпретация : A произошло,B — нет.
Симметричная разность
Симметричной разностью двух подмножеств AиBявляется подмножество
Соответственно и интерпретация : произошло только одно из этих двух событий.
Количество элементов в подмножестве
Если количество элементов в подмножестве A конечно, то будем обозначать его так

Отношения между подмножествами
Вложение
Подмножество В вложено в подмножествоA, если любой элементарный исход, содержащийся вBтакже содержится и вA.

Интерпретация:
Стрелкой | из BследуетA |
Т.е, если произошло B, то произошло и A.
Несовместность
Подмножества A и B называются несовместными (непересекающимися), если они не содержат общих элементарных исходов.
В теории вероятностей это означает, что A и B одновременно произойти не могут.
Противоположность
Подмножества A и B называются противоположными или дополнительными друг к другу, если они несовместны и их объединение достоверно.
В теории вероятностей это означает, что в опыте обязательно произойдет одно и только одно из этих событий.
Убывающая последовательность событий
Пусть
последовательность событий.
Она называется убываюшей, если каждое следующее событие этой последовательности вложено в предыдущее.
Аналогично можно определить возрастающую последовательность событий.
Формулы
Для доказательства равенства двух подмножеств AиBдостаточно показать, чтоAвложено вB,и чтоBвложено вA | Следующие формулы позволяют выразить одни операции с подмножествами через другие. Доказательства проведите сами. |
Полная группа подмножеств
Полной группой подмножеств называется конечный набор или счетная последовательность попарно несовместных подмножеств объединение которых достоверно:

В опыте обязательно произойдет одно и только одно из этих событий.
Любые два противоположных подмножества образуют полную группу подмножеств.
Если пространство элементарных исходов конечно или счетно, то сами элементарные исходы являются полной группой подмножеств.
Алгебра и сигма-алгебра
При построении математической модели случайного объекта необходимо не только указать все возможные элементарные исходы опыта, но и определить (перечислить) все возможные события, которые могут произойти в этом опыте. Принято следующее определение:
Алгебра
событий A это набор подмножеств
пространства элементарных исходов для которого выполняются следующие
условия:
для которого выполняются следующие
условия:
Сигма —
алгебра событий F это набор подмножеств
пространства элементарных исходов для которого выполняются следующие
условия:
для которого выполняются следующие
условия:
и для любой счетной последовательности
Очевидно, что любая сигма-алгебра является алгеброй, но не наоборот.
Колмогоров показал, что естественной математической моделью для множества событий является сигма-алгебра.
Очевидным примером сигма-алгебры является набор всех подмножеств пространства элементарных исходов – это наибольшая сигма-алгебра, возможная на данном пространстве элементарных исходов.
Наименьшая (тривиальная) сигма-алгебра это следующий набор подмножеств
Если алгебра или сигма-алгебра содержит событие A , то она обязана содержать и отрицаниеA. Поэтому минимальное число подмножеств в нетривиальной сигма-алгебре равно 4.
Алгебры и сигма-алгебры обозначаем жирными наклонными латинскими буквами.
studfiles.net
Советы по построению пространства элементарных исходов.
Имейте в виду задачу, которую вы хотите решить — то случайное событие, вероятность которого вам необходимо найти, должно описываться с помощью указания элементарных исходов, приводящих к этому событию.
На первых порах старайтесь вводить наиболее детальное описание опыта, – потом начнете понимать, в каких случаях можно, без ущерба для конечного результата, упростить модель.
Между разными подходящими моделями предпочтительнее выглядит модель, в которой элементарные исходы симметричны и равновероятны.
Очень удобно выбирать элементарные исходы в виде векторов (в смысле точек в пространстве), размерность которых равна количеству различных случайных факторов (источников) в случайном явлении, а координаты которых соответствуют различным вариантам значений этих факторов. Например, при бросании двух костей элементарный исход имеет размерность 2 и каждая координата 6 значений. При одновременном бросании монеты и кости вектор имеет размерность 2, первая координата 2 значения, вторая – 6 (или наоборот). Если бросаем 10 монет, то в качестве пространства элементарных исходов можно взять множество различных двоичных векторов размерности 10 из нулей и единиц.
Определения Подмножества
Если пространство элементарных исходов определено, то появляется возможность описать любое событие, происшедшее в опыте, просто указав, какие элементарные исходы ему соответствуют.
Пример.3.5 Элементарные исходы, 5 вариант: числа очков на костях с различением игральных костей [(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…] –36 исходов.
Элементарный исход можно представить в виде
 ,
,где i – число очков на первой кости, j – второй кости.
Тогда событие «на двух костях выпало в сумме 7 очков» можно представить в виде следующего подмножества элементарных исходов:
Заметим, что порядок перечисления элементарных исходов может быть произвольным. В дальнейшем подмножества пространства элементарных исходов будем обозначать большими латинскими буквами A, B, C…
A =
Пустое подмножество обозначим

Так как пустое подмножество не содержит никаких элементарных исходов, в теории вероятностей оно обозначает невозможное событие.
Множество всех элементарных событий называется, естественно, достоверное событие.
Элементарный исход как случайное событие представляет собой одноточечное подмножество.
Операции над подмножествами
Стандартные операции над подмножествами применяются в теории вероятностей и имеют вероятностную интерпретацию.
Дополнение
Дополнение до подмножества A — это подмножество
т. е. дополнением к Aявляется подмножество, включающее в себя все элементарные исходы, не содержащиеся вA. С точки зрения теории вероятностей подмножествоAпредставляет событие, которое естественно назвать отрицаниеAили не-A. Т.е.A в опыте не произошло («не наступило»).
Объединение
Объединением двух подмножеств AиBявляется подмножество
Соответственно и интерпретация : произошло или A илиB.
Пересечение
Пересечением двух подмножеств : AиBявляется подмножество
Соответственно и интерпретация : и A иB произошли одновременно.
Разность
Разностью двух подмножеств AиBявляется подмножество
Соответственно и интерпретация : A произошло,B — нет.
Симметричная разность
Симметричной разностью двух подмножеств AиBявляется подмножество
Соответственно и интерпретация : произошло только одно из этих двух событий.
Количество элементов в подмножестве
Если количество элементов в подмножестве A конечно, то будем обозначать его так

Отношения между подмножествами
Вложение
Подмножество В вложено в подмножествоA, если любой элементарный исход, содержащийся вBтакже содержится и вA.

Интерпретация:
Стрелкой | из BследуетA |
Т.е, если произошло B, то произошло и A.
Несовместность
Подмножества A и B называются несовместными (непересекающимися), если они не содержат общих элементарных исходов.
В теории вероятностей это означает, что A и B одновременно произойти не могут.
Противоположность
Подмножества A и B называются противоположными или дополнительными друг к другу, если они несовместны и их объединение достоверно.
В теории вероятностей это означает, что в опыте обязательно произойдет одно и только одно из этих событий.
Убывающая последовательность событий
Пусть
последовательность событий.
Она называется убываюшей, если каждое следующее событие этой последовательности вложено в предыдущее.
Аналогично можно определить возрастающую последовательность событий.
Формулы
Для доказательства равенства двух подмножеств AиBдостаточно показать, чтоAвложено вB,и чтоBвложено вA | Следующие формулы позволяют выразить одни операции с подмножествами через другие. Доказательства проведите сами. |
Полная группа подмножеств
Полной группой подмножеств называется конечный набор или счетная последовательность попарно несовместных подмножеств объединение которых достоверно:

В опыте обязательно произойдет одно и только одно из этих событий.
Любые два противоположных подмножества образуют полную группу подмножеств.
Если пространство элементарных исходов конечно или счетно, то сами элементарные исходы являются полной группой подмножеств.
Алгебра и сигма-алгебра
При построении математической модели случайного объекта необходимо не только указать все возможные элементарные исходы опыта, но и определить (перечислить) все возможные события, которые могут произойти в этом опыте. Принято следующее определение:
Алгебра
событий A это набор подмножеств
пространства элементарных исходов для которого выполняются следующие
условия:
для которого выполняются следующие
условия:
Сигма —
алгебра событий F это набор подмножеств
пространства элементарных исходов для которого выполняются следующие
условия:
для которого выполняются следующие
условия:
и для любой счетной последовательности
Очевидно, что любая сигма-алгебра является алгеброй, но не наоборот.
Колмогоров показал, что естественной математической моделью для множества событий является сигма-алгебра.
Очевидным примером сигма-алгебры является набор всех подмножеств пространства элементарных исходов – это наибольшая сигма-алгебра, возможная на данном пространстве элементарных исходов.
Наименьшая (тривиальная) сигма-алгебра это следующий набор подмножеств
Если алгебра или сигма-алгебра содержит событие A , то она обязана содержать и отрицаниеA. Поэтому минимальное число подмножеств в нетривиальной сигма-алгебре равно 4.
Алгебры и сигма-алгебры обозначаем жирными наклонными латинскими буквами.
studfiles.net

 ,
, будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем
будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем
 ,
, будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем
будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем
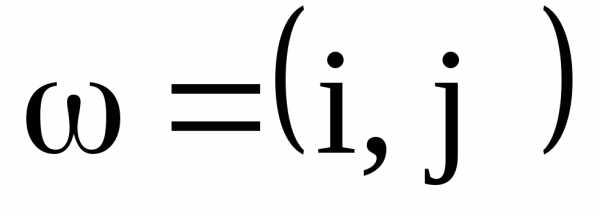 ,
, будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем
будем пользоваться также и для
утверждений типа: “из A следует B” в
формулировках определений и теорем