Скалярное произведение это: Скалярное произведение векторов — урок. Геометрия, 9 класс.

Содержание

Скалярное произведение — Энциклопедия по экономике

Кроме того, определено скалярное произведение двух векторов [c.32]

На основе понятия скалярного произведения модель (3.3) можно представить в сокращенном виде [c.32]

Тогда стоимость потребительской корзины описывается скалярным произведением векторов Р и X. [c.95]

Условием перпендикулярности пары векторов является равенство нулю их скалярного произведения (11.27) [c.77]

Вектор ОР есть ортогональная проекция вектора Y на вектор S. Из векторной алгебры известно, что длина такого вектора равна отношению скалярного произведения векторов Y и S к длине вектора S, т. е. [c.77]

Скалярным произведением двух векторов х = (х, х2,…, х ) и [c.270]

Евклидовым пространством называется векторное (линейное) пространство, в котором задано скалярное произведение векторов, удовлетворяющее следующим свойствам [c.271]

Два вектора называются ортогональными, если их скалярное произведение равно нулю. [c.271]

Каждый узел многослойной сети проектирует свой входной вектор на вектор весов посредством скалярного произведения. Таким [c.24]

В другом варианте победителем считается элемент, весовой вектор которого имеет наибольшее скалярное произведение с входным вектором. Эта величина также является некоторой мерой близости, потому что скалярное произведение — это проектирование входного вектора на вектор весов. Очевидно, такая проекция будет наибольшей, если векторы имеют близкие направления. При этом методе, однако, оба вектора — весовой и входной — должны быть нормированы по длине, например, быть равными единице. Напротив, евклидово расстояние позволяет работать с векторами произвольной длины. [c.43]

Угловыми скобками здесь и далее обозначается скалярное произведение [c.67]

Дюрация портфеля равна скалярному произведению векторов долей вложений в обли- [c.34]

Напомним, что символ (о, b) для ш-мерных векторов а и Ь означает п(. [c.62]

Этот результат немедленно вытекает из формулы (2.

6) с учетом линейности скалярного произведения векторов пространства Ят. [c.66]

Скалярное произведение и линейная (не-) зависимость векторов [c.133]

Объясните связь между скалярным произведением векторов и векторами включенного угла. [c.133]

Рис. 3.1. Скалярное произведение и включенный угол

На рис. 3.1, а два вектора включают в себя угол, который меньше 90 градусов. Это приводит к тому, что скалярное произведение этих двух векторов положительно. Векторы, расположенные друг к другу перпендикулярно, называются ортогональными (рис. 3.1, в). Их скалярное произведение равно нулю. Векторы, которые образуют друг с другом угол, превышающий 90 градусов, имеют отрицательное скалярное произведение (рис. 3.1, б). Если обозначить включенный угол символом а, то мы можем обобщенно записать [c.134]

С помощью двумерных векторов можно сформировать скалярные произведения [c.134]

Лишь vi и v3 расположены перпендикулярно друг к другу. Проверка скалярных произведений трехмерных векторов дает [c.134]

Доказательство заметим, что скалярное произведение векторов-столбцов а и b может быть записано в виде произведения матриц либо как аТЬ, либо как Ъта. На этом основании можно записать [c.263]

Перрона следует, что существует неотрицательный вектор р, такой, что Ар = ЛАр. Выше было доказано, что неотрицательный собственный вектор положительной матрицы является положительным. Поэтому в действительности р >0. Рассмотрим скалярное произведение (р,Ау). Имеем [c.264]

Скалярным произведением векторов х и у называется число, равное сумме произведений соответствующих компонент этих В. [c.42]

Когда в пространстве введено понятие скалярного произведения векторов, можно определить и понятие К., двойственного к данному. Пусть С— выпуклый К., тогда множество С, состоящее из векторов, скалярные произведения которых с любым вектором, принадлежащим С, — отрицательны, называется двойственным конусом. [c.

153]

СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ [c.330]

Скалярное произведение векторов 42, 330 [c.488]

Транспортная работа ML определяется как скалярное произведение транспортной массы М на векторный путь L. При определении транспортной работы ML первый из сомножителей может быть взят в измеряемых единицах массы, а второй — как действительно пройденный путь или как тарифное расстояние. [c.44]

П — вычисление скалярного произведения векторов ху = 2х,у, [c.47]

Доказательство. Достаточно учесть знак скалярного произведения (b, N/s(T)) при всех возможных положениях векторов NIS(T) в ОД /х. [c.79]

Различие между векторами и и и2 приводит к появлению движущих сил Xjj каждая из которых определяется только u j и t/2j, удовлетворяет условиям, аналогичным (2.1), и имеет тот же знак, что и поток Jj. Производство энтропии, характеризующее необратимость процесса, равно среднему значению скалярного произведения вектора потоков на вектор движущих сил [c.54]

В этой таблице /-е строки отражают виды КПТ, а /-е столбцы — соответствующие отрасли промышленности и народного хозяйства (см. п. 4.4.1). При этом каждому /(/=1,. .., 10) соответствуют три соседних столбца, из которых средний х) служит для представления переменных х) при меняющемся /, а крайние — соответствующих ограничений из условий (4.53). Таким образом, переменная х) отображается клеткой на пересечении своих /-й строки и /-го столбца. При этом левая часть условия (4.51) отображается суммой значений х) во всех заполненных клетках /-й строки, а значение х) из правой части условия (4.51) представлено на пересечении /-й строки и столбца 5 и определяется при решении подзадач, реализующих модели 01, 02, 04 и 06. В этих моделях задаются и ограничения из. условий (4.55). Левая часть условий (4.52) формально представима как скалярное произведение соответствующих векторов, представленных столбцами 7 и x) i. Значение х пт из правой части условия (4.52) в других моделях не определялось. Оно заносится после расчета в 0-ю строку табл. 4.2 как выходного документа над столбцом ху ,. В две соседние клетки этой строки могут быть априорно занесены ограничения из условий (4.

54), которые ранее также не вводились. [c.104]

Векторы х и у называются ортогональными, если их скалярное произведение равно нулю. Равенство В. — компонентное, т. е. два В. равны, если равны их соответствующие компоненты. Вектор 0 — (0,. .., 0) нулевой и-мерный В. — положительный (х > 0), если все его компоненты х больше нуля, неотрицательный (х > 0), если все его компоненты х. больше 0 или равны нулю, т. е. х. > 0 и полуположительный, если при этом хотя бы одна компонента х > 0 (обозначение х > 0) если В. имеют равное количество компонент, возможно их упорядочение (полное или частичное), т. е. введение на множестве векторов бинарного отношения «>» х > у, х > у, х > у в зависимости от того, положительна, полуположительна или неотрицательна разность х — у. [c.42]

Lagrangian] — вспомогательная функция, применяемая при решении задач математического программирования, в частности линейного программирования. Образуется путем прибавления к целевой функции скалярного произведения двух векторов вектора разностей между константами ограничений и функциями ограничений и вектора (неизвестных) множителей, называемых множителями Лагранжа [c.

166]

Гиперплоскость Н = х е EJ (с, х) = h (см. Гиперпрострапство, Гиперплоскость, а также Скалярное произведение векторов) называется опорной по отношению к множеству М в его граничной точке х ), если удовлетворяются следующие условия (с, х) [c.241]

Часть Доказательство базируется на учете знака скалярного произведения (8,4 (7)) при всех (ПеОД . [c.80]

Здесь суммирование производится по всем г, включая г = г/, с учетом того, что qjsjs — dw — 0 r (t) — получаемая от г -й подсистемы механическая работа, если г > 0, и затрачиваемая, если г квадратных скобках представляет собой скалярное произведение, т.е. сумму по индексу j от единицы до m для каждого сочетания г и v. [c.92]

Содержание модели 05 простое требование обеспечения всеми видами КПТ заданной на расчетный год общей потребности народного хозяйства БАССР в КПТ в целом. Суть отражающего модель условия (4.50) состоит в том, что сумма всех выделенных 11 видов КПТ, приведенных в тыс. т условного топлива (это соответствует скалярному произведению столбцов 5 и 7 в табл.

4.2), должна быть не меньше априорно заданной величины общей потребности народного хозяйства БАССР в КПТ (Вих») в тыс. тут. Входящие в модель неотрицательные объемы использования 10 отдельных видов КПТ в народном хозяйстве Башкирии определяются в других моделях (коды их указаны в столбце 3 табл. 4.2), а объем использования группы прочих видов КПТ — хпр в тыс. тут, так же как и общее потребление всего КПТ ( нхТ). определяется в результате расчетов. [c.103]

Геометрия Метод координат в пространстве. Скалярное произведение векторов

Для изучения новой темы понадобится повторить теорему о трех перпендикулярах.

Если прямая а, проведенная на плоскости α через основание О наклонной с, перпендикулярна её проекции

в, то она перпендикулярна и самой наклонной.

Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними. Скалярное произведение двух векторов это число.

Скалярное произведение векторов и обозначается так: (произведение вектора а на вектор бэ).

Таким образом:

(произведение вектора а на вектор бэ равно произведению модуль вектора а на модуль вектора бэ и на косинус угла между векторами а и бэ)

Справедливы утверждения:

1°. Скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.

Действительно, скалярное произведение вектора A на вектор B равно произведению их длин на косинус угла между ними. Но cos 90° = 0 следовательно b= 0.

2°. Скалярный квадрат вектора (то есть скалярное произведение вектора на себя) равен квадрату его длины.

Скалярное произведение двух векторов можно вычислить через произведение соответственных координат этих векторов:

скалярное произведение векторов {х₁; у₁; z₁} и {х₂; у₂; z₂} выражается формулой:

х₁х₂ + у₁у₂ + z₁z₂ (скалярное произведение двух векторов равно сумме произведений соответственных координат этих векторов).

Докажем утверждение:

Косинус угла α между ненулевыми векторами {х₁; у₁; z₁} и {х₂; у₂; z₂}

вычисляется по формуле:

cos α =Косинус угла альфа равен частному от деления суммы произведений соответственных координат векторов, которые составляют угол альфа, на произведение длин, выраженных координатами этих векторов

косинус угла альфа равен частному от деления скалярного произведения векторов на произведение их длин.

Таким образом, подставив вместо скалярного произведения вектора формулу суммы произведений соответственных координат векторов х₁х₂ + у₁у₂ + z₁z₂ , а также заменив произведение длин векторов на произведение длин векторов, выраженных через координаты

Получим: косинус угла альфа равен частному от деления скалярного произведения векторов на произведение их длин, отсюда следует, что косинус угла альфа равен частному от деления суммы произведений соответственных координат векторов, которые составляют угол альфа, на произведение длин, выраженных координатами этих векторов

Что и требовалось доказать.

Сформулируем основные свойства скалярного произведения векторов.

Для любых векторов и любого числа k справедливо следующее:

1°. Скалярный квадрат вектора всегда больше либо равен нулю

2.переместительный закон – от перестановки мест векторов в скалярном произведении скалярное произведение не меняется.

3 (распределительный закон – скалярное произведение суммы двух

Что такое скалярное произведение?

По

Роберт Шелдон

Что такое скалярное произведение?
Скалярное произведение, также называемое скалярным произведением, является мерой того, насколько точно совпадают два вектора с точки зрения направлений, в которых они указывают. Мера представляет собой скалярное число (одно значение), которое можно использовать для сравнения двух векторов и понимания влияния изменения положения одного или обоих из них. Скалярный продукт получается путем выполнения математических расчетов векторных свойств.
Вектор — это величина, которая имеет как направление, так и величину (длину вектора). На рис. 1 показаны два вектора ( a и b ) на двумерной декартовой плоскости. Вектор a имеет величину 8 и расположен под углом 115 градусов к оси x (движется против часовой стрелки). Вектор b имеет величину 10 и расположен под углом 45 градусов к оси x. Угол между двумя векторами, представленный греческой буквой тета (θ), составляет 70 градусов, что вычисляется путем вычитания 45 градусов из 115 градусов.
Рис. 1. Диаграмма, показывающая два вектора (a и b) на двумерной декартовой плоскости.
Если известна величина двух векторов и угол между ними, легко вычислить скалярное произведение. Скалярный продукт представлен точкой между двумя векторными ссылками, в данном случае a и b , как показано в следующей формуле:
а • б
Полное уравнение для нахождения скалярного произведения несколько сложнее. Это влечет за собой умножение величины вектора a на величину вектора b , а затем произведение на косинус (cos) угла между векторами, как показано в следующем уравнении:
а • б = |а| × |б| × cos(θ)
Вертикальные полосы показывают, что эти значения являются величиной вектора. Иногда вместо одинарных стержней используются двойные стержни. Если значения с рисунка 1 подставить в уравнение, можно быстро вычислить скалярное произведение для этих двух векторов, как показано в следующем уравнении:0014
a • b = 8 × 10 × cos(70 градусов)
a • b = 8 × 10 × 0,342
a • b = 27,36
Косинус угла округлен до трех знаков после запятой, поэтому конечный результат (27,36) является лишь приблизительным, хотя и близким.
Если величина двух векторов и угол между ними неизвестны, используйте следующую формулу для вычисления скалярного произведения:
a • b = (a _x × b _x) + (a _y × b _y)
Рис. 2. Схема добавления длин векторов, отраженных на каждой оси, к рис. 1.
В этом случае умножьте длины векторов, поскольку они проецируются на оси x и оси y декартовой плоскости. Чтобы лучше понять, как это работает, рассмотрите рис. 2, который был обновлен по сравнению с рис. 1, чтобы включить длины векторов, отраженные на каждой оси.
Vector a измеряет -3,4 по оси x и 7,3 по оси y. (Эти числа были округлены до одного десятичного знака в меньшую сторону.) Вектор b измеряет 7,1 по оси x и 7,1 по оси y. Для этого вектора измерения одинаковы по каждой оси, потому что вектор находится под углом 45 градусов. Эти суммы можно подставить в следующую новую формулу:
.
a • b = (a _x × b _x ) + (a _y × b _y )
a • b = (-3,4 × 7,1) + (7,3 × 7,1)
a • b = -24,12 + 51,83
а • b = 27,71
Поскольку числа были округлены, окончательная цифра немного отличается от предыдущей (27,36), но они достаточно близки, чтобы продемонстрировать, как можно использовать два разных метода для вычисления скалярного произведения для пары векторов.
Аналогичный подход можно использовать для вычисления скалярного произведения векторов в трехмерном пространстве. Для этого измените формулу следующим образом, чтобы включить третье измерение (представленное осью Z):
a • b = (a _x x b _x) + (a _y x b _y) + (a _z x b _z)
Формула теперь включает в свои расчеты ось Z, но исходные компоненты остаются прежними. Чтобы проверить обновленную формулу, предположим, что оба вектора измеряют 5 по оси Z. Теперь расчеты будут выглядеть следующим образом:
a • b = -(3,4 × 7,1) + (7,3 × 7,1) + (5 x 5)
a • b = -24,12 + 51,83 + 25
a • b = 52,71
Неудивительно, что скалярное произведение равно 52,71, что на 25 больше, чем 27,71 в предыдущем расчете. Число 25 является результатом добавления компонента a _z × b _z (5 x 5) к уравнению для включения трехмерного пространства.
Скалярное произведение используется в таких областях, как физика, математика и другие области, способами, которые имеют практическое применение в реальном мире. Например, скалярное произведение можно использовать при установке солнечной панели на крыше. Сравнивая угол наклона солнца с углом панели, инженеры могут рассчитать наилучшее положение панели, чтобы максимизировать количество солнечной энергии, поглощаемой в течение дня.

См. также: Математические символы
Последнее обновление: октябрь 2022 г.
Продолжить чтение О точечном произведении (скалярном произведении)
11 навыков работы с данными для машинного обучения и искусственного интеллекта
18 инструментов обработки данных, которые следует рассмотреть в 2022 году
8 лучших приложений для обработки данных и вариантов использования для бизнеса
Наука о данных, машинное обучение и искусственный интеллект: как они работают вместе
СБОМ
Спецификация программного обеспечения (SBOM) — это список всех составляющих компонентов и программных зависимостей, участвующих в разработке и доставке приложения.
ПоискСеть
беспроводная ячеистая сеть (WMN)
Беспроводная ячеистая сеть (WMN) — это ячеистая сеть, созданная путем соединения узлов беспроводной точки доступа (WAP), установленных в …
Wi-Fi 7
Wi-Fi 7 — это ожидаемый стандарт 802.11be, разрабатываемый IEEE.
сетевая безопасность
Сетевая безопасность охватывает все шаги, предпринятые для защиты целостности компьютерной сети и данных в ней.
ПоискБезопасность
Что такое модель безопасности с нулевым доверием?
Модель безопасности с нулевым доверием — это подход к кибербезопасности, который по умолчанию запрещает доступ к цифровым ресурсам предприятия и …
RAT (троянец удаленного доступа)
RAT (троян удаленного доступа) — это вредоносное ПО, которое злоумышленник использует для получения полных административных привилегий и удаленного управления целью . ..
атака на цепочку поставок
Атака на цепочку поставок — это тип кибератаки, нацеленной на организации путем сосредоточения внимания на более слабых звеньях в организации …
ПоискCIO
пространственные вычисления
Пространственные вычисления широко характеризуют процессы и инструменты, используемые для захвата, обработки и взаимодействия с трехмерными данными.
Пользовательский опыт
Дизайн взаимодействия с пользователем (UX) — это процесс и практика, используемые для разработки и внедрения продукта, который обеспечит положительные и …
соблюдение конфиденциальности
Соблюдение конфиденциальности — это соблюдение компанией установленных правил защиты личной информации, спецификаций или …
SearchHRSoftware
Поиск талантов
Привлечение талантов — это стратегический процесс, который работодатели используют для анализа своих долгосрочных потребностей в талантах в контексте бизнеса . ..
удержание сотрудников
Удержание сотрудников — организационная цель сохранения продуктивных и талантливых работников и снижения текучести кадров за счет стимулирования …
гибридная рабочая модель
Гибридная модель работы — это структура рабочей силы, включающая сотрудников, работающих удаленно, и тех, кто работает на месте, в офисе компании…
SearchCustomerExperience
CRM (управление взаимоотношениями с клиентами) аналитика
Аналитика CRM (управление взаимоотношениями с клиентами) включает в себя все программные средства, которые анализируют данные о клиентах и представляют…
разговорный маркетинг
Диалоговый маркетинг — это маркетинг, который привлекает клиентов посредством диалога.
цифровой маркетинг
Цифровой маркетинг — это общий термин для любых усилий компании по установлению связи с клиентами с помощью электронных технологий.
Скалярное произведение векторов — GeeksforGeeks
Можно перемножить два вектора или вектор и скаляр. В физике в основном есть два вида произведений векторов: скалярное умножение векторов и векторное произведение (перекрестное произведение) двух векторов. Результатом скалярного произведения двух векторов является число (скаляр). Обычно скалярное произведение используется для определения отношений работы и энергии, таких как нахождение работы, выполняемой над объектом силой (вектором), вызывающей смещение объекта, эта работа может быть определена как скалярное произведение вектора силы с вектором смещения.
Скалярные и векторные величины определяются как:
Скаляры: это такие величины, которые могут быть полностью описаны только величиной (или числовым значением). например. длина объекта, вес объекта, скорость тела и т. д.
Векторы: это такие величины, которые могут быть полностью описаны как по величине, так и по направлению. например скорость тела, так как она имеет как величину, так и направление.
Скалярное произведение
Скалярное произведение или скалярное произведение двух векторов — это алгебраическая операция, которая берет две последовательности чисел одинаковой длины и возвращает одно число в качестве результата. С геометрической точки зрения, скалярные произведения можно найти, взяв компонент одного вектора в направлении другого вектора и умножив его на величину другого вектора.
Скалярное произведение двух векторов A и B определяется формулой
A.B = |A| × |В| cos ∅
где
|А| величина вектора A,
|B| — величина вектора B, а
∅ — угол между векторами A и B.
Поскольку скалярное произведение обозначается точкой (.), его также называют точечным произведением .
Скалярное произведение в представлении единичного вектора
В представлении векторов единичным вектором, где i, j, k расположены вдоль оси x, оси y и оси z соответственно. Скалярное произведение можно рассчитать как:
A.B = A _x × B _x + A _y × B _y + A _z × B _z
where,
A = A _x I +A _Y J +A _Z K
B = B _x I +B _Y J +B _Z K
GEOMETRICLACT
Произведение двух ненулевых векторов можно представить как произведение величины любого из векторов на величину проекции на него другого вектора.
Случай 1: Когда угол между двумя векторами больше 0 градусов и меньше 90 градусов, результат скалярного произведения равен положительному .
0 < ∅ < 90
Случай 2: Когда угол между двумя векторами больше 90 градусов и меньше 180 градусов, результат скалярного произведения равен отрицательному .
90 < ∅ < 180
Случай 3: Когда угол между двумя векторами равен 90 градусов, то результат скалярного произведения равен 0 .
∅ = 90
Особые случаи скалярного произведения
(1) Скалярное произведение двух параллельных векторов: Скалярное произведение двух параллельных векторов — это просто произведение величин двух векторов. Поскольку угол между векторами, когда они параллельны, равен 0 градусов, а cos 0 = 1.
Следовательно,
a.b = |a| × |б| cos 0
= |a| × |б|
(2) Скалярное произведение двух антипараллельных векторов: Скалярное произведение двух антипараллельных векторов отрицательно от произведения модулей двух векторов.
ab cos 180 = −|a| × |б| (С тех пор, COS 180 = -1)
(3) Скалярное произведение двух ортогональных векторов: Скалярное произведение двух ортогональных векторов составляет 0.
A.B COS 90 = 0 (с тех пор, COS 90 = 0)
Матричное представление скалярного произведения векторов
В матричной форме векторы могут быть представлены в виде матриц-строк или матриц-столбцов. Если рассматривать векторы как матрицы-строки их компонентов x, y и z, то транспонирование этих векторов будет матрицей-столбцом, содержащим компоненты x, y и z.
Таким образом, векторы A и B можно рассматривать следующим образом:
A =
A _x A _y A _z
B =
B _x
B _y
B _z
SO,
A.B = A _x B _x + A _Y B _Y + A _Z B _Z
9 .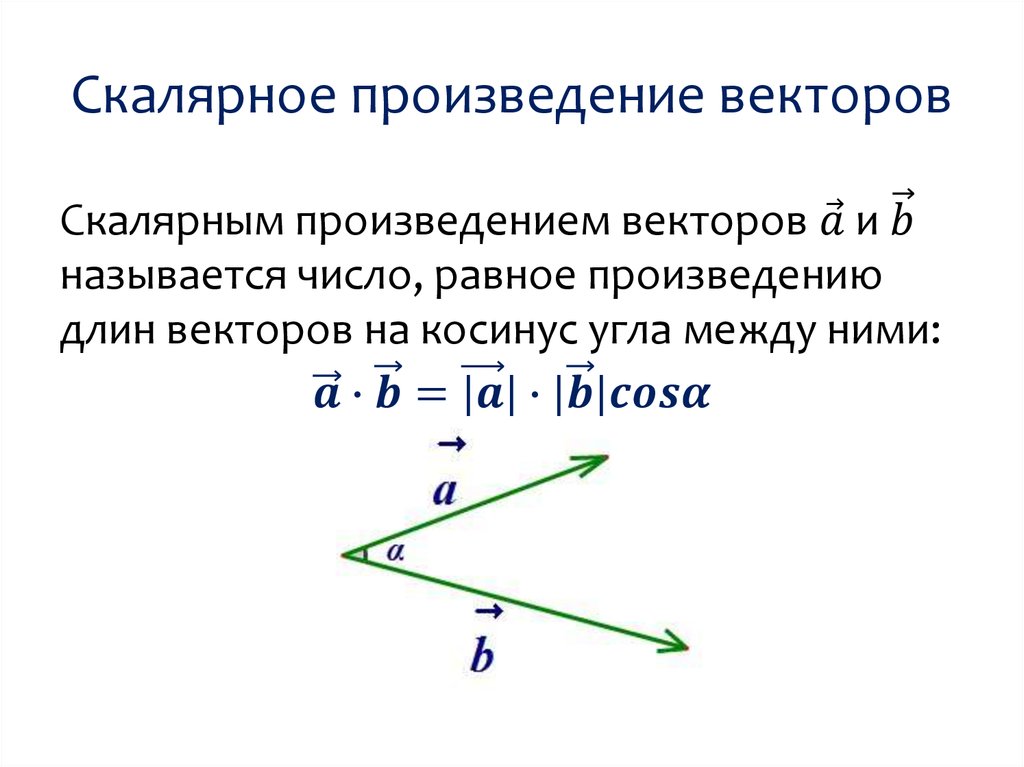 0021
1. Коммутативные свойства скалярного умножения:
, если A и B — два вектора:
A.B = B.A
AS, B.A
AS, A.A
AS, B.A
AS, B.A
AS, = B.A
AS, A.A
A.B . б| cos θ , и
b.a = |b||a| cos θ
So a.b = b.a
0026 тогда вектор,
а. (B + C) = A.B + A.C
3. Ассоциативное свойство:
, если A — векторы, а C, D — скалары. d a ) = (cd) a
4. Identity Property:
If a is a vector then,
1⋅ a = a
5. Мультипликативное свойство 0:
, если A — вектор, а затем вектор
0 ( A ) = 0
Проблемы с образцами
Проблема 1: Найдите продукт Scalar веко. вектор B= 3i + j +2k.
Решение:
A. B = (2 * 3) + (5 * 1) + (3 * 2)
= 6 + 5 + 6
= 17
. 2: Частица перемещается из положения 2i + j + 2k в положение 3i + 2j + 5k под действием равномерной силы (7i + 5j +2k) Н. Если перемещение выражено в метрах, вычислите проделанную работу.
Решение:
. +2 k
Force F = ( 7 i + 5 j + 2 k ) N
So
The displacement D = P2 – P1
Д = ( 3 – 2 ) i + ( 2 -1 ) j + ( 5 – 2 ) k
= i + j + 3 k 5
работа выполнена D
= (7 i + 5 j + 2 k ). ( i + j + 3 k )
= ( 7 * 1 ) + ( 5 * 1 ) + ( 2 * 3 )
= 7 + 5 + 6
= 18 1J 9002 Задача 3. Найдите такое значение m, что векторы A = 2 i + 3j + k и B = 3 i + 2 j + mk могут быть перпендикулярны.
Решение:
Дано,
A и B перпендикулярны
, поэтому A . B = 0
(2 i + 3 j + k ). ( 3 i + 2 j + m k ) = 0
( 2 * 3 ) + ( 3 * 2 ) + ( 1 * m ) = 0
6 + 6 + m = 0
12 + m = 0
m = -12
Задача 4. Докажите, что векторы U = 2i + 3j + k и V = 4i – 2j + 2k перпендикулярны друг другу.
Решение:
.
, чтобы доказать, что U и V перпендикулярны друг другу
U .
No related posts.