Косинус квадрат и синус квадрат
Разбираемся с простыми понятиями: синус и косинус и вычисление косинуса в квадрате и синуса в квадрате.
Синус и косинус изучаются в тригонометрии (науке о треугольниках с прямым углом).
Поэтому для начала вспомним основные понятия прямоугольного треугольника:
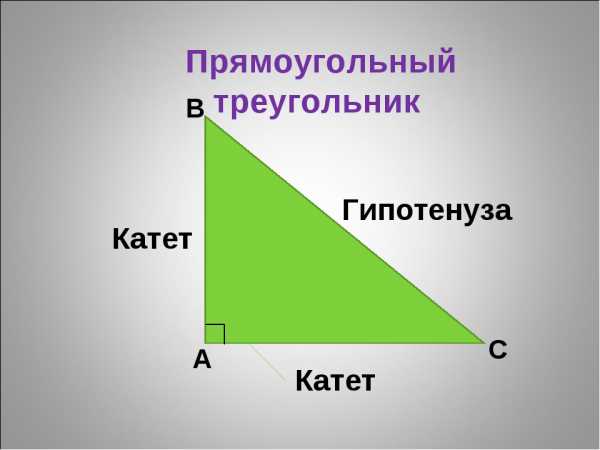
Гипотенуза — сторона, которая всегда лежит напротив прямого угла (угла в 90 градусов). Гипотенуза — это самая длинная сторона треугольника с прямым углом.
Оставшиеся две стороны в прямоугольном треугольнике называются катетами.
Также следует помнить, что три угла в треугольнике всегда имеют сумму в 180°.
Теперь переходим к косинусу и синусу угла альфа (∠α) (так можно назвать любой непрямой угол в треугольнике или использовать в качестве обозначение
Синус угла альфа (sin ∠α) — это отношение противолежащего катета (сторона, лежащая напротив соответствующего угла) к гипотенузе. Если смотреть по рисунку, то sin ∠ABC = AC / BC
Косинус угла альфа (cos ∠α) — отношение прилежащего к углу катета к гипотенузе. Если снова смотреть по рисунку выше, то cos ∠ABC = AB / BC
И просто для напоминания: косинус и синус никогда не будут больше единицы, так как любой катит короче гипотенузы (а гипотенуза — это самая длинная сторона любого треугольника, ведь самая длинная сторона расположена напротив самого большого угла в треугольнике).
Косинус в квадрате, синус в квадрате
Теперь переходим к основным тригонометрическим формулам: вычисление косинуса в квадрате и синуса в квадрате.
Для их вычисления следует запомнить основное тригонометрическое тождество:
sin2α + cos2α = 1 (синус квадрат плюс косинус квадрат одного угла всегда равняются единице).
Из тригонометрического тождества делаем выводы о синусе:
sin2α = 1 — cos2α
или более сложный вариант формулы: синус квадрат альфа равен единице минус косинус двойного угла альфа и всё это делить на два.
sin2α = (1 – cos(2α)) / 2
Из тригонометрического тождества делаем выводы о косинусе:
cos2α = 1 — sin2α
или более сложный вариант формулы: косинус квадрат альфа равен единице плюс косинус двойного угла альфа и также делим всё на два.
cos2α = (1 + cos(2α)) / 2
Эти две более сложные формулы синуса в квадрате и косинуса в квадрате называют еще «понижение степени для квадратов тригонометрических функций». Т.е. была вторая степень, понизили до первой и вычисления стали удобнее.
Добавить новость и получить деньги
Добавить анкету репетитора и получать бесплатно заявки на обучение от учеников
uchilegko.info
Косинус в квадрате, формула и примеры
ОПРЕДЕЛЕНИЕ Квадрат косинуса можно выразить следующим образом
Эта формула называется формулой понижения степени косинуса.
Примеры решения задач
ПРИМЕР 2| Задание | Упростить выражение
|
| Решение | Упростим выражение с помощью формулы квадрата косинуса:
Преобразуем каждый из членов разности следующим образом:
и
Тогда
Полученное выражение представляет собой правую часть формулы произведения синусов, т.е.
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Квадрат — синус — Большая Энциклопедия Нефти и Газа, статья, страница 1
Квадрат — синус
Cтраница 1
Квадраты синусов определяют на выходе вторую гармонику. [1]
Преобразуя квадрат синуса, находим. [2]
Сумма квадратов синуса и косинуса одного угла равна единице. [3]
Среднее значение квадрата синуса и квадрата косинуса равно, как известно, половине. [4]
Формулы удвоения позволяют квадраты синуса, косинуса и их произведения заменить линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения. [5]
Для исследования суммы квадратов синусов этих углов воспользуйтесь теоремой косинусов. [6]
Доказать, что сумма квадратов синусов трех углов, образуемых произвольным лучом с ребрами прямого трехгранного угла, равна двум. [7]Так как в выражении (5.21) присутствует квадрат синуса, то мгновенная мощность всегда является положительной величиной. Положительный знак мгновенной мощности отражает тот факт, что происходит, односторонний процесс поглощения энергии в цепи переменного тока. [9]
Эту теорему можно сформулировать так: квадрат синуса любого угла плюс квадрат косинуса того же угла равен единице. [10]
Для получения подобного ряда следует взять отношения квадрата синуса 6 — каждой из линий Кка дифракционной картины рент-генограммы к квадрату синуса 9i первой линии. [11]
Для получения подобного ряда следует взять отношения
Формула или закон, известный обычно как закон квадрата синуса сопротивления воздуха Ньютона, относится к силе, действующей на наклонную плоскую пластину, омываемую равномерным воздушным потоком. [14]
Косинус двойного угла равен квадрату косинуса данного угла минус квадрат синуса того же угла. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Формулы (тождества) синус, косинус, тангенс, котангенс тройного угла
1. Формула стороны квадрата через диагональ
a — сторона квадрата
d — диагональ квадрата
Формула стороны квадрата, (a):
2. Формула стороны квадрата через радиус вписанной окружности
a — сторона квадрата
R — радиус вписанной окружности
D — диаметр вписанной окружности
Формула стороны квадрата, (a):
3. Формула стороны квадрата через радиус описанной окружности
a — сторона квадрата
R — радиус описанной окружности
D — диаметр описанной окружности
d — диагональ
Формула стороны квадрата, (a):
4. Формула стороны квадрата через площадь и периметр
a — сторона квадрата
S — площадь квадрата
P — периметр квадрата
Формула стороны квадрата, (a):
5. Формула стороны квадрата через линию выходящую из угла на середину стороны квадрата
a — сторона квадрата
C — линия выходящая из угла на середину стороны квадрата
Формула стороны квадрата, (a):
Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
Диагонали прямоугольника равны между собой. Диагональ делит прямоугольник на два равных прямоугольных треугольника ABC и ACD. Диагональ равна диаметру описанной окружности.
1. Формулы длины диагонали в прямоугольнике.
d — диагональ прямоугольника
a, b — стороны
α, β — углы полученные от деления, диагональю, прямого угла
Формула диагонали через стороны, (d):
Формулы диагонали через сторону и угол, (d):
Формулы величины углов через диагональ и стороны, (
2. Формулы углов между диагоналями в прямоугольнике.
d — диагонали прямоугольника
a, b — стороны
α, β — углы между диагоналями
Формулы углов между диагоналями через стороны и диагональ, (α, β ):
1. Формулы диагонали квадрата через стороны, площадь, периметр
a — сторона квадрата
S — площадь квадрата
P — периметр квадрата
d — диагональ квадрата
Формулы диагонали квадрата, (d ):
2. Формула диагонали квадрата через радиус вписанной окружности
R — радиус вписанной окружности
D — диаметр вписанной окружности
d — диагональ квадрата
Формула диагонали квадрата, (d ):
3. Формула диагонали квадрата через радиус описанной окружности
R — радиус описанной окружности
D — диаметр описанной окружности
d — диагональ
Формула диагонали квадрата, (d ):
4. Формула диагонали квадрата через линию выходящую из угла на середину стороны квадрата
C — линия выходящая из угла на середину стороны квадрата
d — диагональ
Формула диагонали квадрата, (d ):
Формула площади квадрата
Формула периметра квадрата
Все формулы по геометрии
www-formula.ru
Тригонометрические тождества и преобразования
Для решения некоторых задач будет полезной таблица тригонометрических тождеств, которая позволит гораздо проще совершать преобразования функций:Простейшие тригонометрические тождества
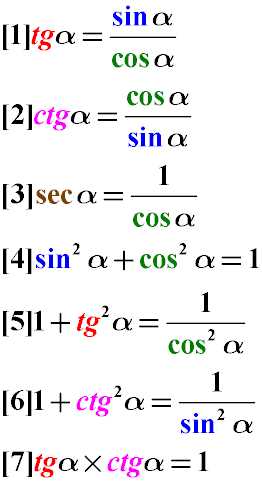
Частное от деления синуса угла альфа на косинус того же угла равно тангенсу этого угла (Формула 1). См. также доказательство правильности преобразования простейших тригонометрических тождеств.
Частное от деления косинуса угла альфа на синус того же угла равно котангенсу этого же угла (Формула 2)
Секанс угла равен единице, деленной на косинус этого же самого угла (Формула 3)
Сумма квадратов синуса и косинуса одного и того же угла равна единице (Формула 4). см. также доказательство суммы квадратов косинуса и синуса.
Сумма единицы и тангенса угла равна отношению единицы к квадрату косинуса этого угла (Формула 5)
Единица плюс котангенс угла равна частному от деления единицы на синус квадрат этого угла (Формула 6)
Произведение тангенса на котангенс одного и того же угла равно единице (Формула 7).
Преобразование отрицательных углов тригонометрических функций (четность и нечетность)
Для того, чтобы избавиться от отрицательного значения градусной меры угла при вычислении синуса, косинуса или тангенса, можно воспользоваться следующими тригонометрическими преобразованиями (тождествами), основанными на принципах четности или нечетности тригонометрических функций.

Как видно, косинус и секанс является четной функцией, синус, тангенс и котангенс — нечетные функции.
Синус отрицательного угла равен отрицательному значению синуса этого же самого положительного угла (минус синус альфа).
Косинус «минус альфа» даст тоже самое значение, что и косинус угла альфа.
Тангенс минус альфа равен минус тангенс альфа.
Формулы приведения двойного угла (синус, косинус, тангенс и котангенс двойного угла)
Если необходимо разделить угол пополам, или наоборот, перейти от двойного угла к одинарному, можно воспользоваться следующими тригонометрическими тождествами:
Преобразование двойного угла (синуса двойного угла, косинуса двойного угла и тангенса двойного угла) в одинарный происходит по следующим правилам:
Синус двойного угла равен удвоенному произведению синуса на косинус одинарного угла
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла
Тангенс двойного угла равен дроби, числитель которой — удвоенный тангенс одинарного угла, а знаменатель равен единице минус тангенс квадрат одинарного угла.
Котангенс двойного угла равен дроби, числитель которой — квадрат котангенса одинарного угла минус единица, а знаменатель равен удвоенному котангенсу одинарного угла
Формулы универсальной тригонометрической подстановки
Указанные ниже формулы преобразования могут пригодиться, когда нужно аргумент тригонометрической функции ( sin α, cos α, tg α) разделить на два и привести выражение к значению половины угла. Из значения α получаем α/2 .Данные формулы называются формулами универсальной тригонометрической подстановки. Их ценность заключается в том, что тригонометрическое выражение с их помощью сводится к выражению тангенса половины угла, вне зависимости от того, какие тригонометрические функции (sin cos tg ctg) были в выражении изначально. После этого уравнение с тангенсом половины угла решить гораздо проще.
Тригонометрические тождества преобразования половины угла
Указанные ниже формулы тригонометрического преобразования половинной величины угла к его целому значению.Значение аргумента тригонометрической функции α/2 приводится к значению аргумента тригонометрической функции α.
Тригонометрические формулы сложения углов
cos (α — β) = cos α · cos β + sin α · sin β
sin (α + β) = sin α · cos β + sin β · cos α
sin (α — β) = sin α · cos β — sin β · cos α
cos (α + β) = cos α · cos β — sin α · sin β
Тангенс и котангенс суммы углов альфа и бета могут быть преобразованы по следующим правилам преобразования тригонометрических функций:
Тангенс суммы углов равен дроби, числитель которой — сумма тангенса первого и тангенса второго угла, а знаменатель — единица минус произведение тангенса первого угла на тангенс второго угла.
Тангенс разности углов равен дроби, числитель которой равен разности тангенса уменьшаемого угла и тангенса вычитаемого угла, а знаменатель — единице плюс произведение тангенсов этих углов.
Котангенс суммы углов равен дроби, числитель которой равен произведению котангенсов этих углов плюс единица, а знаменатель равен разности котангенса второго угла и котангенса первого угла.
Котангенс разности углов равен дроби, числитель которой — произведение котангенсов этих углов минус единица, а знаменатель равен сумме котангенсов этих углов.
Данные тригонометрические тождества удобно применять, когда нужно вычислить, например, тангенс 105 градусов (tg 105). Если его представить как tg (45 + 60), то можно воспользоваться приведенными тождественными преобразованиями тангенса суммы углов, после чего просто подставить табличные значения тангенса 45 и тангенса 60 градусов.
Формулы преобразования суммы или разности тригонометрических функций
Выражения, представляющие собой сумму вида sin α + sin β можно преобразовать с помощью следующих формул:Формулы тройного угла — преобразование sin3α cos3α tg3α в sinα cosα tgα
Иногда необходимо преобразовать тройную величину угла так, чтобы аргументом тригонометрической функции вместо 3α стал угол α.В этом случае можно воспользоваться формулами (тождествами) преобразования тройного угла:
Формулы преобразования произведения тригонометрических функций
Если возникает необходимость преобразовать произведение синусов разных углов косинусов разных углов или даже произведения синуса на косинус, то можно воспользоваться следующими тригонометрическими тождествами:В этом случае произведение функций синуса, косинуса или тангенса разных углов будет преобразовано в сумму или разность.
Формулы приведения тригонометрических функций
Пользоваться таблицей приведения нужно следующим образом. В строке выбираем функцию, которая нас интересует. В столбце — угол. Например, синус угла (α+90) на пересечении первой строки и первого столбца выясняем, что sin (α+90) = cos α .
См. также Полный список формул приведения тригонометрических функций.
| Угол |
α + 90 α + π/2 |
α + 180 α + π |
α + 270 α + 3π/2 |
90 — α π/2- α |
180 — α π- α |
270 — α 3π/2- α |
360 — α 2π- α |
| sin | cos α | -sin α | -cos α | cos α | sin α | -cos α | -sin α |
| cos | -sin α | -cos α | sin α | sin α | -cos α | -sin α | cos α |
| tg | -ctg α | tg α | -ctg α | ctg α | -tg α | ctg α | -tg α |
| ctg | -tg α | ctg α | -tg α | tg α | -ctg α | tg α | -ctg α |
profmeter.com.ua
Квадрат — синус — Большая Энциклопедия Нефти и Газа, статья, страница 3
Квадрат — синус
Cтраница 3
Итак, дифференциал котангенса какой-либо дуги равняется дифференциалу дуги, взятому с обратным знаком и разделенному на квадрат синуса той же дуги. [31]
Например, можно взять k k 2 и попробовать построить фильтры поч-свой косинусный член, и сумма квадратов синусов делится на две части. [32]
Какая формула называется формулой: а) синуса двойного угла; б) косинуса двойного угла; в) квадрата синуса половинного угла; г) квадрата косинуса половинного угла. [33]
Для получения подобного ряда следует взять отношения квадрата синуса 6 — каждой из линий Кка дифракционной картины рент-генограммы к квадрату синуса 9i первой линии. [34]
Для получения подобного ряда следует взять отношения квадрата синуса в — каждой из линий ХЛа дифракционной картины рентгенограммы к квадрату синуса 0Г первой линии. [35]
Действительно, при различных значениях числа п, например при п пг и п — 2 N — 1, квадраты синусов угла nnJN и n ( N — n / N ( а следовательно, и частоты) будут одинаковы, хотя фазы колебаний будут различны. IN 2л — ( fv Эги пары одинаковых частот называются вырожденными. [36]
Если в уравнении есть синус или косинус в четной степени, то степень уравнения может быть понижена с помощью формул 14 и 15, выражающих соответственно квадраты синуса и косинуса угла через косинус двойного угла. [37]
В процессе колебаний кинетическая энергия переходит в потенциальную и обратно. Это видно из приведенных выражений: значение кинетической энергии определяется квадратом синуса, а потенциальной — квадратом косинуса одного и того же аргумента. [38]
Предположим, что и — Ulm sin ю U2m sin co2 /, причем со2 и о1 вообще не кратны друг другу. Подставим это выражение для и в формулу для i и заменим квадраты синусов выражениями через косинусы двойных углов, а произведение синусов через косинусы разности и суммы углов. [39]
Из (98.5) следует, что плотность энергии в каждый момент времени в разных точках пространства различна. В одной и той же точке плотность энергии изменяется со временем по закону квадрата синуса. [40]
Из (98.5) следует, что плотность энергии в каждый момент времени в разных точках пространства различна. В одной и той же точке плотность энергии изменяется со временем по закону квадрата синуса. [41]
Эта добавочная составляющая ЭДС вызывает появление погрешностей. Аналогично в косинусной обмотке при нагрузке поперечным потоком Ф9 индуцируется добавочная ЭДС ECtI, пропорциональная току нагрузки и квадрату синуса 0, которая также вызывает появление погрешностей. [42]
Формула (13.16) выражает условие существования телеанастигматической линзы. Рассматривая ее, видим, что величина Г — увеличение телеанастигматической линзы — всегда должна быть положительной, так как она определяется отношением квадратов синусов углов в. Сами же эти углы могут иметь как одинаковые, так и различные знаки. [43]
Результаты этих опытов, опубликованные в отчете Новые эксперименты о сопротивлении жидкостей ( 1777 г.), подвергали сомнению одно из существенных положений теории сопротивления Ньютона, а именно пропорциональность сопротивления тела квадрату синуса угла между направлениями скорости потока и касательной к поверхности тел. В настоящее время формула Ньютона применяется для приближенного решения ряда задач газовой динамики. [44]
Страницы: 1 2 3 4
www.ngpedia.ru
Формулы (тождества) синус, косинус, тангенс, котангенс двойного угла
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
sin(2α)- через tg и ctg:
cos(2α)- через sin и cos:
cos(2α)- через tg и ctg:
tg(2α):
сtg(2α):
- Подробности
- Автор: Administrator
www-formula.ru
